平衡二叉树详解——PHP代码实现

一、什么是平衡二叉树

平衡二叉树（Self-Balancing Binary Search Tree 或者 Height-Balancing Binary Search Tree）译为 自平衡的二叉查找树或者高度平衡的二叉查找树，简称平衡二叉树，也叫 AVL 树，是一种二叉排序树。每个节点的左子树和右子树的高度差至多等于 1，我们将二叉树上结点的左子树深度减去右子树深度的值称为平衡因子 BF（Balance Factor），那么平衡二叉树上所有结点的平衡因子只可能是  -1，0，1。只要树上有结点的平衡因子的绝对值大于 1，则该二叉树就是不平衡的。

下面举四个例子：

• 图1不满足平衡二叉树定义，58和88这两个结点的平衡因子BF分别是2和-2，不是平衡二叉树
• 图2不是平衡二叉树，因为平衡二叉树首要要是二叉排序树，59比58大却是58的左子树，这是不符合二叉排序树的定义的
• 图3不满足平衡因子小于等于1的要求，对58这个节点来说，平衡因子BF的值是3，因而不是平衡二叉树
• 图4满足平衡二叉树的定义，是平衡二叉树

二、平衡二叉树的实现原理

平衡二叉树构建的基本思想就是在构建二叉排序树的过程中，每当插入一个结点时，先检查是否因插入而破坏了树的平衡性，若是，则找出最小不平衡子树。在保持二叉排序树特性的前提下，调整最小不平衡子树中各结点之间的链接关系，进行相应的旋转（左旋或右旋），使之成为新的平衡子树。 

最小不平衡子树

距离插入结点最近的，且平衡因子的绝对值大于1的结点为根的子树，我们称为最小不平衡子树。

如下图，当新插入结点37时，距离它最近的平衡因子绝对值超过1的结点是58 (即它的左子树高度2减去右子树高度0)，所以从58开始以下的子树为最小不平衡子树。

左旋/右旋

• 当右子树比左子树高，即平衡因子小于-1，需要进行左旋，如下图

 

• 当右子树比左子树低，即平衡因子大于1，需要进行右旋，如下图

实例

 假设插入节点的顺序是{3,2,1,4,5,6,7,10,9,8}

 根据二叉排序树的特性，我们通常会将它构建成如下图1的样子。虽然它完全符合二叉排序树的定义，但是对这样高度达到8的二叉树查找是非常不利的。我们更期望能构建成下图2的样子，这样才能提供高效的查询效率。

 

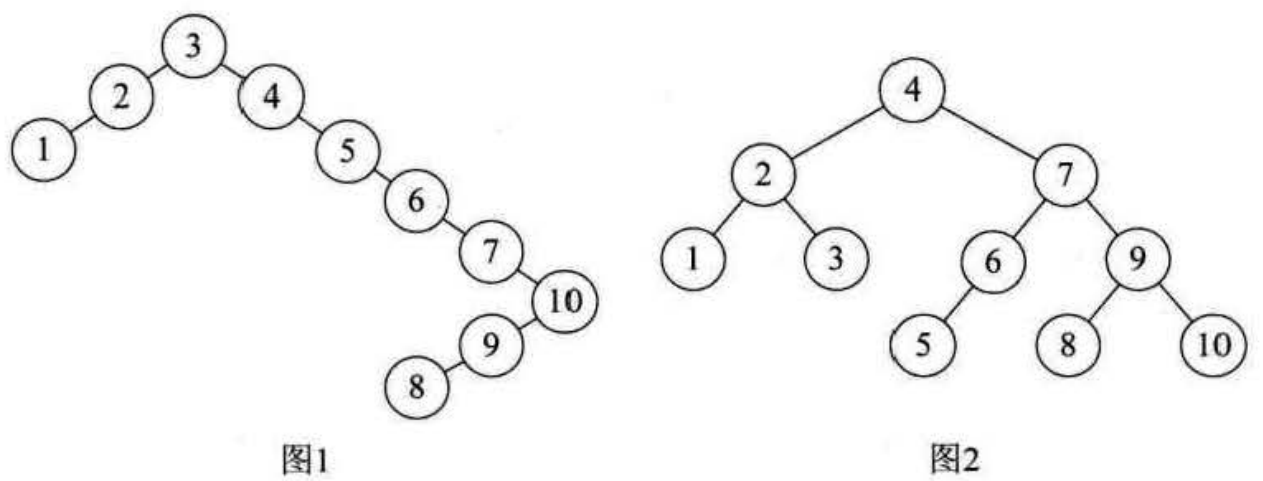
下面就开始构建上图2

 对于{3,2,1,4,5,6,7,10,9,8}的前两位3和2，我们正常的构建，到了第三个数1时发现根节点的平衡因子变成了2，需要把以 3 为根节点的子树进行右旋

 

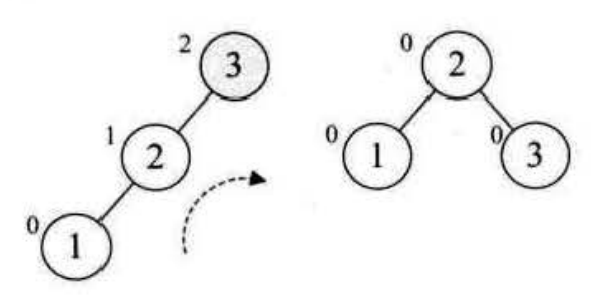
 插入第四个节点 4 的时候，左右子树高度为 -1，符合平衡二叉树要求，继续插入第五个节点，此时又不符合平衡二叉树的要求了，这个时候右子树比较高，需要左旋：旋转的时候以最小不平衡子树为单位，此时最小的不平衡子树是3、4、5节点构成的子树，我们以4为中心进行左旋

 

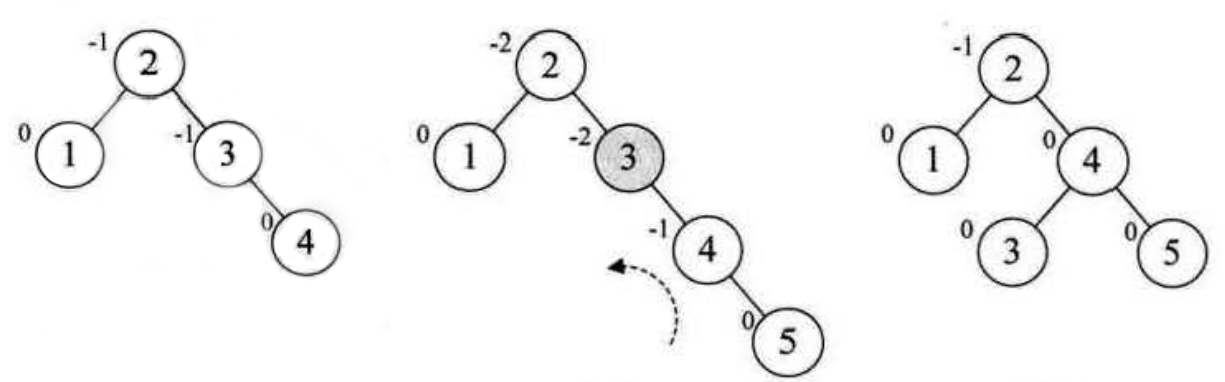
继续增加节点，当插入节点 6 时，发现根节点 2 上维护的高度差值为 -2，又不满足平衡二叉树了，这个时候，需要以 2 为中心对树进行左旋：如下图所示（右子树中旋转到根节点的节点对应子树需要移到旋转后二叉树的左子树中）：

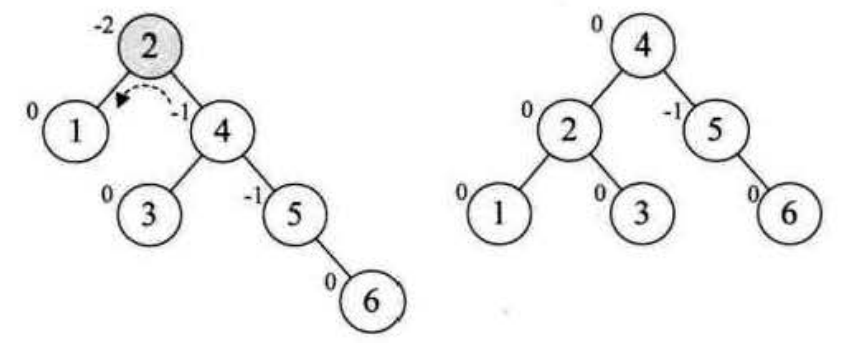
增加结点7，同样的左旋，使得整棵树达到平衡

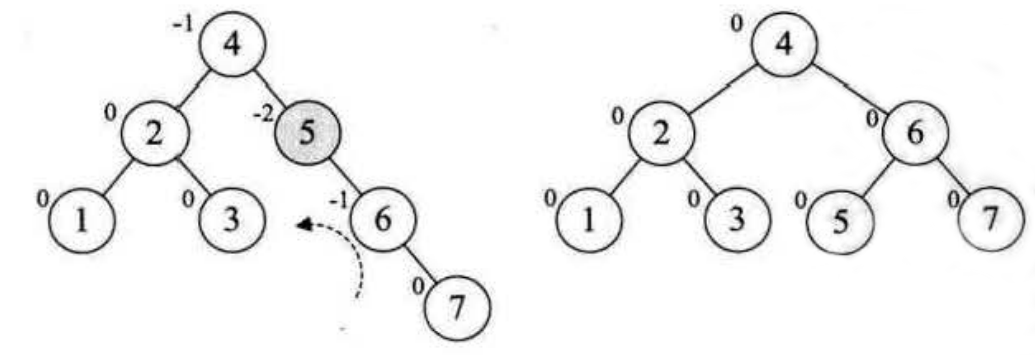
 继续增加节点 10，结构无变化。再插入节点 9，发现结点7的BF变成-2又需要调整。但是这次调整需要绕个弯，不能简单的进行简单的左旋，需要先将以10作为根节点的子树做一次右转，再将以7为根节点的子树做一次左转，让这棵不平衡子树转化为平衡子树

最后，插入节点8，此时情况和刚才类似，这个时候，我们以 9 为根节点对子树进行右旋，再以6为根节点对子树进行左旋，最终达到平衡状态

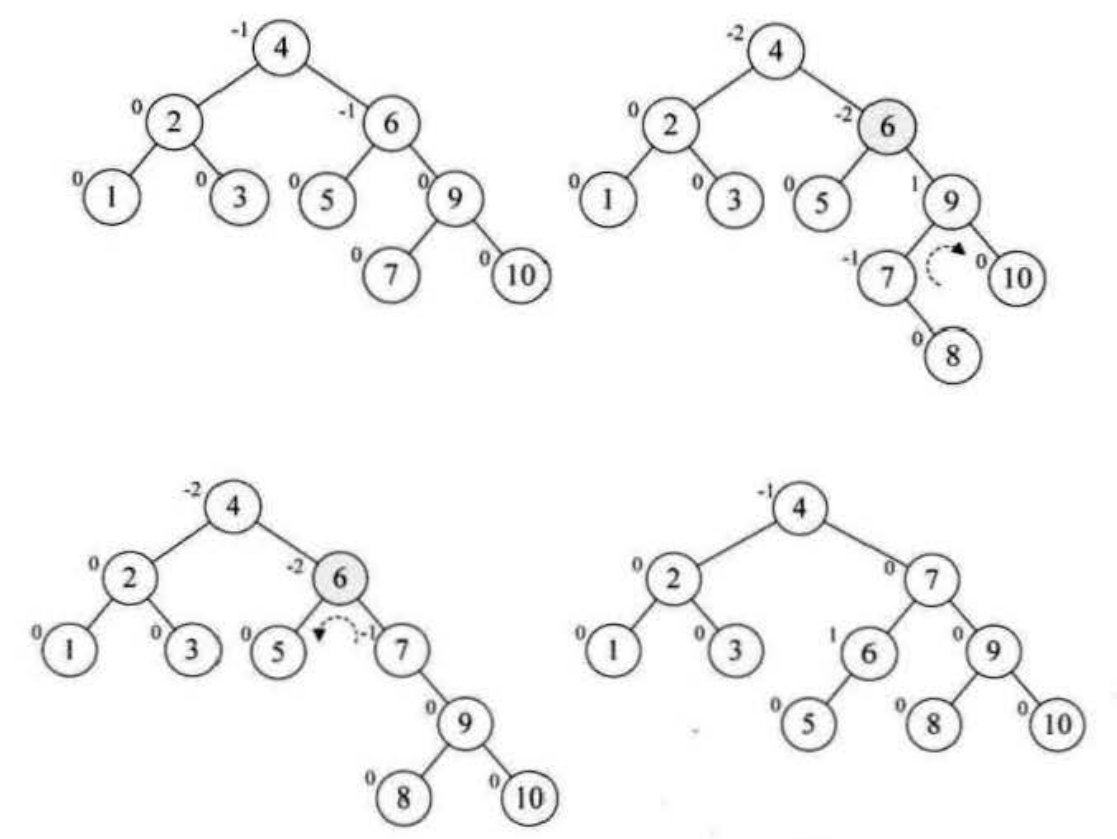
相信大家应该有点明白，所谓的平衡二叉树，其实就是在二叉排序树创建过程中保证它的平衡性，一旦发现有不平衡的情况，马上处理，这样就不会造成不可收拾的情况出现。

通过刚才这个例子，你会发现，当最小不平衡子树根结点的平衡因子BF是大于1时，就右旋，小于-1时就左旋 

三、平衡二叉树PHP代码实现

平衡二叉树结点类

<?php
/**
 * AVLNode.php
 * Created on 2019/4/27 16:44
 * Created by Wilin
 */

class AVLNode
{
    public $data;
    public $left = null;
    public $right = null;
    public $bf = 0;
    public $parent = null;

    public function __construct($data) {
        $this->data = $data;
    }
}

 

 中序遍历

<?php
/**
 * Traverse.php 遍历
 * Created on 2019/4/27 11:10
 * Created by Wilin
 */
function midOrderTraverse($tree) {
    if($tree == null) {
        return;
    }

    midOrderTraverse($tree->left);
    printf("%s\n", $tree->data);
    midOrderTraverse($tree->right);
}

 

平衡二叉树

<?php
/**
 * AVLTree.php
 * Created on 2019/4/27 16:51
 * Created by Wilin
 */

include "AVLNode.php";
include "../Traverse.php";

class AVLTree
{
    private $root;

    const LH = 1;
    const EH = 0;
    const RH = -1;

    public function getTree() {
        return $this->root;
    }

    public function insert(int $data) {
        $this->insert_node($data, $this->root);
    }

    /**
     * 插入节点
     * @param int $data
     * @param $tree
     * @return bool 是否需要调整树结构，true：是，false：否
     */
    protected function insert_node(int $data, &$tree) {

        //创建节点
        if (!$tree) {
            $tree = new AVLNode($data);
            $tree->bf = self::EH;
            return true;                            //插入成功之后需要判断是否需要调整
        }

        if ($data < $tree->data) {
            //递归插入节点
            if (!$this->insert_node($data, $tree->left)) {
                return false;
            } else {
                //更正新插入节点对父节点的指向
                if (empty($tree->left->parent)) {
                    $tree->left->parent = $tree;
                }
                //判断是否需要调整子树
                switch ($tree->bf) {
                    case self::LH:                  //左子树偏高，需要对左子树进行调整
                        $this->left_balance($tree);
                        return false;               //已经进行过调整，不需要继续调整
                    case self::EH:
                        $tree->bf = self::LH;
                        return true;                //由等高变为左高，树的整体高度发生变化，需要继续判断上层节点是否需要调整
                    case self::RH:
                        $tree->bf = self::EH;
                        return false;               //由右高变为等高，树的整体高度没有发生变化，不需要调整
                }
            }
        } else {
            if (!$this->insert_node($data,$tree->right)) {
                return false;
            } else {
                if (empty($tree->right->parent)) {
                    $tree->right->parent = $tree;
                }
                switch ($tree->bf) {
                    case self::LH:
                        $tree->bf = self::EH;
                        return false;
                    case self::EH:
                        $tree->bf = self::RH;
                        return true;
                    case self::RH:
                        $this->right_balance($tree);
                        return false;
                }
            }
        }
    }

    /**
     * 右旋
     * @param $tree
     */
    protected function right_rotate(&$tree) {
        //修改父节点与子树之间的指向时需要特别注意根节点

        $subTree = $tree->left;
        //修改子树对父节点的指向
        if ($tree->parent) {
            $subTree->parent = $tree->parent;
            $left = false;              //调整之前记录当前调整的子树是父节点的左子树还是右子树
            if($tree->parent->left == $tree){
                $left = true;
            }
        } else {
            $subTree->parent = null;    //根节点的父节点为空
        }
        //交换节点位置
        $tree->left = $subTree->right;
        $tree->parent = $subTree;
        $subTree->right = $tree;

        $tree = $subTree;
        //修改父节点对子树的指向
        if (!$tree->parent) {
            $this->root = $tree;
        } else {
            if ($left) {
                $tree->parent->left = $tree;
            } else {
                $tree->parent->right = $tree;
            }
        }
    }

    /**
     * 左旋
     * @param $tree
     */
    protected function left_rotate(&$tree) {

        $subTree = $tree->right;
        if ($tree->parent) {
            $subTree->parent  = $tree->parent;
            $left = true;
            if ($tree->parent->right == $tree) {
                $left = false;
            }
        } else {
            $subTree->parent = null;
        }

        $tree->right = $subTree->left;
        $tree->parent = $subTree;
        $subTree->left = $tree;
        $tree = $subTree;
        if (!$tree->parent) {
            $this->root = $tree;
        } else {
            if ($left) {
                $tree->parent->left = $tree;
            } else {
                $tree->parent->right = $tree;
            }
        }
    }

    /**
     * 调整左子树
     * @param $tree
     */
    protected function left_balance(&$tree) {
        $subTree = $tree->left;
        switch ($subTree->bf) {
            case self::LH:
                $tree->bf = $subTree->bf = self::EH;            //先修改平衡因子，再进行旋转
                $this->right_rotate($tree);
                break;
            case self::RH:
                $subTree_r = $subTree->right;
                switch ($subTree_r->bf) {
                    case self::LH:
                        $tree->bf = self::RH;
                        $subTree->bf = self::EH;
                        break;
                    case self::RH:
                        $tree->bf = self::EH;
                        $subTree->bf = self::LH;
                        break;
                }
                $subTree_r->bf = self::EH;
                $this->left_rotate($subTree);
                $this->right_rotate($tree);
                break;
        }
    }

    /**
     * 调整右子树
     * @param $tree
     */
    protected function right_balance(&$tree) {
        $subTree = $tree->right;
        switch ($subTree->bf) {
            case self::RH:
                $tree->bf = $subTree->bf = self::EH;
                $this->left_rotate($tree);
                break;
            case self::LH:
                $subTree_l = $subTree->left;
                switch ($subTree_l->bf) {
                    case self::RH:
                        $tree->bf = self::LH;
                        $subTree->bf = self::EH;
                        break;
                    case self::EH:
                        $tree->bf = $subTree->bf = self::EH;
                        break;
                    case self::LH:
                        $tree->bf = self::EH;
                        $subTree->bf = self::RH;
                        break;
                }
                $subTree_l->bf = self::EH;
                $this->right_rotate($subTree);
                $this->left_rotate($tree);
        }
    }
}

$avlTree = new AVLTree();
$avlTree->insert(3);
$avlTree->insert(2);
$avlTree->insert(1);
$avlTree->insert(4);
$avlTree->insert(5);
$avlTree->insert(6);
$avlTree->insert(7);
$avlTree->insert(10);
$avlTree->insert(9);
$avlTree->insert(8);
midOrderTraverse($avlTree->getTree());
print_r($avlTree->getTree());

 

打印结果如下

E:\www\tree\2>php AVLTree.php
1
2
3
4
5
6
7
8
9
10
AVLNode Object
(
    [data] => 4
    [left] => AVLNode Object
        (
            [data] => 2
            [left] => AVLNode Object
                (
                    [data] => 1
                    [left] =>
                    [right] =>
                    [bf] => 0
                    [parent] => AVLNode Object
 *RECURSION*
                )

            [right] => AVLNode Object
                (
                    [data] => 3
                    [left] =>
                    [right] =>
                    [bf] => 0
                    [parent] => AVLNode Object
 *RECURSION*
                )

            [bf] => 0
            [parent] => AVLNode Object
 *RECURSION*
        )

    [right] => AVLNode Object
        (
            [data] => 7
            [left] => AVLNode Object
                (
                    [data] => 6
                    [left] => AVLNode Object
                        (
                            [data] => 5
                            [left] =>
                            [right] =>
                            [bf] => 0
                            [parent] => AVLNode Object
 *RECURSION*
                        )

                    [right] =>
                    [bf] => 1
                    [parent] => AVLNode Object
 *RECURSION*
                )

            [right] => AVLNode Object
                (
                    [data] => 9
                    [left] => AVLNode Object
                        (
                            [data] => 8
                            [left] =>
                            [right] =>
                            [bf] => 0
                            [parent] => AVLNode Object
 *RECURSION*
                        )

                    [right] => AVLNode Object
                        (
                            [data] => 10
                            [left] =>
                            [right] =>
                            [bf] => 0
                            [parent] => AVLNode Object
 *RECURSION*
                        )

                    [bf] => 0
                    [parent] => AVLNode Object
 *RECURSION*
                )

            [bf] => 0
            [parent] => AVLNode Object
 *RECURSION*
        )

    [bf] => -1
    [parent] =>
)

参考书籍：《大话数据结构》

其他参考：https://articles.zsxq.com/id_dgm8kpxzw4xo.html