哈夫曼树详解——PHP代码实现

在介绍哈夫曼树之前需要先了解一些专业术语

• 路径和路径长度

　　在一棵树中，从一个结点往下可以达到的孩子或孙子结点之间的通路，称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1，则从根结点到第L层结点的路径长度为L-1。

• 结点的权及带权路径长度

　　若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。结点的带权路径长度为：从根结点到该结点之间的路径长度与该结点的权的乘积。

• 树的带权路径长度

　　树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为WPL =（W1*L1+W2*L2+W3*L3+...+Wn*Ln），N个权值Wi（i=1,2,...n）构成一棵有N个叶结点的二叉树，相应的叶结点的路径长度为Li（i=1,2,...n）。

1、什么是哈夫曼树

给定n个权值作为n个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近，可以证明哈夫曼树的WPL是最小的。

2、哈夫曼树的构造规则

假设有n个权值，则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn，则哈夫曼树的构造规则为：

1. 将w1、w2、…，wn看成是有n 棵树的森林(每棵树仅有一个结点)；
2. 在森林中选出两个根结点的权值最小的树合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；
3. 从森林中删除选取的两棵树，并将新树加入森林； 
4. 重复2、3步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。

3、哈夫曼编码

哈夫曼树的目的是为了解决当年远距离通信(主要是电报)的数据传输的最优化问题

比如，我们需要在网络上传输「BADCADEEFD」字符串序列给其他人，显然用二进制的数字（0和1）来表示是很自然的想法。每个字符占一个字节，如果要压缩的话可以通过二进制编码的方式进行传输，这个字符串包含了6个字符：ABCDEF，我们可以用对应的二进制表示如下：

这样，真正传输的数字编码就是「001000011010000011100100101011」，对方接收时按照3位一分来译码，如果文章很长，这个序列串也会非常长。

而事实上，不管是英文还是中文，不同字母或汉字的出现频率是不同的，完全可以用哈夫曼树的思想进行优化。

上述「BADCADEEFD」中不同字符的出现大致概率是这样的：

合起来是100%，我们可以这样来构建哈夫曼树：

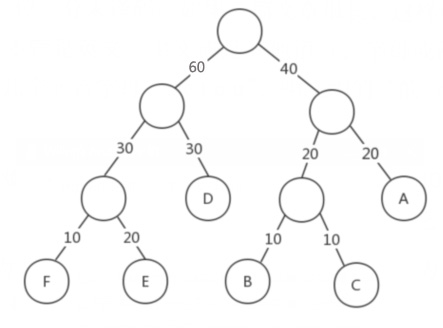
 再将左分支改为0，右分支改为1，对应的哈夫曼树如下：

 

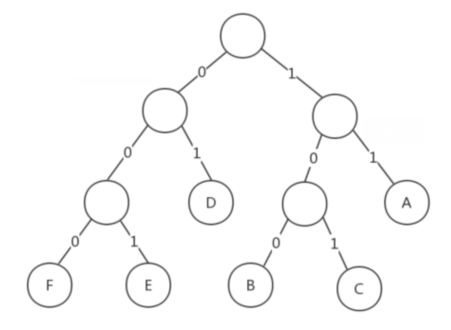
此时，我们对这6个字母用其从树根到叶子所经过路径的 0或1 来编码，可以得到如下图的定义

 

我们将文字内容为「BADCADEEFD」再次编码，对比可以看到结果串变小了

原编码二进制串：001000011010000011100100101011（30个字符）
新编码二进制串：1001101101110100100100001（25个字符）

也就是说，我们的数据被压缩了，节约了大约 17%的存储或传输成本 随着字符的增加和多字符权重的不同，这种压缩会更加显出其优势。

哈夫曼编码的结果会导致不同字符编码长短不一，很容易混淆。因此在解码时，还是要用到哈夫曼编码，即发送方和接收方必须要约定好同样的哈夫曼编码规则。

4、PHP代码实现

<?php
/**
 * HNode.php
 * Created on 2019/5/4 13:11
 * Created by Wilin
 */

class HNode
{
    public $data;
    public $weight;

    public $code = '';
    public $left = null;
    public $right = null;

    public function __construct($data, $weight = 1) {
        $this->data = $data;
        $this->weight = $weight;
    }
}

<?php
/**
 * HuffmanTree.php
 * Created on 2019/5/4 13:11
 * Created by Wilin
 */
include "HNode.php";

class HuffmanTree
{
    private $wpl = 0;
    private $root;
    private $nodes;

    public function getTree() {
        return $this->root;
    }

    public function getWpl() {
        return $this->wpl;
    }

    private function sortByWeight() {
        usort($this->nodes, function ($nodeA, $nodeB) {
            return $nodeA->weight <=> $nodeB->weight;
        });
    }

    public function create($text) {

        $text = str_replace(' ','',strtolower($text));

        for ($i = 0; $i < mb_strlen($text); $i++) {
            $index = $data = $text[$i];
            if (empty($this->nodes[$index])) {
                $newNode = new HNode($data);
                $this->nodes[$index] = $newNode;
            } else {
                $this->nodes[$index]->weight++;
            }
        }

        while (sizeof($this->nodes) > 1) {
            $this->sortByWeight();
            $min1 = array_shift($this->nodes);
            $min2 = array_shift($this->nodes);

            $newNode = new HNode(null, $min1->weight + $min2->weight);
            $newNode->left = $min1;
            $newNode->right = $min2;
            array_push($this->nodes, $newNode);
        }

        $this->root = array_shift($this->nodes);
        $this->fillCW($this->root);
    }

    private function fillCW($tree, $code = '') {
        if($tree == null) {
            return;
        }
        $tree->code = $code;
        if(!$tree->left && !$tree->right){
            $this->wpl += mb_strlen($tree->code)*$tree->weight;
        }
        $this->fillCW($tree->left, $code.'0');
        $this->fillCW($tree->right, $code.'1');
    }

    private function preOrderTraverse($tree) {
        if($tree == null) {
            return;
        }
        if(!$tree->left && !$tree->right){
            printf("%s : %s\n", $tree->data, $tree->code);
        }
        $this->preOrderTraverse($tree->left);
        $this->preOrderTraverse($tree->right);
    }

    public function traverse() {
        $this->preOrderTraverse($this->root);
    }
}

$HTree = new HuffmanTree();
$HTree->create('BADCADEEFD');
$HTree->traverse();
printf("WPL : %s\n", $HTree->getWpl());
print_r($HTree->getTree());

打印结果如下：

E:\www\tree\4>php HuffmanTree.php
e : 00
b : 010
c : 011
d : 10
f : 110
a : 111
WPL : 25
HNode Object
(
    [data] =>
    [weight] => 10
    [code] =>
    [left] => HNode Object
        (
            [data] =>
            [weight] => 4
            [code] => 0
            [left] => HNode Object
                (
                    [data] => e
                    [weight] => 2
                    [code] => 00
                    [left] =>
                    [right] =>
                )

            [right] => HNode Object
                (
                    [data] =>
                    [weight] => 2
                    [code] => 01
                    [left] => HNode Object
                        (
                            [data] => b
                            [weight] => 1
                            [code] => 010
                            [left] =>
                            [right] =>
                        )

                    [right] => HNode Object
                        (
                            [data] => c
                            [weight] => 1
                            [code] => 011
                            [left] =>
                            [right] =>
                        )

                )

        )

    [right] => HNode Object
        (
            [data] =>
            [weight] => 6
            [code] => 1
            [left] => HNode Object
                (
                    [data] => d
                    [weight] => 3
                    [code] => 10
                    [left] =>
                    [right] =>
                )

            [right] => HNode Object
                (
                    [data] =>
                    [weight] => 3
                    [code] => 11
                    [left] => HNode Object
                        (
                            [data] => f
                            [weight] => 1
                            [code] => 110
                            [left] =>
                            [right] =>
                        )

                    [right] => HNode Object
                        (
                            [data] => a
                            [weight] => 2
                            [code] => 111
                            [left] =>
                            [right] =>
                        )

                )

        )

)