力扣动态规划中等题困难题+字符串DP专题20210807

力扣动态规划中等题困难题+字符串DP专题20210807

 

总结：

二叉树的DP，采用哈希表map进行存储。自底向上类似后序遍历。

搜索有DFS和BFS，可以理解为，DFS搜索是递归的子集。

 

一维数组存储可以替换为两个变量或者滚动数组（如果可以的话）。

 

vector的二维数组申请以及初始化：

 vector<vector<int>> dp(n+1,vector<int>(3,0));

 

vector二维数组的行列大小定义：

    int maximalSquare(vector<vector<char>>& matrix) {
        int m=matrix.size();
        int m=matrix[0].size();
}

 

总结：回溯，就是试探性穷举，不成功就退回到上一个状态，继续尝试下一个分支。

 

 

 

力扣 的 139题 一个字符串是否可以在字典集合里完全找到

方法一：采用回溯

代码如下：

class Solution {
private:
    //回溯思想，时间复杂度o(2^n)，空间复杂度O(n)。
    bool backs(string& s, unordered_set<string>& wordSet,vector<int>& memo,int startindex)
    {
        if(startindex==s.size())
        {
            return true;
        }
        if(memo[startindex]!=-1)
        {
            return memo[startindex];
        }
        for(int i=startindex;i<s.size();i++)
        {
            string word = s.substr(startindex,i-startindex+1);

            if(wordSet.find(word)!=wordSet.end()&& backs(s,wordSet,memo,i+1))
            {
                memo[i]=1;
                return true;
            }
            
        }
        memo[startindex]=0;
        return false;
    }

public:
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<string> wordSet(wordDict.begin(),wordDict.end());
        vector<int> memo(s.size(),-1);//设计一个备忘录，存储重复子问题，比如ab和ab，在第二次扫描到ab的时候，可以直接调用值，而不需要重新计算。
        return backs(s,wordSet,memo,0);
    }
};

 

参考链接：https://leetcode-cn.com/problems/word-break/solution/dai-ma-sui-xiang-lu-139-dan-ci-chai-fen-50a1a/

 

方法二：动态规划

类似01背包问题，

01背包问题模板

 

代码如下：

 

class Solution {

public:
    //采用动态规划的思想
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<string> wordSet(wordDict.begin(),wordDict.end());
        vector<bool> dp(s.size()+1,false); // dp[i]表示长度为i的时候，可拆分成1个或者多个在wordSet（字典集合） 里面的单词
        dp[0]=true;
        for(int i=1;i<=s.size();i++)//这是遍历字符串，相当于物品
        {
            for(int j=0;j<i;j++)//这个是单词，相当于背包
            {
                string word = s.substr(j,i-j);
                if((wordSet.find(word) != wordSet.end()) && dp[j])
                {
                    dp[i]=true;
                }
            }
        }
        return dp[s.size()];
    }
};

 

 

力扣 279题 完全平方数

采用动态规划的思想

代码如下：

class Solution {
public:
    int numSquares(int n) {
        //动态规划的思想
        vector<int> dp(n+1);
        dp[0]=0;//dp[0]需要初始化为0

        for(int i=1;i<=n;i++)
        {
            int m = INT_MAX;
            for(int j=1;j*j<=i;j++)
            {
                m = min(m,dp[i-j*j]); //m表示已有一个平方数的基础上，需要的最少数量
                dp[i]=1+m;   //       
            }
        }
        return dp[n];
    }
};

 

 

力扣583题 两个字符串的删除

两个字符串的最长公共子串模板：

定义：

dp[i][j]表示以i,j结尾的最长公共子串。

转移公式：

dp[i][j]= （dp[i]==dp[j] ? (dp[i-1][j-1]+1) ：0）

C++代码模板：

#include<iostream>
#include<cstring>
#include<cmath>
#include<cstdio>
using namespace std;
 
char s1[1000],s2[1000];
int dp[1000][1000];
int main()
{
    while (~scanf("%s %s",s1+1,s2+1))
    {
        int len1 = strlen(s1+1);
        int len2 = strlen(s2+1);
        int ans = 0;
        for (int i = 1;i <= len1; i++)
          for (int j = 1;j <= len2; j++)
          {
              if (s1[i] == s2[j])
              {
                  dp[i][j] = dp[i-1][j-1]+1;
                  ans = max(ans,dp[i][j]);
              }
 
          }
        printf("%d\n",ans);
        memset(dp,0,sizeof(dp));
        memset(s1,0,sizeof(s1));
        memset(s2,0,sizeof(s2));
    }
}

 

Java代码模板：

public static int lcs(String str1, String str2) {
 int len1 = str1.length();
 int len2 = str2.length();
 int result = 0; //记录最长公共子串长度
 int c[][] = new int[len1+1][len2+1];
 for (int i = 0; i <= len1; i++) {
 for( int j = 0; j <= len2; j++) {
  if(i == 0 || j == 0) {
  c[i][j] = 0;
  } else if (str1.charAt(i-1) == str2.charAt(j-1)) {
  c[i][j] = c[i-1][j-1] + 1;
  result = max(c[i][j], result);
  } else {
  c[i][j] = 0;
  }
 }
 }
 return result;
}

参考链接：https://www.iamivan.net/a/MNv05oM.html

 

滚动优化：主要是考虑到两个状态可以滚动

C++代码如下：

#include<iostream>
#include<cstring>
#include<cmath>
#include<cstdio>
using namespace std;
 
char s1[1000],s2[1000];
int dp[2][1000];
int main()
{
    while (~scanf("%s %s",s1+1,s2+1))
    {
        int len1 = strlen(s1+1);
        int len2 = strlen(s2+1);
        int ans = 0, cur = 0;
        for (int i = 1;i <= len1; i++)
        {
            cur ^= 1;
            for (int j = 1;j <= len2; j++)
            {
                if (s1[i] == s2[j])
                {
                    dp[cur][j] = dp[cur^1][j-1]+1;
                    ans = max(ans,dp[cur][j]);
                }
                else dp[cur][j] = 0;
 
            }
        }
 
        printf("%d\n",ans);
        memset(dp,0,sizeof(dp));
        memset(s1,0,sizeof(s1));
        memset(s2,0,sizeof(s2));
    }
}

参考链接：https://blog.csdn.net/sugarbliss/article/details/80731688

 

 

题目代码：

class Solution {
public:
    int minDistance(string word1, string word2) {
        //动态规划的思想
        int a = word1.size();
        int b = word2.size();
        vector<vector<int>> dp(a+1,vector<int>(b+1,0));
        int ans = 0;
        int res=0;
        for(int i=1;i<=a;i++)
        {
            for(int j=1;j<=b;j++)
            {

                if(word1[i-1]==word2[j-1])
                {
                    dp[i][j]= dp[i-1][j-1]+1;
                    ans = max(ans,dp[i][j]);
                }
                else
                {
                    dp[i][j] = max(dp[i-1][j],dp[i][j-1]);//当i,j不相等时，dp[i][j]等于前一个状态的值，max(dp[i-1][j],dp[i][j-1])
                }
            }
        }
        res = (a+b-(2*dp[a][b]));
        //cout<<res<<endl;
        return res;
    }
};

 

 

 参考链接：https://leetcode-cn.com/problems/delete-operation-for-two-strings/solution/dai-ma-sui-xiang-lu-dai-ni-xue-tou-dpzi-8cai1/

 

 

力扣 678题 有效的括号字符串

方法一：采用两个栈

代码如下：

class Solution {
public:
    bool checkValidString(string s) {
    //设两个栈，一个存左括号，一个存星号，遇右括号，先匹配左括号组，再匹配星号组，都没有返回false
    //匹配完剩余星号和左括号匹配，注意左括号要在星号左侧，左括号不能有剩余
    stack<int> left,star;

    for(int i=0;i<s.size();i++)//把（ 和 * 放进两个两个栈里面，遇到 ），就先判断（的栈有的话，就抛出一个；如果（的栈没有，就抛出*的栈里面的一个；都为空，就返回false。
    {
        if(s[i]=='(')
        {
            left.push(i);
        }
        else if(s[i]=='*')
        {
            star.push(i);
        }
        else
        {
            if(left.empty() && star.empty())
            {
                return false;
            }
            if(!left.empty())
            {
                left.pop();
            }
            else
            star.pop();
        }
    }
    while(!left.empty() && !star.empty())//判断左括号和* 可能还没完全消除的情况，如果左括号在*的右边，就是返回false，因为*变成三种方式的任何一种，都不是有效字符串。
    {
        if(left.top()>star.top())//这是*(的情况，不是有效字符串
        {
            return false;
        }
        left.pop();
        star.pop();
    }
    return left.empty();
    }
};

 

方法二：两个变量的方法

代码如下：

class Solution {
public:
    bool checkValidString(string s) {
        //两个变量的方法
        //对未匹配的左括号设置一个变化的范围，用两个变量分别表示范围的最小值和最大值。一般的括号匹配都是左括号设置一个栈，有右括号，则左括号出栈。可以不用栈，用一个变量表示未匹配的左括号即可。 本题加了*，则需要两个变量表示未匹配的左括号的数量
        int min=0;
        int max=0;
        int n=s.size();
        for(int i=0;i<n;i++)
        {
            if(s[i]=='(')//左括号的时候，最小值加一，最大值也是加一
            {
                min++;
                high++;
            }
            else if(s[i]==')')//右括号的时候，最小值是0和减一的最大值，最大值是肯定减一的
            {
                min = max(0,min-1);
                high--;
            }
            else{          //当出现*的时候，最小值*看成右括号，是0和减一的最大值，最大值是*看成左括号，最大值加一
                min = max(0,min-1);
                high++;
            }

        }
        return min<=0; //当未匹配的左括号的数量小于等于0的时候才是返回true，否则返回false

    }
};


/**class Solution {
public:
    bool checkValidString(string s) {
    //设两个栈，一个存左括号，一个存星号，遇右括号，先匹配左括号组，再匹配星号组，都没有返回false
    //匹配完剩余星号和左括号匹配，注意左括号要在星号左侧，左括号不能有剩余
    stack<int> left,star;

    for(int i=0;i<s.size();i++)//把（ 和 * 放进两个两个栈里面，遇到 ），就先判断（的栈有的话，就抛出一个；如果（的栈没有，就抛出*的栈里面的一个；都为空，就返回false。
    {
        if(s[i]=='(')
        {
            left.push(i);
        }
        else if(s[i]=='*')
        {
            star.push(i);
        }
        else
        {
            if(left.empty() && star.empty())
            {
                return false;
            }
            if(!left.empty())
            {
                left.pop();
            }
            else
            star.pop();
        }
    }
    while(!left.empty() && !star.empty())//判断左括号和* 可能还没完全消除的情况，如果左括号在*的右边，就是返回false，因为*变成三种方式的任何一种，都不是有效字符串。
    {
        if(left.top()>star.top())//这是*(的情况，不是有效字符串
        {
            return false;
        }
        left.pop();
        star.pop();
    }
    return left.empty();
    }
};**/

 

方法三：从前往后和从后往前，两次遍历的方法

代码如下：

class Solution {
public:
    bool checkValidString(string s) {
        //两次遍历的方法
        int n = s.size();
        int left = 0;//左括号数量
        int right = 0;//右括号数量
        int star = 0;//*的数量
        for(int i=0;i<n;i++)//从前往后遍历，遇到）的时候，先删除（，没有（就删除* 
        {
            if(s[i]=='(')
            {
                left++;
            }
            else if(s[i]=='*')
            {
                star++;
            }
            else
            {
                if(left>0)
                {
                    left--;
                }
                else if(star>0)
                {
                    star--;
                }
                else return false;
            }
        }
        star = 0;
        for(int i=n-1;i>=0;i--)//从后往前遍历，遇到（的时候，先删），没有）就删除* 
        {
            if(s[i]=='*')
            {
                star++;
            }
            else if(s[i]==')')
            {
                right++;
            }
            else
            {
                if(right>0) right--;
                else if(star>0) star--;
                else
                {
                    return false;//此时左括号没有，所以返回false
                }
            }

        }
        return true;
    }
};

 

方法四：回溯

代码如下：

class Solution {
private:
    bool check(string& s,int start,int count)//有开始点的下标位置，有count记录未匹配的左括号的数量
    
    {
        if(count<0)
        {
            return false;
        }
        for(int i=start;i<s.size();i++)
        {
            if(s[i]=='(')
            {
                count++;
            }
            else if(s[i]==')')
            {
                if(count==0)
                {
                    return false;
                }
                count--;
            }
            else if(s[i]=='*')
            {
                return check(s,i+1,count) || check(s,i+1,count+1) || check(s,i+1,count-1);
            }
        }
        return count==0;
    }


public:
    bool checkValidString(string s) {
        //DFS，回溯的方法
        return check(s,0,0);    
    }
};

以上代码会超时，可以用map或者vector存储start和count的值，达到优化效果，感兴趣可以试一试。

 参考链接：https://leetcode-cn.com/problems/valid-parenthesis-string/solution/fen-zhi-tan-xin-shuang-xiang-bian-li-shuang-zhan-j/

 

 

926. 将字符串翻转到单调递增

采用动态规划思想，

代码如下：

class Solution {
public:
    int minFlipsMonoIncr(string s) {
        //动态规划思想
        int n = s.size();
        vector<int> dp(n+1);
        dp[n] = 0;//dp[i]表示下标是i的时候，i~n-1之间1的数量

        for(int i=n-1;i>=0;i--)
        {
            if(s[i]=='1')
            {
                dp[i]=dp[i+1]+1;
            }
            else
            {
                dp[i]=dp[i+1];
            }
          //  cout<<i<<" "<<dp[i]<<endl;
        }

        int r = INT_MAX;
        for(int i=1;i<n;i++)
        {
            r = min(r,dp[0]-dp[i]+n-i-dp[i]);//dp[0]-dp[i]表示0~i-1之间1的数量,n-i-dp[i]表示i+1~n-1之间的0的数量。两者的和就是需要修改的数量
           // cout<<r<<" "<<dp[0]-dp[i]+n-i-dp[i]<<endl;
        }
        int count=0;
        for(int i=0;i<n;i++)
        {
            if(s[i]=='1')
            {
                count++;
            }
        }
        if(count<r || (n-count)<r)//修改成全0或者全1的情况，需要的次数，小于之前的修改次数的时候，可以取最小值，并返回这个最小值
        {
            return min(count,n-count);
        }
        return r;
    }
};

 

背包问题刷题指南：

 

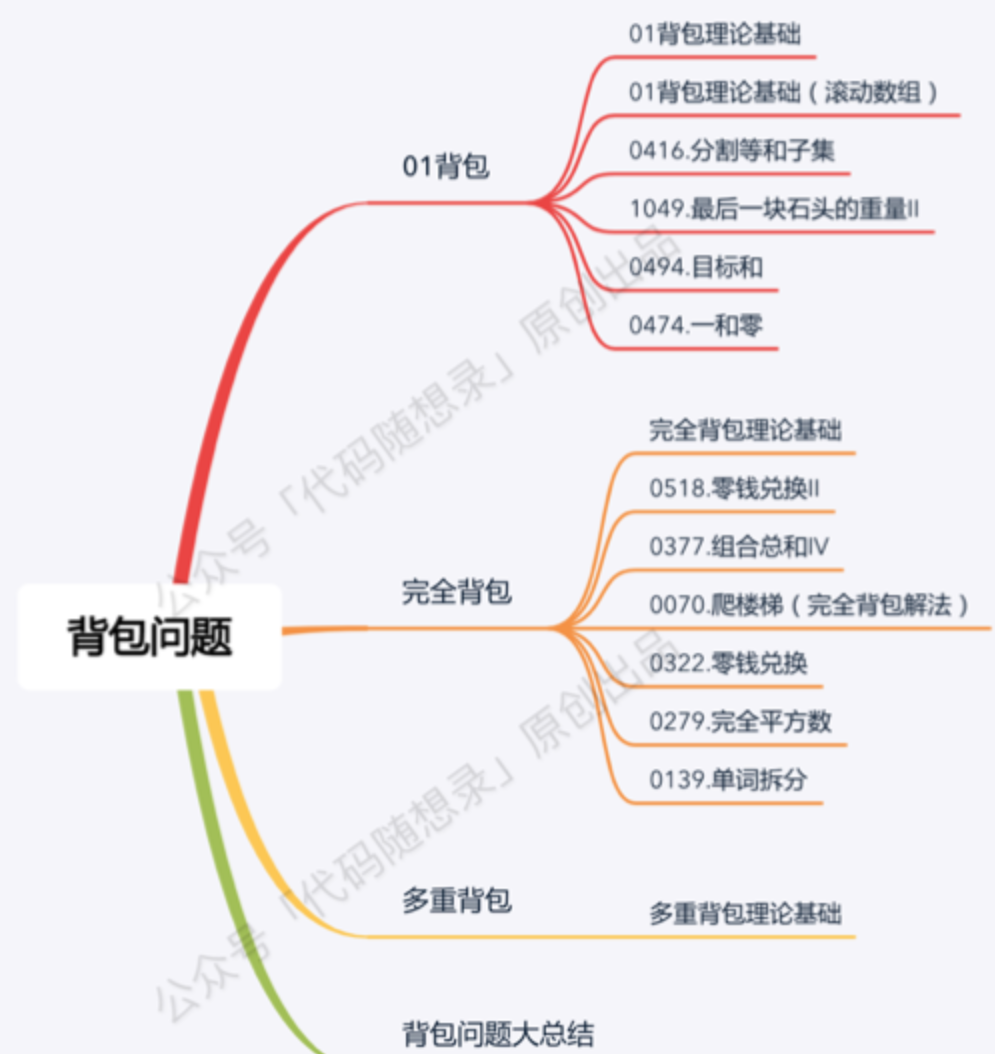
 参考链接：https://blog.csdn.net/youngyangyang04/article/details/114253921