机器学习第八堂课20210422

聚类

应用在无监督学习中。

X=[X1,X2,X3,,,,Xn]

上节课讲的降维实际是把每个数据的特征维度降低了，通过对数据本身进行分析，进行降维。

聚类，是在数据量这个角度 通过方法，对数据进行分析，找到K个代表，可以代表整个n个数据，n个数据归类到K个代表中。

聚类任务相关概念

定义：依据样本的相似度或距离，将其划分为若干个通常不相交的子集（“簇”，cluster）的数据分析问题。

目的：既可以用于发现数据内在的分布结构，也可作为分类等其他学习任务的数据处理过程。

应用：例子1购物网站上，用户的消费类性分析（书籍、服饰......）；例子2根据各个时刻统计的车流量，定义高峰时刻。

聚类的模型表达：

硬聚类：样本只从属于一个簇。例如Kmeans算法。软聚类：样本以概率从属于多个簇。例如高斯混合模型。

样本的相似度度量：用距离衡量相似度时，距离越小样本越相似。

距离的性质：非负性、同一性、对城性、直递性。

闵可父斯基距离：p=2欧式距离、p=1曼哈顿距离。

 

 夹角余弦：夹角余弦越大，样本越相似。

簇的距离：簇内的距离、簇间的距离。有以下四种典型的距离情况。

平均距离：含义：簇类C1和C2的距离等于两个簇类所有样本对的距离平均。

 

 

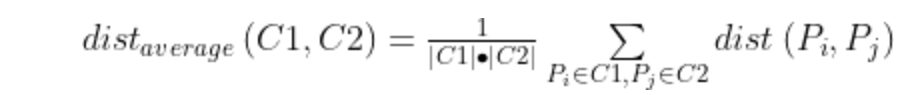
最远距离

最近样本间距离

中心点间的距离

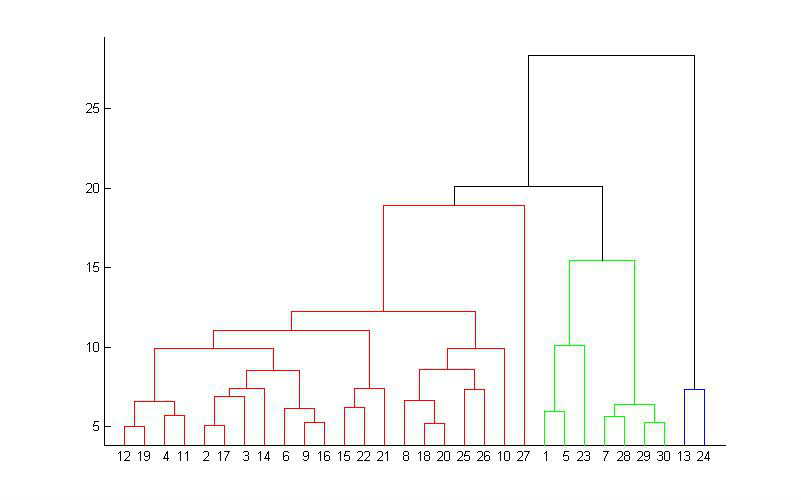
层次聚类方法

主要特点：在不同层次

算法过程：

层次聚类，是一种很直观的算法。顾名思义就是要一层一层地进行聚类，可以从下而上地把小的cluster合并聚集，也可以从上而下地将大的cluster进行分割。所谓从下而上地合并cluster，具体而言，就是每次找到距离最短的两个cluster，然后进行合并成一个大的cluster，直到全部合并为一个cluster。整个过程就是建立一个树结构。

 

基于原型的方法

K-Means聚类

目标：给定N个样本的集合，K均值聚类的目标是将N个样本划分为K个不同的类或者簇中。

模型表达：用C表示划分...

目标函数最小化样本与其所属簇的中心之间的距离的总和。

 

 K-Means的不足，簇的数目K需要人为指定；对簇中心的初始化比较敏感，不能保证收敛到全局最优。

 

 

基于密度的方法

 

 

参考链接：https://baike.baidu.com/item/%E9%97%B5%E6%B0%8F%E8%B7%9D%E7%A6%BB/22677930?fromtitle=%E9%97%B5%E5%8F%AF%E5%A4%AB%E6%96%AF%E5%9F%BA%E8%B7%9D%E7%A6%BB&fromid=23665511&fr=aladdin

https://blog.csdn.net/qq_33384379/article/details/103579917

https://blog.csdn.net/ycy0706/article/details/90439245

https://blog.csdn.net/u014694994/article/details/94972668

https://zhuanlan.zhihu.com/p/70414047