最短路径问题
由于要考试了,这里只是简单的罗列一下,考试完毕之后继续完善~
单元最短路径
单元最短路径有很多变体问题,比如单元目的最短路径,最短路径也有很多性质~,这些性质是算法正确性的基础,这些考试之后来完善,
关于每个算法都要用到的松弛操作如下
RELAX(u,v,w)
if d[v] > d[u]+w(u,v)
d[v]= d[u]+w(u,v)
father[v]=u
关于每个算法的初始化操作也写在前面
INITIALIZE-SINGLE-SOURCE(G,s)
for each vertex v in G
d[v]= MAX
father[v]=NIL
d[s]=0
首先重点是Bellman-Ford算法,该算法能够识别负权重环
BELLMAN-FORD(G,w,s)
INITIALIZE-SINGLE-SOURCE(G,s)
for i = 1 to |V|-1
do for each edge (u,v) in E(G)
RELAX(u,v,w)
for each edge (u,v) in E(G) //没有收敛,存在负权环
if d[v]>d[u]+w(u,v)
return FALSE
return TRUE
时间复杂度为O(VE)
接下来是DAG有向无环图的单元最短路径
//这里考虑是针对顺序进行松弛,但是根据路径松弛性质,必须按照路径的顺序进行,所以这里结合拓扑排序进行计算
DAG-SHORTEST-PATH(G,w,s)
topologically sort the vertices of G
INITIALIZE-SINGLE-SOURCE(G,s)
for each vertex u, taken in toplogically sorted order
for each vertex v in Adj[u]
RELAX(u,v,w)
时间复杂度为O(V+E)
接下来是Dijkstra算法
DIJKSTRA(G,w,s)
INITIALIZE-SINGLE-SOURCE(G,s)
S=空集
Q=V[G]
while Q!=空集
do u=EXTRACT-MIN(Q)
S=S+{u}
for each vertex v in Adj[u]
RELAX(u,v,w)
这个时间复杂度的分析和Prim算法的时间复杂度分析相同
V次EXTRACT-MIN操作,内隐含E次的DECREASE-KEY操作
则分析如下表:

这个算法在后面算任意两点之间计算最短距离的时候,可以通过变化权重转换为此算法,针对稀疏图增加能够提升效率
差分约束和最短路径
这里描述的是一个解决的实际问题,差分约束问题转换为单元最短路径问题的解决
差分约束的一个问题描述:线性规划的一种,目标是找出可满足解,而不是线性规划中的最优解。而且条件式的形式比较固定,每一项中有两个变量的差组成,变换为矩阵每行只有一个1和一个-1 。实例如下:

线面是此问题转换为最短路径的方法,针对矩阵进行转置,得到一个n*m的矩阵,转置后的矩阵为这样一种矩阵n为顶点,m为边,位置i,j的数值信息表示边的信息,信息如下,0第i个顶点和第j条边无关系,1表示第j条边进入i,-1表示第j条边离开i,权中为对应的后面的j位置的信息
一个简单的方法可以直接根据公式换图更方便,某个减去某个表示第i个顶点到减去顶点有一个大小的权重...

上例转换如下图:
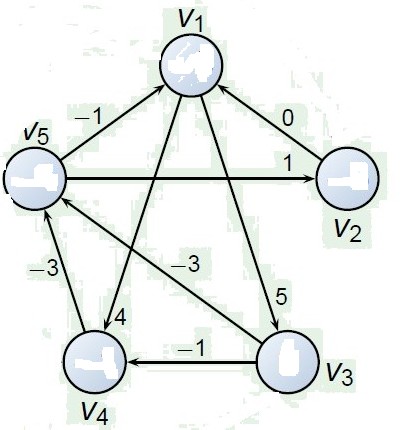
接下来添加一个虚拟的点,其到各个顶点的权重为0,这时候求的该点单元最短路径的及为差分的一个满足解
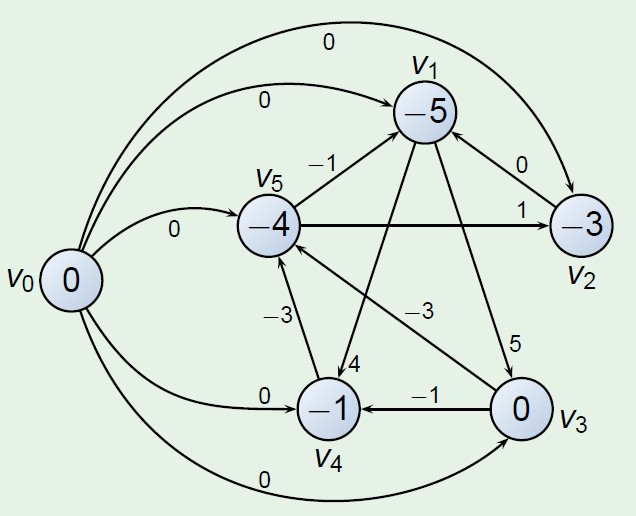
证明后续补充...
每对顶点间的最短路径问题
根据前置矩阵输出最短路径的伪代码这里就不给出了,比较简单。
首先说明最短路径具有最优子结构,所以这里考虑动态规划算法~
首先是一个跟矩阵相乘很相似的算法,其考虑是根据边考虑子结构,比如把路径p的最短路径分解为i到k的最短路径+k到j的权重,这里是每个子问题减去1,
伪代码比较容易实现:


算法导论一书中进行优化的时候是转换为矩阵的乘方问题,所以可以递归,但是这里可以直接从动态规划子结构的划分方面考虑,比如最短路径p分解为i到k的最短路径和k到j的最短路径,这也是一个子结构,这里可以从1扩展到2,然后路径长度为2的扩展到4,4的扩展到8...所以书中的伪代码相似;

这样就行了,因为上面慢的时间复杂度为V的四次方,这里提升到V的三次方*lgV,效率还是比较低。
接下来介绍另外一个更加优秀的动态规划方法,其子结构考虑非常好。
Floyd-Warshall
这个算法的最短路径的子结构考虑的是其路径包含的中间节点的个数
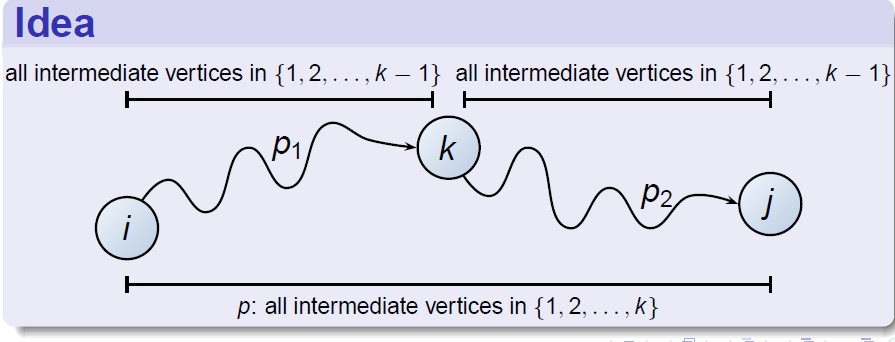
伪代码如下:
FOLYD-WARSHALL(W)
n = rows[w]
D0 = w
for k =1 to n
for i = 1 to n
for j=1 to n
dij(k) = min(dij(k-1),dik(k-1),dkj(k-1))
计算过程中保持计算前置矩阵。

算法导论一书中该处印刷有些错误,第二版...
时间复杂度为V的三次方
有向图的传递闭包
上面的算法稍微修改即可,针对上述算法中的min和+法直接利用逻辑或和逻辑与代替即可。
稀疏图上的Johnson算法
原理将图转换为无负权重的图,利用上面的Dijkstra算法。
每个顶点加一个权重函数,最短路径不变,增加权重方法和差分约束转换方法很相似:
每个顶点增加的权重就是增加新的节点到该节点的最短路径...
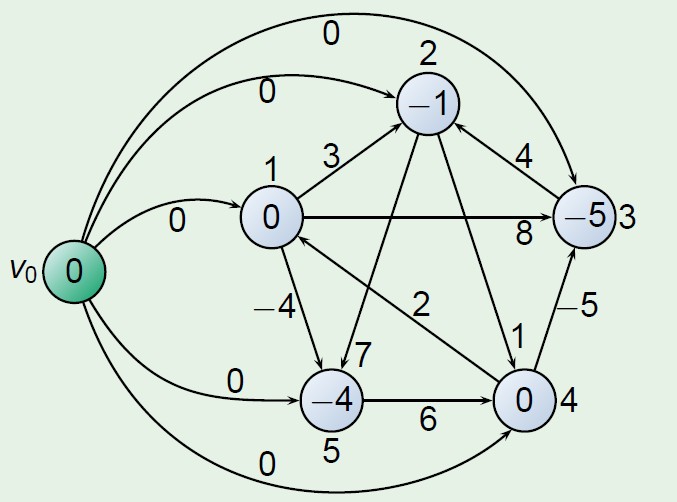
伪代码:


重点的轮廓给出了,我会慢慢补充一些知识进来的~
转载请注明出处,谢谢~


