AC 自动机
概述
-
坐,都坐。我知道各位都很激动,但这个缩写的全称是 Aho-Corasick automaton,AC 是两位发明者的姓氏,automaton:自动机。
-
AC 自动机通过将 trie 的结构和 KMP 的思想结合起来,利用 trie 的结构存储多模式串(或者说构建对应的图论模型),然后将 KMP 自动机的后缀链接推广到多串情况,利用 trie 的结构将状态从匹配位置推广到 trie 上的点,建立对应的后缀链接树并与 trie 的正边合并得到 trie 图,从而高效解决多个模式串相对文本串的各种出现问题。
-
记 \(\Sigma\) 为字符集,则 AC 自动机的空间复杂度和建立时间复杂度均为 \(O(\sum |P|\times |\Sigma|)\)。这里认为预先输入的是模式串,询问相关的是文本串,因一般是求输入的串在询问串中的出现。
实现原理
-
trie 部分参见“字典树”。
-
朴素实现:
-
\(fail\) 数组表示当前节点代表的状态的最大有效后缀对应的节点。
-
我们需要谈谈什么是有效。考虑一个只插入了 \(abca\) 的 AC 自动机:
-
\(abca\) 的最大真后缀显然是 \(bca\),\(bca\) 的是 \(ca\),\(ca\) 的是 \(a\)。但 \(bca,ca\) 对我们来说都是无效的:它不是任何一个模式串的前缀。
-
事实上,我们不妨把 \(bca,ca\) 都建出来:我们会发现,这里 \(abca\) 是“关键点”,而我们只要保留“关键点”相关的点——这是个虚树!而这里的相关,或者说“lca”,是前缀。
-
这也是 AC 自动机必须全部插完之后才构建的理由:如果在线,那么旧有的 fail 边可能是错误的,并没有指向最大有效后缀。
-
-
当查询某个文本串时,如果发现不存在对应的 \(e_{now,c}\),那么 \(now=fail_{now}\) 并再次尝试,直到匹配成功或 \(now=0\) 且仍然匹配失败,此时放弃前面所有的字符从头开始。
-
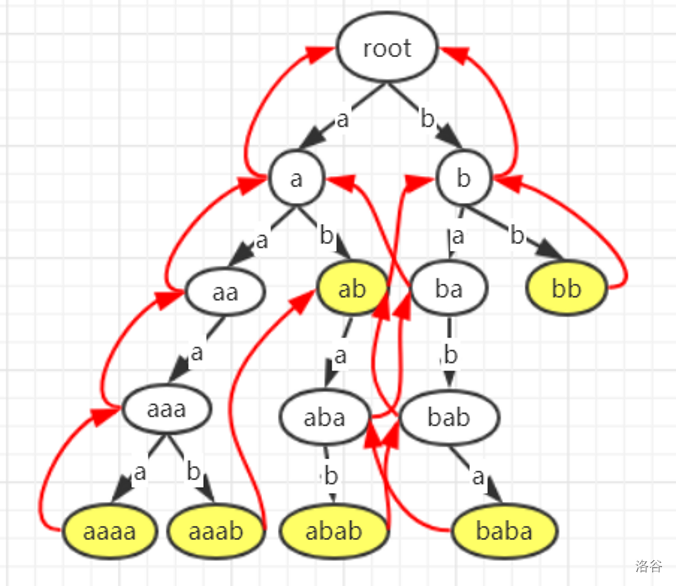
实际形态的话,我们看一张图。黄点为字符串结束点,黑边为 trie 边,红边为 fail 边。
-
-
称黑边即 trie 边构成的树为 trie 树,红边即 fail 边构成的树为 fail 树。两者是 AC 自动机的灵魂;trie 图也只是由这两者共同递推出的罢了。
-
-
trie 图实现:
-
容易看出,上面这个算法的主要弊病在于可能会连续多次失配,于是回跳次数太多。
-
考虑路径压缩!
-
显而易见 \(dep_{fail_{now}}<dep_{now}\),从而我们使用 bfs 实现,并设法让子节点的 \(fail\) 利用上父节点的 \(fail\)。
-
我们站在父亲处理儿子。假如我有这个儿子,那么 \(fail_{e_{now,c}}=e_{fail_{now},c}\),即我儿子的最大有效后缀 \(=\) 我的最大有效后缀 \(+c\)。
-
咦?万一我的最大有效后缀没有对应 \(c\) 的边怎么办?
-
这就不得不谈及非常妙的第二种操作了。假如我没有这个儿子,那么 \(e_{now,c}=e_{fail_{now},c}\)!让虚边来承担 \(fail\),或者说,把 \(fail\) 的效果等效到 \(e\) 里。
-
考虑 \(fail_{now}\) 没有对应 \(c\) 的转移的情况,此时我们有 \(e_{fail_{now},c}=e_{fail_{fail_{now}},c}\)!
-
即,这实质上不是 \(fail\) 了一次,而是不断 \(fail\) 直到找到匹配。
-
如果一直找不到匹配,则最终会达到根节点的某个子节点,从而有 \(e_{fail_{now},c}=e_{0,c}=0=rt\),抛弃了所有前缀。
-
相当于这是一种自动的路径压缩。相较于并查集的由儿子递归地压缩父亲,这里父亲已经压好了,儿子只要连上去就相当于把自己也压了(妙啊)。
-
为了避免把每个 \(dep=1\) 的节点的 \(fail\) 以及无匹配的 \(e_{rt,c}\) 都设为 \(1\) 带来的繁琐特判,我们选择令 \(rt=0\)。
-
-
给出 trie 图实现的示范代码(年久失修):
struct AC_automaton{
int e[maxn][26],tot;
int cnt[maxn],fail[maxn];
il void ins(string &s){
int now=0,to=s.size()-1;
For(i,0,to){
if(!e[now][s[i]-'a'])
e[now][s[i]-'a']=++tot;
now=e[now][s[i]-'a'];
}
++cnt[now]; return;
}
int q[maxn],hd,tl;
il void build(){
hd=1,tl=0;
For(i,0,25)
if(e[0][i])
q[++tl]=e[0][i];
while(tl>=hd){
int now=q[hd++];
For(i,0,25)
if(e[now][i]){
fail[e[now][i]]=e[fail[now]][i];
q[++tl]=e[now][i];
}
else e[now][i]=e[fail[now]][i];
}
}
};
例题
P5357 【模板】AC 自动机(二次加强版)
-
题意:求文本串 \(T\) 中 \(n\) 个模式串 \(P_{1\sim n}\) 分别的出现次数。
-
数据范围:\(n\leqslant 2\times 10^5,\sum |P|\leqslant 2\times 10^5,|T|\leqslant 2\times 10^6\)。
-
直觉上我们可以在 trie 图上,即按 \(e\),把 \(T\) 跑一遍。访问到的点标上 \(vis\)。但这不对。
-
我们知道这里的 \(e_{now,c}\) 很多本质上都是 \(fail\) 边的等效,是舍弃了一部分前缀之后再接一个的结果。
-
通过这些边走到的点,其实相当于从根走到了那个点,这条链上的所有点都是文本串的一部分!
-
考虑一种暴力做法:每到一个点,暴力回跳 \(fail\),每个点都打 \(vis\)。
-
啊...复杂度很不乐观啊,极限情况(虽然不可能)为 \(\sum |P|\times AC.dep\)。
-
考虑把指向没有打 \(vis\) 必要的点(不是字符串结尾)的 \(fail\) 压缩成另一个 \(FAIL\) 用于回跳。
-
假优化。这上界是一样的。
-
-
铛铛!正解:树形 DP(??)!
-
考虑把 \(fail\) 数组对应的 \(fail\) 树建出来(不是 \(fail\) 边这种反边构成的内向树,是正边,正常的可以 dfs 的外向树)。
-
而我们假做法中打的 \(vis\) 的含义其实是从这里到根的路径都 \(vis\) 了,就是说任意的直接/间接 fail...任意的有效后缀,即可能是某个模式串前缀的后缀,都 \(vis\) 了...咦?
-
树形 DP。\(rvis_{now}=\sum rvis_{sons}+vis_{now}\)。
-
从而我们有一个稳定的单次询问复杂度为 \(O(|T|+|AC|)\)。
-
模板题的对偶问题
-
求文本串中所有模式串的总出现次数,多组询问,\(n=Q=\sum |P|=\sum |T|\)。
-
发现瓶颈在于 \(O(|AC|)\) 部分太大了。但不要求对每个模式串分别求出现次数,故考虑反其道而行之,预先做树形 DP!将 \(w\) 推下去(\(w\) 表示有多少个串在该点结尾,准确地说是从根到该点在 trie 上的链对应的串的插入次数),算出 \(rw\) 表示从该点到根在 fail 树上的链的 \(\sum w\),其相当于“有多少个串恰右对齐地和该点对应的串匹配”,于是只要单次 \(O(|T|)\) 即可求出。
P2292 [HNOI2004] L 语言
-
题意:给出 \(n\) 个模式串 \(P_{1\sim n}\),给出 \(Q\) 组询问,每组询问形如求 \(T\) 的最大可理解前缀长度。所谓“可理解”,指的是可以划分成若干个可重的模式串。
-
数据范围:\(n,|P|\leqslant 20,Q\leqslant 50,|T|\leqslant 2\times 10^6\)。实际上似乎并没有 \(10^8\) 的输入,不然不管怎么挣扎都 T 了。
-
首先我们肯定不能上去跑,这就退化成暴搜了,多种并行决策没法决策。
-
故考虑设计 dp:
-
状态设计:\(dp_i\) 表示长为 \(i\) 的前缀是否可理解。
-
初始化:\(dp_0=1\)。
-
状态转移:...我们下面慢慢说。
-
-
首先考虑一个朴素转移:\(dp_i=\bigvee_{j<i} dp_j\land [T_{j+1\sim i}\in P]\)。
-
我们可以暴力枚举是 \(P\) 中那个,然后用字符串 hash 来比较。
-
然而,端下去罢。\(\sum |T|\sim 10^8\),你怎么敢转移不 \(O(1)\) 的?你怎么敢?
-
考虑利用 AC 自动机的性质。既然 \(|P|\leqslant 20\),就把 \(T_{i-19,i}\) 扔上去跑一遍,利用如上题中的 \(rw\) 般预处理出的
\(rsta\)(表示有哪些串恰右对齐地和该点对应的串匹配),可以 \(O(20)\) 地检查出来每个串是否合法。 -
不行,还是不够快。考虑暴力转递推,既然可以跑 \(T_{i-19,i}\),那岂不是也可以 \(O(1)\) 递推到 \(T_{i-18,i+1}\)?毕竟过程中经过的点其实是啥用都没有,我们关心的是它最后停在了哪里。
-
它是个 \(20\) 位二进制状态。那么,我们把 \(dp_{i-20\sim i-1}\) 也压成 \(20\) 位二进制状态!显然它也可以 \(O(1)\) 递推,每次把高位挤掉加个低位就行了,而 \(dp\) 和 \(rsta\) 取交的结果就是 \(dp_i\)(这是未压的,压后应该是 \(dp_{i,0}\))。
-
好了,解决了。\(O(\sum |T|)\)。
-
P2414 阿狸的打字机
- 见树形 DP-欧拉环游序式。


