平衡树

二叉查找树（BST,binary search tree）

概述

• 二叉查找树是一种建立在一个数组（序列）上并用于对其的高效查找的二叉树。

• 满足以下条件的一棵树是二叉查找树：

  1. 空树是二叉查找树。

  2. 二叉查找树的任意一棵子树还是一个二叉查找树。

  3. 二叉查找树的每一个节点都对应着原数组的某个节点（并存储相应的值，相对于线段树只有叶节点才有真值）。

  4. 二叉查找树的根，左子树（如果不空），右子树（如果不空，下同）之间满足某种偏序关系，使得：

     • 对于严格二叉查找树，序相同的点必须唯一（多则合并）（完全偏序），左子树 \(<\) 根 \(<\) 右子树；

     • 对于不严格二叉查找树，允许有序相同的点（不完全偏序）。习惯上让左子树 \(\leqslant\) 根 \(<\) 右子树。请一定一定注意这导致的各种判等后该进左子树还是右子树的问题！！！

     • 准确地说，\(2,4\) 两条联立代表着二叉查找树的左子树的任意一个节点 \(<\) 根 \(<\) 右子树的任意一个节点。

操作

• 二叉查找树支持如下操作：

  1. 插入。直接在上面二分（二叉搜索树本身就是二分的），找到地方之后看情况是合并/插成新儿子。

  2. 查找（按 \(rank\) 查数或按数查 \(rank\)。这里定义 \(rank=\sum (v[i]<val)+1\)）。直接二分，找到或找不到返回。

  3. 找前驱（比它小的最大的）/后继（比它大的最小的）：树上二分。

     • 以查找后继和严格二叉查找树为例，每个节点判一下是否大于，大于则更新\(ret\)并进左子树查，小于等于则进右子树查。

  4. 删除某个数。

     • 先查找到，然后如果只有一个儿子/没有儿子，模仿线段树合并，删掉后直接连边。

     • 如果都有，说明该节点有右子树，从而其后继一定在其右子树中，且其后继一定没有左儿子（否则这个左儿子才是后继）。

     • 删掉后把后继提到当前点的位置，显然提出的后继一定大于左子树，而且小于右子树（因为它是右子树最小的）。

复杂度分析

• 朴素二叉查找树的时间复杂度没有保证：单次查找大体上是跑满一条链，但树高没有限制，只在随机数据下表现为近似 \(\log\) 级，可以构造单链卡到 \(O(n)\)。

平衡树概述

• 平衡树是通过旋转/分裂合并/暴力重构/...等方式限制深度以保证时间复杂度的二叉查找树的统称。

• 不同平衡树中有着不同的平衡定义，但大体上都是深度和子树大小的相对平均。

• 显而易见的是，同构的二叉查找树有很多种，所以我们可以给这棵树加上更严格的限制来选取其中有特殊性质的某一些，使得均摊复杂度稳定在 \(O(\log_2 n)\) 级别（注意，本质上还是能卡，不过至多卡成大常数罢了）。

• 因为平衡树的种类实在太多，所以我们无法收录所有，并且收录的也很可能只有介绍。

简单平衡树：treap

概述

• treap 是一种通过将 BST 和 heap 结合，通过旋转来限制 BST 的深度以保证时间复杂度的数据结构。

操作

• treap 支持旋转，插入，删除，查询，查前驱后继。

复杂度分析

• treap 的各种操作复杂度都在 \(O(\log_2 n)\) 级别。尽管常数不小，但在常数巨大的一众平衡树间，\(treap\) 以常数小和好写而著称。

实现原理：旋转。

• 注意，这不是 treap 独有的旋转。

• 旋转分为左旋和右旋。

• 我们定义 \(fa,ls[],rs[],LS[],RS[]\) 分别为父节点，某节点的左右子节点，某节点的左右子树（中的所有节点）。

• 左旋：将右儿子提升为父节点。

• 根据二叉搜索树的性质，我们有（所有符号都是旋转前的）：\(v[RS[fa]]<v[fa]<v[LS[rs[fa]]]<v[rs[fa]]<v[RS[rs[fa]]]\)。

• 所以现在原父节点做原右儿子的左儿子。原右儿子的原左子树怎么办？没关系，原父节点现在正好没有右儿子，连给它做右子树就好了。

• 

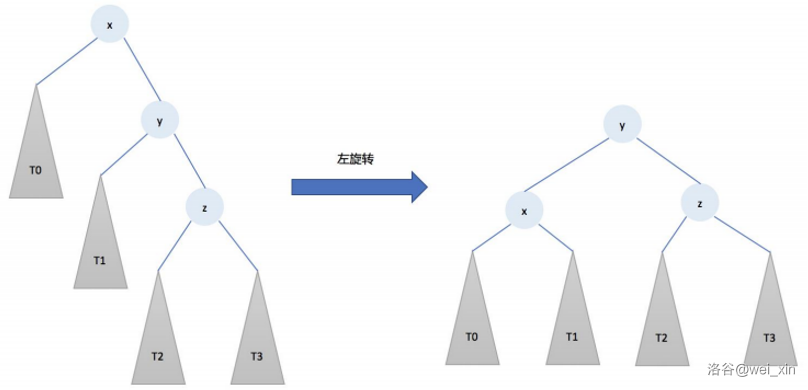
• 右旋：类比左旋，将左儿子提升为父节点，而原父节点成为原左儿子的右儿子，原左儿子的原右儿子连线到原父节点做左子树。

• 

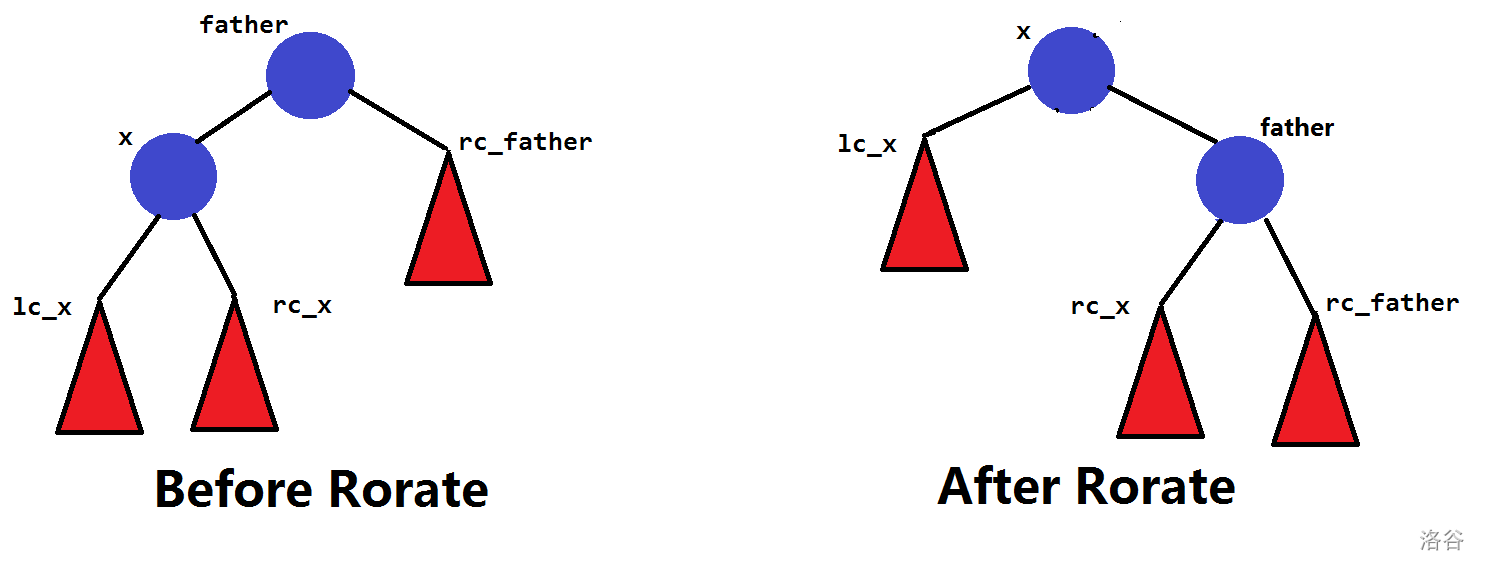
• 可以看到，旋转后的树仍然满足二叉查找树的性质。

• 但简单旋转未必能让整棵树更平衡：考虑一条链的情况，如果只自下而上进行一种旋转操作，那么始终是一条链（最多拐弯方向变了）。

• 一种解决方式是给旋转加上各种顺序。这是 splay 的思路。

• treap(tree+heap) 则是观察到了 BST 和 heap 的互补之处：前者不关心根，关心左右子树；后者关心根，不关心左右子树。所以如果我们能够将两者的性质结合起来，就能获得形态唯一确定的树！

• 但显而易见的也是，两者的性质是不可共存的。怎么办？

• 要素分离！我们给每个节点随机地赋一个 \(pri\)（priority），将这个值作为 heap 的偏序关系。

• 我们接下来讨论 treap 的各种操作，下面的一切讨论基于非严格二叉查找树，同值点不合并，左子树 \(\leqslant\) 根 \(<\) 右子树。

  • 插入：和普通二叉查找树一样。不同的是插完之后利用回溯过程把这个新插入的点旋转到满足堆性质的位置。

  • 删除：先找到，如果左右不全有同前，如果左右都有，模仿可并堆（虽然我也不知道这算啥可并堆但是这样是对的就成了）的做法，旋转它和在堆意义下较优先的儿子，然后继续删除它。

  • 查找/查前驱后继：没变。

  • 注意旋转相关的操作使用了非常见鬼的传参，详细逻辑见代码注释。

  • 复杂度保证：因为堆意义下的\(pri\)是随机生成的，所以我们可以认为我们是随机生成了一棵二叉树。期望意义下可以认为树高近似 \(\log_2 n\)。注意，rand() 未必那么靠谱，mt19937 才是正道的光。

示范代码

mt19937 _rand(time(0)^clock());
struct treap_weixin{
	int rt,tot;
	struct node{
		int v,sz;//the value of the point;the size of this subtree
		int pri;//priority.for heap
		int s[2];
	}a[maxn]; 
	void newnode(int &now,int val){now=++tot; a[now].v=val; a[now].sz=1; a[now].pri=_rand();}
	void pu(int now){a[now].sz=a[a[now].s[0]].sz+a[a[now].s[1]].sz+1;}
	void spin(int &now,bool to){//交换now和它的to儿子 
		int t=a[now].s[to]; a[now].s[to]=a[t].s[!to]; a[t].s[!to]=now;
		pu(now),pu(t); now=t;
	}
	void ins(int &now,int val){//插入 
		if(!now){newnode(now,val); return;}
		bool to=(val>a[now].v);//左子树<=，右子树> 
		ins(a[now].s[to],val);
		if(a[now].pri>a[a[now].s[to]].pri) spin(now,to);
		else pu(now);//否则上面做过了 
	}//这个操作非常妙。在我们下行的时候，我们的now代表考虑到哪个平衡树上节点，注意它虽然是传参的，但每一层都不一样（传下去的不是now，是son）；
	//在我们上行的时候，如果没有旋转那么now毫无意义（不和最下面那个父亲换就更不可能和祖先换）
	//如果有旋转，那么now一开始表示的是最下层节点，回跳一下处的now是回跳一下处的自己，然后它会和son spin一下，spin完了之后now会被改成son，而这层的now因为传参，其实就是回跳两下处的son。
    //所以spin先把边连好，再利用每层都不同但是实际上每层的now本质上都是a[?].son的传参来维护旋转的两个点和原父亲的父亲的关系。
	void del(int &now,int val){//删除 
		if(!now) return;//没有这个数
		if(a[now].v==val){
			if(!a[now].s[0] || !a[now].s[1]) {now=a[now].s[0]|a[now].s[1]; return;}//把我（我父亲的儿子）改成我儿子就好
			if(a[a[now].s[0]].pri<=a[a[now].s[1]].pri) spin(now,0),del(a[now].s[1],val);
			//这个操作也非常鬼。注意，操作之后的now已经被修改成了现在是父亲的原儿子
    		//所以现在是父亲的原儿子的另一侧儿子便是被换下去的准备删的点，详见旋转部分讲解
			else spin(now,1),del(a[now].s[0],val);
		}
		else{//这里已经不会有等于情况了 
			if(a[now].v>val) del(a[now].s[0],val);
			else del(a[now].s[1],val);
		}
		pu(now); return;
	}
	int srank(int now,int val){//求某数是第多少小 
		if(!now) return 1;
		if(a[now].v>=val) return srank(a[now].s[0],val);//这个判等非常妙，使得我们可以求一个不在平衡树里的数字的rank 
		else return a[a[now].s[0]].sz+1+srank(a[now].s[1],val);
	}
	int find(int now,int k){//求第k小数 
		if(a[a[now].s[0]].sz==k-1) return a[now].v;//注意是k-1 
		if(a[a[now].s[0]].sz>=k) return find(a[now].s[0],k);
		else return find(a[now].s[1],k-a[a[now].s[0]].sz-1);
	}
	int pre(int now,int val){
		if(!now) return -inf;
		if(a[now].v>=val) return pre(a[now].s[0],val);
		else return max(a[now].v,pre(a[now].s[1],val));
	}
	int nxt(int now,int val){
		if(!now) return inf;
		if(a[now].v<=val) return nxt(a[now].s[1],val);
		else return min(a[now].v,nxt(a[now].s[0],val));
	}
};

简单平衡树：fhq treap（无旋treap）

概述

• fhq treap 通过各种暴力的拆分和合并来相对较为随机地构造堆，从而限制二叉查找树的深度。

• fhq treap 的核心思路在于 heap。既然是 BST 和 heap 的结合，为什么不能考虑反客为主，用盘外招确保不管怎么乱搞都还是 BST ，使劲利用 heap 可拆并的性质？

操作

• fhq treap 支持拆分，合并（之所以不把它视为一个可合并数据结构，是因为合并就是它的数据结构所在，而非与数据结构本身相异的功能），以及 treap 支持的所有操作（旋转除外）。

复杂度分析

• fhq treap 的复杂度保证也是所有操作都是 \(O(\log_2 n)\)。

扩展

• fhq treap 是一种可持久化数据结构。

实现原理：分裂与合并。

• 分裂（split）：模仿主席树！考虑两种分裂：按数量或按值。

  • 建两个新根（注意这里我们只是需要一个地方来存根。一旦函数开始，原来的 \(rt\) 就失去了它的价值，也可以作为空容器使用）。

  • 两个新根同步往下走，每次，拆出的“左树”（第一棵树）尝试一下能不能把当前节点及其左子树一口吃掉（注意一下用 \(val\) 和用 \(num\) 的判定方法并不一样，前者靠 bst 的性质，后者靠 \(sz\)，前者在根处判，后者捆绑判）。

    • 如果可以，则用（现在还没有的）右子树去和“右树”瓜分当前节点右子树。

    • 如果不行，那么当前节点及其右子树归“右树”，然后“右树”（现在还没有的）左子树去和“左树”争。

    • 这个描述很形象，但不够严谨。观察代码我们可以看出，这里实际上的代表“左树”和“右树”的节点，一开始是根，后来是根的左右儿子。

    • 之所以“左树”要左儿子，“右树”要右儿子，这是为了让拆出的“左树”在 bst 序上严格小于“右树”。

    • 我们可以看到 fhq treap 对于破坏 bst 序的操作避之唯恐不及，这正是所谓的“用盘外招解决 bst，使劲用 heap性质乱搞”。

    • 注意，如果最后“没分到”，那么要把当前的子树根改为 \(0\)，以免拆分前的旧关系残留。

• 合并（merge）：必须保证第一棵树在 bst 序上时刻严格小于第二棵。

  • 按堆的性质比较合并。然后如果是“左树”作根，“右树”去右子树；如果是“右树”做根，“左树”去左子树（竭尽所能不干扰 bst 序！）。

• 插入：找到插入位置，左右拆开，\(newnode\) 充当一棵新树，从左往右 \(merge\) 过去。

• 删除：找到删除位置，左右拆开，将根为删除值的那棵的根抛弃，合并左右子树，然后从左到右 \(merge\)。

• 查询：没啥区别（这就 bst 序的本职工作，找不到位置的话其他操作都是白给）。

• 前驱/后继：找到位置，拆成两棵，前驱查左，一路向右；后继查右，一路向左。

• 区间翻转（注意，这个操作和上面所有操作都没啥关系）：

  • 拆成三棵（\(1\sim l-1,l\sim r,r+1\sim n\)），给中间那棵打一个翻转标记，然后从左到右 \(merge\)。

  • 以后再需要分裂或合并到这部分里面时下传标记（对就是像线段树）。

  • 注意，打过标记之后，每个值的位置就不可知了，相当于黑箱。

  • 一定想知道的话，只能暴力下传把标记推没，然后反手前序遍历。

  • 这个标记的实质是，时刻保证先序遍历下下标的正确性。换句话说，这时 bst 序对应的东西是下标！

  • 询问某个下标的值倒是可以暴力树上二分个数来找到对应的 \(node\)，如果预先存了 \(val\) 可以提出（这个 \(val\) 只是个捆绑值罢了，和 bst 以及 heap 其实都啥关系没有！）。但是询问某个值的位置根本不可行！

  • 想插入也只能按下标插入（拜托都是乱序数了好不好，按值插也不知道插到哪里）。

  • 删除同理，只能按下标。

  • 前后驱根本没变！这一部分可以，且应当，建一棵不带翻转操作的平衡树来维护！

示范代码

mt19937 _rand(time(0)^clock());
struct fhq_treap_weixin{
	int rt,tot;
    struct node{
        int v,sz;//the value of the point;the size of this subtree
        int pri;//priority.for heap
        bool lz; 
        int s[2];
    }a[maxn];
    void newnode(int &now,int val){now=++tot; a[now].v=val; a[now].sz=1; a[now].pri=_rand();}
    void pu(int now){a[now].sz=a[a[now].s[0]].sz+a[a[now].s[1]].sz+1;}
    void pd(int now){
    	swap(a[now].s[0],a[now].s[1]);
    	a[a[now].s[0]].lz^=1,a[a[now].s[1]].lz^=1;
    	a[now].lz=0;
	}
	void predfs(int now){
		if(a[now].lz) pd(now);
		if(a[now].s[0]) predfs(a[now].s[0]);
		wtk(a[now].v);
		if(a[now].s[1]) predfs(a[now].s[1]);
	}
    void splitv(int now,int val,int &x,int &y){//按value来拆，<=val的拆进x，>val的进y 
    	if(!now) {x=y=0; return;}//拆到树底了
    	if(a[now].v<=val) x=now,splitv(a[now].s[1],val,a[x].s[1],y);
    	else y=now,splitv(a[now].s[0],val,x,a[y].s[0]);
    	pu(now);//注意到了吧？只要这样我们就把所有点都整上了 
	}
	void splitn(int now,int k,int &x,int &y){//前k个拆进x 
		if(!now) {x=y=0; return;}
		if(a[now].lz) pd(now);
		if(a[a[now].s[0]].sz+1<=k) x=now,splitn(a[now].s[1],k-a[a[now].s[0]].sz-1,a[x].s[1],y);
		else y=now,splitn(a[now].s[0],k,x,a[y].s[0]);
		pu(now);
	}
	int merge(int now1,int now2){//为了保证我们只需要像合并堆一样simple和naive地合并它，我们得时刻确保他俩本身是具有bst序的：1<2 
		if(!now1 || !now2) return now1|now2;
		if(a[now1].lz) pd(now1); if(a[now2].lz) pd(now2);
		if(a[now1].pri<a[now2].pri) {a[now1].s[1]=merge(a[now1].s[1],now2); pu(now1); return now1;}//这种决定和哪一棵子树合并的操作正是基于bst序 
		else {a[now2].s[0]=merge(now1,a[now2].s[0]); pu(now2); return now2;}
	}
	void ins(int val){
		int x,nn; newnode(nn,val);
		splitv(rt,val,rt,x);
		rt=merge(merge(rt,nn),x);
	}
	void turn(int l,int r){
		int x,y;//放0的主要目的是避免整棵树都被拆到一边之后，另一边的根不为空导致误判。
		splitn(rt,l-1,rt,x);
		splitn(x,r-l+1,x,y);
		a[x].lz^=1;
		rt=merge(merge(rt,x),y);
	}
};

ARC153B Grid Rotations

• 题意略。容易发现每次置换中，行和列互相独立，行之间和列之间分别平等，于是用 fhq 分别维护两者的翻转情况，最后拼到一起就可以得到最后的置换结果。

简单平衡树：splay

简单平衡树：AVL 树

进阶平衡树：替罪羊树

高级平衡树：红黑树

• 这东西鬼知道啥时候我才学。放在这里主要是为了一个事情：

• STL 中的 \(set\) 和 \(multiset\) 的内部实现都是红黑树。

• 作为一种高级平衡树，它除了不能查第 \(k\) 大/小（这得怪写 STL 的人，不怪 RBT）外几乎完美无缺，唯一的弊病是作为 STL 非常依赖 \(\text{O2}\)。

广义平衡树：K-D Tree（K-Dimensions Tree）

• 待补完。