常数优化
数据类型
-
显而易见地,越小的型的运算越快。
-
大体来讲
long long的常数比int大一倍,但__int128的比long long大一倍不止(因为没有 128 位机,故__int128的实现是“不自然”的)。 -
short和char的表现特别差,不论什么环境。原因?它们在任何算术运算(哪怕是纯short/char环境)都会被强转成int。
条件语句
-
if/else,switch,?:的逻辑各不相同。 -
if/else语句中,如果if的内容一直对,那么就会很快。 -
?:中的:优先级比,高,故如果是?...,...:...,...那么左边没问题,但右边只会执行第一个逗号之前的,换言之,语义为?(...,...):(...) , ...,相当于?(...,...):(...); ...;。
中央寄存器
-
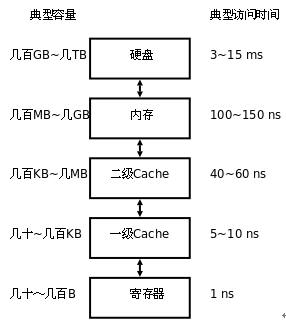
大体来讲,我们的程序使用的内存都是运行内存,即高速缓存。
-
但高速缓存是分级的。据 \(\text{P4604 [WC2017]挑战}\),一级 Cache 的大小大约为 \(256\) 个
int。 -
优先度越高的 Cache,空间越来越小,但访问越来越快。具体地,
内联函数
-
C++ 中的
inline关键字允许我们将函数设置为内联的。这一函数的范畴是广泛的,至少允许对operator,namespace甚至于结构体构造函数使用。 -
内联的本质是在调用函数时不进行实质的函数调用,而是将函数的代码复制到调用处执行其功能,省却了函数初始化(主要是开栈帧之类的)和退出的时间。
-
对于有复杂行为的函数,将其定义为内联会导致负优化,但实际上编译器会自动忽略
inline关键字,所以该关键字可以随便用。 -
特别地,有说法认为递归函数不应定义为内联,但在实际实践中递归函数加
inline仍然是正优化,虽然与非递归函数相比差了一些。 -
效果大约是常数 \(/2\)。
循环展开
-
NOI 系列比赛所使用的的评测机芯片是 i7 8700k@GHz3.7,该芯片为 \(12\) 线程。
-
但在实际的程序运行过程中,单个循环的计算任务只能分配给一个线程。
-
所以我们可以考虑将最后一层的循环展开,这里举 Floyd 算法为例:
il void floyd(){
void work(){
For(k,1,n)
For(i,1,n){
ri int j=1;
for(;j+11<=n;j+=12){
if(dis[i][j]>dis[i][k]+dis[k][j])
dis[i][j]=dis[i][k]+dis[k][j];
if(dis[i][j+1]>dis[i][k]+dis[k][j+1])
dis[i][j+1]=dis[i][k]+dis[k][j+1];
if(dis[i][j+2]>dis[i][k]+dis[k][j+2])
dis[i][j+2]=dis[i][k]+dis[k][j+2];
if(dis[i][j+3]>dis[i][k]+dis[k][j+3])
dis[i][j+3]=dis[i][k]+dis[k][j+3];
if(dis[i][j+4]>dis[i][k]+dis[k][j+4])
dis[i][j+4]=dis[i][k]+dis[k][j+4];
if(dis[i][j+5]>dis[i][k]+dis[k][j+5])
dis[i][j+5]=dis[i][k]+dis[k][j+5];
if(dis[i][j+6]>dis[i][k]+dis[k][j+6])
dis[i][j+6]=dis[i][k]+dis[k][j+6];
if(dis[i][j+7]>dis[i][k]+dis[k][j+7])
dis[i][j+7]=dis[i][k]+dis[k][j+7];
if(dis[i][j+8]>dis[i][k]+dis[k][j+8])
dis[i][j+8]=dis[i][k]+dis[k][j+8];
if(dis[i][j+9]>dis[i][k]+dis[k][j+9])
dis[i][j+9]=dis[i][k]+dis[k][j+9];
if(dis[i][j+10]>dis[i][k]+dis[k][j+10])
dis[i][j+10]=dis[i][k]+dis[k][j+10];
if(dis[i][j+11]>dis[i][k]+dis[k][j+11])
dis[i][j+11]=dis[i][k]+dis[k][j+11];
}
for(;j<=n;++j)
if(dis[i][j]>dis[i][k]+dis[k][j])
dis[i][j]=dis[i][k]+dis[k][j];
}
}
-
实测可以在 \(2\times 10^3\) 的数据下跑过 \(90\%\) 的点。这就是因为这一操作使得 \(12\) 个线程同时运行,但需要注意的是并没有复杂度 \(\dfrac{O}{12}\) 的神奇效果,在已有的实验中即使展开到 \(12\) 个,也只能使运行时间 \(/2\sim /3\).
-
类似地,自增(
i++,++i)等操作也不利于多线程的充分利用,if的表现不如没有default的switch(上面的扫尾工作就可以用switch解决),以及如求和时开 \(12\) 个sum的效果就要比开一个更好,开sum1,sum2,...比开sum[12]要好。
访问连续性
-
C++ 中的数组本质上是一个数组头地址+平移下标个位置来找对应的元素,显而易见地,这一平移越短(可以从上次的平移结果继续),访问越快。
-
并且,高速缓存在运行中并不是“用到哪个取哪个”,而是将包含目标下标的一段全部取过来。所以这可能可以省去去内存中找的时间。
-
从而多维数组的定义顺序是有一定意义的。举一个简单的例子,在倍增求 \(lca\) 算法中我们会用到一个倍增的
fa数组,符合常人想法的应当是fa[maxn][log],表示从 \(i\) 出发走 \(2^j\) 步到哪里。 -
但如果我们仔细考察的话,会发现如果把这个数组倒过来变成
fa[log][maxn]然后跑一遍 dfs 处理出fa[0][i]之后用For来形如 dp 地从本层推下一层,会有好得多的下标连续性(因为都是在fa[step]这个数组里。多维数组的实际存储方式,以这个为例,是log个maxn的数组首尾相接)。 -
类似地,考察矩阵乘法中的三重循环:
mat operator*(mat A,mat B){
mat ret=mat(A.n,B.m);
for(int i=1;i<=ret.n;++i)
for(int j=1;j<=ret.m;++j)
for(int k=1;k<=A.m;++k)
ret.v[i][j]=(ret.v[i][j]+A.v[i][k]*B.v[k][j])%mod;
return ret;
}
- 在这种写法中,
ret.v[i][j]和A.v[i][k]的下标是连续访问的,但B.v[k][j]显然不是,所以我们可以改变循环顺序(容易证明,改变后的枚举总情况是和改变前全同的),得到如下的写法:
mat operator*(mat A,mat B){
mat ret=mat(A.n,B.m);
for(int i=1;i<=ret.n;++i)
for(int k=1;k<=A.m;++k)
for(int j=1;j<=ret.m;++j)
ret.v[i][j]=(ret.v[i][j]+A.v[i][k]*B.v[k][j])%mod;
return ret;
}
-
本写法具备完美的下标连续性,可以优化大约一半的常数。
-
另,之所以较小的数据类型运算较快,不仅是运算的原因,也有访问的原因(更紧凑)。
-
注意,有可能滚维比展开快:乍一看滚维是时间换空间的手法,但事实上在三级乃至更低级的 cache 意义下,可能卡进去了,故反而快了。
STL
-
queue和stack比vector快(在功能相同的时候),list和他们差不多,但实际上哪怕开了O2也还是不如手写。不过,在需要循环队列的时候(说实话用到这个的情况很少,除非卡空间,否则用到这个基本就代表着 T 了),手写的没有 STL 快。 -
不要用
deque!!!也不要用deque来实现priority_queue(指声明里面的第二项,容器)!!!作为对比,上面提到的那几个 STL 基本都是能用的。 -
bitset在不使用位运算的时候似乎是负优化,尽管因为“窄”比较好卡 cache,但bitset的访问是“不自然”的。在使用位运算的时候,不如手动压位(实测__int128的表现至少比bitset好一倍,即时间少一半)。


