解怪题选择性报告

6.5

P1127 词链

• 题意：给定字符串，前一个尾字母=后一个首字母的可以相连（不重叠并且在中间插一个 .），求字典序最小的相连方式,使得每个字符串恰出现一次。无解输出无解。

• 数据范围：$n⩽1000,len⩽20$。

• 首先TSP下显然不可解。

• 注意到一点，这里是可以贪的：每步选当前字典序最小的字符串，同长意义下显然最棒。

• 对于诸如 aca-acaba 两个相连的情况，本来是会出 bug 的，但因为插入的 . 的字典序远小于 a（. 为 $46$，a 为 $97$），所以无论何时想办法接一个短的也就是小的是一定划算的。这就很妙。

• 转换思路，把首尾字母当成点，字符串做边。于是就是一个欧拉路径问题。

6.13

P4551 最长异或路径

• 题意：求一棵边有权的树上的最长路径异或长度，异或长度指 $le{n}_1\oplus le{n}_2\oplus ...$。

• 数据范围：$n⩽1e5,w<2^{31}$。

• 观察异或运算的性质：$ifa⨁b=c,c⨁a=b$。

• 证明：$x⨁a⨁a=x$，所以上式显然

• dfs 一遍，求出每个点到 $1$ 的路径异或长度。

• 然后枚举一个点，按位贪心地求最大路径异或长度。别忘了$1$的要在上一步算好。$O(n\log w)$。

• 主要是异或的性质比较...有趣。差点想到了，但只想到前缀异或和来着。

7.27

P4934 礼物

• 题意：求一种方案将 $a_{1\dots n}$ 分入 $m$ 个集合使得 $\nexists a_i\mathrm{\&}{a}_j=min(a_i,a_j)\mathrm{\&}i,j\in A$。输出最小的 $m$ 及方案。

• 数据范围：$0⩽a_i⩽2^{20},n⩽{10}^6$。

• 容易看出其实就是不允许包含。

• 从而（鬼的从而），想到建图。每个数字都向它在二进制上多一位为 $1$ 的每个数字连边，有向边。

• 从而（这个还算可以），能够看出同一条链上的点不可以共集。进一步地，我们有：$m=maxlen$，其中 $len$ 为链长。

• 则容易想到拓扑排序，对每个点维护一个 $dep$。需要注意的是虚点（不在 $a$ 中的点）对 $dep$ 无贡献，仅仅是中转。

• $O(2^k\times k)$。

9.7

某 T4 通信网络

• 题意：

  • 给一棵的带点权树，所有有序点对 $(u,v)$ 会对其路径上（包括 $u,v$）所有 $w_z+P⩾max(w_u,w_v)$ 的点造成 $1$ 的负荷。

  • 求最大的 $P$，使得最大负荷 $⩽K$。

• 数据范围；$n⩽3\times {10}^5,1⩽w⩽{10}^6$。

• 显然答案单调，所以二分。但是这个的 check 复杂度似乎很高。怎么办？

• 首先可以暴力模拟，用类似点分树的换根 dfs 方式来做（树剖模拟炸飞，$O(n^2{\log }^{3}n)$）。$O(n^2\log n)$。

• 注意到每次询问的其实是某点各方向子树的情况，更进一步地询问的其实是子树内 $w⩽w_x+P$ 的点数。

• 容易想到线段树，对每个点分别做二分，子树内的话...dfs 序拉下来做一下主席树差分就好了。$O(n{\log }^{2}n)$。

• 很遗憾这个东西过不了，因为常数很大。什么，zkw？那个可能不行，可能得用猫树，但我不会，所以想点别的办法。

• 我会乱搞！回到一开始直接二分 $P$ 然后对每个点 check 一下的方式。

• 从二分的性质出发，如果有一个 check 不成立，答案一定小于本次二分的结果；更进一步地，成立的那些点以后一定仍然成立。

• 于是想到在总体的 check 不成立时抛弃掉成立的点做下一轮。有很好的常数优化效果，应该能过。

• 正解：把二分转成树上二分。在儿子数量 $+1$ 棵（这一棵是前置树和后置树的结合）差分树上同时跑，从而每个点只需要大常数 $O(\log )$ 的复杂度就能过。

• 什么，树太多？可以证明，只有 $2n+n-1$ 棵差分树，前者为外置树，后者为子树即度数。

• 另外这个也可以剪枝，如果某个点的答案已经 $⩾ans$，那么直接 return。

9.13

某 T1 猜数字游戏

• 题意：在 $5\times 4$ 的方格纸内写数字（形态略）。现在给了一张写了很多个数字（重叠覆写）的方格纸，已知每个格子被写的次数，求字典序最小的可行解，即字典序最小的每个数字被写的次数。特别地，答案按 $1234567890$ 顺序输出，字典序也是相较这个而言的。

• 数据范围：$an{s}_i⩽9$，注意可能存在更大但是字典序更小的解，请舍弃它们。

• 乍一看就是个暴搜题目对吧，这种状态过于复杂的东西（斗地主、三国杀、华容道、(这个是 DP！)...）一看就很不可设计状态。

• 于是搜了，T 了。40pts。

• 想办法加速搜索。那还是要从题目本身的性质出发。

• 把那个方格纸自己手推一下，看一下每个格子受哪些数字影响。

• 然后想到一个强剪枝，就是重规划枚举顺序，从 $1234567890$ 改成譬如 $8062594371$，当然这样搜到的第一个解不一定是最优解，得更新一下。

• 为什么这样更快？因为某些点（譬如 $(3,0)$）只受少数数字影响，从而可以边搜边剪枝：如果过了那几个之后，对应位置还不是 $0$，那么剪掉。

• 不错的思路。回过头考虑一下复杂度，${10}^{10}$。嗯？

• 可以折半搜索！上多模数哈希记录已经搞掉的/还需要搞的矩阵，然后匹配一下。复杂度...跑满也就 ${10}^5\times 20\times hash$，即使把哈希复杂度视为 $\log$ 也能过。

• 但是其实有一个更妙的解法。看到那个影响矩阵具有一定的方程组性质（当然是不定的），考虑观察法，发现有些方程之间只差了一个数字的存在与否。

• 直接手动消元，操作一下发现 $012347$ 都是定死的，其他随便搜一下也能过。

9.23

P1736 创意吃鱼法

• 题意：给定 $n\times m$ 的 $01$ 矩阵，求其中最大的方阵，使得该方阵一条对角线上的数字都为 $1$，其他地方都为 $0$。输出该方阵边长即可。

• 数据范围：$n,m⩽2.5\times {10}^3$。

• 我一看这个数据范围，就啪的一下站起来了，说我要做 $n^2\log n$，很快啊。

• 首先我们二分答案，显然答案满足单调性，考虑怎么 check，我们需要一个 $O(n^2)$ 的 check。

• 回想理想的正方形等奇怪的矩阵题目，我们想到扫描线。

• 每次二分的答案相当于矩阵的边长，考虑 $n^2$ 地枚举它的左上角，递推地求出当前矩阵内 $1$ 的个数，显然每个点只会计入/弹出 $1$ 次。

• 当然这个写法要复杂得多，不仅要横向递推，还要纵向递推。

  • 具体来讲，先暴力出左上角在第 $1$ 行的所有矩阵的 $cnt$，显然复杂度为 $O(n\times len)$，$len$ 为矩阵边长。

  • 同理暴力出左上角在第 $1$ 列的。

  • 然后，从 $cn{t}_{2,1}$ 到 $cn{t}_{2,2}$ 的转移，并不需要再去处理 $2\times len$ 个点，而可以基于 $cn{t}_{1,1}$ 到 $cn{t}_{1,2}$ 的转移：$cn{t}_{2,2}-cn{t}_{2,1}=cn{t}_{1,2}-cn{t}_{1,1}+a_{1,1}-a_{1,1+len}-a_{1+len,1}+a_{1+len,1+len}$。故 $O(n^2)$ 可做。

  • 即我们可以 $O(n^2)$ 地求任意给定长宽子矩阵的满足差分性的信息。作为对比，理想的正方形那道题是 $O(n\times m\times len)$ 的，不过它的信息不可差分就是了。

• 可这没完，即使我们知道对应矩阵内恰有 $len$ 个 $1$，也不保证 $1$ 恰构成一条对角线。怎么 check？

• 考虑另外维护一个递推数组（和二分的 $now$ 无关）$m{x}_{0/1,x,y}$，表示以 $x,y$ 为左上起点/右上起点的极长对角线长度。

• 这个转移显然是可以做到 $O(n^2)$ 的，因为是 $1$ 的点在 $m{x}_0,m{x}_1$ 中都只会被考虑 $1$ 次（扩展），不是 $1$ 的点被考虑就意味着 $m{x}_{which,i,j}$ 的扩展尝试结束了，这样的结束也最多有 $n^2$ 次，得证。

• 但是这个写法恶心死了。这只是一道蓝题啊。看了题解之后发现我被切了...

• 觉不觉得最后那个东西很 DP？觉得？那它和正解差什么？哦，不保证矩阵内 $1$ 的个数正确。

• 考虑重定义。这里为了方便我们还把起点改为了终点，因为转移顺序是从上到下的（反过来的话，就是起点好转移）：

  • 状态设计：$d{p}_{0/1,i,j}$ 表示以 $i,j$ 为左/右下角的极大合法方阵边长。

  • 初始化：$d{p}_{0/1,i,j}=[a_{i,j}=1]$。

  • 状态转移方程（以 $d{p}_0$ 为例）：$d{p}_{0,i,j}=\{\begin{array}{l}{a}_{i,j}=1min(d{p}_{0,i-1,j+1},min(u{p}_{i-1,j},ri{g}_{i,j+1}))+1\\ a_{i_j}=00\end{array}$。

  • 其中 $up$ 的定义如下，$lef$ 和 $rig$ 可以参照：$u{p}_{i,j}=\{\begin{array}{l}{a}_{i,j}=0u{p}_{i-1,j}+1\\ a_{i,j}=10\end{array}$。

  • 用自然语言说大概就是向上考虑这一列的最大合法长度。

• 显然这个预处理可以做到 $O(n^2)$，DP 本身也是 $O(n^2)$，结束了。而且比那个做法好写 $10$ 倍甚至 $9$ 倍啊！！！

• 所以说，不要看到二维平面就放弃 DP。

9.26

P3978 [TJOI2015] 概率论

• 题意：求 $n$ 个点的二叉树的期望叶子个数。这里的期望是所有不同形态的叶子数之和除以总形态数，区分左右儿子。

• 数据范围：$n⩽{10}^9$。

• 假结论天堂......

• 不妨记 $f_i$ 为 $i$ 个节点的二叉树形态数，$g_i$ 为这些形态的叶子数量和。

• 结论 $1$：$f_i=Ca{t}_i$。

  • 暴力枚举左子树的节点数量，有 $f_i=\sum _{l=0}^{i-1}{f}_l\times f_{i-l-1}$。其中 $f_0=1$。

  • 这就是卡特兰数的递推式。

• 结论 $2$：$g_i=i\times f_{i-1}$。

  • 不妨将 $i$ 个点的二叉树上的叶子，单儿子节点，双儿子节点的数量分别记为 $a,b,c$。

  • 不那么显然地，有 $a+b-1=i-a$。

    • 考虑所有节点的父亲，除根外所有节点都有父亲，故名义父亲数为 $a+b+c-1$。

    • 鉴于 $c$ 类点在名义父亲数中出现两次，$-c$ 得实际父亲数为 $a+b-1$。

    • 显然实际父亲数就是 $i-a$。

  • 化式子容易得到 $2a+b=i+1$，即 $i$ 个节点的二叉树有 $i+1$ 个地方可以挂新节点。

  • 换言之，从 $i-1$ 推到 $i$，每种树扩展出了 $i$ 种形态的树。

  • 考虑 $f_i$ 中的每一种树，考虑它们的每个叶节点。显然，删去其中某一个之后，它就变成了 $f_{i-1}$ 中的一个；如果我们知道有多少种删法，也就知道了 $g_i$。

  • 而 $f_{i-1}$ 中的每一种扩展出了 $i$ 种，也即 $i$ 种删法的结果。

  • 故得证。

10.10

PJudge NOIP2 T3 图同构

• 题意：

  • 给出两张相同的图 $A,B$。每个点都是红黑二色之一，点权为 $a_i$，这里的颜色和点权可能在 $A,B$ 中不同。

  • 你可以执行以下操作任意次：

    1. 选择一张图和相邻的两个点 $u,v$。

    2. 交换 $a_u$ 和 $a_v$。

    3. 如果 $u$ 和 $v$ 同色，则将他们同时反色，否则颜色保持不变。

  • 问两张图能否变得相同，即所有点的颜色和点权对应相同。

• 数据范围：

  • $T⩽3\times {10}^4$。

  • $\sum n,\sum m⩽{10}^6$。

• 这道题是实在的妙妙题...首先我们对题目中的操作做一个转化：

  1. 选择一张图和相邻的两个点 $u,v$。

  2. 将 $u,v$ 同时反色。

  3. 交换 $u,v$ 的颜色和点权。

• 容易发现这是等价变换。这一变换的主要意义在于，对于每个二元组 $c,a$，它的 $c$ 的最终结果只受交换次数的奇偶性的影响。

• 接下来我们对每个连通块分类讨论：

  • 该连通块为二分图：

    • 此时交换次数的奇偶性等价于起始点和结束点所在的部。

    • 从而容易发现，一个点要么是左部红点右部黑点，要么是左部黑点右部红点，相当于两个剩余系。

    • 则首先两图中两剩余系大小需对应相等，更进一步地，对每种点权都要满足这个条件，这是必要的。接下来构造证明这是充分的：

    • 当只有 $1$ 个点，显然可行。注意此时并没有什么“部”。

    • 设 $n-1$ 个点可行。

      • 随便拉一个对应连通块的生成树，任取一个叶子在 $B$ 中的点权，找到其在 $A$ 中的同余对应点，把对应点一路换过来。

      • 于是问题化归为 $n-1$ 规模的问题，done。

  • 该连通块不为二分图：此时一定有奇环。奇环是个好东西啊！

    • 一个二元组 $(c,a)$ 在经过一个奇环（即至少经过其上一条边）之后的颜色是任意的，证明平凡：有两条路可以走到下奇环的点，一条为奇长度，一条为偶长度。

    • 故显然非奇环点可以任意换色，大不了上去走一圈。

    • 则在上述转化完成后，问题归约为令奇环合法。在奇环上我们可以用如下的操作交换相邻两点的颜色：令 $u$ 绕远路和 $v$ 换，再把 $v$ 绕远路走到 $u$，可以证明两者走的长度都为偶，因为两者之间为奇。

    • 但注意到颜色无法任意，颜色分配任意。考虑到每次操作是令两个点反色，发现黑点和红点的奇偶性是不变的。则只要奇偶性对应，就一定可以交换到奇环上色合法。

    • 最后注意还要有点权的对应。

• 总复杂度 $O(\sum (n+m)\alpha )$，并查集成时间大头了。

10.20

某 T2 DS

• 题意：单点修改，区间取模，区间求最大。

• 数据范围：$n,m⩽{10}^5,a⩽{10}^9$。

• 要敢写...我们这里假设区间取模不占用操作次数嗷。

• 考察 Euclid 算法，它的复杂度为什么是对的？

  • $a⩾b\to amodb⩽a/2$。

• 那我们考虑用 sgt 维护一个区间 $mx$，每次取模对于 $mx⩾v$ 的一边暴力递归。

  • 每个 $⩾v$ 的单点会拉出一条单链，这个单链最多拉 ${\log }_{2}a$ 次。

  • 则每次单点修改会导致 $\log n\log a$ 的复杂度，总复杂度 $O(n\log n\log a)$。

12.5

ABC280F Pay or Receive

• 题意略。

• 注意到这里正环和负环是等价的(大不了换个方向来转圈)，于是如果有环，只能是零环。

• 故先判连通，判完连通之后，在每个连通块内 bfs 一下。

• 随便选一个起点 $s$，给所有点赋一个距离 $dis$。

• 如果某个点有两种不同的 $dis$，既然来源不同显然构环，不同代表着不是零环，于是整个连通块寄掉。

• 否则，答案等于终点的 "$dis$" 减去起点的 "$dis$"，因为此时路径唯一（可以认为零环不具有效力，于是不存在），故距离确定。

• $O(n\alpha (n))$。

AGC059A My Last ABC Problem

• 题意略。

• 孤立考虑我们要修改的串，我们可以认为其是环状即首尾相接的，我们可以修改任意一段。

• 显然这等价于修改某一段或同时修改前后缀，前者是操作本身，后者等价于对中间那一段做相反的操作（把置换反过来）。

• 不妨设有 $k$ 个分界点，即左右字符不同的地方。容易感觉到，一次操作至少消去一个分界点，至多消去两个。换言之，答案下界为 $\lceil {\displaystyle \frac{k}{2}}\rceil$。

• 下面证明一定能取到。

  • 对于 $k⩾4$：每次取相同的两个分界。

    • 这里 AC 和 CA 被认为是相同的，以此类推。

    • 譬如 AC......AC，那么操作 C......A 这一段。容易将之变成 AA......CC。

    • 其他情况显然有类同的操作。这样我们至少可以把 $k$ 消到 $k^{\prime }⩽3$，并花费 ${\displaystyle \frac{k-k^{\prime }}{2}}$。

    • 不用在意被包含的那一段发生了什么。这里我们相当于预先把相同字符的连续段缩成一个字符，于是中间一定全是分界，不管怎么翻转都相当于一个长度更小的子问题。

  • 对于 $k⩽3$：构造已在样例中给出。

• 故线段树维护之即可。$O(n\log n)$。

• 感觉没有完全懂。为什么首尾相接那里也算分界点？

12.6

P1419 寻找段落

• 题意略。典中典之被红/橙/黄/绿爆切...

• 首先不考虑 $len\in [S,T]$ 这个一看就很刻意的限制，我们考虑来做一个无限制情况的。

• 发现扫描线之类的遍历所有区间的想法都不太可做，对齐了新加的点长度就不齐，长度齐了 $delta$ 又是分别的，很烦。

• 故考虑二分答案 $ave$，对于所有的合法区间 $[l,r]$，有 ${\displaystyle \frac{su{m}_{l\sim r}}{r-l+1}}⩾k$。

• 化式子，变成 $su{m}_{l\sim r}⩾k(r-l+1)$。发现式右只和长度相关，于是考虑暴力枚举区间长度来 check。

• 那么问题变成对于 $len=S\sim T$ 的，求对应长度区间的区间和最大值。很遗憾我不会，故我们考虑进一步简化问题，即令 $b_i=a_i-k$，然后求 $su{m}_r-su{m}_{l-1}⩾0$。

• 唔...那么这是个区间最小值问题。大概可以用 multiset 或者 sgt 做到 $O(n{\log }^2)$，${10}^5$ 好像能过了，但我们考虑其实际转移式（这显然像个 1D1D DP），发现其显然可以单调队列优化。

• 遂得解。

• 若没有 $[S,T]$ 的限制，还有一种更妙的做法：把前缀和视为二维平面上的点 $(i,su{m}_i)$，发现问题变成求最大斜率。

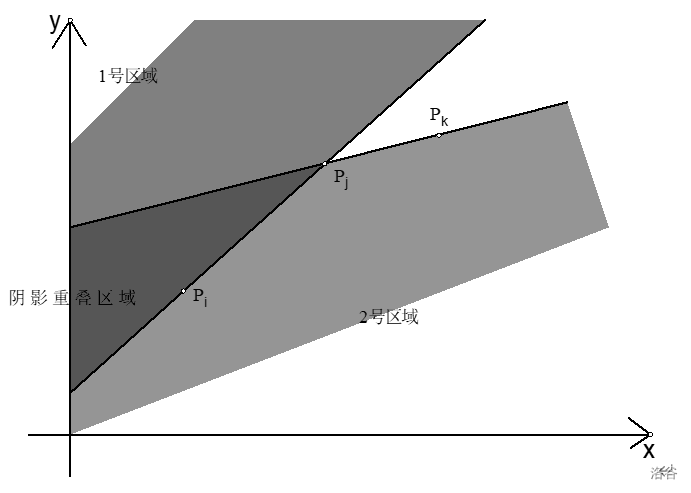
• 斜率的问题往往绕不过凸包。让我们来画一张图看一看（图源《浅谈数形结合思想在信息学竞赛中的应用》，周源）（原论文中限制为 $[S,+\mathrm{\infty })$，但我没看懂证明）：

• 

• 如图，图中 $P_i,P_j,P_k$ 分别是 $(i,su{m}_i),(j,su{m}_j),(k,su{m}_k)$ 三个点。

• 不妨假设将要计算 $P_{now}(now>k)$ 和它们的斜率，若 $P_{now}$ 和 $P_j$ 的连线有贡献，则必有 $K_{P_j{P}_{now}}>K_{P_i{P}_j}\mathrm{\&}{K}_{P_j{P}_{now}}>K_{P_j{P}_k}$。

• 两者分别对应图中 $1$ 号和 $2$ 号区域。显然，两者都满足则应位于重叠区域中，但这与 $now>k$ 矛盾，故上凸点无意义。

• 于是我们知道这是一个下凸壳。求和下凸壳上点连线的最大斜率，显然是切线。更进一步地，和下凸壳上点连线的斜率，一定构成一个自变量为下凸壳上点的编号的单峰函数！

• 于是从左向右暴力枚举凸壳中还剩的点，如果后者的连线斜率大于前者则将前者删除，直到找到切线。$O(n)$。

• 为什么可以删除：感性理解，容易发现更靠前的点对应的切线斜率一定小于当前的切线。

• 23.1.11 upd：容易看出这是一个限制为必须连续和数量在 $[S,T]$ 之间的分数规划问题，显然，二分是自然的。

P7073 [CSP-J2020] 表达式

• 题意略。

• 容易建出表达式树，然后我们做 DDP。

• 注意到结果为 $0$ 或 $1$，则任何一个有意义的数字被改变都恰导致结果改变。所谓一个数字有意义，指的是它到根的路径上没有被 $\mathrm{\&}0$ 或者 $\mid 1$。

• 直接暴力打标记，dfs 一遍推下去，然后结束，$O(n+Q)$。

P5582 【SWTR-01】Escape

• 题意略。妙妙数学题！

• 首先我们知道一件事，如果在一条链上，可以向前走，也可以向后走，可用步长为 $s_1,s_2,\dots ,s_n$，则最小坐标变化量为 $g=gcd(s_1,s_2,\dots ,s_n)$。证明较为显然，因为能走的长度无非是 $\sum _{i=1}^n{k}_i{s}_i$，而这本质是多元裴蜀定理的充分性方面。

• 但这里是同余系...首先容易看出的是，$(g,n)>1$ 时还是不行，由裴蜀定理易得。事实上，我们有结论：当且仅当 $(g,n)=1$，有解，且恰好 $n$ 次即可遍历 $0\sim n-1$。

• 证明如下：

  • 首先我们考虑 $g_1=s_1$，若 $(g_1,n)=1$ 则显然可以 $n$ 次遍历所有剩余系。

  • 否则，问题变成遍历 $mod(g_1,n)$ 意义下的剩余系：只要我们能以 $g_1$ 次遍历 $0\sim g_1-1$，那么可以先不断走 $g_1$ 直到走完 $\equiv 0(\mathrm{mod}{g}_1)$ 的点，然后走到另一个剩余系上，如此反复。

  • 为什么是 $(g_1,n)$：由裴蜀定理易得，最短步长为 $(g_1,n)$。

  • 显然，问题是不断递归的，只要 $gcd(s_1,s_2,\dots ,n)=1$，那么上述构造方案就存在。

• 妙啊...这种归纳，真的很妙。复杂度 $O(\sum _{i=1}^T{n}_i\log )$。

23.2.9

P1007 独木桥

• 题意略。

• 注意到两人都折返相当于两人互相穿过，毕竟人是本质相同的，故变成简单算数题。

2.13

[AGC017B] Moderate Differences

• 题意略。

• 考虑枚举有多少个是加，于是可以视为先加若干 $C$，再减若干 $D$，之后可以将这 $n-1$ 个数调大 $[0,D-C]$ 即可行范围为 $res+[0,(D-C)\ast (n-1)]$。我好傻...复杂度 $O(n)$。

2.18

[AGC017C] Snuke and Spells

• 题意略。

• 仔细一想发现这东西挺典的，大概就是颜色为 $1\sim x$ 的必须恰好有 $x$ 个，且必须有颜色恰为 $x$ 的，这个条件递归一下就是对的。

• 如果我们按颜色排序，就是颜色小于等于下标（数量），当然不能一次走一步，得一次走一种颜色。对于不合法的部分，多的余出来，少的欠着，其实就是和需要的量的差的绝对值求和除二即为答案。

• 然而事实上这玩意不支持带修，因为它没有结合律，你不管线段树还是分块都是错的...看了粉兔题解之后很显然，即将每个阶梯具现化出来，从 $c$ 到 $c-cn{t}_c+1$ 这一段是它所覆盖的，那么覆盖应当是唯一的，维护空的地方（的数量）就好，修改显然 $O(1)$，总复杂度 $O(n)$，典。

2.20

AT_agc012_d [AGC012D] Colorful Balls

• 题意略。

• 手推可以证明对长为三的链满足传递性（可以交换成全排列中的任意一个），于是归纳得到可交换性满足传递性。

• 故问题变成怎么优化建图。首先把每个色内前缀可交换（即可以与本色最小值交换）的一段直接优化建图成一个虚点（不一定真的要实现出来），然后考察全局最小值，和它不同色的如果不能和它连那么一定孤立，接着考察不是这个颜色的全局次小值，它的作用是和刚才那个占着的色连一下，因为连的都是前缀段所以我们可以直接标这个前缀段的长度（容易发现只有一个有意义的，即跨色的连通块），完了。

• 结束战斗，组合数之即可。$O(n)$，哦要排序，那可能是 $O(n\log )$。