排列组合与计数基础
排列组合
定义
排列数
-
\(n\) 个中选 \(m\) 个,考虑顺序。
-
\(A_n^m=P_n^m\) 。特别地, \(A_n^n\) 可以记为 \(A_n\) (全排列)。
-
从定义来求。
组合数:
-
\(n\) 个中选 \(m\) 个,不考虑顺序。
-
\(C_n^m=C(n,m)=\binom{n}{m}\)。
-
可以借助 \(A\),即先依次选出所需数量,然后除以内部排列数。
性质
排列数
-
错位排列
-
\(1\sim n\) 的错位排列是任意排列 \(a\) 使得 \(\nexists\ a_i=i\)。
-
如何计数?显然可以容斥但是也显然不可接受,考虑一种递推做法。
-
记 \(D_i\) 为 \(1\sim i\) 的错位排列数,对于 \(D_{i+1}\),容易看出,我们有:
-
\(D_{i+1}=D_i\times i+D_{i-1}\times i\)。
-
证明如下:
-
考虑新增的一个数往哪里放。
-
如果其原本就是一个完整的错排,那么我们可以将 \(i+1\) 与任意一个数交换。
-
如果其本身不是一个完整的错排,那么必然只存在一个 \(j\ s.t.\ a_j=j\),否则不可能在只处理新增的 \(i+1\) 的前提下将之化为一个 \(i+1\) 的错排。
-
从而其“对排处”有 \(i\) 种选择,综上,证毕。
-
-
-
鉴于组合有着极为优异的递推性,我们往往把排列问题化归成组合-阶乘问题。
组合数,杨辉三角与二项式定理
-
-
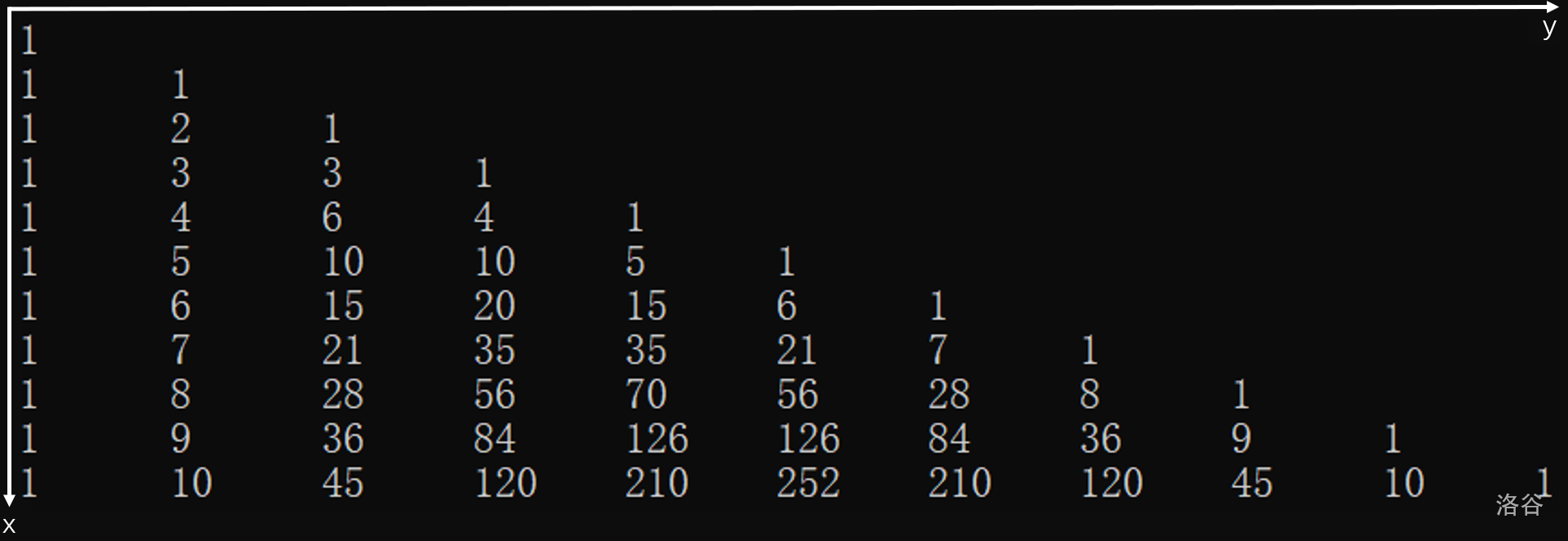
我们先来看一张杨辉三角。为了符合信竞的习惯,坐标轴已经做过了调整,左上角的第一个为 \(C(0,0)\)。
-
我们知道,杨辉三角的实质是组合数,其具有如下的性质:\((i,j)=(i-1,j-1)+(i-1,j)\)。
-
这实质上可以通过 dp 得到。考虑我们已经有了 \(\binom{i}{x}\),如何求 \(\binom{i+1}{j}\)?
-
分两种情况讨论:
-
选第 \(i+1\) 个数,则方案数相当于在前 \(i\) 个数中选 \(j-1\) 个数的方案数,即 \(\binom{i}{j-1}\)。
-
不选第 \(i+1\) 个数,则方案数相当于在前 \(i\) 个数中选 \(j\) 个数的方案数。
-
综上,我们有 \(\binom{i}{j}=binom{i-1}{j-1}+\binom{i-1}{j}\)。
-
-
利用这一性质,我们可以进行如下的简单求和:
-
求对角线和(杨辉三角的对角线定义为平行于斜边的线),即求 \(\sum\limits_{k=0}^l \binom{i+k}{j+k}\)。
-
考虑配凑一个。
-
配首项 \(\binom{i}{j}\) 左边的那一项 \(\binom{i}{j-1}\),从而两者相加得到 \(\binom{i+1}{j}\),恰为第二项 \(\binom{i+1}{j+1}\) 的左边一项,从而全部合并。
-
从而我们有 \(\sum\limits_{k=0}^l \binom{i+k}{j+k}=\binom{i+l+1}{i+l}-\binom{i}{j-1}\)。
-
-
求列和,即求 \(\sum\limits_{k=0}^l \binom{i+k}{j}\)。
-
同上,配首项的右项 \(\binom{i}{j+1}\)。
-
从而我们有 \(\sum\limits_{k=0}^l \binom{i+k}{j}=\binom{i+l+1}{j+1}-\binom{i}{j+1}\)。
-
-
求行和,即求 \(\sum\limits_{k=0}^l \binom{i}{j+k}\)。
-
这个真没法直接求,但我们可以 \(O(1)\) 地从当前行递推到下一行。
-
容易看出,\(2\sum\limits_{k=0}^l \binom{i-1}{j+k}\) 合并后为 \(\sum\limits_{k=0}^l \binom{i}{j+k}-\binom{i}{j}+\binom{i-1}{j}+\binom{i-1}{j+l}\)。
-
从而有 \(\sum\limits_{k=0}^l \binom{i}{j+k}=2\sum\limits_{k=0}^l \binom{i-1}{j+k}+\binom{i}{j}-\binom{i-1}{j}-\binom{i-1}{j+l}\)。
-
单次递推无法 \(O(1)\),但如果是连续递推的话,我们可以存下上次的边界处理结果,从而根据组合数的定义式可以很容易地递推新的边界处理。
-
-
-
二项式定理:\((a+b)^n=\sum\limits_{k=0}^n \binom{n}{i}a^kb^{n-k}\)。
-
证明比较显然,毕竟拆括号相当于任意对位乘。而其中 \(a\) 的次数为 \(k\) 的就相当于选了 \(k\) 个括号取 \(a\)。
-
二项式定理的结果展开后,如果按 \(a\) 降次排序,系数恰为 \(n\) 行的杨辉三角(注意杨辉三角最上面那行是第 \(0\) 行)。
-
各种结论
-
以下所有结论都可以通过暴力推式子得到,但不建议那么做。
-
同一个式子有很多种化法,但关键的是它们的实际意义。这才是我们需要的。
-
\(\sum\limits_{i=0}^n \binom{n}{i}=2^n\):显然,由加法原理相当于选任意个,于是每个都是爱选不选。
可重组合
-
从 \(n\) 个数中可重地选出 \(k\) 个数的方案数为 \(\binom{n+k-1}{k}\)。
-
不妨将第 \(i\) 个数被选取的次数记为 \(x_i\),则该问题等价于求方程 \(x_1+x_2+\dots+x_n=k(x_i\geqslant 0)\) 的解集数。
-
则可以将之视为把 \(k\) 个球用 \(n-1\) 个隔板分成 \(n\) 段的方案数。\(\binom{n+k-1}{n-1}=\binom{n+k-1}{k}\),得证。
-
可重排列显然是 \(n^k\),故不予讨论。
-
可重集的排列组合,目前我会的方式主要是 DP,即转化成 \(\sum\limits_{i=1}^m x_i(0\leqslant x_i \leqslant a_i)=k\) 来做,其中 \(m,a_i,x_i\) 分别为元素种数,第 \(i\) 种元素的个数和选的个数。
-
组合有生成函数解法,但 NTT,故略。
-
排列的话,DP 中需要不断 \(C\) 出插进去的系数。
-
计数基础
加法原理与乘法原理
-
加法原理:若做某事的某一步有 \(n\) 类方式,第 \(i\) 类方式有 \(a_i\) 种方案,则总方案数为 \(\sum\limits_{i=1}^n a_i\)。
-
乘法原理:若做某事有 \(n\) 个互相独立的步骤,第 \(i\) 步的方案数为 \(a_i\),则总方案数为 \(\prod\limits_{i=1}^n a_i\)。
例题
[ABC281G] Farthest City
-
题意略。
-
容易想到设计 dp 状态为 \(dp_{i,j}\) 表示 \(i\) 个点构成的图,最深层有 \(j\) 个点的方案数。初始化为 \(dp_{1,1}=1\),但发现好像没法转移:
-
新加一个点加到第 \(k\) 层怎么办呢,即使我们只要求往最后一层加点,似乎也没法整啊...这需要倒数第二层的点数,然后又可能要在这一维上转移,又需要倒数第三层...无穷递归了。
-
发挥 DP 的思想:最优子结构。已有的子结构,你不要去动它。每次暴力转移一整层新的出来!
-
转移系数:层内随意连边,层间每个点至少有一个连。即,\(dp_{i,j}\to dp_{i+k,k}\),转移系数为 \(2^{\binom{k}{2}}\times (\sum\limits_{l=1}^j \binom{j}{l})^k\)。
-
注意到 \(\sum\limits_{l=1}^j \binom{j}{l}=2^j-1\),显然 \(2^j\) 可以预处理,于是两个系数都可以随着 \(k\) 的增大 \(O(1)\) 递推到新系数,没有 \(\log\),很优秀(事实上带 \(\log\) 实现精细也容易过)。
CF1515E Phoenix and Computers
-
题意:求将 \(1\sim n\) 的灯打开的方案数。如果 \(i-1,i+1\) 都被打开,那么 \(i\) 会自动打开,不能再被手动打开。两个方案不同,当且仅当打开的灯不同,或打开的顺序不同。
-
数据范围:\(n\leqslant 400\)。
-
首先容易发现最后的序列一定是形如
____.____.____.__的,即一段手动-一个自动-一段手动-...,如此反复。 -
考察将长为 \(n\) 的一段灯全部手动打开的方案数(其前后没有预先打开的灯)。容易看出,第一手是随意的,但之后其左边只能一路向左,右边只能一路向右;不过两者可以相互穿插。换言之,方案数为 \(\sum\limits_{i=1}^n \binom{n-1}{i-1}=2^{n-1}\)。
-
转而考虑设计 dp 如下:
-
状态设计:\(dp_{i,j}\) 表示打开了 \(1\sim i\) 的灯,其中 \(j\) 盏是手动打开的,保证 \(i\) 一定是一个连续手动段的结尾,的方案数。
-
初始化:\(dp_{i,i}=2^i\)。
-
状态转移:\(dp_{i,j}\to dp_{k,j+(k-i-1)}\),转移系数为 \(2^{k-i-1}\times \binom{j+(k-i-1)}{j}\)。其中后项非常重要,它将新段的操作序列和原有的操作序列插到了一起,也正是这一点使得这个有顺序的开灯过程变成了从左到右扫过去的。
-
-
复杂度 \(O(n^3)\),足够通过本题。不过本题还有一个 \(O(n^2)\) 的妙妙区间 dp 做法,参看区间 dp。
P3773 [CTSC2017] 吉夫特
-
题意略。
-
我会暴力 DP!注意到“是奇数”相当于“所有 \(2\) 全部消掉”,且发现所求的式子可以化为 \(\dfrac{a_{b_1}!}{a_{b_k}!\prod_{i=1}^{k-1} (a_{b_i}-a_{b_{i+1}})!}\),于是设计如下 DP:
-
状态设计:\(dp_{i,j}\) 表示考虑了前 \(i\) 个元素,包含 \(i\) 且含 \(j\) 个 \(2\) 的所有“半序列”个数。
- 所谓半序列,即只计算了分子和分母中的后一项,在尾部还有端口的子序列。
-
初始化:\(dp_{i,get2(a_i!)}=1\)。注意到其实 \(get2()\) 就是 \(ctz()\),但阶乘太大,不过我们可以预处理,直接把 \(ctz()\) 连乘就好啦。
-
状态转移:
-
\(dp_{i,j}\to ans\),系数为 \([get2(a_i!)=j]\)。特别地,对于 \(j=get2(a_i!)\),其在参与这个转移的时候要先 \(-1\),毕竟要求的子序列长度至少为 \(2\) 嘛。
-
\(dp_{i,j}\to dp_{k,j-get2((a_i-a_k)!)}\),系数为 \([a_i\geqslant a_k]\)。这个倒是没什么说的。
-
-
-
分析一下复杂度,发现对于 \(n=2017\) 这一档分绰绰有余(打表发现第二维的大小至多 \(2010\)),\(O(n^2)\) 暴力即可获得 \(70\) 分!
-
但这和正解毫无关系(自豪)!正解的话...我们得抛弃“奇偶性”。


