最大流

概述

• 最大流思想主要用于求解“最多能...”的问题。

• 更多的我还没想明白。

增广路

• 若 \(P\) 是网络 \(G\) 中一条连通 \(S,T\) 的路径，且 \(\forall e\in P,c(e)>0\)，则称 \(P\) 为一条增广路。

• 正如二分图最大匹配的增广路一样，网络流中的增广路本质也是带悔贪心。

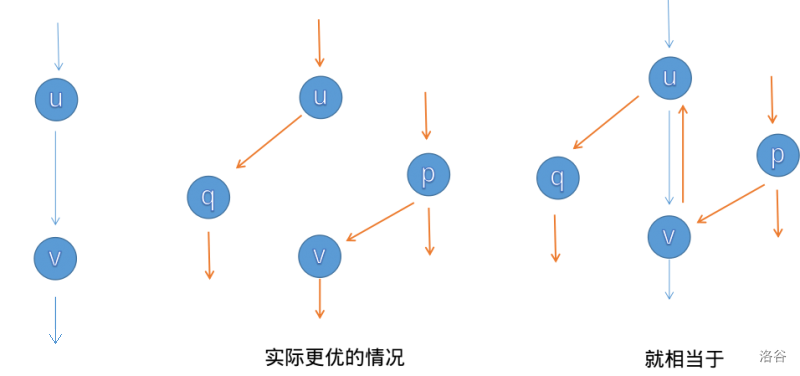
• 它的实现基于“退流”思想。我们先看一张图吧（图源 OI Wiki）：

• 图中我们一开始找了一条“错误”的增广路，即实际上在最大流中不存在的路径。

• 但我们可以做如下操作：根据斜对称性，\(f(u,v)=-f(v,u)\)，从而 \(c(v,u)\) 即 \((v,u)\) 的残量此时相当于 \(f(u,v)\) 即 \((u,v)\) 的容量。

• 可以利用这一反向边的残量，在反向边（虽然实际上不存在）上流过一定的流量。

• 事实上这代表着两者对冲掉了，不过这不是水管，对不对冲我们不关心。

• 从而可以想到一种朴素实现：邻接表存图（需要建反边）后不断从 \(S\) 开始 dfs 求增广路。如果求到，那么在 dfs 的出栈过程中更改边的残量。反复直到不存在增广路为止。

  • 这里可以利用链式前向星存图：第一条边的编号是 \(2\)，其反边编号为 \(3\)，故 \(\oplus 1\) 就能找到对应的反边（不管实际上是正还是反）。

  • 使用这种思路的最大流算法，都可以称为 Ford-Fulkerson 增广路算法，即在求最大流过程中保持流量守恒，并通过寻找增广路来更新最大流。下面谈到的具体实现算法都是 FF 增广路算法。

  • 另一种思路是 Push-Relabel 预流推进算法，这一算法在求解过程中忽略流守恒性，并每次对一个结点更新信息，以求解最大流（这段描述是我从 OI Wiki 贺过来的，等我学了 HLPP 再说）。

• 然而朴素 dfs 的复杂度显然有可能是指数级的（譬如不断走环）。怎么办？

Edmonds-Karp 动能算法（EK 算法）

• 既然 dfs 不行，为什么不考虑 bfs？只要记录队列中每个点的来源，在扩展到 \(T\) 的时候手动出栈改残量就好了。

• 只要找到一条增广路就抛弃队列中所有点，从头开始 bfs。从而每个点只会入队一次（之前没机会之后也没机会，之前有机会就从头开始了），内层复杂度显然是 \(O(n+m)\)。

• 可外层复杂度呢？

• 定理 \(1\)：EK 算法每找到一条增广路，\(\forall v\in V\And v\notin\{S,T\}\)，\(dis'(S,v)\geqslant dis(S,v)\)。

  • 这里的 \(dis\) 定义为经过的边数，即边长为 \(1\)。

  • 这里的 \(dis\) 只能经过 \(c>0\) 的边。

• 证明：考虑使用反证法。

  • 不妨令 \(v\) 为所有 \(dis'(S,v)<dis(S,v)\) 减小的点中，\(dis'(S,v)\) 最小的点。

  • 首先，容易证明 \(dis'(S,v)>1\)。

    • 对于 \(e(S,v)\) 不存在的点，结论显然成立。

    • 对于 \(e(S,v)\) 存在的点：

      • 如果该轮增广前 \(c(S,v)>0\)，显然有 \(dis(S,v)=1\)，故 \(dis'(S,v)\geqslant dis(S,v)\)，与 \(v\) 是 \(dis(S,v)\) 减小的点矛盾。

      • 如果 \(\forall e(S,v)\)（我们考虑上重边情况），\(c(S,v)=0\)，则 \(dis(S,v)>1\)。

      • 但此时不可能有 \(dis'(S,v)=1\)，除非该轮增广中 \(c'(S,v)>0\geqslant c(S,v)\)。然而变大就意味着发生了退流，显然不可能向 \(S\) 退流。

  • 故，在增广后的网络上，\(S\to v\) 的最短路上一定还有至少一个其他点。

  • 从而 \(v\) 在该最短路径中有非 \(S\) 的前驱，不妨记为 \(u\)，于是有 \(dis'(S,u)+1=dis'(S,v),c'(u,v)>0\)。

  • 又由 \(v\) 是 \(dis'(S,v)<dis(S,v)\) 的点中，\(dis'(S,v)\) 最小的点，可以推知 \(dis'(S,u)\geqslant dis(S,u)\)。

  • 故 \(c(u,v)=0 \And c'(u,v)>0\)，否则一定有 \(dis(S,v)\leqslant dis(S,u)+1\leqslant dis'(S,u)+1=dis'(S,v)\)，与 \(dis'(S,v)<dis(S,v)\) 矛盾。

  • 我们看到这里发生了退流。既然 \(c(v,u)\) 减小而 \(c(u,v)\) 增大，一定是在该轮增广中用 \(v\) 扩展出了 \(u\) 并成功增广。

  • 但由 bfs 的性质，每个点一定被最短路上的点先扩展出。我们分两种情况讨论：

    • \(v\) 在 \(dis(S,u)\) 的最短路上：...显然不可能，此时有 \(dis(S,v)<dis(S,u)\leqslant dis'(S,u)<dis'(S,v)\)，与前设矛盾。

    • \(v\) 不在 \(dis(S,u)\) 的最短路上：

      • 对一般的 EK 算法，只要找到了一条增广路就会抛弃队列中所有元素从头开始 bfs。故有一个简单证明：

      • 成功增广：从头开始。

      • 增广失败：\(v\) 也没机会，不必把 \(u\) 二次扩展。

  • 故无论如何，\(c(u,v)\) 不可能增大，与前设矛盾。

• 定理 \(2\)：EK 算法最多增广 \(O(VE)\) 次。

  • 显然，每条增广路的 \(c\) 一定等于至少一条其中的边的 \(c\)。不妨将其称为关键边。

  • 可以证明，每条边最多做关键边 \(O(\dfrac{|V|}{2})\) 次。

  • 不妨记关键边为 \((u,v)\)，显然 \((u,v)\) 在 \(dis(S,v)\) 上，故 \(dis(S,v)=dis(S,u)+1\)。

  • 想要它再做一次关键边，首先需要 \((v,u)\) 做一次关键边。

  • 由定理 \(1\)，\(dis'(S,v)\geqslant dis(S,v)\)。既然 \((v,u)\) 是关键边，则 \(dis'(S,u)=dis'(S,v)+1\)。

  • 故 \(dis'(S,u)=dis'(S,v)+1\geqslant dis(S,v)+1=dis(S,u)+2\)。

  • 可见，从做了一次关键边到再做第二次，距离至少 \(+2\)，故最多做 \(O(\dfrac{|V|}{2})\) 次。

  • 故最多增广 \(O(VE)\) 次。

• 综上，单轮增广的复杂度为 \(O(E)\)，故 EK 算法的复杂度大约在 \(O(VE^2)\sim \Theta(VE^2)\) 之间。能用，但很不乐观。

Dinic 算法

• 我们来考虑一个好像有希望的增强版 EK：不是找到一条增广路就从头开始。事实上，这叫做“多路增广”。

• 注意，此时每个点可以多次入队。同时，有可能队列中的某些点是无效的：

  • 譬如 \(S\to 1\to 2\to 3,4,5,6\to T\)，如果 \(3\to T\) 的增广路就把流推满了，那么 \(4,5,6\) 都是废元素。

  • 解决办法是回溯改残量之前先把整条路径拉出来 check 一下，当然，可能有 \(2\) 倍常数。

• 定理 \(1\)：接着“\(v\) 不在 \(dis(S,u)\) 的最短路上”下面开始证。

  • 此时，\(\forall dis(S,u)<dis(S,v,u)\) 的路径，在它们的本轮增广后、\(dis(S,v,u)\) 的本轮增广前，结果要么是它们 \(c=0\)，要么是 \(c(u,T)=0\)，这里的 \(c\) 是广义残量。

  • 如果 \(c(u,T)=0\)：显然不可能有 \(c(u,v)=0 \And c'(u,v)>0\)，后面没有流量了，不可能让 \(c(v,u)\) 减小，\(c(u,v)\) 增大。

  • 如果 \(c(dis(S,u))=0\)：有点复杂。

    • 此时，在实质上，最新的残量网络中，\(v\) 已经在 \(u\) 的最短路上了。

    • 不妨假设我们在这里强行把本轮增广结束。此时，定理 \(1\) 显然成立（由无穷递降法）。

    • 称此时的 \(dis\) 为 \(disn\)，则我们有 \(disn(S,v)<disn(S,u)\leqslant dis'(S,u)<dis'(S,v)\)，与前设矛盾（其实就是化归到了最短路情况）。

    • 上面这行里面的 \(disn(S,u)\leqslant dis'(S,u)\) 看似没有证明（从 \(dis(S,u)\) 到 \(dis'(S,u)\) 可能先增后减），但事实上一定是对的：每条增广路是平等的且单位的，整个过程是同质的。

    • 或者说，这里也可以无穷递降：如果 \(disn(S,u)>dis'(S,u)\geqslant dis(S,u)\)，那么抛弃后面的增广过程，孤立地考虑到现在为止的情况。

    • \(u\) 变成 \(v\) 了。直到 \(c(u,T)=0\) 或 \(v\) 在 \(dis(S,u)\) 的最短路上。而最平凡的情况可以用原本的定理 \(1\) 来证，所以这个问题是可归纳的。

  • 故无论如何，\(c(u,v)\) 不可能增大，与前设矛盾。

• 定理 \(2\)：显然这个做法的增广次数上界可以用定理 \(2\) 来证明，不需要改动。但我们希望得到一个卡得更紧的复杂度。

• 定理 \(1.5\)：我们尝试证一下定理 \(1\) 的对称定理：每找到一条增广路，\(\forall v\in V\And v\notin\{S,T\}\)，\(dis'(v,T)\geqslant dis(v,T)\)。

  • 仍然取 \(v\) 为 \(dis'(v,T)<dis(v,T)\) 的点中 \(dis'(v,T)\) 最小的。

  • 首先容易证明 \(dis'(v,T)>1\)，此部分证明平凡：不可能从 \(T\) 退流。

  • 故不妨将 \(v\) 在 \(dis'(v,T)\) 上的后继记为 \(u\)，则 \(dis'(v,T)=dis'(u,T)+1\)。由前设，\(dis'(u,T)\geqslant dis(u,T)\)。

  • 从而 \(c(v,u)=0 \And c'(v,u)>0\)，否则一定有 \(dis(v,T)\leqslant dis(u,T)+1\leqslant dis'(u,T)+1=dis'(v,T)\)，与前设矛盾。

  • 故该轮增广中一定用 \(u\) 扩展了 \(v\) 并成功增广。分两种情况讨论：

    • \(v\) 在 \(dis(u,T)\) 上：此时有 \(dis(v,T)<dis(u,T)\leqslant dis'(u,T)<dis'(v,T)\)，与前设矛盾。

    • \(v\) 不在 \(dis(u,T)\) 上：

      • 此时，\(\forall dis(u,T)<dis(u,v,T)\) 的路径，在它们完成本轮增广后，\(dis(u,v,T)\) 完成本轮增广前，结果要么是它们 \(c=0\)，要么是 \(c(S,u)=0\)。

      • 如果 \(c(S,u)=0\)：显然不可能有 \(c(v,u)=0 \And c'(v,u)>0\)，前面没有流量了。

      • 如果 \(c(dis(u,T))=0\)：模仿定理 \(1\) 做无穷递降，递归的初始条件可以用朴素定理 \(1\) 的对称定理，证明平凡。

• 定理 \(3\)：每轮增广后，\(dis(S,T)\) 单增。

  • 考虑使用反证法。如果 \(dis'(S,T)= dis(S,T)\)，那么我们分两种情况讨论：

    • 是某条原有路径：其一定会被增广，增广后一定失去关键边，故路径一定消失。不可能是某条原有路径。

    • 是某条新增路径：

      • 显然其中至少有一条边是新增的反向边（不管它到底反不反，我们总是相对残量网络来谈），不妨记为 \((v,u)\)。

      • 易得 \((u,v)\) 一定在某条增广路上。容易看出，该增广路长度至少为 \(d=dis(S,u)+1+dis(v,T)\)，故 \(dis(S,T)\leqslant d\)。

      • 故此时 \(dis'(S,T)=dis'(S,v)+1+dis'(u,T)=dis(S,T)\leqslant d=dis(S,u)+1+dis(v,T)\)。

      • 即 \(dis'(S,v)+1+dis'(u,T)\leqslant dis(S,u)+1+dis(v,T)\)。

      • 由定理 \(1\) 和 \(1.5\)，我们可以将其置换为 \(dis(S,v)+1+dis(u,T)\leqslant dis(S,u)+1+dis(v,T)\)。则不应当走 \(d\) 增广，应该走式左增广，与前设矛盾。

• 好耶！！！我们终于证明了外层最多做 \(n\) 次了，毕竟 \(dis(S,T)\leqslant n\)。

• 但内层呢？

• 注意到这里内层的问题很大，我们无法保证队列中元素数量。几次失败的推流就会导致复杂度暴涨，考虑链-完全二分图-链的情况，就会发现炸了。

• 为什么炸？因为队列中无用元素太多。为什么无用？因为它们对应的增广路上游用完了。

• 那我能不能判一下不把它们加进去？不行，bfs 不具备即时性，等你知道用完了的时候，早就扩展了一大堆元素了。

• 好，我换 dfs 不就解决了吗！然而不行，内层复杂度还是没有保证，而且外层复杂度中依赖的增广顺序消失了。

• 证明可以刻板，但发明不行。我们得感性理解，不能光靠式子。

• 这里 \(dis(S,T)\) 单调递增，就其根本而言，实质上相当于“较短的增广路被增广了，且没有产生更短的增广路”。这个东西...直觉上应该不和 bfs 的增广顺序绑定。

• 请循其本。我们是希望多路增广能带来复杂度的优化；到底有多少优化，这得证。

• 那无论如何先设法做一个较劣的复杂度。顺着上面的思路，我们第 \(i\) 轮只增广 \(dis(S,T)=i\) 的增广路。

• 毕竟是有顺序的，这相当于总是做 \(dis(S,T)\) 最短的增广路。最短？嗯...这是无边权图...无边权图的最短路显然是 bfs 求得的。则考虑...嗯...

• 回过头来，之所以 dfs 的内层复杂度不对，主要是因为图上有环。而另一个显然的事情是，过环的一定不是最短路。

• 考虑 bfs 建出广义最短路树（即一个点可能有多个父节点），然后在上面跑 dfs。

• 先考虑外层。我们尝试先证明对所有点都有 \(dis'(S,v)\geqslant dis(S,v)\)，再证明 \(dis'(S,T)\neq dis(S,T)\)，就可以证明外层复杂度为 \(O(n)\)。

• 定理 \(1\)：\(dis'(S,v)\geqslant dis(S,v)\)。

  • 故技重施，使用反证法+无穷递降法。

  • 首先容易证明，在分层图的前提下，每轮增广后新出现的边 \((u,v)\) 一定是 \(dis(S,v)+1=dis(S,u)\)。

  • 显然，任何 \(dis'(S,v)<dis(S,v)\) 都可以归约到这种新出现的边上，或者说 \(dis'(S,v)\) 一定至少经过一条新边。

  • 不断回溯直到 \(dis'(S,u)\geqslant dis(S,u)\)，显然这个源头是存在的，这种回溯一定不构成环。

  • 从而 \(dis'(S,v)=dis'(S,u)+1\geqslant dis(S,u)+1=dis(S,v)+2\)，与前设矛盾。得证。

• 定理 \(2\)：\(dis'(S,T)>dis(S,T)\)。

  • 这个更简单。

  • 由定理 \(1\)，如果不大于，只能是等于。

  • 既然是等于，为什么没有被增广掉？显然这是符合该层的增广要求的。

• 故外层复杂度为 \(O(n)\)。考虑证明内层复杂度。

• 定理 \(3\)：每次 dfs 到首次 return，至少导致一条边在本轮的分层图上消失。

  • 如果找到了增广路，关键边消失。

  • 如果没找到，最后一条边消失，而且可能消失得更多。

  • 这一“消失”的实际实现依赖当前弧优化。

  • 显然首次 return 前的复杂度为 \(O(n)\)。

• 故内层复杂度为 \(O(nm)\)，每次 return 至多是一条满链，删 \(m\) 次结束。

• 我们成功了。

• 综上，Dinic 算法的复杂度为 \(O(n^2m)\)。\(\Theta\)？不知道，但似乎是可卡到 \(O\) 的。

• 需要指出的是，Dinic 算法...可以说依赖多路增广，因为定理 \(2\) 的最后一句需要多路增广来把所有对应长度的增广路增广完；也可以说不依赖，因为可以每次找到一条就 return，不过当前弧 \(cur\) 是在 dfs 间继承的罢了。

• 另外应当指出的是，Dinic 算法在单位网络上的复杂度是 \(O(\sqrt{n}m)\)，证明如下：

  • 单位网络：所有边容量均为 \(1\)，且除源汇点外的其他点要么入度为 \(1\)，要么出度为 \(1\) 的网络。

  • 首先，显然有内层复杂度为 \(O(m)\)，因为每条边只会被考虑一次。

  • 然后考虑外层复杂度，不妨假设现已增广了 \(\sqrt{n}\) 次，当前流量为 \(f\)，最大流为 \(f'\)，记两者差值为 \(d=f'-f\)。

  • 既然所有边的 \(c=1\)，显然所有增广路的 \(c\) 也为 \(1\)，于是我们还要找到 \(d\) 条增广路。

  • 由定理 \(2\) 可以推知，增广 \(k\) 轮后的增广路长度至少为 \(k+1\)，于是此时每条增广路的长度都 \(\geqslant \sqrt{n}\)。

  • “除源汇点外的其他点要么入度为 \(1\)，要么出度为 \(1\)”。这句话实际上指出，每个点只能负载 \(1\) 的流量（毕竟边的容量也都为 \(1\)），换言之每个点只在一条增广路中出现，于是总有增广路不交。

  • 故 \(d\) 条增广路一定不交，换言之它们总共需要 \(d\sqrt{n}\) 个点，又 \(d\sqrt{n}\leqslant n\)，于是 \(d\leqslant \sqrt{n}\)，外层最多还要跑 \(\sqrt{n}\) 轮。

• 于是外层复杂度为 \(O(\sqrt{n})\)，内层 \(O(m)\)，总复杂度 \(O(\sqrt{n}m)\)。

• 最后，这里给出示范代码。

namespace dinic{
	int S,T,tot;
	struct edge{
		int to,nxt,c;
		edge(){}
		edge(int _to,int _nxt,int _c){to=_to,nxt=_nxt,c=_c;}
	}e[maxe<<1];
	int ehd[maxv],etot=1;
	il void addedge(int s,int t,int c){
		e[++etot]=edge(t,ehd[s],c),ehd[s]=etot;
		e[++etot]=edge(s,ehd[t],0),ehd[t]=etot;
		return;
	}
	
	int cur[maxv],dep[maxv];
	il bool bfs(){
		memcpy(cur+1,ehd+1,sizeof(int)*tot);
		
		static int q[maxv],hd,tl;
		memset(dep+1,0,sizeof(int)*tot);
		q[hd=tl=1]=S,dep[S]=1;
		int now;
		while(hd<=tl){
			now=q[hd],++hd;
			for(int i=ehd[now];i;i=e[i].nxt)
				if(e[i].c && !dep[e[i].to]){
					dep[e[i].to]=dep[now]+1;
					if(e[i].to==T) return true;
					q[++tl]=e[i].to;
				}
		}
		return false;
	}
	
	il int dfs(int now,int fl){
		if(now==T) return fl;
		int rest=fl,used;
		for(int &i=cur[now];i;i=e[i].nxt)
			if(e[i].c && dep[e[i].to]==dep[now]+1){
				used=dfs(e[i].to,mymin(e[i].c,rest));
				e[i].c-=used,e[i^1].c+=used;
				rest-=used; if(!rest) break;
			}
		if(rest) dep[now]=0;
		return fl-rest;
	}
	
	const int inf=0x3f3f3f3f;
	il int getflow(){
		int ret=0;
		while(bfs()) ret+=dfs(S,inf);
		return ret;
	}
	
	il void clear(){
		memset(ehd+1,0,sizeof(int)*tot);
		etot=1; return;
	}
}

• \(cur\) 为当前弧，显然它是 Dinic 复杂度正确的必要条件。改 \(dep\) 为 \(0\) 是一个常数优化，相当于标记这个点没有前途。

• 视情况写 build 函数之类的来使用吧，这个主要是封装度高，另外记得开 ll。

• p.s.有时候 \(inf\) 难以取到一个足够大的值。一个解决办法是：

ll flow;
while(bfs())
	while((flow=dfs())
    	ret+=flow();

例题

P2071 座位安排

• 题意略。

• 拆点可按二分图匹配板题来做，但我们这里直接使用网络流。

• 应当指出的是，Dinic 算法在单位网络（定义较为繁杂，参看 OI Wiki，至少对二分图匹配建出的网络是单位网络）上的复杂度是 \(O(\sqrt{n}m)\)，优于 Hungarian 算法。

P1231 教辅的组成

• 题意略。

• 多层二分图匹配？爱怎么叫都好，但显然没法按二分图匹配来做。

• 唯一的注意点在于，不与 \(S,T\) 直接相连的点要拆点，因为要限制其使用次数。

CF387D George and Interesting Graph

• 题意略。我们用这道题谈谈建模的优劣。

• 首先容易想到暴力枚举中心点 \(u\)，容易处理所有和 \(u\) 相关的边，然后问题变成：在一张图中，每个点的入度和出度都要为 \(1\)，加/删边代价都为 \(1\)，求最小代价。

• 我一开始想到的建模是最小割。从 \(v\) 出发的所有边互相矛盾，从 \(u\) 出发的所有边互相矛盾，于是最小割就是最少删的边数。

• 但这显然不优，因为此时网络流图的点数为 \(O(m)\)，边数为

\[\begin{aligned} & O(\sum\limits_{i=1}^n [i\neq u]\times (indeg_i^2+outdeg_i^2)) \\ & \approx O(\sum\limits_{i=1}^{n-1}x_i^2),\text{where }\sum\limits_{i=1}^{n-1} x\to m \\ & \to O(n^2) \end{aligned} \]

• 那么 \(O(n(m^2n^2))\) 想跑过去还是...蛮自信的。

• 贺题解后优化建模，考虑这么建图：

  • 将 \(u\) 以外的所有点 \(i\) 拆成 \(in_i\) 和 \(out_i\)。

  • \(\forall i\neq u,S\to out_i\)。

  • \(\forall e.s=i \And e.t\neq u,out_i\to e\)。

  • \(\forall e.s\neq u \And e.t\neq u,e\to in_{e.t}\)。

  • \(\forall i\neq u,in_i\to T\)。

  • 上述所有边容量均为 \(1\)。

• 那么这张图的点数和边数都是 \(O(n+m)\) 的，常数我们不关心。已经可以过了。

• 但是，还可以进一步贺题解后优化建模。

  • \(\forall i\neq u,S\to out_i\)。

  • \(\forall e.s=i \And e.t\neq u,out_i\to in_{e.t}\)。

  • \(\forall i\neq u,in_i \to T\)。

• 这是什么？二分图最大匹配！没事别老把你那边变成网络里的点。。。

• 总之，\(O(n^3m)\)，足够通过本题（网络流，网络流）。

P2526 [SHOI2001] 小狗散步

• 题意略。

• \(\forall i<n \And dis(i,j)+dis(j,i+1)<2dis(i,i+1),i\to j\)。

• 鉴于要输出方案，用匈牙利吧。

• tips：这里有加减，所以必须开方！我想着怕掉精度不开方挂了好久...式右改成 \(4\) 也不对，毕竟式左是完全平方式，无论如何绕不过一次项的。

P2754 [CTSC1999] 家园 / 星际转移问题

• 题意略。

• 考虑按时间拆点。时刻 \(t\) 的空间站向 \(t+1\) 的它自己连容量为 \(+\infty\) 的边，飞船正常连边，\(S\to \text{earth}(+\infty),\text{moon}\to T(+\infty)\)。

• 这一做法的点数是 \(O(tn)\)，边数是 \(O(tm)\)，其中 \(t\) 为答案。

• 如果使用二分答案，忽略建图时间，复杂度趋于 \(O(t^3n^2m\log)\)。

• 如果利用 Dinic 的性质，每次在原图（残量网络）上加一层点，复杂度我不会分析，但似乎优于二分答案。

• 但应当指出的一点是，讨论区已经有数据能够将 \(t\) 构造到 \(749\)。更大的 \(t\)，除非我们能证明它不存在，否则很可能其是存在的。

• 故上述两种方法都只是能过本题的数据而已；更严谨的做法，依我看，需要对飞船的周期求 lcm，于是图的层数不超过 \(lcm\)，二分跑了多少个 \(lcm\)，\(lcm\) 内用 Dinic 加边，注意此时 \(S\) 向所有空间站都要连对应空间站人数的边。

• 显然太复杂了，故，“我偷个懒”，就写个过这道题的数据的做法...吧...哈哈哈。

• 对了，判无解用并查集。\(O(t^3n^2m)\)，不过每一项都是网络流的复杂度，故...大概能过（纸面一京，实际上每个点都是 4ms）。

• p.s.这个在残量网络上加点的做法真的超快（所有点都是 4ms)，但需注意一点：前 k-1 层已经增广完了，本次 Dinic 的返回值不包含它们的流（只包含新增流），故最大流应当累加得到。

P2764 最小路径覆盖问题

• 题意略。这不隔壁二分图的板吗...

• 谈一下输出方案：对于所有满流的正边，它们是路径的一部分，将之取出后随便拼一下就好了。

P2766 最长不下降子序列问题

• 题意略。有趣...

• 第一问容易 DP 解决，这里唯一要指出的是，我们使用 \(dp_i\) 表示以 \(i\) 结尾的最长不下降子序列长度这个状态，后面有用。

• 我首先想到了把一个点拆成 \((i,1\sim dp_i)\)，把选一个数作为决策扔到边上。

  • 但发现这会导致一个数字选很多遍，拆点也没法拆，设计一个临时枢纽当关卡的话，又不知道从枢纽出去往哪里流，在 Ford-Fulkerson 增广路算法下肯定没机会。只能求可交的最长不下降子序列问题。

  • 而事实上，可交的版本可以用和原 DP 同阶的辅助 DP 解决，类似 \(\text{P2516 [HAOI2010] 最长公共子序列}\)，最大流既没有必要，复杂度也过不了（这大概算“模拟最大流”？）。

• 事实上，这一想法在我贺了题解之后发现是很有启发性的。考虑它的本质：分层图。选了几个就是层。

• 这里需要一点我们对 LIS 的深入理解。LIS 中，存在这么一个结论：以 \(k\) 结尾的所有长度 \(<dp_k\) 的合法子序列，都不可能是一个最长合法子序列的前缀。

  • 使用反证法，假设存在，于是把前缀进一步拉长到 \(dp_k\)。

  • 发现最长合法子序列变长了，与原设不符。

• 换言之，所有第二维不为 \(dp_k\) 的点对答案都无贡献！于是，我们可以：

  • 对 \(i\) 只建 \((i,dp_i)\)，因为 \(i\) 只在作为这一层被选时有意义。注意到这也使得我们可以用拆点来限制选择次数。

  • 继续，考虑建立源汇以统计答案。发现显然只能从 \(S\) 向第一层的点连边，从最后一层的点向 \(T\) 连边。建出的网络是单位网络。

• 如何推广到第三问？答：考虑实际意义。

  • 首先注意到和 \(S,T\) 相关的边的流量都可以是 \(+\infty\)，毕竟保证一个点只被选一次，靠的是拆点。

  • 那么它是怎么被选很多次的？多个 \((j,dp_i-1)\) 都尝试推流到 \((i,dp_i)\)，换言之，这条边就代表着选 \(i\)。每个 \(j\) 自然是选 \(i\) 一次，但有多个 \(j\) 都想选 \(i\)。

  • 嘶。为什么每个 \(j\) 只选一次？我们上面说卡元素的被选次数靠的是拆点...拆点...那就是说，这些边的容量也是无所谓的！

  • 于是意识到只要保证拆点的容量为 \(1\)，其他的容量无所谓。现在解除了 \(1\) 和 \(n\) 的限制，那只要把它们的拆点边容量改成 \(+\infty\) 就好咯。

  • 实现上可以玩一点小 trick 来方便偷懒：不重置网络，也不改边权，直接加四条边（可能没有 \(out_n\to T\) 这条，视 dp 情况），然后就着残量网络跑一次最大流增量，即和星际转移问题一样的累加手法。

  • 事实上，这一“动态 Dinic”trick 可以推广到任意的网络，并对常数有一定帮助。据说 \(\text{P2050 [NOI2012] 美食节}\) 就考了这个 trick，不过我还没有做到，故以后再说。

  • 当然，出于常数考虑我们还是把 \((S,1)\) 和 \((n,T)\) 之外的其他边的容量置为 \(1\)。

• 得解，复杂度 \(O(n^2m)\)，\(m\) 难以算出但显然 \(<n^2\)，在网络流意义下可以无压力跑过。

• 需要特别指出的是，当最长不下降子序列长度为 \(1\) 或为 \(2\) 且 \(a_1\leqslant a_n\) 的时候，第三问的答案会有 bug，因为存在从 \(S\) 到 \(T\) 的容量为 \(+\infty\) 的路径，事实上就是 \(1\) 和 \(n\) 本身单独构成的子序列被选了无限次。

• 解决办法：

  • 首先这里我们令非源汇边的容量为 \(1\) 就是有意义的了。这可以避免最长不下降子序列长度为 \(2\) 时的 bug。

  • 如果为 \(1\)，直接特判掉。这是容易的。

P3153 [CQOI2009] 跳舞

• 题意略。首先自然地想到把舞曲作为流量，跑最大流。

• 经过一番调试发现没读 K，最后是这么一个做法：

• \(S\to boy(0),girl\to T(0)\)。

• \(boy\to (liked)girl(1),boy\to ex\to girl(\min(K,n-like))\)。

• 看到 \(ex\) 代表的就是不喜欢情况下的匹配。感觉有点怪，对不对？为什么源汇边是 \(0\)？

• 我们每次把源汇边的流量各 \(+1\)，然后在残量网络上直接跑一轮 Dinic，看增量是否恰好为 \(n\)。是则 ++ans，否则输出答案。

  • 这相当于是尝试放一支舞曲，看是否能恰好配 \(n\) 对。

  • 之前配过的不能再配，所以不要动残量网络，只是把男女的需要各 \(+1\)。

• 两个问题：

  1. 会不会把一个喜欢的当成不喜欢的跳了？

     • 会，但无所谓。

     • 如果用得到这个喜欢，那显然会退流回来。

     • 否则真的浪费一个不喜欢名额也无所谓，反正留着也没用。

  2. 会不会某一对跳了不止一次？

     • 好问题。乍一看是有可能的。

     • 但事实上这只在我们的最大流中有可能，而我们的最大流只在数值上和实际方案跳的舞曲数相等。

     • 换言之，应当总是存在一种方式，可以通过合理的退流/推流，使得同一对不会反复跳。

     • 这一证明是感性的，确实不太好。存在一种方式把它变得严谨，那就是把喜欢额度和不喜欢额度拆开，分别连边，即 \(S\to boy(inf),boy\to like(inf),boy\to unlike(\min(K,n-like)),unlike\to (girl_x)unlike(1)\)。

     • 不过这将导致我们的加流量手段不再可行：不知道给喜欢还是不喜欢加，都加又怕配的对数太多，即这个男孩这一轮和不止一个女孩跳了舞。

     • 于是必须转成二分答案，每次跑一遍检验可行性，我不喜欢。姑且认为这个感性证明是对的吧，毕竟这一问题只在走 \(ex\) 的时候出现，而 \(ex\) 应该总是有办法分配的...

     • 考虑某个倒霉男生和不喜欢的女生一直跳，导致他不得不和某个女生跳了不止一次（某些他不喜欢的女生一直在和不同的喜欢的男生跳舞），那么那些互相喜欢的女生和男生的“不喜欢额度”一定还有很多空余，故应该是能周转过来？

     • upd：到目前为止没想到证明，感觉是假的。可惜我也不会构造数据，只是感觉这种数据应该存在。

• 理论复杂度 \(O(n^2(4n+n^2))\approx O(n^4)\)，哇这次纸面复杂度过了诶！

P3163 [CQOI2014] 危桥

• 题意略。很有趣的一道题。

• 首先做了这么多我们也看出来套路了，这道题多半是直接最大流。

• 考虑将危桥拆成 \(in\) 和 \(out\)，内部连容量为 \(2\) 的边，其他的都是 \(+\infty\)。

• 用 \(key_{i,j}\) 表示第 \(i\) 个人的第 \(j\) 个关键点（\(0\) 为 \(S\)，\(1\) 为 \(T\)，当然他是要往返的）。则先 \(S\to key_{0,0}(req_0),key_{0,1}\to T(req_0)\)，四种都试一下看一下最大流增量对不对。

• 然而样例都过不了。为什么？

• 因为退流啊。反边的存在允许我们通过“流过去再流回来”的“对冲”方式来退流，实际上就是反悔，但这里 \(S,T\) 不断在变，甚至直接 \(S,T\) 互换。

• 于是 \(S\to T\) 的推流路径创建的退流路径就恰好是 \(T\to S\) 的推流路径，寄了（而在固定 \(S,T\) 的时候这种操作的本质是把这个推流反悔了）。

• 怎么办？显然我不可能按着它的头说不许退流。那就根本不是网络流了，算不对的。

• 拆点。进一步拆点。定义一个点为 \(((i,0/1),(j,0/1))\) 表示 Alice 在 \(i\)，是否到达过 \(key_{0,1}\)，Bob 在 \(j\)，是否到达过 \(key_{1,1}\)。

• 连边。不妨假设 \(req_1\geqslant req_2\)：

  • \(S\to ((key_{0,0},0),(key_{1,0},0))(+\infty)\)。

  • \(((key_{0,0},1),(key_{1,0},1))\to T(req_2),((key_{0,0},1)(key_{1,0},0))\to T(req_1-req_2)\)。

• 余下的连边较为显然，只要记得还是要拆危桥即可。

• 啊...哈哈哈。又假了。我们遇到了和最长不下降子序列问题那道题一样的问题：分层之后，边的使用次数无法限制。然而这里可没有“只需要某一个点”这种好事了。

• 考虑到思维过程的完整性，以及我写这个也不是当题解用的，上面的就留着吧。下面我们谈谈我贺了题解之后仔细思考得到的真做法：

• 首先无脑 \(S\to key_{x,0},key_{x,1}\to T(2req_x)\)，中间的不用说了就正常连边，记得拆一下危桥，跑一遍最大流。因为是无向图，所以显然往返=过去两次，这一转化是正确的。

• 等等！这摆明了是假的啊！

  1. 如果 \(S\to key_{x,0}\to key_{!x,1}\to T\)（\(!\) 为取反，将就用吧）了怎么办？这不就越俎代庖，额，或者说偷梁换柱了吗？

  2. 第一种假做法里的退流问题不是还是没有解决吗？如果 \(key_{0,0}\to key_{0,1}\) 和 \(key_{1,0}\to key_{1,1}\) 从不同方向经过某个危桥，那这个危桥的经过次数很可能不对啊。

• 好的，我们来尝试解决：改成 \(S\to key_{0,0},key_{1,1} \And key_{0,1},key_{1,0}\to T(2req_x)\)，再跑一遍，如果最大流还是 \(2\sum req\)，那就是对的。

• 第一个问题：

  • 不妨设原本 \(key_{0,0}\to key_{1,1}\) 的流量为 \(x\)，由网络构建和最大流为 \(2\sum req\)，有：
  \[\begin{cases} & key_{0,0}\to key_{0,1}(req_0-x)\\ & key_{0,0}\to key_{1,1}(x) \\ & key_{1,0}\to key_{1,1}(req_1-x) \\ & key_{1,0}\to key_{0,1}(x) \end{cases} \]
  • 考虑改换源汇边后的情况，既然是无向图显然 \(key_{x,0}\to key_{x,1}\)（或者前后颠倒）的流量可以不变，于是有
  \[\begin{cases} & key_{0,0}\to key_{0,1}(req_0-x)\\ & key_{0,0}\to key_{1,0}(x) \\ & key_{1,1}\to key_{1,0}(req_1-x) \\ & key_{1,1}\to key_{0,1}(x) \end{cases} \]

  • 注意到其中 \(key_{0,0}\to key_{1,0}\geqslant x,key_{0,0}\to key_{1,1}\geqslant x\)，且两者都是在不影响 \(key_{0,0}\to key_{0,1}=req_0-x\) 的前提条件下进行的。

  • 于是考虑将 \(key_{0,0}\to key_{1,0}\) 退流，和 \(key_{0,0}\to key_{1,1}\) 合并得到一条新的流 \(key_{1,0}\to key_{1,1}\geqslant x\)，故显然 \(key_{1,0}\to key_{1,1}\) 一定存在合法构造方案。

  • 同理可证 \(key_{0,0}\to key_{0,1}\) 一定存在合法构造方案，换言之，两次最大流都是 \(2\sum req\) 可以藉由上面的流量关系推出合法构造方案的存在性。

• 第二个问题：

  • 我们第二遍把 \(key_1\) 相关的路径反过来了。所以如果原来是对着走，现在就变成同向走了。

  • 故感性理解上不会出现“退流产生的路径当成了推流路径”的问题。

• 综上，在感性理解范围内，本题得解。复杂度 \(O((n^2)^2n^2)=O(n^6)\)，唉不管了反正会过去的。

• p.s.本题输入数据末尾有多余空格，用快读判 EOF 的，自己注意一下。

P2763 试题库问题

• 题意略。该怎么形容呢？区分于带权二分图匹配（每个点在匹配中提供不同的权重），称为二分图带权匹配（每个点需要的匹配数不一样）？

• 总之既然是这样，流一下就好啦，方案随便构造一下。

P2765 魔术球问题

• 题意略。我是傻狗，图都建出来了还看不出来模型...别骂了别骂了...

• 首先非常容易想到 \(\forall \sqrt{i+j}\in \mathbb{N_+},i\to j\)。

• 那不就完了吗！DAG 的不相交最小路径覆盖啊...每次把球数 \(+1\)，在残量网络上跑一跑...累加最大流，看一看路径数超不超...就好了。

• 本题还有一个非常有趣的贪心做法：每次将新加入的数尝试放在所有柱子上，如果不行则开新柱子。

1. 能够放上去的柱子的数量必然为 \(0\) 或 \(1\)。

   • 定义函数 \(h(x)=\min\{a\mid a^2\geqslant 2x+1\}\)，于是能放在 \(x\) 上的最小的数为 \(h(x)^2-x\)。

   • 显然 \(h(x)^2-x\) 互不相同比原命题更强（原命题中，只要满足任意时刻柱顶的 \(x\) 对应的 \(h(x)^2-x\) 中没有两个同时为 \(i\) 即可，松得多）。

   • 如果 \(h(x)^2-x\) 单调，那将绝杀，可惜单不得（不妨以 \(x=13\sim 18\) 为例手推就发现了，\(h(x)\) 改变时会陡增）。但我们有 \(h(x)\) 单调。

   • 注意到对固定的 \(h(x)\)，\(x\) 为区间；于是 \(h(x)^2-x\) 也为区间。设法证明它们不相交，显然这与 \(h(x)^2-x\) 互不相同等价。

   • 不妨取 \(g(x)=\lfloor\frac{x^2-1}{2}\rfloor\)，可以看出，\(g(x)=\max\{i\mid h(i)=x\}\)。这里下取整是因为上取整可能代表着 \(-1\) 跟没减一样，于是在 \(x\) 为偶数时构造出的其实是 \(g(x)=\frac{x^2}{2}\)，自己上面放自己，显然不对。

   • 于是只要证明 \(x^2-(g(x-1)+1)<(x+1)^2-g(x+1)\)，化简得到 \(2x+2>g(x+1)-g(x-1)\)，不太美观换一下元变成 \(2(x-1)+2=2x>g(x)-g(x-2)=\lfloor\frac{x^2-1}{2}\rfloor-\lfloor\frac{(x^2-4x-5}{2}\rfloor\)。

   • 对 \(x\) 分奇偶讨论拆掉下取整符，发现最后化出来都是 \(2x>2x-2\)。注意到这里我们用到 \(g(x-2)\)，显然 \(g\) 在 \(0\) 处无定义，所以对 \(x=2\) 特判：\(3>0\)。

   • 得证。

2. 设 \(f(n)\) 为 \(n\) 个柱子能放至多多少个球，则 \(f(n)=(n+1)^2-g(n+1)-2\)。

   • 首先我们注意到柱顶的数和 \(x\) 构成双射，除了某些倒霉孩子，即对应着化出来的 \(2x-1\) 的数。

   • 谁对应 \(2x-1\)？\(x^2-(g(x-1)+1)+1=x^2-g(x-1)\) 咯，一个更舒服的写法是 \(x^2-g(x)-1(x\geqslant 2)\)。两种写法并不完全相等，这是因为没有 \(g(0)\)，可以认为是类似混循环的东西吧，分别缺 \(2\) 和 \(1\)。

   • 故 \(f(n)\) 即为第 \(n+1\) 个倒霉孩子 \(-1\)，即 \((n+1)^2-g(n+1)-2\)。

P3254 圆桌问题

• 题意略。感觉上该怎么说呢？二分图带权（指点需要多个匹配）匹配？

• 事实上贪心解法，即先安排大单位的正确性在感性上显然...理性上的话，可以考虑反证法，应该较为容易。