机器学习十讲第八讲
维度灾难
什么是维度灾难

高维空间的欧式距离
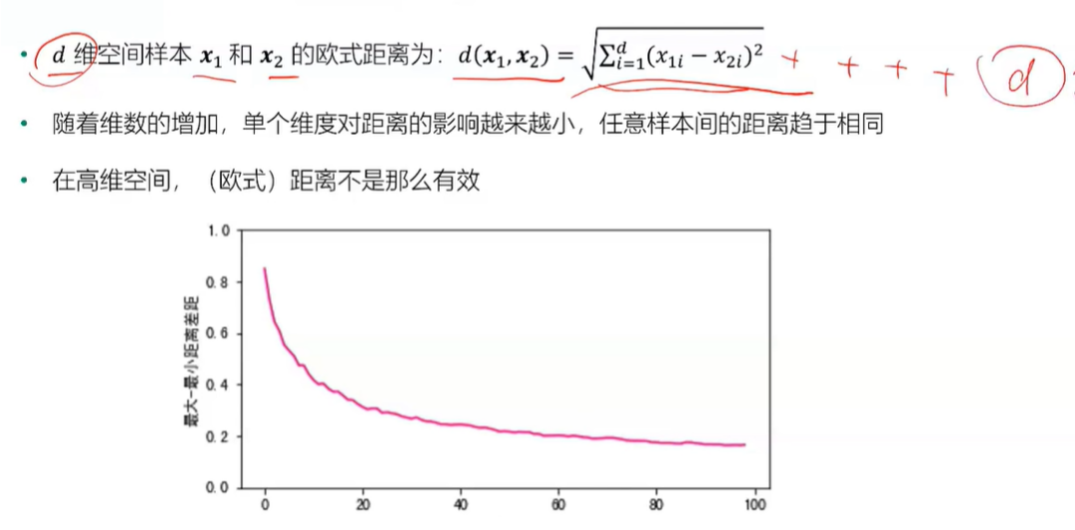
由于距离在高维空间中不再有效,因此一些基于距离的机器学习模型就会收到影响
基于距离的机器学习模型:K近邻(样本间距离),支持向量机(样本到决策面距离),K-Means(样本到聚类中心距离),层次聚类(不同簇之间的距离),推荐系统(商品或用户相似度),信息检索(查询和文档之前的相似度)。
稀疏性与过度拟合
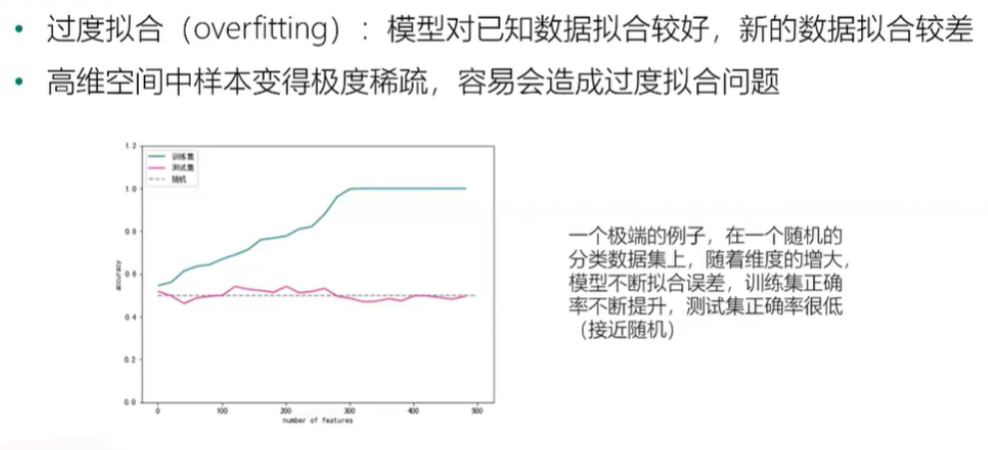
维度灾难举例
决策树

朴素贝叶斯

应对维度灾难
特征选择和降维

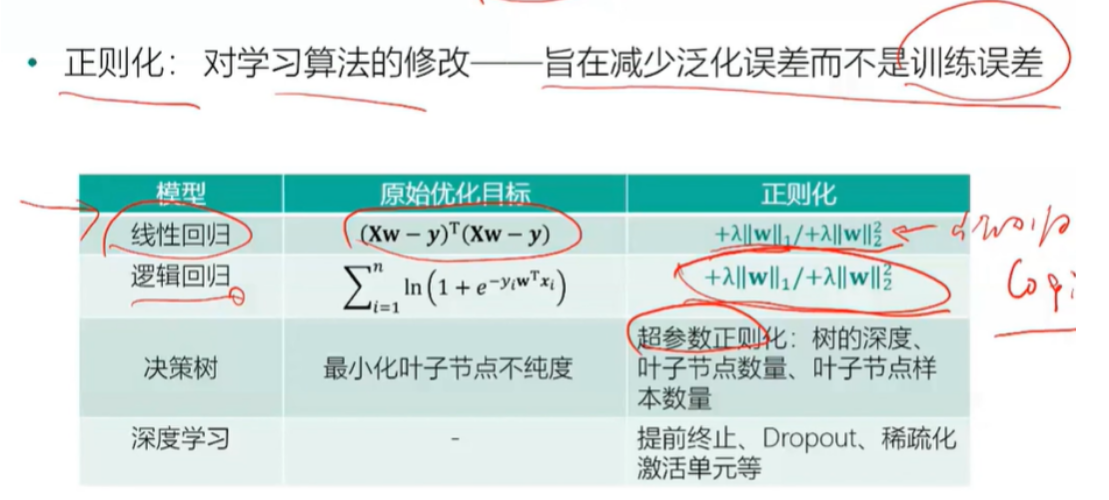
过度拟合与正则化
核技巧

使用Python认识维度问题
单位球体积随着维度的变化
#公式实现
import numpy as np
import math
#引用伽马函数
from scipy.special import gamma
def V(d,r):
return math.pi**(d/2)*(r**d)/gamma(d/2 + 1)
#测试一下
#print(V(1,1))
#使用公式计算1-20维单位球的体积
import pandas as pd
df = pd.DataFrame()
df["d"] = np.arange(1,20)
#半径为1
df["V"] = V(df["d"],1)
df.round(9)
#将单位球体积随着维度的变化进行可视化
##为了方便观察,设置维度为1-70
import matplotlib.pyplot as plt
%matplotlib inline
fig, ax = plt.subplots(figsize=(12, 6)) #设置图片大小
ds = np.arange(1,70)
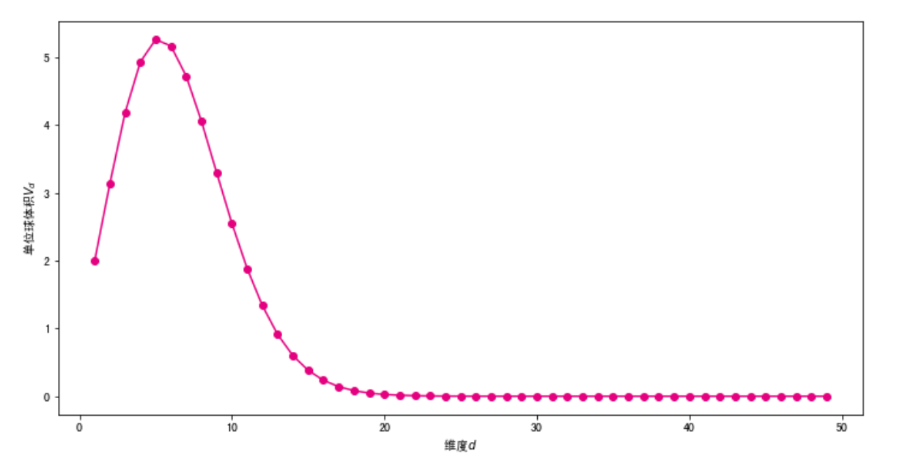
plt.plot(ds,V(ds,1),color="#E4007F",marker="o")
plt.xlabel("维度$d$")
plt.ylabel("单位球体积$V_d$")
#看一下0.1半径体积的比例是多少
##假设边界为0.1
def ratio(d):
return (V(d,1) - V(d,0.9))/ V(d,1)
df["ratio90"] = 1 - 0.9**(df.d)
df.round(6).head(20)
#将0.1边界体积比例可视化
import matplotlib.pyplot as plt
%matplotlib inline
fig, ax = plt.subplots(figsize=(12, 6)) #设置图片大小
ds = np.arange(1,50)
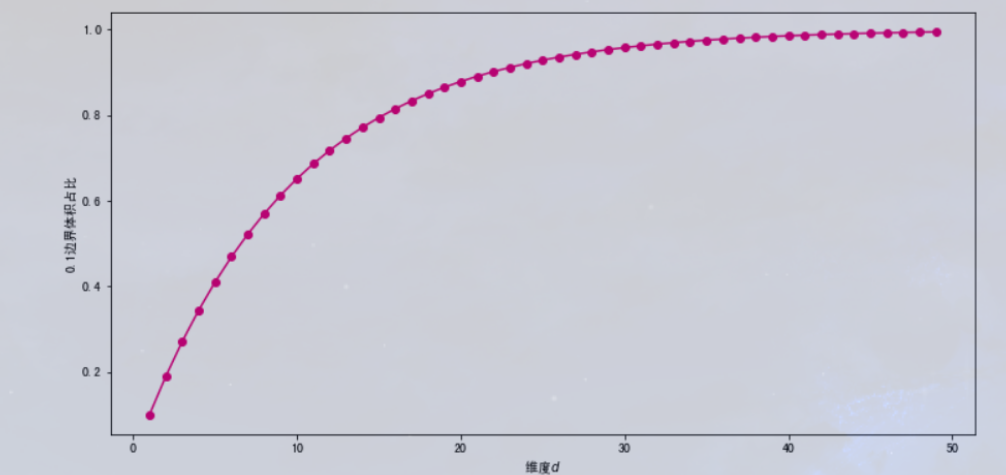
plt.plot(ds,ratio(ds),color="#E4007F",marker="o")
plt.xlabel("维度$d$")
plt.ylabel("0.1边界体积占比")
#刚才的方法是指定边界为0.1,为了能查看任意边界比例的情况,再写一个方法
def volumn_fraction_in_border(d,r):
return(V(d,1)-V(d,1-r))/V(d,1)
#可视化
import numpy as np
#设置维度
ds=[1,2,5,20,100]
#设置颜色
colors=["gray","#E4007F","","","",""]
rs=np.linspace(0,1,100)
result=[]
for d in ds:
vs=[]
for r in rs:
vs.append(volumn_fraction_in_border(d,r))
result.append(vs)
import matplotlib.pyplot as plt
%matplotlib inline
fig, ax = plt.subplots(figsize=(8, 8)) #设置图片大小
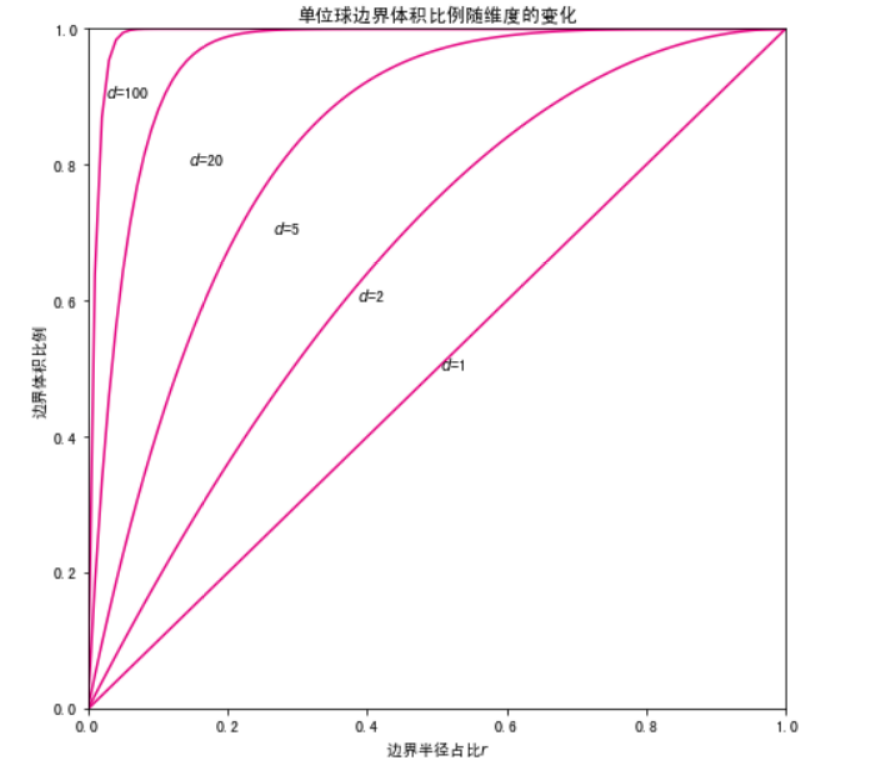
plt.title("单位球边界体积比例随维度的变化")
for i in range(len(ds)):
plt.plot(rs,result[i],color="#E4007F",label="d="+str(ds[i]))
plt.text(rs[50]-i*0.12,0.5+i*0.1,"$d$="+str(ds[i]))
plt.xlim(0,1)
plt.ylim(0,1)
plt.xlabel("边界半径占比$r$")
plt.ylabel("边界体积比例")
- 高维空间中的样本距离
#定义方法计算欧式距离
def data_euclidean_dist(x):
sum_x = np.sum(np.square(x), 1)
dist = np.add(np.add(-2 * np.dot(x, x.T), sum_x).T, sum_x)
return dist
#自定义一个矩阵,计算两两之间的欧式距离
x = np.array([[0, 1, 3], [3, 8, 9], [2, 3, 5]])
dist_matrix = data_euclidean_dist(x)
dist_matrix
#使用mask去掉对角线(0)
##计算该欧式距离中的最小值
mask = np.ones(dist_matrix.shape, dtype=bool)
np.fill_diagonal(mask, 0)
dist_matrix[mask].min()
#生成一个包含5000个样本5000个维度的数据集。每一个维度都是从[-1,1]之间随机生成。
X = np.random.uniform(-1,1,(5000,5000))
#显示
X
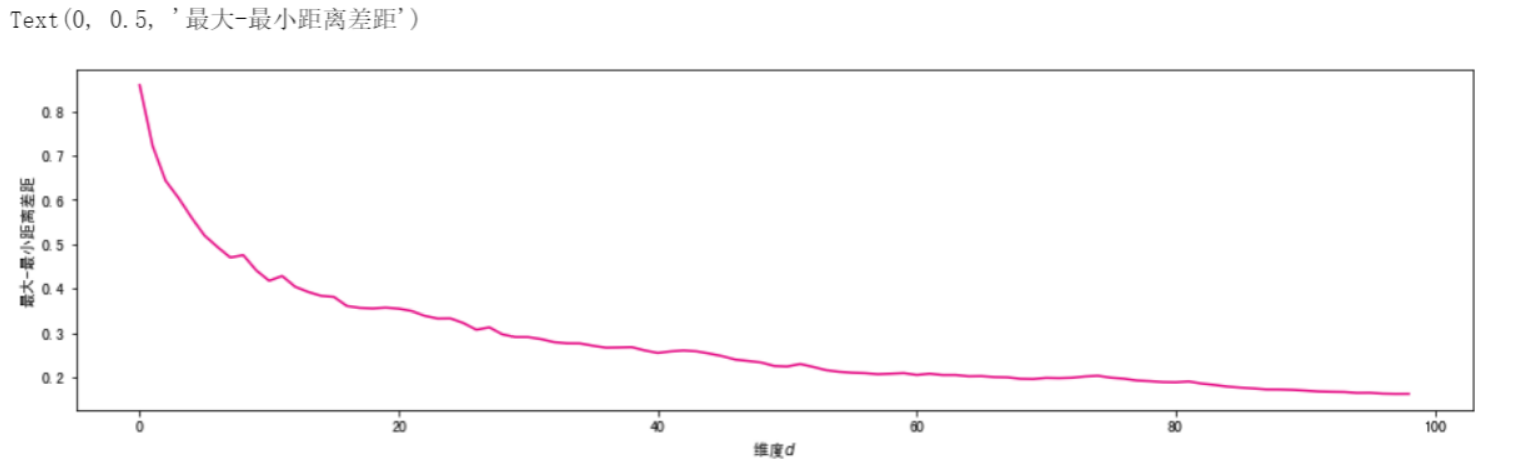
#求随着维度增大,样本间欧式距离最大值与最小值的差值,需要用mask去掉对角0
min_max_list = []
#设置间隔为50
for d in range(50,5000,50):
dist_matrix = data_euclidean_dist(X[:,:d])
mask = np.ones(dist_matrix.shape, dtype=bool)
np.fill_diagonal(mask, 0)
min_max = (dist_matrix[mask].max() - dist_matrix[mask].min())/dist_matrix[mask].max()
if d%50 == 0:
print(d,min_max.round(3))
min_max_list.append(min_max)
#可视化
import matplotlib.pyplot as plt
%matplotlib inline
fig, ax = plt.subplots(figsize=(16, 4)) #设置图片大小
ds = np.arange(0,len(min_max_list))
plt.plot(ds,min_max_list,color="#E4007F")
plt.xlabel("维度$d$")
plt.ylabel("最大-最小距离差距")
- 维度对分类性能的影响
#生成Trunk数据集
import pandas as pd
import numpy as np
max_features,num_samples = 1000,500 #最大特征数量和样本数量
X_pos = pd.DataFrame()
X_neg = pd.DataFrame()
for i in range(max_features):
X_pos["f"+str(i+1)] = np.random.randn(num_samples)+ np.sqrt(1/(i+1)) #生成当前特征的正类样本
X_neg["f"+str(i+1)] = np.random.randn(num_samples)- np.sqrt(1/(i+1)) #生成当前特征的负类样本
X_pos["label"],X_neg["label"] = 0,1 #添加标签
trunk_data = pd.concat([X_pos,X_neg],axis=0) #合并正类和负类样本
trunk_data.head()
#随机选择几个特征,用散点图可视化正负类样本的分布情况。
import matplotlib.pyplot as plt
%matplotlib inline
features = [1,5,10,100]
fig, ax = plt.subplots(figsize=(16, 4)) #设置图片大小
for i in range(len(features)):
plt.subplot(1,4,i+1)
plt.scatter(trunk_data[trunk_data.label == 0]["f" + str(features[i])], trunk_data[trunk_data.label == 0]["f" + str(features[i]+1)], color="#007979")
plt.scatter(trunk_data[trunk_data.label == 1]["f" + str(features[i])], trunk_data[trunk_data.label == 1]["f" + str(features[i]+1)],color="#E4007F")
plt.xlabel("feature " + str(features[i]))
plt.ylabel("feature " + str(features[i]+1))
plt.tight_layout()
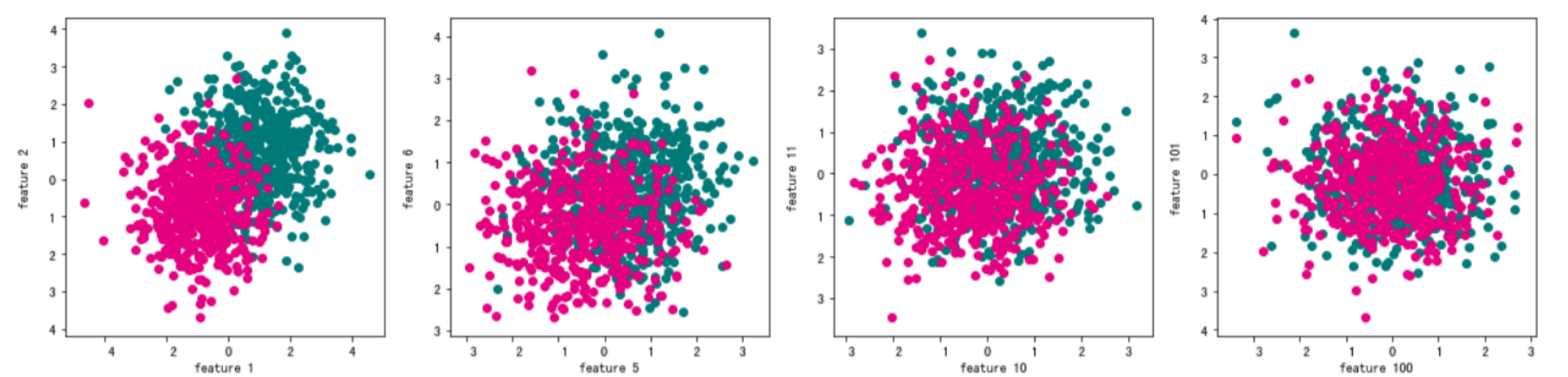
#不断增加特征数量,观察分类性能随着维数的变化。
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(trunk_data.iloc[:,:-1],trunk_data["label"],test_size=0.5)#训练集和测试集划分
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
num_features = np.arange(1,max_features,10)
exp_times = 10 #试验次数
test_result = np.zeros(len(num_features))
train_result = np.zeros(len(num_features))
#实验用到不同维度,所以使用两层for循环控制
for t in range(exp_times): #运行多次试验
scores_train = [] #记录训练集正确率
scores_test = [] #记录测试集正确率
for num_feature in num_features: #使用不同特征数量
clf = LinearDiscriminantAnalysis()#新建分类模型
clf.fit(X_train.iloc[:,:num_feature],y_train)#用训练集对应特征数去训练
score_train = clf.score(X_train.iloc[:,:num_feature],y_train)#记录训练集正确率
score_test = clf.score(X_test.iloc[:,:num_feature],y_test)#记录测试集正确率
scores_train.append(score_train)
scores_test.append(score_test)
train_result += np.array(scores_train)
test_result += np.array(scores_test)
print(t)
#求平均值
test_result /= exp_times
train_result /= exp_times
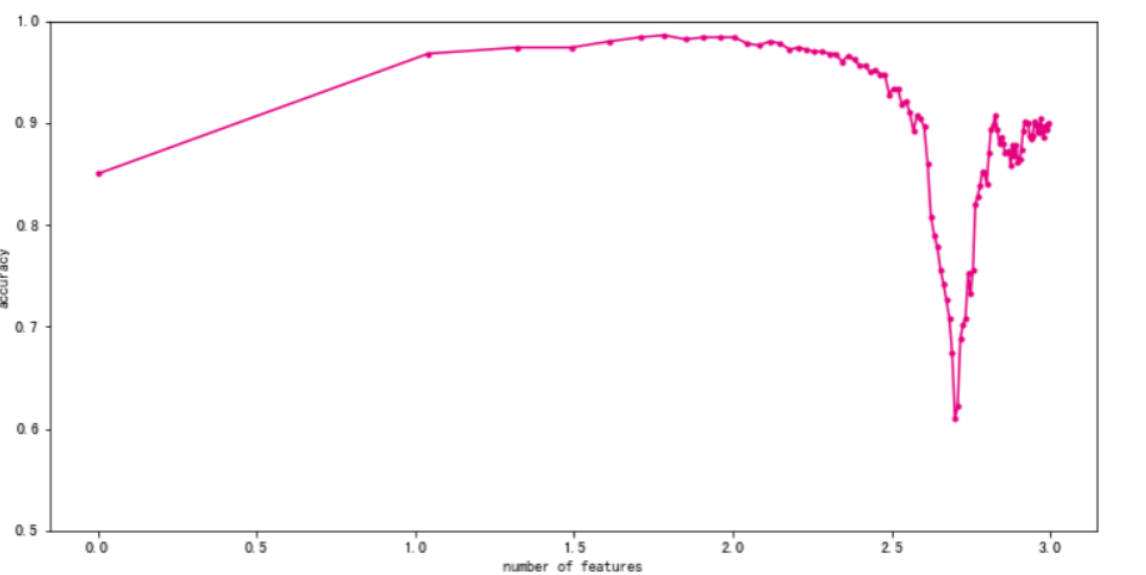
#训练好后进行可视化
fig, ax = plt.subplots(figsize=(12, 6))
ax.plot(np.log10(num_features),test_result,color="#E4007F",marker=".")
plt.ylim(0.5,1)
plt.xlabel("number of features")
plt.ylabel("accuracy")