JM8.6(H.264编码器)源码注释——码率控制部分主要推导
讲解分为三个部分:MAD线性回归参数估计的计算、RQ模型参数计算、Qstep估计,以下分别从JM8.6的源码注释和公式推导进行讲解。更多关于码率控制的注释在我的Github里面。
一、矩阵求解MAD线性回归参数的程序注释:
1 void MADModelEstimator (int n_windowSize)//MAD模型估计 2 { 3 int n_realSize = n_windowSize;//暂时存放当前的窗口大小 4 int i; 5 double oneSampleQ; 6 double a00 = 0.0, a01 = 0.0, a10 = 0.0, a11 = 0.0, b0 = 0.0, b1 = 0.0; 7 double MatrixValue; 8 Boolean estimateX2 = FALSE; 9 10 for (i = 0; i < n_windowSize; i++) {// find the number of samples which are not rejected 11 if (PictureRejected[i])//如果某一帧图像被限制了 n_realSize就减一次 最后记录的是没有被限制使用的图像 12 n_realSize--; 13 } 14 15 // default MAD model estimation results 16 17 MADPictureC1 = MADPictureC2 = 0.0;//某一帧图像MAD线性预测的参数 18 19 for (i = 0; i < n_windowSize; i++) { 20 if (!PictureRejected[i])//如果图像没有被限制 21 //难道是记录最后一帧没有被限制图像的MAD??? 22 oneSampleQ = PictureMAD[i];//把最后一个没有被限制的图像的MAD赋值给oneSampleQ变量 23 } 24 for (i = 0; i < n_windowSize; i++) {// if all non-rejected MAD are the same, take 1st order model 25 if ((PictureMAD[i] != oneSampleQ) && !PictureRejected[i])//图像没有被限制且不是最后一帧被限制的图像 26 estimateX2 = TRUE;//estimateX2标志位赋值为真 27 if (!PictureRejected[i])//如果图像没有被限制 28 //这句话不知道在做怎样的优化??? W值 29 MADPictureC1 += PictureMAD[i] / (ReferenceMAD[i]*n_realSize);// 30 } 31 32 // take 2nd order model to estimate X1 and X2 33 if ((n_realSize >= 1) && estimateX2) { 34 for (i = 0; i < n_windowSize; i++) { 35 if (!PictureRejected[i]) { 36 /*图像没有被限制 好厉害这部分就是在求解参数 37 平方差求和最小来优化 线性回归 38 i从0到n的(MADPictureC1*ReferenceMAD[i]+MADPictureC2-PictureMAD[i])^2求和=平方差求和最小优化 39 相当于我下面公式推导中i从0到n的(W*x[i]+b-y[i])^2求和=平方差求和最小优化 40 41 以下部分是通过矩阵求解两个参数的过程 42 */ 43 a00 = a00 + 1.0; 44 a01 += ReferenceMAD[i]; 45 a10 = a01; 46 a11 += ReferenceMAD[i]*ReferenceMAD[i]; 47 b0 += PictureMAD[i]; 48 b1 += PictureMAD[i]*ReferenceMAD[i]; 49 } 50 } 51 // solve the equation of AX = B 52 MatrixValue=a00*a11-a01*a10;//求矩阵A的行列式 53 if(fabs(MatrixValue)>0.000001)//行列式不为0 A可逆 有解 54 { 55 //通过伴随矩阵求解 56 MADPictureC2=(b0*a11-b1*a01)/MatrixValue;//b 57 MADPictureC1=(b1*a00-b0*a10)/MatrixValue;//W 58 } 59 else//行列式为0 A不可逆 60 { 61 //只是一个特解 62 MADPictureC2=0.0;//b 63 MADPictureC1=b0/a01;//W 64 } 65 66 } 67 if(img->type==P_SLICE)//如果是P帧 把上面刚刚计算的结果覆盖掉前面计算的 68 { 69 PMADPictureC1=MADPictureC1; 70 PMADPictureC2=MADPictureC2; 71 } 72 }
以下是矩阵求解MAD线性回归参数的推导过程:

二、 码率控制模型的线性回归参数估计程序注释:
1 //码率控制模型的核心 2 void RCModelEstimator (int n_windowSize) 3 { 4 int n_realSize = n_windowSize; 5 int i; 6 double oneSampleQ; 7 double a00 = 0.0, a01 = 0.0, a10 = 0.0, a11 = 0.0, b0 = 0.0, b1 = 0.0; 8 double MatrixValue; 9 Boolean estimateX2 = FALSE; 10 11 for (i = 0; i < n_windowSize; i++) {// find the number of samples which are not rejected 12 if (m_rgRejected[i])//如果存在某一帧图像数据被拒绝 13 n_realSize--;//求和遍历的n减少 即被限制的数据不参加优化过程 14 } 15 16 // default RD model estimation results 17 18 m_X1 = m_X2 = 0.0;//码率控制模型参数先清零 19 20 for (i = 0; i < n_windowSize; i++) { 21 if (!m_rgRejected[i])// 22 oneSampleQ = m_rgQp[i];//m_rgQp[i]里面是Qstep值 记录最后一个没有被限制的数据 23 } 24 for (i = 0; i < n_windowSize; i++) {// if all non-rejected Q are the same, take 1st order model 25 if ((m_rgQp[i] != oneSampleQ) && !m_rgRejected[i])//如果当前的数据不是最后一个且当前数据没有被限制使用 26 estimateX2 = TRUE;//标志位置为真 27 if (!m_rgRejected[i])//如果数据没有被拒绝 28 m_X1 += (m_rgQp[i] * m_rgRp[i]) / n_realSize;//为啥这样算??? 29 } 30 31 // take 2nd order model to estimate X1 and X2 看不懂求解过程???? 32 if ((n_realSize >= 1) && estimateX2) { 33 for (i = 0; i < n_windowSize; i++) { 34 if (!m_rgRejected[i]) {//数据没有被限制使用 35 //线性回归优化 36 a00 = a00 + 1.0; 37 a01 += 1.0 / m_rgQp[i]; 38 a10 = a01; 39 a11 += 1.0 / (m_rgQp[i] * m_rgQp[i]); 40 b0 += m_rgQp[i] * m_rgRp[i]; 41 b1 += m_rgRp[i]; 42 } 43 } 44 // solve the equation of AX = B 45 MatrixValue=a00*a11-a01*a10;//A矩阵行列式 46 if(fabs(MatrixValue)>0.000001)//A行列式不为0 满秩 47 { 48 m_X1=(b0*a11-b1*a01)/MatrixValue; 49 m_X2=(b1*a00-b0*a10)/MatrixValue; 50 } 51 else//A的行列式为0 特解 52 { 53 m_X1=b0/a00; 54 m_X2=0.0; 55 } 56 57 } 58 if(img->type==P_SLICE) 59 { 60 Pm_X1=m_X1; 61 Pm_X2=m_X2; 62 } 63 }
以下的码率控制模型的线性回归参数估计推导过程:
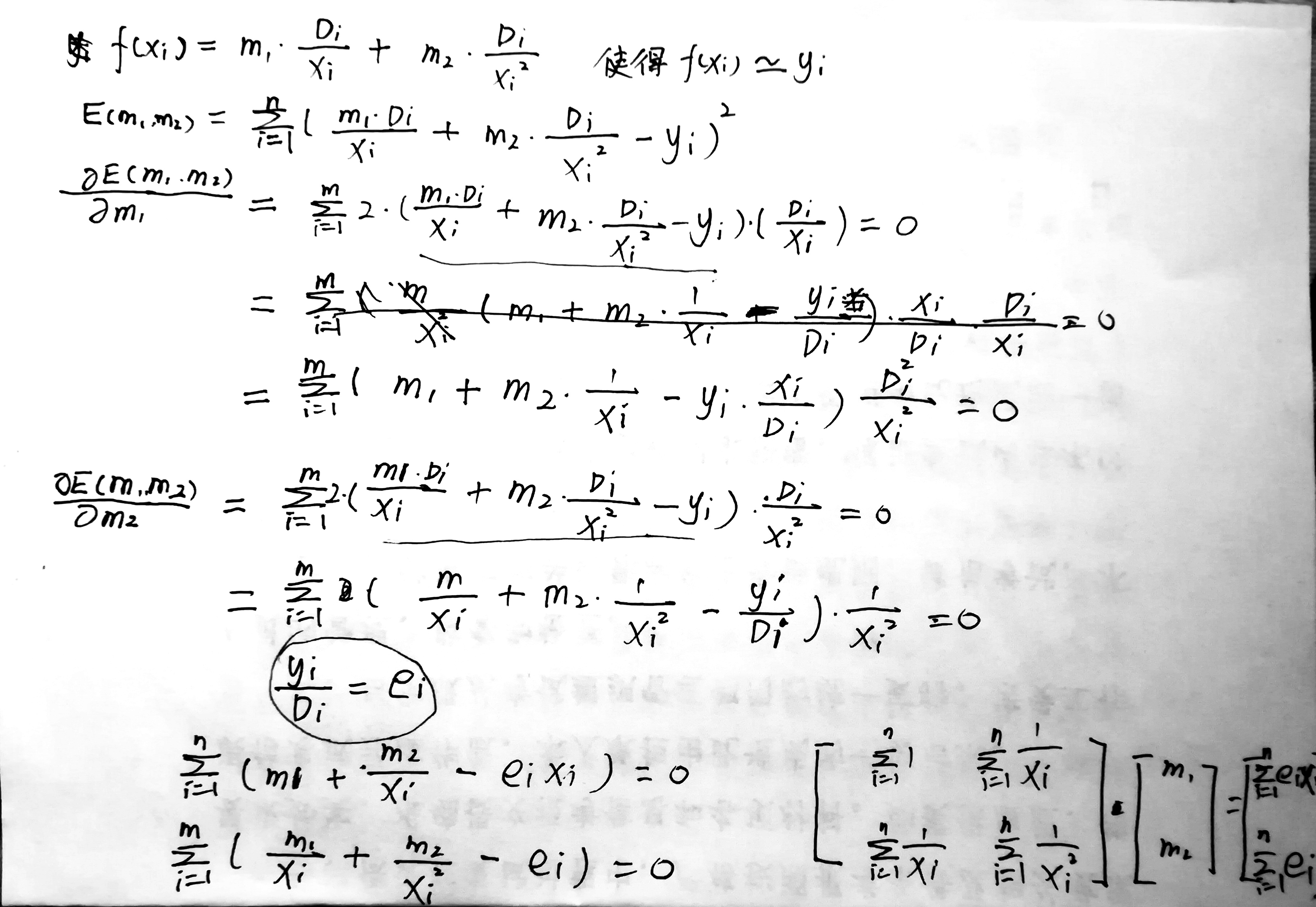
三、Qstep(量化步长)估计的程序注释:
1 //Pm_X1=bit_rate*1.0;//RD模型参数 2 //Pm_X2=0.0; 3 m_X1=Pm_X1;//RD模型的两个参数 4 m_X2=Pm_X2; 5 m_Hp=PPreHeader; 6 m_Qp=Pm_Qp;//前一帧P帧的QP 7 DuantQp=PDuantQp;//量化参数最大的变化量 2 8 MADPictureC1=PMADPictureC1;//PMADPictureC1=1 线性预测的两个参数 9 MADPictureC2=PMADPictureC2;//PMADPictureC1=0 10 PreviousPictureMAD=PPictureMAD[0]; 11 12 /* predict the MAD of current picture*/ 13 CurrentFrameMAD=MADPictureC1*PreviousPictureMAD+MADPictureC2;//线性预测当前帧的MAD 14 15 /*compute the number of bits for the texture*/ 16 17 if(T<0)//当T小于0 直接使用前一个P帧的QP来预测 然后加2 得到当前的QP值 18 { 19 m_Qc=m_Qp+DuantQp;//前一帧P帧的QP加2 DuantQp=2 20 m_Qc = MIN(m_Qc, RC_MAX_QUANT); // clipping 21 } 22 else//当T大于0 执行RD优化 23 { 24 m_Bits =T-m_Hp;//减去头部bits ?? 25 m_Bits = MAX(m_Bits, (int)(bit_rate/(MINVALUE*frame_rate)));//MINVALUE=4 确定一个最大值上界 26 //求解m_Bits(Qstep)=X1*D/Qstep+x2*D/(Qstep*Qstep)一元二次方程解 27 dtmp = CurrentFrameMAD * m_X1 * CurrentFrameMAD * m_X1 \ 28 + 4 * m_X2 * CurrentFrameMAD * m_Bits;//判别式 29 if ((m_X2 == 0.0) || (dtmp < 0) || ((sqrt (dtmp) - m_X1 * CurrentFrameMAD) <= 0.0)) // fall back 1st order mode 30 m_Qstep = (float) (m_X1 * CurrentFrameMAD / (double) m_Bits); 31 else // 2nd order mode 32 m_Qstep = (float) ((2 * m_X2 * CurrentFrameMAD) / (sqrt (dtmp) - m_X1 * CurrentFrameMAD)); 33 34 m_Qc=Qstep2QP(m_Qstep);//0.625到224的Qstep映射到QP 0到51 35 //m_Qp是前一P帧QP的预测 36 m_Qc = MIN(m_Qp+DuantQp, m_Qc); // control variation 37 m_Qc = MIN(m_Qc, RC_MAX_QUANT); // clipping 38 m_Qc = MAX(m_Qp-DuantQp, m_Qc); // control variation 39 m_Qc = MAX(RC_MIN_QUANT, m_Qc);// QP平滑和限幅 40 }
以下的已知码率控制RQ模型的参数后,对当前Qstep(量化步长)的估计过程:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号