吴恩达机器学习第三周：Logistic Regression逻辑回归
先来说说回归的思想吧：
常见的回归就是通过一系列的点，计算得到一条线。当有新的输入时，可以直接计算得到输出。用最小二乘法求解线性回归方程就是我们最早接触到的回归。对于线的表示都不尽相同，如线性回归得到的预测函数是y=w⃗ T∗x⃗ +a，逻辑回归则是一条S型曲线。
逻辑回归和线性回归（Linear Regression）的区别如下：
- 普通线性回归主要用于连续变量的预测，即，线性回归的输出y的取值范围是整个实数区间（y∈R）
- 逻辑回归用于离散变量的分类，即它的输出y的取值范围是一个离散的集合，主要用于类的判别，而且其输出值y表示属于某一类的概
Logistic Regression逻辑回归主要用于分类问题，常用来预测概率，如知道一个人的年龄、体重、身高、血压等信息，预测其患心脏病的概率是多少。经典的LR用于二分类问题（只有0,1两类）。
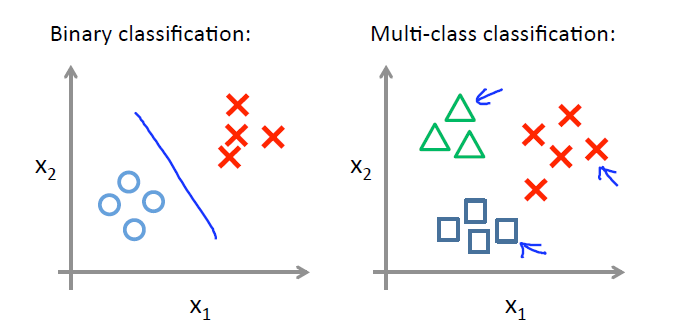
二分类问题
二分类问题是指预测的y值只有两个取值（0或1），二分类问题可以扩展到多分类问题。例如：我们要做一个垃圾邮件过滤系统，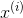
是邮件的特征，预测的y值就是邮件的类别，是垃圾邮件还是正常邮件。对于类别我们通常称为正类（positive class）和负类（negative class），垃圾邮件的例子中，正类就是正常邮件，负类就是垃圾邮件。
逻辑回归
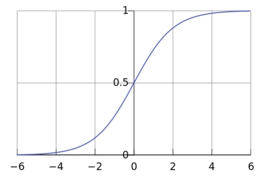
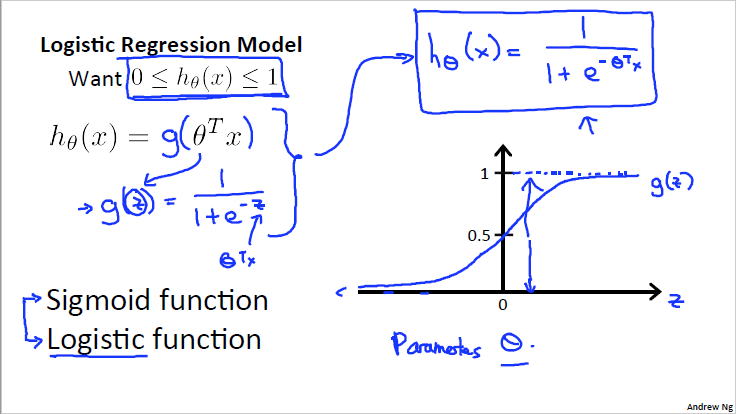
Logistic函数
对于任意的x值，对应的y值都在区间(0,1)内。
函数公式为：
，
决策边界（Decision Boundary）
线性的决策边界，如图所示的决策边界为x1+x2 = 3
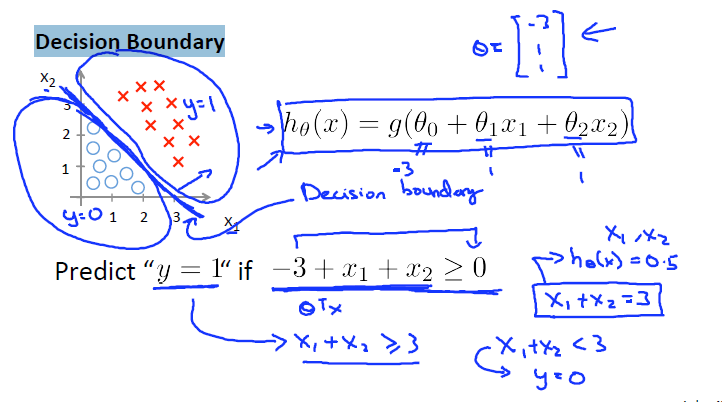
另一种决策边界，决策边界为x1^2+ x2^2 = 1
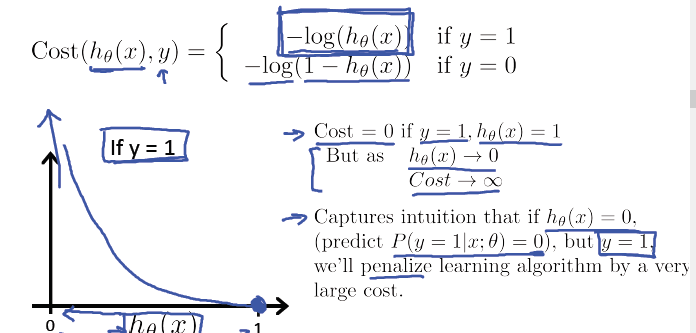
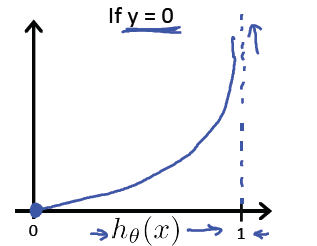
逻辑回归的代价函数：
逻辑回归的代价函数很可能是一个非凸函数(non-convex)，有很多局部最优点，所以如果用梯度下降法，不能保证会收敛到全局最小值。
多分类问题
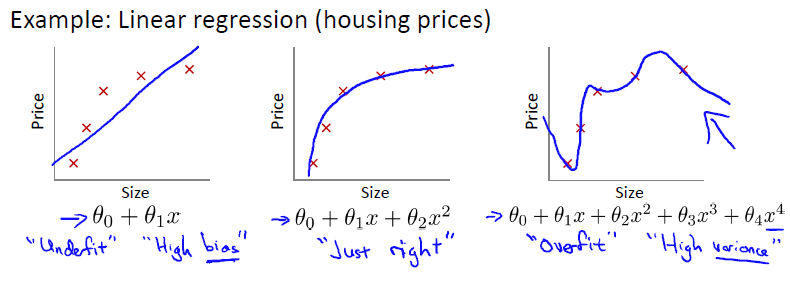
过拟合问题overfitting——正则化Regulation
overfitting:If we have too many features, the learned hypothesis may fit the training set very well , but fail to generalize to new examples (predict prices on new examples).
过拟合：如果特征值过多，学习模型能很好的适应训练集，但无法对新数据进行很好的预测，泛化能力弱。
图三属于overfitting
解决方法：
1、减少特征数量（找主要的，或者用算法找）
2、正则化（保留所有参数，但较少维度或数量级）
正则化项：加入参数过多的惩罚，其中lamda是控制正则化参数
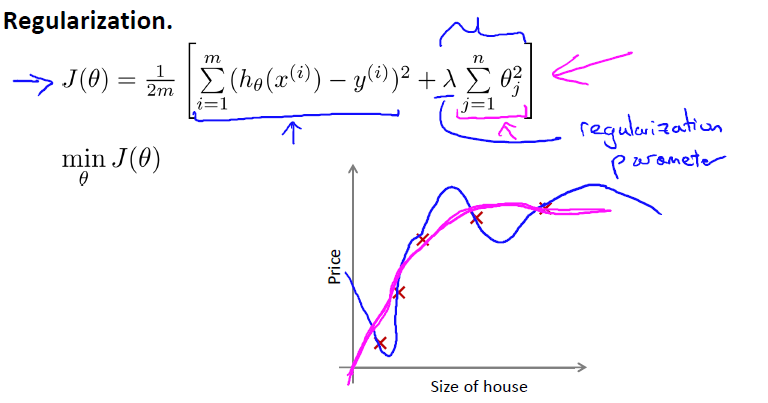
如果lamda过大，会造成欠拟合underfitting，相当于所有theta都约等于0，只剩第一项。
正则化线性回归：正则化+梯度下降结合：
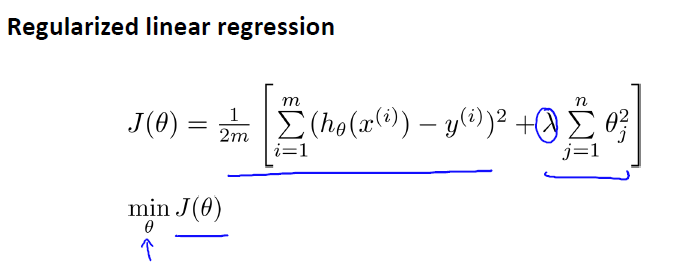
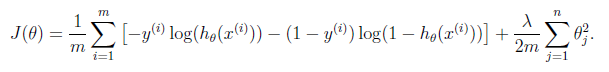
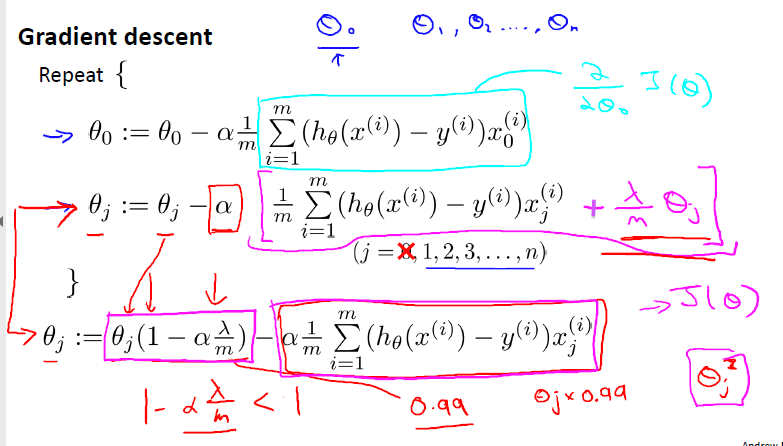
不惩罚theta0
正规方程的求解：
