机车启动模型的理论推导
假设机车启动时初速度为 \(0\),瞬间达到额定功率 \(P\),阻力 \(f\) 恒定。
易得牵引力为
\[F=\dfrac{P}{v}-f
\]
则加速度为
\[\begin{aligned}
a
&=\dfrac{F}{m}\\
&=\dfrac{\dfrac{P}{v}-f}{m}
\end{aligned}
\]
所以
\[\begin{aligned}
\dfrac{\text{d}v}{\text{d}t}
&=\dfrac{\dfrac{P}{v}-f}{m}\\
&=\dfrac{P-vf}{mv}
\end{aligned}
\]
分离变量
\[\text{d}t=\dfrac{mv}{P-fv}\text{d}v
\]
两边积分
\[\begin{aligned}
T_1
&=\int_0^v\dfrac{mv}{P-fv}\text{d}v\\
&=\dfrac{mP}{f^2}\ln\dfrac{P}{P-fv}-\dfrac{mv}{f}
\end{aligned}
\]
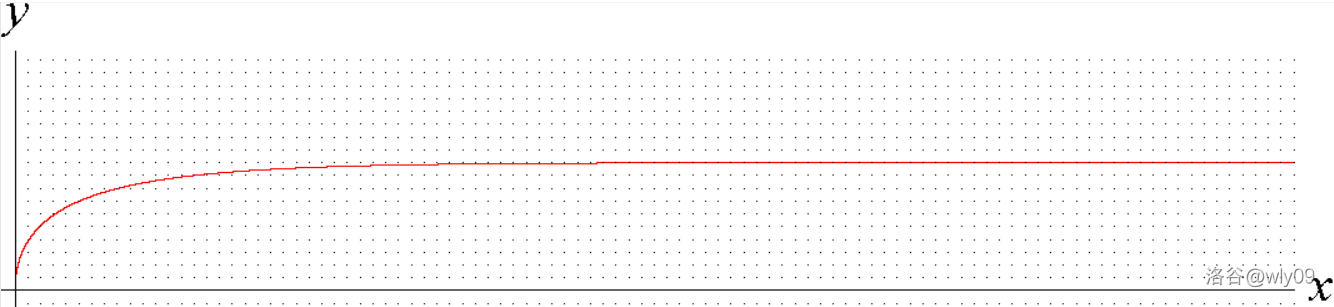
特别地,\(f\to 0\) 时,有
\[T_0=\dfrac{m}{2P}v^2
\]
\(T_0\) 式中 \(v\) 可以被反解出来,但在 \(T_1\) 中不行。
从 \(T_1\) 式中,我们也可以看到,在当前模型下,\(v_\max=\dfrac{P}{f}\) 只能无限接近,不能达到。


