Orderless Recurrent Models for Multi-label Classification

论文信息：地址，代码，CVPR2020.

概述

循环神经网络在处理变长数据时非常有效，并且和CNN搭配之后，也能够用于计算机视觉任务，比如图片注释和图片多标签分类。多标签分类任务需要为图片分配若干个标签或概念，比如物体类别，颜色，材料等。由于标签类别多，模型需要学习标签之间的依赖关系。同时标签概念之间的相似性也使得模型产生不确定性。

在图片分类任务中，LSTM通常被用来生成标签序列。然而，该方法有一个弊端：如果LSTM预测的标签序列与真实标签序列的排序顺序不同，将会对损失施加惩罚，但事实上标签之间可以换顺序，比如识别含有狗和球的图片时输出dog,ball或ball,dog都是对的。这严重阻碍了模型收敛，使训练过程复杂化，并且通常导致模型质量下降。

和其他工作不同，本论文不要求输出序列具有预定义的顺序，而是通过对真实标签序列重新排序使之与预测标签序列尽可能匹配从而让模型损失函数最小。本文提出了两种方法，分别叫作minimal loss alignment(MLA)和predicted label alignment(PLA)。

方法

Image-to-sequence模型

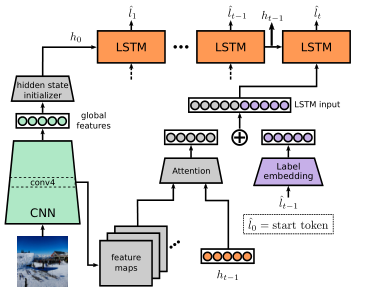
该论文使用如下图所示的CNN-RNN结构进行图片多标签分类，CNN用于抽取图片特征，RNN用于生成标签序列。CNN的特征经过全连接层后输入到RNN中解码，RNN的每一步将会预测一个标签：

\[\begin{aligned} x_t &= E \cdot \hat{l}_{t-1} \\ h_t &= LSTM(x_t, h_{t-1}, c_{t-1}) \\ p_t &= W \cdot h_t + b \end{aligned} \]

其中\(E\)是词嵌入矩阵，用于将标签\(\hat{l}_{t-1}\)转化为向量，\(h_{t-1}, c_{t-1}\)是LSTM的隐状态和记忆单元，\(p_t\)就是预测的标签概率。模型中还用到了Attention机制，用于在不同时间关注图像的不同部分。

模型训练

训练集由图片标签对组成，一个图片标签对表示为\((I,L)\)，其中标签\(L=\{l_1,\dots,l_n\},l_i \in \mathbb{L}, |\mathbb{L}|=m\)。\(P \in \mathbb{R}^{m\times n}\)是LSTM预测的概率矩阵。如果实际的预测标签序列过长或者过短，将会进行截断或者补齐。模型的交叉熵损失可以定义为：

\[\begin{aligned} &\mathcal{L} = tr(T \log (P)) \\ &with \begin{cases} T_{ij}=1 \quad if \ l_t=j \\ T_{ij}=0 \quad otherwise \end{cases} \end{aligned} \]

其中，\(T \in \mathbb{R}^{n \times m}\)是正确标签矩阵。模型损失是通过比较每一步的预测标签与真实标签进行计算。

正如上述公式表示的，正确标签的顺序对于损失的计算非常关键。而对于无序的图像分类任务，标签顺序往往是随机的，因此如何减小不必要的惩罚变得非常重要。已经有多种方法用于解决这个问题，最通用的方法就是根据一个标准对标签进行排序，其中包括rare-first和frequent-first方法，然而这些方法仍然存在诸多不足，如下图所示。

无序循环模型

为了减轻由于对标签施加固定顺序而导致的问题，该文在计算损失之前将正确标签与网络的预测对齐，提出了两种策略。

minimal loss alignment (MLA)

\[\begin{aligned} &\mathcal{L} = tr(T \log (P)) \\ &subject \ to \begin{cases} T_{ij} \in \{0,1\} \ \sum_j T_{tj} = 1 \\ \sum_t T_{tj} = 1 \quad \forall j \in L \\ \sum_t T_{tj} = 1 \quad \forall j \notin L \end{cases} \end{aligned} \]

其中，\(T \in \mathbb{R}^{n \times m}\)是正确标签排列矩阵。在三个约束中，第一个保证了每一个时间步最多一个标签；第二个如果正确标签存在\(j\)标签，则在\(T\)中必须体现；第三个保证了如果正确标签没有\(j\)标签，则排列矩阵也不应该含有\(j\)标签。这是一个分配问题，可以通过匈牙利算法在多项式时间内求解。

predicted label alignment (PLA)

\[\begin{aligned} &\mathcal{L} = tr(T \log (P)) \\ &subject \ to \begin{cases} T_{ij} \in \{0,1\} \ \sum_j T_{tj} = 1 \\ T_{ij} = 1 \quad if \ \hat{l}_t \in L \ and \ j = \hat{l}_t \\ \sum_t T_{tj} = 1 \quad \forall j \in L \\ \sum_t T_{tj} = 1 \quad \forall j \notin L \end{cases} \end{aligned} \]

其中，\(\hat{l}_t\)是模型在时间步\(t\)的预测标签。这个方法首先固定矩阵\(T\)中的那些刚好被预测命中的标签，然后应用匈牙利算法分配其余的标签。由于对\(T\)的限制增多，因此第二种方法比第一种方法通常导致更高的损失，但该方法与LSTM实际预测的标记更加一致。

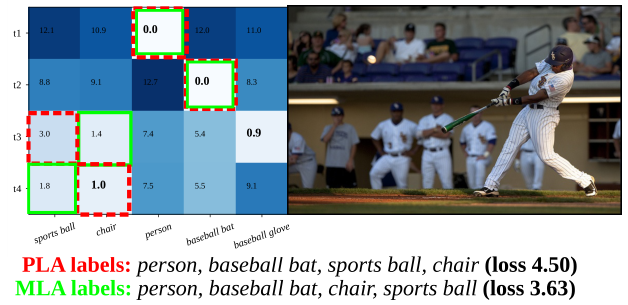
两种方法的预测示例以及对应的分数矩阵(cost matrix)如下图所示。

实验

数据集：MS-COCO，NUS-WIDE，WIDER Attribute和PA-100K四个数据集。

由于本文对计算机视觉领域不是很熟悉，阅读此文只是出于对这个方法感兴趣，因此将重点放在方法介绍。具体的实验结论分析请读者参照原文。