变分自编码器VAE原理

1 概述

在讨论变分自编码器前，我觉得有必要先讨论清楚它与自编码器的区别是什么，它究竟是干什么用的。否则看了一堆公式也不知道变分自编码器究竟有什么用。

众所周知，自编码器是一种数据压缩方式，它把一个数据点\(x\)有损编码为低维的隐向量\(z\)，通过\(z\)可以解码重构回\(x\)。这是一个确定性过程，我们实际无法拿它来生成任意数据，因为我们要想得到\(z\)，就必须先用\(x\)编码。

变分自编码器可以用来解决生成问题，它可以直接通过模型生成隐向量\(z\)，并且生成的\(z\)是既包含了数据信息又包含了噪声，因此用各不相同的\(z\)可以生成无穷无尽的新数据。所以问题的关键就是怎么生成这种\(z\)。

我们更加具体地描述一下需求。我们要生成和原数据相似的数据，那当然得有一个模块能够学习到数据的分布信息，这个被称为编码器。这个编码器获得了数据分布信息，同时也应该融入一些随机性，所以引入了高斯噪声。这两部分信息融合后，应该由另一个模块解码生成新的数据吧，所以又需要一个解码器。如此下来，就出现了VAE的大致结构，如下图这样：

图1 VAE模型结构

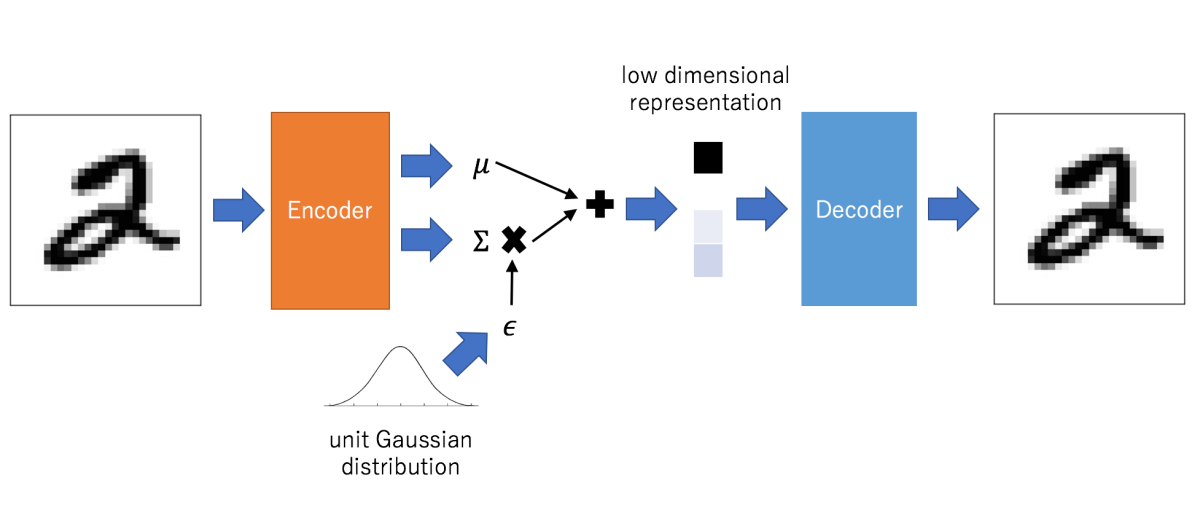
那么还有一个问题，GAN也是生成模型，变分自编码器VAE和GAN有什么区别呢。我的理解是，VAE和GAN都能生成新数据，但在生成质量的判断上，它们的做法不同。VAE使用概率思想，通过计算生成数据分布与真实数据分布的相似度(KL散度)来判断。但GAN直接使用神经网络训练一个判别器，用判别器判断生成的数据是不是真的和原分布差不多。

在对变分自编码器有一个基本的了解后，我们可以来看看它究竟是怎么做的。但问题又来了，变分自编码器既涉及到神经网络，又涉及到概率模型，结果就是搞神经网络和搞概率模型的都看不懂。参照Jaan Altosaar的教程，本文将从神经网络和概率模型两个角度对变分自编码器进行讲解。

2 神经网络角度

以神经网络语言描述的话，VAE包含编码器、解码器和损失函数三部分。编码器将数据压缩到隐空间\((z)\)中。解码器根据隐状态\(z\)重建数据。

图2 神经网络角度看VAE

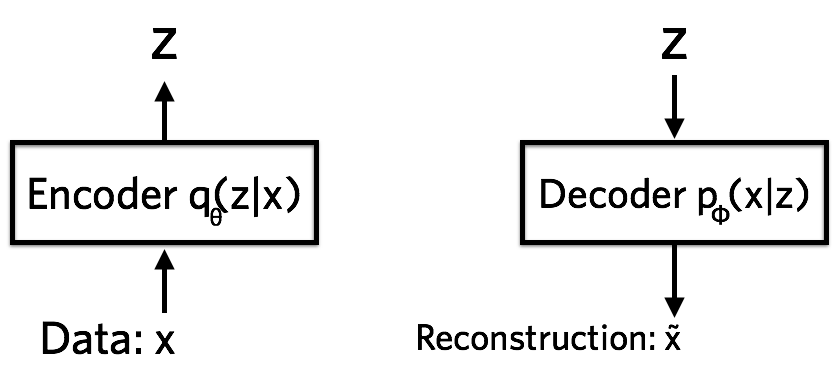
编码器是一个神经网络，它的输入是数据点\(x\)，输出是隐向量\(z\)，它的参数是\(\theta\)，因此编码器可以表示为\(q_{\theta}(z|x)\)。为了更具体地说明，假设\(x\)是784维的黑白图片向量。编码器需要将728维的数据\(x\)编码到隐空间\(z\)，而且\(z\)的维度要比784小很多，这就要求编码器必须学习将数据有效压缩到此低维空间的方法。

此外，我们假设\(z\)是服从高斯分布的，编码器输出\(z\)的过程实际上可以分解成两步：1）首先编码器输出高斯分布的参数(均值、方差)，这个参数对于每个数据点都是不一样的；2）将噪声与该高斯分布融合并从中采样获得\(z\)。

解码器也是一个神经网络，它的输入是隐向量\(z\)，输出是数据的概率分布，它的参数是\(\phi\)，因此解码器可以表示为\(p_{\phi}(x|z)\)。还是以上面例子讲解，假设每个像素取值是0或者1，一个像素的概率分布可以用伯努利分布表示。因此解码器输入\(z\)之后，输出784个伯努利参数，每个参数表示图中的一个像素是取0还是取1。原始784维图像\(x\)的信息是无法获取的，因为解码器只能看到压缩的隐向量\(z\)。这意味着存在信息丢失问题。

变分自编码器的损失函数是带正则项的负对数似然函数。因为所有数据点之间没有共享隐向量，因此每个数据点的损失\(l_i\)是独立的，总损失\(L=\sum_{i=1}^N l_i\)是每个数据点损失之和。而数据点\(x_i\)的损失\(l_i\)可以表示为：

\[l_i(\theta,\phi)=-\mathbb{E}_{z \sim p_{\theta}(z|x_i)}[\log_{p_{\phi}}(x_i|z)] + KL(p_{\theta}(z|x_i)||p(z)) \]

第一项是重构损失，目的是让生成数据和原始数据尽可能相近。第二项KL散度是正则项，它衡量了两个分布的近似程度。

重构损失好理解，它保证了数据压损的质量嘛，但是正则项该如何理解呢？在变分自编码器中，\(p(z)\)被指定为标准正态分布，也就是\(p(z)=\mathcal{N}(\mathbf{0}, \mathbf{I})\)。那正则项的存在就是要让\(p_{\theta}(z|x_i)\)也接近正态分布。如果没有正则项，模型为了减小重构损失，会不断减小随机性，也就是编码器输出的方差，没有了随机性变分自编码器也就无法生成各种数据了。因此，变分自编码器需要让编码的\(z\)，即\(p_{\theta}(z|x_i)\)接近正态分布。如果编码器输出的\(z\)不服从标准正态分布，将会在损失函数中对编码器施加惩罚。这样理解之后，变分自编码器应该长下面这样：

图3 VAE的另一种解释

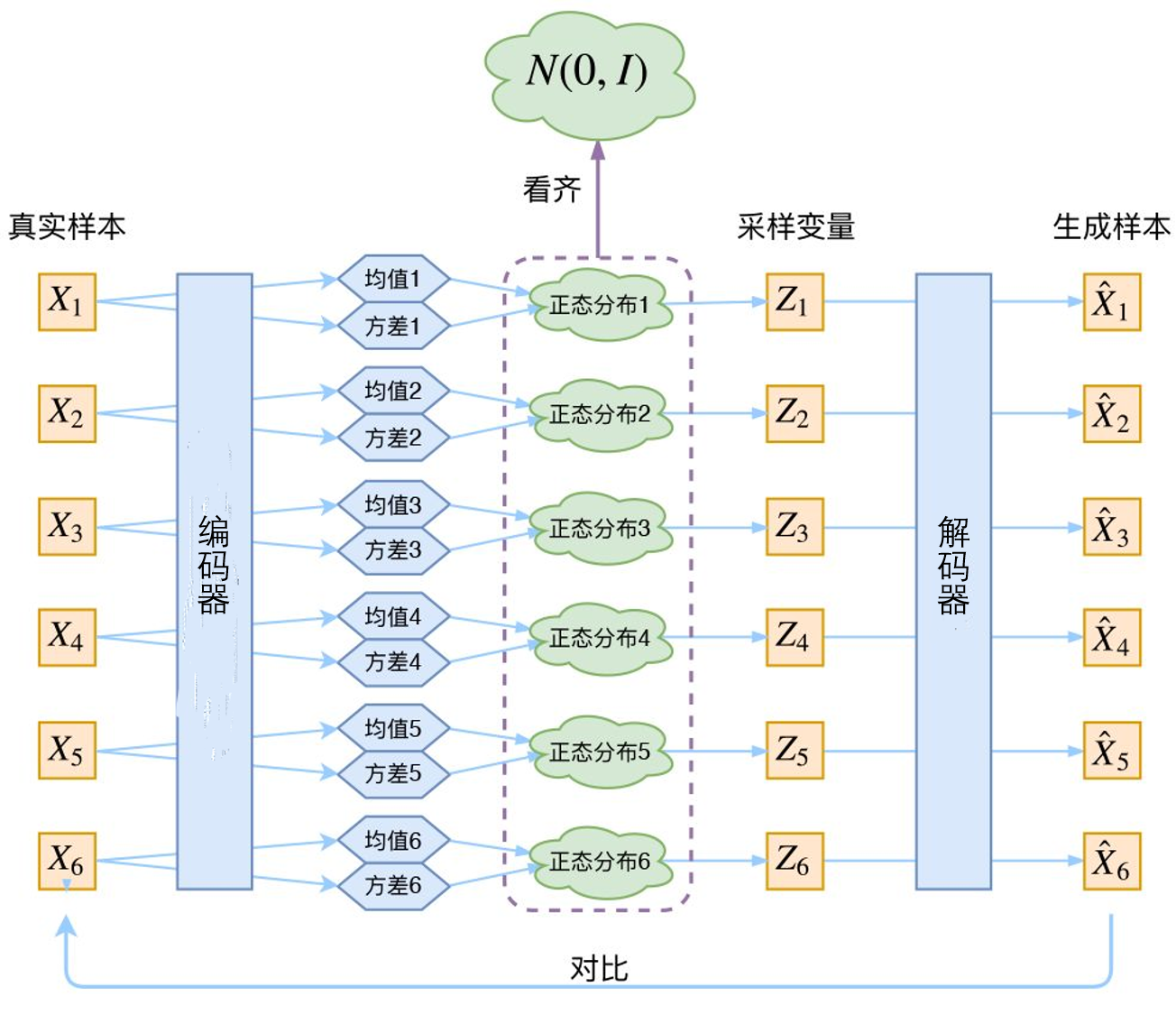
3 概率模型角度

现在，让我们忘掉所有深度学习和神经网络知识，从概率模型的角度重新看变分自编码器。在最后，我们仍然会回到神经网络。

变分自编码器可以用下面概率图模型表示；

图4 VAE对应的概率图模型

隐向量\(z\)从先验分布\(p(z)\)中采样得到，然后数据点\(x\)从以\(z\)为条件的分布\(p(x|z)\)中产生。整个模型定义了数据和隐向量的联合分布\(p(x,z)=p(x|z)p(z)\)，对于手写数字而言，\(p(x|z)\)就是伯努利分布。

上面所说的是根据隐变量\(z\)重构数据\(x\)的过程，但我们如何得到数据\(x\)对应的隐向量\(z\)呢？或者说如何计算后验概率\(p(z|x)\)。根据贝叶斯定理：

\[p(z|x)=\frac{p(x|z)p(z)}{p(x)} \]

考虑分母\(p(x)\)，它可以通过\(p(x)=\int p(x|z)p(z)dz\)计算。但不幸的是，该积分需要指数时间来计算，因为需要对所有隐变量进行计算。没办法直接求解，就只能近似该后验分布了。

假设我们使用分布\(q_{\lambda}(z|x)\)来近似后验分布\(p(x|z)\)，\(\lambda\)是参数。在变分自编码器里，后验分布是高斯分布，因此\(\lambda\)就是每个数据点隐向量的均值和方差，即\(\lambda_{x_i}=(\mu_{x_i},\sigma_{x_i}^2)\)。这也说明了每个数据点的后验分布是不一样的，我们实际上是要求\(q_{\lambda}(z|x_i)\)，要得到每个数据点所对应的\(\lambda_{x_i}\)。

那么怎么知道用分布\(q_{\lambda}(z|x)\)近似真实的后分布\(p(z|x)\)到底好不好呢？我们可以用KL散度来衡量：

\[\begin{aligned} KL\left(q_{\lambda}(z|x)||p(z|x)\right) &= \int q_{\lambda}(z|x) \ln \frac{q_{\lambda}(z|x)}{p(z|x)}dz \\ &=\mathbb{E}_{z \sim q_{\lambda}(z|x)} \ln \frac{q_{\lambda}(z|x)}{p(z|x)} \\ &=\mathbb{E}_{z \sim q_{\lambda}(z|x)} [\ln q_{\lambda}(z|x) - \ln p(z|x)] \\ &=\mathbb{E}_{z \sim q_{\lambda}(z|x)} [\ln q_{\lambda}(z|x) - \ln \frac{p(z)p(x|z)}{p(x)}] \\ &=\mathbb{E}_{z \sim q_{\lambda}(z|x)} [\ln q_{\lambda}(z|x) - \ln p(z) - \ln p(x|z)] + \ln p(x) \\ &=KL(q_{\lambda}(z|x)||p(z)) - \mathbb{E}_{z \sim q_{\lambda}(z|x)} \ln p(x|z) + \ln p(x) \\ \end{aligned} \]

现在的目标就变成了找到使得KL散度最小的参数\(\lambda^*\)。最优的后验分布就可以表示为：

\[q_{\lambda^*}(z|x)=\arg\min_{\lambda}KL\left(q_{\lambda}(z|x)||p(z|x)\right) \]

但是这依然无法进行计算，因为仍然会涉及到\(p(x)\)，我们还需要继续改进。我们整理一下，可以得到下面形式：

\[KL\left(q_{\lambda}(z|x)||p(z|x)\right) - \ln p(x) = -\mathbb{E}_{z \sim q_{\lambda}(z|x)} \ln p(x|z) + KL(q_{\lambda}(z|x)||p(z)) \]

我们需要最小化KL散度，而\(\ln p(x)\)是一个定值，因此我们需要最小化等式右边。注意到没有，这个优化目标和神经网络的优化目标是一致的。

接下来就要引入下面这个ELBO函数，令其等于上式右边取负：

\[ELBO(\lambda)= \mathbb{E}_{z \sim q_{\lambda}(z|x)} \ln p(x|z) - KL(q_{\lambda}(z|x)||p(z)) \]

我们可以将ELBO与上面的KL散度计算公式结合，得到：

\[\ln p(x)= ELBO(\lambda) + KL\left(q_{\lambda}(z|x)||p(z|x)\right) \]

由于KL散度始终是大于等于0的，而\(\ln p(x)\)是一个定值，这意味着最小化KL散度等价于最大化ELBO。ELBO(Evidence Lower Bound)让我们能够对后验分布进行近似推断，可以从最小化KL散度中解脱出来，转而最大化ELBO。而后者在计算上是比较方便的。

在变分自编码器模型中，每个数据点的隐向量\(z\)是独立的，因此ELBO可以被分解成所有数据点对应项之和。这使得我们可以用随机梯度下降来进行学习，因为mini-batch之间独立，我们只需要最大化一个mini-batch的ELBO就可以了。每个数据点的ELBO表示如下：

\[ELBO_i(\lambda)=\mathbb{E}_{z \sim q_{\lambda}(z|x_i)}[\ln p(x_i|z)] - KL(q_{\lambda}(z|x_i)||p(z)) \]

现在可以再用神经网络来进行描述了。我们使用一个编码器\(q_{\theta}(z|x)\)建模\(q_{\lambda}(z|x)\)，该编码器输入数据\(x\)然后输出参数\(\lambda\)（注意\(\lambda\)是正态分布的参数）。再使用一个解码器\(p_{\phi}(x|z)\)建模\(p(x|z)\)，该解码器输入隐向量和参数，输出重构数据分布。\(\theta\)和\(\phi\)是编码器和解码器的参数。此时我们可以使用这两个网络来重写上述ELBO：

\[ELBO_i(\theta,\phi)=\mathbb{E}_{z \sim q_{\theta}(z|x_i)}[\ln p_{\phi}(x_i|z)] - KL(q_{\theta}(z|x_i)||p(z)) \]

可以看到，\(ELBO_i(\theta,\phi)\)和我们之前从神经网络角度提到的损失函数就差一个符号，即\(ELBO_i(\theta,\phi)=-l_i(\theta,\phi)\)。一个需要最大化，一个需要最小化，所以本质上是一样的。我们仍然可以将KL散度看作正则项，将期望看作重构损失。但是概率模型清楚解释了这些项的意义，即最小化近似后验分布\(q_{\lambda}(z|x)\)和模型后验分布\(p(z|x)\)之间的KL散度。

ELBO的计算中重构损失很好计算，但后一项KL散度该怎么计算呢。上面提到，编码器实际上生成的是参数\(\lambda=(\mu, \sigma)\)，\(z\)是一个正态分布，因此有：

\[\begin{aligned} KL(q_{\theta}(z|x)||p(z)) &= KL(q_{\theta}(z|x)|| \mathcal{N}(0, I)) \\ &= \int \frac{1}{\sqrt{2\pi \sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \ln \frac{\frac{1}{\sqrt{2\pi \sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}}{\frac{1}{\sqrt{2\pi \sigma^2}}e^{-\frac{x^2}{2}}} dx \\ &= \int \frac{1}{\sqrt{2\pi \sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \ln \frac{1}{\sqrt{\sigma^2}} \times e^{\frac{x^2}{2} - \frac{(x-\mu)^2}{2\sigma^2}} dx \\ &= \int \frac{1}{\sqrt{2\pi \sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} [-\frac{1}{2}\ln \sigma^2 + \frac{1}{2}x^2 -\frac{1}{2} \frac{(x-\mu)^2}{\sigma^2}] dx \\ &= \frac{1}{2} \int \frac{1}{\sqrt{2\pi \sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} [-\ln \sigma^2 + x^2 - \frac{(x-\mu)^2}{\sigma^2}] dx \\ &= \frac{1}{2} (-\ln \sigma^2 + \mathbb{E}[x^2] - \frac{1}{\sigma^2}\mathbb{E}[(x - \mu)^2]) \\ &= \frac{1}{2} (-\ln \sigma^2 + \sigma^2 + \mu^2 - 1) \end{aligned} \]

因此，KL散度散度这一项最终可以通过\(\lambda\)参数计算出来。那么还剩下最后一个问题，我们怎么从\(q_{\theta}(z|x)\)采样\(z\)呢，这个问题在VAE中使用重参数化技巧来解决。

4 重参数化技巧

实现变分自编码器的最后一件事是如何对随机变量的参数求导数。我们用\(q_{\theta}(z|x)\)确定一个高斯分布，然后从中采样\(z \in \mathcal{N}(\mu, \sigma^2)\)，但采样操作是不可导的，进而导致模型无法反向传播。

这个问题可以使用重参数化技巧实现。从均值\(\mu\)和标准偏差\(\sigma\)的正态分布中采样，等价于先从标准正态分布中采样\(\epsilon\)，然后再对其进行下列变换，这种方式也对应于图1中的\(z\)的计算：

\[z = \mu + \sigma \odot \epsilon \]

从\(\epsilon\)到\(z\)只涉及了线性操作，这是可导的。而\(\epsilon\)的分布是确定的，不需要学习。采样\(\epsilon\)的操作不参与梯度下降，采样得到\(\epsilon\)值才参与梯度下降。

图5 VAE中的重参数化技巧

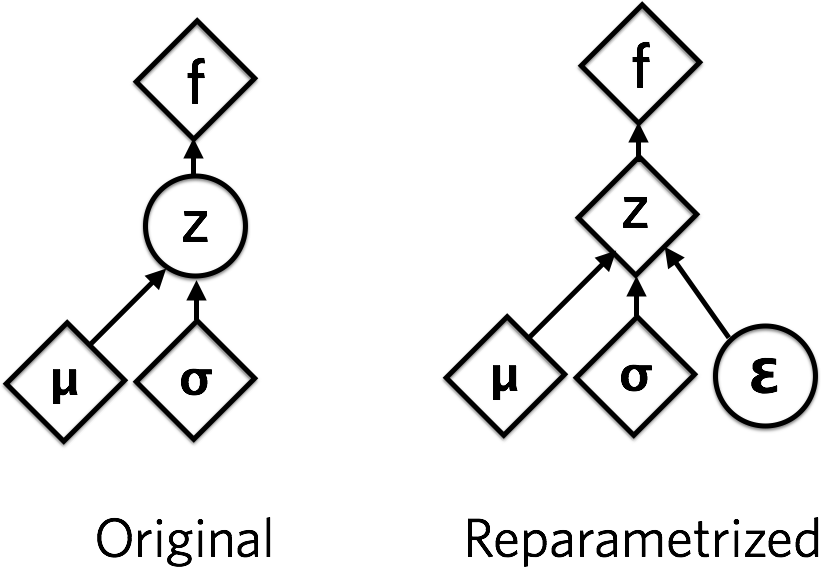
这张图表示了重参数化的形式，其中圆是随机节点，菱形是确定性节点。

5 代码实现

现在可以使用模型进行一些实验了，可以参考Pytorch Examples给出的代码：https://github.com/pytorch/examples/tree/master/vae ，代码比我想象中的的简单。

class VAE(nn.Module):
    def __init__(self):
        super(VAE, self).__init__()

        #  编码器用到的全连接层
        self.fc1 = nn.Linear(784, 400)
        self.fc21 = nn.Linear(400, 20)
        self.fc22 = nn.Linear(400, 20)
        # 解码器用到的全连接层
        self.fc3 = nn.Linear(20, 400)
        self.fc4 = nn.Linear(400, 784)

    def encode(self, x):
	# 编码器，输出均值和log方差的平方，即\mu和\log \sigma^2
        h1 = F.relu(self.fc1(x))
        return self.fc21(h1), self.fc22(h1)

    def reparameterize(self, mu, logvar):
	# 重参数化
        std = torch.exp(0.5 * logvar)
        eps = torch.randn_like(std)
        return mu + eps * std

    def decode(self, z):
	# 解码，从隐向量恢复原始输入
        h3 = F.relu(self.fc3(z))
        return torch.sigmoid(self.fc4(h3))

    def forward(self, x):
        mu, logvar = self.encode(x.view(-1, 784))
        z = self.reparameterize(mu, logvar)
        return self.decode(z), mu, logvar

    # Reconstruction + KL divergence losses summed over all elements and batch
    def loss_function(self, recon_x, x, mu, logvar):
	# 重构损失
        BCE = F.binary_cross_entropy(recon_x, x.view(-1, 784), reduction='sum')
	# KL散度
        KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())

        return BCE + KLD

6 其它

6.1 Mean-field推断和amortized推断

Mean-field变分推断是指在没有共享参数的情况下对\(N\)个数据点进行分布推断：

\[q(z)=\prod_i^N q(z_i;\lambda_i) \]

这意味着每个数据点都有自由参数\(\lambda_i\)（例如对于高斯隐变量，\(\lambda_i =(\mu_i，\sigma_i)\)）。对于新数据点，我们需要针对其mean-field参数\(\lambda_i\)最大化ELBO。

amortized推断是指“摊销”数据点之间的推断成本。一种方法是在数据点之间共享（摊销）变分参数\(\lambda\)。例如，在变分自编码器中，编码器网络的参数\(\theta\)，这些全局参数在所有数据点之间共享。如果我们看到一个新的数据点并想看一下它的近似后验\(q(z_i)\)，我们可以再次运行变分推断（最大化ELBO直到收敛），或者直接使用现有的共享参数。与Mean-field变分推断相比，这很明显可以节省时间。

哪一个更灵活呢？Mean-field变分推断严格来说更具表达性，因为它没有共享参数。每个数据点独立的参数\(\lambda_i\)可以确保近似后验最准确。但另一方面，通过在数据点之间共享参数可以限制近似分布族的容量或表示能力，加入更多约束。

6.2 条件变分自编码器

变分自编码器的生成过程是无监督的，这意味着我们没办法生成特定的数据。比如想要生成数字“2”的图片，我们没办法把信息传递给变分自编码器。

条件变分自编码器(Conditional VAE, CVAE)就是用来解决这个问题的，它可以实现给定一些变量来控制生成某一类数据。

变分自编码器的优化目标是：

\[ELBO_i(\theta,\phi)=\mathbb{E}_{z \sim q_{\theta}(z|x_i)}[\log p_{\phi}(x_i|z)] - KL(q_{\theta}(z|x_i)||p(z)) \]

编码器生成\(z\)只和\(x\)有关，而解码器重构\(x\)也只与\(z\)有关，这就是为什么没办法融合数据\(x\)的其他信息（比如标签）。现在假设对于\(x\)还有额外的信息\(c\)，我们可以这样修改VAE的优化目标：

\[ELBO_i(\theta,\phi)=\mathbb{E}_{z \sim q_{\theta}(z|x_i,c)}[\log p_{\phi}(x_i|z,c)] - KL(q_{\theta}(z|x_i,c)||p(z|c)) \]

现在，编码器和解码器都已经和\(c\)联系起来了。此外，\(p(z|c)\)表示对于每个\(c\)，都有一个\(z\)的分布与之对应。

条件变分自编码器的代码实现可以参考 https://github.com/wiseodd/generative-models

参考资料

posted @ 2020-03-25 17:59 WeilongHu 阅读(17573) 评论(2) 编辑收藏举报

刷新页面返回顶部

胡伟龙的博客

乱花逐流水，古月绕千山