单表密码
定义
单表代替是密码学中最基础的一种加密方式。在加密时用一张自制字母表上的字母来代替明文上的字母(比如说A——Z,B——D)来达到加密。
破解思路
破解方法为统计法。在英语中,最常用的字母为E,所以在密文中代替E 的字母出现的频率也最高,由此便可破解。
分类
凯撒密码(单表密码)
在密码学中,恺撒密码(英语:Caesar cipher),或称恺撒加密、恺撒变换、变换加密,是一种最简单且最广为人知的加密技术。它是一种替换加密的技术,明文中的所有字母都在字母表上向后(或向前)按照一个固定数目进行偏移后被替换成密文。例如,当偏移量是3的时候,所有的字母A将被替换成D,B变成E,以此类推。这个加密方法是以罗马共和时期恺撒的名字命名的,当年恺撒曾用此方法与其将军们进行联系。
根据偏移量的不同,还存在若干特定的恺撒密码名称:
偏移量为10:Avocat(A→K)
偏移量为13:ROT13
偏移量为-5:Cassis (K 6)
偏移量为-6:Cassette (K 7)
备注:只是换为了python2的代码,懒得优化了,见谅。
#!/usr/bin/python
inp = raw_input()
for i in inp:
if i == ' ':
print(" ")
elif i in ['X','Y','Z','x','y','z']:
print(chr(ord(i)-23))
elif 'a'<=i<='w'or 'A'<=i<='W':
print(chr(ord(i)+3))
else:
print(i)
https://blog.csdn.net/aladdinzebra/article/details/88937515
密码破解
即使使用唯密文攻击,恺撒密码也是一种非常容易破解的加密方式。可能有两种情况需要考虑:
(1)攻击者知道(或者猜测)密码中使用了某个简单的替换加密方式,但是不确定是恺撒密码;
(2)攻击者知道(或者猜测)使用了恺撒密码,但是不知道其偏移量。
对于第一种情况,攻击者可以通过使用诸如频率分析或者样式单词分析的方法, 马上就能从分析结果中看出规律,得出加密者使用的是恺撒密码。
对于第二种情况,解决方法更加简单。由于使用恺撒密码进行加密的语言一般都是字母文字系统,因此密码中可能是使用的偏移量也是有限的,例如使用26个字母的英语,它的偏移量最多就是25(偏移量26等同于偏移量0,即明文;偏移量超过26,等同于偏移量1-25)。因此可以通过穷举法,很轻易地进行破解。
其中一种方法是在表格中写下密文中的某个小片段使用所有可能的偏移量解密后的内容——称为候选明文,然后分析表格中的候选明文是否具有实际含义,得出正确的偏移量,解密整个密文。
例如,被选择出的密文片段是"EXXEGOEXSRGI",从右表中的候选明文,我们可以很快看出其正确的偏移量是4。也可以通过在每一个密文单词的每一个字母下面,纵向写下整个字母表其他字母,然后可以通过分析,得出其中的某一行便是明文。
另外一种攻击方法是通过频率分析。当密文长度足够大的情况下,可以先分析密文中每个字母出现的频率,然后将这一频率与正常情况下的该语言字母表中所有字母的出现频率做比较。
例如在英语中,正常明文中字母E和T出现的频率特别高,而字母Q和Z出现的频率特别低,而在法语中出现频率最高的字母是E,最低的是K和W。
可以通过这一特点,分析密文字母出现的频率,可以估计出正确的偏移量。
此外,有时还可以将频率分析从字母推广到单词,例如英语中,出现频率最高的单词是:the, of, and, a, to, in...。我们可以通过将最常见的单词的所有可能的25组密文,编组成字典,进行分析。
比如QEB可能是the,MPQY可能是单词know(当然也可能是aden)。
但是频率分析也有其局限性,它对于较短或故意省略元音字母或者其他缩写方式写成的明文加密出来的密文进行解密并不适用。
另外,通过多次使用恺撒密码来加密并不能获得更大的安全性,因为使用偏移量A加密得到的结果再用偏移量B加密,等同于使用A+B的偏移量进行加密的结果。
频率分析:
https://blog.csdn.net/qq_29185043/article/details/88680267
# -*- coding: utf-8 -*-
s=['A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z']
b=[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
f1=open("D:单表破译.txt","r+")
message=f1.read()#读取文章
sum=0#总数
for i in message:
if('A'<=i<='Z'):#只记录字母
sum=sum+1#记录字母总数
for j in range(0,26):
if(s[j]==i):
b[j]=b[j]+1
print(sum)#字母总数
print(b)#各个字母总数
for i in range(0,26):
result.append((b[i]/sum))
print(s[i],":",(b[i]/sum)*100)
#打印频率
维吉尼亚密码(多表密码)
在一个凯撒密码中,字母表中的每一字母都会作一定的偏移,例如偏移量为3时,A就转换为了D、B转换为了E……而维吉尼亚密码则是由一些偏移量不同的恺撒密码组成。
为了生成密码,需要使用表格法。这一表格包括了26行字母表,每一行都由前一行向左偏移一位得到。具体使用哪一行字母表进行编译是基于密钥进行的,在过程中会不断地变换。

例如,假设明文为:
ATTACKATDAWN
选择某一关键词并重复而得到密钥,如关键词为LEMON时,密钥为:
LEMONLEMONLE
对于明文的第一个字母A,对应密钥的第一个字母L,于是使用表格中L行字母表进行加密,得到密文第一个字母L。类似地,明文第二个字母为T,在表格中使用对应的E行进行加密,得到密文第二个字母X。以此类推,可以得到:
明文:ATTACKATDAWN
密钥:LEMONLEMONLE
密文:LXFOPVEFRNHR
解密的过程则与加密相反。
例如:根据密钥第一个字母L所对应的L行字母表,发现密文第一个字母L位于A列,因而明文第一个字母为A。
密钥第二个字母E对应E行字母表,而密文第二个字母X位于此行T列,因而明文第二个字母为T。以此类推便可得到明文。
用数字0-25代替字母A-Z,维吉尼亚密码的加密文法可以写成同余的形式:
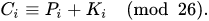
解密方法则能写成:
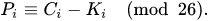
https://www.cnblogs.com/maoguy/p/6002510.html
维吉尼亚密码的Python实现:
#-*-coding:utf-8-*-
#维吉尼亚
'''
fileName : main.py
'''
import VigenereEncrypto
import VigenereDecrypto
print u"维吉尼亚加密"
plainText = raw_input ("Please input the plainText : ")
key = raw_input ("Please input the key : ")
plainTextToCipherText = VigenereEncrypto (plainText , key)
print u"加密后得到的暗文是 : " + plainTextToCipherText
print u"维吉尼亚解密"
cipherText = raw_input ("Please input the cipherText : ")
key = raw_input ("Please input the key : ")
cipherTextToPlainText = VigenereDecrypto (cipherText , key)25 print u"解密后得到的明文是 : " + cipherTextToPlainText
#-*-coding:utf-8-*-
#维吉尼亚加密
'''
fileName : VigenereEncrypto.py
'''
def VigenereEncrypto (input , key) :
ptLen = len(input)
keyLen = len(key)
quotient = ptLen // keyLen #商
remainder = ptLen % keyLen #余
out = ""
for i in range (0 , quotient) :
for j in range (0 , keyLen) :
c = int((ord(input[i*keyLen+j]) - ord('a') + ord(key[j]) - ord('a')) % 26 + ord('a'))
#global output
out += chr (c)
for i in range (0 , remainder) :
c = int((ord(input[quotient*keyLen+i]) - ord('a') + ord(key[i]) - ord('a')) % 26 + ord('a'))
#global output
out += chr (c)
return out
#-*-coding:utf-8-*-
#维吉尼亚解密
'''
fileName : VigenereDecrypto.py
'''
def VigenereDecrypto (output , key) :
ptLen = len (output)
keyLen = len (key)
quotien = ptLen // keyLen
remainder = ptLen % keyLen
inp = ""
for i in range (0 , quotient) :
for j in range (0 , keyLen) :
c = int((ord(output[i*keyLen+j]) - ord('a') + 26 - (ord(key[j]) - ord('a')) % 26 + ord('a')))
#global input
inp += chr (c)
for i in range (0 , remainder) :
c = int((ord(output[quotient*keyLen + i]) - ord('a') + 26 - (ord(key[i]) - ord('a')) % 26 + ord('a')))
#global input
inp += chr (c)
return inp
密码破译
维吉尼亚密码不是一定可以破译的,只有有可能。
破译维吉尼亚密码的关键在于它的密钥是循环重复的。如果我们知道了密钥的长度,那密文就可以被看作是交织在一起的凯撒密码,而其中每一个都可以单独破解。
https://baike.baidu.com/item/%E7%BB%B4%E5%90%89%E5%B0%BC%E4%BA%9A%E5%AF%86%E7%A0%81/4905472?fr=aladdin
https://blog.csdn.net/sarahduo/article/details/51236000
https://www.lmlphp.com/user/56/article/item/10994/
import vigenerecipher
#使用拟重合指数法确定秘钥长度:拟重合指数大于0.6为标志
def length(Ciphertext):
ListCiphertext=list(Ciphertext)
Keylength=1
while True:
#指数初始化为0
CoincidenceIndex = 0
#使用切片分组
for i in range(Keylength):
Numerator = 0
PresentCipherList = ListCiphertext[i::Keylength]
#使用集合去重,计算每一子密文组的拟重合指数
for Letter in set(PresentCipherList):
Numerator += PresentCipherList.count(Letter) * (PresentCipherList.count(Letter)-1)
CoincidenceIndex += Numerator/(len(PresentCipherList) * (len(PresentCipherList)-1))
#求各子密文组的拟重合指数的平均值
Average=CoincidenceIndex / Keylength
Keylength += 1
#均值>0.6即可退出循环
if Average > 0.06:
break
Keylength -= 1
return Keylength
#使用重合指数法确定秘钥内容:遍历重合指数的最大值为标志
def keyword(Ciphertext,keylength):
ListCiphertext = list(Ciphertext)
Standard = {'A':0.08167,'B':0.01492,'C':0.02782,'D':0.04253,'E':0.12702,'F':0.02228,'G':0.02015,'H':0.06094,'I':0.06966,'J':0.00153,'K':0.00772,'L':0.04025,'M':0.02406,'N':0.06749,'O':0.07507,'P':0.01929,'Q':0.00095,'R':0.05987,'S':0.06327,'T':0.09056,'U':0.02758,'V':0.00978,'W':0.02360,'X':0.00150,'Y':0.01974,'Z':0.00074}
while True:
KeyResult = []
for i in range(keylength):
# 使用切片分组
PresentCipherList = ListCiphertext[i::keylength]
#初始化重合指数最大值为0,检验移动位数对应字符以*代替
QuCoincidenceMax = 0
KeyLetter = "*"
#遍历移动的位数
for m in range(26):
#初始化当前移动位数的重合指数为0
QuCoincidencePresent = 0
#遍历计算重合指数:各个字符的频率*对应英文字符出现的标准频率---的和
for Letter in set(PresentCipherList):
LetterFrequency = PresentCipherList.count(Letter) / len(PresentCipherList)
# 标准频率
k = chr( ( ord(Letter) - 65 - m ) % 26 + 65 )
StandardFrequency = Standard[k]
#计算重合指数
QuCoincidencePresent = QuCoincidencePresent + LetterFrequency * StandardFrequency
#保存遍历过程中重合指数的最大值,同时保存对应应对的位数,即对应key的字符
if QuCoincidencePresent > QuCoincidenceMax:
QuCoincidenceMax = QuCoincidencePresent
KeyLetter = chr( m + 65 )
#保存当前位置key的值,退出循环,进行下一组子密文移动位数的尝试
KeyResult.append( KeyLetter )
#列表转为字符串
Key = "".join(KeyResult)
break
return Key
if __name__ == '__main__':
Ciphertext = input("输入密文:").upper()
Keylength = length(Ciphertext)
print("keylength最可能为:",Keylength)
KeyResult = keyword(Ciphertext,Keylength)
print("秘钥最可能为:" , KeyResult)
#已知秘钥可用python自带维吉尼亚解密
ClearText = vigenerecipher.decode( Ciphertext,KeyResult )
print("解密结果为:" , ClearText)


