线性反馈移位寄存器（LFSR）

　　LFSR用于产生可重复的伪随机序列PRBS，该电路有n级触发器和一些异或门组成，如下图所示。

 

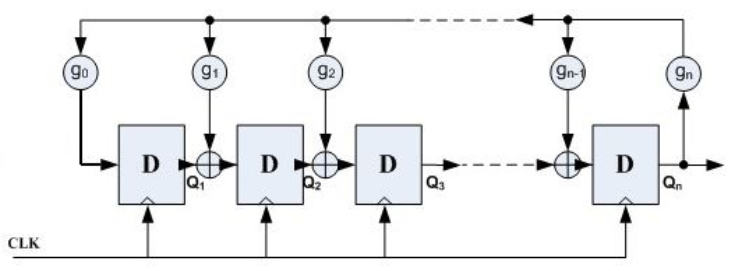
其中，gn为反馈系数，取值只能为0或1，取为0时表明不存在该反馈之路，取为1时表明存在该反馈之路；这里的反馈系数决定了产生随机数的算法的不同。用反馈函数表示成y=a0x^0+a1x+a2x^2.......反馈函数为线性的叫线性移位反馈序列，否则叫非线性反馈移位序列。

 

LFSR的初始值被称为伪随机序列的种子，影响下一个状态的比特位叫做抽头。LFSR的触发器编号一般从1开始，抽头取值范围是1到2ⁿ-1。抽头序列可以用来描述该LFSR的反馈多项式。由n个触发器构成的LFSR电路可以产生一个周期为2ⁿ-1的序列。理论表明，要使LFSR得到最长的周期，这个抽头序列构成的多项式加1就是其反馈多项式，必须是一个本原多项式，也就是说这个多项式不可约，比方下图的抽头序列为（4,1），其对应的反馈多项式为，其对应的线性反馈移位寄存器电路如下所示。

假设的初始值各自是1 0 0 0，反馈函数选取，那么得到例如以下序列

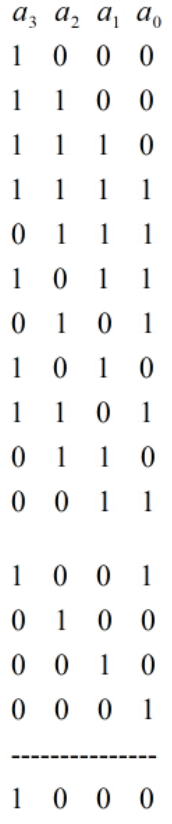
 能够看出周期为15。在这一个周期里面涵盖了开区间内的全部整数，而且都是没有固定顺序出现的，有非常好的随机性。

　　目前常用的LFSR电路可分为斐波那契LFSR和伽罗瓦LFSR。

• 斐波那契LFSR

　　　　斐波那契LFSR也可以称为多到一型LFSR，即抽头序列对应bit位置的多个触发器的输出通过异或逻辑来驱动一个触发器的输入。如下图所示

 

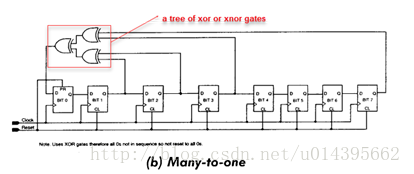
• 伽罗瓦LFSR

　　伽罗瓦LFSR和斐波那契刚好相反，它是一到多型的LFSR，即最后一个触发器的输出通过与抽头序列对应位置触发器前一级触发器的输出异或逻辑驱动多个抽头序列对应位置触发器的输入。如下图所示

 

 

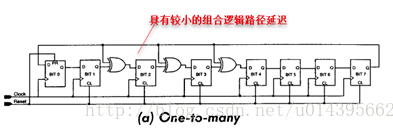
•  虽然这两种电路都产生伪随机序列，但是一到多型的伽罗瓦LFSR具有更高的速度，因为它的两个触发器之间仅使用一个异或门。

 

• 应该避免寄存器进入全为0的禁止态，因为全为0的状态是不用的，而且可能会导致在这个状态出不来。

　　预防办法：

　　（1）想办法给寄存器置位到某个允许的状态

　　（2）用额外的电路让寄存器能够从禁止状态自动进入允许状态