光照不均匀图像的一种二值化方法
“ 在图像处理中,我们经常需要将感兴趣区域与其它区域区别开来,以便于后续步骤的处理。比如生成一副与原图尺寸相同的图像对不同区域进行标记,感兴趣区域像素值标记为255, 其它区域像素值标记为0,该图像就是我们说的二值图。”
前文我们有讲过“大津法”和“最佳阈值迭代法”这两种最常用的图像二值化算法,并对“最佳阈值迭代法”进行了一点改进,使其在光照不均匀的情况下也能一定程度地区分开前景背景,然而有些情况下还是不能很好地区分开:
本文我们参考以下文献,并结合前文我们改进的“最佳阈值迭代法”,使用C++/Opencv来实现一种光照不均匀情况下二值化效果比较好的算法。
[不均匀光照文本图像的二值化] 贺志明
01
—
总体处理流程
总体处理流程主要包括光照补偿-->去噪-->图像增强-->最佳阈值迭代获取阈值-->二值化这几个步骤,如下图所示。其中前面三个步骤属于预处理,后面两个步骤是二值化操作。
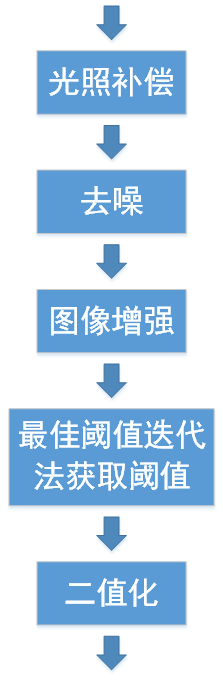
下文我们将依次展开来讲以上步骤的原理与实现。
02
—
光照补偿
根据以上提到的参考文献,光照补偿又分为两个步骤:计算背景信息-->使用背景信息补偿光照。
首先是计算背景信息,在这里前提是背景信息比前景信息的像素值高,如果图像不是这种情况,可以将图像的黑白像素值反转。核心思想是对图像中每一个点取其矩形邻域,然后对矩形邻域内所有点的像素值进行从大到小的排序,取排在前五的几个像素值较大的像素值计算均值,作为该点的背景值。
实现代码:
//src--原图像
//win_2 -- 矩形邻域窗口的长、宽均为(2*win_2+1)
Mat get_background(Mat src, int win_2)
{
int winsize = 2 * win_2 + 1;
Mat src_tmp;
//为了使原图所有点都能取到完整的矩形邻域,首先对原图进行边缘填充
copyMakeBorder(src, src_tmp, win_2, win_2, win_2, win_2, BORDER_REPLICATE);
//中值滤波去噪,减少背景杂志
medianBlur(src_tmp, src_tmp, 9);
Mat dst(src.size(), CV_8UC1);
for (int i = win_2; i < src_tmp.rows-win_2; i++)
{
uchar *pd = dst.ptr<uchar>(i-win_2);
for (int j = win_2; j < src_tmp.cols-win_2; j++)
{
Mat tmp;
//截取每一个点周围的矩形邻域
src_tmp(Rect(j-win_2, i-win_2, winsize, winsize)).copyTo(tmp);
//将二维矩阵转换成一维数据
tmp.reshape(1, 1).copyTo(tmp);
//从大到小排序
cv::sort(tmp, tmp, CV_SORT_EVERY_ROW + CV_SORT_ASCENDING);
uchar *p = tmp.ptr<uchar>(0);
//取排序之后的前5个像素值计算均值作为背景值
pd[j - win_2] = (uchar)((p[tmp.cols - 1] + p[tmp.cols - 2] + p[tmp.cols - 3] + p[tmp.cols - 4] + p[tmp.cols - 5])*0.2);
}
}
return dst;
}
本文我们使用一张光照不均匀的血管图像来检验所实现算法的效果,如下图所示,可以看到原本图像的光照信息就是不均匀的,所以计算出来的背景图像上不同区域的明暗并不一样。
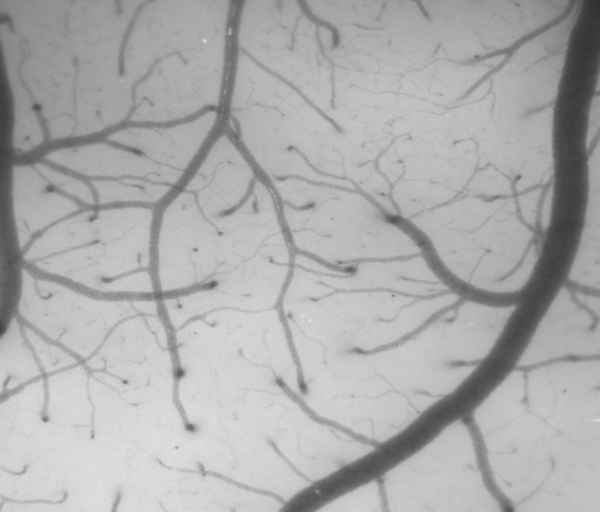
原图

背景图
接着是使用背景信息来补偿光照,对原图每一个点,使用背景图中相同坐标位置的点来计算其光照补偿之后的像素值。假设原图像素值为x,背景图中相同位置点的像素值为xb,光照补偿之后的像素值为y,处理流程如下图所示:
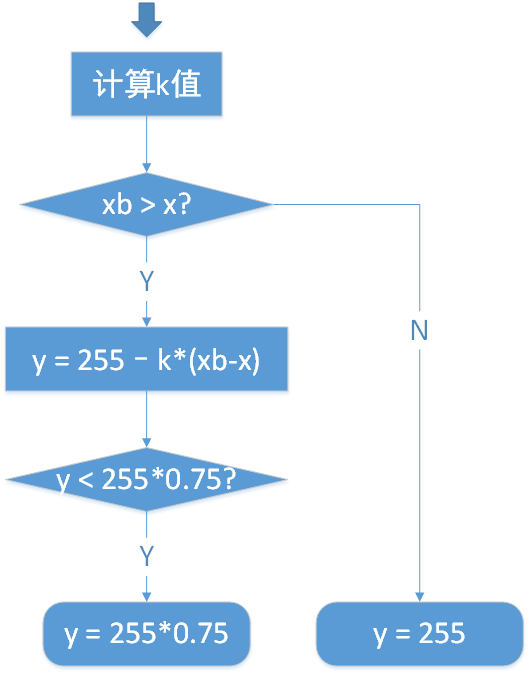
其中计算k值使用以下分段函数公式:
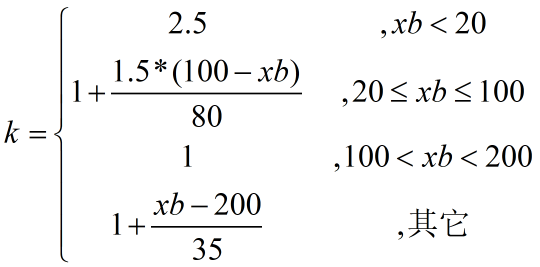
光照补偿之后的血管图及其背景图如下,可以看到,相比原图的背景图,光照补偿之后背景图的光强分布均匀多了。
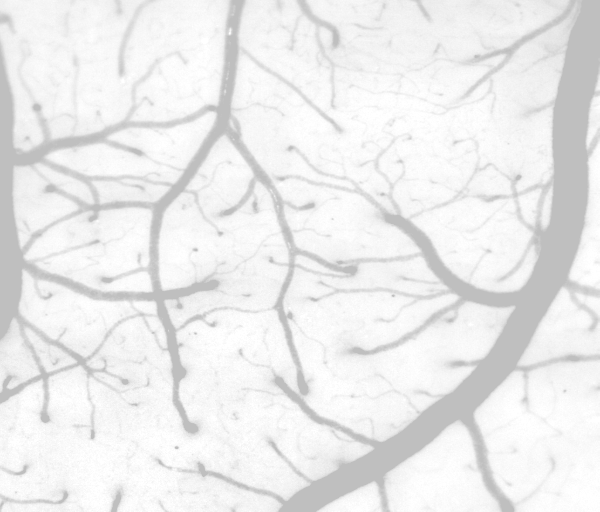
光照补偿之后的图像

光照补偿之后图像的背景图
03
—
去噪
常用的去噪算法有均值滤波、高斯滤波、中值滤波,以及非局部均值滤波等,为了能较好地保留血管边缘,我们使用非局部均值滤波对血管图像进行去噪。前文我们有讲过非局部均值滤波的原理与实现(Opencv里面也有现成的fastNlMeansDenoising函数实现):
非局部均值滤波(NL-means)算法的积分图加速原理与C++实现
对光照补偿之后的图像进行去噪,结果如下图:

去噪图像
04
—
图像增强
常见的图像增强算法有直方图均衡化、拉普拉斯锐化、Gamma校正、USM锐化等。本人试了这几种算法,对比感觉USM锐化的效果相对更好,因此我们使用USM算法对去噪之后的图像进行增强。
在图像中,通常边缘区域属于高频信号,其它区域属于低频信号,如果使用原信号减去低频信号,剩余的为高频信号,也即凸显了边缘信息。高斯滤波可以看成是一个低通滤波器,经过高斯滤波之后图像变得模糊,也即高频信号被滤除了,剩余低频信号,这时可以使用原图减去高斯滤波之后的图像,得到高频信号图像,也即边缘被增强的图像,这就是USM算法的基本原理。
代码实现:
//img--原图像
//dst--增强图像
//alpha1--原图像系数,通常取1.0~1.5
//alpha2--高斯滤波图像系数,通常取-0.5~-0.9
void img_ehance(Mat img, Mat &dst, double alpha1, double alpha2)
{
Mat blur;
GaussianBlur(img, blur, Size(0, 0), 30);
addWeighted(img, alpha1, blur, alpha2, 0, dst);
}
对去噪之后的图像进行增强,效果如下:

增强图像
05
—
最佳阈值迭代法获取阈值
在前文我们已经讲过最佳阈值迭代法的原理与实现:
此处我们直接上代码:
//src--原图像
//T--迭代结束的阈值
//a--控制前景区域范围的参数,a越大被划分为前景的区域越多
float get_threld(Mat src, float T, float a)
{
const int level = 256;
float hist[level] = { 0 };
float sum = 0.0;
for (int i = 0; i < src.rows; i++) //统计直方图
{
uchar *p = src.ptr<uchar>(i);
for (int j = 0; j < src.cols; j++)
{
hist[p[j]] += 1.0;
sum += p[j];
}
}
float hist_add[level] = { 0 };
hist_add[0] = hist[0];
for (int i = 1; i < level; i++) //累加统计直方图
{
hist_add[i] = hist_add[i - 1] + hist[i];
}
const int img_size = src.rows*src.cols;
float T_current = sum / img_size; //求像素平均值作为阈值的初始值
float T_next = 0;
float S0 = 0.0;
float n0 = 0.0;
float S1 = 0.0;
float n1 = 0.0;
float d = abs(T_current - T_next);
float count = 0;
while (d >= T && count < 1000)
{
count++;
uchar TT = (uchar)(T_current);
n1 = hist_add[TT]; //像素值小于等于TT的点数
n0 = img_size - hist_add[TT]; //像素值大于TT的点数
S1 = 0.0;
for (int i = 0; i <= TT; i++) //使用累加直方图快速计算图像中所有像素值小于等于阈值的点的像素值之和
{
S1 += i*hist[i];
}
S0 = sum - S1; //计算图像中所有像素值大于阈值的点的像素值之和
float m0 = S0 / n0; //计算图像中所有像素值大于阈值的平均值
float m1 = S1 / n1; //计算图像中所有像素值小于等于阈值的平均值
T_next = m1 + (m0 - m1)*a; //参数a控制m0、m1的权重
d = abs(T_current - T_next); //当前迭代得到的阈值与下一轮迭代得到的阈值之差的绝对值
T_current = T_next; //把下一轮迭代的阈值赋值给当前轮迭代的阈值
}
return T_current;
}
使用最佳阈值迭代法获取阈值之后,就可以对图像进行二值化了:
void threld_img(Mat src, Mat &dst, float a, double h)
{
//获取背景图
Mat bg = get_background(src, 35);
//光照补偿
Mat gb = guangqiang_buchang(src, bg);
//去噪
fastNlMeansDenoising(gb, gb, h, 7, 25);
//图像增强
img_ehance(gb, gb, 1.0, -0.5);
//获取阈值
float TT = get_threld(gb, 0.01, a);
//二值化
threshold(gb, dst, TT, 255, THRESH_BINARY_INV);
}
对比是否作光照补偿的二值化结果如下,可以,未作光照补偿时,二值化结果并不好,光照不均匀的地方本来是背景,也被划分为前景了。作了光照补偿则没有这个问题。

未作光照补偿的二值化结果

作光照补偿的二值化结果
欢迎扫码关注本微信公众号,接下来会不定时更新更加精彩的内容,敬请期待~


