libtorch Tensor张量的常用操作总结(2)
“前文我们已经讲了一部分常见的张量操作,本文让我们继续吧~”
本文我们继续来讲讲张量的压缩与扩张、张量与张量的运算、求张量的最大最小值、操作第0维、张量的堆叠、调整维度顺序、改变张量的形状等常用操作。
01
—
张量的压缩与扩张
张量的压缩是指删除长度为1的维度,扩张则是相反的操作——在某位置添加长度为1的维度,见以下代码:
注意:当要删除的某个维度长度不是1时,将不作删除。
auto a = torch::zeros({1, 5, 3, 1}); //定义1*5*3*1的张量a
cout << a.sizes() << endl;
//将张量a的所有长度为1的维度删除,变成5*3张量
auto b = torch::squeeze(a);
cout << b.sizes() << endl;
//将张量a的第0维度删除,变成5*3*1张量
b = torch::squeeze(a, 0);
cout << b.sizes() << endl;
//将张量a的第1维度删除,变由于第1维度长度不是1,所以不作删除,还是1*5*3*1张量
b = torch::squeeze(a, 1);
cout << b.sizes() << endl;
//在第0维度增加一个长度为1的维度,变成1*1*5*3*1张量
b = torch::unsqueeze(a, 0);
cout << b.sizes() << endl;
运行结果:

02
—
张量与张量的对应位置运算
对应位置运算,是指两个张量相同位置的数值分别进行加、减、乘、除等运算。如果两个张量的所有维度都相同,则直接对每个位置的值进行运算;如果维度不同,则先对张量进行填充,使两者维度相同,然后再进行运算。
两个张量维度相同
auto a = torch::randint(0, 10, { 3, 5 });
cout << a << endl;
auto b = torch::randint(0, 10, { 3, 5 });
cout << b << endl;
auto c = a + b;
cout << c << endl;
运行结果:

两个张量维度不同
这种情况下只有两个张量同时满足以下两个原则,才可以进行运算:
1. 每个张量至少有一个维度;
2. 两个张量对应位置上的维度要么相同,要么其中一个是1,要么不存在,如果都不是,说明两个张量不能执行对应位置的运算。
auto a = torch::randint(0, 10, { 1, 4, 4 });
cout << a << endl;
auto b = torch::randint(0, 10, { 3, 1, 4 });
cout << b << endl;
auto c = a + b;
cout << c << endl;
b = torch::randint(0, 10, { 3, 1, 3 });
auto c1 = a + b;
cout << c1 << endl;
比如以上代码,张量a的维度为1*4*4,张量b的维度为3*1*4,a和b的维度对应关系如下表,由于它们所有维度均满足条件,因此a和b是可以执行运算的。
| a | b | 是否满足运算条件 | |
| 第0维度长度 | 1 | 3 | 满足 |
| 第1维度长度 | 4 | 1 | 满足 |
| 第2维度长度 | 4 | 4 | 满足 |
运行结果:

运算前,张量a被填充为3*4*4张量:
2 2 5 5
5 5 6 4
3 7 9 6
1 2 9 5
2 2 5 5
5 5 6 4
3 7 9 6
1 2 9 5
2 2 5 5
5 5 6 4
3 7 9 6
1 2 9 5
张量b也被填充为3*4*4张量:
3 3 5 4
3 3 5 4
3 3 5 4
3 3 5 4
2 0 6 6
2 0 6 6
2 0 6 6
2 0 6 6
0 6 2 4
0 6 2 4
0 6 2 4
0 6 2 4
03
—
求张量的最大最小值
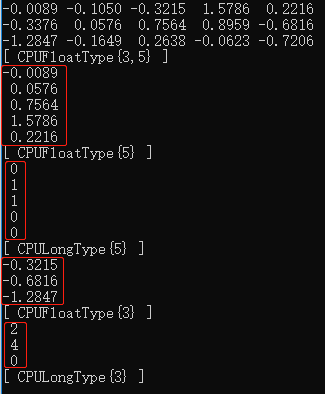
求张量某个维度的最大、最小值,也是很常见的操作:
auto a = torch::randn({ 3,5 });
cout << a << endl;
//求张量a第0维度的最大值,如果要求第1维度的最大值,则为(torch::max)(a, 1)
std::tuple<torch::Tensor, torch::Tensor> max_classes = (torch::max)(a, 0);
auto max_1 = std::get<0>(max_classes); //求得最大值
auto max_index = std::get<1>(max_classes); //求得最大值的索引
cout << max_1 << endl;
cout << max_index << endl;
//求张量a第1维度的最小值
auto min_classes = (torch::min)(a, 1);
auto min_1 = std::get<0>(min_classes); //求得最小值
auto min_index = std::get<1>(min_classes); //求得最小值的索引
cout << min_1 << endl;
cout << min_index << endl;
运行结果:
04
—
操作张量的第0维
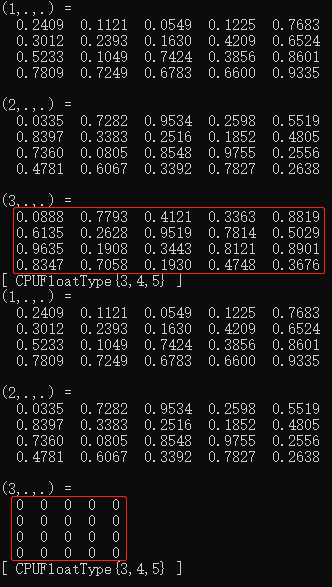
无论张量有几个维度,对张量使用[]符号时都是对其第0维度进行操作:
auto a = torch::rand({ 3, 4, 5 }); //定义维度为3*4*5的张量a
cout << a << endl;
a[2] = torch::zeros({4, 5}); //将a的第0维度的索引号2张量赋值为4*5的0值张量
cout << a << endl;
运行结果:
05
—
张量的堆叠
前文我们讲过张量的cat操作,是指将两个张量直接首尾拼接到一起,但并没有增加新的维度。而堆叠操作stack则在某一个新的维度堆叠多个张量,因此增加了一个新的维度,比如把多个2维张量凑成一个3维的张量、多个3维张量凑成一个4维的张量。
形象的理解为:假设有多张尺寸一样的纸,在平坦的桌面上将多张纸首尾拼接成一张更大的纸,这是cat操作;将多张纸叠到一张纸上面,形成了一本书的操作,则是stack操作。如下图所示:
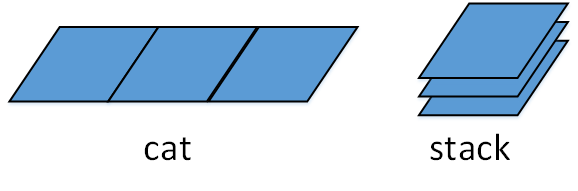
stcak函数有两个输入参数,参数一为张量的列表,列表中所有张量必须维度相同,参数二为所增加的新维度的索引号,假设张量列表中每一个张量具有N个维度,那么参数二的取值范围是[0, N]。
代码如下:
//生成维度为2*5的张量a
auto a = torch::linspace(1, 10, 10).reshape({ 2, 5 });
cout << a << endl;
//生成维度为2*5的张量b
auto b = torch::linspace(11, 20, 10).reshape({ 2, 5 });
cout << b << endl;
//增加第0维度,并在第0维度将a和b堆叠为2*2*5张量
auto c = torch::stack({ a, b }, 0);
cout << c << endl;
//获取一个张量列表,包含10个2*5张量
vector<torch::Tensor> list;
for (int i = 0; i < 10; i++)
{
auto x = torch::linspace(i*10+1, i*10+10, 10).reshape({ 2, 5 });
list.push_back(x);
}
//增加第0维度,并在第0维度将10个2*5张量堆叠为10*2*5张量
auto x_10 = torch::stack(list, 0);
cout << x_10 << endl;
运行结果:

06
—
调整维度顺序
有时候,我们需要调整张量的维度顺序,比如我们前文讲过的:
Opencv Mat存储三通道图像的顺序为[Height, Width, Channels],然而libtorch要求输入神经网络的Tensor张量存储三通道图像的顺序为[Channels, Height, Width],两者的数据维度顺序是不一致的。如果没有转换Mat格式的维度顺序就直接将其数据赋值给Tensor张量,导致网络因为维度顺序不对而不能准确捕获图像特征。
在这种情况下,首先要把[Height, Width, Channels]的Mat格式数据转换为[Height, Width, Channels]的Tensor张量,然后再调用Tensor张量的permute函数把数据的维度顺序调整为[Channels, Height, Width]。
auto a = torch::randn({ 3, 4, 5 });
cout << a.sizes() << endl;
auto b = a.permute({ 1,0,2 }); //将第0维度和第1维度交换顺序
cout << b.sizes() << endl;
运行结果:

07
—
改变张量的形状
有时候我们需要改变张量的形状,在libtorch中通常有这两个函数可以实现形状的改变:view和reshape。虽然这两个函数都可以改变张量的形状,但是它们是有区别的:
调用view函数得到的张量,虽然形状改变了,但是其与原张量是共用内存的,并没有开辟新的内存。而调用reshape得到的张量则开辟了新的内存。
如果张量不连续(比如调用permute函数改变张量的维度顺序之后,张量变得不连续),调用view对其进行改变形状的操作会出错,而reshape则没有这个问题。一种保险的做法是调用view之前,先contiguous一下张量,从而使张量变得连续,另一种做法是干脆使用reshape代替view。
代码:
//定义维度为3*4*5的张量a
auto a = torch::randn({ 3, 4, 5 });
cout << a.sizes() << endl;
//调用view将a的形状改变为12*5
auto b = a.view({12, 5});
cout << b.sizes() << endl;
//用reshape将a的形状改变为12*5
auto c = a.reshape({ 12, 5 });
cout << c.sizes() << endl;
//将a的第1维度和第2维度交换顺序,此时a变得不连续,直接对其调用view会出错
a = a.permute({0, 2, 1});
cout << a.sizes() << endl;
//即使a不连续,调用reshape改变其形状也没有问题
c = a.reshape({ 12, 5 });
cout << c.sizes() << endl;
//调用view之前先contiguous一下,即使a不连续也不会出错
b = a.contiguous().view({ 12, 5 });
cout << b.sizes() << endl;
运行结果:

此外,在分类神经网络的末端,通常需要把除第0维之外的所有其它维数据转换为一维张量,以便输入Affine层:
x = x.view({ x.size(0), -1 });
x = x.reshape({ x.size(0), -1 });
比如本来张量的维度为[32, 3, 512, 512],按照上述代码调用view或reshape之后,其维度将变成[32, 3*512*512],也即[32, 786432]。
欢迎扫码关注本微信公众号,接下来会不定时更新更加精彩的内容,敬请期待~

