基于TPS薄板样条变换与PSO粒子群算法的一种非刚性配准方法
前文我们介绍过一种基于TPS薄板样条与梯度下降法的非刚性配准方法:
我们知道,梯度下降法是一种单线优化算法,也即它只优化目标函数的一组解,这样是很容易陷入局部极值的。而PSO粒子群算法则不一样,它是多线优化算法,也即同时优化目标函数的多组解,最后从多组解中再选择最优的一组解作为最终解,因此相比梯度下降法,PSO算法更不容易陷入局部极值。
本文我们来实现一种基于薄板样条变换与PSO优化算法的非刚性配准方法,该方法使用薄板样条变换作为形变模型,并使用PSO粒子群算法作为优化算法对薄板样条变换的输入参数进行优化。
01
—
目标函数介绍
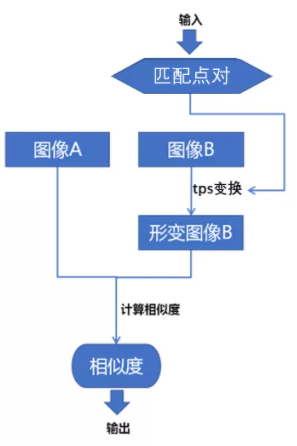
目标函数示意图
目标函数如下图所示,输入参数为参考图像A与浮动图像B的多组匹配点对,然后使用匹配点对计算TPS变换的坐标偏移,接着使用坐标偏移对图像B进行像素重采样,得到TPS形变之后的图像B,最后计算图像A与形变之后图像B的相似度,作为目标函数的输出值。
输入参数的初始化
配准开始之前,需要在参考图像A与浮动图像B上面初始化一系列等间距的点,假设两图中相同位置的点为匹配点对,然后将这些匹配点对作为以上目标函数的初始输入参数。接着使用PSO算法求解目标函数取得最小值(也即图像A与形变图像B最相似)时的输入参数作为最终解。如下图所示:
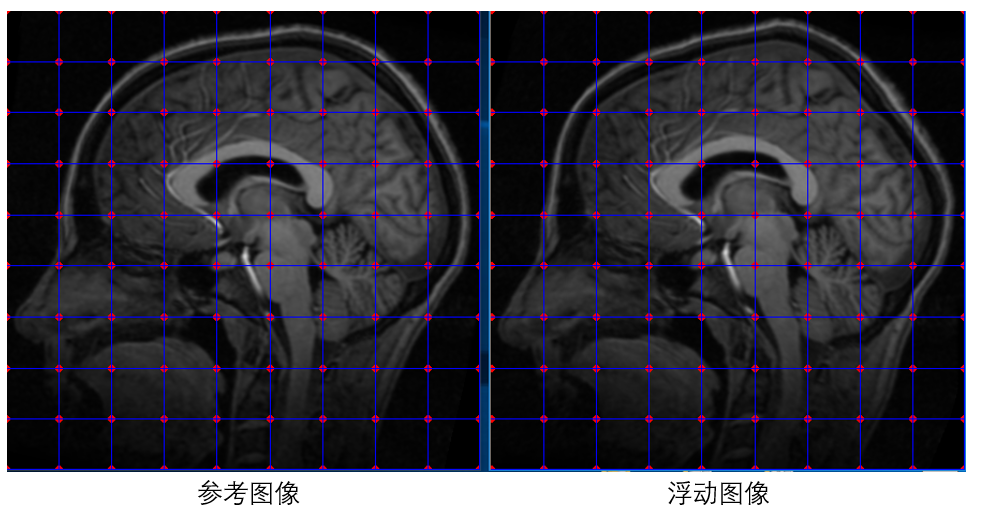
目标函数的输入为图像A与图像B的多组匹配点对,但实际上并不需要优化图像A上点的位置,只需要固定图像A上点的位置,然后优化图像B上点的位置,使其与图像A上点的位置匹配即可。假设图像A与图像B上初始化的等间距的点个数都是N个,每个点包含x坐标和y坐标,那么我们需要优化的参数为图像B上所有初始化点的x、y坐标组成的2*N个参数。
TPS薄板样条变换原理与实现
TPS变换是一种非刚性形变模型,其输入参数为两图像的一系列匹配点对,所有匹配点对共同决定了一张图像到另一张图像的形变坐标偏移。一般通过特征点匹配、光流追踪等方法获取两图的匹配点对,不过本文中我们使用PSO优化算法来获取。
前文我们介绍过TPS变换的原理与C++实现:
由于TPS变换的计算过程很耗时,后来我们又使用GPU CUDA来并行加速其计算过程:
相似度衡量
本文我们使用两图像的差值图均值作为相似度,也即相似度越小,表示两图像越相似。假设图像A与图像B的尺寸都是m行n列,对于图像上任意坐标点(x,y),图像A、图像B上该点的像素值分别为A(x,y)、B(x,y),那么A和B的相似度计算如下式:
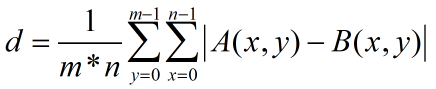
02
—
PSO粒子群算法的基本原理与改进
基本原理
前文我们已经讲过PSO算法的基本原理,此处再简单介绍一下:
简单地理解粒子群算法就是:
(1) 有多个粒子;
(2) 每个粒子就是目标函数的一组解;
(3) 每个粒子具有记忆功能,它在移动过程中,每到达一个位置都计算目标函数值,如果发现目标函数值相对上一个位置有所下降,则把当前位置记住,这个记住的位置也称为局部最优位置pbest(每个粒子都有一个自己的pbest);
(4) 不同粒子之间互相通信,把各自记住的局部最优位置互相告知,并在所有粒子的局部最优位置当中,选择一个目标函数值最小的位置,作为全局最优位置gbest(所有粒子共享一个gbest)。
(5) 当前位置X、局部最优位置pbest、全局最优位置gbest共同决定粒子移动的下一个位置(也即更新粒子参数)。假设目标函数f输入N个参数,那么每个粒子的X、pbest以及所有粒子共享的gbest都可看作长度为N的一维向量:
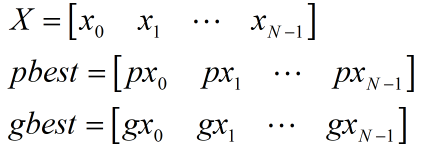
对于X中的任意分量xi(0≤i≤N-1),其下一个位置的值可按下式计算,其中c1和c2为取值范围在1.5~2.5之间的固定值,通常都取1.8,rand(0,1)为0~1的随机数,pxi为pbest中对应xi的分量,gxi为gbest中对应xi的分量。
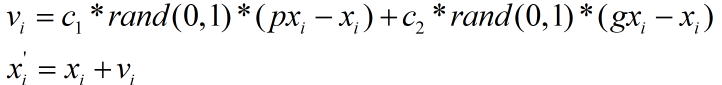
算法改进
增加惯性权重
上式的v相当于粒子移动的速度,根据加速度原理,当前位置的速度与上个位置的速度具有一定关系,因此后来人们又提出了改进算法,改进之后可加速收敛速度,如下式所示。
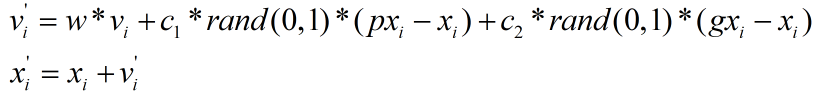
上式中v'为粒子在当前位置的速度,v为粒子在上个位置的速度,w为0~1之间的惯性权重值。w通常取固定值或递减:
(1) 取0~1之间的一个固定值。
(2) 设置最大、最小值,随着迭代次数的增加,由最大值线性递减到最小值。如下式,i为当前迭代次数(0≤i≤num-1),num为总迭代次数。

增加压缩系数
增加压缩系数φ来限制速度的大小,这样也可加速迭代收敛。如下式所示,不过需要注意c1和c2之和必须大于4:
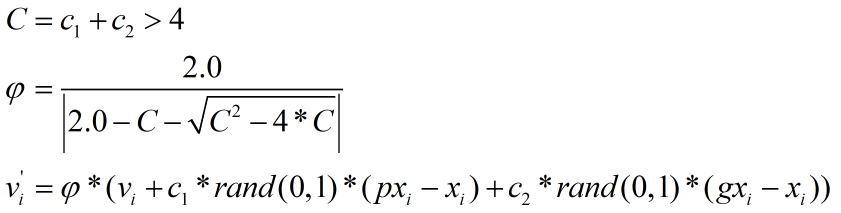
增加粒子的老化处理
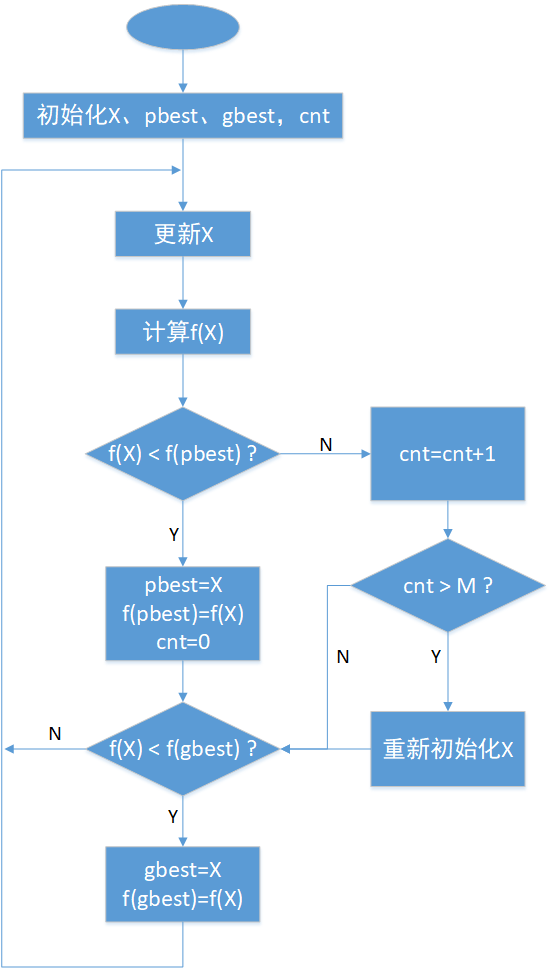
当某一个粒子连续移动M次(M通常设置为5~15之间的一个值)但目标函数值一次都没有下降,则认为该粒子老化了,此时可对该粒子的位置X重新初始化,使其重新焕发活力,这样可以有效避免优化陷入局部极值。如下图所示:
使用所有粒子的pbest的质心位置代替各自的pbest
由上述速度计算公式可知,粒子的移动速度主要由其pbest与X的差值向量,以及gbest与其X的差值向量决定。也就是说,粒子的移动方向由两个差值向量的向量之和决定,这么一来粒子大概率往目标函数值更低的位置移动,如下图所示:
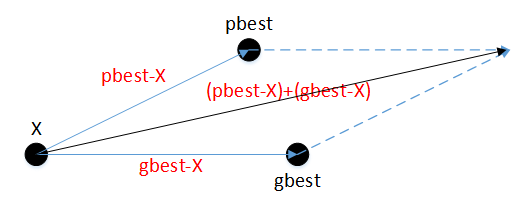
根据统计学原理,多个值的平均值通常比单个值的准确度更高,因此我们计算所有粒子的pbest的质心点,使用质心点代替各个粒子的pbest计算速度,使粒子朝着更加准确的方向移动,所以可加快收敛速度。
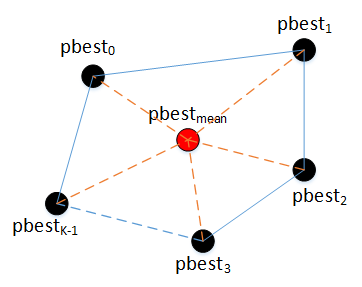
假设有K个粒子,每个粒子都有一个pbest,那么总共有K个pbest,如上图对K个pbest求平均,得到质心位置pbestmean,然后使用pbestmean来代替原来各自的pbest计算速度:
pbestmean的计算如下式:
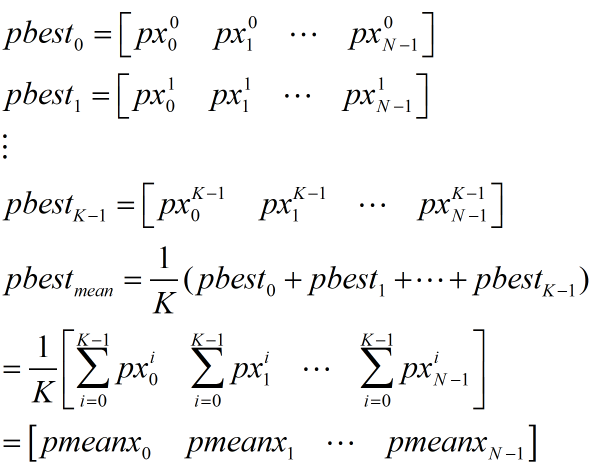
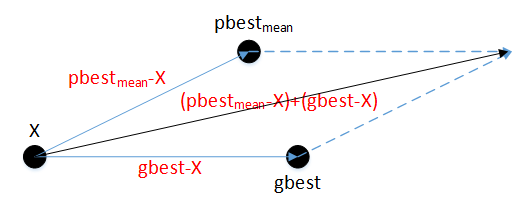
从而速度计算公式修改为:
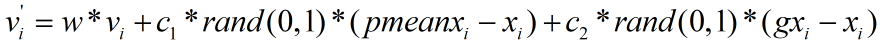
修改后的速度计算公式还有一个优点:我们知道当粒子运行到位置X时,如果f(X)<f(pbest),那么会将X赋值给pbest、将f(x)赋值给f(pbest),此时pxi-xi的值为0;如果f(X)<f(gbest),那么会将X赋值给gbest、将f(x)赋值给f(gbest),此时gxi-xi的值为0。这两种情况下如果按照原速度公式计算,粒子的移动速度将很大程度减小,导致收敛速度变慢。但是修改后的公式则没有这个问题,不管是f(X)<f(pbest)还是f(X)<f(gbest)的情况,pmeanxi-xi都不会为0,这就确保了粒子的移动速度保持在一定水平。
03
—
各部分代码实现
TPS薄板样条变换代码
TPS变换的代码,以及CUDA并行加速代码,我们在前文都已列出,此处不再重复:
值得一提的是,Opencv也有现成的TPS模块可以调用,不过相比自己使用CUDA加速实现的TPS就慢了很多了:
//定义一个tps变换的对象
auto tps = cv::createThinPlateSplineShapeTransformer();
//定义一个DMatch参数,p1为图像A上的点集,p2为图像B上的点集
//p1与p2中对应位置的点互相匹配
vector<cv::DMatch> matches;
for (int i = 0; i < p1.size(); i++)
{
matches.push_back(cv::DMatch(i, i, 0));
}
//计算tps形变坐标偏移
tps->estimateTransformation(p1, p2, matches);
Mat out;
//对图像B进行像素重采样
tps->warpImage(Si, out);相似度计算代码
double cal_diff_gradient(Mat S1, Mat Si)
{
Mat diff = abs(S1 - Si); //计算两图的差值绝对值图
double m = mean(diff)[0]; //求差值绝对值图的均值
return m;
}目标函数代码
float F_fun_tps(Mat S1, Mat Si, vector<Point2f> p1, vector<Point2f> p2)
{
double result;
Mat Si_tmp;
#if 1 //CUDA加速TPS
Mat Tx, Ty;
Tps_warpImage_cuda(Si, Si_tmp, Tx, Ty, p1, p2, 1);
result = cal_diff_gradient(S1, Si_tmp);
#else //Opencv实现的TPS
auto tps = cv::createThinPlateSplineShapeTransformer();
vector<cv::DMatch> matches;
for (int i = 0; i < p1.size(); i++)
{
matches.push_back(cv::DMatch(i, i, 0));
}
tps->estimateTransformation(p1, p2, matches);
Mat out;
tps->warpImage(Si, out);
result = cal_diff_gradient(S1, out);
#endif
return result;
}输入参数初始化代码
在参考图像A与浮动图像B上面初始化一系列等间距的点,假设两图中相同位置的点为匹配点对,然后将这些匹配点对作为目标函数的初始输入参数。
void init_points(Mat src, int row_block_num, int col_block_num, vector<Point2f> &p1, vector<Point2f> &p2)
{
float row_block_size = src.rows * 1.0 / (row_block_num-1);
float col_block_size = src.cols * 1.0 / (col_block_num-1);
p1.clear();
p2.clear();
for (int i = 0; i < row_block_num; i++)
{
for (int j = 0; j < col_block_num; j++)
{
float x = j*col_block_size;
float y = i*row_block_size;
x = x > src.cols - 1 ? src.cols - 1 : x;
y = y > src.rows - 1 ? src.rows - 1 : y;
Point2f p(x, y);
p1.push_back(p);
p2.push_back(p);
}
}
}PSO优化代码
首先是一些全局变量的定义:
const int NUM_tps = 50; //粒子数
const float c1_tps = 1.88; //粒子群参数1
const float c2_tps = 1.88; //粒子群参数2
float xmin_tps = -1.5; //控制参数被初始化为-1.5到1.5之间的随机数
float xmax_tps = 1.5;
const float vmin_tps = -6.5; //粒子的移动速度被钳制在为-6.5到6.5之间,这是经验值,合适的钳制范围可以加快收敛速度
const float vmax_tps = 6.5;
//定义粒子群,粒子个数为NUM_tps,每个粒子为一个结构体
struct particle_tps
{
vector<Point2f> x; //粒子的当前位置
vector<Point2f> bestx; //粒子的局部最优位置
float f; //当前位置对应的目标函数值
float bestf; //局部最优位置对应的目标函数值
}swarm_tps[NUM_tps];其次是原PSO算法代码:
void tps_PSO_0(Mat S0_u8, Mat Si_u8, Mat &out_u8, vector<Point2f> p1, vector<Point2f> &p2, Mat &Tx, Mat &Ty, int iter_num)
{
vector<float> cc_list;
float v_min = vmin_tps;
float v_max = vmax_tps;
float c1 = c1_tps;
float c2 = c2_tps;
srand((unsigned)time(NULL) + rand());
float gbestf = 999999999999.9;
const int len = p1.size();
for (int i = 0; i < NUM_tps; i++) //初始化粒子群
{
particle_tps *p = &swarm_tps[i];
for (int j = 0; j < len; j++)
{
p->x.push_back(p1[j] + Point2f(randf(xmin_tps, xmax_tps), randf(xmin_tps, xmax_tps)));
p->bestx.push_back(p1[j] + Point2f(randf(xmin_tps, xmax_tps), randf(xmin_tps, xmax_tps)));
}
p->f = F_fun_tps(S0_u8, Si_u8, p1, p->x);
p->bestf = p->f;
}
for (int t = 0; t < iter_num; t++) //iter_num次迭代
{
for (int i = 0; i < NUM_tps; i++) //NUM_tps个粒子
{
particle_tps *p = &swarm_tps[i];
for (int j = 0; j < len; j++) //计算速度
{
float Vx = c1*randf(0, 1)*(p->bestx[j].x - p->x[j].x) + c2*randf(0, 1)*(p2[j].x - p->x[j].x);
float Vy = c1*randf(0, 1)*(p->bestx[j].y - p->x[j].y) + c2*randf(0, 1)*(p2[j].y - p->x[j].y);
//钳制速度大小
Vx = (Vx < v_min) ? v_min : ((Vx > v_max) ? v_max : Vx);
Vy = (Vy < v_min) ? v_min : ((Vy > v_max) ? v_max : Vy);
p->x[j].x = p->x[j].x + Vx; //更新粒子位置
p->x[j].y = p->x[j].y + Vy;
}
p->f = F_fun_tps(S0_u8, Si_u8, p1, p->x); //计算当前粒子的当前位置对应的目标函数值
//如果当前粒子的当前位置目标函数值小于其局部最优位置对应的目标函数值,则替换该粒子的局部最优位置
if (p->f < p->bestf)
{
for (int j = 0; j < len; j++)
{
p->bestx[j] = p->x[j];
}
p->bestf = p->f;
}
//如果当前粒子的局部最优位置对应的目标函数值小于全局最优位置对应的目标函数值,则替换全局最优位置
if (p->bestf < gbestf)
{
for (int j = 0; j < len; j++)
{
p2[j] = p->bestx[j];
}
gbestf = p->bestf;
printf("t = %d, gbestf = %lf\n", t, gbestf);
}
}
//速度钳制范围逐渐缩小,6.5->5.5
v_min = vmin_tps - (vmin_tps + 5.5) * t / (iter_num - 1);
v_max = vmax_tps - (vmax_tps - 5.5) * t / (iter_num - 1);
}
Tps_warpImage_cuda(Si_u8, out_u8, Tx, Ty, p1, p2, 1);
}接着是改进的PSO算法代码:
void tps_PSO_1(Mat S0_u8, Mat Si_u8, Mat &out_u8, vector<Point2f> p1, vector<Point2f> &p2, Mat &Tx, Mat &Ty, int iter_num)
{
vector<float> cc_list;
float v_min = vmin_tps;
float v_max = vmax_tps;
float c1 = c1_tps;
float c2 = c2_tps;
srand((unsigned)time(NULL) + rand());
float gbestf = 999999999999.9;
const int len = p1.size();
for (int i = 0; i < NUM_tps; i++) //初始化粒子群
{
particle_tps *p = &swarm_tps[i];
for (int j = 0; j < len; j++)
{
p->x.push_back(p1[j] + Point2f(randf(xmin_tps, xmax_tps), randf(xmin_tps, xmax_tps)));
p->bestx.push_back(p1[j] + Point2f(randf(xmin_tps, xmax_tps), randf(xmin_tps, xmax_tps)));
}
p->f = F_fun_tps(S0_u8, Si_u8, p1, p->x);
p->bestf = p->f;
}
vector<vector<float>> Vx_pre(NUM_tps, vector<float>(len, 0));
vector<vector<float>> Vy_pre(NUM_tps, vector<float>(len, 0));
float Vx, Vy;
float w = 0.25;
vector<int> update_cnt(NUM_tps, 0);
//计算所有粒子的pbest的均值
vector<Point2f> mean_bestx(len, Point2f(0, 0));
for (int t = 0; t < len; t++)
{
for (int k = 0; k < NUM_tps; k++) //NUM个粒子
{
mean_bestx[t] = mean_bestx[t] + swarm_tps[k].bestx[t];
}
mean_bestx[t] = mean_bestx[t] / NUM_tps;
}
for (int t = 0; t < iter_num; t++) //iter_num次迭代
{
//权重线性递减
w = 0.25 - (0.25 - 0.1) * t / (iter_num - 1);
for (int i = 0; i < NUM_tps; i++) //NUM_tps个粒子
{
particle_tps *p = &swarm_tps[i];
for (int j = 0; j < len; j++) //计算速度,并更新位置
{
//改进,使用质心点替代原来的局部最优位置
Vx = Vx_pre[i][j] * w + c1*randf(0, 1)*(mean_bestx[j].x - p->x[j].x) + c2*randf(0, 1)*(p2[j].x - p->x[j].x);
Vy = Vy_pre[i][j] * w + c1*randf(0, 1)*(mean_bestx[j].y - p->x[j].y) + c2*randf(0, 1)*(p2[j].y - p->x[j].y);
Vx = (Vx < v_min) ? v_min : ((Vx > v_max) ? v_max : Vx);
Vy = (Vy < v_min) ? v_min : ((Vy > v_max) ? v_max : Vy);
p->x[j].x = p->x[j].x + Vx; //更新位置
p->x[j].y = p->x[j].y + Vy;
Vx_pre[i][j] = Vx; //将当位置的速度保存到上个位置的速度
Vy_pre[i][j] = Vy;
}
//计算当前粒子的当前位置的目标函数值
p->f = F_fun_tps(S0_u8, Si_u8, p1, p->x);
//如果当前粒子的当前位置目标函数值小于其局部最优位置目标函数值,则替换该粒子的局部最优位置
if (p->f < p->bestf)
{
//因为当前粒子的局部最优位置改变,质心点也将改变,所以重新计算质心点
//这里为了加快计算速度,没有重新计算所有pbest的均值,而是原来的和减去旧值再加上新值,然后再除以粒子数
for (int t = 0; t < len; t++)
{
mean_bestx[t] = mean_bestx[t] * NUM_tps - p->bestx[t] + p->x[t];
mean_bestx[t] = mean_bestx[t] / NUM_tps;
}
for (int j = 0; j < len; j++)
{
p->bestx[j] = p->x[j];
}
p->bestf = p->f;
update_cnt[i] = 0; //计数器清零
}
else
{
//如果目标函数值没有下降,计数器加1,且如果连续10次没有下降,则重新初始化该粒子
update_cnt[i]++;
if (update_cnt[i] >= 10)
{
update_cnt[i] = 0; //计数器清零
//重新初始化该粒子
for (int j = 0; j < len; j++)
{
p->x[j] = p1[j] + Point2f(randf(xmin_tps, xmax_tps), randf(xmin_tps, xmax_tps));
}
}
}
if (p->bestf < gbestf) //如果当前粒子的历史最优值小于全局最优值,则替换全局最优值
{
for (int j = 0; j < len; j++)
{
p2[j] = p->bestx[j];
}
gbestf = p->bestf;
printf("t = %d, gbestf = %lf\n", t, gbestf);
}
}
v_min = vmin_tps - (vmin_tps + 5.5) * t / (iter_num - 1);
v_max = vmax_tps - (vmax_tps - 5.5) * t / (iter_num - 1);
}
Tps_warpImage_cuda(Si_u8, out_u8, Tx, Ty, p1, p2, 1);
}测试代码
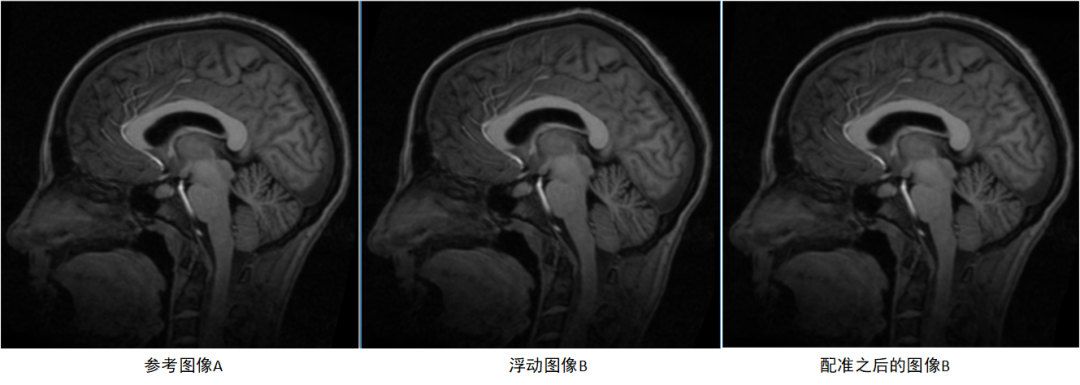
分别使用原PSO算法、改进PSO算法来优化TPS模型,对两张脑部MRI进行配准。
void tps_pso_test(void)
{
Mat img1 = imread("brain3.png", CV_LOAD_IMAGE_GRAYSCALE);
Mat img2 = imread("brain4.png", CV_LOAD_IMAGE_GRAYSCALE);
imshow("image before", img1);
imshow("image2 before", img2);
vector<Point2f> p1, p2;
int row_block_num = 8;
int col_block_num = 8;
//初始化输入参数
init_points(img1, row_block_num, col_block_num, p1, p2);
Mat out, Tx, Ty;
//tps_PSO_0(img1, img2, out, p1, p2, Tx, Ty, 300);
tps_PSO_1(img1, img2, out, p1, p2, Tx, Ty, 300);
//画出配准前后的网格
Mat img1_grid = img1.clone();
Mat img2_grid = img2.clone();
Mat img3_grid = img2.clone();
cvtColor(img1_grid, img1_grid, CV_GRAY2BGR);
cvtColor(img2_grid, img2_grid, CV_GRAY2BGR);
cvtColor(img3_grid, img3_grid, CV_GRAY2BGR);
for (int i = 0; i < row_block_num; i++)
{
for (int j = 0; j < col_block_num; j++)
{
int idx = i*col_block_num + j;
circle(img1_grid, p1[idx], 2, Scalar(0, 0, 255), 2);
circle(img2_grid, p1[idx], 2, Scalar(0, 0, 255), 2);
circle(img3_grid, p2[idx], 2, Scalar(0, 0, 255), 2);
if (i > 0 && j > 0)
{
line(img1_grid, p1[idx], p1[i*(col_block_num)+j - 1], Scalar(255, 255, 255), 1);
line(img1_grid, p1[idx], p1[(i - 1)*(col_block_num)+j], Scalar(255, 255, 255), 1);
line(img2_grid, p1[idx], p1[i*(col_block_num)+j - 1], Scalar(255, 255, 255), 1);
line(img2_grid, p1[idx], p1[(i - 1)*(col_block_num)+j], Scalar(255, 255, 255), 1);
line(img3_grid, p2[idx], p2[i*(col_block_num)+j - 1], Scalar(255, 255, 255), 1);
line(img3_grid, p2[idx], p2[(i - 1)*(col_block_num)+j], Scalar(255, 255, 255), 1);
}
}
}
imshow("img1_grid", img1_grid);
imshow("img2_grid", img2_grid);
imshow("img3_grid", img3_grid);
imshow("img2-img1", abs(img2 - img1));
imshow("tps_out-img1", abs(out - img1));
imshow("tps_out", out);
waitKey();
}04
—
测试结果
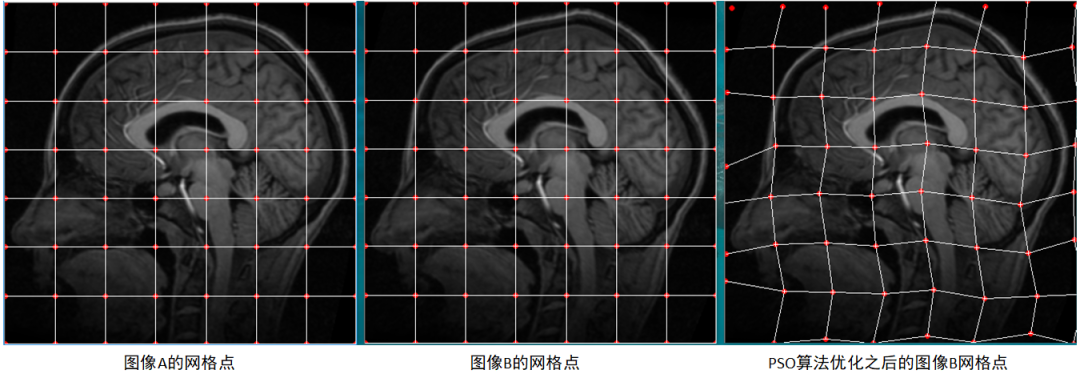
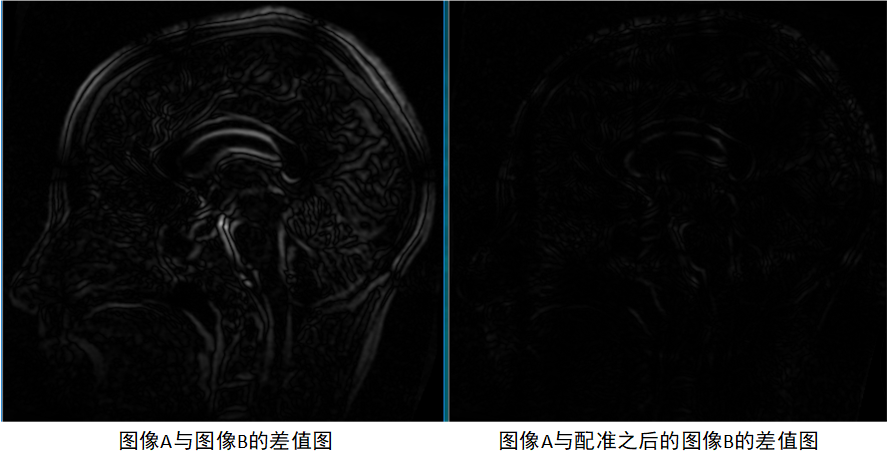
改进PSO算法的配准结果如下图,可以看到经过优化之后图像B上的网格点位置发生了改变,且由差值图可知配准之后图像B的形状达到与图像A相匹配。
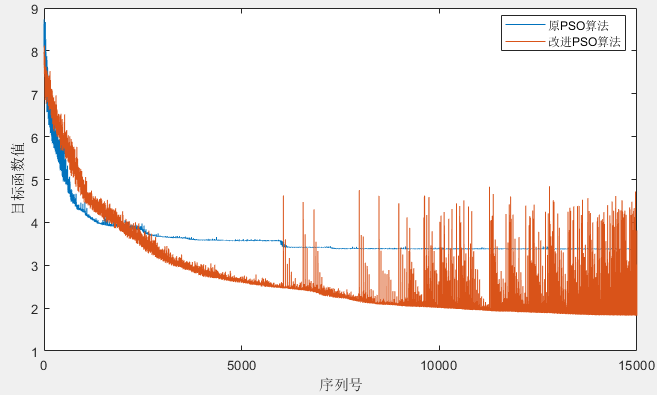
为了对比原PSO算法和改进的PSO算法,记录所有粒子每轮迭代过程中的目标函数值,得到下图。可以看到,原PSO算法迭代到了一定程度之后目标函数值没有明显的下降,但改进算法则持续下降。而且我们注意到,到了中后期改进算法的目标函数值出现较多毛刺波动,这是因为对粒子做了重新初始化的老化处理,重新初始化之后目标函数值难免有波动,但总比原算法陷入局部极值无法自拔好。
欢迎扫码关注以下微信公众号,接下来会不定时更新更加精彩的内容噢~

