堆栈和队列
1 堆栈
1.1 堆栈的概念
表达式求值问题
表达式 = 运算数 + 运算符号
不同的运算符号优先级不一样
一般地, 运算是见到运算符号进行运算, 但是在一般的表达式中, 运算符号前面的值我们能够知道, 但是后面的值不一定是当前运算符运算的值, 因此这个运算增加了很大的困难
中缀表达式: 运算符位于两个运算数之间
后缀表达式: 运算符位于两个运算数之后
前缀表达式(波兰式)
1) 前缀表达式的计算
从右往左看, 遇到运算数就放入堆栈, 遇到运算符就弹出两个运算数进行运算
2) 中缀表达式转为前缀表达式
从右往左扫描, 遇到运算数就输出, 遇到运算符根据规则决定输出还是放入堆栈
规则为:
当运算符为右括号, 直接进栈;
比较当前运算符与栈顶运算符, 只有 当前优先级 < 栈顶优先级, 才输出;
相反则进栈;
遇到左括号, 出栈运算符直到遇到右括号
输出结果的时候, 要从右往左输出就是得到的表达式
(一般地, 输出的结果也放到堆栈中, 要得到表达式输出堆栈就行)
中缀表达式"1+((2+3)×4)-5"转为前缀表达式"- + 1 × + 2 3 4 5"的过程
后缀表达式(逆波兰式)
1) 后缀表达式的计算
从左往右看, 遇到运算数就放入堆栈, 遇到运算符就弹出两个运算数进行运算
2) 中缀表达式转为后缀表达式
方向是从左往右扫描
与前缀表达式区别
当 当前优先级 > 栈顶优先级 进栈, 其余是直接输出
另外, 从左往右输出就是正常的表达式
中缀表达式"1+((2+3)×4)-5"转为后缀表达式"1 2 3 + 4 × + 5 -"的过程
后缀表达式的求值顺序:
从左往右依次扫描, 遇到运算符就运算, 运算的运算数是就近就近就近的两个运算数
62/3-42*+ = ?
62/ -> 3
33- -> 0
042* -> 08
08+ -> 8
完成这种后入先出的效果的就是堆栈(Stack)
堆栈只在一端(栈顶TOP)做插入和删除
栈顶TOP: 堆栈中离出口最近的那一个元素的位置
插入数据: 入栈(Push)
删除数据: 出栈(Pop)
后进先出: LIFO

对于n个不同元素进栈, 出栈序列的个数为卡特兰数

F(n)=c(2n,n)/(n+1)
堆栈元素出现的顺序的可能性
有ABC三个顺序输入, 输出的结果不可能是CAB
1.2 堆栈的顺序存储
栈的顺序存储结构通常由一个一维数组和一个记录栈顶元素位置的变量组成

其中Top不是一个指针, 而是一个整数, 默认的时候为-1, 当进入一个元素之后加1
当Top=-1时表示栈为空
1) 入栈

2) 出栈

关于使用一个数组实现两个堆栈的问题
如果将数组对半分, 自己存自己的, 这样有可能存在空间浪费, 为了避免空间浪费
应该设计两个堆栈都是从数组的两端向里存储
当两个堆栈的Top指针相遇(也就是相邻了, 值相差1了)时, 堆栈就满了

出入栈

1.3 堆栈的链式存储
栈的链式存储结构实际上就是一个单链表, 叫做链栈
插入和删除只能在链栈的栈顶进行
由于单链表在链尾无法找到前一个元素, 因此用单链表存储堆栈的时候, 选择链头作为栈顶

初始化和判空

出栈入栈操作


1.4 堆栈的应用
将中缀表达式转化为后缀表达式
特点: 运算数的相对顺序是不变的, 只是运算符号顺序发生改变
处理办法:
从左往右读, 遇到运算数就输出
遇到运算符的时候, 判断运算符与堆栈中运算符的优先级, 如果堆栈的优先级高, 就弹出, 再比较堆栈的符号与当前的符号直到小于当前的运算符为止; 如果堆栈的运算符优先级低就把当前的运算符压如堆栈中
注意, 在堆栈中的括号优先级是最低的, 当遇到右括号的时候就可以弹出内容了, 直到遇到左括号结束

堆栈的其他应用诸如:
函数调用以及递归的实现
深度优先搜索
回溯算法
...
2 队列
队列具有一定操作约束的线性表
插入和删除: 只能在一端插入, 在另一端删除
特点: 先进先出FIFO

2.1 队列的顺序存储的实现
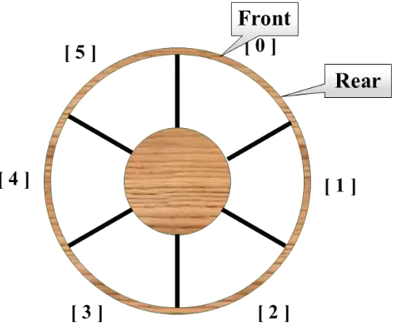
队列的顺序存储结构通常是由一个一维数组和记录队列列头和列尾元素的两个变量组成, 记录列头元素位置的变量是front, 记录队尾元素位置的变量是rear

front和rear是整形数据, 记录的是数组的下标
一般的一维数组表示的队列, front和rear都是-1, 当新增数据时, rear加1, 当输出数据的时候, front加1
rear是最后一个元素的下标
front是第一个元素前一个位置的下标

由于这样会造成资源浪费, 因此产生了循环队列
当front=rear的时候, 表示队列为空
但是如果这么设定的话, 一直存存满的时候, front和rear又相等了, 这样就无法判断是空还是满了
解决方案:
1) 使用额外的标记, size或者tag(判断最后一次操作是添加还是删除)
2) 仅仅使用n-1个数组空间(一般采用这样的方式)
入队列

出队列

2.2 队列的链表实现
队列的链式存储结构也可以用一个单链表实现, 插入和删除操作分别在链表的两头进行
单链表的链投头既可以插入也可以删除, 但是链表尾部插入方便但是删除不方便, 所以Front是链表头, rear是链表尾

不带头结点的链式队列的出队操作

3 多项式的加法运算

主要思路: 相同指数的项系数相加, 其余部分进行拷贝
多项式加法运算采用不带头结点的单向链表, 按照指数递减的顺序排列各项

多项式加法的实现





