IMU 积分进行航迹推算

Reference https://github.com/gaoxiang12/slam_in_autonomous_driving

1.0 递推方程推导

\(\quad\)连续时间内的 IMU 运动学方程：

\[\dot{\mathbf{R}}=\mathbf{R}\omega ^{\wedge} \\ \dot{\mathbf{q}=\frac{1}{2}\mathbf{q}\omega}\\ \dot{\mathbf{p}}=v \\ \dot{\mathbf{v}}=a \]

\(\quad\)这些物理量带上角标之后应该写作 \(\mathbf{R_{wb},p_{wb}}\)，对应世界坐标系，它在求导之后就是车辆在世界坐标系下的速度与加速度 \(\mathbf{v_w}, \mathbf{a_w}\) 。在不考虑地球自传的时候，也可以简单的将车辆行驶的打的视为固定的世界坐标系，这时 IMU 的测量值 \(\widetilde{\omega } ,\widetilde{a}\) 就是车辆本身的角速度，以及车体系下的加速度:

\[\begin{aligned} \tilde{\boldsymbol{a}} & =\boldsymbol{R}^{\top} \boldsymbol{a}, \\ \tilde{\boldsymbol{\omega}} & =\boldsymbol{\omega} . \end{aligned} \]

\(\quad\)注意 \(\mathbf{R}^{\top}\) 带下标之后就是 \(\mathbf{R_{bw}}\)。它将世界系下的物理量转换到车体系。然而，实际的车辆、机器人都在地球表面运行。这些系统受到重力的影响，所以我们应该把重力写在系统方程中。在绝大多数 IMU 系统中，我们可以忽略地球自转的干扰，从而把 IMU 测量值写为：

\[\begin{aligned} \tilde{\boldsymbol{a}} & =\boldsymbol{R}^{\top} \boldsymbol{(a-g)}, \\ \tilde{\boldsymbol{\omega}} & =\boldsymbol{\omega} . \end{aligned} \]

\(\quad\)\(\mathbf{g}\) 为地球的重力。当然，如果在无重力环境下测量物体加速度，就不会出现重力项。注意这里 \(\mathbf{g}\)的符号和坐标系定义相关。我们的车体系和世界系都是 \(Z\) 轴向上，于是 \(\mathbf{g}\) 通常取值 \((0, 0, −9.8)^⊤\)。假设有一个水平放置的IMU，其读数此时应当为 \((0, 0, 9.8)^⊤\)，为什么呢？因为此时真正的加速度应该为 \((0, 0, 0)^⊤\)，但是由于地球重力的影响，其输出结果会减去 \(\mathbf{g}\) ，所以输出结果就是\((0, 0, 9.8)^⊤\)。

\(\quad\)在大多数系统中，我们认为 IMU 的噪声由两部分组成：测量噪声（measurement noise）与零偏（bias）。记陀螺仪和加速度计的测量噪声分别为 \(η_g\), \(η_a\)，同时记零偏为 \(b_g\), \(b_a\)，下标 \(g\) 表示陀螺仪，\(a\) 表示加速度计。那么这几个参数在测量方程中体现为：

\(\quad\)于是，我们直接把测量模型代入运动学方程，忽略测量噪声影响，即可得到连续时间下的积分模型：

\[\begin{aligned} \dot{\boldsymbol{R}} & =\boldsymbol{R}\left(\tilde{\boldsymbol{\omega}}-\boldsymbol{b}_{g}\right)^{\wedge}, \quad \text { 或 } \dot{\boldsymbol{q}}=\boldsymbol{q}\left[0, \frac{1}{2}\left(\tilde{\boldsymbol{\omega}}-\boldsymbol{b}_{g}\right)\right], \\ \dot{\boldsymbol{p}} & =\boldsymbol{v}, \\ \dot{\boldsymbol{v}} & =\boldsymbol{R}\left(\tilde{\boldsymbol{a}}-\boldsymbol{b}_{a}\right)+\boldsymbol{g} . \end{aligned} \]

\(\quad\)有时候我们也把 \(p, v, q\) 称为 \(PVQ\) 状态。该方程可以从时间 \(t\)积分至 \(t + ∆t\),推出下一个时刻的状态情况:

\[\begin{aligned} \boldsymbol{R}(t+\Delta t) & =\boldsymbol{R}(t) \operatorname{Exp}\left(\left(\tilde{\boldsymbol{\omega}}-\boldsymbol{b}_{g}\right) \Delta t\right), \quad \text { 或 } \boldsymbol{q}(t+\Delta t)=\boldsymbol{q}(t)\left[1, \frac{1}{2}\left(\tilde{\boldsymbol{\omega}}-\boldsymbol{b}_{g}\right) \Delta t\right], \\ \end{aligned} \]

\(\quad\)这里我们先不考虑白噪声 \(\boldsymbol{\eta}_{a}\)，则IMU的测量方程有：

\[\begin{aligned} \tilde{\boldsymbol{a}} &=\boldsymbol{R}^{\top}(\boldsymbol{a}-\boldsymbol{g})+\boldsymbol{b}_{a}+\boldsymbol{\eta}_{a}\\ \tilde{\boldsymbol{a}} -\boldsymbol{b}_{a}&=\boldsymbol{R}^{\top}(\boldsymbol{a}-\boldsymbol{g}) \\ \boldsymbol{R}(\tilde{\boldsymbol{a}} -\boldsymbol{b}_{a})&=\boldsymbol{a}-\boldsymbol{g}\\ \boldsymbol{a}&=\boldsymbol{R}(\tilde{\boldsymbol{a}} -\boldsymbol{b}_{a}) + \boldsymbol{g} \end{aligned} \]

\(\quad\)速度的递推，我们知道 \(\boldsymbol{v}(t+\Delta t) = \boldsymbol{v}(t) + \mathbf{a}t\)。

\[\begin{aligned} \boldsymbol{v}(t+\Delta t) & =\boldsymbol{v}(t)+ \mathbf{a}\Delta t \\ & =\boldsymbol{v}(t)+ \left( \boldsymbol{R}(t)\left(\tilde{\boldsymbol{a}}-\boldsymbol{b}_{a}\right) +\boldsymbol{g} \right)\Delta t \\ &=\boldsymbol{v}(t)+\boldsymbol{R}(t)\left(\tilde{\boldsymbol{a}}-\boldsymbol{b}_{a}\right) \Delta t+\boldsymbol{g} \Delta t . \end{aligned} \]

\(\quad\)位置的递推，我们知道 \(\boldsymbol{p}(t+\Delta t) =\boldsymbol{p}(t)+\mathbf{v}\Delta t + \frac{1}{2}\mathbf{at^2}\)，则有：

\[\begin{aligned} \boldsymbol{p}(t+\Delta t) & =\boldsymbol{p}(t)+\boldsymbol{v} \Delta t+\frac{1}{2} \mathbf{a}t^2\\ & =\boldsymbol{p}(t)+\boldsymbol{v} \Delta t+\frac{1}{2} \left(\boldsymbol{R(t)}(\tilde{\boldsymbol{a}} -\boldsymbol{b}_{a}) + \boldsymbol{g} \right)t^2\\ & =\boldsymbol{p}(t)+\boldsymbol{v} \Delta t+\frac{1}{2}\left(\boldsymbol{R}(t)\left(\tilde{\boldsymbol{a}}-\boldsymbol{b}_{a}\right)\right) \Delta t^{2}+\frac{1}{2} \boldsymbol{g} \Delta t^{2}\\ \end{aligned} \]

2.0 代码实现

2.1 数据集介绍

这里使用的高博书中带的数据集，数据集的格式为：

# timestamp gx gy gz ax ay az

2.2 具体代码实现

代码实现主要有三个文件

common.hpp 主要用户存放 IMU 数据结构体和读取和保存数据。
imu_integration.hpp 主要存放 IMU数据的处理和航迹推算实现类。
run_imu_integration.cpp 程序入口函数。

如下命令运行

./run_imu_integration --txt_file_path="../slam_in_auto_driving/chapter3/dataset/10.txt" --output_inter_trajectory_path="./output_trajectory.txt"

common.hpp

#ifndef COMMON_HPP
#define COMMON_HPP

#include <eigen3/Eigen/Core>
#include <eigen3/Eigen/Dense>
#include <fstream>
#include <iomanip>
#include <iostream>
#include <string>
#include <vector>

struct IMUMsg
{
  IMUMsg() = default;
  IMUMsg(double timestamp, Eigen::Vector3d gyro, Eigen::Vector3d acc)
      : timestamp_(timestamp), acc_(acc), gyro_(gyro){};

  double timestamp_{0.0};
  Eigen::Vector3d acc_;
  Eigen::Vector3d gyro_;
};

struct IMUIntegrationResult
{
  IMUIntegrationResult() = default;
  IMUIntegrationResult(const double &timestamp, const Eigen::Vector3d &P,
                       const Eigen::Quaterniond &Q, const Eigen::Vector3d &V)
      : timestamp_(timestamp), P_(P), V_(V), Q_(Q){};

  double timestamp_{0.0};
  Eigen::Vector3d P_;
  Eigen::Vector3d V_;
  Eigen::Quaterniond Q_;
};

inline void ReadImuMsg(std::ifstream &fin, std::vector<IMUMsg> &imu_msg)
{
  if (!fin)
  {
    std::cerr << "Coule not find file\n";
    return;
  }
  while (!fin.eof())
  {
    std::string line;
    std::getline(fin, line);
    if (line.empty())
    {
      continue;
    }

    if (line[0] == '#')
    {
      continue;
    }

    std::stringstream ss;
    ss << line;
    std::string data_type;
    ss >> data_type;
    if (data_type == "IMU")
    {
      double time, gx, gy, gz, ax, ay, az;
      ss >> time >> gx >> gy >> gz >> ax >> ay >> az;
      imu_msg.push_back(IMUMsg(time, Eigen::Vector3d(gx, gy, gz),
                               Eigen::Vector3d(ax, ay, az)));
    }
  }
  std::cout << "Read IMU msgs success\n";
}

inline void SaveImuIntegrationResult(
    const std::string &file_path,
    const std::vector<IMUIntegrationResult> &imu_inte_result)
{
  std::ofstream fout(file_path);
  for (const auto &imu_traj : imu_inte_result)
  {
    fout << std::setprecision(18) << imu_traj.timestamp_ << " " << std::setprecision(9);
    fout << imu_traj.P_(0) << " " << imu_traj.P_(1) << " " << imu_traj.P_(2) << " ";
    fout << imu_traj.Q_.w() << " " << imu_traj.Q_.x() << " " << imu_traj.Q_.y() << " " << imu_traj.Q_.z() << " ";
    fout << imu_traj.V_(0) << " " << imu_traj.V_(1) << " " << imu_traj.V_(2) << " ";
    fout << std::endl;
  }
}

#endif  // COMMON_HPP

imu_integration.hpp

#include <eigen3/Eigen/Core>
#include <eigen3/Eigen/Dense>
#include <sophus/so3.hpp>

#include "common.hpp"

class ImuIntegration
{
 public:
  ImuIntegration() = default;
  ~ImuIntegration() = default;
  ImuIntegration(const Eigen::Vector3d &gravity, const Eigen::Vector3d &init_bg,
                 const Eigen::Vector3d &init_ba)
      : gravity_(gravity), init_ba_(init_ba), init_bg_(init_bg)
  {
  }

  void AddNewImgMessage(const IMUMsg &imu_msg)
  {
    // Final P: -3.38794e+06  5.73752e+06  -512933
    // 其实第一帧 IMU 数据也可以不判断，因为后面有 dt<0.1 的判断
    if (first_imu_)
    {
      first_imu_ = false;
      timestamp_ = imu_msg.timestamp_;
    }

    double dt = imu_msg.timestamp_ - timestamp_;

    if (dt > 0 && dt < 0.1)
    {
      P_ = P_ + V_ * dt + 0.5 * (R_ * (imu_msg.acc_ - init_ba_)) * dt * dt +
           0.5 * gravity_ * dt * dt;
      V_ = V_ + R_ * (imu_msg.acc_ - init_ba_) * dt + gravity_ * dt;
      R_ = R_ * Sophus::SO3d::exp((imu_msg.gyro_ - init_bg_) * dt);
    }

    timestamp_ = imu_msg.timestamp_;
  }

  Eigen::Vector3d GetPosition() const { return P_; }
  Eigen::Vector3d GetVelocity() const { return V_; }
  Eigen::Quaterniond GetRotation() const { return R_.unit_quaternion(); }

 private:
  Sophus::SO3d R_;
  Eigen::Quaterniond R_quaternion_ = Eigen::Quaterniond::UnitRandom();
  Eigen::Vector3d P_ = Eigen::Vector3d::Zero();
  Eigen::Vector3d V_ = Eigen::Vector3d::Zero();
  Eigen::Vector3d gravity_ = Eigen::Vector3d(0, 0, -9.81);
  Eigen::Vector3d init_ba_ = Eigen::Vector3d::Zero();
  Eigen::Vector3d init_bg_ = Eigen::Vector3d::Zero();
  double timestamp_{0.0};
  bool first_imu_{true};
};

run_imu_integration.cpp

#include <gflags/gflags.h>

#include <eigen3/Eigen/Core>
#include <eigen3/Eigen/Dense>
#include <iostream>
#include <ostream>

#include "common.hpp"
#include "imu_integration.hpp"

DEFINE_string(txt_file_path, "../slam_in_auto_driving/chapter3/dataset/10.txt",
              "Imu integration file");
DEFINE_string(output_inter_trajectory_path, "./output_trajectory.txt",
              "output trajectory file");

int main(int argc, char *argv[])
{
  google::ParseCommandLineFlags(&argc, &argv, true);
  std::ifstream fin(FLAGS_txt_file_path);
  std::vector<IMUMsg> imu_msgs;
  std::vector<IMUIntegrationResult> imu_inter_result;
  ReadImuMsg(fin, imu_msgs);

  // 该实验中，我们假设零偏已知
  Eigen::Vector3d gravity(0, 0, -9.8);  // 重力方向
  Eigen::Vector3d init_bg(00.000224886, -7.61038e-05, -0.000742259);
  Eigen::Vector3d init_ba(-0.165205, 0.0926887, 0.0058049);

  ImuIntegration imu_integration(gravity, init_bg, init_ba);

  for (auto &imu_msg : imu_msgs)
  {
    imu_integration.AddNewImgMessage(imu_msg);
    imu_inter_result.push_back(IMUIntegrationResult(
        imu_msg.timestamp_, imu_integration.GetPosition(),
        imu_integration.GetRotation(), imu_integration.GetVelocity()));
  }

  SaveImuIntegrationResult(FLAGS_output_inter_trajectory_path,
                           imu_inter_result);
  // 高博书中程序输出的结果
  // T: 1624429630.2702086
  // P : -3387943.36 5737523.81 -512933.307
  // Q : 0.982857044 -0.132676506 0.0940114453 0.0868954789
  // V : -572.166705 4626.10758 -496.605214
  std::cout << "Final P: " << imu_integration.GetPosition().transpose()
            << std::endl;
  std::cout << "Final V: " << imu_integration.GetVelocity().transpose()
            << std::endl;
  std::cout << "Final Q: " << imu_integration.GetRotation().coeffs().transpose()
            << std::endl;

  return 0;
}

输出结果可视化：

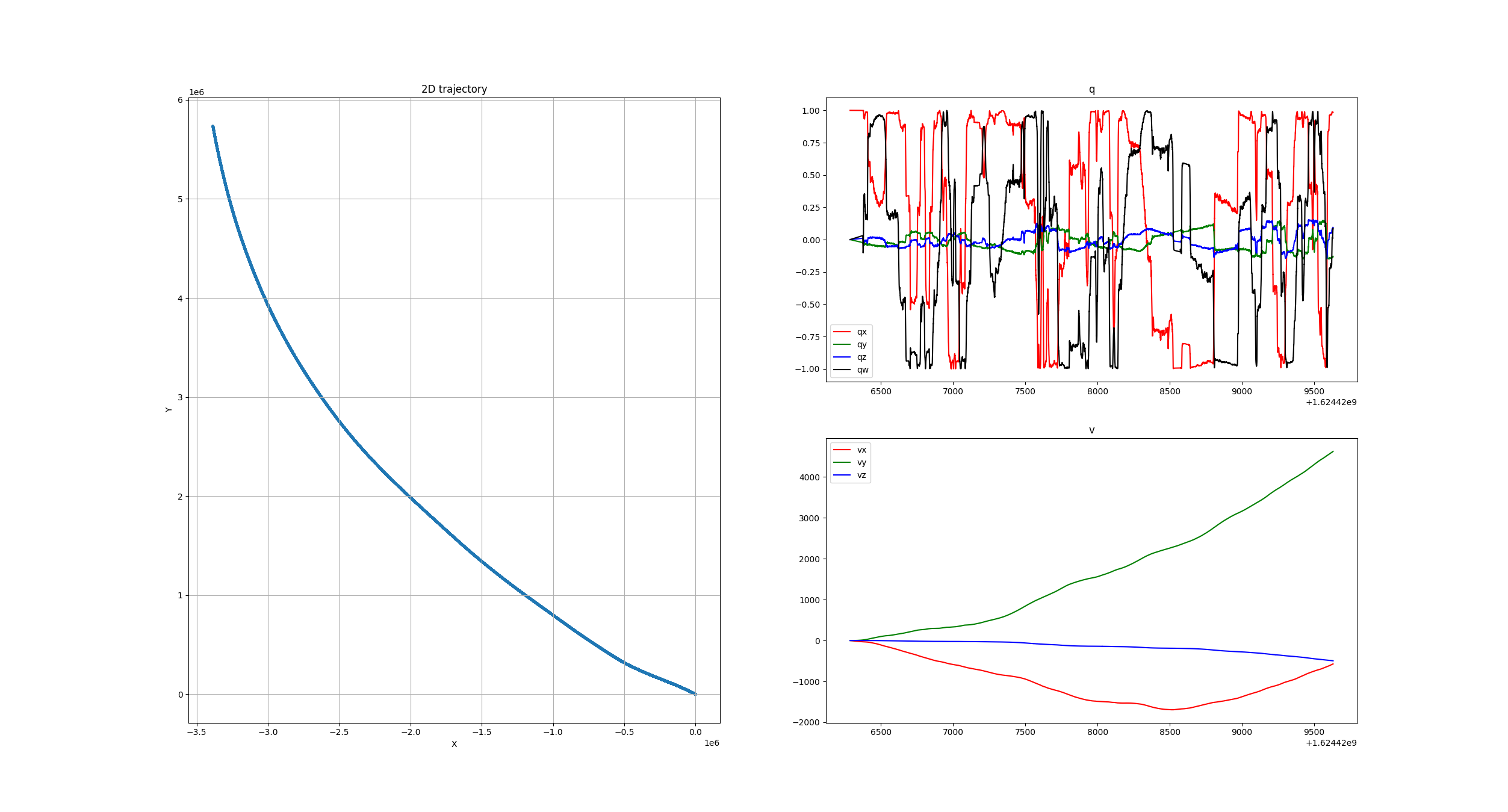
可视化程序，运行：

python3 draw_imu_integration.py ./output_trajectory.txt

# coding=UTF-8
import sys
import numpy as np
import matplotlib.pyplot as plt

if __name__ == "__main__":
    if len(sys.argv) != 2:
        print('Please input valid file')
        exit(1)
    else:
        path = sys.argv[1]
        path_data = np.loadtxt(path)
        plt.rcParams['figure.figsize'] = (16.0, 12.0)
        
        # 轨迹
        plt.subplot(121)
        plt.scatter(path_data[:, 1], path_data[:, 2], s=2)
        plt.xlabel('X')
        plt.ylabel('Y')
        plt.grid()
        plt.title('2D trajectory')
        
        # 姿态
        plt.subplot(222)
        plt.plot(path_data[:, 0], path_data[:, 4], 'r')
        plt.plot(path_data[:, 0], path_data[:, 5], 'g')
        plt.plot(path_data[:, 0], path_data[:, 6], 'b')
        plt.plot(path_data[:, 0], path_data[:, 7], 'k')
        plt.title('q')
        plt.legend(['qx', 'qy', 'qz', 'qw'])

        # 速度
        plt.subplot(224)
        plt.plot(path_data[:, 0], path_data[:, 8], 'r')
        plt.plot(path_data[:, 0], path_data[:, 9], 'g')
        plt.plot(path_data[:, 0], path_data[:, 10], 'b')
        plt.title('v')
        plt.legend(['vx', 'vy', 'vz'])

        plt.show()
        exit(1)

posted @ 2023-05-21 14:56 weihao-ysgs 阅读(620) 评论(0) 编辑收藏举报

刷新页面返回顶部

weihao-ysgs

IMU 积分进行航迹推算

IMU 积分进行航迹推算

1.0 递推方程推导

2.0 代码实现

2.1 数据集介绍

2.2 具体代码实现

公告