IMU 预积分（仅供参考）

IMU Pre-Integration

本文章记录在学习 VIO 的过程中对 IMU 预积分的一些理解和公式的证明，也看了很多的文章和论文，知识点和证明过于复杂，特此记录，方便复习回顾，参考文献和网址也已经在文章最后给出，大家也可以自行查阅。

目录

• IMU Pre-Integration
  • 0. 部分先验知识
  • 1.0 预积分定义
    • 1.1 引出预积分
    • 1.2 预积分量
  • 2.0 IMU 的预积分误差
    • 2.1 定义
    • 2.2 预积分的离散形式
    • 2.3 预积分量的方差
    • 2.4 状态误差线性递推公式的推导
      • 2.4.1 简介
      • 2.4.2 基于一阶泰勒展开的误差递推方程
      • 2.4.3 基于误差随时间变化的递推方程
      • 2.4.4 对比分析
    • 2.5 预积分的误差递推公式推导

0. 部分先验知识

$${\mathit{\omega }}^{\wedge }={\left[\begin{array}{c}{\omega }_1\\ {\omega }_2\\ {\omega }_3\end{array}\right]}^{\wedge }=\left[\begin{array}{ccc}0& -{\omega }_3& {\omega }_2\\ {\omega }_3& 0& -{\omega }_1\\ -{\omega }_2& {\omega }_1& 0\end{array}\right]\in \mathfrak{s}\mathfrak{o}(3).$$

$${\mathbf{a}}^{\wedge }\mathbf{b}=-{\mathbf{b}}^{\wedge }\mathbf{a},\mathrm{\forall }\mathbf{a},\mathbf{b}\in {\mathbb{R}}^3$$

$$\exp \left({\varphi }^{\wedge }\right)=\mathbf{I}+\frac{\sin (\Vert \varphi \Vert )}{\Vert \varphi \Vert }{\varphi }^{\wedge }+\frac{1-\cos (\Vert \varphi \Vert )}{\Vert \varphi {\Vert }^2}{\left({\varphi }^{\wedge }\right)}^2.$$

$$\begin{gathered} \exp \left({\varphi }^{\wedge }\right)\approx \mathbf{I}+{\varphi }^{\wedge } \\ TaylorExpansionapprox \end{gathered}$$

$$\begin{array}{rl}\frac{\partial (\exp \left({\varphi }^{\wedge }\right)\mathrm{p})}{\partial \varphi }& =\underset{\delta \varphi \to 0}{lim}\frac{\exp ((\varphi +\delta \varphi {)}^{\wedge })\mathrm{p}-\exp \left({\varphi }^{\wedge }\right)\mathrm{p}}{\delta \varphi }\\ 1:& =\underset{\delta \varphi \to 0}{lim}\frac{\exp \left({\left({\mathrm{J}}_1\delta \varphi \right)}^{\wedge }\right)\exp \left({\varphi }^{\wedge }\right)\mathrm{p}-\exp \left({\varphi }^{\wedge }\right)\mathrm{p}}{\delta \varphi }\\ 2:& \approx \underset{\delta \varphi \to 0}{lim}\frac{(\mathrm{I}+{\left({\mathrm{J}}_1\delta \varphi \right)}^{\wedge })\exp \left({\varphi }^{\wedge }\right)\mathrm{p}-\exp \left({\varphi }^{\wedge }\right)\mathrm{p}}{\delta \varphi }\\ 3:& =\underset{\delta \varphi \to 0}{lim}\frac{{\left({\mathrm{J}}_1\delta \varphi \right)}^{\wedge }\exp \left({\varphi }^{\wedge }\right)\mathrm{p}}{\delta \varphi }\\ 4:& =\underset{\delta \varphi \to 0}{lim}\frac{-{(\exp \left({\varphi }^{\wedge }\right)\mathrm{p})}^{\wedge }{\mathrm{J}}_1\delta \varphi }{\delta \varphi }\\ 5:& =-(\mathrm{Rp}{)}^{\wedge }{\mathrm{J}}_1\end{array}$$

1.0 预积分定义

1.1 引出预积分

​ 与传统IMU的运动学积分不同，预积分可以将一段时间内的IMU测量数据累计起来，建立预积分测量，因而十分适合以关键帧为基础单元的激光或视觉SLAM系统。

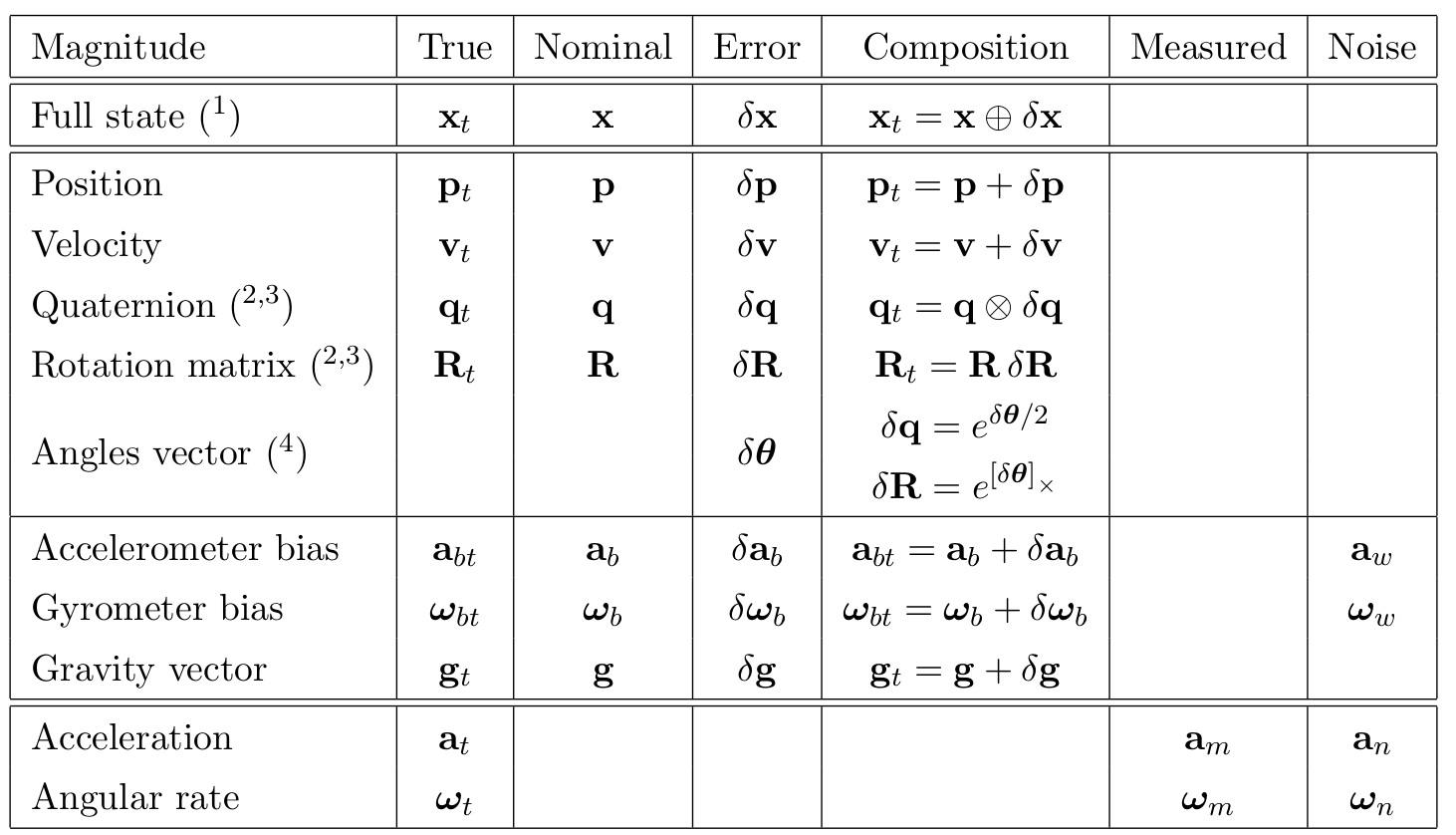
​ IMU 的真实值为 $\mathit{\omega },\mathbf{a}$ , 测量值为 $\tilde{\mathit{\omega }}$, $\tilde{\mathbf{a}}$, 则有：

$$\begin{array}{rl}{\tilde{\mathit{\omega }}}^b& ={\mathit{\omega }}^b+{\mathbf{b}}^g+{\mathbf{n}}^g\\ {\tilde{\mathbf{a}}}^b& ={\mathbf{q}}_{bw}({\mathbf{a}}^w+{\mathbf{g}}^w)+{\mathbf{b}}^a+{\mathbf{n}}^a\end{array}$$

​ 上标 $g$ 表示 $gyro$, $a$ 表示 $acc$， $w$ 表示在世界坐标系 $world$, $b$ 表示 $imu$ 机体坐标系 $body$。$\mathrm{PVQ}$ 对时间的导数可写成:

$$\begin{array}{l}{\dot{\mathbf{p}}}_{w{b}_t}={\mathbf{v}}_t^w\\ {\dot{\mathbf{v}}}_t^w={\mathbf{a}}_t^w\\ {\dot{\mathbf{q}}}_{w{b}_t}={\mathbf{q}}_{w{b}_t}\otimes \left[\begin{array}{c}0\\ \frac{1}{2}{\mathit{\omega }}^{b_t}\end{array}\right]\end{array}$$

​ 预积分的过程可以用如下图来示意：

​ 从第 $i$ 时刻的 $\mathrm{PVQ}$ 对 IMU 的测量值进行积分得到第 $j$ 时刻的 $\mathrm{PVQ}$:

$$\begin{array}{l}{\mathbf{p}}_{w{b}_j}={\mathbf{p}}_{w{b}_i}+{\mathbf{v}}_i^w\mathrm{\Delta }t+{\iint }_{t\in [i,j]}({\mathbf{q}}_{w{b}_t}{\mathbf{a}}^{b_t}-{\mathbf{g}}^w)\delta t^2\\ {\mathbf{v}}_j^w={\mathbf{v}}_i^w+{\int }_{t\in [i,j]}({\mathbf{q}}_{w{b}_t}{\mathbf{a}}^{b_t}-{\mathbf{g}}^w)\delta t\\ {\mathbf{q}}_{w{b}_j}={\int }_{t\in [i,j]}{\mathbf{q}}_{w{b}_t}\otimes \left[\begin{array}{c}0\\ \frac{1}{2}{\mathit{\omega }}^{b_t}\end{array}\right]\delta t\end{array}$$

问题:每次 $q_{w{b}_t}$ 优化更新后,都需要重新进行积分,运算量较大。

​ 一个很简单的公式转换,就可以将积分模型转为预积分模型:

$${\mathbf{q}}_{w{b}_t}={\mathbf{q}}_{w{b}_i}\otimes {\mathbf{q}}_{b_i{b}_t}$$

​ 那么,$\mathrm{PVQ}$ 积分公式中的积分项则变成相对于第 $i$ 时刻的姿态,而不是相对于世界坐标系的姿态:

$$\begin{array}{l}{\mathbf{p}}_{w{b}_j}={\mathbf{p}}_{w{b}_i}+{\mathbf{v}}_i^w\mathrm{\Delta }t-\frac{1}{2}{\mathbf{g}}^w\mathrm{\Delta }{t}^2+{\mathbf{q}}_{w{b}_i}{\iint }_{t\in [i,j]}\left({\mathbf{q}}_{b_i{b}_t}{\mathbf{a}}^{b_t}\right)\delta t^2\\ {\mathbf{v}}_j^w={\mathbf{v}}_i^w-{\mathbf{g}}^w\mathrm{\Delta }t+{\mathbf{q}}_{w{b}_i}{\int }_{t\in [i,j]}\left({\mathbf{q}}_{b_i{b}_t}{\mathbf{a}}^{b_t}\right)\delta t\\ {\mathbf{q}}_{w{b}_j}={\mathbf{q}}_{w{b}_i}{\int }_{t\in [i,j]}{\mathbf{q}}_{b_i{b}_t}\otimes \left[\begin{array}{c}0\\ \frac{1}{2}{\mathit{\omega }}^{b_t}\end{array}\right]\delta t\end{array}$$

1.2 预积分量

​ 预积分量仅仅跟 IMU 测量值有关,它将一段时间内的 IMU 数据直接积分起来就得到了预积分量:

$$\begin{array}{l}{\mathit{\alpha }}_{b_i{b}_j}={\iint }_{t\in [i,j]}\left({\mathbf{q}}_{b_i{b}_t}{\mathbf{a}}^{b_t}\right)\delta t^2\\ {\mathit{\beta }}_{b_i{b}_j}={\int }_{t\in [i,j]}\left({\mathbf{q}}_{b_i{b}_t}{\mathbf{a}}^{b_t}\right)\delta t\\ {\mathbf{q}}_{b_i{b}_j}={\int }_{t\in [i,j]}{\mathbf{q}}_{b_i{b}_t}\otimes \left[\begin{array}{c}0\\ \frac{1}{2}{\omega }^{b_t}\end{array}\right]\delta t\end{array}$$

​ 其中 $\mathbf{a}$ 表示的是位移的增量，$\mathbf{b}$ 表 示的是速度的增量，$\mathbf{q}$ 表示的是旋转的增量。很显然，对加速度进行一次积分即得到了速度增量，对加速度进行两次积分即得到了位移增量。

​ 将上面三个量分别带入公式$(5)$重新整理下 $\mathrm{PVQ}$ 的积分公式,有:

$$\left[\begin{array}{c}{\mathbf{p}}_{w{b}_j}\\ {\mathbf{v}}_j^w\\ {\mathbf{q}}_{w{b}_j}\\ {\mathbf{b}}_j^a\\ {\mathbf{b}}_j^g\end{array}\right]=\left[\begin{array}{c}{\mathbf{p}}_{w{b}_i}+{\mathbf{v}}_i^w\mathrm{\Delta }t-\frac{1}{2}{\mathbf{g}}^w\mathrm{\Delta }{t}^2+{\mathbf{q}}_{w{b}_i}{\mathit{\alpha }}_{b_i{b}_j}\\ {\mathbf{v}}_i^w-{\mathbf{g}}^w\mathrm{\Delta }t+{\mathbf{q}}_{w{b}_i}{\mathit{\beta }}_{b_i{b}_j}\\ {\mathbf{q}}_{w{b}_i}{\mathbf{q}}_{b_i{b}_j}\\ {\mathbf{b}}_i^a\\ {\mathbf{b}}_i^g\end{array}\right]$$

2.0 IMU 的预积分误差

2.1 定义

​ 定义:一段时间内 IMU 构建的预积分量作为测量值,对两时刻之间的状态量进行约束

$${\left[\begin{array}{c}{\mathbf{r}}_p\\ {\mathbf{r}}_q\\ {\mathbf{r}}_v\\ {\mathbf{r}}_{ba}\\ {\mathbf{r}}_{bg}\end{array}\right]}_{15\times 1}=\left[\begin{array}{c}{\mathbf{q}}_{b_{i}w}({\mathbf{p}}_{w{b}_j}-{\mathbf{p}}_{w{b}_i}-{\mathbf{v}}_i^w\mathrm{\Delta }t+\frac{1}{2}{\mathbf{g}}^w\mathrm{\Delta }{t}^2)-{\mathit{\alpha }}_{b_i{b}_j}\\ 2{[{\mathbf{q}}_{b_j{b}_i}\otimes ({\mathbf{q}}_{b_{i}w}\otimes {\mathbf{q}}_{w{b}_j})]}_{xyz}\\ {\mathbf{q}}_{b_{i}w}({\mathbf{v}}_j^w-{\mathbf{v}}_i^w+{\mathbf{g}}^w\mathrm{\Delta }t)-{\mathit{\beta }}_{b_i{b}_j}\\ {\mathbf{b}}_j^a-{\mathbf{b}}_i^a\\ {\mathbf{b}}_j^g-{\mathbf{b}}_i^g\end{array}\right]$$

​ 其实就是将公式$(7)$ 中的等式单独拿出来，然后做了一个差的运算，作为误差项。例如公式 $(7)$ 中的第一行：

$$\begin{array}{r}{\mathbf{p}}_{w{b}_j}={\mathbf{p}}_{w{b}_i}+{\mathbf{v}}_i^w\mathrm{\Delta }t-\frac{1}{2}{\mathbf{g}}^w\mathrm{\Delta }{t}^2+{\mathbf{q}}_{w{b}_i}{\mathit{\alpha }}_{b_i{b}_j}\\ {\mathbf{q}}_{w{b}_i}{\mathit{\alpha }}_{b_i{b}_j}={\mathbf{p}}_{w{b}_j}-{\mathbf{p}}_{w{b}_i}+{\mathbf{v}}_i^w\mathrm{\Delta }t-\frac{1}{2}{\mathbf{g}}^w\mathrm{\Delta }{t}^2\\ {\mathit{\alpha }}_{b_i{b}_j}={\mathbf{q}}_{b_{i}w}({\mathbf{p}}_{w{b}_j}-{\mathbf{p}}_{w{b}_i}+{\mathbf{v}}_i^w\mathrm{\Delta }t-\frac{1}{2}{\mathbf{g}}^w\mathrm{\Delta }{t}^2)\\ {\mathbf{r}}_p={\mathbf{q}}_{b_{i}w}({\mathbf{p}}_{w{b}_j}-{\mathbf{p}}_{w{b}_i}+{\mathbf{v}}_i^w\mathrm{\Delta }t-\frac{1}{2}{\mathbf{g}}^w\mathrm{\Delta }{t}^2)-{\mathit{\alpha }}_{b_i{b}_j}\end{array}$$

​ 公式 $(10)$ 中的其他项也是如此

​ 上面误差中位移, 速度, 偏置都是直接相减得到。第二项是关于四元 数的旋转误差, 其中 $[\cdot {]}_{xyz}$ 表示只取四元数的虚部 $(x,y,z)$ 组成的三维向量。

2.2 预积分的离散形式

​ 这里使用 mid-point 方法,即两个相邻时刻 $k$ 到 $k+1$ 的位姿是用两个时刻的测量值 $\mathbf{a}$, $\mathit{\omega }$ 的平 均值来计算:

$$\begin{array}{rl}\mathit{\omega }& =\frac{1}{2}(({\mathit{\omega }}^{b_k}-{\mathbf{b}}_k^g)+({\mathit{\omega }}^{b_{k+1}}-{\mathbf{b}}_k^g))\\ {\mathbf{q}}_{b_i{b}_{k+1}}& ={\mathbf{q}}_{b_i{b}_k}\otimes \left[\begin{array}{c}1\\ \frac{1}{2}\mathit{\omega }\delta t\end{array}\right]\\ \mathbf{a}& =\frac{1}{2}({\mathbf{q}}_{b_i{b}_k}({\mathbf{a}}^{b_k}-{\mathbf{b}}_k^a)+{\mathbf{q}}_{b_i{b}_{k+1}}({\mathbf{a}}^{b_{k+1}}-{\mathbf{b}}_k^a))\\ {\mathit{\alpha }}_{b_i{b}_{k+1}}& ={\mathit{\alpha }}_{b_i{b}_k}+{\mathit{\beta }}_{b_i{b}_k}\delta t+\frac{1}{2}\mathbf{a}\delta t^2\\ {\mathit{\beta }}_{b_i{b}_{k+1}}& ={\mathit{\beta }}_{b_i{b}_k}+\mathbf{a}\delta t\\ {\mathbf{b}}_{k+1}^a& ={\mathbf{b}}_k^a+{\mathbf{n}}_{{\mathbf{b}}_k^a}\delta t\\ {\mathbf{b}}_{k+1}^g& ={\mathbf{b}}_k^g+{\mathbf{n}}_{{\mathbf{b}}_k^g}\delta t\end{array}$$

2.3 预积分量的方差

​ question: 一个 IMU 数据作为测量值的噪声方差我们能够标定。现在,一段时间内多个 IMU 数据积分形成的预积分量的方差呢?

• Covariance Propagation
  已知一个变量 $\mathbf{y}=\mathbf{A}\mathbf{x},\mathbf{x}\in \mathcal{N}(0,{\mathbf{\Sigma }}_x)$, 则有 ${\mathbf{\Sigma }}_y=A{\mathbf{\Sigma }}_x{A}^{\mathrm{\top }}$

$$\begin{array}{rl}{\mathbf{\Sigma }}_y& =E((\mathbf{A}\mathbf{x})(\mathbf{A}\mathbf{x}{)}^{\mathrm{\top }})\\ & =E\left(\mathbf{A}\mathbf{x}{\mathbf{x}}^{\mathrm{\top }}{\mathbf{A}}^{\mathrm{\top }}\right)\\ & =A{\mathbf{\Sigma }}_x{A}^{\mathrm{\top }}\end{array}$$

​ 所以,要推导预积分量的协方差,我们需要知道 imu 噪声和预积分量之间的线性递推关系。

​ 假设已知了相邻时刻误差的线性传递方程:

$${\mathit{\eta }}_{ik}={\mathbf{F}}_{k-1}{\mathit{\eta }}_{ik-1}+{\mathbf{G}}_{k-1}{\mathbf{n}}_{k-1}$$

​ 比如: 状态量误差为 ${\mathit{\eta }}_{ik}=[\delta {\mathit{\theta }}_{ik},\delta {\mathbf{v}}_{ik},\delta {\mathbf{p}}_{ik}]$ , 测量噪声为 ${\mathbf{n}}_k={[{\mathbf{n}}_k^g,{\mathbf{n}}_k^a]}_{\text{。 }}$

​ 误差的传递由两部分组成:当前时刻的误差传递给下一时刻，当前时刻测量噪声传递给下一时刻。

​ 协方差矩阵可以通过递推计算得到:

$${\mathbf{\Sigma }}_{ik}={\mathbf{F}}_{k-1}{\mathbf{\Sigma }}_{ik-1}{\mathbf{F}}_{k-1}^{\mathrm{\top }}+{\mathbf{G}}_{k-1}{\mathbf{\Sigma }}_{\mathbf{n}}{\mathbf{G}}_{k-1}^{\mathrm{\top }}$$

​ 其中, ${\mathrm{\Sigma }}_{\mathbf{n}}$ 是测量噪声的协方差矩阵, 方差从 $i$ 时刻开始进行递推, ${\mathbf{\Sigma }}_{ii}=\mathbf{0}$ 。

2.4 状态误差线性递推公式的推导

state variables in error kalman filter

2.4.1 简介

​ 通常对于状态量之间的递推关系是非线性的方程如 ${\mathbf{x}}_k=f({\mathbf{x}}_{k-1},{\mathbf{u}}_{k-1})$, 其中状态量为 $\mathbf{x},\mathbf{u}$ 为系统的输入量。

​ 我们可以用两种方法来推导状态误差传递的线性递推关系:

• 一种是基于一阶泰勒展开的误差递推方程。
• 一种是基于误差随时间变化的递推方程。

2.4.2 基于一阶泰勒展开的误差递推方程

​ 令状态量为 $\mathbf{x}=\hat{\mathbf{x}}+\delta \mathbf{x}$, 其中, 真值为 $\hat{\mathbf{x}},\mathrm{误}\mathrm{差}\mathrm{为}\delta \mathbf{x}$ 。另外, 输入量 $u$ 的噪声为 $n$ 。

​ 基于泰勒展开的误差传递（应用于 EKF 的协方差预测）

​ 非线性系统 ${\mathbf{x}}_k=f({\mathbf{x}}_{k-1},{\mathbf{u}}_{k-1})$ 的状态误差的线性递推关系如下:

$$\delta {\mathbf{x}}_k=\mathbf{F}\delta {\mathbf{x}}_{k-1}+\mathbf{G}{\mathbf{n}}_{k-1}$$

​ 其中, $\mathbf{F}$ 是状态量 $\mathrm{x}{k} $ 对状态量 ${\mathrm{x}}_{k-1}$ 的雅克比矩阵, $\mathbf{G}$ 是状态量 $ \mathrm{x}$\mathrm{对}\mathrm{输}\mathrm{入}\mathrm{量}$\mathbf{u}_{k-1} $ 的雅克比矩阵。

​ 证明：对非线性状态方程进行一阶泰勒展开有:

$$\begin{array}{rl}{\mathbf{x}}_k& =f({\mathbf{x}}_{k-1},{\mathbf{u}}_{k-1})\\ {\hat{\mathbf{x}}}_k+\delta {\mathbf{x}}_k& =f({\hat{\mathbf{x}}}_{k-1}+\delta {\mathbf{x}}_{k-1},{\hat{\mathbf{u}}}_{k-1}+{\mathbf{n}}_{k-1})\\ \underset{―}{{\hat{\mathbf{x}}}_k}+\delta {\mathbf{x}}_k& =\underset{―}{f({\hat{\mathbf{x}}}_{k-1},{\hat{\mathbf{u}}}_{k-1})}+\mathbf{F}\delta {\mathbf{x}}_{k-1}+\mathbf{G}{\mathbf{n}}_{k-1}\end{array}$$

2.4.3 基于误差随时间变化的递推方程

如果我们能够推导状态误差随时间变化的导数关系,比如:

$$\dot{\delta }\mathbf{x}=\mathbf{A}\delta \mathbf{x}+\mathbf{B}\mathbf{n}$$

则误差状态的传递方程为:

$$\begin{array}{rl}\delta {\mathbf{x}}_k& =\delta {\mathbf{x}}_{k-1}+\dot{\delta }{\mathbf{x}}_{k-1}\mathrm{\Delta }t\\ \to \delta {\mathbf{x}}_k& =(\mathbf{I}+\mathbf{A}\mathrm{\Delta }t)\delta {\mathbf{x}}_{k-1}+\mathbf{B}\mathrm{\Delta }t{\mathbf{n}}_{k-1}\end{array}$$

对上面式子作个简单展开即可得到：

$$\begin{array}{rl}\delta {\mathbf{x}}_k& =\delta {\mathbf{x}}_{k-1}+\dot{\delta }{\mathbf{x}}_{k-1}\mathrm{\Delta }t\\ \delta {\mathbf{x}}_k& =\delta {\mathbf{x}}_{k-1}+(\mathbf{A}\delta {\mathbf{x}}_{k-1}+{\mathbf{Bn}}_{\mathbf{k}\mathbf{-}\mathbf{1}})\mathrm{\Delta }t\\ \delta {\mathbf{x}}_k& =\delta {\mathbf{x}}_{k-1}+\mathbf{A}\delta {\mathbf{x}}_{k-1}\mathrm{\Delta }t+{\mathbf{Bn}}_{\mathbf{k}\mathbf{-}\mathbf{1}}\mathrm{\Delta }t\\ \\ \to \delta {\mathbf{x}}_k& =(\mathbf{I}+\mathbf{A}\mathrm{\Delta }t)\delta {\mathbf{x}}_{k-1}+\mathbf{B}\mathrm{\Delta }t{\mathbf{n}}_{k-1}\end{array}$$

这两种推导方式的可以看出有:

$$\mathbf{F}=\mathbf{I}+\mathbf{A}\mathrm{\Delta }t,\mathbf{G}=\mathbf{B}\mathrm{\Delta }t$$

2.4.4 对比分析

​ 第一种方法不是很好么,为什么会想着去弄误差随时间的变化呢 ? 这是因为 VIO 系统中已经知道了状态的导数和状态之间的转移矩阵。
​ 如: 我们已经知道速度和状态量之间的关系:

$$\dot{\mathbf{v}}=\mathbf{R}{\mathbf{a}}^b+\mathbf{g}$$

​ 那我们就可以推导速度的误差和状态误差之间的关系,再每一项上都加上各自的误差就有:

$$\begin{array}{rl}\dot{\mathbf{v}}+\dot{\delta }\mathbf{v}& =\mathbf{R}(\mathbf{I}+[\delta \mathit{\theta }{]}_{\times })({\mathbf{a}}^b+\delta {\mathbf{a}}^b)+\mathbf{g}+\delta \mathbf{g}\\ \dot{\delta \mathbf{v}}& =\mathbf{R}\delta {\mathbf{a}}^b+\mathbf{R}[\delta \mathit{\theta }{]}_{\times }({\mathbf{a}}^b+\delta {\mathbf{a}}^b)+\delta \mathbf{g}\\ \dot{\delta \mathbf{v}}& =\mathbf{R}\delta {\mathbf{a}}^{\mathbf{b}}-\mathbf{R}{\left[{\mathbf{a}}^b\right]}_{\times }\delta \mathit{\theta }+\delta \mathbf{g}\end{array}$$

​ 由此就能以此类推，写出整个 $\mathbf{A}$ 和 $\mathbf{B}$ 其他方程了。

2.5 预积分的误差递推公式推导

​ 首先回顾预积分的误差递推公式,将测量噪声也考虑进模型:

$$\begin{array}{rl}\mathit{\omega }& =\frac{1}{2}(({\mathit{\omega }}^{b_k}+{\mathbf{n}}_k^g-{\mathbf{b}}_k^g)+({\mathit{\omega }}^{b_{k+1}}+{\mathbf{n}}_{k+1}^g-{\mathbf{b}}_k^g))\\ {\mathbf{q}}_{b_i{b}_{k+1}}& ={\mathbf{q}}_{b_i{b}_k}\otimes \left[\begin{array}{c}1\\ \frac{1}{2}\mathit{\omega }\delta t\end{array}\right]\\ \mathbf{a}& =\frac{1}{2}({\mathbf{q}}_{b_i{b}_k}({\mathbf{a}}^{b_k}+{\mathbf{n}}_k^a-{\mathbf{b}}_k^a)+{\mathbf{q}}_{b_i{b}_{k+1}}({\mathbf{a}}^{b_{k+1}+{\mathbf{n}}_{k+1}^a-{\mathbf{b}}_k^a))}\\ {\mathit{\alpha }}_{b_i{b}_{k+1}}& ={\mathit{\alpha }}_{b_i{b}_k}+{\mathit{\beta }}_{b_i{b}_k}\delta t+\frac{1}{2}\mathbf{a}\delta t^2\\ {\mathit{\beta }}_{b_i{b}_{k+1}}& ={\mathit{\beta }}_{b_i{b}_k}+\mathbf{a}\delta t\\ {\mathbf{b}}_{k+1}^a& ={\mathbf{b}}_k^a+{\mathbf{n}}_{{\mathbf{b}}_k^a}\delta t\\ {\mathbf{b}}_{k+1}^g& ={\mathbf{b}}_k^g+{\mathbf{n}}_{{\mathbf{b}}_k^g}\delta t\end{array}$$

​ 确定误差传递的状态量,噪声量,然后开始构建传递方程。

• 预积分误差传递的形式:

  用前面一阶泰勒展开的推导方式,我们希望能推导出如下的形式:

  $$\left[\begin{array}{c}\delta {\mathit{\alpha }}_{b_{k+1}}{b}_{k+1}^{\prime }\\ \delta {\mathit{\theta }}_{b_{k+1}{b}_{k+1}^{\prime }}\\ \delta {\mathit{\beta }}_{b_{k+1}{b}_{k+1}^{\prime }}\\ \delta {\mathbf{b}}_{k+1}^a\\ \delta {\mathbf{b}}_{k+1}^g\end{array}\right]=\mathbf{F}\left[\begin{array}{c}\delta {\mathit{\alpha }}_{b_{k+1}}{b}_k^{\prime }\\ \delta {\mathit{\theta }}_{b_{k+1}{b}_k^{\prime }}\\ \delta {\mathit{\beta }}_{b_{k+1}{b}_k^{\prime }}\\ \delta {\mathbf{b}}_k^a\\ \delta {\mathbf{b}}_k^g\end{array}\right]+\mathbf{G}\left[\begin{array}{c}{\mathbf{n}}_k^a\\ {\mathbf{n}}_k^g\\ {\mathbf{n}}_{k+1}^a\\ {\mathbf{n}}_{k+1}^g\\ {\mathbf{n}}_{{\mathbf{b}}_k^a}\\ {\mathbf{n}}_{{\mathbf{b}}_k^g}\end{array}\right]$$

  $\mathbf{F},\mathbf{G}$ 为两个时刻间的协方差传递矩阵

$$\begin{array}{r}\mathbf{F}=\left[\begin{array}{ccccc}\mathbf{I}& {\mathbf{f}}_{12}& \mathbf{I}\delta t& -\frac{1}{4}({\mathbf{q}}_{b_i{b}_k}+{\mathbf{q}}_{b_i{b}_{k+1}})\delta t^2& {\mathbf{f}}_{15}\\ \mathbf{0}& \mathbf{I}-[\mathit{\omega }{]}_{\times }& \mathbf{0}& \mathbf{0}& -\mathbf{I}\delta t\\ \mathbf{0}& {\mathbf{f}}_{32}& \mathbf{I}& -\frac{1}{2}({\mathbf{q}}_{b_i{b}_k}+{\mathbf{q}}_{b_i{b}_{k+1}})\delta t& {\mathbf{f}}_{35}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{I}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& & \mathbf{I}\end{array}\right]\\ \mathbf{G}=\left[\begin{array}{cccccc}\frac{1}{4}{\mathbf{q}}_{b_i{b}_k}\delta t^2& {\mathbf{g}}_{12}& \frac{1}{4}{\mathbf{q}}_{b_i{b}_{k+1}}\delta t^2& {\mathbf{g}}_{14}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \frac{1}{2}\mathbf{I}\delta t& \mathbf{0}& \frac{1}{2}\mathbf{I}\delta t& \mathbf{0}& \mathbf{0}\\ \frac{1}{2}{\mathbf{q}}_{b_i{b}_k}\delta t& {\mathbf{g}}_{32}& \frac{1}{2}{\mathbf{q}}_{b_i{b}_{k+1}}\delta t& {\mathbf{g}}_{34}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{I}\delta t& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{I}\delta t\end{array}\right]\end{array}$$

其中的系数为：

$$\begin{array}{rl}& {\mathbf{f}}_{12}=\frac{\partial {\mathit{\alpha }}_{b_i{b}_{k+1}}}{\partial \delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}}=-\frac{1}{4}({\mathbf{R}}_{b_i{b}_k}{[{\mathbf{a}}^{b_k}-{\mathbf{b}}_k^a]}_{\times }\delta t^2+{\mathbf{R}}_{b_i{b}_{k+1}}{\left[({\mathbf{a}}^{b_{k+1}}-{\mathbf{b}}_k^a)\right]}_{\times }(\mathbf{I}-[\mathit{\omega }{]}_{\times }\delta t)\delta t^2)\\ & {\mathbf{f}}_{32}=\frac{\partial {\mathit{\beta }}_{b_i{b}_{k+1}}}{\partial \delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}}=-\frac{1}{2}({\mathbf{R}}_{b_i{b}_k}{[{\mathbf{a}}^{b_k}-{\mathbf{b}}_k^a]}_{\times }\delta t+{\mathbf{R}}_{b_i{b}_{k+1}}{\left[({\mathbf{a}}^{b_{k+1}}-{\mathbf{b}}_k^a)\right]}_{\times }(\mathbf{I}-[\mathit{\omega }{]}_{\times }\delta t)\delta t)\\ & {\mathbf{f}}_{15}=\frac{\partial {\mathit{\alpha }}_{b_i{b}_{k+1}}}{\partial \delta {\mathbf{b}}_k^g}=-\frac{1}{4}\left({\mathbf{R}}_{b_i{b}_{k+1}}{\left[({\mathbf{a}}^{b_{k+1}}-{\mathbf{b}}_k^a)\right]}_{\times }\delta t^2\right)(-\delta t)\\ & {\mathbf{f}}_{35}=\frac{\partial {\mathit{\beta }}_{b_i{b}_{k+1}}}{\partial \delta {\mathbf{b}}_k^g}=-\frac{1}{2}\left({\mathbf{R}}_{b_i{b}_{k+1}}{\left[({\mathbf{a}}^{b_{k+1}}-{\mathbf{b}}_k^a)\right]}_{\times }\delta t\right)(-\delta t)\\ & {\mathbf{g}}_{12}=\frac{\partial {\mathit{\alpha }}_{b_i{b}_{k+1}}}{\partial {\mathbf{n}}_k^g}={\mathbf{g}}_{14}=\frac{\partial {\mathit{\alpha }}_{b_i{b}_{k+1}}}{\partial {\mathbf{n}}_{k+1}^g}=-\frac{1}{4}\left({\mathbf{R}}_{b_i{b}_{k+1}}{\left[({\mathbf{a}}^{b_{k+1}}-{\mathbf{b}}_k^a)\right]}_{\times }\delta t^2\right)\left(\frac{1}{2}\delta t\right)\\ & {\mathbf{g}}_{32}=\frac{\partial {\mathit{\beta }}_{b_i{b}_{k+1}}}{\partial {\mathbf{n}}_k^g}={\mathbf{g}}_{34}=\frac{\partial {\mathit{\beta }}_{b_i{b}_{k+1}}}{\partial {\mathbf{n}}_{k+1}^g}=-\frac{1}{2}\left({\mathbf{R}}_{b_i{b}_{k+1}}{\left[({\mathbf{a}}^{b_{k+1}}-{\mathbf{b}}_k^a)\right]}_{\times }\delta t^2\right)\left(\frac{1}{2}\delta t\right)\end{array}$$

• 证明：

公式简化约定，考虑到公式的编辑篇幅,为了对一些求导公式进行简化,这里做一些简单的约定, 比如求导公式:

$$\frac{\partial {\mathbf{x}}_a}{\partial \delta \mathit{\theta }}=\underset{\delta \theta \to 0}{lim}\frac{{\mathbf{R}}_{ab}\exp ([\delta \mathit{\theta }{]}_{\times }){\mathbf{x}}_b-{\mathbf{R}}_{ab}{\mathbf{x}}_b}{\delta \mathit{\theta }}$$

后续直接简写为 :

$$\frac{\partial {\mathbf{x}}_a}{\partial \delta \mathit{\theta }}=\frac{\partial {\mathbf{R}}_{ab}\exp ([\delta \mathit{\theta }{]}_{\times }){\mathbf{x}}_b}{\partial \delta \mathit{\theta }}$$

雅克比矩阵 F 的推导:

$\mathbf{\beta }$ 对各状态量的雅克比推导,即 $\mathbf{F}$ 第三行，速度预积分量 $\mathbf{\beta }$ 的递推计算形式:

$$\begin{array}{rl}{\mathit{\beta }}_{b_i{b}_{k+1}}& ={\mathit{\beta }}_{b_i{b}_k}+\mathbf{a}\delta t\\ & ={\mathit{\beta }}_{b_i{b}_k}+\frac{1}{2}({\mathbf{q}}_{b_i{b}_k}({\mathbf{a}}^{b_k}-{\mathbf{b}}_k^a)+{\mathbf{q}}_{b_i{b}_{k+1}}({\mathbf{a}}^{b_{k+1}}-{\mathbf{b}}_k^a))\delta t\end{array}$$

${\mathrm{f}}_{33}$ : 对上一时刻速度预积分量的 $Jacobian$

$${\mathbf{f}}_{33}=\frac{\partial {\mathit{\beta }}_{b_i{b}_{k+1}}}{\partial \delta {\mathit{\beta }}_{b_k{b}_k^{\prime }}}={\mathbf{I}}_{3\times 3}$$

${\mathrm{f}}_{32}$ : 对角度预积分量的 $Jacobian$
首先将速度预积分量 $\mathbf{\beta }$ 的递推计算形式写成如下形式:

$${\mathit{\beta }}_{b_i{b}_{k+1}}={\mathit{\beta }}_{b_i{b}_k}+\frac{1}{2}({\mathbf{q}}_{b_i{b}_k}({\mathbf{a}}^{b_k}-{\mathbf{b}}_k^a)+{\mathbf{q}}_{b_i{b}_k}\otimes \left[\begin{array}{c}1\\ \frac{1}{2}\mathit{\omega }\delta t\end{array}\right]({\mathbf{a}}^{b_{k+1}}-{\mathbf{b}}_k^a))\delta t$$

${\mathrm{f}}_{32}$ : 对角度预积分量的$Jacobian$
那么,速度的预积分量对角度预积分量的 $Jacobian$:

$$\frac{\partial {\mathit{\beta }}_{b_i{b}_{k+1}}}{\partial \delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}}=\frac{\partial \mathbf{a}\delta \mathbf{t}}{\partial \delta {\theta }_{{\mathbf{b}}_{\mathbf{k}}{\mathbf{b}}_{\mathbf{k}}^{\prime }}}$$

其中分子和一写成：

$$\begin{array}{rl}\mathbf{a}\delta t=& \frac{1}{2}{\mathbf{q}}_{b_i{b}_k}\otimes \left[\begin{array}{c}1\\ \frac{1}{2}\delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}\end{array}\right]({\mathbf{a}}^{b_k}-{\mathbf{b}}_k^a)\delta t\\ & +\frac{1}{2}{\mathbf{q}}_{b_i{b}_k}\otimes \left[\begin{array}{c}1\\ \frac{1}{2}\delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}\end{array}\right]\otimes \left[\begin{array}{c}1\\ \frac{1}{2}\mathit{\omega }\delta t\end{array}\right]({\mathbf{a}}^{b_{k+1}}-{\mathbf{b}}_k^a)\delta t\\ =& \underset{\text{Part }1}{\underbrace{\frac{1}{2}{\mathbf{R}}_{b_i{b}_k}\exp \left({\left[\delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}\right]}_{\times }\right)({\mathbf{a}}^{b_k}-{\mathbf{b}}_k^a)\delta t}}\\ & +\underset{\text{Part }2}{\underbrace{\frac{1}{2}{\mathbf{R}}_{b_i{b}_k}\exp \left({\left[\delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}\right]}_{\times }\right)\exp ([\mathit{\omega }\delta t{]}_{\times })({\mathbf{a}}^{b_{k+1}}-{\mathbf{b}}_k^a)\delta t}}\end{array}$$

$Part1$ 对应的的雅克比为:

$$\begin{array}{rl}\frac{\partial {\mathbf{R}}_{b_i{b}_k}\exp \left({\left[\delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}\right]}_{\times }\right)({\mathbf{a}}^{b_k}-{\mathbf{b}}_k^a)\delta t}{\partial \delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}}& =\frac{\partial {\mathbf{R}}_{b_i{b}_k}(\mathbf{I}+{\left[\delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}\right]}_{\times })({\mathbf{a}}^{b_k}-{\mathbf{b}}_k^a)\delta t}{\partial \delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}}\\ & =\frac{\partial -{\mathbf{R}}_{b_i{b}_k}{\left[({\mathbf{a}}^{b_k}-{\mathbf{b}}_k^a)\delta t\right]}_{\times }\delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}}{\partial \delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}}\\ & =-{\mathbf{R}}_{b_i{b}_k}{\left[({\mathbf{a}}^{b_k}-{\mathbf{b}}_k^a)\delta t\right]}_{\times }\end{array}$$

$Part2$ 对应的雅可比为：

$$\begin{array}{rl}& \frac{\partial {\mathbf{R}}_{b_i{b}_k}\exp \left({\left[\delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}\right]}_{\times }\right)\exp ([\mathit{\omega }\delta t{]}_{\times })({\mathbf{a}}^{b_{k+1}}-{\mathbf{b}}_k^a)\delta t}{\partial \delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}}\\ & =\frac{\partial {\mathbf{R}}_{b_i{b}_k}(\mathbf{I}+{\left[\delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}\right]}_{\times })\exp ([\mathit{\omega }\delta t{]}_{\times })({\mathbf{a}}^{b_{k+1}}-{\mathbf{b}}_k^a))\delta t}{\partial \delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}}\\ & =-\frac{\partial {\mathbf{R}}_{b_i{b}_k}{[\exp ([\mathit{\omega }\delta t{]}_{\times })({\mathbf{a}}^{b_{k+1}}-{\mathbf{b}}_k^a)\delta t]}_{\times }\delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}}{\partial \delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}}\\ & =-\frac{\partial {\mathbf{R}}_{b_i{b}_k}\exp ([\mathit{\omega }\delta t{]}_{\times }){\left[({\mathbf{a}}^{b_{k+1}}-{\mathbf{b}}_k^a)\delta t\right]}_{\times }\exp ([-\mathit{\omega }\delta t{]}_{\times })\delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}}{\partial \delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}}\\ & =-{\mathbf{R}}_{b_i{b}_{k+1}}{\left[({\mathbf{a}}^{b_{k+1}}-{\mathbf{b}}_k^a)\delta t\right]}_{\times }\exp ([-\mathit{\omega }\delta t{]}_{\times })\\ & \approx -{\mathbf{R}}_{b_i{b}_{k+1}}{\left[({\mathbf{a}}^{b_{k+1}}-{\mathbf{b}}_k^a)\delta t\right]}_{\times }(\mathbf{I}-[\mathit{\omega }\delta t{]}_{\times })\end{array}$$

将上面两部分综合起来就能得到

$${\mathbf{f}}_{32}=\frac{\partial {\mathit{\beta }}_{b_i{b}_{k+1}}}{\partial \delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}}=-\frac{1}{2}({\mathbf{R}}_{b_i{b}_k}{[{\mathbf{a}}^{b_k}-{\mathbf{b}}_k^a]}_{\times }\delta t+{\mathbf{R}}_{b_i{b}_{k+1}}{\left[({\mathbf{a}}^{b_{k+1}}-{\mathbf{b}}_k^a)\right]}_{\times }(\mathbf{I}-[\mathit{\omega }{]}_{\times }\delta t)\delta t)$$

${\mathrm{f}}_{35}$ : 速度预积分量对 $k$ 时刻角速度 $bias$ 的 $Jacobian$
递推公式如下：

$$\begin{array}{rl}\mathit{\omega }& =\frac{1}{2}(({\mathit{\omega }}^{b_k}-{\mathbf{b}}_k^g)+({\mathit{\omega }}^{b_{k+1}}-{\mathbf{b}}_k^g))=\frac{1}{2}({\mathit{\omega }}^{b_k}+{\mathit{\omega }}^{b_{k+1}})-{\mathbf{b}}_k^g\\ {\mathit{\beta }}_{b_i{b}_{k+1}}& ={\mathit{\beta }}_{b_i{b}_k}+\frac{1}{2}({\mathbf{q}}_{b_i{b}_k}({\mathbf{a}}^{b_k}-{\mathbf{b}}_k^a)+\underbrace{{\mathbf{q}}_{b_i{b}_k}\otimes \left[\begin{array}{c}1\\ \frac{1}{2}\mathit{\omega }\delta t\end{array}\right]({\mathbf{a}}^{b_{k+1}}-{\mathbf{b}}_k^a))\delta t}\end{array}$$

只有括号中的公式部分和角速度 bias 有关系, 因此雅克比的推导只考括号中的公式部分。

$$\begin{array}{rl}{\mathbf{f}}_{35}=\frac{\partial {\mathit{\beta }}_{b_i{b}_{k+1}}}{\partial \delta {\mathbf{b}}_k^g}& =\frac{\partial \frac{1}{2}{\mathbf{q}}_{b_i{b}_k}\otimes \left[\begin{array}{c}1\\ \frac{1}{2}\mathit{\omega }\delta t\end{array}\right]\otimes \left[\begin{array}{c}1\\ -\frac{1}{2}\delta {\mathbf{b}}_k^g\delta t\end{array}\right]({\mathbf{a}}^{b_{k+1}}-{\mathbf{b}}_k^a)\delta t}{\partial \delta {\mathbf{b}}_k^g}\\ & =\frac{1}{2}\frac{\partial {\mathbf{R}}_{b_i{b}_{k+1}}\exp \left({[-\delta {\mathbf{b}}_k^g\delta t]}_{\times }\right)({\mathbf{a}}^{b_{k+1}}-{\mathbf{b}}_k^a)\delta t}{\partial \delta {\mathbf{b}}_k^g}\\ & =\frac{1}{2}\frac{\partial {\mathbf{R}}_{b_i{b}_{k+1}}(\mathbf{I}+{[-\delta {\mathbf{b}}_k^g\delta t]}_{\times })({\mathbf{a}}^{b_{k+1}}-{\mathbf{b}}_k^a)\delta t}{\partial \delta {\mathbf{b}}_k^g}\\ & =\frac{1}{2}\frac{\partial -{\mathbf{R}}_{b_i{b}_{k+1}}\left({\left[({\mathbf{a}}^{b_{k+1}}-{\mathbf{b}}_k^a)\delta t\right]}_{\times }\right)(-\delta {\mathbf{b}}_k^g\delta t)}{\partial \delta {\mathbf{b}}_k^g}\\ & =-\frac{1}{2}\left({\mathbf{R}}_{b_i{b}_{k+1}}{\left[({\mathbf{a}}^{b_{k+1}}-{\mathbf{b}}_k^a)\right]}_{\times }\delta t\right)(-\delta t)\end{array}$$

旋转预积分量的 $Jacobian$,即 $F$ 第二行，旋转预积分的递推公式为：

$$\begin{array}{l}\mathit{\omega }=\frac{1}{2}(({\mathit{\omega }}^{b_k}-{\mathbf{b}}_k^g)+({\mathit{\omega }}^{b_{k+1}}-{\mathbf{b}}_k^g))\\ {\mathbf{q}}_{b_i{b}_{k+1}}={\mathbf{q}}_{b_i{b}_k}\otimes \left[\begin{array}{c}1\\ \frac{1}{2}\mathit{\omega }\delta t\end{array}\right]\\ ={\mathbf{q}}_{b_i{b}_k}\otimes \left[\begin{array}{c}1\\ \frac{1}{2}(\frac{1}{2}({\mathit{\omega }}^{b_k}+{\mathit{\omega }}^{b_{k+1}})-{\mathbf{b}}_k^g)\delta t\end{array}\right]\end{array}$$

${\mathrm{f}}_{22}$ : 前一时刻的旋转误差 $\delta {\theta }_{b_k{b}_k^{\prime }}$ 如何影响当前旋转误差 $\delta {\theta }_{b_{k+1}{b}_{k+1}^{\prime }}$。假设两个时刻的真值为 ${\mathbf{q}}_{b_i{b}_{k+1}}{\mathbf{q}}_{b_i{b}_k}$ , 两个时刻间的增量真值为 ${\mathbf{q}}_{b_k{b}_{k+1}}$ 。推导过程只考虑一个变量, 即旋转误差$\delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}$的影响, 而不 考虑测量值角速度 $bias$ 误差影响。可以假设

$${\mathbf{q}}_{b_k{b}_{k+1}}\approx \left[\begin{array}{c}1\\ \frac{1}{2}\mathit{\omega }\delta t\end{array}\right]$$

另外, 三元组四元数相乘有如下性质：

$$\mathbf{q}\otimes \mathbf{p}\otimes {\mathbf{q}}^{\ast }=[\mathbf{q}{]}_L[\mathbf{q}{]}_R^{\mathrm{\top }}\mathbf{p}=\left[\begin{array}{c}{p}_w\\ \mathbf{R}{\mathbf{p}}_v\end{array}\right]$$

其中 $\mathbf{R}$ 是和 $\mathbf{q}$ 对应的旋转矩阵, $p_w$ 为 $\mathbf{p}$ 的实部， ${\mathbf{p}}_v$ 为 $\mathbf{p}$ 的虚部。
下面开始详细推导:

$$\begin{array}{rl}{\mathbf{q}}_{b_i{b}_{k+1}}\otimes \left[\begin{array}{c}1\\ \frac{1}{2}\delta {\mathit{\theta }}_{b_{k+1}{b}_{k+1}^{\prime }}\end{array}\right]& ={\mathbf{q}}_{b_i{b}_k}\otimes \left[\begin{array}{c}1\\ \frac{1}{2}\delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}\end{array}\right]\otimes \left[\begin{array}{c}1\\ \frac{1}{2}\mathit{\omega }\delta t\end{array}\right]\\ \left[\begin{array}{c}1\\ 2\end{array}\right]& ={\mathbf{q}}_{b_{k+1}{b}_{k+1}^{\prime }}^{\ast }]\otimes {\mathbf{q}}_{b_i{b}_k}\otimes \left[\begin{array}{c}1\\ \frac{1}{2}\delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}\end{array}\right]\otimes \left[\begin{array}{c}1\\ \frac{1}{2}\mathit{\omega }\delta t\end{array}\right]\\ & ={\mathbf{q}}_{b_{k+1}{b}_k}\otimes \left[\begin{array}{c}1\\ \frac{1}{2}\delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}\end{array}\right]\otimes \left[\begin{array}{c}1\\ \frac{1}{2}\mathit{\omega }\delta t\end{array}\right]\\ & \approx \left[\begin{array}{c}1\\ -\frac{1}{2}\mathit{\omega }\delta t\end{array}\right]\otimes \left[\begin{array}{c}1\\ \frac{1}{2}\delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}\end{array}\right]\otimes \left[\begin{array}{c}1\\ \frac{1}{2}\mathit{\omega }\delta t\end{array}\right]\\ & =\left[\begin{array}{c}1\\ \frac{1}{2}\mathbf{R}\delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}\end{array}\right]\end{array}$$

只考虑公式中的虚部:

$$\begin{array}{rl}\delta {\mathit{\theta }}_{b_{k+1}{b}_{k+1}^{\prime }}& =\mathit{R}\delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}\\ & =\exp ([-\mathit{\omega }\delta t{]}_{\times })\delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}\\ & \approx (\mathbf{I}-[\mathit{\omega }\delta t{]}_{\times })\delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}\end{array}$$

那么, 第 $k+1$ 时刻的旋转预积分的误差相对于第 $k$ 时刻的 $Jacobian$ 为:

$${\mathbf{f}}_{22}=\frac{\partial \delta {\mathit{\theta }}_{b_{k+1}{b}_{k+1}^{\prime }}}{\partial \delta {\mathit{\theta }}_{b_k{b}_k^{\prime }}}=\mathbf{I}-[\mathit{\omega }\delta t{]}_{\times }$$

渔已授完,$F$, $G$ 中的其他鱼靠大家去捞了...

• 四元数求导的直观理解（不够严谨） https://zhuanlan.zhihu.com/p/395511536