梯度下降算法原理 神经网络(Gradient Descent)
在求解神经网络算法的模型参数,梯度下降(Gradient Descent)是最常采用的方法。下面是我个人学习时对梯度下降的理解,如有不对的地方欢迎指出。
1、✌ 梯度定义
微积分我们学过,对多元函数的各个变量求偏导数,把求得的各个参数的偏导数以向量的形式写出来,就是梯度。比如函数f(x,y), 分别对x,y求偏导数,求得的梯度向量就是(∂f/∂x, ∂f/∂y)T,简称grad f(x,y)或者▽f(x,y)。对于在点(x0,y0)的具体梯度向量就是(∂f/∂x0, ∂f/∂y0)T.或者▽f(x0,y0),如果是3个参数的向量梯度,就是(∂f/∂x, ∂f/∂y,∂f/∂z)T,以此类推。
那么这个梯度向量求出来有什么意义呢?他的意义从几何意义上讲,就是函数变化增加最快的地方。具体来说,对于函数f(x,y),在点(x0,y0),沿着梯度向量的方向就是(∂f/∂x0, ∂f/∂y0)T的方向是f(x,y)增加最快的地方。或者说,沿着梯度向量的方向,更加容易找到函数的最大值。反过来说,沿着梯度向量相反的方向,也就是 -(∂f/∂x0, ∂f/∂y0)T的方向,梯度减少最快,也就是更加容易找到函数的最小值。
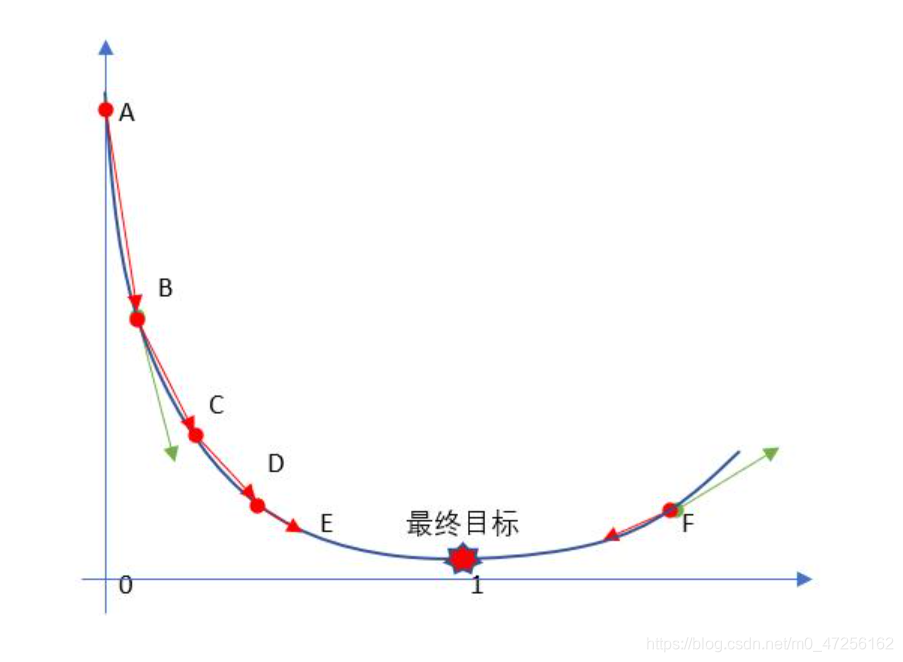
对于F点来说,F点的梯度为绿色向量的方向,那么它的反方向即为下降最快的地方
对于B点来说,B点的梯度为负,所以梯度的反方向为右下方,也是函数下降最快的地方
可见,他们都朝着使函数到达最小值的方向努力。
2、✌ 梯度下降和梯度上升
一般我们要求取损失函数最小值时就要利用梯度下降,对应求取最大值就应该用梯度上升,两种方法都是将参数进行迭代更新。
下面进行介绍梯度下降的原理。
3、✌ 梯度下降的图示

首先我们看这张图,z轴为损失函数,x、y轴分别为两个参数,现在问题就是我们要求取损失函数达到最小对应参数的取值,可能会想,穷举每个参数,这个方法显然不行,参数取值不限,不可能取到所有值,或者对损失函数求导,求极值,这种方法按理来说可能没有问题,但是因为我们每次遇到的损失函数不同,把这种方法封装成一个函数较难,函数类型不同,求导不同,无法做到通解,那么应该怎么做呢?
把它看成一个碗,当我们向碗里放一个小球时,按自然现象来说,小球肯定会向下滚,那么小球滚的路径有什么特别之处呢?当让是坡度大的地方,越陡的地方越容易下来而且越快,那不就和我们的梯度对应上了吗,小球每次沿着梯度的反方向滚动总会有一个时刻达到最低点。
梯度下降就是这个原理,可是又有了新的问题,我们看一张图。
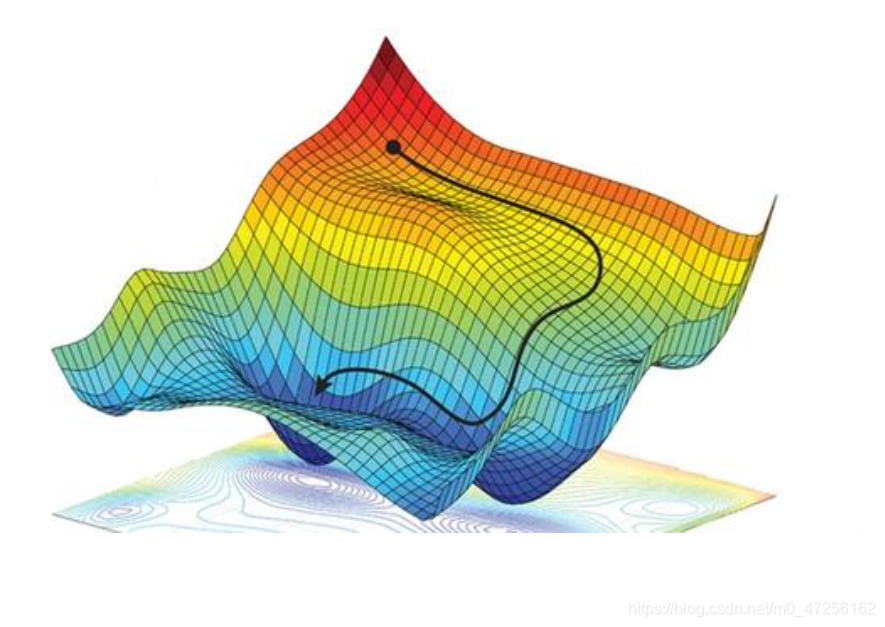
按照上面的理论,小球肯定会滚到一个最低点,那么这个点一定是最低点吗?肯定不是,根据上面的图可以看出,如果小球一旦陷入某一个凹陷的区域,就会终止,并没有达到最低点,那么就说我们获得的是局部最优,而不是全局最优,这里有一个补充,如果我们的损失函数为凸函数,那么我们一定会得到全局最优解。
学过高数可能知道,取得极小值的位置,并不一定是最小值,它只是局部的最小值,那么应该怎么做呢,由此产生了很多优化的算法,利用各种数学的推导衍生新的公式,这里不予说明,本文只为讲解梯度下降原理,有兴趣可自行查找相关文献。
4、✌ 梯度下降的相关概念
这个就是梯度下降的核心公式,用这个公式来进行更新w的取值,这里问什么用减号呢?话不多说看图。
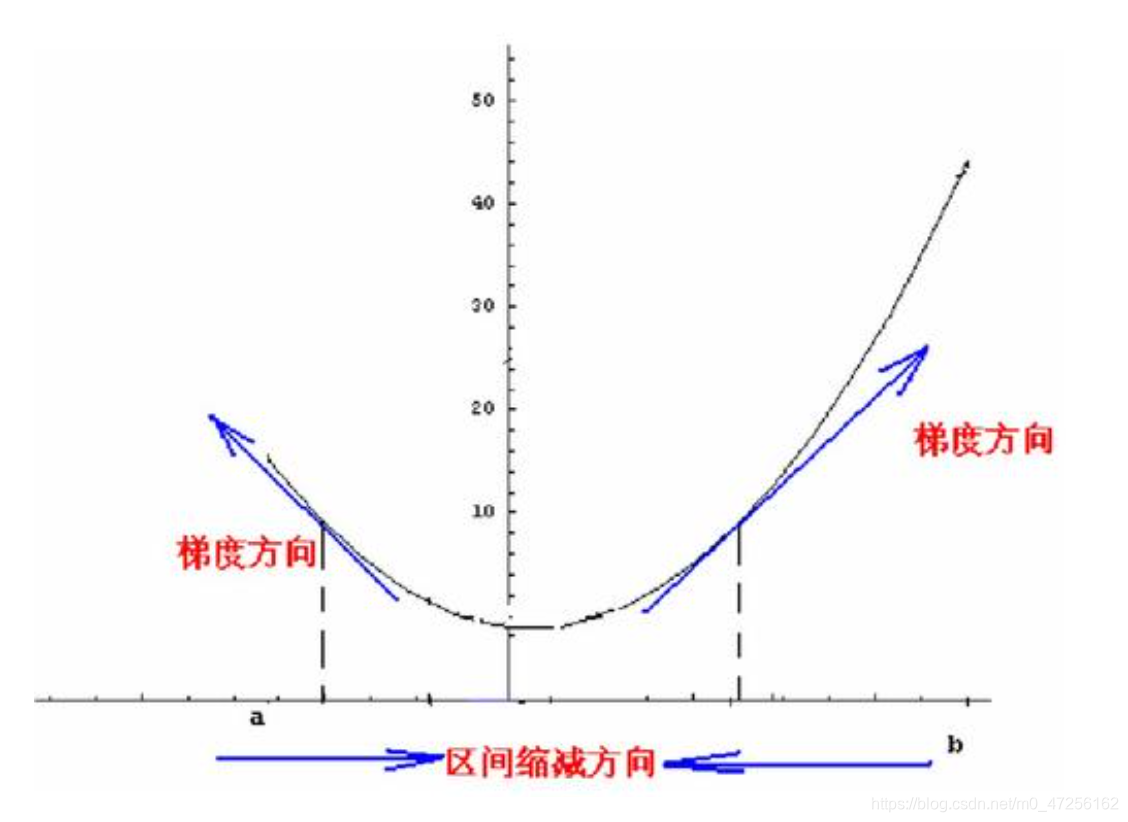
当我们的点是b点时,梯度为正(导数值),那么我们想要取到最小值,肯定是要左移,那么就需要减去该值*学习率
如果是a点,梯度为负(导数值为负),那么就需要右移,导数值为负就应该加上它
- 损失函数:学过线性回归可能知道,我们评估它的好坏利用的就是MSE(均方误差),利用它进行度量模型拟合的程度。
显然这个函数越小越好,那么我们就是要求取最优的w1和w2取值使我们的损失函数达到最小值,这就用到了梯度下降。
2. 学习率:就是上面公式中的a,有的地方也叫做步长,我感觉很矛盾,这个地方我感觉有些问题,我个人认为就是一个起调节作用的数,因为w和它对应的导数有可能数量级不同,这时就需要将导数乘一个小点的数调节一下
5、✌ 梯度下降的计算过程
其中涉及到多维矩阵运算以及特别多的符号,对于初学者很难理解,这里我们简化一下,用一个简易版的来代替,不过原理是一样的,就是将低维推广到多维。
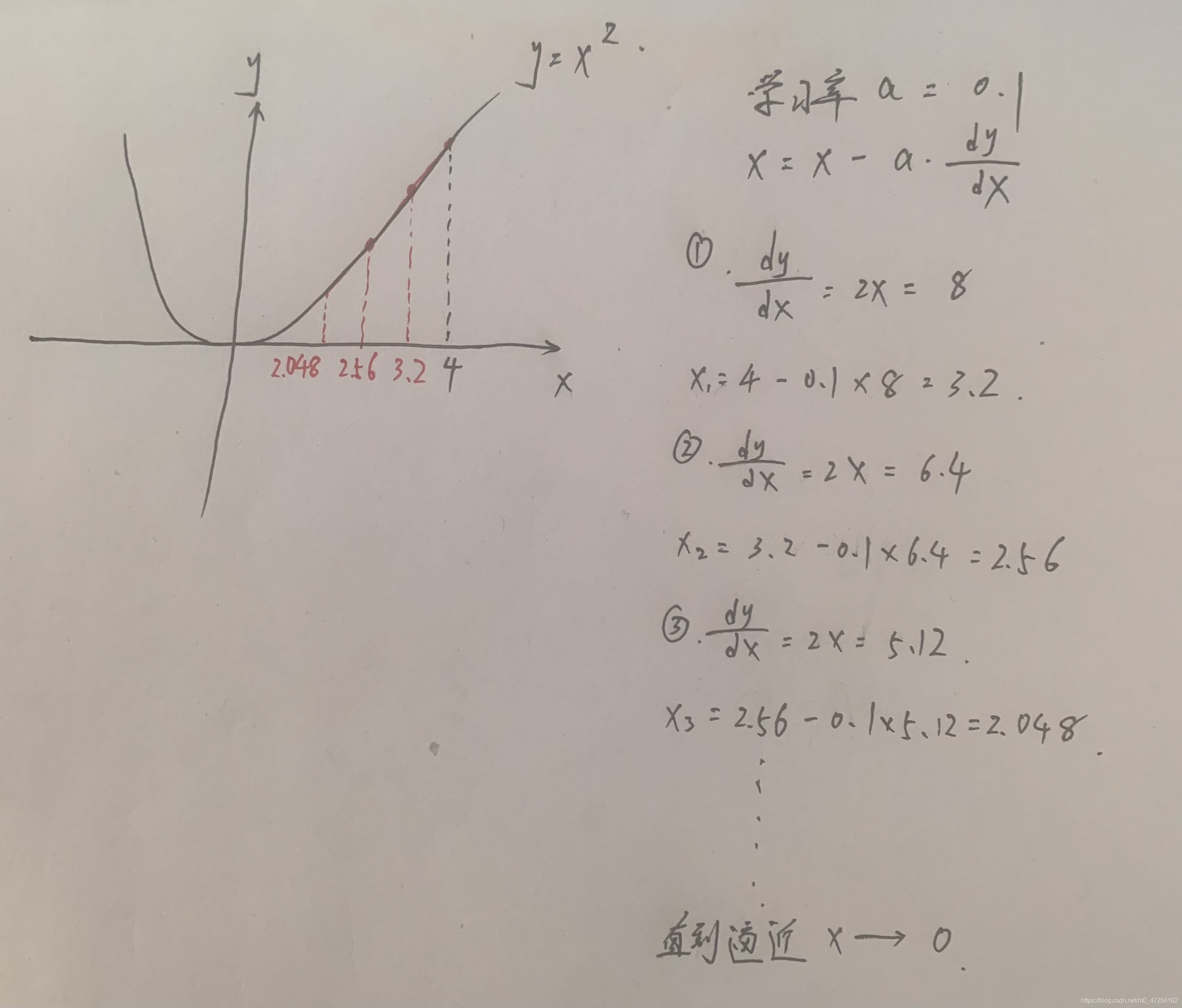
话不多说(因为编辑文档公式不好写,所有我在草纸上演示了下过程),来看图!!!
6、✌ 算法过程:
-
确定当前参数所在位置的梯度(导数)$$dJ/dw$$
-
用学习率乘以梯度,得到参数更新的距离,即a*dJ/dw
-
确定迭代次数和阈值,分为两种情况
3.1 第一种达到迭代次数,计算结束
3.2 第二种参数更新值小于阈值,说白了就是a*dJ/dw趋于0,说明近乎达到了最优位置
7、✌ 算法优化:
有没有什么地方可以优化呢?
-
学习率的选择:
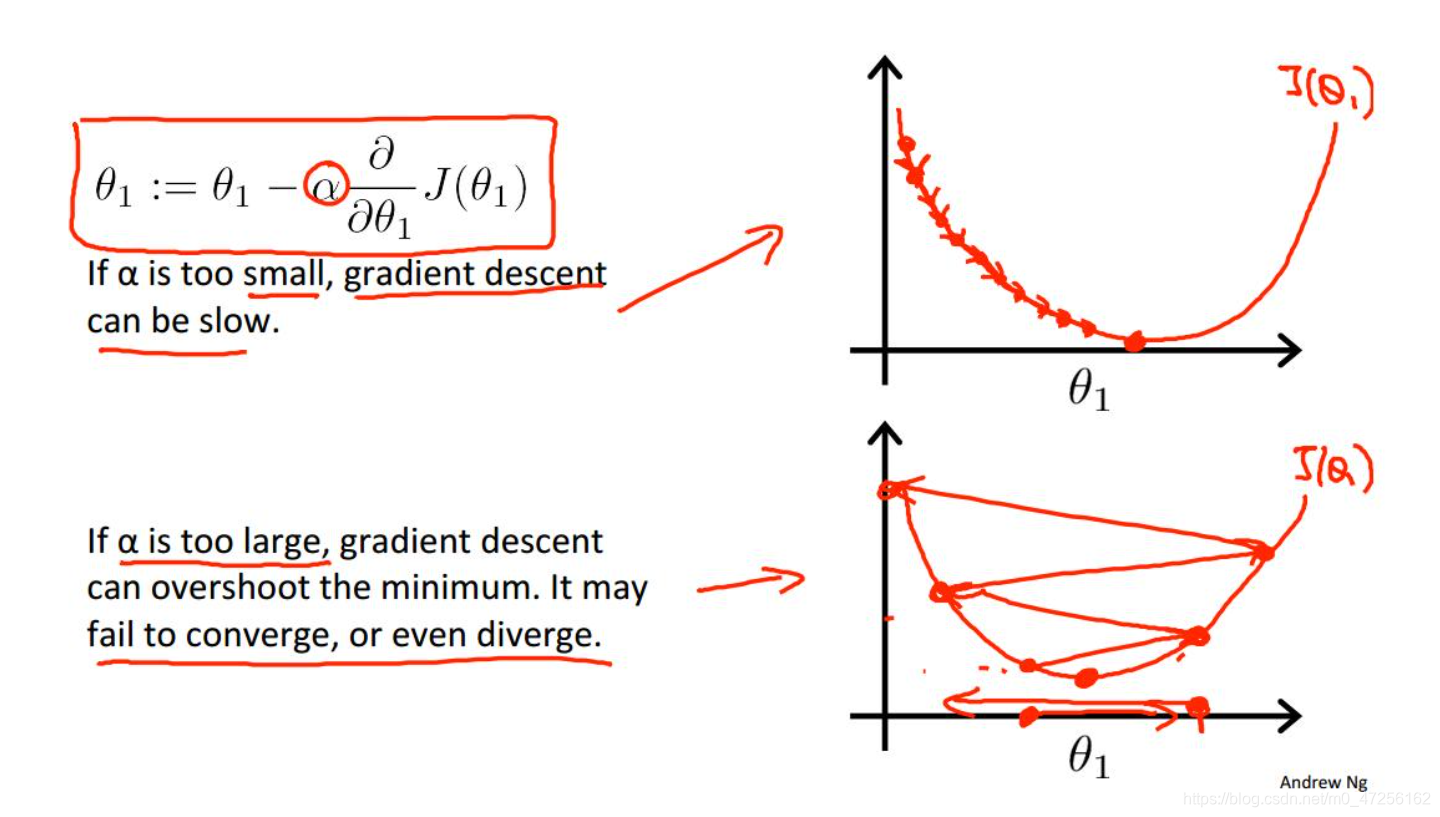
很容易知道,如果学习率过小的化,会导致参数更新率较小,变化小,导致迭代次数增加,增加模型训练时间,如果学习率过大的化,会导致参数变化太大,迭代过快,导致跳过最优解的位置
看张图就明白了
-
参数的初始值:
初始值的不同也会影响模型的效果,因为梯度下降有时会得到局部最优解,而如果位置选择得当的化会避免这种状况 -
数据的归一化,消除量纲影响 :
归一化后不同特征的取值范围会划分到同一范围,会减少一定的计算量
样本减去均值除以标准差,这样处理后的数据会符合高斯分布