特征工程
上周参加了学校的数据挖掘竞赛,总的来说,在还需要人工干预的机器学习相关的任务中,主要解决两个问题:(1)如何将原始的数据处理成合格的数据输入(2)如何获得输入数据中的规律。第一个问题的解决方案是:特征工程。第二个问题的解决办法是:机器学习。
相对机器学习的算法而言,特征工程的工作看起来比较low,但是特征工程在机器学习中非常重要。特征工程,是机器学习系列任务中最耗时、最繁重、最无聊却又是最不可或缺的一部分。这些工作先行者们已经总结的很好,作为站在巨人的肩膀上的后来者,对他们的工作表示敬意。主要内容转载自http://www.cnblogs.com/jasonfreak/p/5448385.html
这篇文章在该文章的基础上做了添加或修改,仍在更新中
特征工程
1、特征工程是什么:
工业界流传者这么一句话:数据和特征决定了机器学习的上限,而模型和算法只是逼近这个上限而已。
那么,到底什么是特征工程?我们知道,数据是信息的载体,但是原始的数据包含了大量的噪声,信息的表达也不够简练。因此,特征工程的目的,是通过一系列的工程活动,将这些信息使用更高效的编码方式(特征)表示。使用特征表示的信息,信息损失较少,原始数据中包含的规律依然保留。此外,新的编码方式还需要尽量减少原始数据中的不确定因素(白噪声、异常数据、数据缺失…等等)的影响。
经过前人的总结,特征工程已经形成了接近标准化的流程,如下图所示:
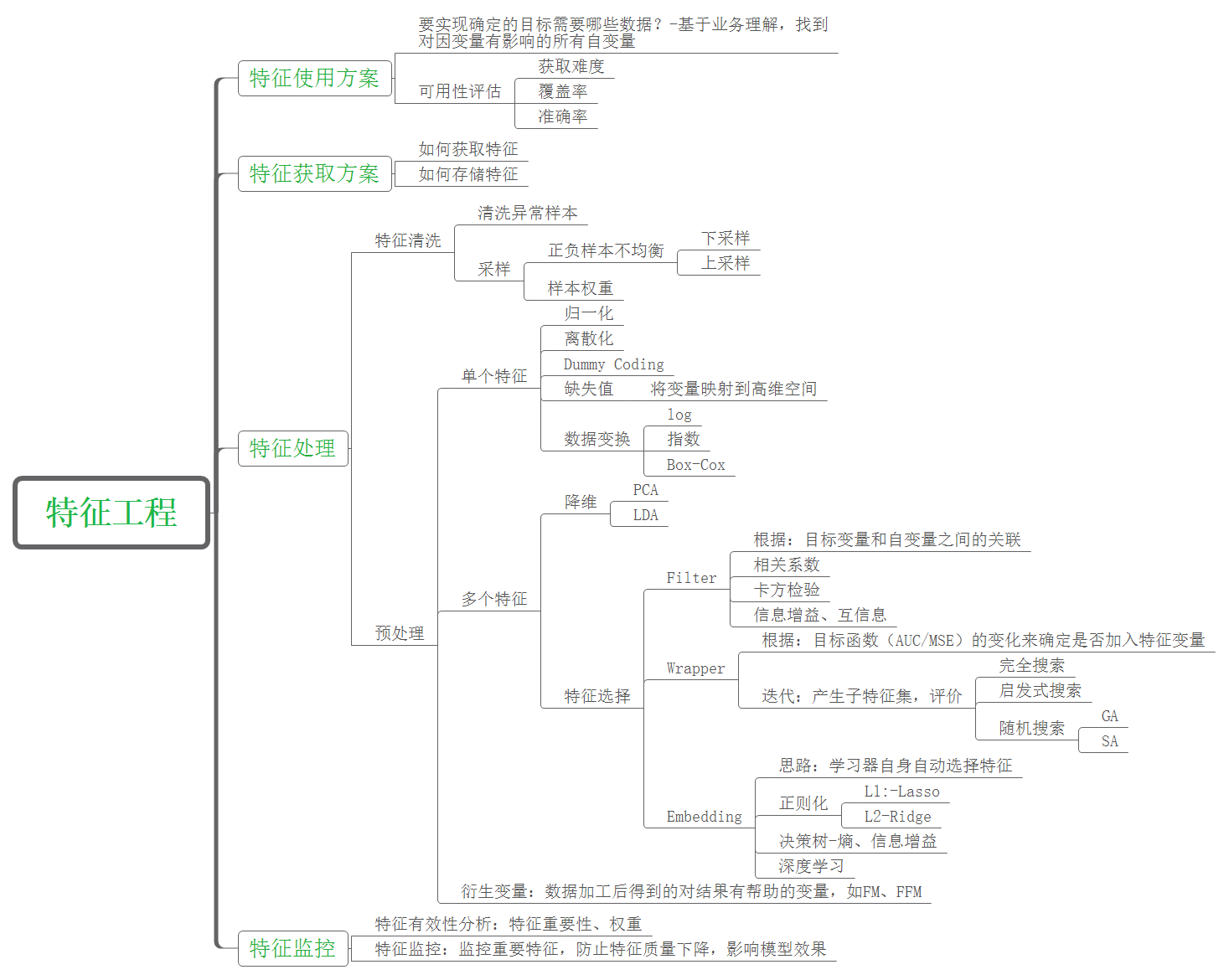
2、异常数据的清洗和样本的选取
异常数据的清洗,目标是将原始数据中异常的数据清除。 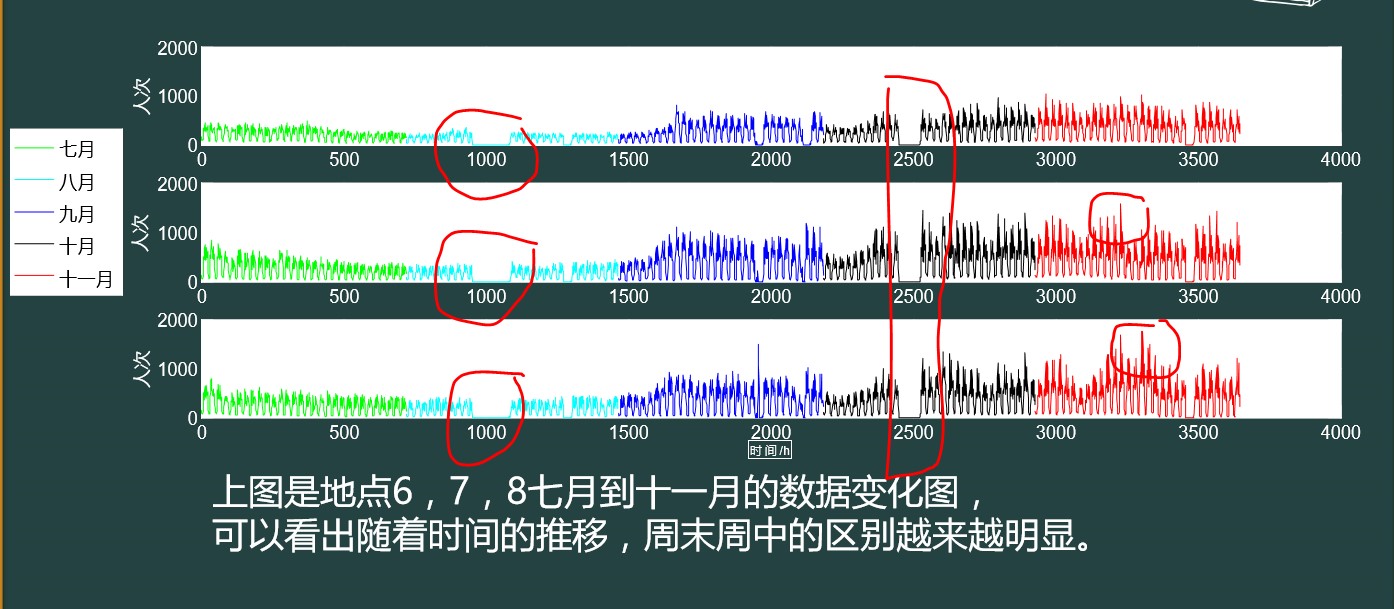
上图表示了2015年7月到11月某个地点人流量的变化。数据的分析图可以看到,红色的框框内表示了数据的缺失和异常的峰值。这些异常的数据需要在特征的预处理前清除。一般情况下,直接将这些数据舍弃。
除了使用肉眼观察的办法来判断数据的合理性,工业中,更多采用算法或者公式对数据的是否异常进行判断。
(1) 结合业务情况进行过滤:比如去除crawler抓取,spam,作弊等数据
(2) 异常点检测采用异常点检测算法对样本进行分析,常用的异常点检测算法包括
² 偏差检测:聚类、最近邻等
² 基于统计的异常点检测
例如极差,四分位数间距,均差,标准差等,这种方法适合于挖掘单变量的数值型数据。全距(Range),又称极差,是用来表示统计资料中的变异量数(measures of variation) ,其最大值与最小值之间的差距;四分位距通常是用来构建箱形图,以及对概率分布的简要图表概述。
² 基于距离的异常点检测
主要通过距离方法来检测异常点,将数据集中与大多数点之间距离大于某个阈值的点视为异常点,主要使用的距离度量方法有绝对距离 ( 曼哈顿距离 ) 、欧氏距离和马氏距离等方法。
² 基于密度的异常点检测
考察当前点周围密度,可以发现局部异常点,例如LOF算法
3、数据预处理
通过特征提取,我们能得到未经处理的特征,这时的特征可能有以下问题:
² 不属于同一量纲:即特征的规格不一样,不能够放在一起比较。无量纲化可以解决这一问题。
² 信息冗余:对于某些定量特征,其包含的有效信息为区间划分,例如学习成绩,假若只关心“及格”或不“及格”,那么需要将定量的考分,转换成“1”和“0”表示及格和未及格。二值化可以解决这一问题。
² 定性特征不能直接使用:某些机器学习算法和模型只能接受定量特征的输入,那么需要将定性特征转换为定量特征。最简单的方式是为每一种定性值指定一个定量值,但是这种方式过于灵活,增加了调参的工作。通常使用独热编码的方式将定性特征转换为定量特征:假设有N种定性值,则将这一个特征扩展为N种特征,当原始特征值为第i种定性值时,第i个扩展特征赋值为1,其他扩展特征赋值为0。独热编码的方式相比直接指定的方式,不用增加调参的工作,对于线性模型来说,使用独热编码后的特征可达到非线性的效果。
² 存在缺失值:缺失值需要补充。
² 信息利用率低:不同的机器学习算法和模型对数据中信息的利用是不同的,之前提到在线性模型中,使用对定性特征独热编码可以达到非线性的效果。类似地,对定量变量多项式化,或者进行其他的转换,都能达到非线性的效果。
² 特征缺失:在本次的比赛中,影响人流量的因素还有天气、温度…等等,而这些因素在原始数据中并不存在,因此,需要在数据预处理的时候,将这些影响因素添加进来。
3.1无量纲化
无量纲化使不同规格的数据转换到同一规格。常见的无量纲化方法有标准化和区间缩放法。标准化的前提是特征值服从正态分布,标准化后,其转换成标准正态分布。区间缩放法利用了边界值信息,将特征的取值区间缩放到某个特点的范围,例如[0, 1]等。
3.1.1标准化
常用的方法是z-score标准化,经过处理后的数据均值为0,标准差为1,处理方法是:
$x'=\frac{x-\mu}{\delta}$ (1)
公式一中,x’是标准化后的特征,x是原始特征值, 是样本均值, 是样本标准差。它们可以通过现有样本进行估计。在已有样本足够多的情况下比较稳定,适合现代嘈杂大数据场景。
3.1.2 区间缩放法
常用的方法是通过对原始数据进行线性变换把数据映射到[0,1]之间,变换函数为:
$x'=\frac{x-\min}{\max-\min} $ (2)
其中 min 是样本中最小值, max是样本中最大值,注意在数据流场景下最大值与最小值是变化的。另外,最大值与最小值非常容易受异常点影响,所以这种方法鲁棒性较差,只适合传统精确小数据场景。
3.1.3归一化
简单来说,标准化是依照特征矩阵的列处理数据,其通过求z-score的方法,将样本的特征值转换到同一量纲下。归一化是依照特征矩阵的行处理数据,其目的在于样本向量在点乘运算或其他核函数计算相似性时,拥有统一的标准,也就是说都转化为“单位向量”。规则为 的归一化公式如下:
$x'=\frac{x}{\sqrt{\sum_j^m x^2_j}} $ (3)
使用preproccessing库的Normalizer类对数据进行归一化的代码如下:
3.2 对定量特征二值化(离散化)[1]
定量特征二值化的核心在于设定一个阈值,大于阈值的赋值为1,小于等于阈值的赋值为0,公式表达如下:
$x'=\left\{\begin{aligned}1&,& \ \ x>threshold\\0&,& x\leq threshold\end{aligned}\right.$ (4)
3.3 对定性特征进行独热编码
独热编码:使用一个二进制的位来表示某个定性特征的出现与否
3.4 缺失值的处理
现实世界中的数据往往非常杂乱,未经处理的原始数据中某些属性数据缺失是经常出现的情况。另外,在做特征工程时经常会有些样本的某些特征无法求出。下面是几种处理数据中缺失值的主要方法。
3.4.1. 删除
最简单的方法是删除,删除属性或者删除样本。如果大部分样本该属性都缺失,这个属性能提供的信息有限,可以选择放弃使用该维属性;如果一个样本大部分属性缺失,可以选择放弃该样本。虽然这种方法简单,但只适用于数据集中缺失较少的情况。
3.4.2. 统计填充
对于缺失值的属性,尤其是数值类型的属性,根据所有样本关于这维属性的统计值对其进行填充,如使用平均数、中位数、众数、最大值、最小值等,具体选择哪种统计值需要具体问题具体分析。另外,如果有可用类别信息,还可以进行类内统计,比如身高,男性和女性的统计填充应该是不同的。
3.4.3. 统一填充
对于含缺失值的属性,把所有缺失值统一填充为自定义值,如何选择自定义值也需要具体问题具体分析。当然,如果有可用类别信息,也可以为不同类别分别进行统一填充。常用的统一填充值有:“空”、“0”、“正无穷”、“负无穷”等。
3.4.4 预测填充
我们可以通过预测模型利用不存在缺失值的属性来预测缺失值,也就是先用预测模型把数据填充后再做进一步的工作,如统计、学习等。虽然这种方法比较复杂,但是最后得到的结果比较好。
3.4.5具体分析
上面两次提到具体问题具体分析,为什么要具体问题具体分析呢?因为属性缺失有时并不意味着数据缺失,缺失本身是包含信息的,所以需要根据不同应用场景下缺失值可能包含的信息进行合理填充。下面通过一些例子来说明如何具体问题具体分析,仁者见仁智者见智,仅供参考:
- “年收入”:商品推荐场景下填充平均值,借贷额度场景下填充最小值;
- “行为时间点”:填充众数;
- “价格”:商品推荐场景下填充最小值,商品匹配场景下填充平均值;
- “人体寿命”:保险费用估计场景下填充最大值,人口估计场景下填充平均值;
- “驾龄”:没有填写这一项的用户可能是没有车,为它填充为0较为合理;
- ”本科毕业时间”:没有填写这一项的用户可能是没有上大学,为它填充正无穷比较合理;
- “婚姻状态”:没有填写这一项的用户可能对自己的隐私比较敏感,应单独设为一个分类,如已婚1、未婚0、未填-1。
3.5 数据变换
常见的数据变换有基于多项式的、基于指数函数的、基于对数函数的。4个特征,度为2的多项式转换公式如下:
$(x'_1,x'_2...x'_{15})=(1,x_1,x_2,x_3,x_4,x_1^2,x_1*x_2,x_1*x_3,x_1*x_4,x_2^2,x_2*x_3,x_2*x_4,x_3^2,x_3*x_4,x_4^2)$ (5)
多项式特征变换,目标是将特征两两组合起来,使得特征和目标变量之间的的关系更接近线性,从而提高预测的效果
4、特征选择
当数据预处理完成后,我们需要选择有意义的特征输入机器学习的算法和模型进行训练。通常来说,从两个方面考虑来选择特征:
- 特征是否发散:如果一个特征不发散,例如方差接近于0,也就是说样本在这个特征上基本上没有差异,这个特征对于样本的区分并没有什么用。
- 特征与目标的相关性:这点比较显见,与目标相关性高的特征,应当优选选择。除方差法外,本文介绍的其他方法均从相关性考虑。
根据特征选择的形式又可以将特征选择方法分为3种:
- Filter:过滤法,按照发散性或者相关性对各个特征进行评分,设定阈值或者待选择阈值的个数,选择特征。
- Wrapper:包装法,根据目标函数(通常是预测效果评分),每次选择若干特征,或者排除若干特征。
- Embedded:嵌入法,先使用某些机器学习的算法和模型进行训练,得到各个特征的权值系数,根据系数从大到小选择特征。类似于Filter方法,但是是通过训练来确定特征的优劣。
我们使用sklearn中的feature_selection库来进行特征选择。
4.1 Filter
4.1.1 方差选择法
使用方差选择法,先要计算各个特征的方差,然后根据阈值,选择方差大于阈值的特征。
4.1.2 相关系数法
使用相关系数法,先要计算各个特征对目标值的相关系数以及相关系数的P值。
4.1.3 卡方检验
经典的卡方检验是检验定性自变量对定性因变量的相关性。假设自变量有N种取值,因变量有M种取值,考虑自变量等于i且因变量等于j的样本频数的观察值与期望的差距,构建统计量:
$x^2=\sum\frac{(A-E)^2}{E} $ (6)
这个统计量的含义简而言之就是自变量对因变量的相关性。选择卡方值排在前面的K个特征作为最终的特征选择
4.1.4 互信息法
经典的互信息也是评价定性自变量对定性因变量的相关性的,互信息计算公式如下:
$I(X:Y)=\sum_{x\in X}\sum_{y\in Y}p(x,y)log\frac{p(x,y)}{p(x)p(y)}$ (7)
同理,选择互信息排列靠前的特征作为最终的选取特征
4.2 Wrapper
4.2.1 递归特征消除法
递归消除特征法使用一个基模型来进行多轮训练,每轮训练后,消除若干权值系数的特征,再基于新的特征集进行下一轮训练。
4.3 Embedded
4.3.1 基于惩罚项的特征选择法
使用带惩罚项的基模型,除了筛选出特征外,同时也进行了降维。由于$L_1$范数有筛选特征的作用,因此,训练的过程中,如果使用了$L_1$范数作为惩罚项,可以起到特征筛选的效果
4.3.2 基于树模型的特征选择法
训练能够对特征打分的预选模型:GBDT、RandomForest和Logistic Regression等都能对模型的特征打分,通过打分获得相关性后再训练最终模型;
GBDT: http://breezedeus.github.io/2014/11/19/breezedeus-feature-mining-gbdt.html
4.4 特征组合
通过特征组合后再来选择特征:如对用户id和用户特征最组合来获得较大的特征集再来选择特征,这种做法在推荐系统和广告系统中比较常见
5、降维
当特征选择完成后,可以直接训练模型了,但是可能由于特征矩阵过大,导致计算量大,训练时间长的问题,因此降低特征矩阵维度也是必不可少的。常见的降维方法除了以上提到的基于L1惩罚项的模型以外,另外还有主成分分析法(PCA)和线性判别分析(LDA),线性判别分析本身也是一个分类模型。PCA和LDA有很多的相似点,其本质是要将原始的样本映射到维度更低的样本空间中,但是PCA和LDA的映射目标不一样:PCA是为了让映射后的样本具有最大的发散性;而LDA是为了让映射后的样本有最好的分类性能。所以说PCA是一种无监督的降维方法,而LDA是一种有监督的降维方法。
5.1 主成分分析法(PCA)
使用decomposition库的PCA类选择特征的代码如下:
1from sklearn.decomposition import PCA
2
3#主成分分析法,返回降维后的数据
4#参数n_components为主成分数目
5 PCA(n_components=2).fit_transform(iris.data)
5.2 线性判别分析法(LDA)
使用lda库的LDA类选择特征的代码如下:
1from sklearn.lda import LDA
2
3#线性判别分析法,返回降维后的数据
4#参数n_components为降维后的维数
5 LDA(n_components=2).fit_transform(iris.data, iris.target)
参考文献:
(1)维基百科


 浙公网安备 33010602011771号
浙公网安备 33010602011771号