NOJ1002将军问题
-
[1002] 将军问题
- 时间限制: 1000 ms 内存限制: 65535 K
- 问题描述
-
关于中国象棋,想必大家都很熟悉吧。我们知道,在走棋的时候,被对方將军的这种情形是很容易被人察觉的(不然,你也太粗心了)。但是我们的计算机是如何识别这种情形的呢?它显然没有人的这种“直觉”。这就是我们今天要解决的问题,你的任务就是写一段计算机代码,根据当前局面信息,判断是否存在一方正在被另一方將军的情形,并给出正确结果。
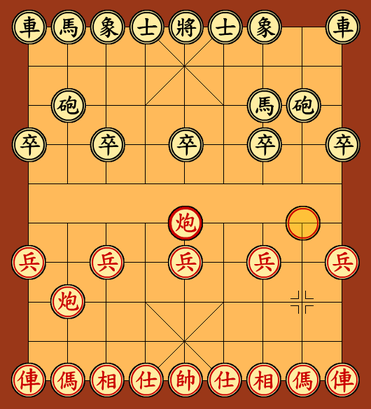
![./1.png]()
图片一
如图一,象棋棋盘由九条竖线和十条横线交叉组成。棋盘上共有九十个交叉点,象棋子就摆放在和活动在这些交叉点上。棋盘中间没有画通直线的地方,叫做“九宫”。棋子共有三十二个,分为红、黑两组,每组共十六个,各分七种,其名称和数目如下:
-
红棋子: 帅一个,车、马、炮、相、仕各两个,兵五个。
-
黑棋子: 将一个,车、马、炮、象、士各两个,卒五个。
各种棋子的走法如下:
-
将(帅)每一步只许前进、后退、横走,但不能走出“九宫”。
-
士(仕)每一步只许沿“九宫”斜线走一格,可进可退。
-
象(相)不能越过“河界”,每一步斜走两格,可进可退,即俗称“象(相)走田字“。当田字中心有别的棋子时,俗称”塞象(相)眼“,则不许走过去。
-
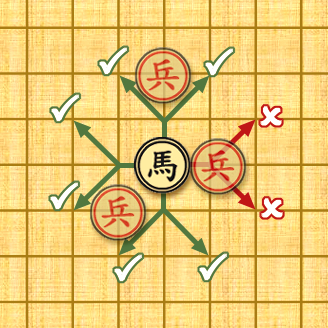
马每步一直(或一横)一斜,可进可退,即俗称”马走日字“。如果在要去的方向有别的棋子挡住,俗称”蹩马腿”,则不许走过去。具体可参考图二。
![./2.png]()
图片二
-
车每一步可以直进、直退、横走,不限步数。
-
炮在不吃子的时候,走法跟车一样。在吃子时必须隔一个棋子(无论是哪一方的)跳吃,即俗称“炮打隔子”。
-
卒(兵)在没有过“河界”前,没步只许向前直走一格;过“河界”后,每步可向前直走或横走一格,但不能后退。
另外,在一个局面中,如果一方棋子能够走到的位置有对方将(帅)的存在,那么该局面就称为將军局面,我们的任务就是找出这样的局面。根据上述规则,我们很容易就能推断出只有以下几种方式才会造成將军局面:
-
将(帅)照面。即将和帅在同一直线上。
-
马对将(帅)的攻击。(注意马有蹩脚)
-
车对将(帅)的攻击。
-
炮对将(帅)的攻击。(注意炮要隔一子)
-
过河兵对将(帅)的攻击。
-
- 输入
-
输入的第一行为一个正整数n(1<=n<=100)。表示有n个测试局面。
接下来的n次测试,每次输入10行,每行输入9个特定正整数,用来表示一个局面(上黑下红)。其中数字0表示该处无棋子,其他数字具体表示如下:
黑方:将(1)、士(2,3)、象(4,5)、马(6,7)、车(8,9)、炮(10,11)、卒(12,13,14,15,16)
红方:帅(17)、仕(18,19)、相(20,21)、马(22,23)、车(24,25)、炮(26,27)、兵(28,29,30,31,32)
提示:样例中的第一组数据表示的是初始局面,第二组数据表示的是图一的局面。 - 输出
-
如果存在将军局面,则输出"yes"。反之,输出"no"。
- 样例输入
-
2 8 6 4 2 1 3 5 7 9 0 0 0 0 0 0 0 0 0 0 10 0 0 0 0 0 11 0 12 0 13 0 14 0 15 0 16 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 28 0 29 0 30 0 31 0 32 0 26 0 0 0 0 0 27 0 0 0 0 0 0 0 0 0 0 24 22 20 18 17 19 21 23 25 8 6 4 2 1 3 5 0 9 0 0 0 0 0 0 0 0 0 0 10 0 0 0 0 7 11 0 12 0 13 0 14 0 15 0 16 0 0 0 0 0 0 0 0 0 0 0 0 0 27 0 0 0 0 28 0 29 0 30 0 31 0 32 0 26 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 24 22 20 18 17 19 21 23 25
- 样例输出
-
no yes
- 提示
-
无
- 来源
-
Timebug
-
没啥好解释,直接模拟。
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 using namespace std; 6 int borad[10][10]; 7 int f[4][2]={0,1,-1,0,0,-1,1,0},ffma[8][2]={-1,1,1,1,-1,1,-1,-1,1,-1,-1,-1,1,1,1,-1}; 8 int hx,hy,bx,by; 9 void init() 10 { 11 for(int i=0;i<10;i++) 12 for(int j=0;j<9;j++) 13 { 14 scanf("%d",&borad[i][j]); 15 if(borad[i][j]==1)hx=i,hy=j; 16 if(borad[i][j]==17)bx=i,by=j; 17 } 18 19 } 20 bool jug(int x,int y) 21 { 22 if(x<0||x>9||y<0||y>8)return false; 23 return true; 24 } 25 bool is_che(int x,int y) 26 { 27 int p=y,q=x,other=0; 28 while(1) 29 { q--; 30 if(q<0)break; 31 if(borad[q][y]!=0) 32 { 33 if(borad[q][y]==17&&borad[x][y]<17)return true; 34 if(borad[q][y]==1&&borad[x][y]>=17)return true; 35 break; 36 } 37 } p=y,q=x; 38 while(1) 39 { q++; 40 if(q>9)break; 41 if(borad[q][y]!=0) 42 { 43 if(borad[q][y]==17&&borad[x][y]<17)return true; 44 if(borad[q][y]==1&&borad[x][y]>=17)return true; 45 break; 46 } 47 } p=y,q=x; 48 while(1) 49 { p--; 50 if(p<0)break; 51 if(borad[x][p]!=0) 52 { 53 if(borad[x][p]==17&&borad[x][y]<17)return true; 54 if(borad[x][p]==1&&borad[x][y]>=17)return true; 55 break; 56 } 57 } p=y,q=x; 58 while(1) 59 { p++; 60 if(p>8)break; 61 if(borad[x][p]!=0) 62 { 63 if(borad[x][p]==17&&borad[x][y]<17)return true; 64 if(borad[x][p]==1&&borad[x][y]>=17)return true; 65 break; 66 } 67 } 68 return false; 69 } 70 bool is_ma(int x,int y) 71 { 72 for(int i=0;i<4;i++) 73 { 74 int xx=x+f[i][0];int yy=y+f[i][1]; 75 if(jug(xx,yy)&&borad[xx][yy]==0) 76 { int tx=xx,ty=yy; 77 for(int j=0;j<2;j++) 78 { 79 xx=tx+ffma[i*2+j][0];yy=ty+ffma[i*2+j][1]; 80 if(jug(xx,yy)&&borad[xx][yy]==17&&borad[x][y]<17)return true; 81 if(jug(xx,yy)&&borad[xx][yy]==1&&borad[x][y]>17)return true; 82 } 83 } 84 } 85 return false; 86 } 87 bool is_pao(int x,int y) 88 { 89 int p=y,q=x,shan; 90 shan=0; 91 while(1) 92 { q--; 93 if(q<0)break; 94 if(borad[q][y]!=0) 95 { 96 if(!shan)shan=1; 97 else if(borad[q][y]==17&&borad[x][y]<17&&shan)return true; 98 else if(borad[q][y]==1&&borad[x][y]>=17&&shan)return true; 99 else if(shan)break; 100 } 101 } p=y,q=x;shan=0; 102 while(1) 103 { q++; 104 if(q>9)break; 105 if(borad[q][y]!=0) 106 { if(!shan)shan=1; 107 else if(borad[q][y]==17&&borad[x][y]<17&&shan)return true; 108 else if(borad[q][y]==1&&borad[x][y]>=17&&shan)return true; 109 else if(shan)break; 110 } 111 } p=y,q=x;shan=0; 112 while(1) 113 { p--; 114 if(p<0)break; 115 if(borad[x][p]!=0) 116 { if(!shan)shan=1; 117 else if(borad[x][p]==17&&borad[x][y]<17&&shan)return true; 118 else if(borad[x][p]==1&&borad[x][y]>=17&&shan)return true; 119 else if(shan)break; 120 } 121 } p=y,q=x;shan=0; 122 while(1) 123 { p++; 124 if(p>8)break; 125 if(borad[x][p]!=0) 126 { if(!shan)shan=1; 127 else if(borad[x][p]==17&&borad[x][y]<17&&shan)return true; 128 else if(borad[x][p]==1&&borad[x][y]>=17&&shan)return true; 129 else if(shan)break; 130 } 131 } 132 return false; 133 } 134 bool is_jiang(int x,int y) 135 { 136 for(int i=0;i<4;i++) 137 { if(borad[x][y]==1&&i==1)continue; 138 if(borad[x][y]==17&&i==3)continue; 139 int xx=x+f[i][0],yy=y+f[i][1]; 140 if(jug(xx,yy)) 141 { 142 if(borad[x][y]==1) 143 { 144 if(borad[xx][yy]==28||borad[xx][yy]==29||borad[xx][yy]==30||borad[xx][yy]==31||borad[xx][yy]==32)return true; 145 } 146 else if(borad[x][y]==17) 147 { 148 if(borad[xx][yy]==12||borad[xx][yy]==13||borad[xx][yy]==14||borad[xx][yy]==15||borad[xx][yy]==16)return true; 149 } 150 } 151 } 152 int xx=x,yy=y; 153 while(1) 154 { 155 xx++; 156 if(xx>9)break; 157 if(borad[xx][yy]!=0) 158 { 159 if(borad[x][y]==1&&borad[xx][yy]==17)return true; 160 if(borad[x][y]==17&&borad[xx][yy]==1)return true; 161 return false; 162 } 163 }xx=x,yy=y; 164 while(1) 165 { 166 xx--; 167 if(xx<0)break; 168 if(borad[xx][yy]!=0) 169 { 170 if(borad[x][y]==1&&borad[xx][yy]==17)return true; 171 if(borad[x][y]==17&&borad[xx][yy]==1)return true; 172 return false; 173 } 174 } 175 return false; 176 } 177 bool check(int x,int y) 178 { 179 if(borad[x][y]==8||borad[x][y]==9||borad[x][y]==24||borad[x][y]==25) 180 { 181 if(is_che(x,y))return true;return false; 182 } 183 if(borad[x][y]==6||borad[x][y]==7||borad[x][y]==22||borad[x][y]==23) 184 { 185 if(is_ma(x,y))return true;return false; 186 } 187 if(borad[x][y]==10||borad[x][y]==11||borad[x][y]==26||borad[x][y]==27) 188 { 189 if(is_pao(x,y))return true;return false; 190 } 191 if(borad[x][y]==1||borad[x][y]==17) 192 { 193 if(is_jiang(x,y))return true;return false; 194 } 195 return false; 196 } 197 void solve() 198 { int flag=0; 199 for(int i=0;i<10&&!flag;i++) 200 { 201 for(int j=0;j<9&&!flag;j++) 202 { 203 if(check(i,j))flag=1; 204 } 205 } 206 if(flag)printf("yes\n"); 207 else printf("no\n"); 208 } 209 int main() 210 { int T; 211 scanf("%d",&T); 212 while(T--) 213 { 214 init(); 215 solve(); 216 } 217 return 0; 218 }

 浙公网安备 33010602011771号
浙公网安备 33010602011771号