结对项目
| 这个作业属于哪个课程 | 班级的链接 |
|---|---|
| 这个作业要求在哪里 | 作业要求的链接 |
| 这个作业的目标 | 组队合作实现一个自动生成小学四则运算题目的命令行程序 |
一、结对组合成员介绍
| 结对成员姓名 | 学号 | GitHub项目地址 |
|---|---|---|
| 梁志聪 | 3122004650 | 项目地址 |
| 李永杰 | 3122004652 | 项目地址 |
二、PSP表
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 30 | 30 |
| ·Estimate | ·估计这个任务需要多少时间 | 30 | 30 |
| Development | 开发 | 660 | 660 |
| ·Analysis | ·需求分析 (包括学习新技术) | 180 | 60 |
| · Design Spec | · 生成设计文档 | 30 | 30 |
| · Design Review | · 设计复审 | 30 | 30 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 30 | 30 |
| · Design | · 具体设计 | 120 | 60 |
| · Coding | · 具体编码 | 120 | 180 |
| · Code Review | · 代码复审 | 30 | 180 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 30 | 90 |
| Reporting | 报告 | 90 | 130 |
| · Test Repor | · 测试报告 | 30 | 60 |
| · Size Measurement | · 计算工作量 | 30 | 10 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 30 | 60 |
| 合计 | 780 | 910 |
三、效能分析
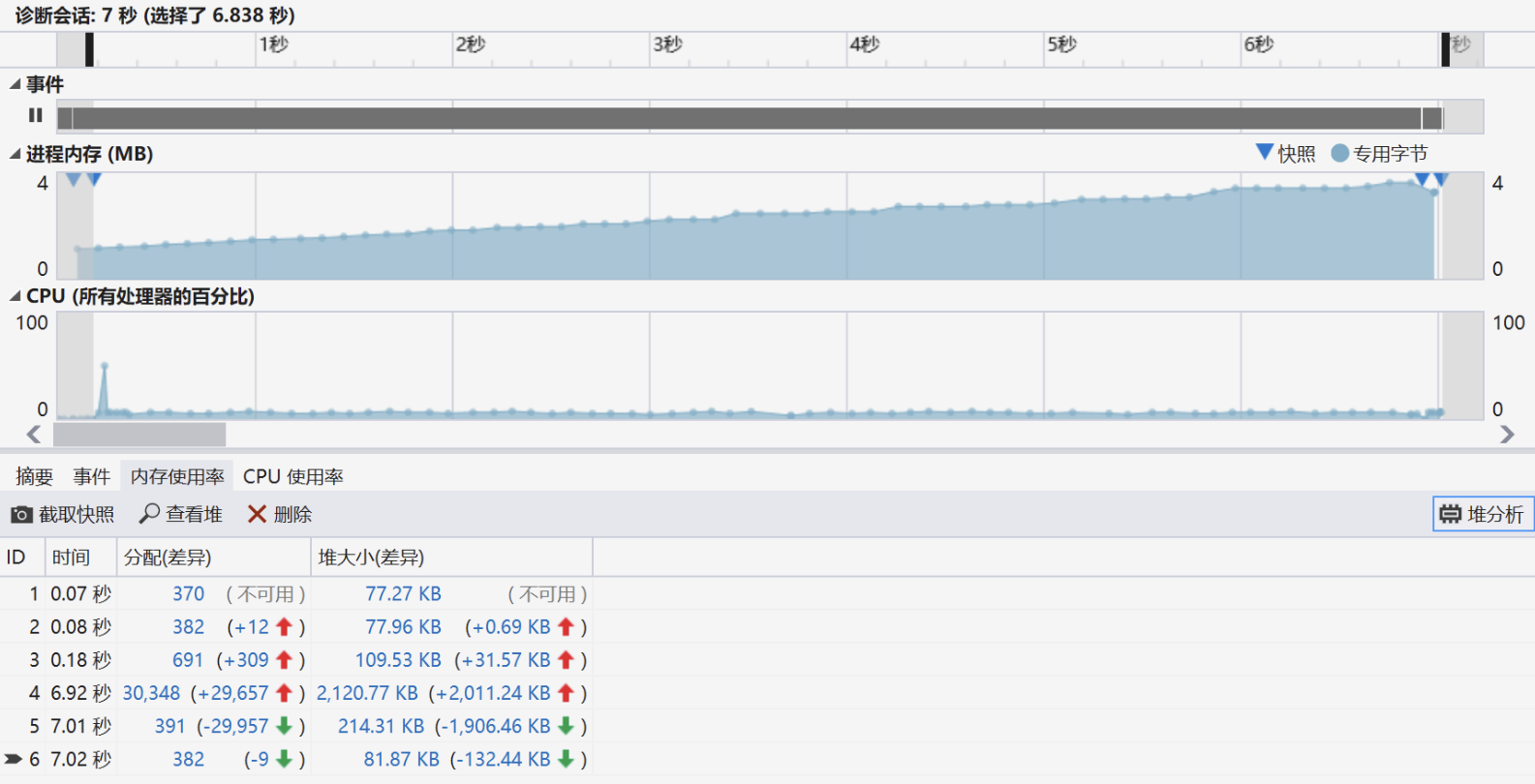
快照1:刚进入函数时;快照2:即将调用算式生成函数;快照3:已经生成了100条算式;
快照4:已经生成了10000条算式;快照5:清空查重用哈希表后;快照6:函数结束后;
分析6个快照可知程序内存主要使用在于存储查重用的字符串,总体来说内存花销较小,并且对比快照1和6可以判断程序无内存泄漏
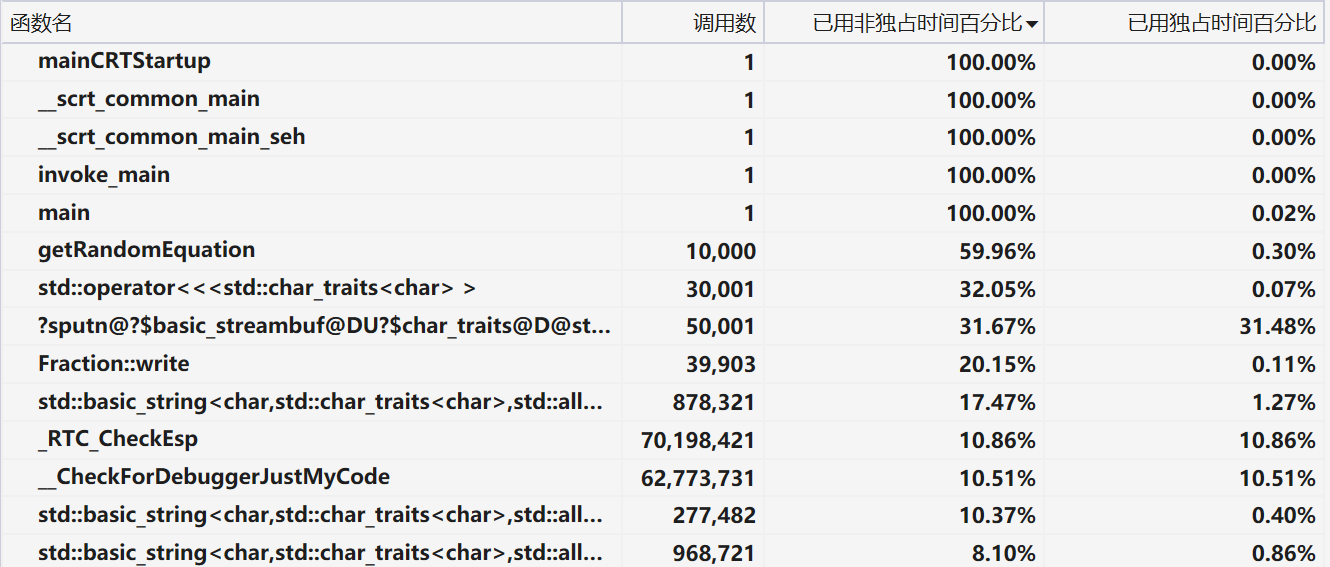
由上图可知,getRandomEquation及其子函数耗时占比最大,其次则是数据输出的耗时占比。
对比数据输出耗时和getRandomEquation及其子函数耗时和函数设计,得出以下结论:生成算式函数的耗时跟算式输出到文件耗时接近,个人认为算法优化对性能提升的空间有限,可以通过多线程来进一步提升性能。
最终生成10000条算式,数字限制在100时的耗时在109ms左右,个人认为效率优秀。
四、设计实现过程
1.设计2个全局变量numLimit和countLimit分别控制算式中数值的上限和算式的生成数量,和1个全局常量operatorLimit控制算式中运算符的上限。
2. 设计一个Fraction分数类来实现分数间的四则运算操作:
(1)类内私有变量numerator和denominator表示分母和分子。
(2)类内私有函数reduction()用于分母和分子的通分,使分数为最简分数
(3)类内公共函数random_init()用于分数的随机生成,分数大小取决于全局变量numLimit
(4)类内剩余操作包括构造函数和运算符重载
(5)类内公共函数write()将分数转换成合法的真分数字符串
3.设计一些辅助函数简化一些基础操作
(1)stringToFraction(string s):将合法字符串转换为分数类(不支持负数,非法字符串会抛出异常)
(2)autoCal(Fraction x, string op, Fraction y):识别字符串形式的运算符,进行分数四则运算
(3)getPriority(string x):获取运算符优先级,其他字符优先级均为0
(4)getRandomOperator():随机生成一个运算符并返回
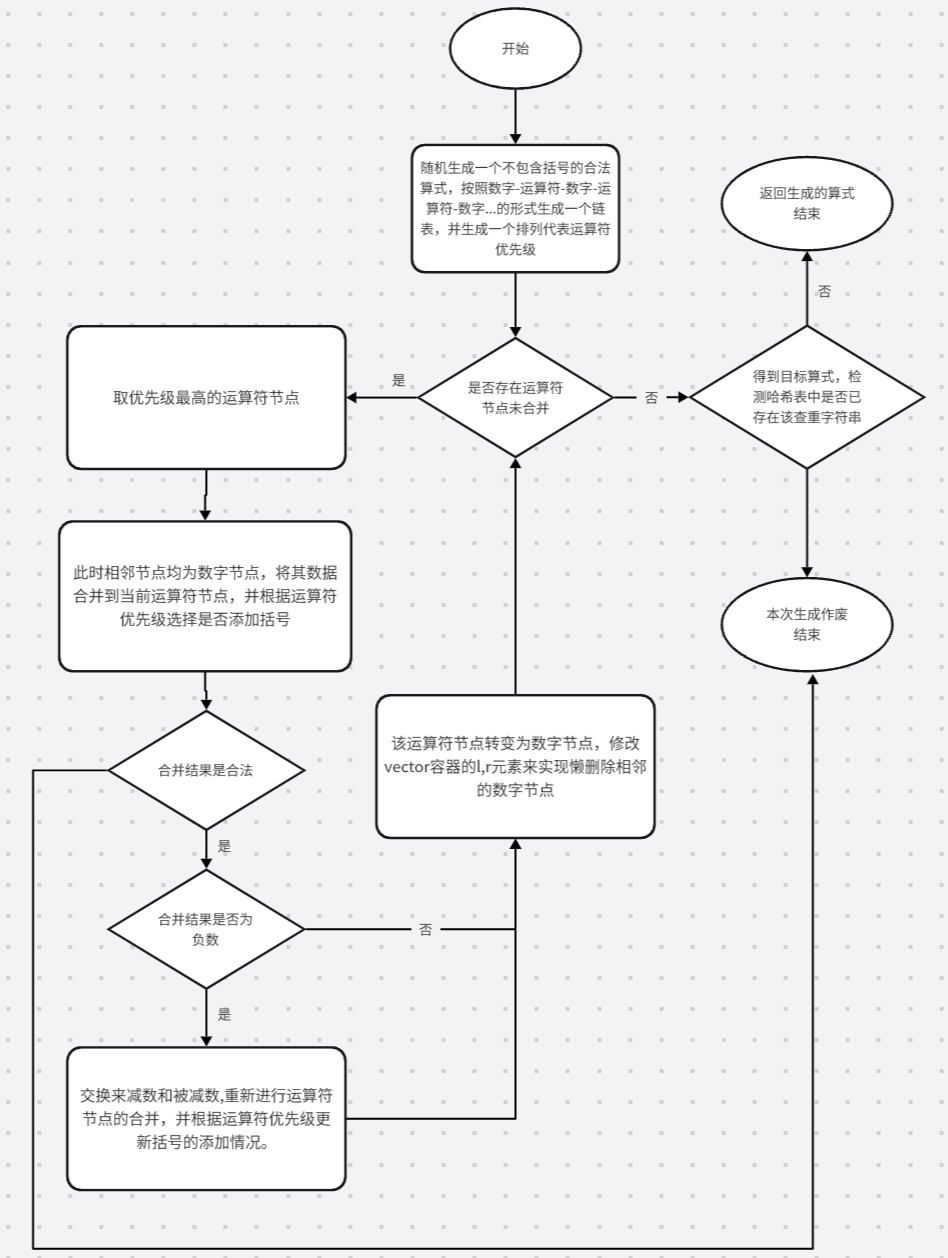
4.getRandomEquation():实现算式随机生成,流程图如下:
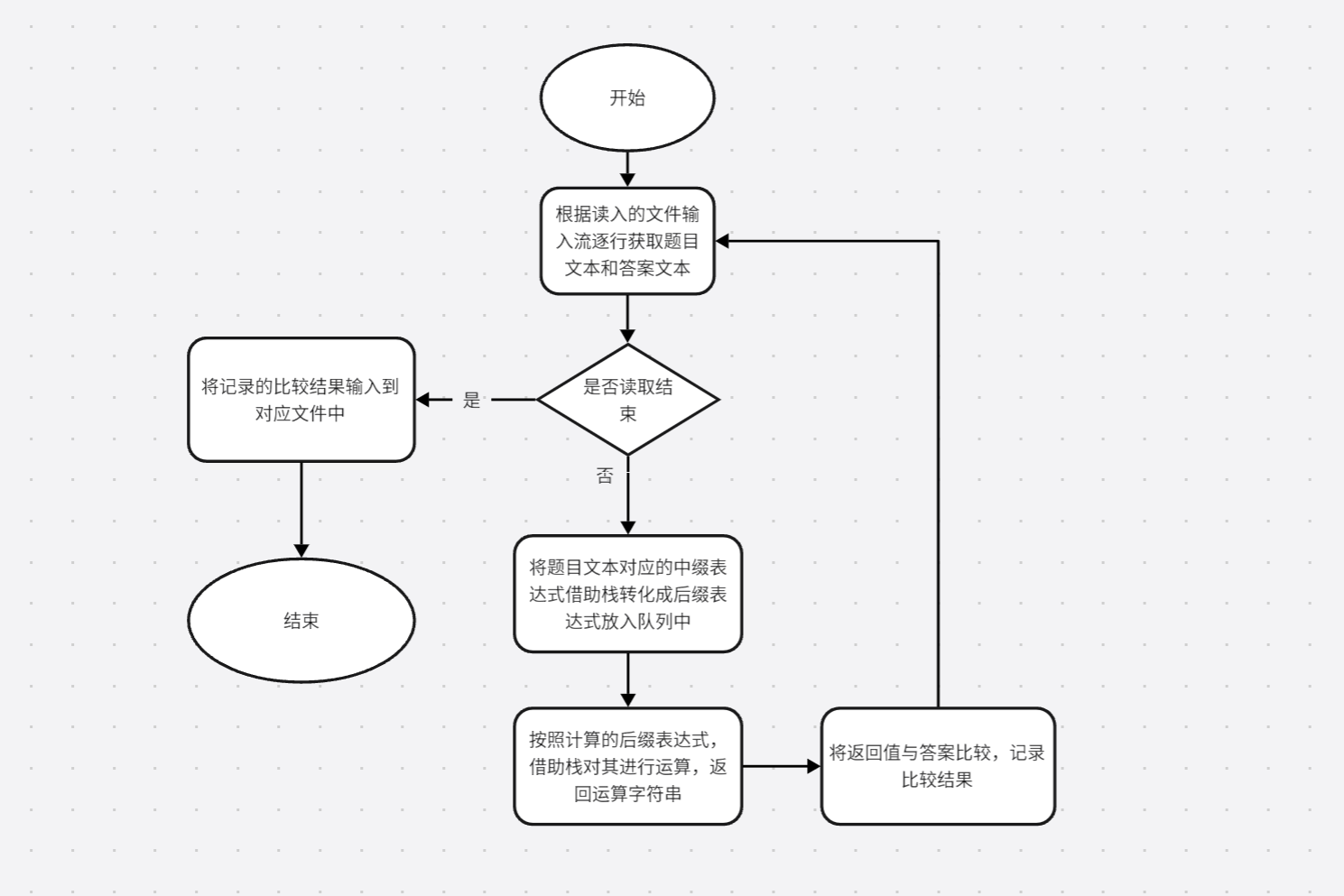
5.calculate(string eq):实现将合法四则运算字符串计算出结果
checkexample(ifstream &fileExample,ifstream &fileAnswer)通过文件流读取样例和答案文件调用calculate函数进行答案比较,并将比较结果存入Grade.txt文件
流程图如下:
6.main()函数:实现对从命令行读入数据的分析,根据分析选择具体要实现功能,或进行报错处理,通过return不同的结果代表发生不同的异常。
命令行输入要求:使用随机生成算式时 -n参数必须要有且为正整数,-r参数不存在则默认为零;使用比较答案模式时-e和-a参数必须同时存在且文件路径正确。
五、代码说明
getRandomEquation()代码如下:
点击查看代码
Node getRandomEquation() {
int siz = (rand() % operatorLimit + 1) * 2 + 1;
vector <Node> List(siz);//用vector实现将链缩成点的过程
vector <int> priority;//优先级
List[0].fr.random_init(); List[0].checkeq = List[0].eq = List[0].fr.write();
List[0].l = -1, List[0].r = 1; List[0].bracketadd = 0;
for (int i = 1; i < siz; i += 2) {//节点数据初始化,使链呈现数字与运算符交替的结构(即是一条合法的无括号四则运算算式)
List[i].l = i - 1; List[i].r = i + 1;
List[i].op = getRandomOperator();
List[i].checkeq = List[i].eq = List[i].op;
List[i].bracketadd = false;
priority.push_back(i);
List[i + 1].l = i; List[i + 1].r = i + 2;
List[i + 1].fr.random_init();
List[i + 1].checkeq = List[i + 1].eq = List[i + 1].fr.write();
List[i + 1].bracketadd = false;
}
random_shuffle(priority.begin(), priority.end());//随机排序以获得运算符的运算优先级
for (auto id : priority)
{
/*
该合并过程可以看作将链根据节点优先级缩成一个点
初始每个节点对应分别一条合法的无括号四则运算算式的数字和运算符
按优先级逐级操作链上的运算符节点,每次对一个运算符节点操作时,
首先根据两个相邻数字节点的数据更新当前运算符节点从而得到新的数字节点,并根据运算符优先级判断是否添加括号。
然后将两个相邻的数字节点从链中删除(该操作通过修改下标实现懒删除)
此时可以看作链上的一个运算符节点和其相邻的数字节点合并成了新的数字节点。
重复上述操作,将链上的所有节点合并完成,最终剩下的节点包含的四则运算式即是目标算式。
查重字符串则是数字节点在合并中按字典序较小来进行合并且始终添加括号的结果(可确保有限次交换相同的字符串其查重字符串一样)
*/
int lid = List[id].l, rid = List[id].r;//获取进行运算元素的下标
string lop = List[lid].l == -1 ? "#" : List[List[lid].l].op;//获取该运算符左边的运算符
string rop = List[rid].r == siz ? "#" : List[List[rid].r].op;//获取该运算符右边的运算符
List[id].fr = autoCal(List[lid].fr, List[id].op, List[rid].fr);
if (List[id].fr < 0) {//合并节点值小于0,交换合并顺序并更新括号
if ((List[lid].op == "-" || List[lid].op == "+") && List[lid].bracketadd == false) {
List[lid].eq = '(' + List[lid].eq + ')';
List[lid].bracketadd = true;
}
if ((List[rid].op == "-" || List[rid].op == "+") && List[rid].bracketadd == true) {
List[rid].eq = List[rid].eq.substr(1, (int)List[rid].eq.size() - 2);
List[rid].bracketadd = false;
}
List[lid].swapkey(List[rid]);//交换节点的关键值
List[id].fr = autoCal(List[lid].fr, List[id].op, List[rid].fr);
if (List[id].fr.error_check())//算式运算过程发生除0错误
return { Fraction(),"","","",0,0 };
}
if (getPriority(lop) < getPriority(List[id].op) && getPriority(List[id].op) >= getPriority(rop))//根据优先级判断是否添加括号
List[id].eq = List[lid].eq + List[id].eq + List[rid].eq;
else
{
if (getPriority(lop) >= getPriority(List[lid].op) && getPriority(List[lid].op) >= getPriority(List[id].op) && List[lid].bracketadd == true) {
List[lid].eq = List[lid].eq.substr(1, (int)List[lid].eq.size() - 2);//移除不需要的括号
List[lid].bracketadd = false;
}
List[id].eq = '(' + List[lid].eq + List[id].eq + List[rid].eq + ')';
List[id].bracketadd = true;
}
if ((List[id].op == "+" || List[id].op == "*") && List[lid].checkeq > List[rid].checkeq)//根据字典序增序生成查重用字符串
List[id].checkeq = List[rid].checkeq + List[id].checkeq + List[lid].checkeq;
else
List[id].checkeq = List[lid].checkeq + List[id].checkeq + List[rid].checkeq;
List[id].r = List[rid].r;
List[id].l = List[lid].l;
if (List[id].l != -1) List[List[id].l].r = id;
if (List[id].r != siz) List[List[id].r].l = id;
}
Node ans = List[priority.back()];
if (vis.find(ans.checkeq) != vis.end())
return { Fraction(),"","","",0,0 };
vis.insert(ans.checkeq);
return ans;
}
关于代码中注释的解释图如下:
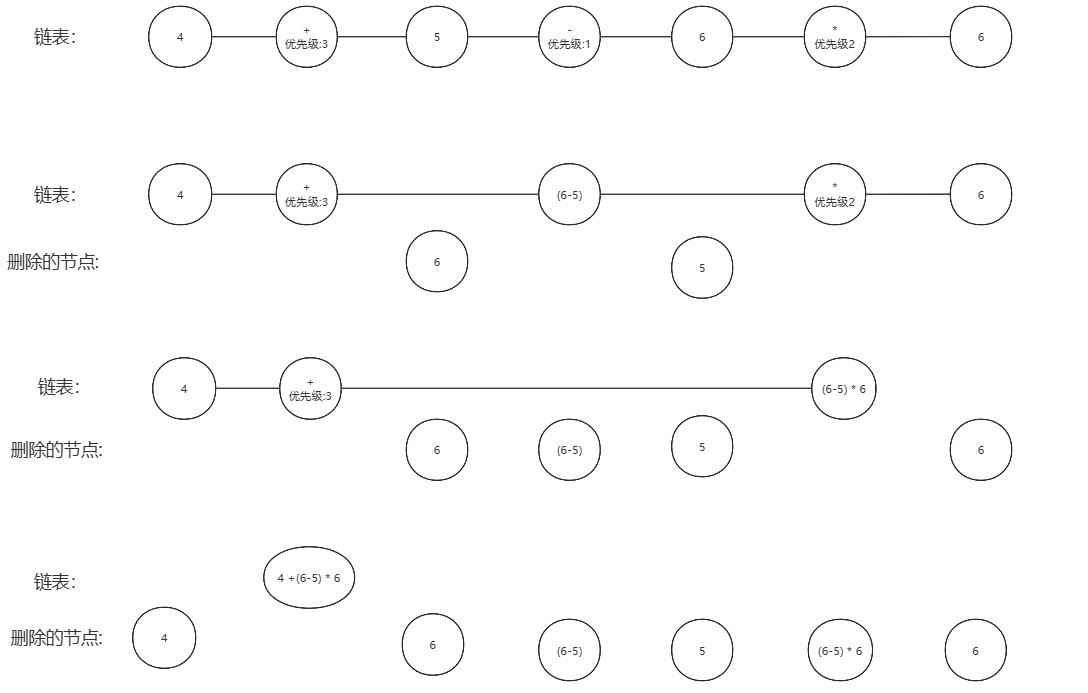
代码总体思路如下:
随机生成一个不包含括号的合法算式,按照数字-运算符-数字-运算符-数字...的形式生成一个链表,并生成一个排列代表运算符优先级。
然后根据优先级进入如图所示的合并,合并详情可以看代码注释。
合并结束和得到算式结果和查重用字符串,查重用字符串先根据哈希表判重,没有重复则放入哈希表并返回生成的算式,否则生成失败。
calculate函数代码如下:
点击查看代码
string calculate(string eq) {
stack<string> opt;
queue<pair<string, Fraction>> postOrder;
size_t last = 0;
for (size_t i = 0; i < eq.size(); i++) { //求后缀表达式
if (eq[i] == '=') {//算式存在等于号,加载最后一个数字
if (last != i)
postOrder.push({ "",Fraction(stringToFraction(eq.substr(last,i - last))) });
last = i + 1;
continue;
}
else if (eq[i] == '+' || eq[i] == '-' || eq[i] == '*') {
if (last != i)
postOrder.push({ "",Fraction(stringToFraction(eq.substr(last,i - last))) });
last = i + 1;
while (!(opt.empty() || getPriority(eq.substr(i, 1)) > getPriority(opt.top()))) {
postOrder.push({ opt.top(),Fraction() });
opt.pop();
}
opt.push(eq.substr(i, 1));
}
else if (eq.substr(i, 2) == "÷") {
if (last != i)
postOrder.push({ "",Fraction(stringToFraction(eq.substr(last,i - last))) });
last = i + 2;
while (!(opt.empty() || getPriority(eq.substr(i, 2)) > getPriority(opt.top()))) {
postOrder.push({ opt.top(),Fraction() });
opt.pop();
}
opt.push(eq.substr(i, 2));
}
else if (eq[i] == '(') {
opt.push(eq.substr(i, 1));
last++;
}
else if (eq[i] == ')') {
if (last != i)
postOrder.push({ "",Fraction(stringToFraction(eq.substr(last,i - last))) });
last = i + 1;
while (!opt.empty() && opt.top() != "(") {
postOrder.push({ opt.top(),Fraction() });
opt.pop();
}
if (!opt.empty()) opt.pop();
}
}
if (last < eq.size())//算式不存在等于号时,加载最后一个数字
postOrder.push({ "",Fraction(stringToFraction(eq.substr(last))) });
while (!opt.empty()) {
postOrder.push({ opt.top(),Fraction() });
opt.pop();
}
stack<Fraction> st;
while (!postOrder.empty())
{
if (postOrder.front().first != "") {
Fraction fra1 = st.top();
if (!st.empty()) st.pop();
Fraction fra2 = st.top();
if (!st.empty()) st.pop();
st.push(autoCal(fra2, postOrder.front().first, fra1));
}
else {
st.push(postOrder.front().second);
}
postOrder.pop();
}
if (st.empty())
throw out_of_range("Index out of range");
return st.top().write();
}
六、测试运行
1.按题目要求命令行输入:main.exe -n - 10000 -r 100得到如下结果
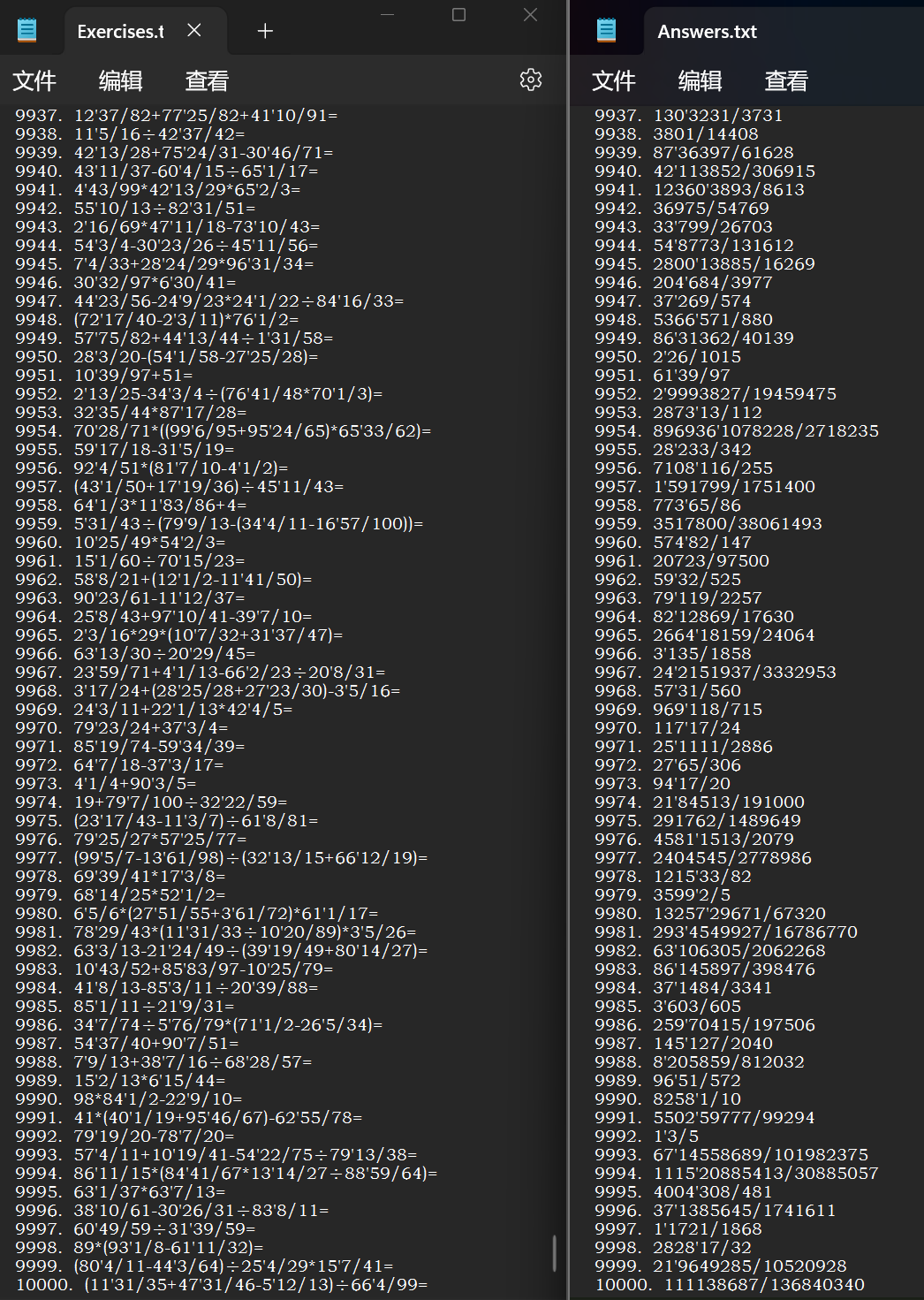
2.命令行输入:main.exe -n -10 -r 10 得到如下结果:
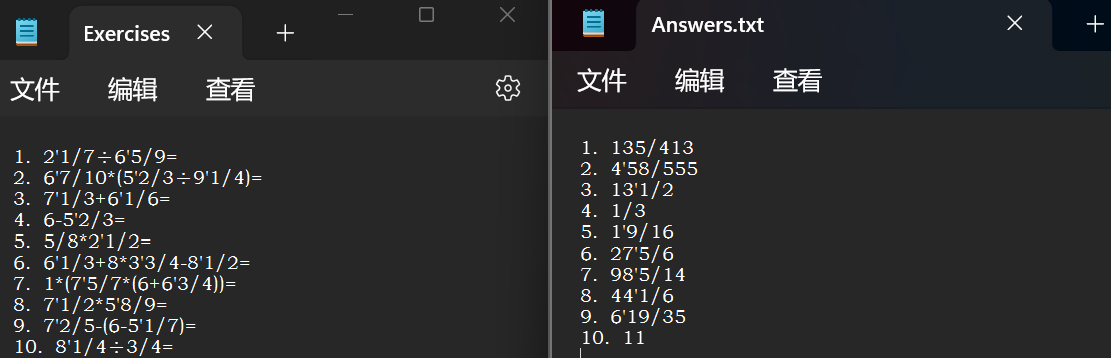
可以看出程序正常生成了10条合法的不重复的算式,且给出了算式的答案。
3.命令行输入:main.exe -e Exercises.txt -a Answers.txt 得到如下结果:
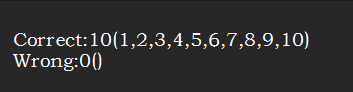
此时进行答案比较可以看出答案均正确
4.修改答案文件后再输入:main.exe -e Exercises.txt -a Answers.txt 得到如下结果:
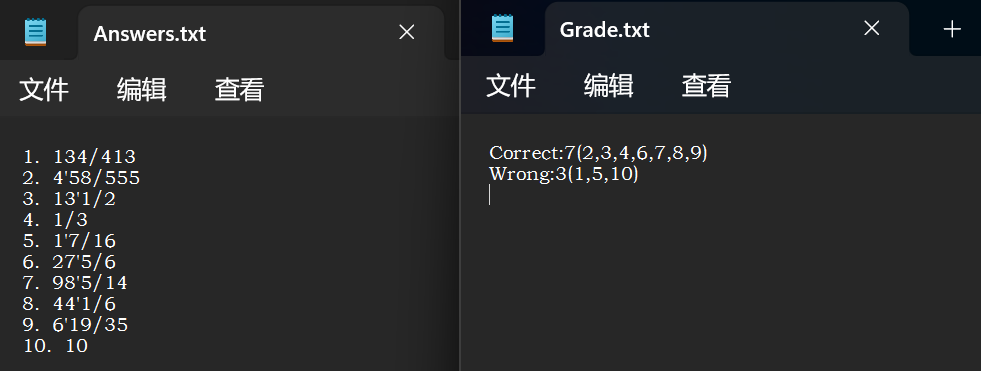
此时进行答案比较可以发现1,5,10号题目答案错误共3题
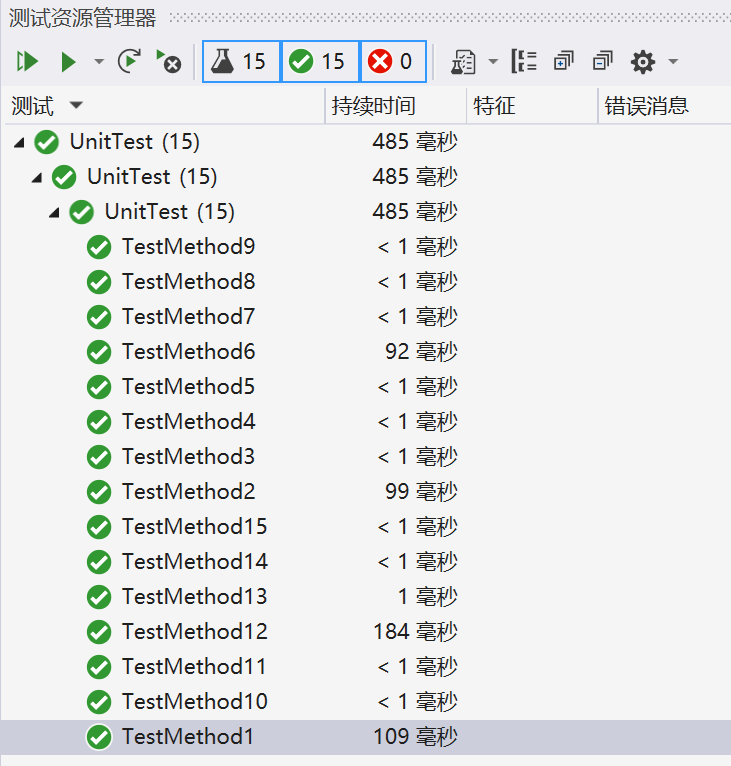
5.设计15个单元测试进行白盒测试,覆盖绝大部分异常情况,代码,测试情况和覆盖率如下图所示:
点击查看代码
namespace UnitTest
{
TEST_CLASS(UnitTest)
{
public:
TEST_METHOD(TestMethod1)
{
char* argv[5] = { "main.exe","-n","10000","-r","100" };
Assert::AreEqual(main(5, argv), 0);
}
TEST_METHOD(TestMethod2)
{
char* argv[3] = { "main.exe","-n","10000" };
Assert::AreEqual(main(3, argv), 0);
}
TEST_METHOD(TestMethod3)
{
char* argv[3] = { "main.exe","-n","-10000" };
Assert::AreEqual(main(3, argv), 1);
}
TEST_METHOD(TestMethod4)
{
char* argv[5] = { "main.exe","-e","10000","-a","100" };
Assert::AreEqual(main(5, argv), 3);
}
TEST_METHOD(TestMethod5)
{
char* argv[4] = { "main.exe","-e","10000","-a" };
Assert::AreEqual(main(4, argv), -1);
}
TEST_METHOD(TestMethod6)
{
char* argv[5] = { "main.exe","-e","Exercises.txt","-a","Answers.txt" };
Assert::AreEqual(main(5, argv), 0);
}
TEST_METHOD(TestMethod7)
{
Assert::AreEqual(getPriority("+"), 1);
Assert::AreEqual(getPriority("-"), 1);
Assert::AreEqual(getPriority("*"), 2);
Assert::AreEqual(getPriority("÷"), 2);
Assert::AreEqual(getPriority("#"), 0);
}
TEST_METHOD(TestMethod8)
{
string eq = "1. 3'5/7+(1*6'2/3-6)=";
string str = "1. 4'8/21";
Assert::IsTrue(str.compare(calculate(eq)));
}
TEST_METHOD(TestMethod9)
{
Fraction x(100, 10), y(-50, 10);
string op1 = "+";
string op2 = "-";
string op3 = "*";
string op4 = "÷";
string ans = "15";
Assert::IsTrue(ans.compare(autoCal(x, op1, y).write()));
ans = "5";
Assert::IsTrue(ans.compare(autoCal(x, op2, y).write()));
ans = "50";
Assert::IsTrue(ans.compare(autoCal(x, op3, y).write()));
ans = "2";
Assert::IsTrue(ans.compare(autoCal(x, op4, y).write()));
}
TEST_METHOD(TestMethod10)
{
string eq = "1'1/10";
string str = "101/10";
Assert::IsTrue(str.compare(stringToFraction(eq).write()));
}
TEST_METHOD(TestMethod11)
{
char* argv[5] = { "main.exe","-n","10000","-r","0" };
Assert::AreEqual(main(5, argv), 2);
}
TEST_METHOD(TestMethod12)
{
char* argv[5] = { "main.exe","-n","100000","-r","2" };
Assert::AreEqual(main(5, argv), 5);
}
TEST_METHOD(TestMethod13)
{
char* argv[5] = { "main.exe","-a","Exercises.txt","-e","Answers.txt" };
ofstream fileExample("Exercises.txt");
ofstream fileAnswer("Answers.txt");
fileExample << "1. " << "1+1" << "=" << endl;
fileExample << "2. " << "10+1" << "=" << endl;
fileExample << "3. " << "1+15" << "=" << endl;
fileAnswer << "1. " << "0" << endl;
fileAnswer << "2. " << "5" << endl;
fileAnswer << "3. " << "8" << endl;
Assert::AreEqual(main(5, argv), 0);
}
TEST_METHOD(TestMethod14)
{
char* argv[5] = { "main.exe","-x","Exercises.txt","-t","Answers.txt" };
Assert::AreEqual(main(5, argv), 7);
}
TEST_METHOD(TestMethod15)
{
char* argv[5] = { "main.exe","-e","Exercises.txt","-a","Answers.txt" };
ofstream fileExample("Exercises.txt");
fileExample << "%#%$" << "=" << endl;
Assert::AreEqual(main(5, argv),6);
}
};
}
测试结果:
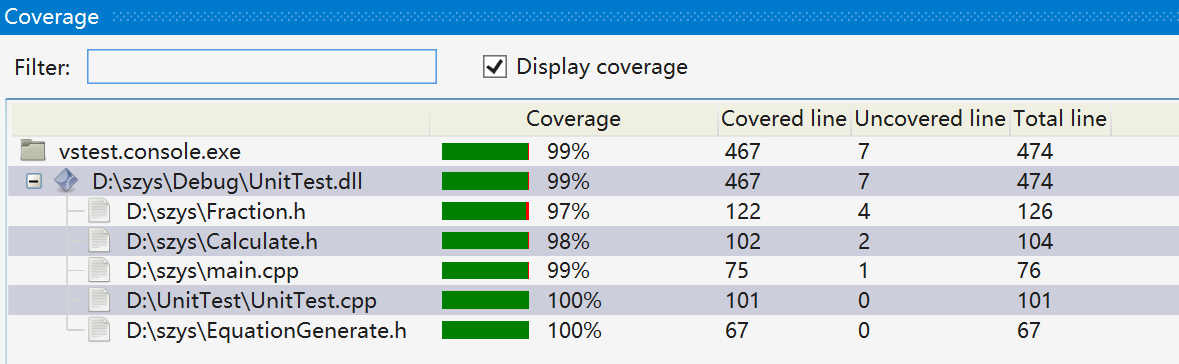
覆盖率:
七、项目小结
梁志聪结对感受:这次结对项目,我负责代码的构思和编写,李永杰同学负责博客的编写和单元测试的设计,虽然我在项目花费的时间更多,但是有李永杰同学帮忙处理博客编写和单元测试的设计,也是减轻了我的工作量,使我可以更专注于程序的设计之中,通过这次结对项目,我体会到了团队合作分工对于软件设计的重要性。
李永杰结对感受:此次结对项目,主导者为梁志聪同学,他包揽了几乎大部分的代码,我负责博客等有关文本的编写,可以说我花费的时间是不足以与梁志聪同学相比的,他在此次结对项目中多次精益求精,从完成基本需求,到考虑更多特殊情况,最后完善附加需求,这些都是由他所推动。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号