Codeforces Round #403 (Div. 2, based on Technocup 2017 Finals) C Andryusha and Colored Balloons
地址:http://codeforces.com/contest/782/problem/C
题目:
Andryusha goes through a park each day. The squares and paths between them look boring to Andryusha, so he decided to decorate them.
The park consists of n squares connected with (n - 1) bidirectional paths in such a way that any square is reachable from any other using these paths. Andryusha decided to hang a colored balloon at each of the squares. The baloons' colors are described by positive integers, starting from 1. In order to make the park varicolored, Andryusha wants to choose the colors in a special way. More precisely, he wants to use such colors that if a, b and c are distinct squares that a and b have a direct path between them, and b and c have a direct path between them, then balloon colors on these three squares are distinct.
Andryusha wants to use as little different colors as possible. Help him to choose the colors!
The first line contains single integer n (3 ≤ n ≤ 2·105) — the number of squares in the park.
Each of the next (n - 1) lines contains two integers x and y (1 ≤ x, y ≤ n) — the indices of two squares directly connected by a path.
It is guaranteed that any square is reachable from any other using the paths.
In the first line print single integer k — the minimum number of colors Andryusha has to use.
In the second line print n integers, the i-th of them should be equal to the balloon color on the i-th square. Each of these numbers should be within range from 1 to k.
3
2 3
1 3
3
1 3 2
5
2 3
5 3
4 3
1 3
5
1 3 2 5 4
5
2 1
3 2
4 3
5 4
3
1 2 3 1 2
In the first sample the park consists of three squares: 1 → 3 → 2. Thus, the balloon colors have to be distinct.
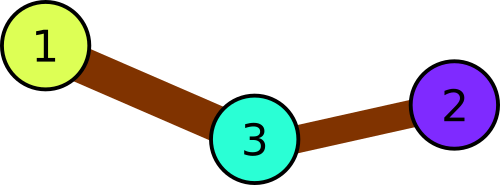 Illustration for the first sample.
Illustration for the first sample.
In the second example there are following triples of consequently connected squares:
- 1 → 3 → 2
- 1 → 3 → 4
- 1 → 3 → 5
- 2 → 3 → 4
- 2 → 3 → 5
- 4 → 3 → 5
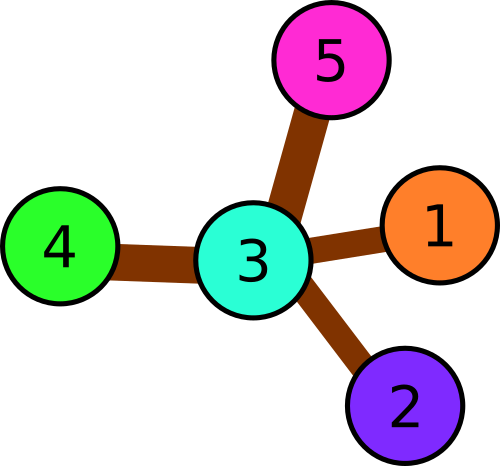 Illustration for the second sample.
Illustration for the second sample.
In the third example there are following triples:
- 1 → 2 → 3
- 2 → 3 → 4
- 3 → 4 → 5
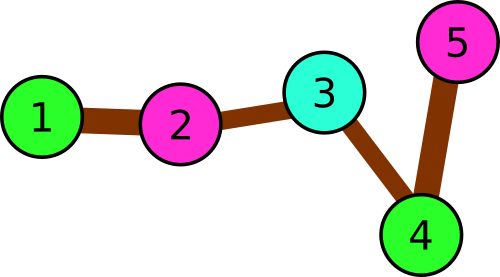 Illustration for the third sample.
Illustration for the third sample. 1 #include <bits/stdc++.h>
2
3 using namespace std;
4
5 #define MP make_pair
6 #define PB push_back
7 typedef long long LL;
8 typedef pair<int,int> PII;
9 const double eps=1e-8;
10 const double pi=acos(-1.0);
11 const int K=2e5+7;
12 const int mod=1e9+7;
13
14 int n,ans,col[K],vis[K];
15 vector<int>mp[K];
16
17 void dfs(int x,int f)
18 {
19 for(int i=0,t=1;i<mp[x].size();i++)
20 if(mp[x][i]!=f)
21 {
22 while(t==col[x]||t==col[f])t++;
23 col[mp[x][i]]=t++;
24 }
25 for(int i=0;i<mp[x].size();i++)
26 if(mp[x][i]!=f)
27 dfs(mp[x][i],x);
28 }
29 int main(void)
30 {
31 cin>>n;
32 for(int i=1,x,y;i<n;i++)
33 scanf("%d%d",&x,&y),mp[x].PB(y),mp[y].PB(x);
34 col[1]=1;
35 dfs(1,0);
36 for(int i=1;i<=n;i++)
37 vis[col[i]]=1;
38 for(int i=1;i<=n;i++)
39 ans+=vis[i];
40 cout<<ans<<endl;
41 for(int i=1;i<=n;i++)
42 printf("%d ",col[i]);
43 return 0;
44 }
作者:weeping
出处:www.cnblogs.com/weeping/
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号