Codeforces Round #395 (Div. 2) D. Timofey and rectangles

地址：http://codeforces.com/contest/764/problem/D

题目：

D. Timofey and rectangles

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

One of Timofey's birthday presents is a colourbook in a shape of an infinite plane. On the plane n rectangles with sides parallel to coordinate axes are situated. All sides of the rectangles have odd length. Rectangles cannot intersect, but they can touch each other.

Help Timofey to color his rectangles in 4 different colors in such a way that every two rectangles touching each other by side would have different color, or determine that it is impossible.

Two rectangles intersect if their intersection has positive area. Two rectangles touch by sides if there is a pair of sides such that their intersection has non-zero length

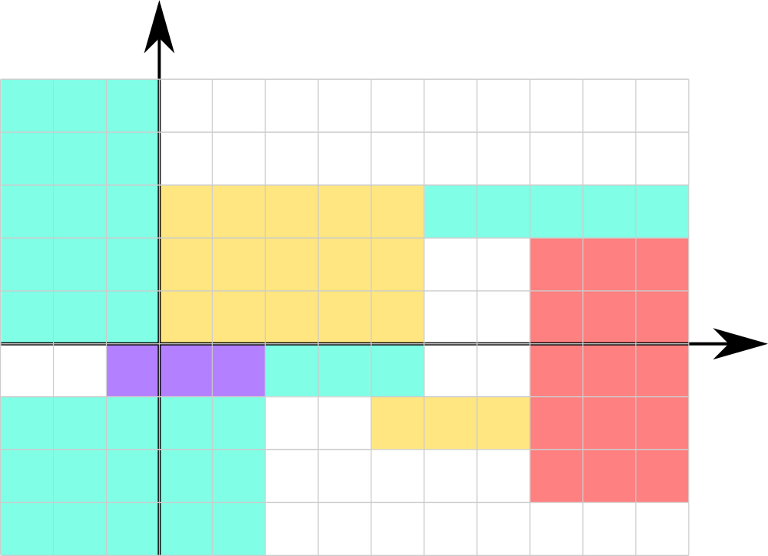The picture corresponds to the first example

Input

The first line contains single integer n (1 ≤ n ≤ 5·105) — the number of rectangles.

n lines follow. The i-th of these lines contains four integers x1, y1, x2 and y2 ( - 109 ≤ x1 < x2 ≤ 109,  - 109 ≤ y1 < y2 ≤ 109), that means that points (x1, y1) and (x2, y2) are the coordinates of two opposite corners of the i-th rectangle.

It is guaranteed, that all sides of the rectangles have odd lengths and rectangles don't intersect each other.

Output

Print "NO" in the only line if it is impossible to color the rectangles in 4 different colors in such a way that every two rectangles touching each other by side would have different color.

Otherwise, print "YES" in the first line. Then print n lines, in the i-th of them print single integer ci (1 ≤ ci ≤ 4) — the color of i-th rectangle.

Example

input

8
0 0 5 3
2 -1 5 0
-3 -4 2 -1
-1 -1 2 0
-3 0 0 5
5 2 10 3
7 -3 10 2
4 -2 7 -1

output

YES
1
2
2
3
2
2
4
1
题意：给你n个边长都为奇数的长方形，问你能否使用四种颜色使所有相邻的长方形涂成不用颜色。
思路：　这题一定有解的，因为四色定理嘛，，然而比赛时想歪了，想先把长方形转化成图，相邻的长方形直接建一条无向边，然后用图的着色方法进行求解，这一点可以百度图的着色。
　　然而发现建图的时间复杂度太高，然后就GG了。。。。（其实可以扫描线建图，不过感觉太麻烦了）
　　做这题感觉智商被碾压了，其实这个题没有这么复杂。因为边长都为奇数，所以可以根据长方形的某一个顶点的坐标的奇偶进行染色。
　　以左下顶点为例，进行反证：
　　　　1.如果（a,b）与（c,d）涂了相同颜色，那么有a与c同奇偶，b与d同奇偶。（用长方形的左下顶点代表长方形）
　　　　2.因为长方形相邻，有 奇数（第一个长方形的顶点坐标x）+奇数（任意一个长方形的边长）=偶数（另一个长方形的对应顶点）
　　　　可以得出1与2相悖，所以假设不成立，其他情况同理可证。
　　所以按照长方形的某一个顶点的坐标的奇偶进行染色即可，，，感觉智商被碾压0.0

#include <bits/stdc++.h>

using namespace std;

#define MP make_pair
#define PB push_back
typedef long long LL;
typedef pair<int,int> PII;
const double eps=1e-8;
const double pi=acos(-1.0);
const int K=1e6+7;
const int mod=1e9+7;


int main(void)
{
    int n;cin>>n;
    printf("YES\n");
    for(int i=1,a,b,c,d,ans;i<=n;i++)
    {
         scanf("%d%d%d%d",&a,&b,&c,&d);
         if(a&1)
         {
             if(b&1)
                ans=1;
             else
                ans=2;
         }
         else
         {
             if(b&1)
                ans=3;
             else
                ans=4;
         }
         printf("%d\n",ans);
    }

    return 0;
}