poj1696 Space Ant
地址:
题目:
Space Ant
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 4295 | Accepted: 2697 |
Description
The most exciting space discovery occurred at the end of the 20th century. In 1999, scientists traced down an ant-like creature in the planet Y1999 and called it M11. It has only one eye on the left side of its head and just three feet all on the right side of its body and suffers from three walking limitations:
The pictures transmitted by the Discovery space ship depicts that plants in the Y1999 grow in special points on the planet. Analysis of several thousands of the pictures have resulted in discovering a magic coordinate system governing the grow points of the plants. In this coordinate system with x and y axes, no two plants share the same x or y.
An M11 needs to eat exactly one plant in each day to stay alive. When it eats one plant, it remains there for the rest of the day with no move. Next day, it looks for another plant to go there and eat it. If it can not reach any other plant it dies by the end of the day. Notice that it can reach a plant in any distance.
The problem is to find a path for an M11 to let it live longest.
Input is a set of (x, y) coordinates of plants. Suppose A with the coordinates (xA, yA) is the plant with the least y-coordinate. M11 starts from point (0,yA) heading towards plant A. Notice that the solution path should not cross itself and all of the turns should be counter-clockwise. Also note that the solution may visit more than two plants located on a same straight line.
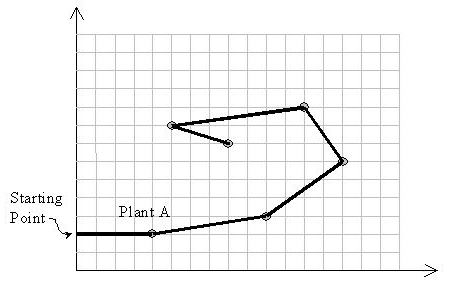
- It can not turn right due to its special body structure.
- It leaves a red path while walking.
- It hates to pass over a previously red colored path, and never does that.
The pictures transmitted by the Discovery space ship depicts that plants in the Y1999 grow in special points on the planet. Analysis of several thousands of the pictures have resulted in discovering a magic coordinate system governing the grow points of the plants. In this coordinate system with x and y axes, no two plants share the same x or y.
An M11 needs to eat exactly one plant in each day to stay alive. When it eats one plant, it remains there for the rest of the day with no move. Next day, it looks for another plant to go there and eat it. If it can not reach any other plant it dies by the end of the day. Notice that it can reach a plant in any distance.
The problem is to find a path for an M11 to let it live longest.
Input is a set of (x, y) coordinates of plants. Suppose A with the coordinates (xA, yA) is the plant with the least y-coordinate. M11 starts from point (0,yA) heading towards plant A. Notice that the solution path should not cross itself and all of the turns should be counter-clockwise. Also note that the solution may visit more than two plants located on a same straight line.

Input
The first line of the input is M, the number of test cases to be solved (1 <= M <= 10). For each test case, the first line is N, the number of plants in that test case (1 <= N <= 50), followed by N lines for each plant data. Each plant data consists of three integers: the first number is the unique plant index (1..N), followed by two positive integers x and y representing the coordinates of the plant. Plants are sorted by the increasing order on their indices in the input file. Suppose that the values of coordinates are at most 100.
Output
Output should have one separate line for the solution of each test case. A solution is the number of plants on the solution path, followed by the indices of visiting plants in the path in the order of their visits.
Sample Input
2 10 1 4 5 2 9 8 3 5 9 4 1 7 5 3 2 6 6 3 7 10 10 8 8 1 9 2 4 10 7 6 14 1 6 11 2 11 9 3 8 7 4 12 8 5 9 20 6 3 2 7 1 6 8 2 13 9 15 1 10 14 17 11 13 19 12 5 18 13 7 3 14 10 16
Sample Output
10 8 7 3 4 9 5 6 2 1 10 14 9 10 11 5 12 8 7 6 13 4 14 1 3 2
思路:直接用卷包裹法求凸包即可
代码:
1 /* 二维几何 */ 2 /* 需要包含的头文件 */ 3 #include <cstdio> 4 #include <cmath > 5 #include <iostream> 6 #include <algorithm> 7 #include <cstring> 8 #include <map> 9 using namespace std; 10 /** 常用的常量定义 **/ 11 const double INF = 1e200; 12 const double eps = 1e-10; 13 const double PI = acos(-1.0); 14 const int Max = 100; 15 /** 基本几何结构 **/ 16 struct Point 17 { 18 double x,y; 19 Point(double a=0, double b=0){x=a,y=b;} 20 bool operator<(const Point &ta)const 21 { 22 if(x==ta.x) return y<ta.y; 23 return x<ta.x; 24 } 25 friend Point operator+(const Point &ta,const Point &tb) 26 { 27 return Point(ta.x+tb.x,ta.y+tb.y); 28 } 29 friend Point operator-(const Point &ta,const Point &tb) 30 { 31 return Point(ta.x-tb.x,ta.y-tb.y); 32 } 33 }; 34 struct Vec2D //二维向量,*重载为点乘,/重载为叉乘 35 { 36 double x,y; 37 Vec2D(double ta,double tb){x=ta,y=tb;} 38 Vec2D(Point &ta){x=ta.x,y=ta.y;} 39 friend double operator*(const Vec2D &ta,const Vec2D &tb) 40 { 41 return ta.x*tb.x+ta.y*tb.y; 42 } 43 friend double operator/(const Vec2D &ta,const Vec2D &tb) 44 { 45 return ta.x*tb.y-ta.y*tb.x; 46 } 47 friend Vec2D operator+(const Vec2D &ta,const Vec2D &tb) 48 { 49 return Vec2D(ta.x+tb.x,ta.y+tb.y); 50 } 51 friend Vec2D operator-(const Vec2D &ta,const Vec2D &tb) 52 { 53 return Vec2D(ta.x-tb.x,ta.y-tb.y); 54 } 55 Vec2D operator=(const Vec2D &ta) 56 { 57 x=ta.x,y=ta.y; 58 return *this; 59 } 60 }; 61 struct LineSeg //线段,重载了/作为叉乘运算符,*作为点乘运算符 62 { 63 Point s,e; 64 LineSeg(){s=Point(0,0),e=Point(0,0);} 65 LineSeg(Point a, Point b){s=a,e=b;} 66 double lenth(void) 67 { 68 return sqrt((s.x-e.x)*(s.x-e.x)+(s.y-e.y)*(s.y-e.y)); 69 } 70 friend double operator*(const LineSeg &ta,const LineSeg &tb) 71 { 72 return (ta.e.x-ta.s.x)*(tb.e.x-tb.s.x)+(ta.e.y-ta.s.y)*(tb.e.y-tb.s.y); 73 } 74 friend double operator/(const LineSeg &ta,const LineSeg &tb) 75 { 76 return (ta.e.x-ta.s.x)*(tb.e.y-tb.s.y)-(ta.e.y-ta.s.y)*(tb.e.x-tb.s.x); 77 } 78 LineSeg operator=(const LineSeg &ta) 79 { 80 s=ta.s,e=ta.e; 81 return *this; 82 } 83 }; 84 struct Line // 直线的解析方程 a*x+b*y+c=0 为统一表示,约定 a >= 0 85 { 86 double a,b,c; 87 Line(double d1=1, double d2=-1, double d3=0){ a=d1,b=d2,c=d3;} 88 }; 89 90 double getdis(Point &ta,Point &tb) 91 { 92 return sqrt((ta.x-ta.x)*(ta.x-tb.x)+(ta.y-tb.y)*(ta.y-tb.y)); 93 } 94 /** ************凸包graham算法**************** 95 寻找凸包的graham 扫描法 96 PS(PointSet)为输入的点集; 97 tb为输出的凸包上的点集,按照逆时针方向排列; 98 n为PointSet中的点的数目 99 num为输出的凸包上的点的个数 100 ****************************************** **/ 101 bool cmp(const Point &ta,const Point &tb)// 选取与最后一条确定边夹角最小的点,即余弦值最大者 102 { 103 // double tmp=LineSeg(ps[0],ta)/LineSeg(ps[0],tb); 104 // if(fabs(tmp)<eps) 105 // return getdis(ps[0],ta)<getdis(ps[0],tb); 106 // else if(tmp>0) 107 // return 1; 108 return 0; 109 } 110 void graham(Point ps[],Point tb[],int n,int &num) 111 { 112 int cur=0,top=2; 113 for(int i=1;i<n;i++) 114 if(ps[cur].y>ps[i].y || (ps[cur].y==ps[i].y &&ps[cur].x>ps[i].x)) 115 cur=i; 116 swap(ps[cur],ps[0]); 117 sort(ps+1,ps+n,cmp); 118 tb[0]=ps[0],tb[1]=ps[1],tb[2]=ps[2]; 119 for(int i=3;i<n;i++) 120 { 121 while(LineSeg(tb[top-1],tb[top])/LineSeg(tb[top-1],ps[i])<0) 122 top--; 123 tb[++top]=ps[i]; 124 } 125 num=top+1; 126 } 127 /** 卷包裹法求点集凸壳,参数说明同graham算法 **/ 128 void ConvexClosure(Point ps[],Point tb[],int n,int &num) 129 { 130 LineSeg lx,ly; 131 int cur; 132 bool vis[Max]; 133 num=-1,cur=0; 134 memset(vis,0,sizeof(vis)); 135 for(int i=1;i<n;i++) 136 if(ps[cur].y>ps[i].y || (ps[cur].y==ps[i].y &&ps[cur].x>ps[i].x)) 137 cur=i; 138 tb[++num]=ps[cur]; 139 lx.s=Point(ps[cur].x-1,ps[cur].y),lx.e=ps[cur]; 140 vis[cur]=1; 141 // 选取与最后一条确定边夹角最小的点,即余弦值最大者 142 while(num!=n) 143 { 144 int ch; 145 double mxcross=-2,midis,tmxcross; 146 ly.s=lx.e; 147 for(int i=0;i<n;i++)if(!vis[i]) 148 { 149 ly.e=ps[i]; 150 tmxcross=(lx*ly)/lx.lenth()/ly.lenth(); 151 if(tmxcross>mxcross ||(fabs(tmxcross-mxcross)<eps && getdis(ly.s,ly.e)<midis)) 152 mxcross=tmxcross,midis=getdis(ly.s,ly.e),ch=i; 153 } 154 tb[++num]=ps[ch],vis[ch]=1; 155 lx.s=tb[num-1],lx.e=tb[num],ly.s=tb[num]; 156 } 157 } 158 159 map<Point,int>mp; 160 Point ps[Max],tb[Max]; 161 int main(void) 162 { 163 int t;cin>>t; 164 while(t--) 165 { 166 mp.clear(); 167 int n,ans;cin>>n; 168 for(int i=0,id,x,y;i<n;i++) 169 scanf("%d%d%d",&id,&x,&y),ps[i]=Point(x,y),mp[ps[i]]=id; 170 ConvexClosure(ps,tb,n,ans); 171 printf("%d ",ans); 172 for(int i=0;i<ans;i++) 173 printf("%d%c",mp[tb[i]],i==ans-1?'\n':' '); 174 } 175 return 0; 176 }
作者:weeping
出处:www.cnblogs.com/weeping/
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号