深度之眼(三)——矩阵的行列式
文章目录
一、行列式的定义
1.1 二阶行列式

二阶行列式:主对角线相乘 - 副对角线相乘
1.2 三阶行列式

暂时不管怎么算的
D2的话就是吧第二列换成b1、b2、b3,D3就是把第三列换成换成b1、b2、b3,
二、行列式的计算
2.1 全排列和逆序列

2.2 计算定义

首先看是n*n的矩阵有n的全排列,正负号由逆序数决定,逆序数为奇数,则为负,逆序数为偶数,则为正,依次可推广
三、特殊矩阵的行列式与行列式的性质
3.1 特殊矩阵的行列式
根据这个,观察某一项,可知,都是从第一行中取出一个乘以第二行中取出与第一行的不同列,依次类推,形成求和项。
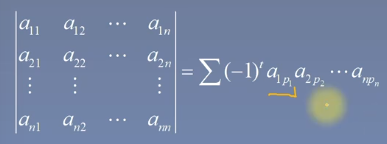
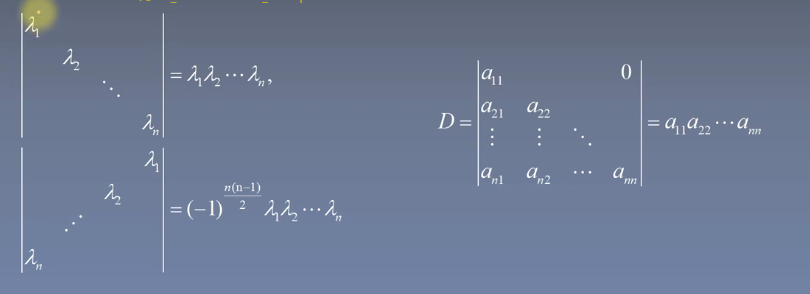
所以,针对第一幅图(主对角矩阵),虽然有n的全排列,但是既满足不会有0的一项(因为有0的话,这个项就是0了),又要满足不同列,所以只有主对角线相乘,正负号由于是正常排序,所以逆序数为0,所以为正号
第二幅图(负对角矩阵)(第一幅图的下面那张)只有符号问题,进行计算即可
第三张图,下三角矩阵
第一行只会取第一列(因为其他列都是0,乘起来为0,无影响),第二行就只会取第二列了,以此类推,还是和第一张图一样
3.2 行列式的性质



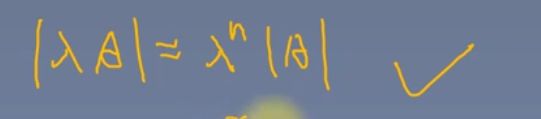
这个的话,自己推一遍,主要理解本质,这些性质只是对本质进行提炼归纳,不要死记
四、行列式按行(列)展开,代数余子式
降阶处理,用低阶的行列式来计算高阶的行列式


就是利用在特殊矩阵那得想法,某一行或者某一列只有一个不为0,则则对于那行而言只有那列有效,而那一列根据其余行不同的原则,所以不用看,因此得到上述结论
定理3
推论
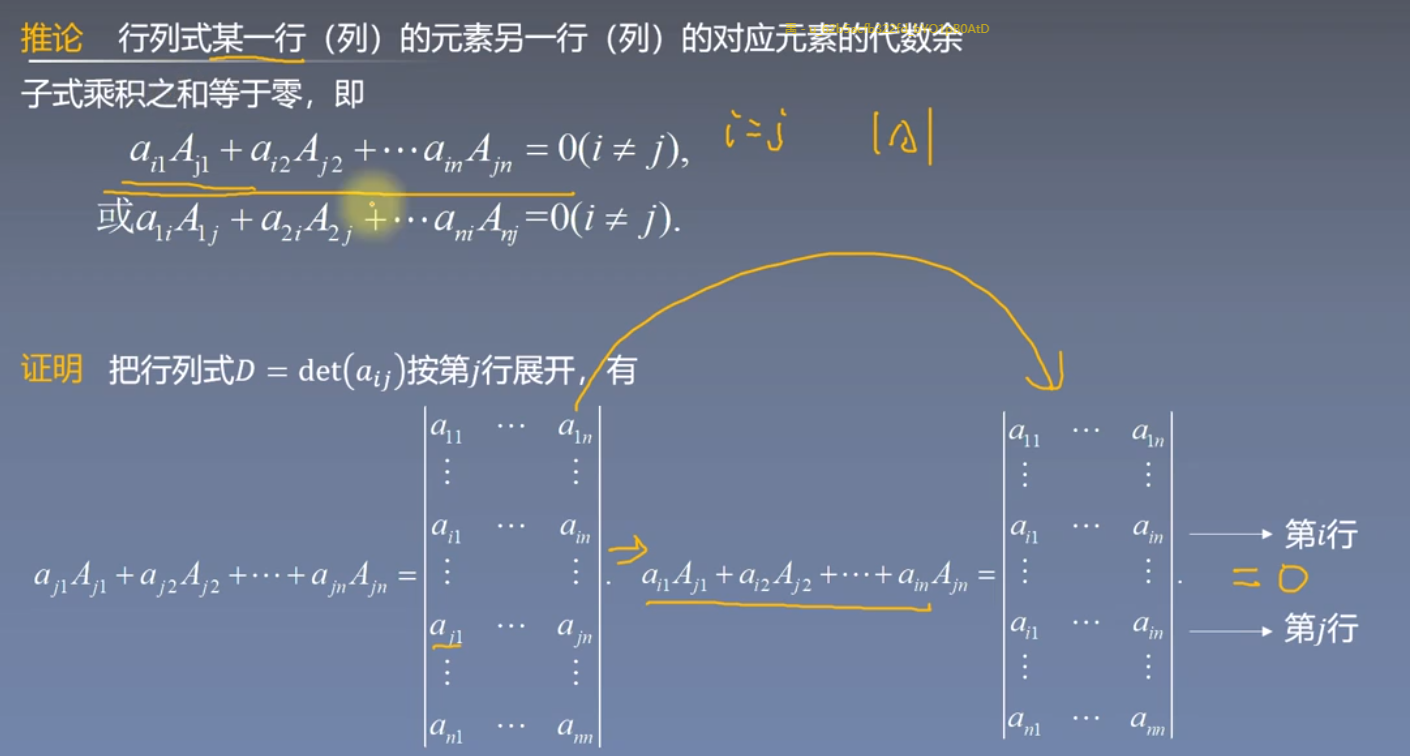
五、行列式在线性方程组中的应用:克莱姆法则
克莱姆法则(理想化):未知数与方程组数相同,且方程的系数行列式不等于0,则方程有唯一解

Dj把对应列去掉,换成b的常数列

左边非齐次,右边齐次



