数字图像处理——图像变换（二维离散傅里叶正逆变换fft2/fft2、离散余弦正逆变换dct2/idct2、频谱正逆平移fftshift/ifftshift、幅度谱与相位谱）| 例题与分析
文章目录
零、前言
不想看的，可以跳过哈~~~
首先，我们为什么要学习傅里叶正逆变换、余弦正逆变换、频谱正逆平移
首先，根据章节情况，我们知道，傅里叶和余弦都是对图像的一种变换方式，而图像处理中所用的变换都是酉变换，即变换核满足正交条件的变换。经过酉变换后的图像往往更有利于特征抽取、增强、压缩和图像编码。
上面是百度解释，根据解释，可以说明，图像的变换是为了后续特征抽取、增强、压缩和图像编码，这下我们就明白了，图像的变换，是为了后面处理做的铺垫,也是为了更快做图像分析处理
下面一个问题，图像变换为什么学习傅里叶变换和余弦变换，首先，emmmm,它是简单的，虽然它也很难，但是其他的变换更难，所以现在只有学这两个变换，其次，傅里叶变换为什么可以被用到图像变换里面
看看下面这些，连接附上
通俗讲解：图像傅里叶变换
哈哈哈，下面就回归正题
一、二维离散的傅里叶正逆变化(fft2/ifft2)、频谱平移(fftshift)
直接上代码
第一行就是读取图像
第二行就是图像数据进行预处理也就是进行归一化（如果不归一化，那么在傅里叶逆变换时就需要加上uint8才能恢复至原图像）
第三行就是二维离散傅里叶变换
第四行就是首先abs取绝对值，实际上就是找个表示频谱图的量，
至于uint8
官方给出的解释是这样
打开abs处理后的数据是这样的
所以这里给出的想法是，uint8是对数据进行四舍五入到整型，另一个作用是，当超出范围时归并到255，起到限制作用
第五行就是显示频谱图的
第六行有注释，就是频谱平移，将低频移至中间
第七行就是abs+uint8进行图像显示
第八行就是傅里叶逆变换
最后就是还原成原图像
f1 = imread ('pout.tif');
f=im2double(f1);
F=fft2(f);
S=uint8(abs(F));
imshow(S);
S1=fftshift(F); %频谱平移，将直流分量移到频谱中心
figure;imshow(uint8(abs(S1)));
f11=ifft2(F);
figure;imshow(f11);
二、幅度谱与相位谱和有无im2double处理的显示区别
看下面的图吧
clc,clear
close all
f = imread ('pout.tif');
f_y = im2double(f);
f_n = fft2(f); % 未im2double的傅里叶变换
f_y = fft2(f_y); % 经过im2double的傅里叶变换
RR_y = real(f_y); %实部
II_y = imag(f_y); %虚部
RR_n = real(f_n);
II_n = imag(f_n);
A_y = sqrt(RR_y.^2+II_y.^2); % 求取距离（频谱）
B_y = angle(f_y); % 求取相位
C_y = abs(f_y); % 求取距离
A_n = sqrt(RR_n.^2+II_n.^2);
B_n = angle(f_n);
C_n = abs(f_n);
S_y = fftshift(f_y); %频谱平移
S_n = fftshift(f_n);
% 有im2double
figure
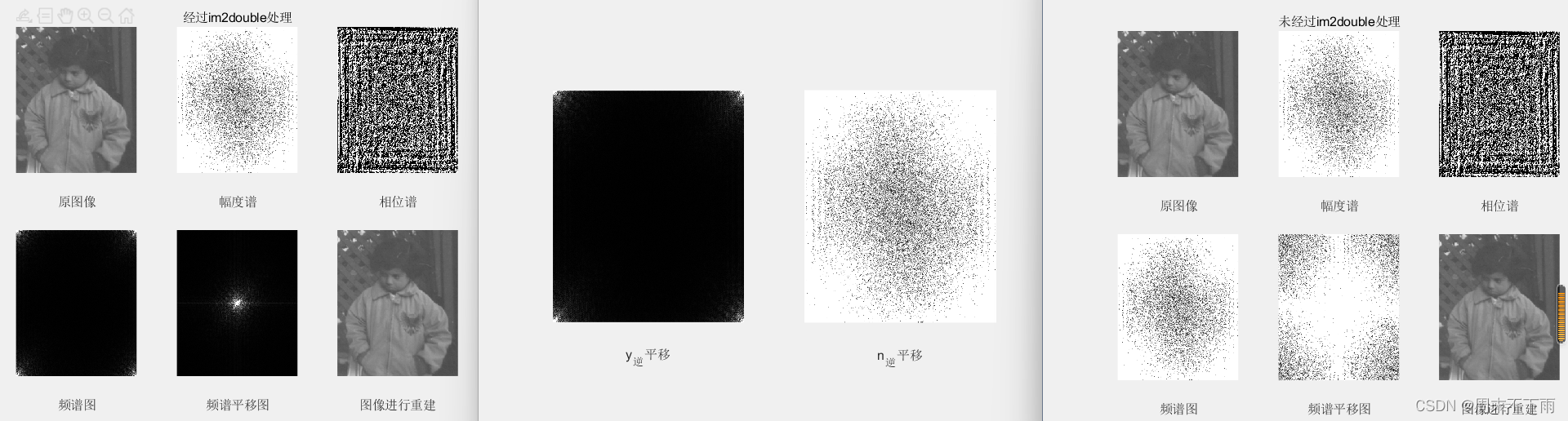
subplot(2,3,1);imshow(f);xlabel('原图像')
subplot(2,3,2);imshow(A_y);xlabel('幅度谱');title('经过im2double处理')
subplot(2,3,3);imshow(B_y);xlabel('相位谱')
subplot(2,3,4);imshow(uint8(A_y));xlabel('频谱图')
subplot(2,3,5);imshow(uint8(abs(S_y)));xlabel('频谱平移图')
subplot(2,3,6);imshow(ifft2(f_y));xlabel('图像进行重建')
% 没有im2double
figure
subplot(2,3,1);imshow(f);xlabel('原图像')
subplot(2,3,2);imshow(uint8(C_n));xlabel('幅度谱');title('未经过im2double处理')
subplot(2,3,3);imshow(B_n);xlabel('相位谱')
subplot(2,3,4);imshow(uint8(abs(A_n)));xlabel('频谱图')
subplot(2,3,5);imshow(uint8(abs(S_n)));xlabel('频谱平移图')
subplot(2,3,6);imshow(uint8(ifft2(f_n)));xlabel('图像进行重建')
三、频谱的逆平移(ifftshift)
I_y = ifftshift(S_y);
I_n = ifftshift(S_n);
figure
subplot(1,2,1);imshow(uint8(abs(I_y)));xlabel('y_逆平移')
subplot(1,2,2);imshow(uint8(abs(I_n)));xlabel('n_逆平移')
四、离散余弦正逆变换dct2/idct2
f = imread ('pout.tif');
f1 = im2double(f);
f_dct = dct2(f1);
f_idct = idct2(f_dct);
Z = zeros(291,240);
Z(1:33,1:33) = 1; %做了改变参数，只选取左上33*33的矩阵作为信息量
f_dct_d = Z.*f_dct;
f_idct_d = idct2(f_dct_d);
figure
subplot(2,2,1);imshow(f);xlabel('原图像')
subplot(2,2,2);imshow(abs(f_dct));xlabel('频谱图')
subplot(2,2,3);imshow(f_idct);xlabel('直接重建图像')
subplot(2,2,4);imshow(f_idct_d);xlabel('改变系数后重建图像')
分析
对于流程，其实是和傅里叶一样的，关键在于低频区域
通过傅里叶变换的频谱图，低频分布在四个角上，而通过余弦变换的，直接就集中在左上角
我做了部分信息获取，也就是33*33，可以看出，逆变换后的图，虽然模糊，但是大部分的信息量已经提取出来了
