树上前缀和&树上差分
学习本文需要提前掌握前缀和、差分和 LCA。
简介
树上前缀和,简单来说就是把前缀和思想运用到树上。可以通过前缀和 \(O(n+m)\) 求解所有点到某一点的距离(边权和)或权值和(点权和),一般这个点是根,\(O(1)\) 求解某两个点之间的树上路径的距离或权值和。
树上差分,同样,简单来说就是把差分运用到树上。可以通过差分 \(O(1)\) 维护在树上修改点权或边权的操作,求所有点权或边权的时间复杂度约为 \(O(n+m)\)。
思想
树上前缀和
比较简单,也是很常用的求树上两点间路径的方法。
设 \(x\),\(y\) 为所求的两个点,假设根为 \(rt\),设 \(len_{i,j}\) 表示点 \(i\longrightarrow j\) 的路径长度,设 \(val_{i,j}\) 表示点 \(i\longrightarrow j\) 的路径点权和。
- 对于点 \(x\longrightarrow y\) 的路径长度 \(len_{x,y}\),可求得
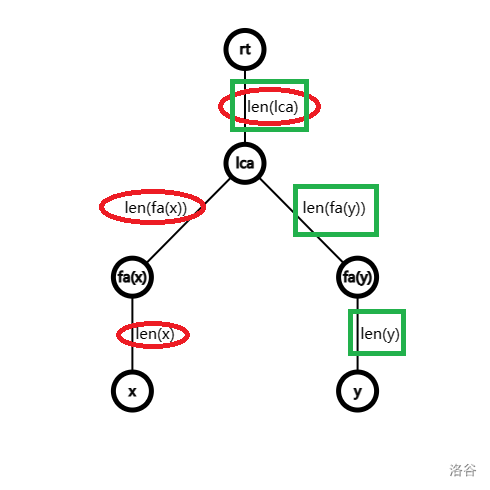
可以看图理解一下,其中红色标记表示 \(len_{rt,x}\) 包含的边,绿色标记表示 \(len_{rt,y}\) 包含的边。
式子可以结合图理解一下:
设 \(len_i\) 表示从根节点向下遍历时以 \(i\) 为终点的边,则有
因此就有
- 对于点 \(x\longrightarrow y\) 的点权和 \(val_{x,y}\),可求得
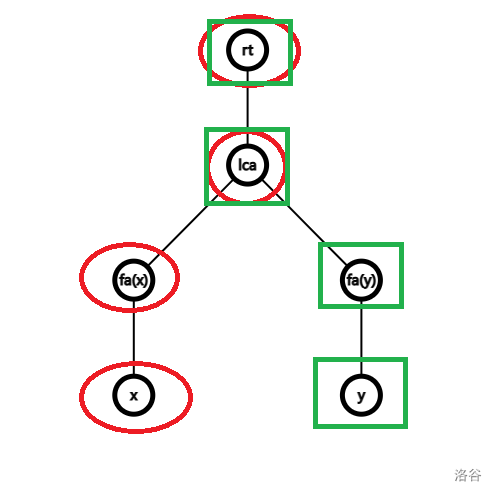
同样可以看图理解一下,其中红色标记表示 \(val_{rt,x}\) 包含的点,绿色标记表示 \(val_{rt,y}\) 包含的点。
式子也可以结合图理解一下:
设 \(val_i\) 表示 \(i\) 的点权,则有
因此就有
时间复杂度分析:
处理前缀和时会遍历所有的点和边,时间复杂度为 \(O(n+m)\),每次查询时间复杂度为 \(O(1)\)。因此,树上前缀和适用于静态的查询问题,如果修改其中的某个值,会需要重新进行前缀和的处理,这和普通前缀和类似。
树上差分
树上差分同样也被分为点差分和边差分。
点差分
相当于对修改点权的操作进行差分,一般点权就是当前点的询问次
数。
我们设 \(d_i\) 表示点 \(i\) 记录询问次数的差分数组,设询问次数为 \(t_i=0\),刚开始时 \(d_i=t_i=0\)。
普通的差分要保证对于 \(t_i=\sum_{j=1}^id_i\),对于树上差分,则要保证 \(t_i=\sum_{son \in i}d_{son}\),这个式子就是说:当前点的询问次数 \(t_i\) 是它所有儿子的差分数组 \(d_i\) 之和(自己也是自己的儿子)。如何保证这个条件呢?我们用图举例一下。
同样还是用刚才的图:
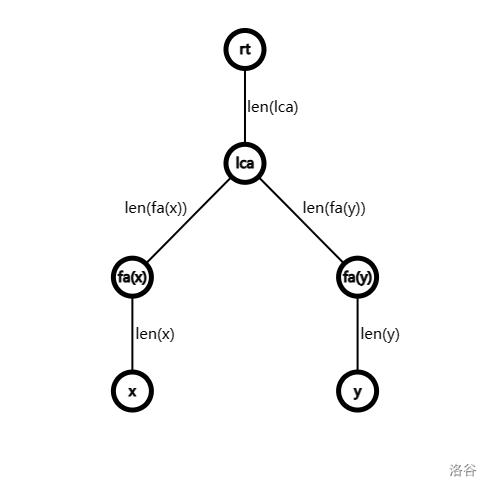
初始状态为:
| 点编号 | \(d_i\) | 询问次数 |
|---|---|---|
| \(x\) | \(0\) | \(0\) |
| \(fa_x\) | \(0\) | \(0\) |
| \(y\) | \(0\) | \(0\) |
| \(fa_y\) | \(0\) | \(0\) |
| \(lca\) | \(0\) | \(0\) |
| \(rt\) | \(0\) | \(0\) |
当我们访问了路径 \(x\longrightarrow y\) 上的所有点时,不难猜到先改变边界的差分数组,即 \(d_x+1,d_y+1\)。但是我们发现,如果只是这样的话,通过上面的式子求解会得到以下结果。
| 点编号 | \(d_i\) | \(t_i\) |
|---|---|---|
| \(x\) | \(1\) | \(1\) |
| \(fa_x\) | \(0\) | \(1\) |
| \(y\) | \(1\) | \(1\) |
| \(fa_y\) | \(0\) | \(1\) |
| \(lca\) | \(0\) | \(2\) |
| \(rt\) | \(0\) | \(2\) |
本来不属于路径上的 \(rt\) 变成了 \(2\),\(lca\) 会多算一次。这是因为在修改 \(x\) 和 \(y\) 后,我们并没有限制差分后的值在 \(fa_{lca}\) 处停止,同时 \(x\) 和 \(y\) 都会经过 \(lca\) 处,造成贡献算重。
因此我们考虑在 \(lca\) 和 \(fa_{lca}\) 处做一下限制,令 \(d_{lca}-1,d_{fa_{lca}}-1\),最后求解出来的结果就是这样的。
| 点编号 | \(d_i\) | \(t_i\) |
|---|---|---|
| \(x\) | \(1\) | \(1\) |
| \(fa_x\) | \(0\) | \(1\) |
| \(y\) | \(1\) | \(1\) |
| \(fa_y\) | \(0\) | \(1\) |
| \(lca\) | \(-1\) | \(1\) |
| \(rt\) | \(-1\) | \(0\) |
而对于查询,我们只需要每次从最深的节点向上记录贡献,直到根节点为止。
这就点差分的所有操作。
总结一下:
- 对于修改点 \(x\longrightarrow y\) 路径上所有点的点权,就令
- 对于查询操作,从下往上依次遍历所有点,记录 \(\sum d_i\) 即可。
边差分
将点权改变边权,与点权类似。
修改点 \(x\) 和 \(y\) 上的路径 \(x\longrightarrow y\) 的所有边的边权。
这个要不你先推推?经过前面的磨练,相信这个你一定能推出来。

没错,设 \(d_i\) 表示差分数组,其中 \(i\) 表示从根到 \(i\) 的路径上终点为 \(i\) 的边。
答案就是
这里就不具体推了,手玩玩就能推出来。
时间复杂度分析:
修改路径点权时间复杂度为 \(O(1)\),完成所有修改后处理答案需要遍历所有的点和边,时间复杂度为 \(O(n+m)\)。
例题
点差分模板题
一句话题意:给定一颗树和很多条路径,求被遍历最多次的点。
标准的点差分模板题,有了结论就非常简单,这里用倍增实现。
代码
#include<iostream>
using namespace std;
const int N=5e4+10,M=N<<1;
int n,m,res;
int h[N],e[M],ne[M],idx;
int dep[N],fa[N][20],lg[N],d[N];
void add(int a,int b)
{
e[++idx]=b,ne[idx]=h[a],h[a]=idx;
}
void init()//初始化 lg 数组
{
for(int i=1;i<=n;i++)lg[i]=lg[i-1]+(1<<lg[i-1]==i);
}
void dfs(int u,int father)//处理倍增数组fa和深度dep
{
fa[u][0]=father,dep[u]=dep[father]+1;
for(int i=1;i<=lg[dep[u]];i++)
fa[u][i]=fa[fa[u][i-1]][i-1];
for(int i=h[u];i;i=ne[i])
{
int j=e[i];
if(j==father)continue;
dfs(j,u);
}
}
int lca(int x,int y)//倍增求lca
{
if(dep[x]<dep[y])swap(x,y);
while(dep[x]>dep[y])x=fa[x][lg[dep[x]-dep[y]]-1];
if(x==y)return x;
for(int i=lg[dep[x]]-1;i>=0;i--)
if(fa[x][i]!=fa[y][i])
{
x=fa[x][i];
y=fa[y][i];
}
return fa[x][0];
}
void dfs(int u)
{
for(int i=h[u];i;i=ne[i])
{
int j=e[i];
if(j==fa[u][0])continue;
dfs(j);
d[u]+=d[j];//自底向上求解差分数组
}
res=max(res,d[u]);//取最大值
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<n;i++)
{
int a,b;
cin>>a>>b;
add(a,b),add(b,a);
}
init();
dfs(1,0);
while(m--)
{
int a,b;
cin>>a>>b;
int father=lca(a,b);
d[a]++,d[b]++,d[father]--,d[fa[father][0]]--;
}//根据推出的公式进行树上差分
dfs(1);
cout<<res;
return 0;
}
边差分模板题
题意:给定一棵树,每条边有两种边权 \(c_{i1},c_{i2}\),花费 \(c_{i1}\) 只能走一次当前边,花费 \(c_{i2}\) 可以走无限次当前边。
求 \(\min{\sum_{i=1}^{n-1}dist_{i,i+1}}\),即每个 \(i\) 到 \(i+1\) 的路径的距离和的最小值。
简单的边差分问题,每次将选定的两个点之间的边进行差分,最后统计一下差分结果。直接根据公式写即可,注意在统计答案时要用 long long。
下面给出树剖和倍增两种类型的代码,主要在求 lca 和 统计差分的最终结果时不同。
树剖
代码
#include<iostream>
using namespace std;
const int N=2e5+10,M=N<<1;
typedef long long ll;
int n,t1[N],t2[N],d[N];
int h[N],e[M],w1[M],w2[M],ne[M],idx;
void add(int a,int b,int c,int d)
{
e[++idx]=b,w1[idx]=c,w2[idx]=d,ne[idx]=h[a],h[a]=idx;
}
int s[N],fa[N],dep[N],top[N],son[N],rw[N],cnt;
void dfs(int u,int father,int depth)
{
s[u]=1,fa[u]=father,dep[u]=depth,rw[++cnt]=u;
for(int i=h[u];i;i=ne[i])
{
int j=e[i];
if(j==father)continue;
t1[j]=w1[i],t2[j]=w2[i];
dfs(j,u,depth+1);
s[u]+=s[j];
if(s[son[u]]<s[j])son[u]=j;
}
}
void dfs(int u,int t)
{
top[u]=t;
if(!son[u])return;
dfs(son[u],t);
for(int i=h[u];i;i=ne[i])
{
int j=e[i];
if(j==fa[u]||j==son[u])continue;
dfs(j,j);
}
}
int LCA(int x,int y)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])swap(x,y);
x=fa[top[x]];
}
if(dep[x]>dep[y])swap(x,y);
return x;
}
int read()
{
int x=0;
char ch=getchar();
while(!isdigit(ch))ch=getchar();
while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
return x;
}
int main()
{
n=read();
for(int i=1;i<n;i++)
{
int a=read(),b=read(),c=read(),d=read();
add(a,b,c,d),add(b,a,c,d);
}
dfs(1,0,0);
dfs(1,1);
for(int i=1;i<n;i++)d[i]++,d[i+1]++,d[LCA(i,i+1)]-=2;
for(int i=n;i;i--)d[fa[rw[i]]]+=d[rw[i]];
ll res=0;
for(int i=2;i<=n;i++)res+=min((ll)t1[i]*d[i],(ll)t2[i]);
cout<<res;
return 0;
}
倍增
代码
#include<iostream>
using namespace std;
typedef long long ll;
const int N=2e5+10,M=N<<1,P=18;
int n,t1[N],t2[N];
ll d[N];
int h[N],e[M],ne[M],w1[M],w2[M],idx;
void add(int a,int b,int c,int d)
{
e[++idx]=b,w1[idx]=c,w2[idx]=d,ne[idx]=h[a],h[a]=idx;
}
int fa[N][P],lg[N],dep[N];
void init()
{
for(int i=1;i<=n;i++)lg[i]=lg[i-1]+(1<<lg[i-1]==i);
}
void dfs(int u,int father)
{
fa[u][0]=father,dep[u]=dep[father]+1;
for(int i=1;i<=lg[dep[u]];i++)
fa[u][i]=fa[fa[u][i-1]][i-1];
for(int i=h[u];i;i=ne[i])
{
int j=e[i];
if(j==father)continue;
t1[j]=w1[i],t2[j]=w2[i];
dfs(j,u);
}
}
int LCA(int x,int y)
{
if(dep[x]<dep[y])swap(x,y);
while(dep[x]>dep[y])x=fa[x][lg[dep[x]-dep[y]]-1];
if(x==y)return x;
for(int i=lg[dep[x]]-1;i>=0;i--)
if(fa[x][i]!=fa[y][i])
x=fa[x][i],y=fa[y][i];
return fa[x][0];
}
void dfs(int u)
{
for(int i=h[u];i;i=ne[i])
{
int j=e[i];
if(j==fa[u][0])continue;
dfs(j);
d[u]+=d[j];
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;
init();
for(int i=1,a,b,c,d;i<n;i++)
{
cin>>a>>b>>c>>d;
add(a,b,c,d),add(b,a,c,d);
}
dfs(1,0);
for(int i=2;i<=n;i++)d[i-1]++,d[i]++,d[LCA(i,i-1)]-=2;
dfs(1);
ll res=0;
for(int i=2;i<=n;i++)res+=min(d[i]*t1[i],(ll)t2[i]);
cout<<res;
return 0;
}
没想到去掉快读后无论是空间,码量还是时间树剖都碾压倍增。
下面再来一道真题
P2680 [NOIP2015 提高组] 运输计划
题意:给定一棵树和 \(m\) 条路线,你可以令树中一条边的边权变为 \(0\),要让改变后所有路径的最大值最小,求这个最小的最大值。
题目要求求最大值最小,这是二分很明显的特点,因此可以考虑二分解决本题,每次二分判断当前是否有解。
首先我们先找找性质。
我们发现,对于所有路线,我们要改变的边权一定是在最大路线上的。这也很好证明,假设我们要改变的边权不在最大路线上,那么我们无论怎么修改边权都不会让答案更优,因此答案一定是在最大路线上的。
此外,如果在最大边权上贪心做是错误的。一般贪心有两种想法:
- 第一种是贪最大的边,很容易举到反例:一棵树,有两条有重复边的路线都是最长的,但是重复边的边权很小,此时我们选定这条边的答案一定是最优的,只是贪心的选择最大的边不会不会令答案更优。
- 第二种是贪经过次数最多的边,也可以举一个反例:一棵树,只有一条极长的最长路线,但是最长路线上有一条边权很小的边多次被其他较短路线经过,贪心的选择这条边,不如选定这条最长路线上最大的边更优。
考虑如何判断是否有解。看时间复杂度应该需要每次 \(O(n)\) 判断有无解情况。
因此我们可以考虑使用树上差分,一来它擅长处理树上路径的问题,二来它的时间复杂度是正确的。
我们可以先预处理出来所有 lca 和树上前缀和,这个我们用树剖实现。每次二分最大路线长度,每次对于所有大于当前最大路线长度的路线进行树上差分统计经过次数,每次自底向上更新差分数组,如果找到其中一条从树根到当前点的边的边权大于原来最长路线 \(-\) 当前二分的最大路线长度并且所有大于当前二分值的路线都经过当前边,说明就找到一组解。
细节还是比较多的,看看代码也许可以更好的理解。
代码
#include<iostream>
#include<cstring>
using namespace std;
const int N=3e5+10,M=N<<1;
int n,m,u[N],v[N],d[N],p[N],lca[N],l,r;
int h[N],e[M],ne[M],w[M],idx,edge[N];
void add(int a,int b,int c)
{
e[++idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx;
}
int dep[N],fa[N],top[N],rw[N],s[N],son[N],dist[N],cnt;
void dfs(int u,int father,int depth)
{
s[u]=1,dep[u]=depth,fa[u]=father,rw[++cnt]=u;
for(int i=h[u];i;i=ne[i])
{
int j=e[i];
if(j==fa[u])continue;
edge[j]=w[i];
dist[j]=dist[u]+w[i];
dfs(j,u,depth+1);
s[u]+=s[j];
if(s[son[u]]<s[j])son[u]=j;
}
}
void dfs(int u,int t)
{
top[u]=t;
if(!son[u])return;
dfs(son[u],t);
for(int i=h[u];i;i=ne[i])
{
int j=e[i];
if(j==fa[u]||j==son[u])continue;
dfs(j,j);
}
}
int LCA(int x,int y)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])swap(x,y);
x=fa[top[x]];
}
if(dep[x]>dep[y])swap(x,y);
return x;
}
bool check(int x)
{
int sum=0;
memset(p,0,sizeof p);//清空差分数组
for(int i=1;i<=m;i++)
if(d[i]>x)//对于所有大于x的路径
{
p[u[i]]++,p[v[i]]++,p[lca[i]]-=2;//统计所有边的遍历次数
sum++;//统计路径个数
}
for(int i=n;i;i--)//自底向上更新差分数组求解
{
p[fa[rw[i]]]+=p[rw[i]];//借用dfs序,很精妙
if(edge[rw[i]]>=r-x&&p[rw[i]]==sum)return 1;
}//当前边的边权大小符合二分的要求并且所有不合法的路径都包含当前边
return 0;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<n;i++)
{
int a,b,c;
cin>>a>>b>>c;
add(a,b,c),add(b,a,c);
l=max(l,c);//记录最大边权
}
dfs(1,0,1);//第一次预处理深度dep,父亲fa,子树大小s,dfs序rw,从树根到以i为节点为终点的边edge,到根的距离dist,重儿子son
dfs(1,1);//处理树链链顶top
for(int i=1;i<=m;i++)
{
cin>>u[i]>>v[i];
lca[i]=LCA(u[i],v[i]);//预处理所有路线上的lca
d[i]=dist[u[i]]+dist[v[i]]-2*dist[lca[i]];//用树上前缀和求所有路线长度
r=max(r,d[i]);//找一个最长路线作为二分的边界
}
int ll=r-l,rr=r,ans;
while(ll<=rr)//注意这里不能直接用r,因为会修改check函数中的r
{
int mid=ll+rr>>1;
if(check(mid))rr=mid-1,ans=mid;
else ll=mid+1;
}
cout<<ans<<"\n";
return 0;
}
如果还有问题或者哪里没有讲明白可以联系我。
本文可能略有疏漏,各位大佬请多指教,蒟蒻在此感激不尽。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号