表达式求值
好一阵子木有学习数据结构相关的东东,大脑得生锈啦~~赶紧再来练练大脑,这次学习一下如何用二叉树和栈来实现表达式的求值,这里只以简单的四则运算表达式来实现。
思考:对于表达式如何在电脑中进行表式,其优先级怎么解决?
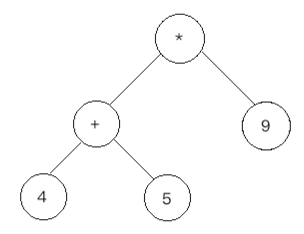
在正式篇码之前,先思考一下,对于这样一个表达式"(4 + 5) * 9",在计算机中如何来表达它呢?其实可以用一颗二叉树来表达,将其数字做为树的叶子结点,而运算符做为树的父结点,表示如下:
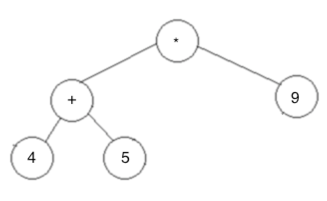
貌似中序遍历刚好可以表达:4、+、5、*、9,但是!!!如何表达(4+5)的这个先算的优先级呢?貌似做不到。
其实可以采用后序遍历来解决,先看下后序遍历的结果:4、5、+、9、*,对于这个结果可能不一定能想到求解,但是,肉眼可以看出貌似是先算4、5,然后再算9,可以体现一个顺序,事实上确实是可以通过后序遍历的序列来达到表达式求解的目的,下面编码走起~
实现第一步:表达式解析
首先搭建框架,还是跟上一次的方式一样定义一个二叉树数据结构,不过这里直接采用系统的stack来编写(因为会用到size()方法,这个咱们自己手动写的是木有实现滴,偷个懒~):

首先来实现如何将表达式解析成一个二叉树结构,先直接上代码,之后再debug一下:
#include <iostream> #include <stack> //用来表示二叉树 struct treenode{ char data;//由于表达式中有数字字每,所以这里用一个字节来表达 treenode* left;//左结点 treenode* right;//右结点 treenode(int value):data(value), left(nullptr), right(nullptr){} }; class BET { treenode* root; public: BET() : root(nullptr) {} //解析表达式为树形结构 void parse(const char exp[]) { const char* p = exp; std::stack<treenode*> s; while(*p != '\0') { if(*p >= '0' && *p <= '9') { s.push(new treenode(*p)); } else { treenode* new_node = new treenode(*p); new_node->right = s.top(); s.pop(); new_node->left = s.top(); s.pop(); s.push(new_node); } p++; } if(s.size() != 1) { std::cout << "Illegal Expression:"; root = nullptr; } else { root = s.top(); } } //求值 int evaluate() { //TODO return 0; } }; int main(void) { return 0; }
下面debug看一下实现的思路:

①、 ,声明一个存放树结点的栈,之后在解析表达式的时候会用到它。
,声明一个存放树结点的栈,之后在解析表达式的时候会用到它。
②、循环遍历整个表达式,然后生成一个之前我们说的叶子结点是数字,而父接点是运算符这样结构的二叉树,这里还是以"(4 + 5) * 9"这样的表达式来进行分析,由于是采用后序遍历的方式进行解析,所以其解析字符串为"45+9*",其解析结果应该是这样:

下面开始拆解其解析过程:
Loop1:判断当前要解析的字符是否不是结束符,当前字符为"4",条件为真,执行循环体:
a、判断当前字符是不是数字字符,条件为真,执行条件体,将4生成一个新结点压入到栈s中,如下:
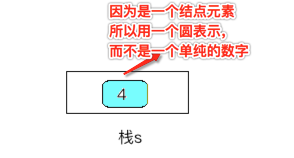
c、p++,这里p指向字符"5"
Loop2:判断当前要解析的字符是否不是结束符,当前字符为"5",条件为真,执行循环体:
a、判断当前字符是不是数字字符,条件为真,执行条件体,将5生成一个新结点压入到栈s中,如下:
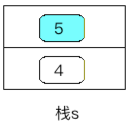
c、p++,这里p指向字符"+"
Loop3:判断当前要解析的字符是否不是结束符,当前字符为"+",条件为真,执行循环体:
a、判断当前字符是不是数字字符,条件为假,执行b。
b、碰到了运算符结点,则需要将栈中的数字进行连接成二叉树结构,看下具体连接过程:
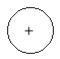
ba、 ,新建一个结点,结点内容为"+",如下:
,新建一个结点,结点内容为"+",如下:
bb、 ,将栈顶的元素【5】取出做为当前新结点的右结点,所以此时的结构为:
,将栈顶的元素【5】取出做为当前新结点的右结点,所以此时的结构为:

并将栈顶的元素从栈中弹出,所以此时栈s的内容为:

bc、 ,继续取出栈顶的元素【4】做为当前新结点的左结点,所以此时的结构为:
,继续取出栈顶的元素【4】做为当前新结点的左结点,所以此时的结构为:
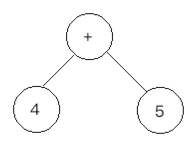
并将栈顶的元素从栈中弹出,所以此时栈s的内容就为空了。
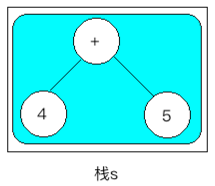
bd、 ,此时再将新生成的结点压入到栈s中,但是注意:此时的结点就已经是按我们要求生成的一个二叉树了,如下:
,此时再将新生成的结点压入到栈s中,但是注意:此时的结点就已经是按我们要求生成的一个二叉树了,如下:
c、p++,这里p指向字符"9"
Loop4:判断当前要解析的字符是否不是结束符,当前字符为"9",条件为真,执行循环体:
a、判断当前字符是不是数字字符,条件为真,执行条件体,将9生成一个新结点压入到栈s中,如下:

c、p++,这里p指向字符"*"
Loop5:判断当前要解析的字符是否不是结束符,当前字符为"*",条件为真,执行循环体:
a、判断当前字符是不是数字字符,条件为假,执行b。
b、碰到了运算符结点,则需要将栈中的数字进行连接成二叉树结构,看下具体连接过程:
ba、 ,新建一个结点,结点内容为"*",如下:
,新建一个结点,结点内容为"*",如下:

bb、 ,将栈顶的元素【9】取出做为当前新结点的右结点,所以此时的结构为:
,将栈顶的元素【9】取出做为当前新结点的右结点,所以此时的结构为:
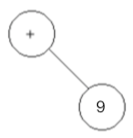
并将栈顶的元素从栈中弹出,所以此时栈s的内容为:
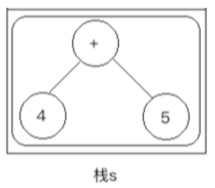
bc、 ,继续取出栈顶的元素【+】做为当前新结点的左结点,所以此时的结构为:
,继续取出栈顶的元素【+】做为当前新结点的左结点,所以此时的结构为:
如我们的预期,并将栈顶的元素从栈中弹出,所以此时栈s的内容就为空了。
bd、 ,此时再将新生成的结点压入到栈s中,但是注意:此时的结点就已经是按我们要求生成的一个二叉树了,如下:
,此时再将新生成的结点压入到栈s中,但是注意:此时的结点就已经是按我们要求生成的一个二叉树了,如下:
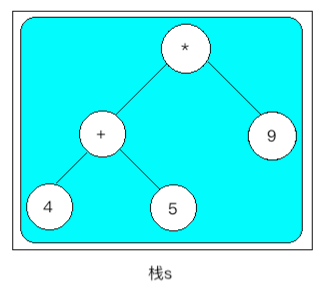
c、p++,这里p指向字符"\0"
Loop6:判断当前要解析的字符是否不是结束符,条件为假,退出循环并往下执行③。
③、给类的root变量赋值:
a、 ,如果表达式是正常的,肯定栈最终的元素只有一个,且里面是已经生成二叉树结构滴,所以如果栈大小不为1则表示表达式非法,给出非法提示,并将root变量置为空。由于此时条件不满足所以执行b。
,如果表达式是正常的,肯定栈最终的元素只有一个,且里面是已经生成二叉树结构滴,所以如果栈大小不为1则表示表达式非法,给出非法提示,并将root变量置为空。由于此时条件不满足所以执行b。
b、 ,直接将栈元素弹出并赋给root变量。
,直接将栈元素弹出并赋给root变量。
实现第二步:表达式计算
当将表达式解析成相应的二叉树之后,接下来就可以对它进行求解了,其具体实现如下:
#include <iostream> #include <stack> //用来表示二叉树 struct treenode{ char data;//由于表达式中有数字字每,所以这里用一个字节来表达 treenode* left;//左结点 treenode* right;//右结点 treenode(int value):data(value), left(nullptr), right(nullptr){} }; class BET { treenode* root; public: BET() : root(nullptr) {} //解析表达式为树形结构 void parse(const char exp[]) { const char* p = exp; std::stack<treenode*> s; while(*p != '\0') { if(*p >= '0' && *p <= '9') { s.push(new treenode(*p)); } else { treenode* new_node = new treenode(*p); new_node->right = s.top(); s.pop(); new_node->left = s.top(); s.pop(); s.push(new_node); } p++; } if(s.size() != 1) { std::cout << "Illegal Expression:"; root = nullptr; } else { root = s.top(); } } //求值 int evaluate() { if(root == nullptr) return std::numeric_limits<int>::max(); return evaluate(root); } private: int evaluate(treenode* node) { switch(node->data) { case '-': return evaluate(node->left) - evaluate(node->right); case '+': return evaluate(node->left) + evaluate(node->right); case '*': return evaluate(node->left) * evaluate(node->right); default: return node->data - '0'; } } };
先来写个用例来运行一下:
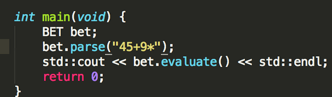
编译运行:
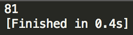
下面来debug看一下计算过程:
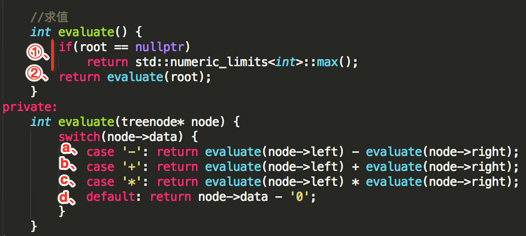
①、由于root为空,则返回一个int的最大值,条件不成立,向下执行②。
②、会调用私有的evaluate方法进行递归计算,将root传给它,目前的二叉树的结构为:
 ,其root= new node('*'),所以会执行c:
,其root= new node('*'),所以会执行c:
 ,return evaluate(new node('+')) * evaluate(new node('9'));
,return evaluate(new node('+')) * evaluate(new node('9'));
下面左右继续递归:
evaluate(new node('+'))会执行b:
 ,return evaluate(new node('4')) * evaluate(new node('5'));继续左右递归:
,return evaluate(new node('4')) * evaluate(new node('5'));继续左右递归:
evaluate(new node('4'));会执行d:
 ,return '4' - '0' = 4
,return '4' - '0' = 4
evaluate(new node('5'));会执行d:
 ,return '5' - '0' = 5
,return '5' - '0' = 5
所以这次的执行后的结果为:return 4 + 5 = 9
evaluate(new node('9'));会执行d:
 ,return '9' - '0' = 9
,return '9' - '0' = 9
所以最后的结果为:9 * 9 = 81



