遍历二叉树 - 基于栈的DFS
之前已经学过二叉树的DFS的遍历算法【http://www.cnblogs.com/webor2006/p/7244499.html】,当时是基于递归来实现的,这次利用栈不用递归也来实现DFS的遍历,这里先只学习如何用它进行二叉树的前序遍历,具体何为前序遍历这里不多解释,可以参考之前写的博客有详细的说明,下面开始实现。
实现一个栈:
为了能让栈里面可以放任何类型的数据,则使用C++的模板来实现,先新建一个stack头文件,以便在我们需要用的文件中只要引用头文件既可:
然后再新建一个Stack类,里面定义栈的几个经典方法: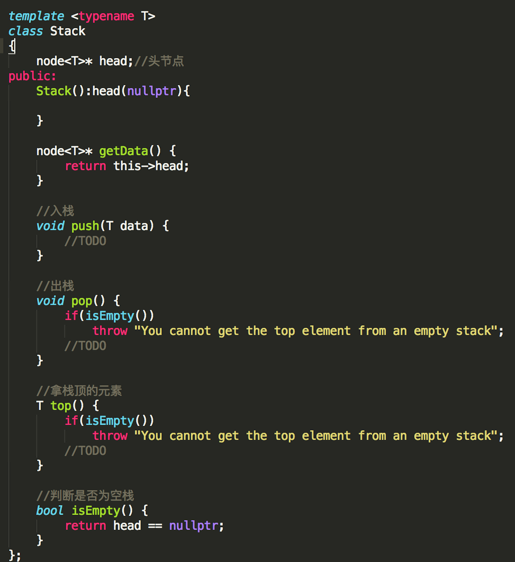
由于比较好理解,下面直接给出具体实现,不多解释:
/* * 利用模板来实现一个栈,可以往里面添加任意一个元素 */ template <typename T> struct node { T data; struct node* next; node(T data) {this->data = data;}; }; template <typename T> class Stack { node<T>* head;//头节点 public: Stack():head(nullptr){ } node<T>* getData() { return this->head; } //入栈 void push(T data) { node<T>* new_node = new node<T>(data); new_node->next = head; head = new_node; } //出栈 void pop() { if(isEmpty()) throw "You cannot get the top element from an empty stack"; node<T>* temp = head; head = temp->next; delete temp; } //拿栈顶的元素 T top() { if(isEmpty()) throw "You cannot get the top element from an empty stack"; return head->data; } //判断是否为空栈 bool isEmpty() { return head == nullptr; } };
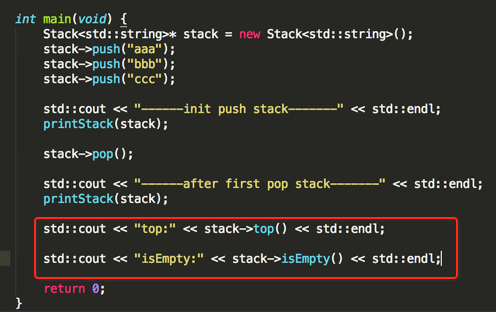
下面来使用一下咱们实现的Stack,如下:
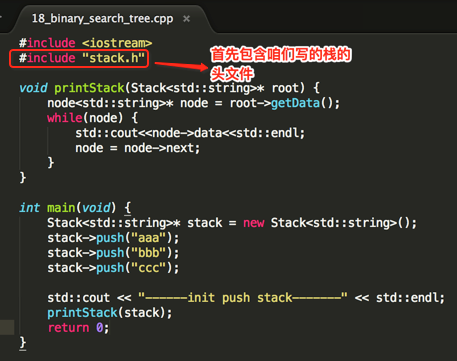
编译运行:

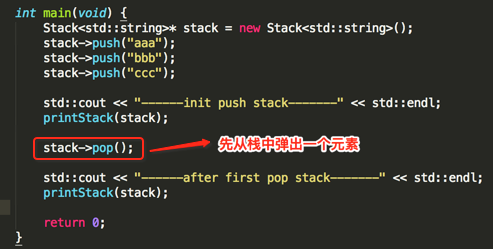
编译运行:
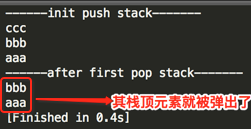
编译运行:
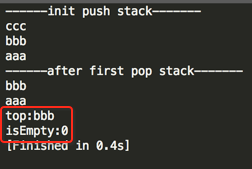
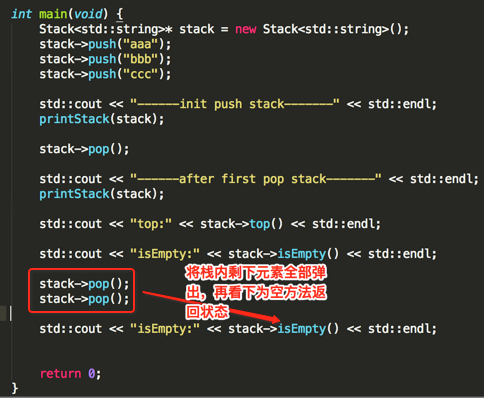
编译运行:

ok,一切如预期~
利用栈构建一个二叉树:
新建一个结构体用来构造二叉树:
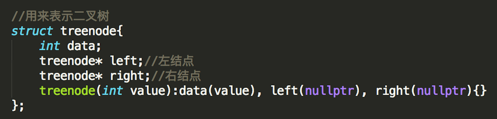
接着用它来构建一个二叉树,还是构建之前已经使用过的如下二叉树:

下面开始构建:

利用栈对二叉树进行前序遍历:
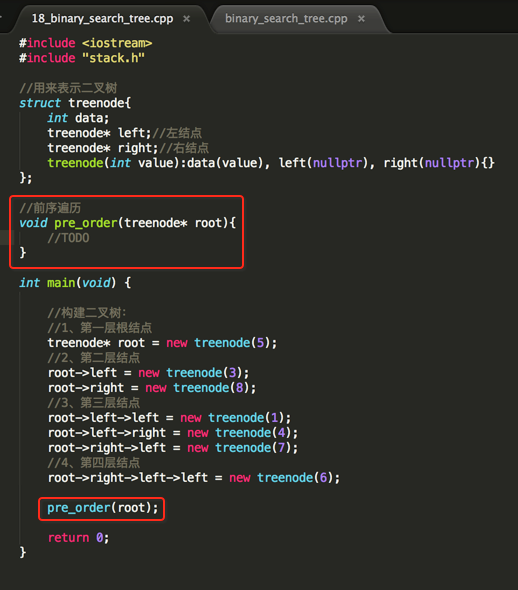
下面看下具体实现:
#include <iostream> #include "stack.h" //用来表示二叉树 struct treenode{ int data; treenode* left;//左结点 treenode* right;//右结点 treenode(int value):data(value), left(nullptr), right(nullptr){} }; //前序遍历 void pre_order(treenode* root){ Stack<treenode*> stack;//声明一个栈 treenode* current_node = root; while(current_node) { //1、首先打印当前结点,因为是前序遍历 std::cout << current_node->data << std::endl; //2、如果存在右结点则将其入栈暂存,待左结点输出完之后再去处理这些右结点 if(current_node->right) stack.push(current_node->right); //3、不断去处理左结点,直到左结点处理完了,则从栈中拿右点进行处理 if(current_node->left)//如果有左结点,则将它做为当前处理的结点不断输出 current_node = current_node->left; else { //这时左结点已经处理完了 if(stack.isEmpty())//如果缓存栈已经为空了则说明整个二叉树的遍历结束了 current_node = nullptr; else { //则取出栈顶的右结点进行处理,由于是后进先出,所以拿出来的永远是最新插入的右结点 current_node = stack.top(); stack.pop();//将其元素从栈顶弹出 } } } } int main(void) { //构建二叉树: //1、第一层根结点 treenode* root = new treenode(5); //2、第二层结点 root->left = new treenode(3); root->right = new treenode(8); //3、第三层结点 root->left->left = new treenode(1); root->left->right = new treenode(4); root->right->left = new treenode(7); //4、第四层结点 root->right->left->left = new treenode(6); pre_order(root); return 0; }
可见其遍历过程并未用到递归,编译运行:

Debug分析:

root = new treenode(5);
①、 ,新建一个栈,用来存放暂存的结点。
,新建一个栈,用来存放暂存的结点。
②、
③、开始进行循环遍历:
Loop1: current_node = new treenode(5);
a、打印当有结点【5】。
b、current_node->right = new treenode(8);条件为真,则将它添加入栈暂存。此是栈为:

c、current_node->left = new treenode(3);有左结点,条件为真,current_node = new treenode(3);
Loop2:current_node = new treenode(3);
a、打印当有结点【3】。
b、current_node->right = new treenode(4);条件为真,则将它添加入栈暂存。此是栈为:

c、current_node->left = new treenode(1);有左结点,条件为真,current_node = new treenode(1);
Loop3:current_node = new treenode(1);
a、打印当有结点【1】。
b、current_node->right = null;条件为假,继续c:
c、current_node->left = null;木有左结点,条件为假,执行d;
d、这时左结点已经处理完,则从栈中去处理右结点
①、当前栈不为空,条件不满足执行②。
②、取出栈顶的右结点进行处理:current_node = new treenode(4);并将这上结点从栈中弹出。
Loop4:current_node = new treenode(4);
a、打印当有结点【4】。
b、current_node->right = null;条件为假,继续c:
c、current_node->left = null;木有左结点,条件为假,执行d;
d、这时左结点已经处理完,则从栈中去处理右结点
①、当前栈不为空,条件不满足执行②。
②、取出栈顶的右结点进行处理:current_node = new treenode(8);并将这上结点从栈中弹出。
Loop5:current_node = new treenode(8);
a、打印当有结点【8】。
b、current_node->right = null;条件为假,继续c:
c、current_node->left = new treenode(7);有左结点,条件为真,current_node = new treenode(7);
Loop6:current_node = new treenode(7);
a、打印当有结点【7】。
b、current_node->right = null;条件为假,继续c:
c、current_node->left = new treenode(6);有左结点,条件为真,current_node = new treenode(6);
Loop7:current_node = new treenode(6);
a、打印当有结点【6】。
b、current_node->right = null;条件为假,继续c:
c、current_node->left = null;木有左结点,条件为假,执行d;
d、这时左结点已经处理完,则从栈中去处理右结点
①、当前栈为空,条件满足,current_node = null;
Loop8:current_node = null;其循环条件不满足退出循环。
复杂度分析:
时间复杂度:由于每个结点都会循环到,所以说它的复杂度是O(N)。
空间复杂度:从上面的debug分析结果可以看出,栈中最多只会存树的深度大小,所以说空间复杂度正常情况下是:O(logN);除非是一个极端的二叉树,结点都放到一边了,那最差也是O(N)。



