用循环链表实现约瑟夫环问题

 

什么是约瑟夫环问题？

而这实际上就是一个经典的数学问题：

而用一个更生活化的例子来阐述：几个人围坐在一张圆桌上，然后开始数数，数到指定数则淘汰，然后再重1开始数，直到还剩最后一个人则为胜利者。

而具体代码如何来实现呢？

首先还是基于上次的那个链表进行扩展：

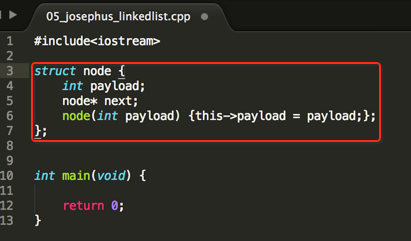
接着构造一个循环链表，为了使代码更加的清晰，这里采用面向对象的方法来进行封装

接下来就是去实现这个add方法，如何在这个方法中实现一个循环链表呢？下面用图来模拟下整个组建的一个过程从而形成一个实现思路：

1、添加第一个元素“0”：

由于目前里面只有一个元素，所以自身指向自已形成一个环，而tail变量是有用的，这个等下面就可以看出来。 

2、添加第一个元素“1”

 

将之前元素的下一个节点指向新建的结点，而新建结点的下一个节点指向tail的next，也就是node1，而将tail指向新建的结点。

3、添加第一个元素“2”：

同样的也是新建节点的next指向之前tail的next，tail的next指向新建的结点，而tail变更为指向新节点。

而tail变量的作用也比较清楚了，就是最后可以用它来遍历，并且对于组成环也有比较重要的作用。

通过上面三个步骤，可以总结点这个添加成环有两种情况：一个是添加第一个元素的时候；另一个则是非第一个元素，有了上面的思路之后下面看代码具体实现：

上面的实现比较好理解，下面编写一个打印方法看否里面添加的元素都正常打印了，这时tail变量就发挥作用啦：

编译运行：

正确打印，接下来就到了最关键的步骤，开始实现数数淘汰的问题，这个首先先声明一个方法：

 

那具体如何实现呢？还是先画图整理思路，假如是如下四个结点：

 

这里以数3就淘汰的规则来整理【从node1开始数数】：

1、首先判断边界条件：如果链表则空或链表只有一个元素时，则没必要进行数数了。

2、首先数3-1=2下，为啥不数满3下呢？因为如果如图中所示，第一次要淘汰的是node3，也就是要删掉node3之前，得将node3这个元素获取出来，不然的话数满三下到了node3直接将其删掉会导致程序无法继续了，所以这里是数到第二下到node2这个节点就暂停。

3、获得要淘汰的元素node3，并将node2.next=node2.next.next:

4、在删除node3之前，有一种特珠情况需要注意，如图：

那在删除node4之前，首先需要将tail指向p，也就是node2,不然到的把node4删掉了tail也为null了，这样整个状态就不对了，这是需要注意到的。

5、删除要淘汰的无毒，而C++中则是将无用的内存delete掉既可。

有了上面的思路之后，下面的具体实现就不难啦，具体如下：

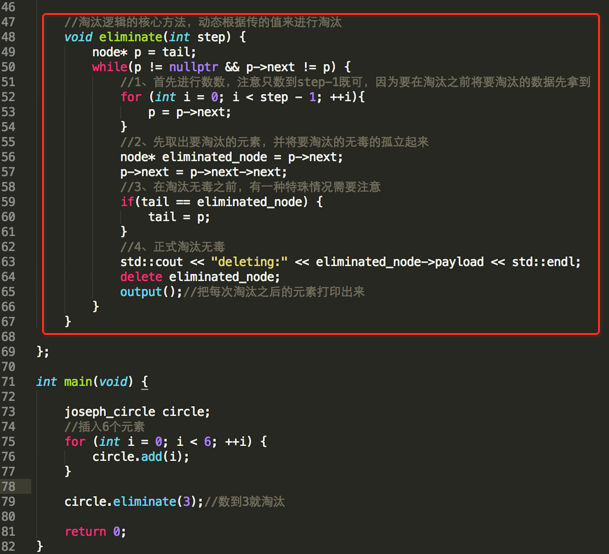
编译运行:

那对于这个算法的时间复杂度是多少呢？下面来看一下：

所以T(n) = (n - 1) * ((k-1) + c[假设常量级别用c表示]) 

而将常量级别的c给忽略掉，则进一步换算T(n) = (n-1) * (k - 1) = nk - n - k + 1

进一步将常量1给忽略掉，而T(n) = nk - n - k = nk - c0[加上一个系数]n - c1[加上一个系数]k 

所以它的时间复杂度为：O(nk)

其实对于约瑟夫环问题还可以用数组来更好的实现,而它的时间复杂度跟用链表实现是一样的，这个在下篇继续学习~