普林斯顿微积分读本05第四章--求解多项式的极限问题

接着https://www.cnblogs.com/webor2006/p/16521502.html继续往下学习。在上一次主要是从概念的角度学习了极限，这次则是时候学习一下求解极限的一些技巧了。

x->a时的有理函数的极限：

对于x->a的有理函数的极限的样式是这样的：

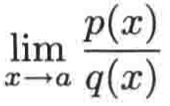
其中p和q都是多项式，对于多项式的定义可能也忘得差不多了，借此回顾一下：

另外a是一个有限的数，另外要记住，两个多项式之比p(x)/q(x)被称作有理函数：

代入法：

对于这种有理函数的极限的求解，首先就是尝试将a的值直接替换x，如果分母不为0，那么极限值就是你替换后所得到的值，举个例子：

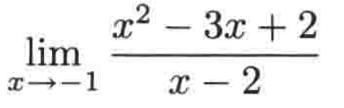
将x=-1代入到式子中就有：

很幸运，分母不为0，-2就是极限值，简单~~

但是有个细节需要提一下，对于x->-1和x=1完全是两码事，在上章中曾经说过函数在极限点上的值是无关紧要的，比如我们举例的这个，就是在x=-1处的值是无关紧要的，那你这种直接代入的方法求极限应该会有问题吧？其它在下一章，学到连续性的概念后，它将证明这种“代入”法是没有问题的。

不定式极限：

在上面代入法的例子中，提到了一个“很幸运”，对立的肯定也有“不幸运”的对吧，也就是用代入法之后，分母会为0，比如：

例一：

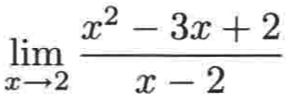
很明显代入之后会变成：

(4 - 6 + 2) / (2 - 2) = 0 / 0，它被称为不定式极限，注意这里的0并不是指整数0，而是代表趋于无穷小（趋于0）的极限形式。对于零比零的形式的极限，如下情况都有可能发生：极限或许是有限的、极限或许是∞或-∞、极限或许不存在。

对于零比零的形式的极限，通常可以用因式分解这一重要技巧来求解上例：

化简之后，再将x=2代入到表达式（x-1）中，此时得到的结果为1，它也就是极限值。

这里会容易产生一个误解：对于这两个函数，它们是同一个么？

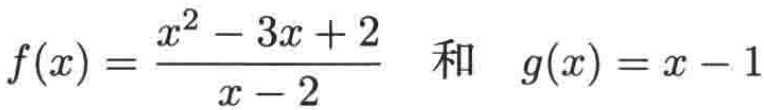
当然是呀，因为可以化简一下：

注意：不是哟，因为2不在函数f的定义域中，却在函数g的定义域中，所以它们俩是不同的函数。

但是！！！如果求这些函数的极限就不一样了，因为对于x=2处的值在求极限时是不关心的，极限只关心在x=2附近的值，所以这也是为啥在分母代入为0的情况下极限的解也存在的原因，一定要区分函数和极限的区别。

例二：

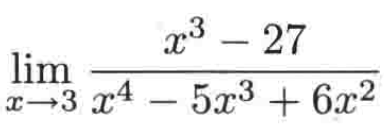
将3代入，其实也是0/0型，好，接下来做因式分解来避免分母为0，对于这个多项式你还记得咋因式分解不，这里得先复习一个立方差的公式：

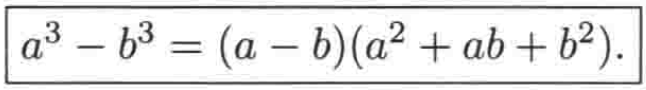
所以分子可以分解成：

然后分母明显有一个因子可以提出来，如下：

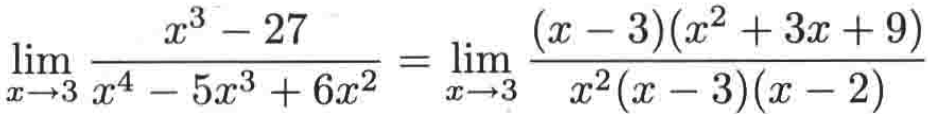
此时可以消去分子和分母的公因子(x - 3)，此时就可以用代入法了，如下：

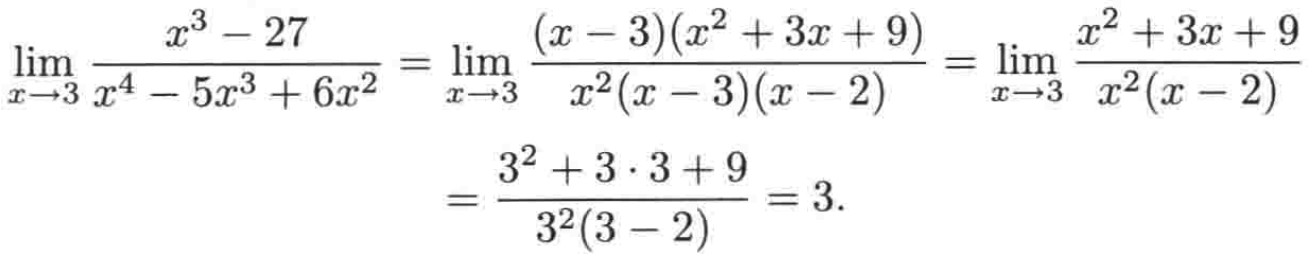
(!=0)/0型的极限：

概述：

还有一种情况，就是分母是0，但是分子不是0， 那它的极限又是怎样的呢？这里先将结论描述出来，之后再来用具体例子进行巩固理解：

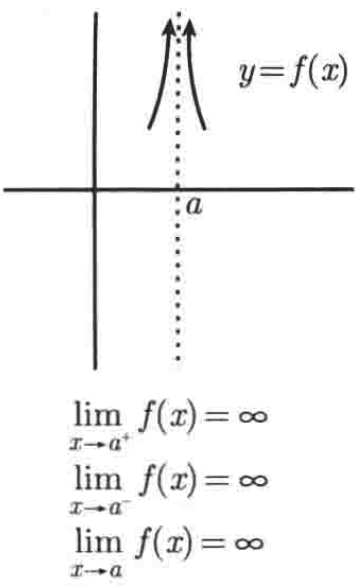
在这种情况下，将总会牵扯到一条垂直渐近线，既有理函数的图像在你感兴趣的x值上会有一条垂直渐近线，而此时它的极限会有四种情况出现，如下，f是我们所关心的有理函数，而x=a处的极限情况如下：

那么问题来了，你如何知道你所处理的极限是属于这四种情形中的哪一种呢？其实只需要查看f(x)在x = a两边的符号就可以了。比如：如果它在两边都是正的，那么你一定是在处理第二种情形：

实践：

下面来举两个具体的例子：
例一：

还是按步骤来进行求解：

1、将x=1代入式子，最终的结果是-5/0，此时不是0/0型，而是正是我们现在探讨的这种情况对吧；

2、接下来就得确定它属于上述四种情况哪一种对吧，就得观察当移动x到1的附近时会有什么情况发生，具体做法如下：

• 分子在正负先确定，直接代入1，为-5，所以是负的；
• 接下来就是需要来确定分母的正负性了，因子是x=1，它是大于0的，此时分母的正负性很明显你不能直接代入1，而应该是来研究左右无限逼迫x=1这个点再来看分母的正负性，好来看一下：x>1时，很明显分子是大于0的，所以整个的结果的正负性为：
  
  再来换一个条件，当x<1时，其正负性为：
  
  这里注意：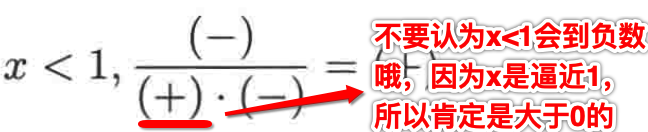
  

3、当我们求出了x附近左右的正负性之后：当x>1，f(x)是负的，当x<1，f(x)是正的，此时就可以来对照上述四种情况进行对应了，很明显属于这种情况：

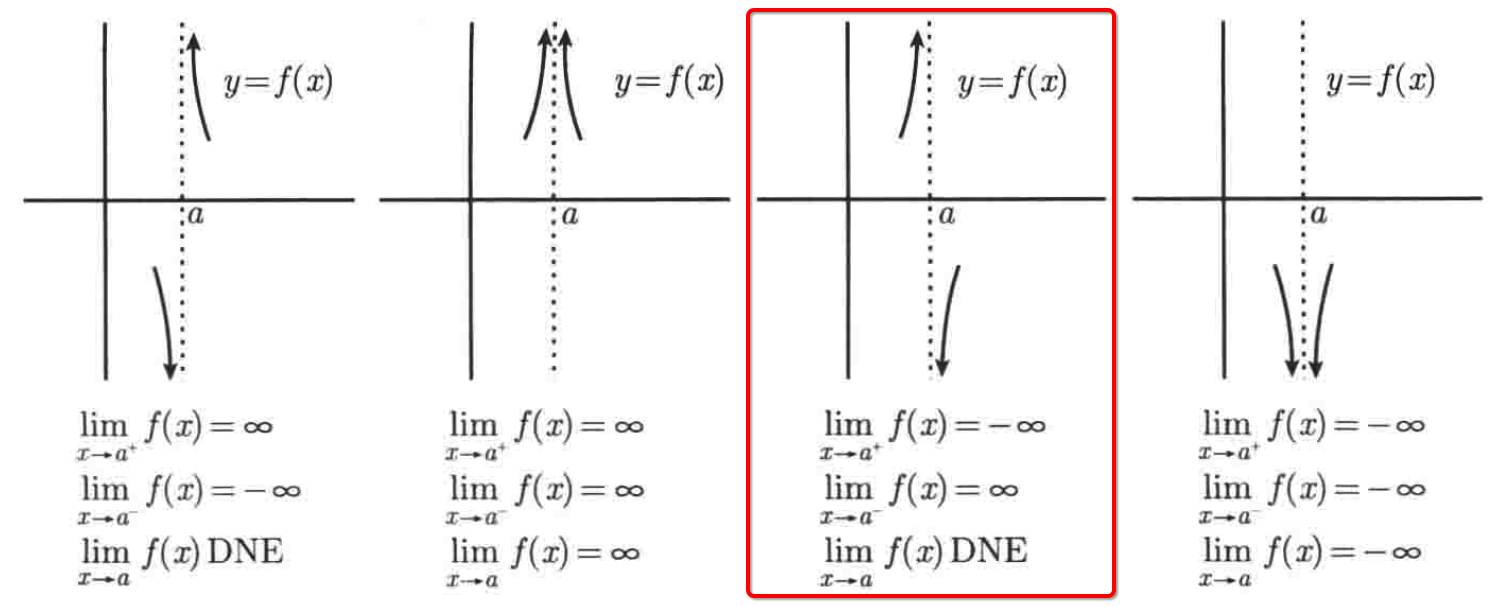
也就是此函数的极限是不存在双侧极限的，只有两个单侧极限，如下：

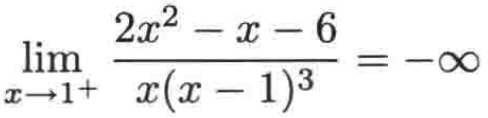
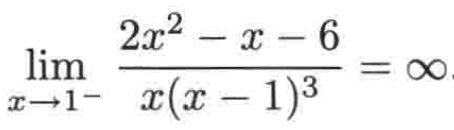
例二：

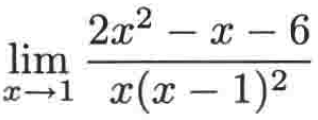
同样的求解步骤：

1、由于当1代入，它属于"分子不为0/0"型；

2、分子是负数；

3、当x>1时是负的：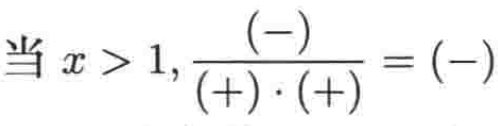

而当<1时，也是负的：

4、对照四种情况，可以得结果：

所以此函数的极限为：

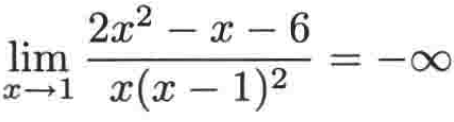
当然左右极限都是-∞。

x->a时的平方根的极限：

比如要求这个函数的极限：

好，先来按着目前所学的一些套路来求：

1、直接代入，你会发现可以得到0/0型的不定式；

2、因式分解法，可以将：

但，貌似起不了太大的作用，因为分子上还有一个-4存在。

3、“分子非0/0”型，貌似也不是；

你会发现，上面所学的三个套路，在这个求极限中已经完全不好使了，此时要解此题，则需要再学另一个新的套路了，式子中你会发现有平方根：

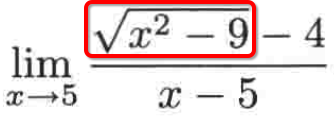
遇到有这样平方根的式子，此时可以乘以这个式子的共轭表达式，此时就需要学习一下共轭复数的概念了：

也就是对于式子a-b而言，它的共轭表达式则是a+b，所以同理：

它的共轭表达式为：

而做法就是让分子和分母同时乘以这个式子，如：

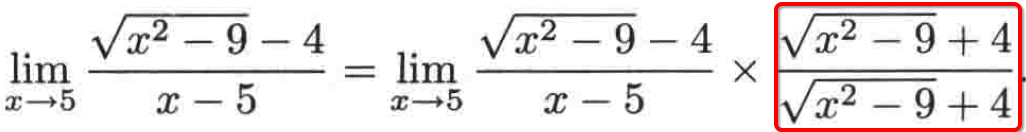
擦勒，表面上貌似变得更复杂了，但是其实是往一个好方面在转变，因为：

所以我们可以将分子进行一下变形为：

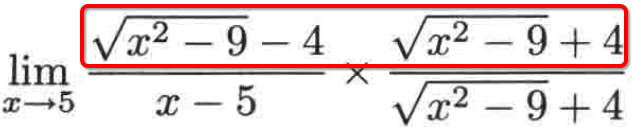
它等于：

既：

所以此时的式子就可以变为：

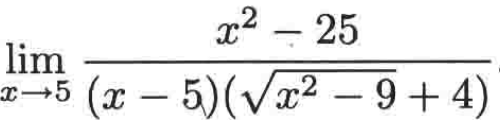
而分子又可以分解为(x - 5)(x + 5)，此时就有公因子可以消去了，具体如下：

此时将x=5再代入就可以得到结果10/8，既5/4。

总结：

对于这种情况的求解总结一下就是：如果你碰到一个平方根加上或减去另一个量，就可以试着把分子和分母同时乘以其共轭表达式，惊喜也许就会出现！！！

x->∞时的有理函数的极限：

概述：

在前面我们学习了x->a时的有理函数的极限了对吧，接下来则来讨论x->∞求有理函数的极限，也就是：

其中p和q是多项式，对于多项式，有这么一个非常重要的性质：

当x很大时，首项决定一切【注意：首项并不是指第一项，而是指次数最高的那一项】。也就是说，如果你有一个多项式p，那么当x越来越大时，p(x)的表现就好像只有它的首项存在一样。

比如这么一个多项式：

其中设首项为：

当x变得非常非常大时，p(x)和pL(x)会非常接近，也就是这个极限会为1：

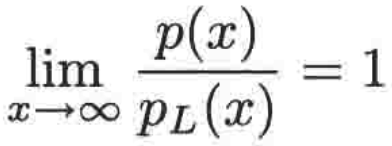
这里来看一下它想要表达的意义，这里用到的是极限的方式来表达这个等式，那如果不用极限符号呢，则是这样子：

如果没有极限符号，这就意味p(x)=pL(x)，很明显这不是真的，只是越来越趋于真的，那么用极限符号来表达是最为合适的。

那如果写成下面这种式子可以么？

貌似是真的，但是由于两边x都是趋于∞，很明显这种式子是毫无意义的，所以还得用其比接近于1来表达p(x)和pL(x)非常接近比较适合，也就是随着x越来越大，其比趋于1，而不是等于1。

理解：

为啥当x->∞大时，式子只跟首项差不多大，而不是其它项中的一项呢？下面以一个实际大的x值来进行检验你就能知道为啥是首项了。

还是拿这个多项式来进行举例：

1、x=100：可以看到3x^3=三百万，10000(x^2)=一千万，5x=500，所有值加起来，可以看到p(100)大概是负七百万，你会发现，它跟pL(100)首项的三百万完全不同对吧，不要灰心，因为此时的x值还不够大。

2、x = 1 000 000，可以看到3x^3会变得非常之大，它是三百万万亿，10000(x^2)=一千万亿，5x=五百万，而最后的-7此时就可以忽略不计了，此时再来计算p(100)，你会发现结果还是接近于三百万万亿，它不就是pL(1 000 000)的值么？

经过上面这个具体值的代入来看，当x变大时，最高次数项比其它项要增长得更快，这也就是为啥当x->∞时跟首项一样的原因。

证明：

接下来咱们来看一下真正的数学证明，也就是要证：

还是以这个多项式为例：

就有：

 

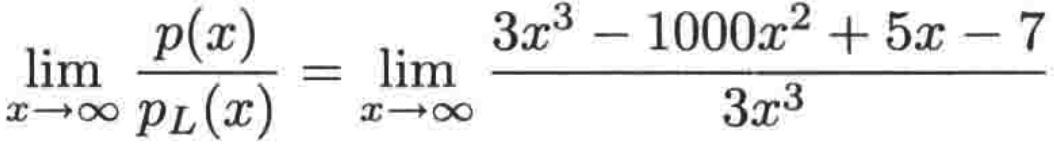
进一步进行简化：

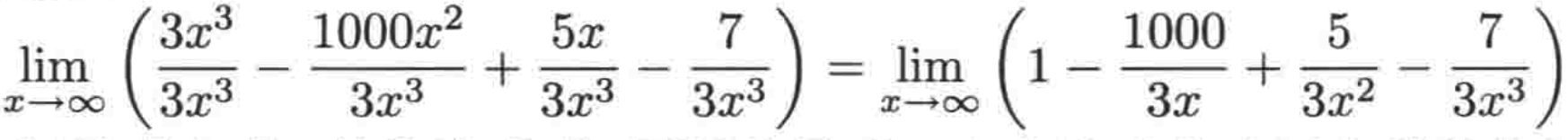
而对于这个式子，根据“在所有极限都是有限的时候，和的极限等于极限的和”，所以我们可以将这个式子拆开来求四个极限，最后再把四个极限加起来得到最终的极限结果。

那么下面分别求出这四个极限：

1、第一个是1，所以不管x是什么，它总是1；

2、

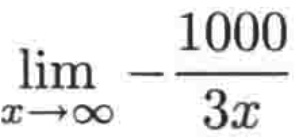
求这个式子的诀窍就是将因子提出来，就可以变成：

由于-1000/3是常数，不管x是什么，它都不会改变，所以此时可以将它提到极限符号之外，变为：

 

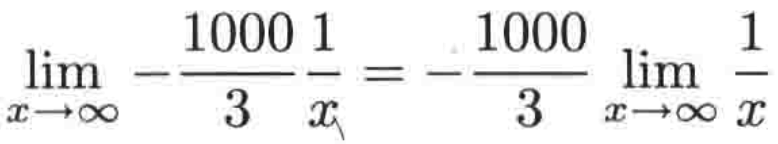
此时的关键就是求：

对极限有了解的一看它就是0，因为非常大的倒数是一个非常小的数，也就是当x->∞，它接近于0，所以最终此极限为0：

 

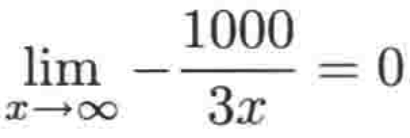
根据这个，接下来先来抛出一个定理【重要！！！】：

对于任意的n>0，只要C是常数，就有：

基于这个定理，剩下的两个极限都不用求了，一看都是0，所以完整的论证为：

这样：

就得到论证了，这个方法适用于任意的多项式哟~~

实践：

方法：

接下来举几个例子加以巩固，在正式解题之前，先来对方法思想进行一个阐述，因为它是解题的思路：

当看到某个关于p的多项式p(x)是多于一项时，把它代以：

对于每一个多项式都这样做，这里的要点是当x->∞时，以上表达式中的分式的极限是1，也就是：

并且首项比原来的表达式要简单很多。可能这块的思想有点模糊，下面以具体例子来理解一下。

例一：

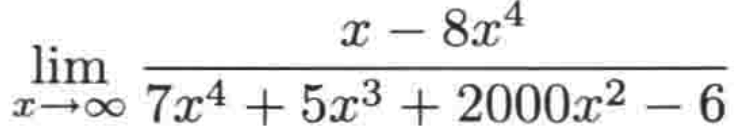
分子和分母都是多项式，所以下面来看如何用上面的思想来求解。 

1、对于分子，它的首项是：

所以，对于该多项式就可以按这种来进行变换：

 

为：

 

2、同样的，对于分母的首项是：

所以可以代以：

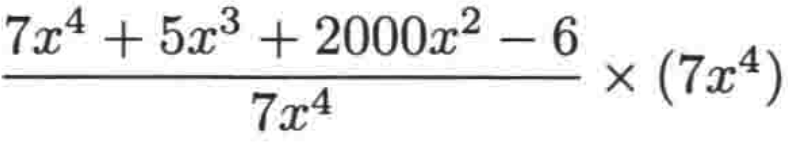
3、做完分子和分母的替换之后，式子就可以变为：

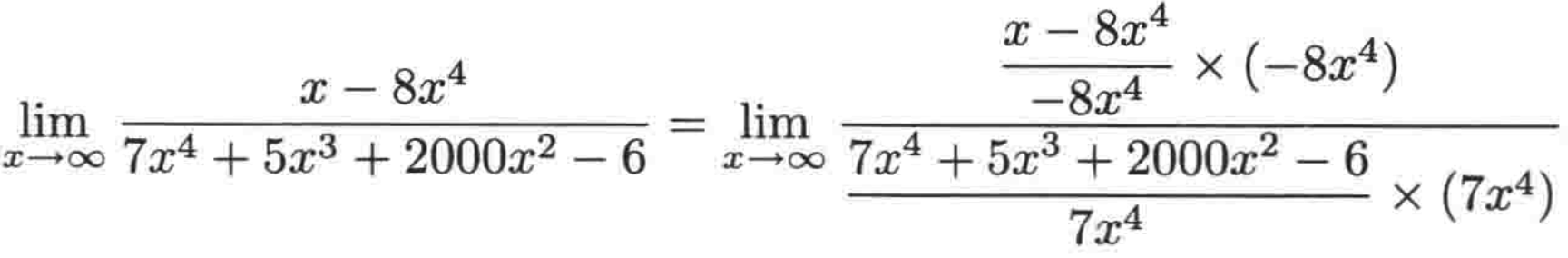
4、此时可以求出这些分式的极限都是1：

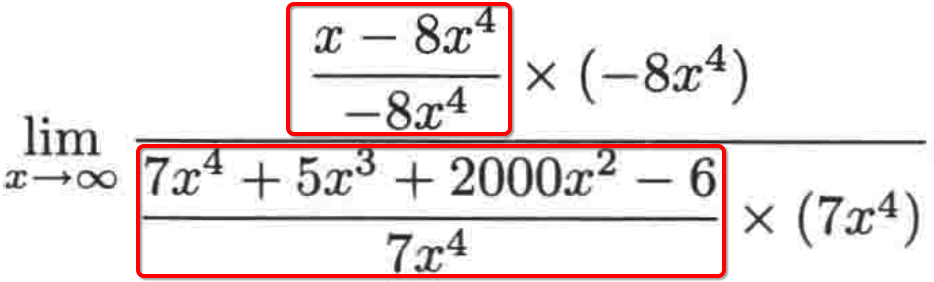
至于为啥，下面来化简一下就知道了：

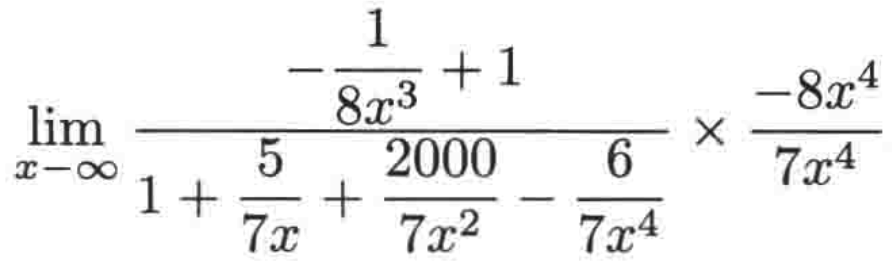
根据前面的这个定理：

很明显这些项都是0：

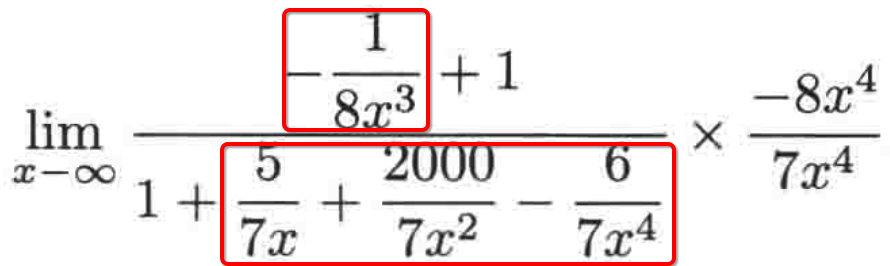
所以这么复杂的式子，经过：

这样的变换之后，最终只留下这么精简的式子了：

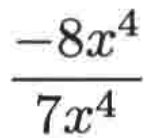
最终该极限就为：

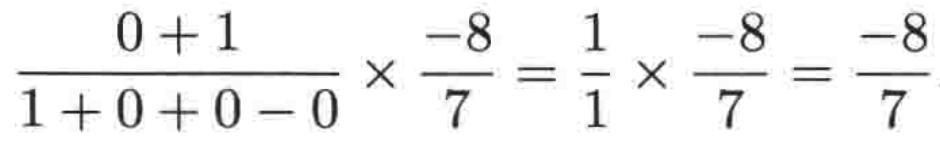
有木有感受到这种变化的魅力？下面再来看一个例子。

例二：

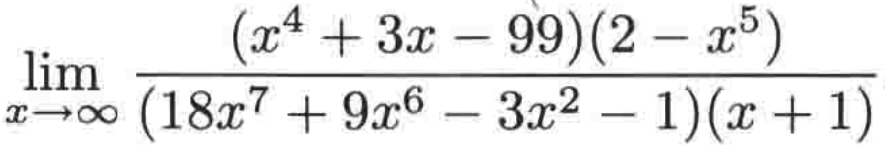
1、这里有四个多项式，找出首项，很明显是：

2、每个多项式使用此大法：

3、萃取出各首项：

4、进一步进行化简，完整求解如下：

例三：

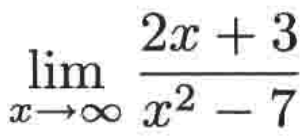
这里直接给出整个求解过程：

 

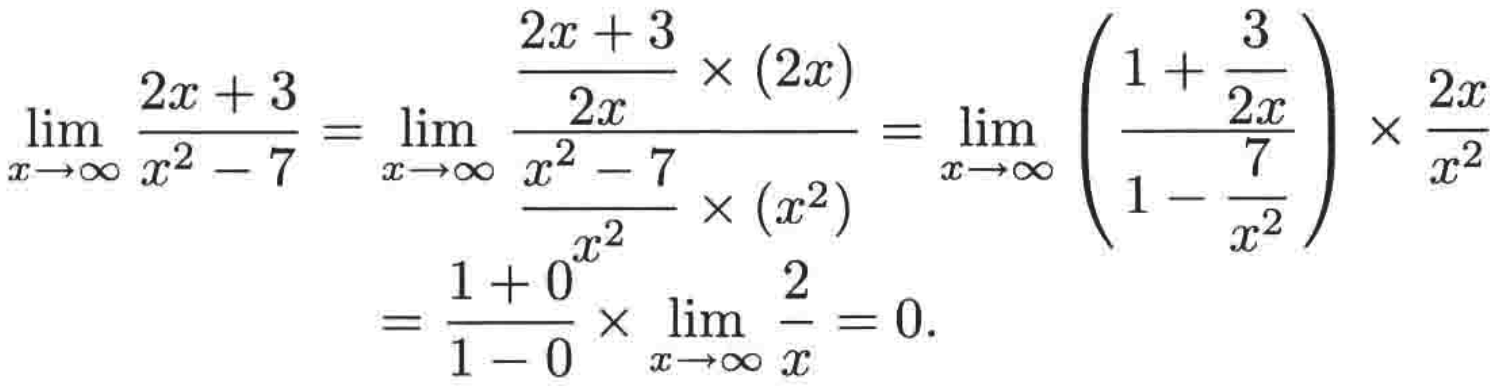
总结：

在上面举的三个例子而言，其实是比较有代表性的，这块有规律可以总结：

1、第一个例子的分子和分母次数都是4，得到的极限有可能是有限的且非零（得到答案-8/7）；

2、第二个例子的分子的次数是4，分子的次数是4和5的多项式的乘积，会得到一个次数为9的多项式，而分母是次数为7和1的多项式的乘积，因此它的总次数是8次，也就是分子的次数大于分母，得到的极限有可能是无限的（得到答案-∞）；

3、第三个例子分母的次数为2，大于分子的次数为1，其结果为0；

好，接下来就可以有一个通用的总结了，对于这样的极限：

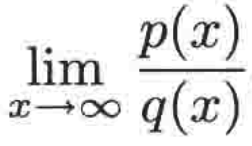
其中p和q为多项式，我们可以说：

(1)、如果p的次数等于q的次数，则极限是有限的且非零；【如例一】

(2)、如果p的次数大于q的次数，则极限是∞或-∞；【如例二】

(3)、如果p的次数小于q的次数，则极限是0；【如例三】

同样的，对于：

 

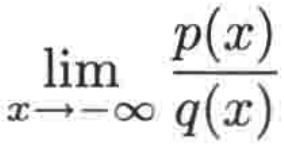
也满足这样的结论。

不过，对于这些结论，在解题时其实不用记它，重点是知道:

大法。

x->∞时的多项式型函数的极限：

概述：

在上面我们已经学会求解有理函数多项式的极限了对吧，下面再来看如下三个函数：

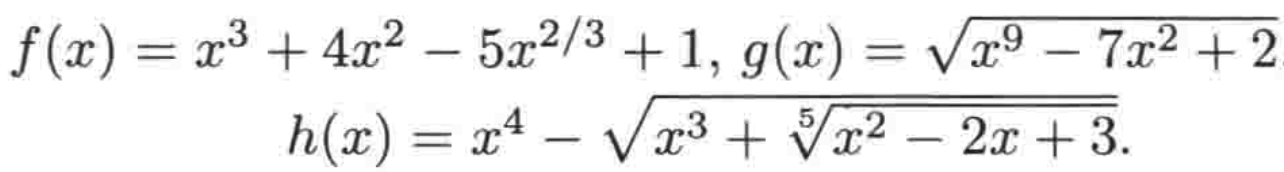
这些其实都不是多项式了，因为它们含有分数次数或n次根，关于这块，特意问了一下度娘，确实多项式的次数只能是自然数，不能是分数：

但是！！！它们其实看起来有点像是多项式，所以对于这些函数，我们称之为“多项式型函数”，其上面学习的有理函数的求解方法同样也适用于多项式型函数。

所以对于这三种类型的函数，其求解思路跟上面所学的有理函数的求解方法一样，只是说对于多项式型函数的首项不是那么清晰，下面以实际例子来看一下求解过程。

实践：

例一：

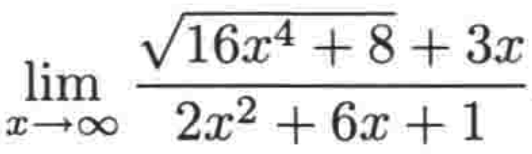
1、确认首项：分母的首项很好确认，它是2(x^2)；而分子的首项就不太好确定了， 其实按如下步骤你也很好的可以对带根号的这种式子来确定首项，先确认平方根下的式子的首项，很明显是：

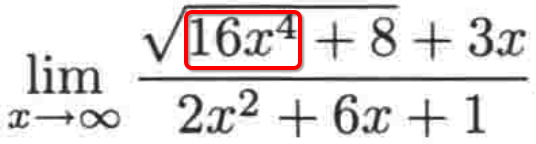
而它开根号之后，其实就是4(x^2)对吧，此时对于分子你就可以简单理解为4(x^2) + 3x，所以分子的首项是4(x^2)。

2、进行如下大法：

也就是：

3、对分子进行化简：

对于分子的这个式子的化简：

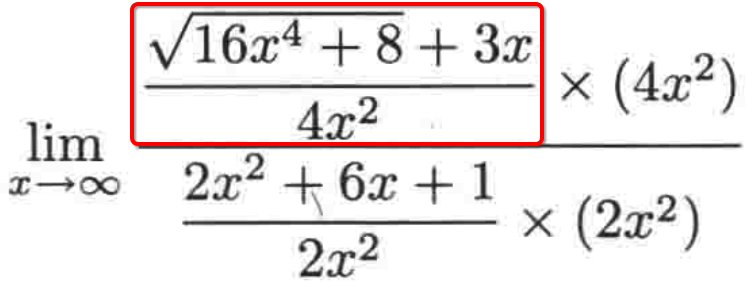
其实方法就是将4(x^2)拖进平方根符号里面，如下：

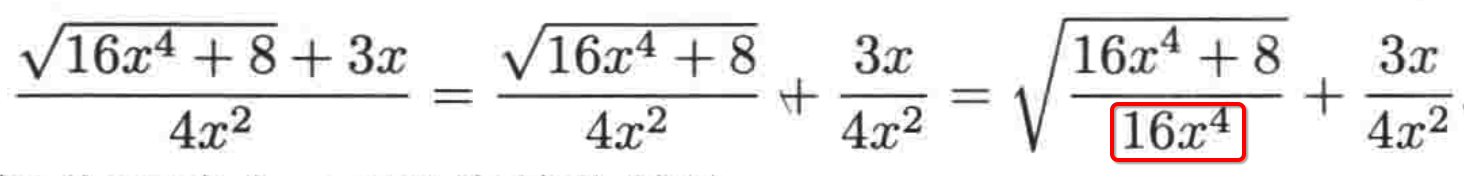
进一步化简就为：

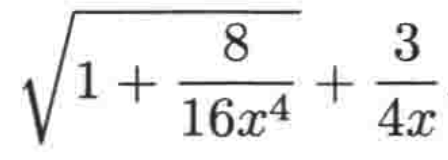
而由于x->∞，有前面的一个定理：

所以最终就为：

4、对分母进行化简：

而对于分母的化简就比较简单了，这里直接将整个求解的过程展现出来，比较好理解：

是不是针对这种“多项式型函数”的极限求解方法跟有理数函数的求解方法是一样的？

例二：

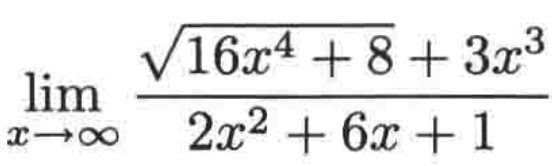
同样的步骤进行求解：

1、确定首项，很明显分子的首项是3(x^3)，分母是2(x^2)。

2、接下来的就直接把整个过程展示出来的，其套路是一模一样的：

这个例子对于分母的首项是由它后面的3(x^3)，因为它的次数是3，比2(x^2)要大，那如果后面的次数跟根号中的首项的次数一样呢？下面看一下这种情况的例子。

例三：

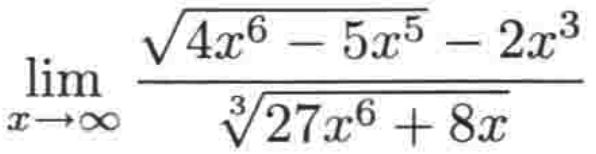
1、确认分子的首项，你会发现根号的那个首项2(x^3)，然后跟后面一减，貌似没有分子了。。所以这里可以使用在上面所学的共轭表达式方式让分子和分母都乘以分子的共轭表达式来避免这样的尴尬【有木有感受到，求极限就是当你发现问题时，用其它的一些已知的定理进行转换来避免这些问题，再进一步进行极限的求解】：

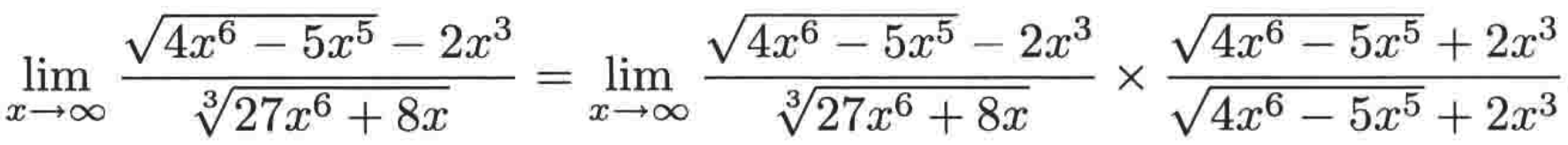
根据：

可以将上式子又转换为：

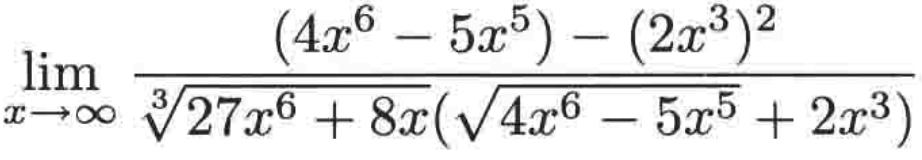
进一步把分子化简就为：

2、确认分母的首项，然后进行化简：

对于分母其实是由两个式子来决定的：

先来确定前面的根号式子，比较简单，它的首项是3(x^2)，为了方便根号化简，这里可以化为：

也就是：

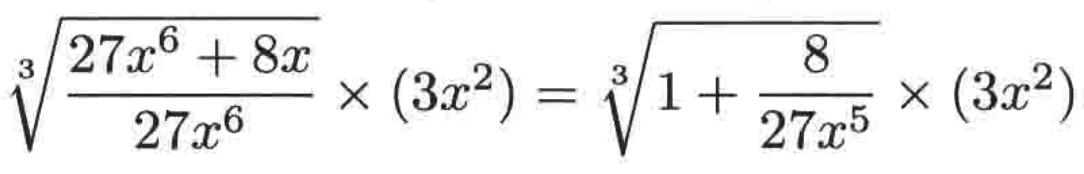
而当x->∞时，立方根的那部分就为1。

接下来再来处理右边的这个式子：

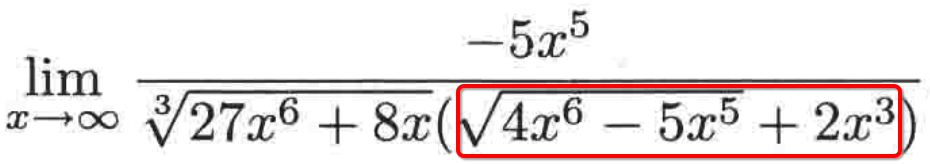
根号的首项是2(x^3)，再加上后面的，也就是整个的首项就是4(x^3)，于是就可以分子和分母都乘以它：

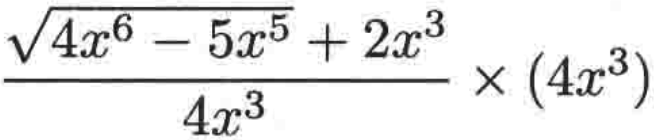
然后将4(x^3)拖到平方根中进行进一步化简就为：

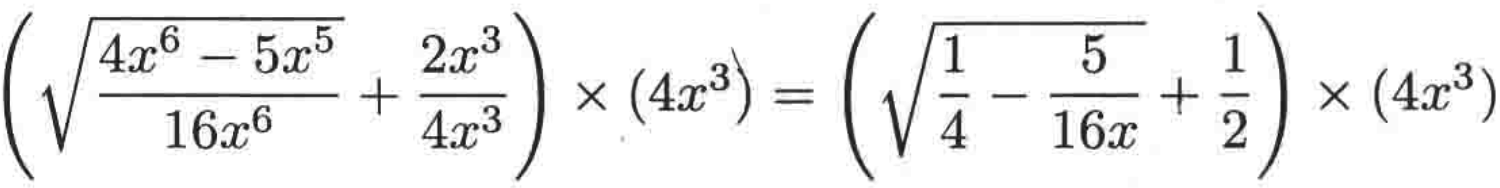
当x->∞时，最终就可以化为：

3、最后求解整个串起来，先是分子乘以了共轭表达式就化简为：

 

然后进一步就可以化为：

 

将首项都提出来就有：

 

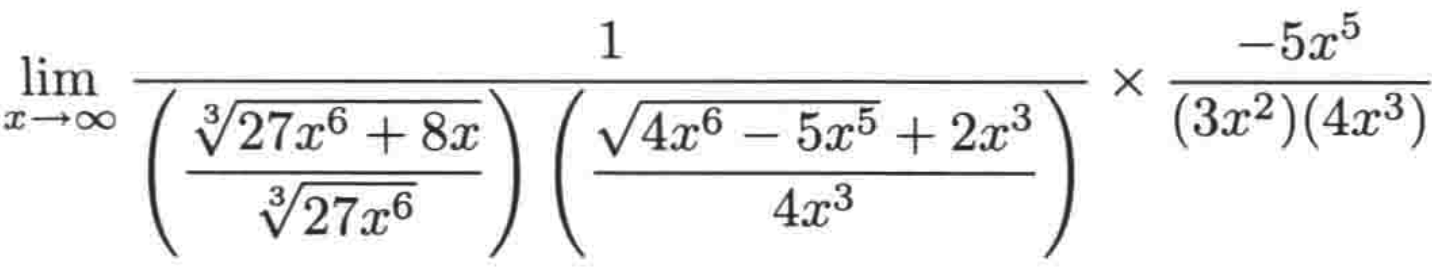
而由于：

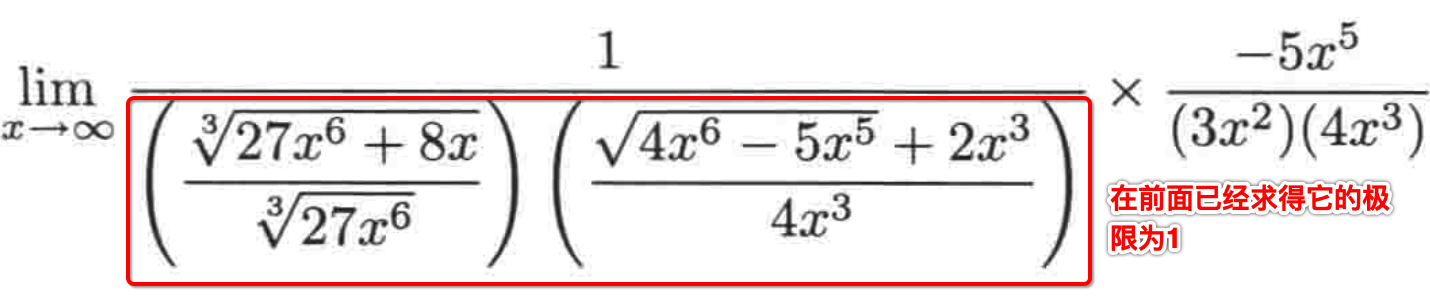
最后其实就只剩它了：

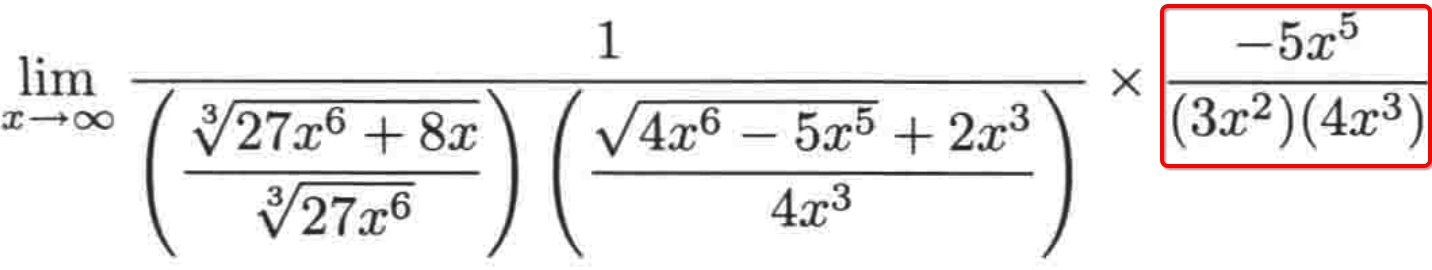
最后该式子的极限就是-5/12，这个函数的求解相对而言要麻烦很多，但是万变不离其宗，其采用的套路基本上都是那些，需要有一定的耐心。

x->-∞时的有理函数的极限：

概述：

在前面咱们已经学过了x->∞时有理函数的极限的求解了，接下来重点关注一下负无穷的情况，也就是：

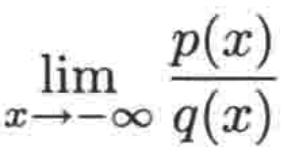
其中p和q是多项式或者多项式型函数， 而我们之前所学的原理在这里同样适用：当x是一个非常大的负数时，在任意和中，其最高次数项仍然会占主导；另外当x->-∞时，只要C是常数，且n是一个正整数，C/(x^n)仍然趋于0，下面以之前在有理函数中举过的例子看一下。

实践：

例一：

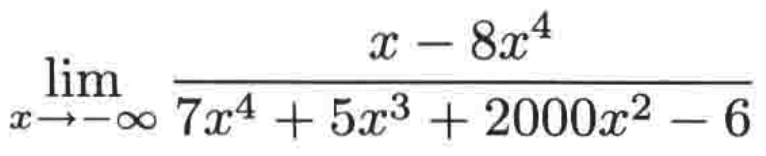
对于这个例子的求解跟x->∞是一模一样的，这里直接分子和分母乘以首项既可，这里就不一步步求了，之前在x->∞已经详细说明过，直接给出整个求解的过程：

是不是它的解跟之前的无穷大的是一样的？

例二：

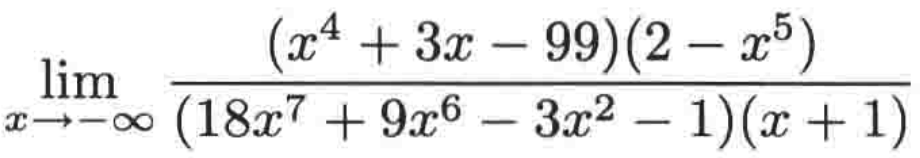
这个解题步骤也跟之前的差不多，不过，最终的结果有些差别，整个过程如下：

而对比一下之前的刚好是相反的结果：

 

例三：

 这个例子需要说明一个问题，就是对于x->-∞：

 

因为x是负数了，所以对于这个式子的分母首项比较容易确定，是2(x^3)，但是对于分子的首项是它对吧：

由于x是负的，所以它化简注意负号，应该为：

 

就注意这个小细节既可，整个求解过程如下：

 

类似地，在x为负数时，如果在处理四次方根、六次方根等偶数次方根时，都需要小心负号，比如：

 

但是如果是奇数次方根时，则有：

另外当x<0，还有：

 

因为x^2是不可能为负的，根号下x^4也不可能为负。

总结：

关于这种场景的极限求解就是注意一下小细节，就是关于符号，总结如下：

包含绝对值的函数的极限：

有时候会面临求解包含绝对值函数的极限，比如：

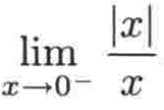
如何求解呢，这里设：

很明显0不可能在函数f的定义域中，因为分母不能为0，接下来分两种情况来看一下：

1、x>0时，f(x) = 1；

2、x<0时，f(x) = -1；

具体图像为：

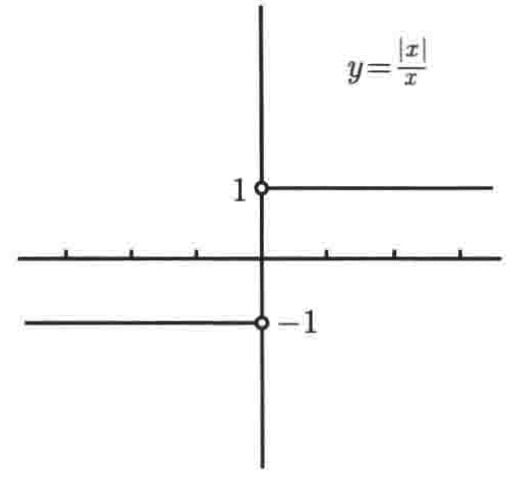
所以很明显左右极限的情况为：

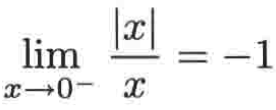
由于左右极限不相等，所以双侧极限不存在：

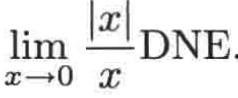
所以对于绝对值函数的极限求法也就是这样求的。

下面再来看一个例子：

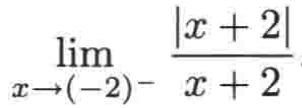
很明显这个绝对值主要取决于x+2>0还是x+2<0。

1、x+2>0时，|x + 2| = x + 2；

2、x+2<0时，|x + 2| = -(x + 2)；

所以当x>-2时，|x + 2| / (x + 2) = 1；而当x< -2时，它则是-1。事实上y = |x + 2| / (x + 2)的图像就是y = |x| / x的图像向左平移两个单位得到的，如下：

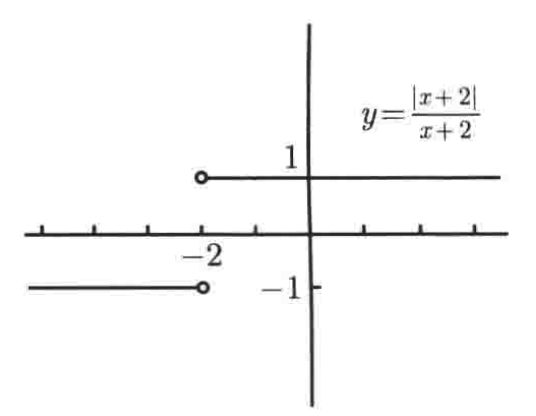
也就是此双侧极限也不存在，因为左右权限不相等。

总结：

至此，这章已经学完了，总体来说就是学一些求解极限的套路，当个备忘吧，不可能记得住，下一章准备学习函数的连续性和可导性，加油！！！