普林斯顿微积分读本02第一章--函数的复合、奇偶函数、函数图像

继续接着https://www.cnblogs.com/webor2006/p/16486101.html高数的学习。

函数的复合：

接着还是复习函数相关的基础，“函数的复合”，这个从字面意思也比较好理解，就是一个函数是由多个函数复合而成嘛， 下面来具体看一下书本对它的介绍。

假设有这么一个函数：

咱们可以把x替换成任何使函数有意义的对象，比如：

其中对于(x+5)需要加上小括号，不然写出来的结果是错的，这个没啥好说的，也就是你需要将f(x)写成f(某表达式)，可以将每一个x替换成（某表达式），这时候记得要加一个小括号，不过有一种情况小括号可以不加，那就是指数函数，如下：

比如代一个这个式子：

定义：

接下来看一下函数的复合的定义，比如这么一个函数：

我们就可以将这个函数拆成两个，如下：

这样的话，函数形式就可以变成由g和h函数复合而成了，如下：

也可以用另一种形式表达：

其中有个注意点了：我们计算是需要从右到左，也就是g计算完了，然后再将结果给到h，这一点要搞清楚。

这里的圈表示“与....的复合”，既f函数是g函数和h函数的复合。

练习：

函数的复合计算练习：

书中说到“练习求两个或多个函数的复合是很有用的”，具体多有用随着之后的学习再见分晓，这里先来练习这么三个函数的复合：

那么函数f = g o h o j的表达式是什么？根据函数的复合的定义，其计算是从右到左的，也就是先计算j，然后再j的结果给h，最后再将h的结果给到g，所以其复合的过程为：

复合函数拆解练习：

同样，给定一个复合的函数，你需要练习一下它的拆解过程，也就是复合的逆过程，比如这么一个复合函数：

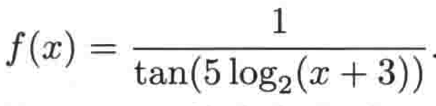
那如何将f分解为几个简单函数呢？步骤如下：

1、从函数式中找到x，首先它是需要+3的对吧，所以可以设这么一个函数：

2、需要对g函数取得的值取以2为底的的对数，所以又可能设一个函数：

 

3、然后需要乘以5，所以设函数：

 

4、再求tan正切值，所以设函数：

5、最后取倒数：所以设函数：

所以把上面5个函数一复合，就有：

而用另一种复合符号的形式写就是：

当然还可以有其它种类的复合，比如将j和h复合成另一个函数n，如下：

这样整个函数f的样式就变为：

这两种形式都木有错，看自己的喜爱，这里还是重点要提醒的是，计算是从右向左，而定义复合时是从左向右。

函数的复合和函数的乘积的区别：

对于函数的复合一定不要把它理解成了函数的乘积了，比如这么一个函数：

它就不是两个函数的复合了，因为对于任意给定的x，计算f(x)的值需要求解x^2和sin(x)，重点是先求哪个值都没有关系，这个很明显跟复合函数是不同的，复合函数的计算是严格区分顺序的（也就是从右向左来进行计算），比如我们尝试将它还是拆解一下就更加容易理解了：

此时函数就可以写成：

而我们写一下g和h函数的复合形式就是：

 

换成另一种形式为：

而我们也可以这么复合：

它的另一种形式为：

是不是清楚的可以看到：函数的乘积和复合是完全不同的，最大的区别就是函数的乘积是跟函数的顺序无关，而函数的复合是跟函数的顺序是有关的。

特殊复合函数：

对于复合函数，有这么一个比较简单但是又很重要的复合情况：

将函数f和g(x) = x -a (a是常数，关于常数是啥可以百科一下，简言之就是确定的数（不会变）)进行复合，复合之后得到的新函数为h(x) = f(x -a)，这里需要关注的g 一个特性就是：

y = h(x)和 y = f(x)的函数图像是一样的，只不过复合后的y = h(x)函数图像向右平移了a个单位；如果a是负的，那么就是向左平移【这个向左平移可以这样理解，向右平移-3个单位与向左平移3个单位是一样的】，下面就来举几个例子来理解这一特性：

比如这么一个函数：

它的画像可能你不一定能想到对吧，但是：

它的图像你肯定比较容易想到：

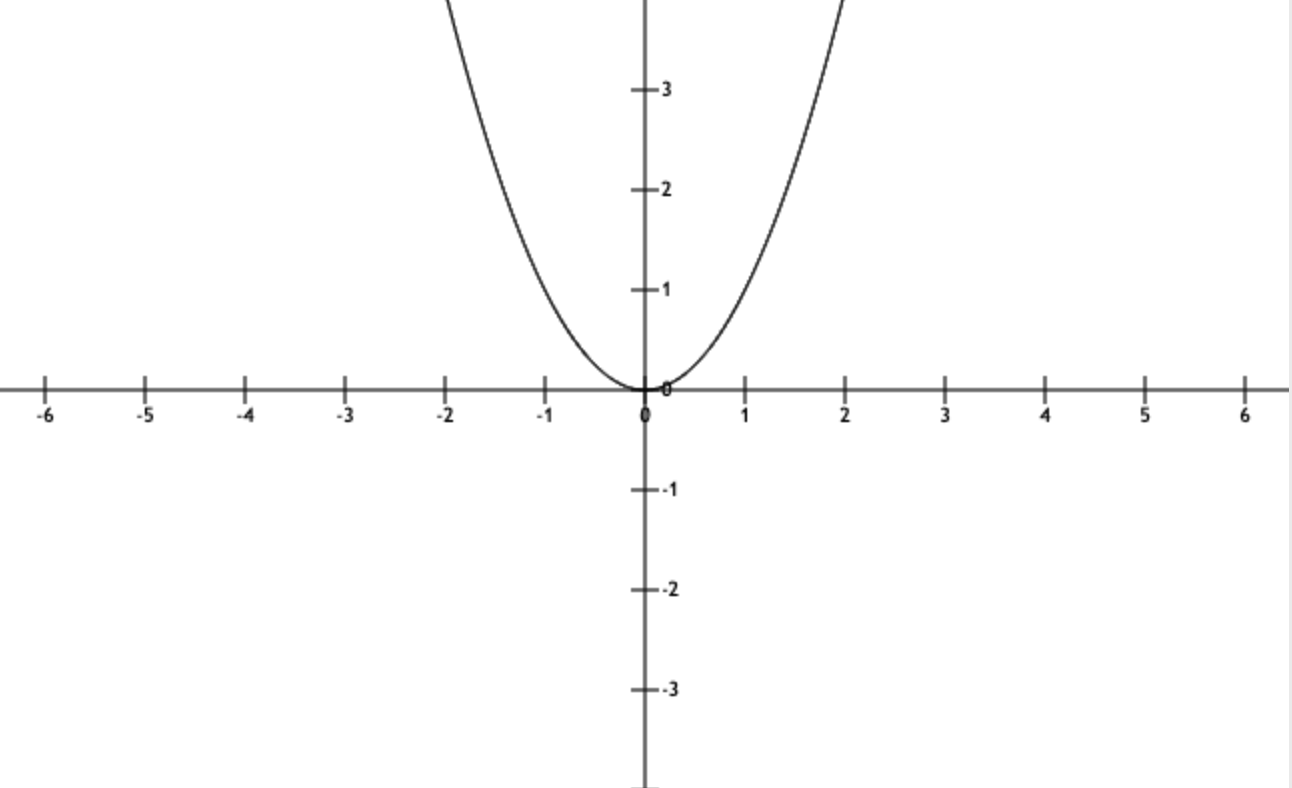
而我们就可以利用这一特性，因为这俩的图像是一样的，只是用x-1来代替x，是不是它就是f(x -a)的形式？其中a是>0的，则向右平移一个单位，如下：

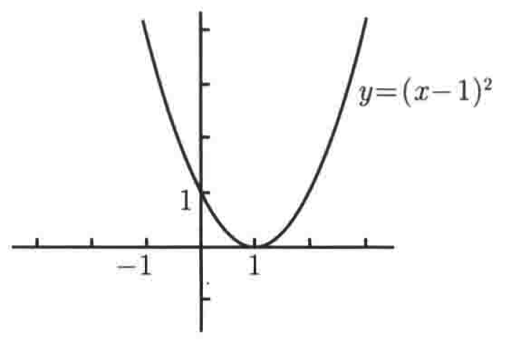
也就是只要满足：

这种特性，你就可以用简单的函数的图像根据a来很容易的联想起来，这也就是这个特性的意义之所在，再举一个例子加深一下理解：

同样的道理，将x+2来代表x，其中x+2不满足f(x-a)的形式，但是我们可以将它变形成这种形式，也就是(x-(-2))对不，也就是此时的a<0，根据规则：

所以它的图像就是：

这里推荐一个在线生成函数图像的工具：https://zuotu.91maths.com/#W3sidHlwZSI6MCwiZXEiOiIoeCsyKV4yIiwiY29sb3IiOiIjMDAwMDAwIn0seyJ0eXBlIjoxMDAwLCJ3aW5kb3ciOlsiLTYuNTU5OTk5OTk5OTk5OTg5IiwiNi40Mzk5OTk5OTk5OTk5ODgiLCItNC4wMzk5OTk5OTk5OTk5OTQiLCIzLjk1OTk5OTk5OTk5OTk5MzMiXSwiZ3JpZCI6WyIxIiwiMSJdLCJzaG93Z3JpZCI6MH1d

 

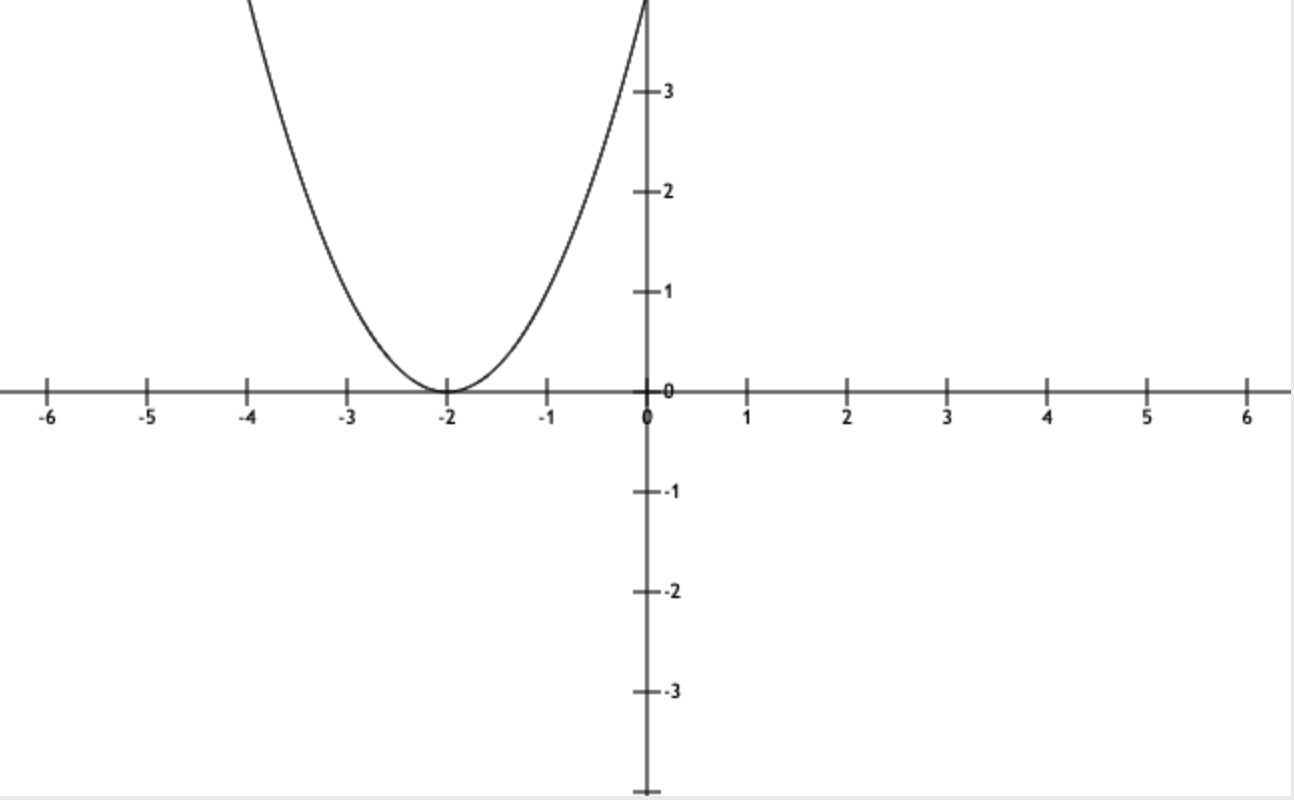
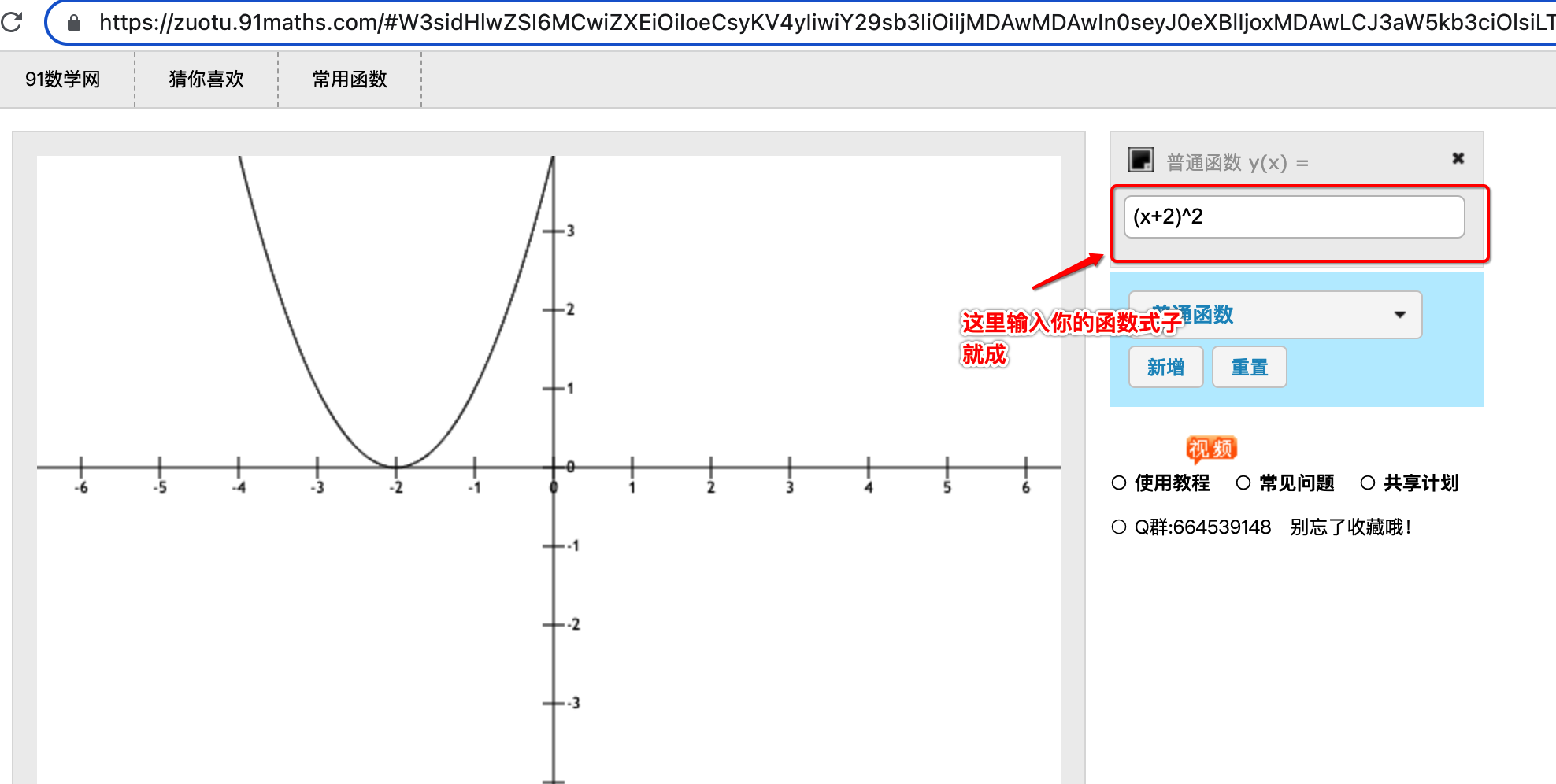
其中还有很多其它的一些图像可以设置：

对于图像不太熟悉的借助这个工具还是挺方便的。

奇偶函数：

定义：

偶函数：

比如这么一个函数：

是不是对于f函数的定义域中的所有x都有这个等式成立？

可能这样说有点抽像，下面举几个例子就明白了：

比如这个x我取3，是不是f(-3)=f(3)=9？其实对于这样的函数也有同样的性质：

事实上，当n是偶数时（n可以是负数）：

都具有相同的性质，这种函数其实就叫偶函数，好，基于这个性质，下面就可以给偶函数来个正式的数学定义了：

如果对于f定义域里的“所有”x都有： 

则此f函数就称之为偶函数。

注意：这个等式对“某些”x值成立是不够的，它必须对定义域里的“所有”x都成立哟！

奇函数：

有了偶函数的定义，对于奇函数它的定义理解就非常自然了，这里就直接给出了：

当f定义域内所有的x都有：

则称f是奇函数。

举个简单的例子：

是不是当x=3是，其结果等27，而x=-3是，结果等于-27，刚好符合奇函数的定义。

非奇非偶/既奇又偶：

对于大多数的函数， 其实是非奇非偶的，还有一种是既奇又偶，对于既奇又偶的函数，只有它：

也就是非常单调的对所有x都成立的零函数，那为啥这函数是唯一的既奇又偶的呢？下面简单证明一下：

如果它是奇函数，有：

而如果它有偶函数，有：

然后这两个可以列一个等式，用下面的式子减去上面的式子就有：

0 = 2f(x)，既f(x) = 0。

另外还有一个有用的结论：

如果一个函数是奇函数，并且0在其定义域内，则f(0) = 0

这是为啥呢？根据奇函数的定义，对定义域里的所有x，都有：

我们用0代一下，就有f(-0) = -f(0)，但是-0等于0，所以就可以化简为2f(0) = 0，既f(0) = 0。

性质：

想一个问题：对于一个函数f，怎么来判断它是奇函数、偶函数或都不是呢？若是奇函数或偶函数又怎么样呢？下面来进行一下这方面的探讨，先从后者这个问题开始探讨。

若是奇函数或偶函数又怎么样呢？

其实当你知道一个函数的奇偶性之后，一个比较好的事情就是画函数图像比较容易了，事实上，如果你能将这个函数的右半边图像画出来，那对于它左半边的图像就是小菜一碟了。

偶函数：

先说偶函数图的性质：

偶函数的图像关于y轴具有镜面对称性。

由于是偶函数，所以有：

此时y=f(x)的图像在x和-x坐标上方具有相同的高度，且对所有的x都成立，下面用一个图例直观感受下这一性质：

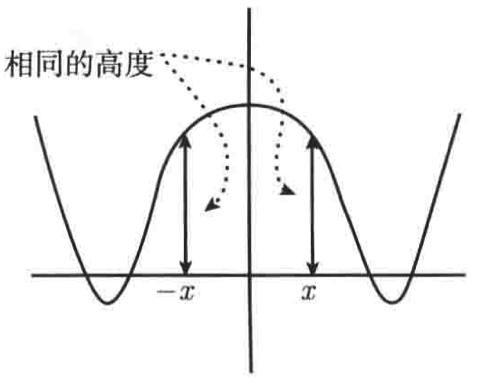
很明显图像是基于y轴进行对称的，而且y=f(x)的图像在x和-x坐标上方是具有相同的高度的。

所以，如果你知道一个函数是偶函数，当你画出偶函数的右半边图像后，就可以通过将其图像关于y轴反射得到它的左半边图像，这个特性是不是对于画图是有很大帮助？

奇函数： 

也同样先把奇函数图的性质说出来：

奇函数的图像关于原点有180°的点对称性。

由于是奇函数，所以：

此时y=f(x)图像在x坐标上方和-x的坐标下方具有相同的高度【注意：若f(x)是负的，那么需要调换一下“上方”、“下方”的词】，下面直观看一下奇函数的图像：

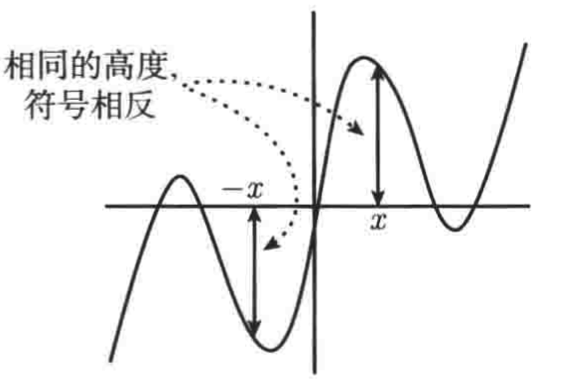
假设你只有奇函数的右半边图像，书中介绍了一个这样的方法让你可以很轻松的得到它的另一半边的图像：

1、首先在原点处把曲线给钉住：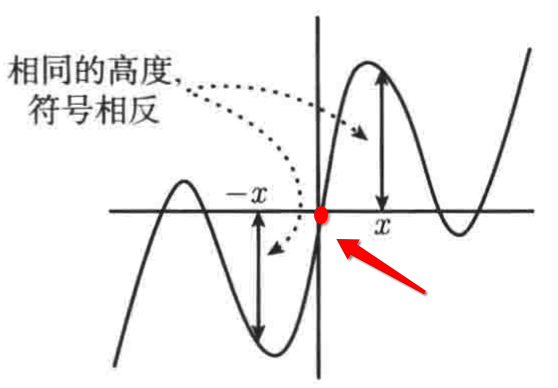

2、然后将整个曲线旋转180°：

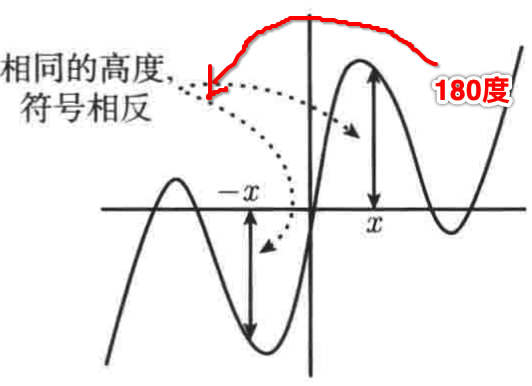
这样就得到了左边图像了，注：如果曲线是不连续的，既不是连在一起的一条，那么此方法是不适用的。

怎么来判断它是奇函数、偶函数或都不是呢？

其实方法比较简单，先描述出来：

将每一个x替换为（-x）并计算f(-x)，其中注意一定要给-x加上小括号，然后化简结果，如果你得出了原始表达式f(x)，那么此函数为偶函数；如果得到的原始表达式的负值f(-x)，f就是

奇函数；如果得到的结果既不是f(x)，也不是-f(x)，则f就是非奇非偶；

下面来具体实践一下：

举例一：

那它是啥函数呢？咱们来求一下f(-x)既可，如下：

 

是不是满足偶函数的定义： ，所以此函数是一个偶函数。

举例二：

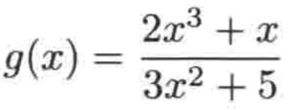
同样，求g(-x)：

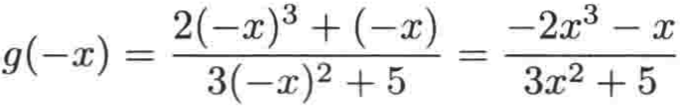
然后我们把负号提到前面，就有：

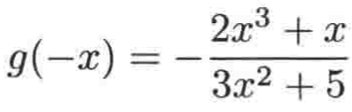
是不是满足奇函数的定义：，所以此函数是一个奇函数。

举例三：

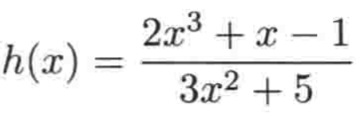
同样求h(-x)：

 

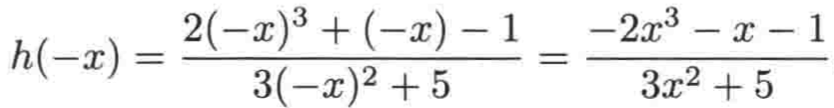
然后把负号提到前面来：

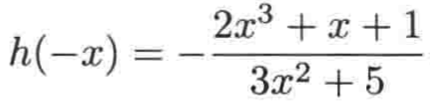
很明显它是满足：，是奇函数。

错！！！！注意看它跟原函数不是成负的关系：

 

这块一定要看仔细，其实这个函数是非奇非偶的。

奇偶函数的积：

最后还有一个性质，其实这个非常好理解，先给出结论：

奇函数x奇函数=偶函数；

偶函数x偶函数=偶函数；

奇函数x偶函数=奇函数；

这里只证明一个就可以了，其它的都类似，这里就证明一下两个奇函数的积是偶函数：

假设有两个奇函数f和g，它们的乘积的函数为h，那么就有：

h(x) = f(x)g(x)

要想证明h函数是偶函数，则需要求h(-x)，来吧：

h(-x) = f(-x)g(-x)，而f和g都是奇函数，根据它的性质我们都知道：

f(-x) = -f(x)，g(-x) = -g(x)，所以：

h(-x) = (-f(x))(-g(x))=f(x)g(x)=h(x)

最后把整个转换的过程式子输出来就是：

偶函数就可以得证了。 

函数图像：

线性函数的图像：

线性函数了解：

线性函数是一个比较简单的函数，它的形式是：f(x) = mx + b，百度百科了一下，这种表示形式叫斜截式：

，它的图像比较简单，就是一条直线，如下：

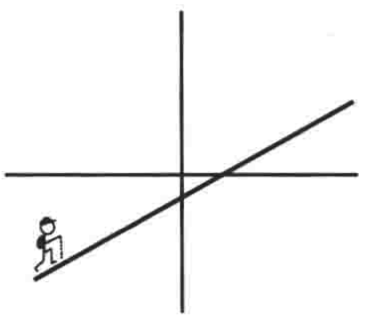
如图中有个人在山上行走一样，这里涉及到一个斜率的概念，当斜率m为正数时，说明你正在上山，m越大其这段上坡就越陡；而如果斜率m为负数， 那么就是在下山，m的数值越小（既绝对值越大），这段下坡也就越陡；如果斜率m为0，说明这段山路是水平的。

如何绘制线性函数的图像？

对于线性函数的图像，其实就是需要确定两个点，好，下面来看下如何来找这两点：

第一个点：其中有一个很容易找，那就是y轴的截距，其实在上面百科定义中也提到了它：

那啥叫截距呢？继续百科：

哦，也就是图中的这个点：

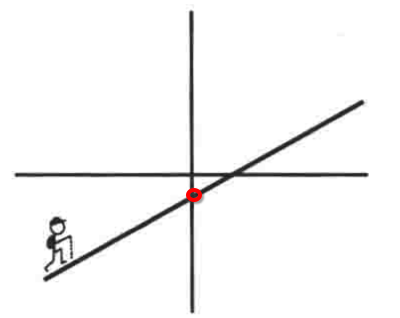
所以算y轴的截距非常之简单，把线性函数中的x用0代入就可以求得：

y = m x 0 + b = b，所以，百度百科中也描述了线性函数中的b就是y轴的截距了，所以这个点就为(0, b)

第二个点：当然就是找x轴的截距喽，也就是设y=0，求x对吧，也就是mx+b = 0，求x=-b/m，那么第二个点就为（-b/m,0），有了两个点，你就可以画出该线性函数的图像啦，

不过，这种方法【找x轴和y轴的截距来确定直线的方法】在如下两种特殊情况下是不适用的，下面来看一下：

情况一：b = 0，此时函数变为了y = mx，直线通过原点，x轴和y轴的截距都为0，很明显无法确定直线，这里需要再算另一个点，可以把x=1代入，可得y = m，所以直线y = mx是通过原点和(1, m)这两点，所以像这种y = -2x，它的函数图像就可以知道了，它是通过原点和(1, -2)的两点，所以图就是：

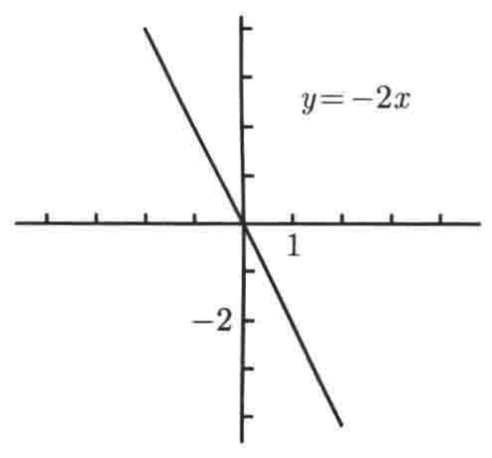
情况二：当m=0时，这时的直线函数就变为y = b，是一条通过(0, b)的水平直线。

总之，你要记住的是： 

 

记住之后，下面再来练习一下这个函数：

 

你知道它的函数图像长啥样不，如果你不学习基本的套路肯定是很难想到的，下面来把上面所学的思路再来挼一下：

1、y轴的截距是-1，斜率是1/2；

2、为了画这条直线，我们还需要求得x轴的截距对吧，那就是让y=0，求出x，很简单0 = 1/2x - 1，可以求得x=2；

有了x,y轴的截距之后，两点就可以确定一条直线了，所以其函数图像就为：

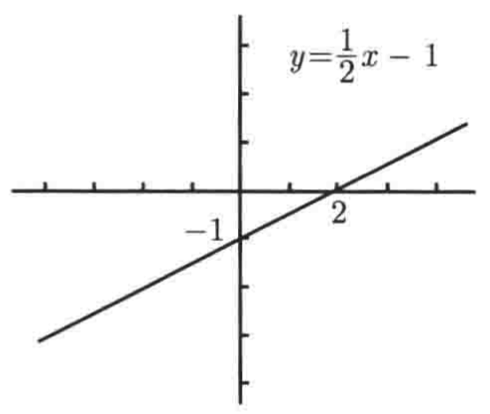
是不是很简单，当然简单的前提你要学会这些套路才行。

直线方程的点斜式：【重要！！！】

定义：

这个就非常非常重要啦，在之后的学习中会经常用到，也就是假设你知道平面上有一条直线，但是不知道它的方程。如果你知道这条直线通过某一个固定的点以及它的斜率，那就能容易地找到它的方程，这个公式就叫直线方程的点斜式，其定义为：

如果已知直线通过点(x0, y0)，斜率为m，则它的方程为y - y0 = m(x - x0)。

但是有时你可能不知道直线的斜率，但是知道它通过哪两个点，那怎么求方程呢？技巧就是先求得它的斜率，然后再用上面的点斜式公式就行了，所以这里需要知道另一个求两点的斜率的公式了，如下：

如果一条直线通过点(x1, y1)和(x2, y2)，则它的斜率等于(y2 - y1)/(x2 - x2)。

实践：

例一：

如果已知一条直线通过（-2, 5），斜率为-3，求它的方程？如果你记得直线方程的点斜式公式，一下就可以写出来：

y - 5 = -3(x - (-2))，化简后方程为y = -3x = 1。

例二：

通过(-3, 4) 和 (2, -6)的直线方程是什么？这个就需要用到求斜率的公式了，具体如下：

1、求斜率：

2、由于经过(-3, 4)这点，斜率为-2，那么就可以利用直线方程的点斜式来一口气写出它的方程了：

y - 4 = -2(x - (-3))，化简后为y = -2x - 2；

同样我们也可以使用另一个点(2, -6)和斜率-2，得出方程，其实是一样的：

y - (-6) = -2(x - 2)，化简后也是y = -2x -2; 

常用函数及图像：

以下函数是我们应该知道的最重要的一些函数，因为如果你不知道，会对之后的学习效率大大打扣【未来学习微信分中会大量运用到】，所以这里好好的回顾一下。 

多项式：

定义：

比如这样的函数就是一个多项式：

这种函数是基于x的非负次幂建立起来的，你可以以

等为基本项，然后用实数同这些基本项做乘法，最后把有限个这样的项加起来。像举的这个多项式它就是由x⁴的5倍+x³的-4倍+10而形成的，其中我们也可以加中间的基本项x²和x，由于它们木有出现在式子中，我们可以说是零倍的x²和零倍的x。

其中基本项xⁿ的倍数叫作xⁿ的系数，如咱们举的这个多项式：

它们的常数项的系统分别为5、-4、0、0、10。其中最大的幂指数n（该项系数不能为零）叫作多项式的次数。对于举例的这个多项式很明显它的次数为4次：

下面对于n次多项式的公式进行一个定义：

次数为n的多项式的数学通式为：

其中an为xⁿ的系统，an-1为x^n-1的系统，以此类推，直到最后一项1的系数为a0。

函数图像： 

由于xⁿ是所有多项式的基本项，因此你应该知道它们的图像是什么样的。偶次幂的图像之间是非常类似的，同样奇次幂的图像之间也很类似，比如下面看一下从x⁰到x⁷的图像：

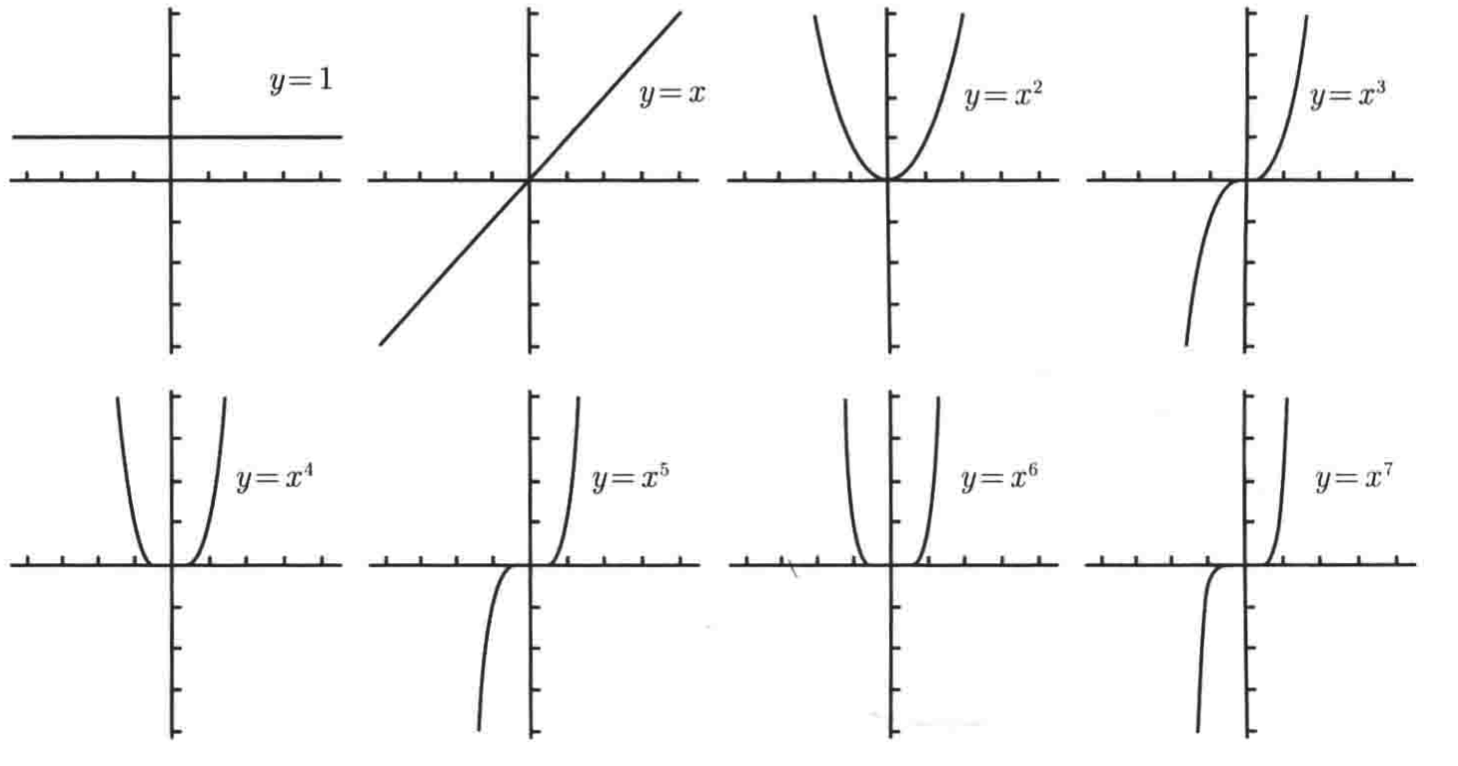
但是！！！很多时候多项式的图像是很难画的，除非是简单的多项式，否则连x轴的截矩都很难找到。

不过，多项式的图像左右两端的走势倒是很容易判断。这是由最高次数的项的系数决定的，该系统叫作首项系数，如我们所举的多项式的例子中5x⁴-4x³+10，其中5则为它的首项系数。实际上，我们只需考虑首项系数正负以及多项式次数的奇偶就能判断图像两端的走势了，具体图像两端的走势共有如下四种情况：

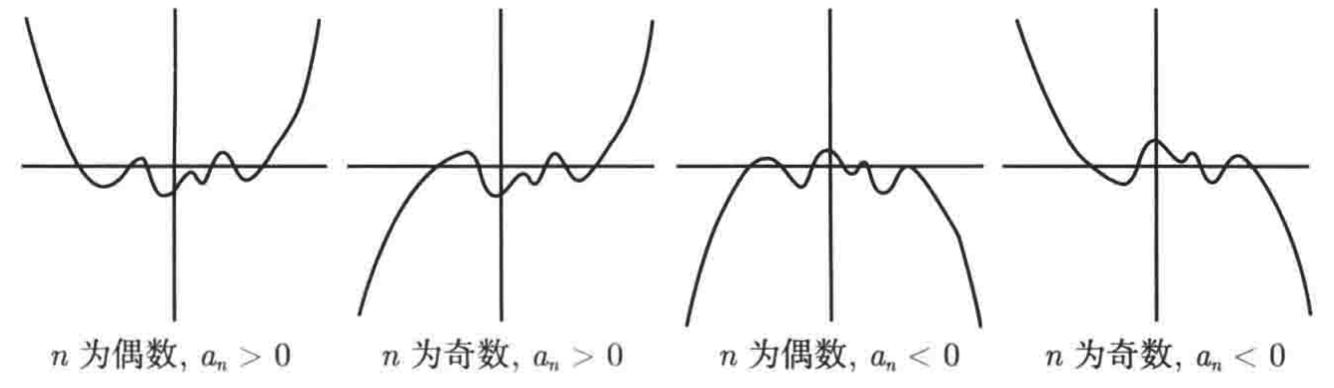
注意：上述图像的中间部分是由多项式的其他项决定的，上图仅仅是为了显示图像左右两端的走势。那对于我们举例的这个多项式5x⁴-4x³+10，它的图像同最左边的图像类似，因为n=4为偶数，a_{n=5为奇数。}

二次函数：

定义：

通常对于次数为2的多项式叫二次函数，注意，它的形式不写成p(x) = a2x² + a1x + a0，而把系统分别写成a、b、c会更简单一些，既：

p(x) = ax² + bx + c

求解：

而这个x的解是啥呢？这里涉及到判别式的一个东东：

其中是用的希腊字母Δ(读做“delta”)来表示判别式=b²-4ac，根据它的正负可以决定这个二次函数的解的情况，如下：
1、Δ > 0，有两个不同的解，解为：

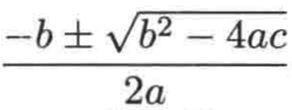
2、Δ = 0，只有一个解，解为：

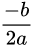
3、Δ < 0，在实数范围内是无解的。

配方：

对于二次函数它有一个重要的技术就是配方，书中也说到在之后的第18章和第19章会大量运用这个技巧：

所以，咱们来看一下是如何进行配方的，这里以这个二次函数为例：2x² - 3x + 10

第一步：把二次项的系数提出来，此时的多项式就变成了：

此时括号里面就得到了一个二次项系数为1的首一多项式（这个词是不是也忘了，其实就是首项系数为 1 的多项式）

第二步：把首一多项式中x的系数，也就是-3/2，除以2，再平方，此时就变成了9/16
第三步：将常数项也要有9/16，此时就需要进行如下变换了：

为啥需要化成这种形式呢？因为：

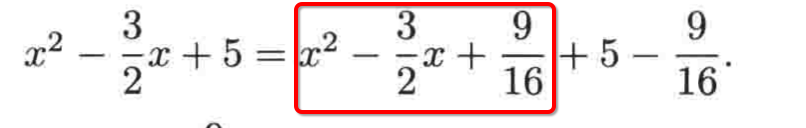
它可以写成这种平方形式：

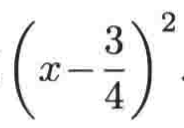
所以式子就可以变为：

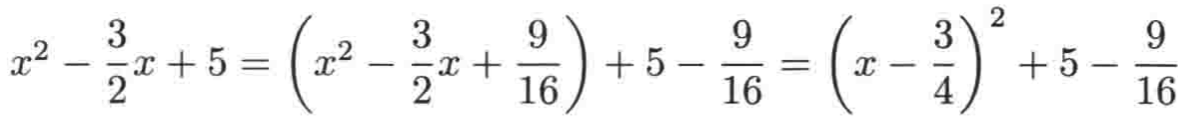
最后将5 - 9/16计算出来为：

第四步：恢复系统2，就有：

至于化成它有啥用，待之后的学习中再来感受，先记住这么有一个技巧。

有理函数：

定义：

形如：

其中p和q为多项式的函数，则把这个函数就称之为有理函数，比如：

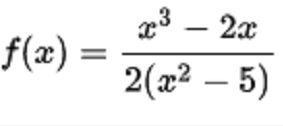
其中最简单的有理函数是多项式本身，既q(x)为1的有理函数；另一个简单的例子是1/xⁿ，其中n为正整数。

函数图像： 

有理函数变化多样，它的图像根据p和q两个多项式的变化而变化，下面来感觉一下1/xⁿ这个简单的有理函数的图像：

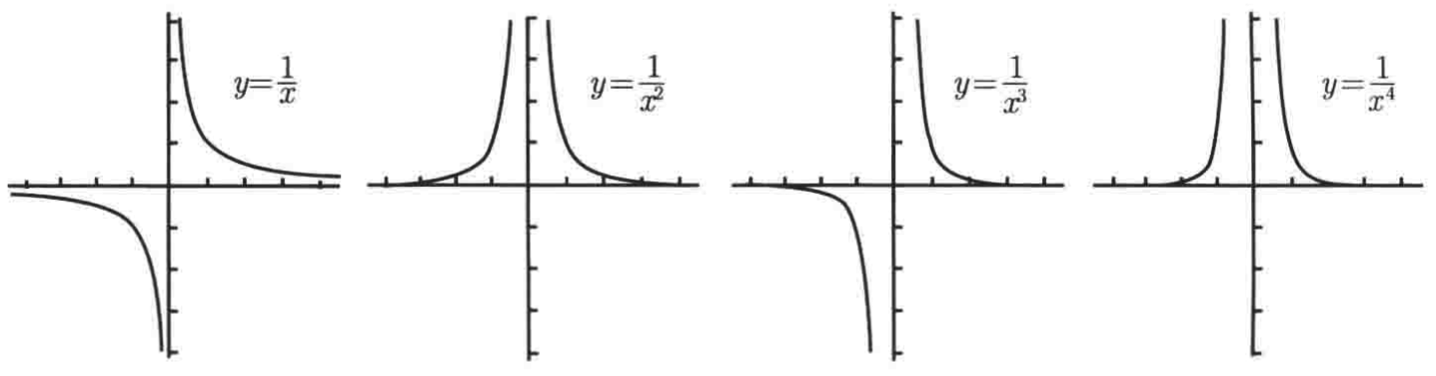
奇次幂的图像之间类似，偶次幂的图像之间也很类似。

指数函数和对数函数：

对于指数和对数函数，也是必须要掌握的，不然之后的学习会很吃力，但是呢这块的函数又是一个很容易陌生的一个知识，好好必须好好学一学。

指数函数：

指数函数的形式是y = b^x(b > 1)，它的图像基本上都类似，比如y = 2^x，它的函数图像是：

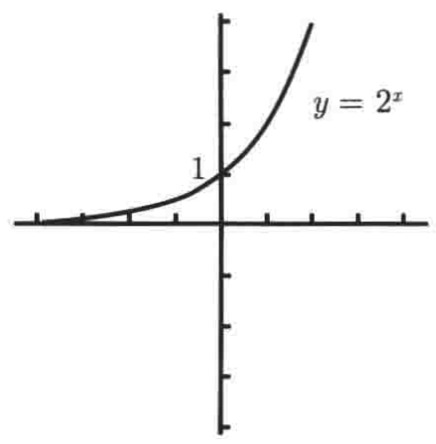
有几个需要注意的：

1、该函数定义域是全体实数；

2、y轴的截距为1并且值域为大于0的所有实数；

3、左端的水平渐近线为x轴；关于啥是渐近线可以百科一下：

其中提到了极限的概念，是的，在极限中会大量运用指数函数，这也是为啥要学习它的原因，另外渐近线其实就是趋向于0，但是不等于0。

另外对于y=2^-x的图像是关于y=2^{x关于y轴对称的，如下：}

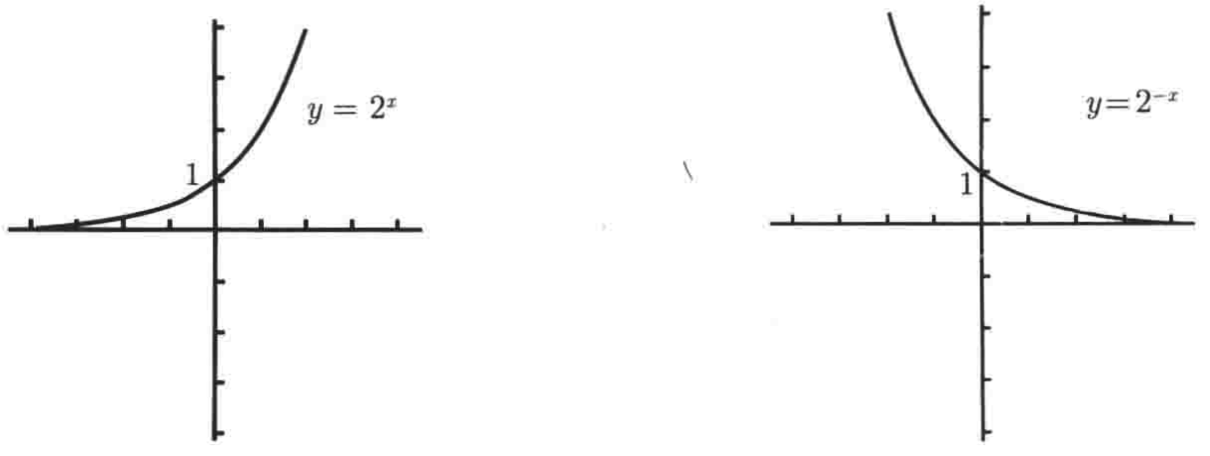
再问一下：这俩是反函数么？不是哟，反函数是基于y=x的函数进行对称的，这一点不要搞混了。

 

如果底小于1，情况会怎么样呢？比如：

 

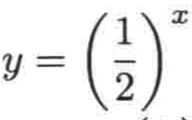
由于(1/2)^x=1/2^x=2^-x,所以它的图像其实也就是y = 2^-x的图像，所以也可以得出y = b^x(0<b<1)的图像。

对数函数： 

由于y = 2^x图像满足水平线检验，证明该函数是有反函数的，这个反函数其实就是y = log₂(x)，图像为：

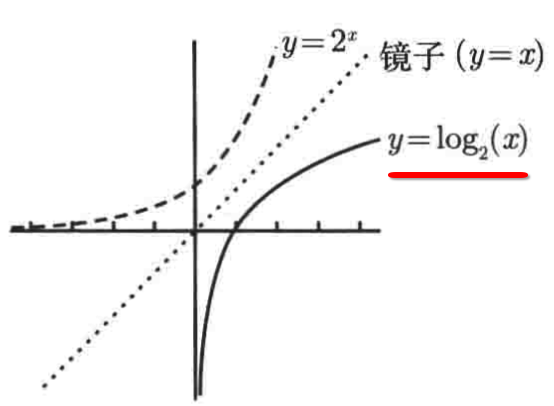
该对数函数的定义域为(0, +∞)，这也验证了之前https://www.cnblogs.com/webor2006/p/16486101.html所说的负数和0是不能求对数的说法：

 

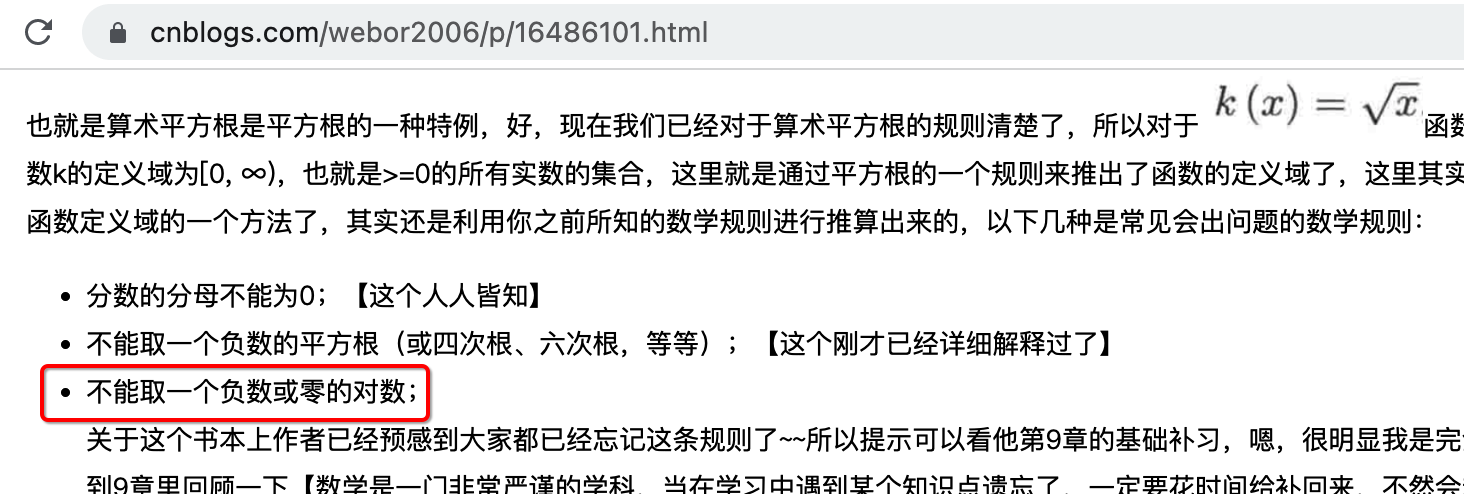
该函数的值域为全体实数，y轴为垂直渐近线，对于log_b(x)（b > 1）的图像其实都很类似。

提示：对数函数在微积分的学习中是很重要的。

三角函数：

这个非常重要，在下一篇中会集中进行学习，这里先略过。 

带有绝对值的函数：

定义：

它的形式为f(x) = |x|，这种就叫绝对值函数，具体定义如下：

比如好理解，另一个看待这个绝对值函数的方法是：它表示数轴上0和x的距离。

更一般而言，你还得知道这么一点：

|x - y| 是数轴上x和y两点间的距离。

举个例子：假设需要在数轴上找到区域|x - 1| ≤ 3，按照上面这句话来理解就可以阐释为x和1之间的距离≤3，换言之我们就是要找到所有与1之间的距离不大于3的点。所以下面来画一个数轴并标记出1的位置：

那么距离不大于3的点最左是到-2，最右到4，所以如图：

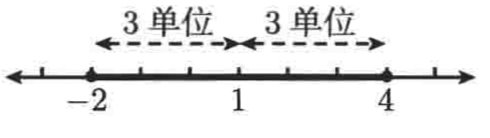
所以区域|x - 1| ≤ 3也可以表示为[-2, 4]。

另外再来看一个绝对值函数：

 

根据绝对值函数的定义，这里分两个条件来看：

1、x≥0，显然

2、x<0，显然

是不是就已经论证了：

它是成立的【两个条件的右侧是x和-x，这不就是|x|嘛】，也就是对于绝对值函数得要以分段函数去定义。

函数图像： 

先来看一下书中的描述：

如果你知道一个函数的图像，那么可以这样得到这个函数的绝对值的图像：既以x轴为镜子，把x轴下方的图像映射上来，x轴上方的图像保持不变。

可能光看文字你不知道它说的是啥意思，下面举两个例子就明白了：

例一：

对于y=|x|这个绝对值函数，你知道它的图像是啥不，不知道对吧，此时你就先把y=x【先不管绝对值】先画出来，这个肯定熟悉，然后再把x轴下方的那部分映射到x上方来，那这么个图像就是y=|x|的图像了，如下：

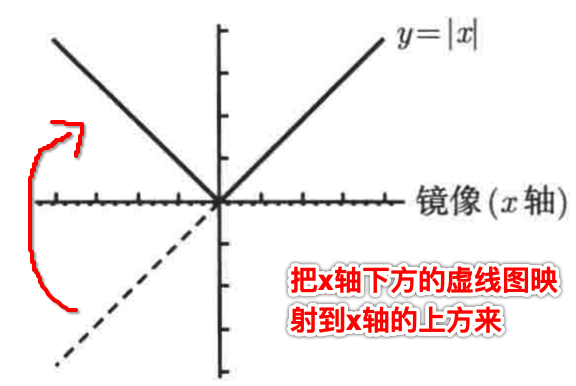
这样对于上面的描述是不是就理解了。

例二：

再来举另一个例子，假如要你画y = |log₂(x)|的图像，同样的套路，先把不带绝对值的函数图画出来，这个我们之前已经学过，其图像是这样的：

 

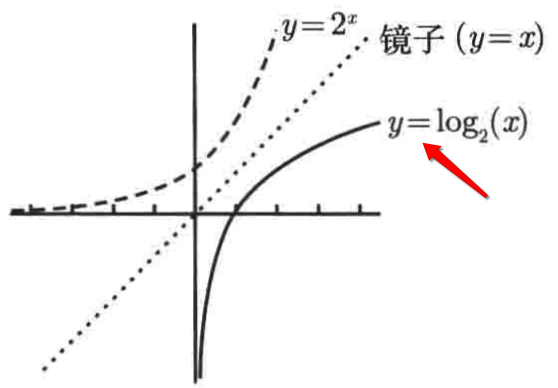
而要画它的绝对值图像，也是把x轴下方的图映射到x轴上方来既可，最终的图像就为：

 

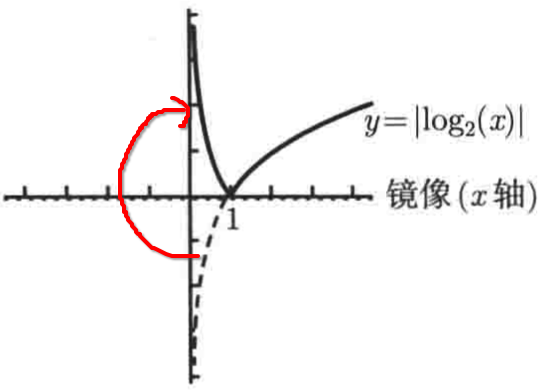
所以，只要你知道原函数的图像，对于它的绝对值函数图像就按这个套路来你就知道怎么画像了。

总结：

至此，第一章的内容就已经全部一字不落的学习完了，基本都是基础知识回顾，其中函数这部分还差非常非常重要的三角函数，在下章就重点来复习它。通过这个小章节，真的弥补了自己好多的数学基础，真的这本书对于小白真的是太适合了，基本上你可以一字不落的看完，且看得很明白，磨刀不误砍柴工，相信这些基础会为之后学习更加高级的知识带来巨大的帮助，加油！！！