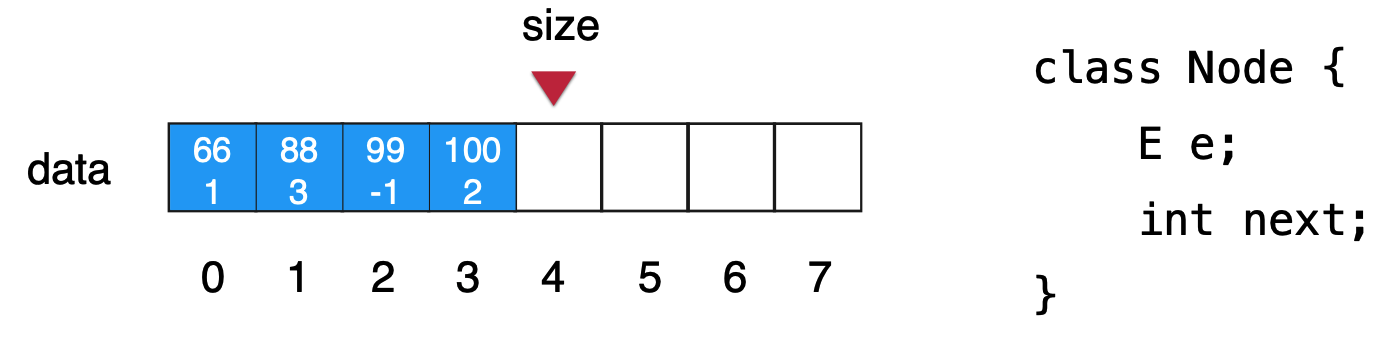
算法与数据结构基础<四>----数据结构基础之动态数据结构基础:链表<下>
链表与递归:
在上一次https://www.cnblogs.com/webor2006/p/15575331.html对于递归进行了一个初步的学习,其中在文末提到了我们在写递归算法时一定要站在递归的宏观语意上来理解,这样会简单很多,很多时候我们可以将递归算法理解成它的一个子过程就好了,这里继续对链表与递归的关系进行进一步的探讨。
链表天然的递归性:
对于链表,它其实天然就具有递归性的,如何理解?比如这么一个链表:
![]()
而它其实可以把它想像成这样:
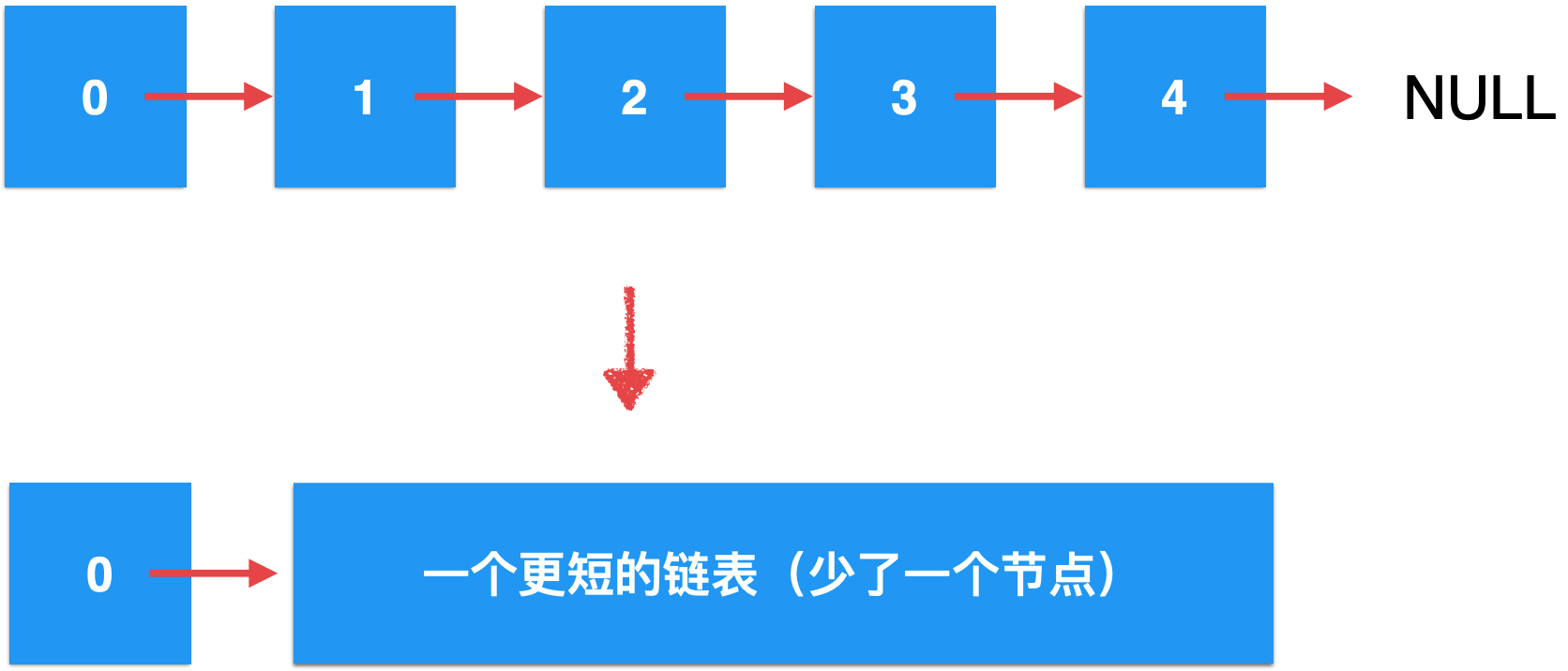
也就是第一个元素0后面又挂了一个更短的链表,这就是所谓的“天然性”,对于一个链表,我们可以将它理解成一个个节点的挂接,也可以把它理解成一个头节点它后面挂接了一个更小的链表,有了这么一个思考之后,其实对于链表的很多操作都可以用递归的逻辑方式来完成,比如下面的这个操作。
解决链表中删除元素的问题:
思路整理:
还是以删除链表中的指定元素为例,在上次已经实现了两种方式了:

但是这俩都不是使用的递归来实现的,而接下来则会使用递归的思路来完成同样的功能,先来整理一下思路【这块概述得有点抽象,先大致了解一下】,先来回忆一下对于这个问题所定义的方法:

根据链表天然具有递归性,对于原始的链表我们可以理解成这样的结构:
![]()
而对于这个更短的链表,经过递归函数,从宏观语义上来看,就变为它:
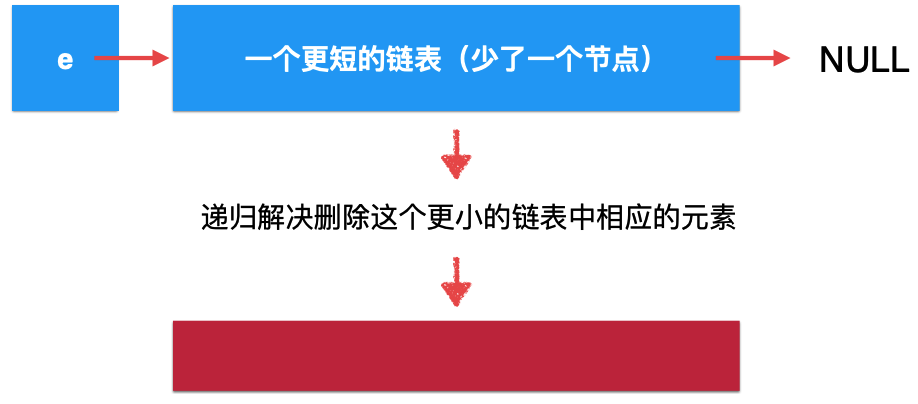
而目前它不是一个原问题的解,因为还少了一个头节点,所以此时咱们将头节点考虑进来,就会是:
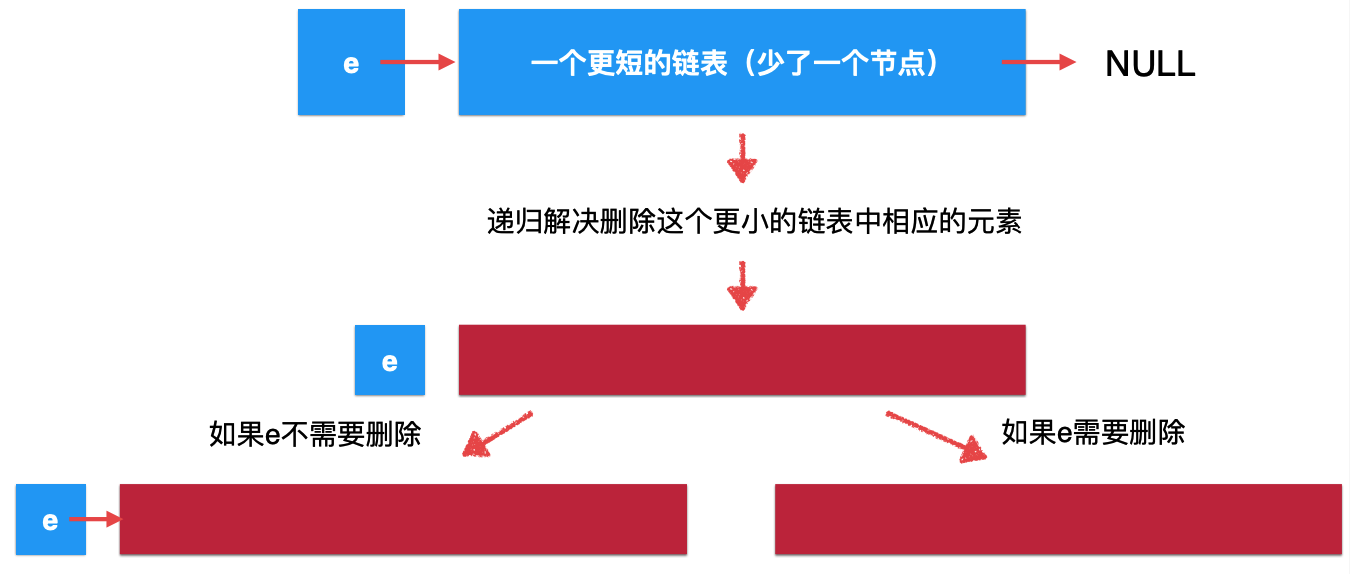
是不是比较抽象?木关系,下面结合具体代码可以进一步理解这个递归删除链表元素的思想。
实现:
1、新建文件:
其模板代码还是套用上一次咱们实现的,接下来就用递归来实现一下,先来回忆一下对于一个递归的实现它有两大步骤:
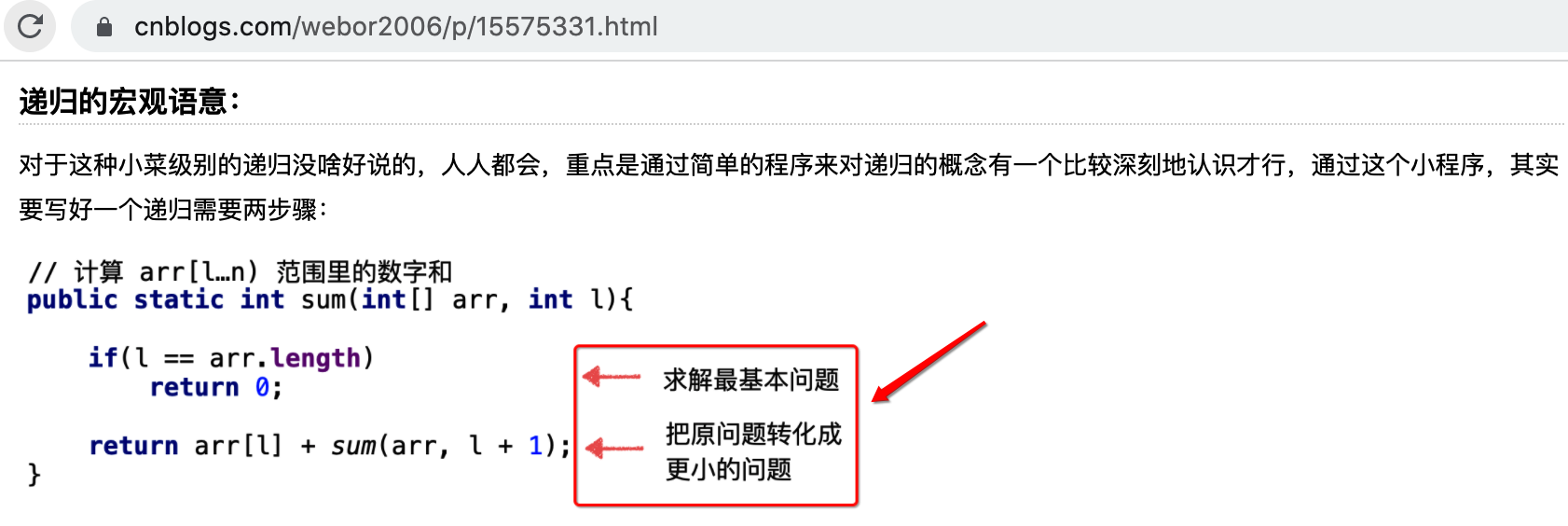
所以下面按这思路进行递归实现。
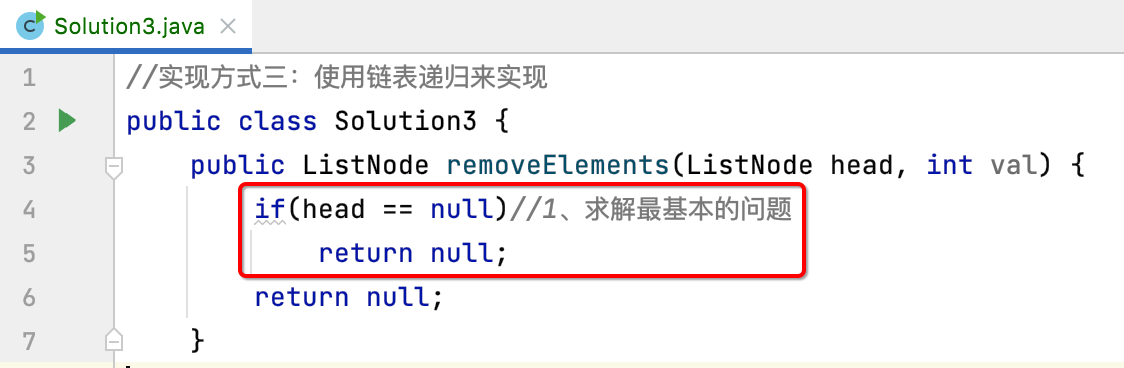
2、求解最基本的问题:
其实也就是先写好递归的结束条件,很明显当递归的最小的链表为null的时候,则整个递归就需要结束了,所以代码如下:
3、把原问题转化成更小的问题:
这里则是递归实现的重点,注意一定要以“宏观”的语意来去思考这个递归的编写,按着上面整理的思路,首先是需要将更小的链表进行递归删除元素调用: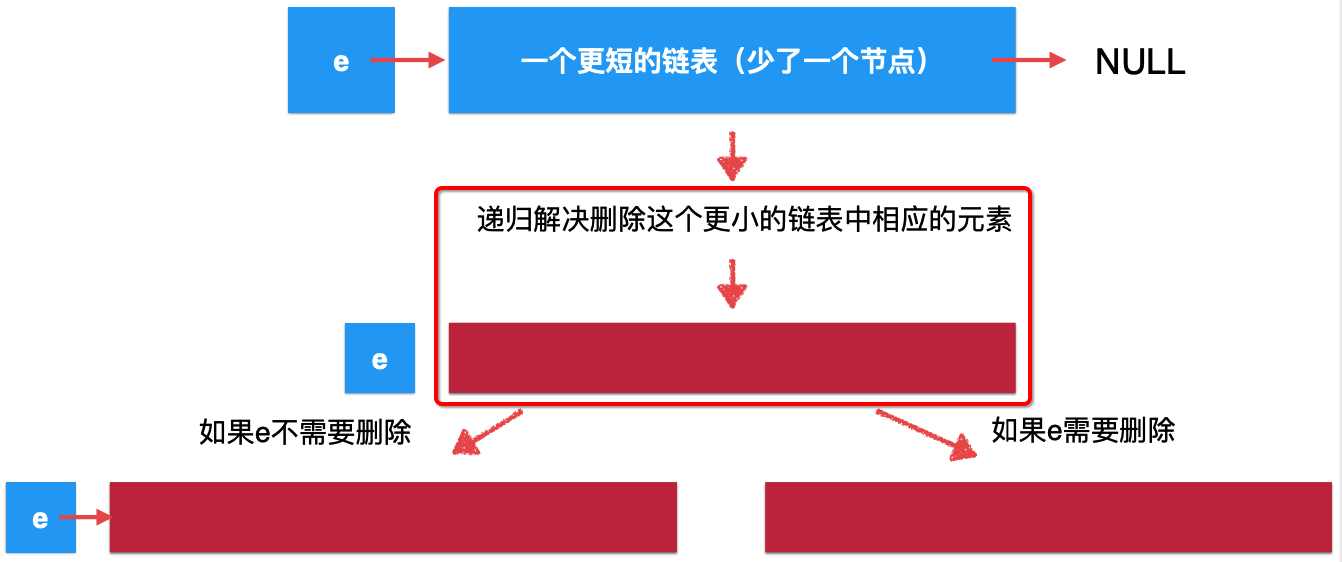
怎么写呢?递归的套路如下:

接下来则需要处理头节点了:
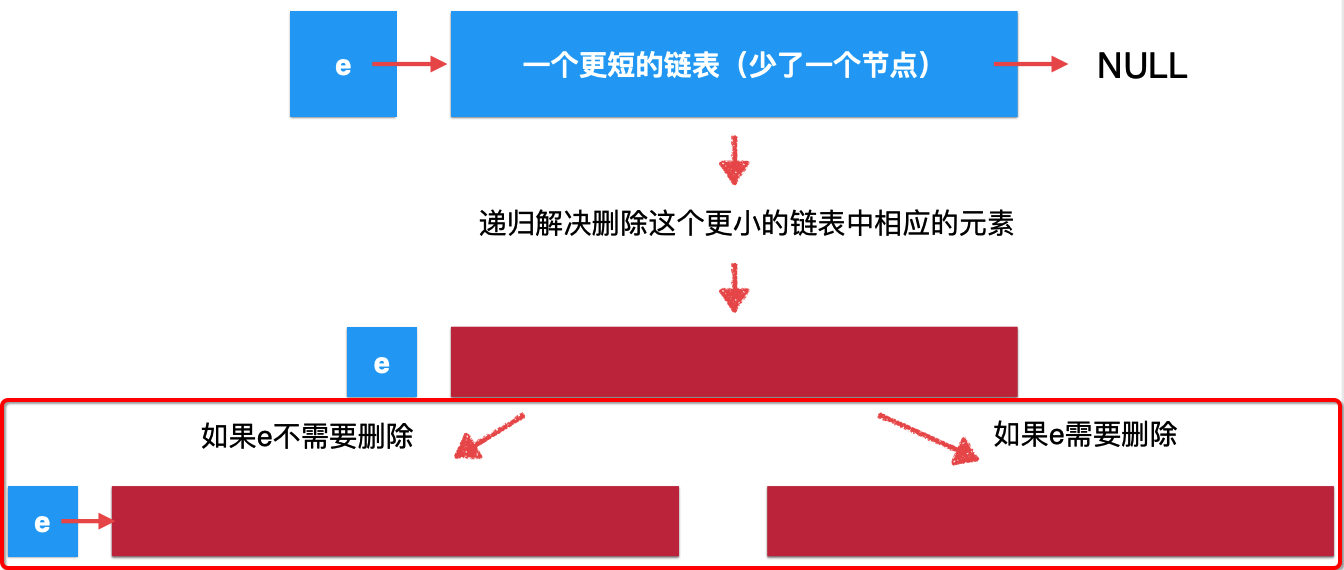
这块就比较简单了,如下:
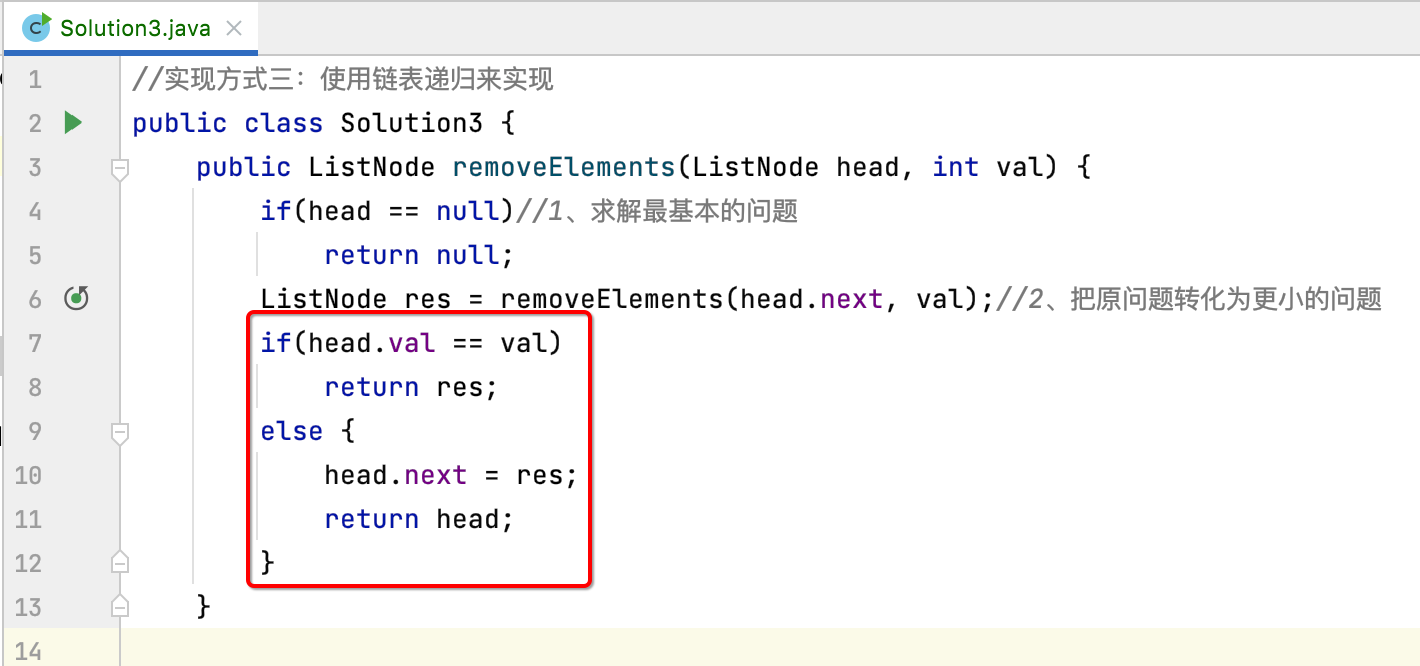
也就是用一个更小的问题的解来构建原问题。
4、测试:

木有问题。
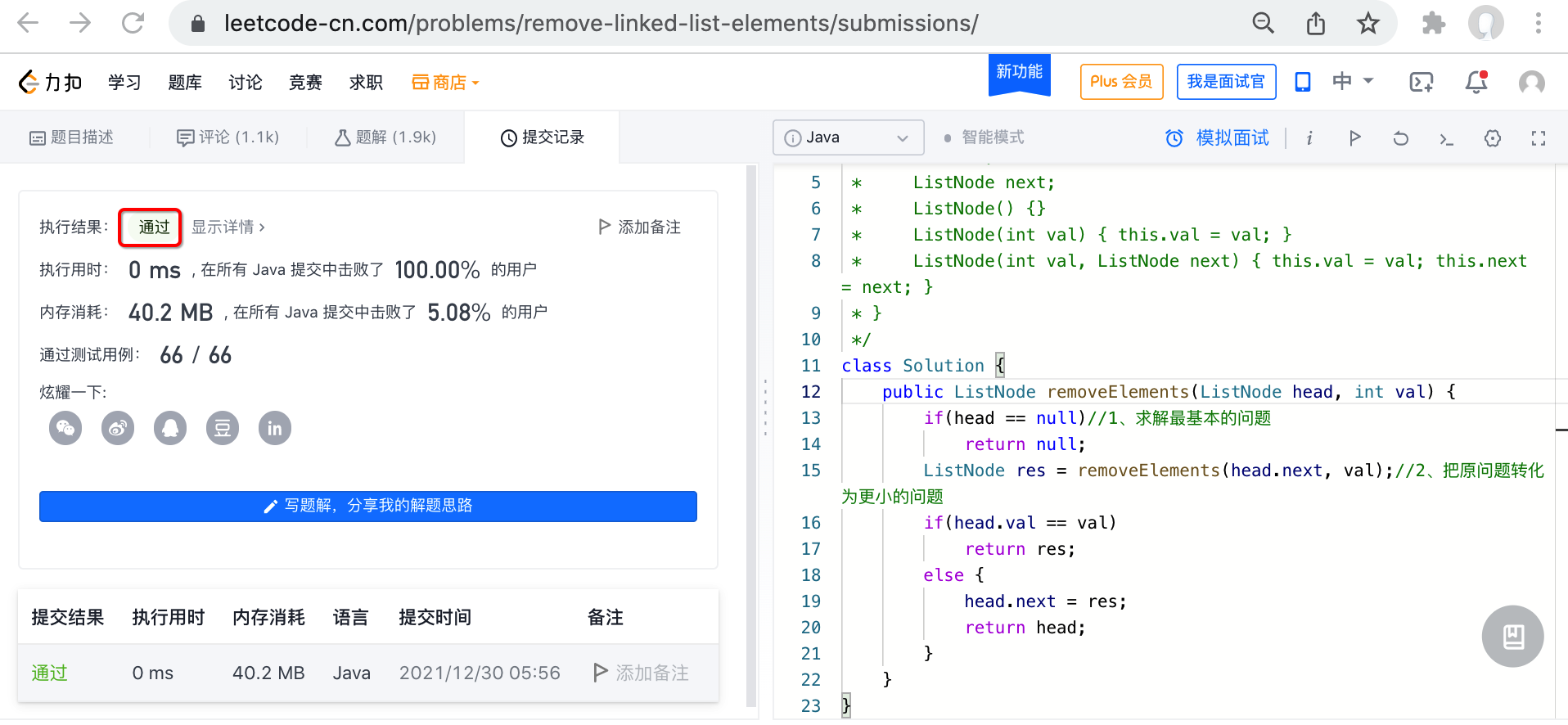
leetcode验证:
接下来将咱们的实现拷到leetcode上进行验证:
代码优化:
对于这段逻辑,其实可以精简:

怎么精简呢?如下:

而对于这个条件又可以精简为三目运算语句:
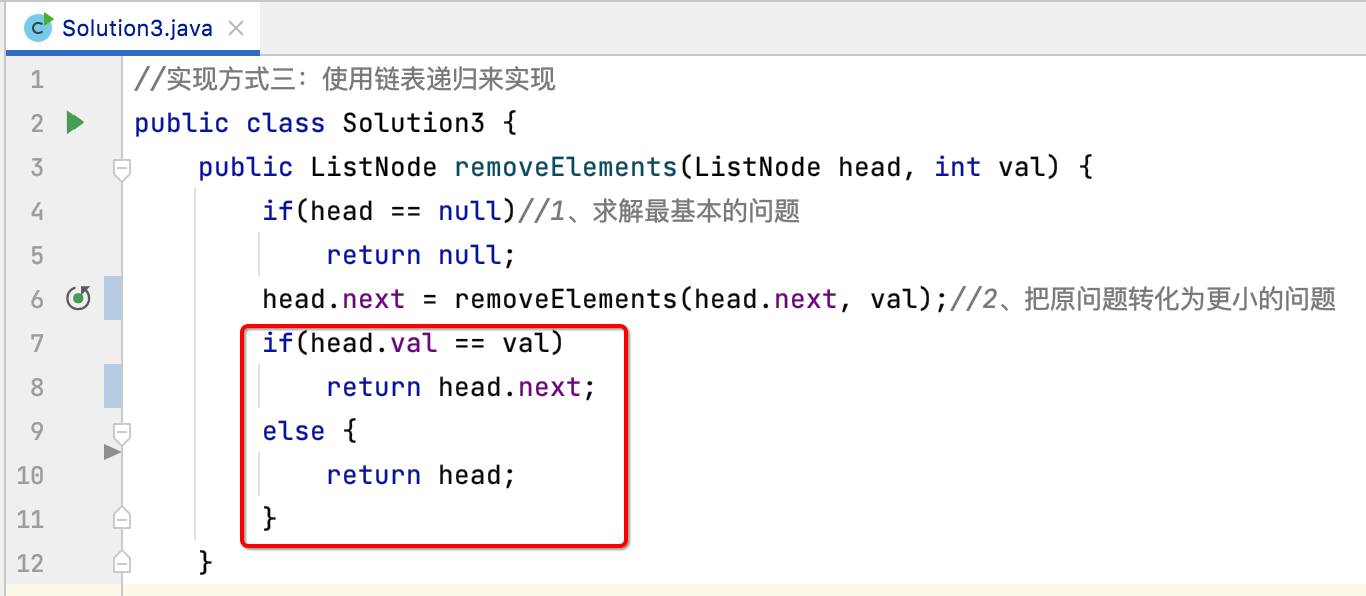

同样提交到leetcode中进行验证:

是不是相比之前非递归的方式代码更加精简?可以对比一下:
这也就是一个正常演化的过程【一上来就让你用递归的方式来写不一定能写出来,但最起码我可以用非递归的方式呀】,最终你会发现使用递归实现出来的代码是比较精练的,另外再强调一下:在写递归逻辑时,是站在宏观的语义来输写的,如果你写递归还要纠结它里面的运行机制的话会非常之痛苦,绕来绕去的很容易晕,这是一个写递归的经验之道。
递归运行的机制:递归的微观解读:
在上面输写递归的时候一直强调一定要站着“宏观”的角度来输写,因为这样能容易理解一些,但是!!!对于递归内部运行的机理难道就完全可以忽视么,当然不是,所以接下来则以“微观”的角度来从递归的内部运行机制进行一下剖析,这样不管是宏观还是微观角度来理解递归你就都了解了。
回忆栈的应用:
对于递归逻辑从本质上来说还是函数调用函数对吧,而程序调用其实是一个系统栈,关于这块其实在之前https://www.cnblogs.com/webor2006/p/14216904.html已经学习过了:

其整个系统栈的过程如下:
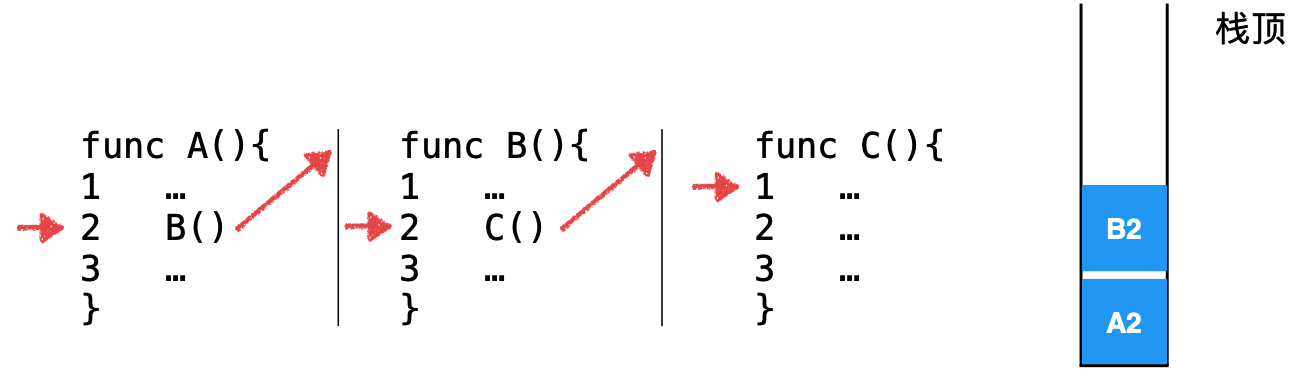
而当子函数C调用完成之后,则会从系统栈中找到上次在父函数调用该子函数的位置继续往下执行,而递归的调用跟它木有区别,只是函数调用自身罢了。
分析一:使用递归的方式来求解数组元素的和
在之前咱们实现过这么一个简单的递归程序:
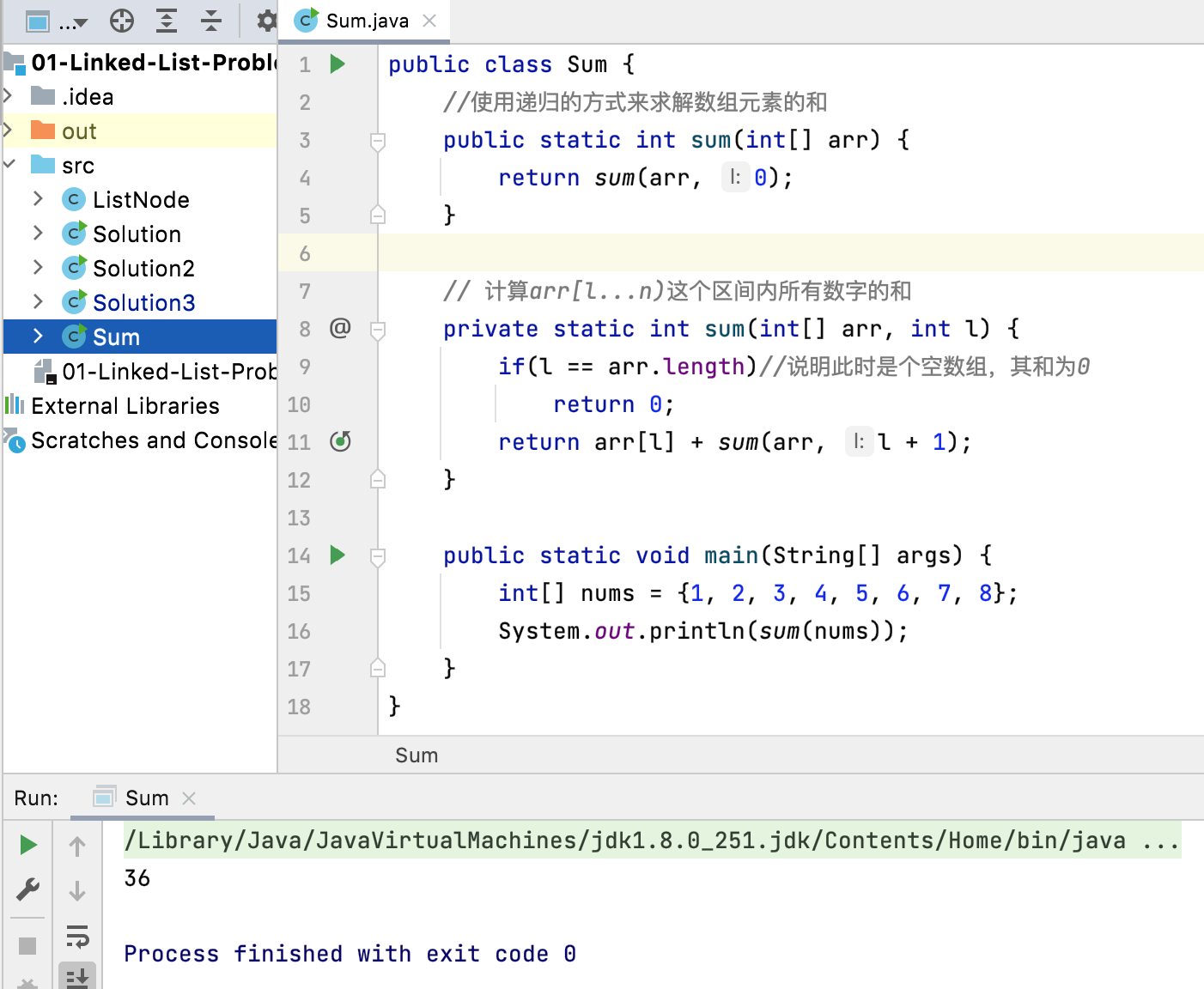
接下来咱们则先来分析该递归程序的整个内部运行的过程。
调整代码:
为了方便程序的分析,咱们将递归的实现调整一下:

也就是将原来写一行的拆成二行了:
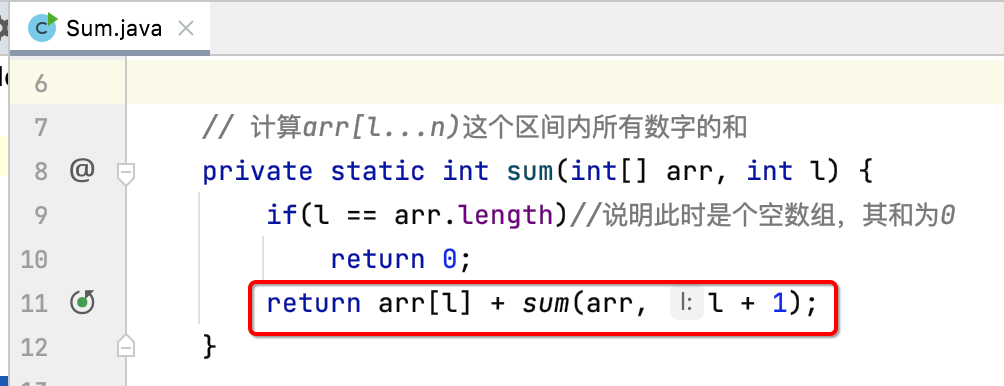
另外将第一个条件也变换一下:

开始分析:
这里以这么一个简单的数组为例进行分析:
![]()
1、调用sum(arr, 0)

此时会执行第一句话:

很明显是不成立的对吧,所以接着执行它:

此时就进入了一次递归调用了对吧,而对于递归调用其实就是调用了一下函数如下。
2、调用sum(arr, 1)

其实跟第一次函数调用的逻辑是一模一样的,但是为了便于理解这里将其拆开来分解了, 同样的,此时又执行函数中的第一句:

很明显条件又不满足对吧,继续往下执行:

此时又发生了一次递归调用,又是一个子函数的调用过程。
3、调用sum(arr, 2)

此时第一个条件已经成立了,所以直接返回0了,所以此时:

4、sum(arr, 1)继续往下执行:

此时该函数就可以返回了,于是:

4、sum(arr, 0)继续往下执行:
此时继续往下执行:

最终整个递归结束,其结果就是16:

总结:
至此,关于这个简单的递归程序的整个内部运转机制就已经梳理完了,这其实也揭示了当你对某个递归函数它的运转机制有点难理解的时候,用这种方式进行梳理会比较清晰易懂。
分析二:删除链表中的元素
对于上面的递归程序可能太简单了,下面咱们再以这个程序为例进行微观层面的剖析:
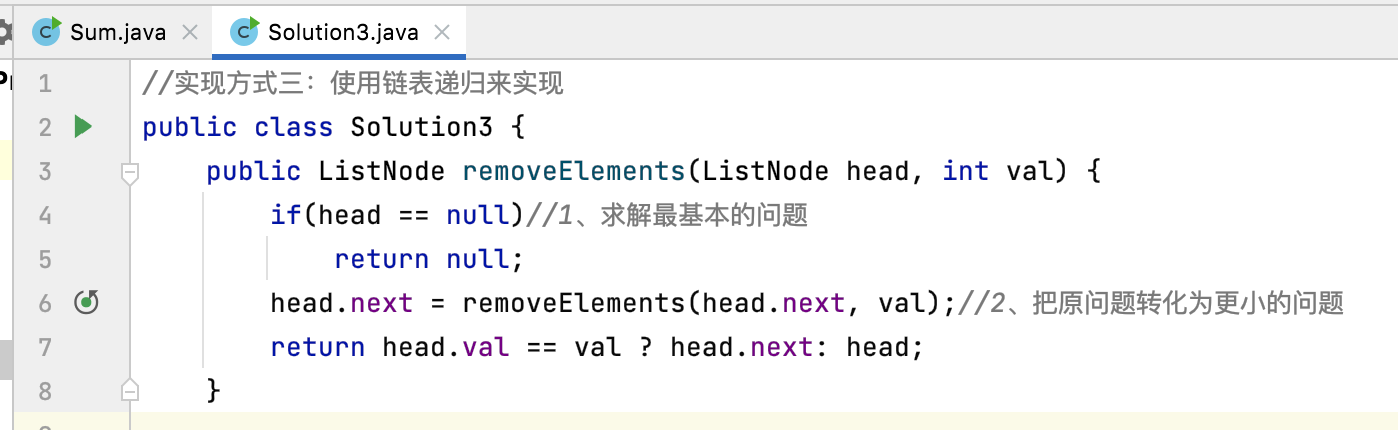
为了便于分析,先给里面函数的代码标个序号:

同样这里以一个简单的链表数据进行模拟:
![]()
开始分析:
1、第一次removeElements调用:
此时传进来的head链表为:
![]()
此时执行第一步:

接着执行第二步,开始了递归调用了:
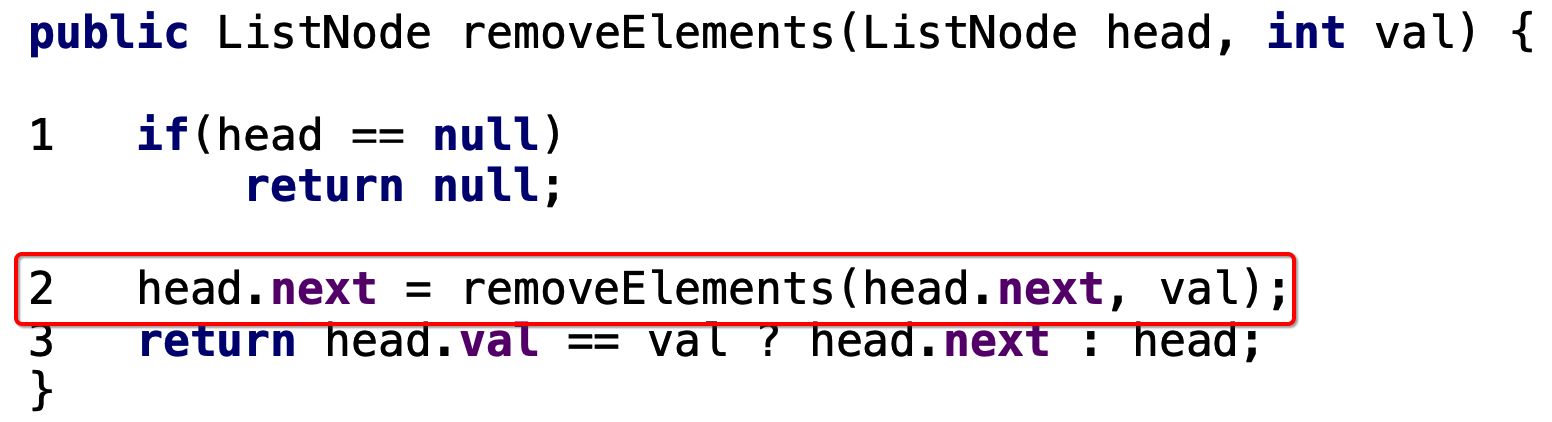
此时的状态就为:
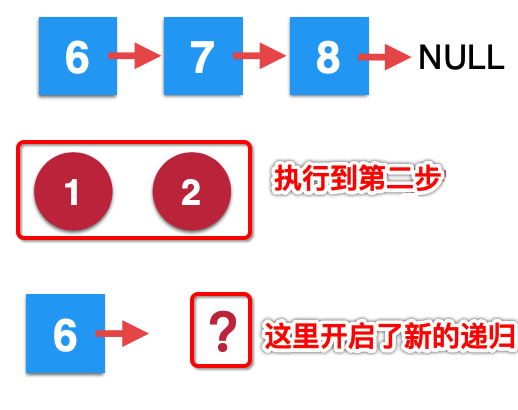
2、第二次removeElements调用:
接着看第二次递归调用:
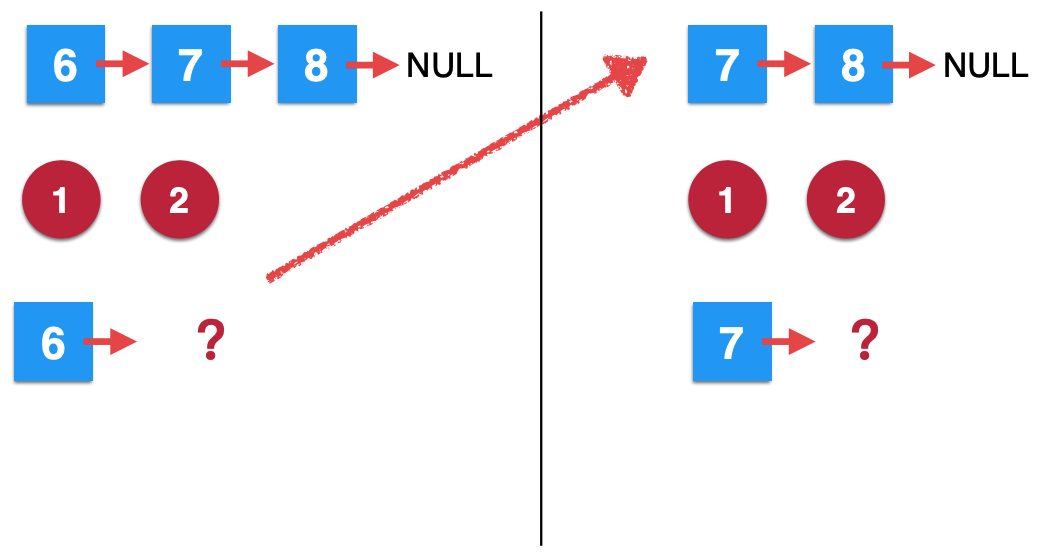
此时也停在了第二步,新的一个递归又开启了。
3、第三次removeElements调用:
同样的,看第三次递归:
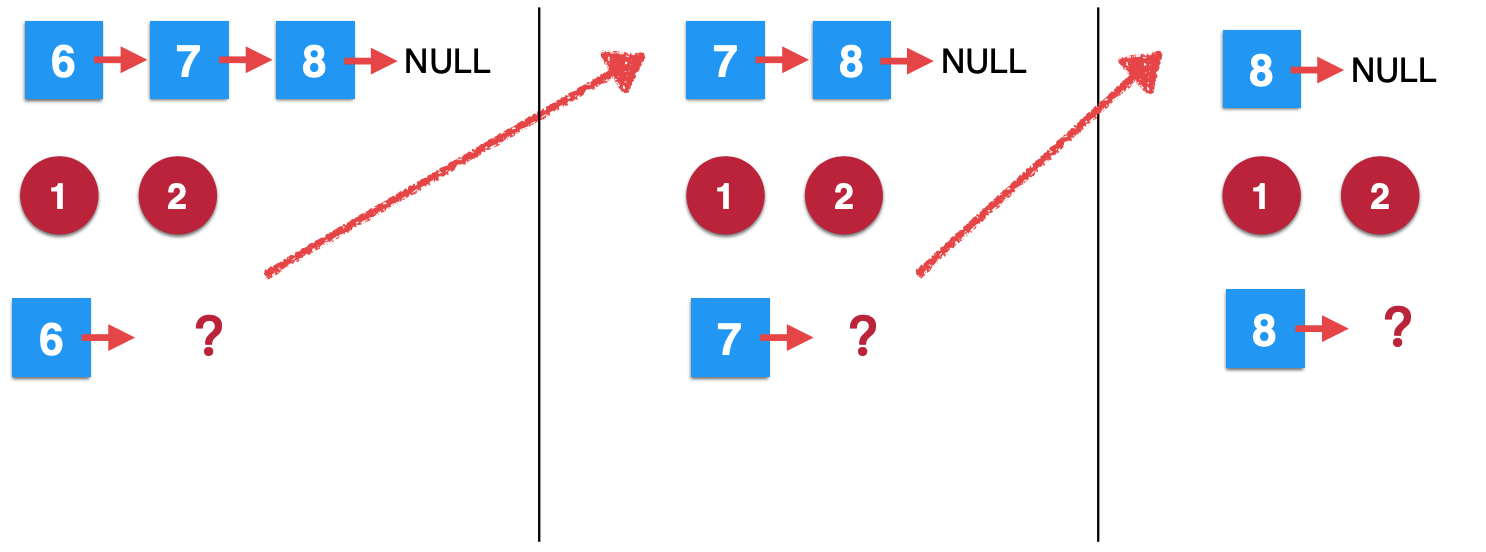
此时也停在了第二步,新的一个递归又开启了。
4、第四次removeElements调用:
同样的,看第四次递归:
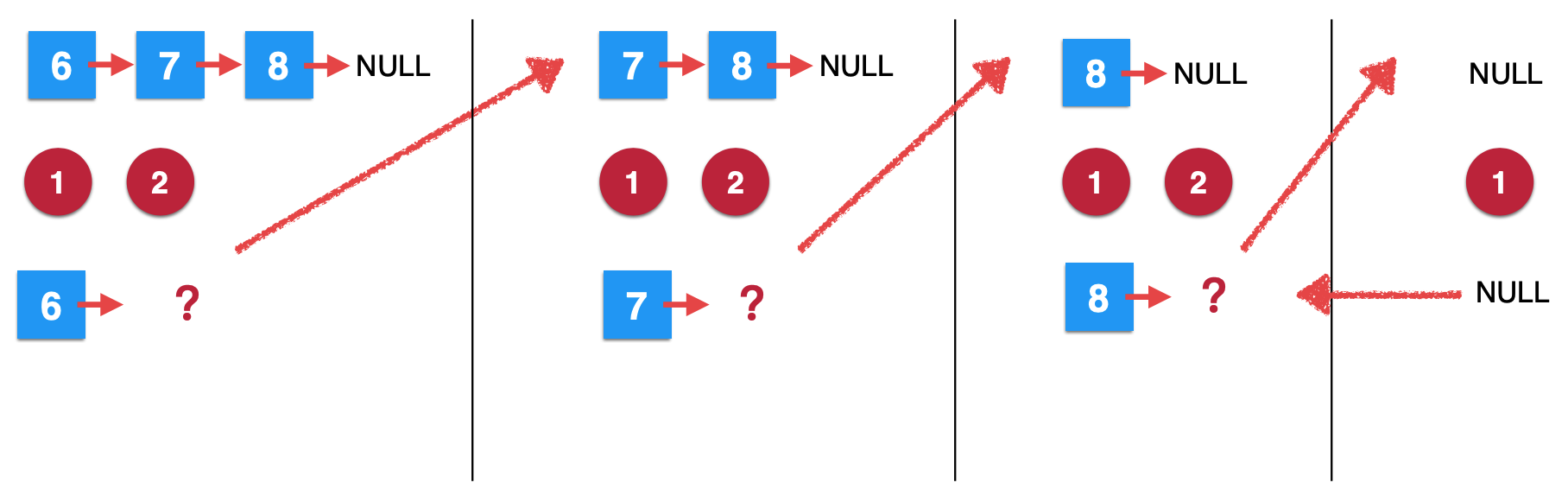
发现执行第一句时就已经满足条件了,于是乎该次函数调用返回结束。
5、第三次removeElements调用继续往下:
此时这个调用的结果就出来了:
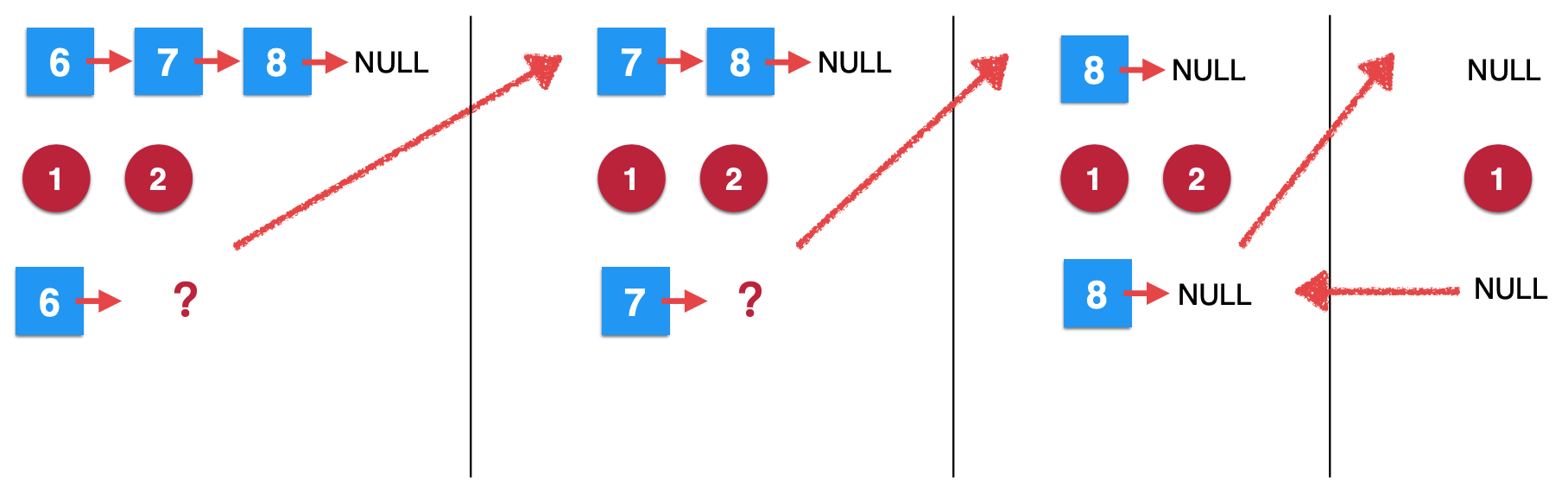
接下来可以继续执行第三步了,执行完之后,其实就是:
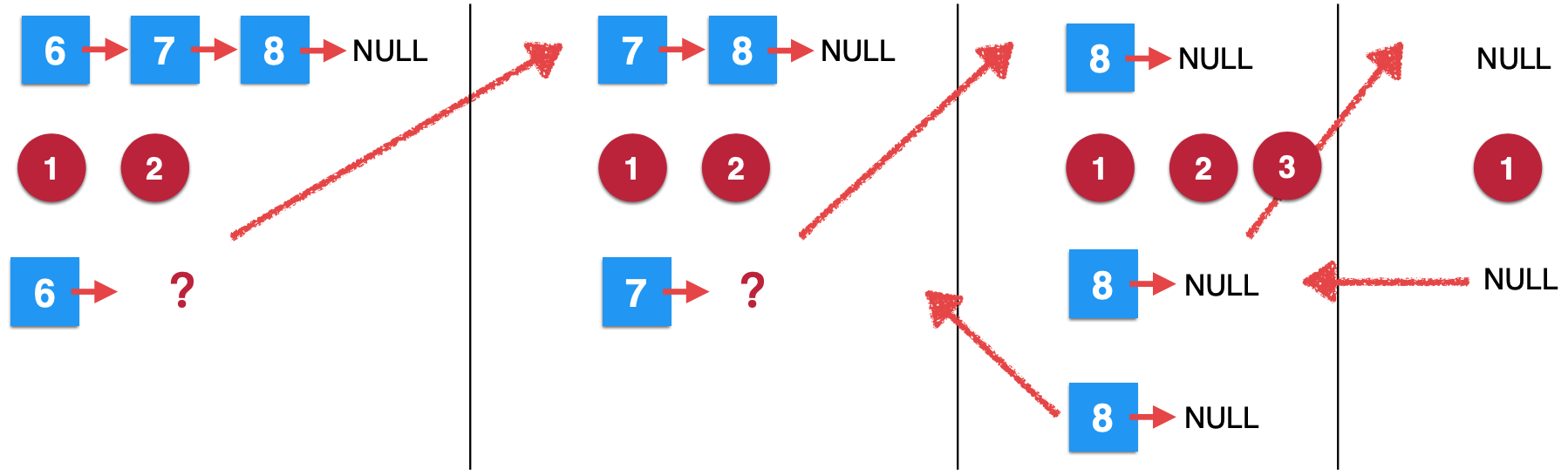
6、第二次removeElements调用继续往下:
此时第二次的递归结果出来了:
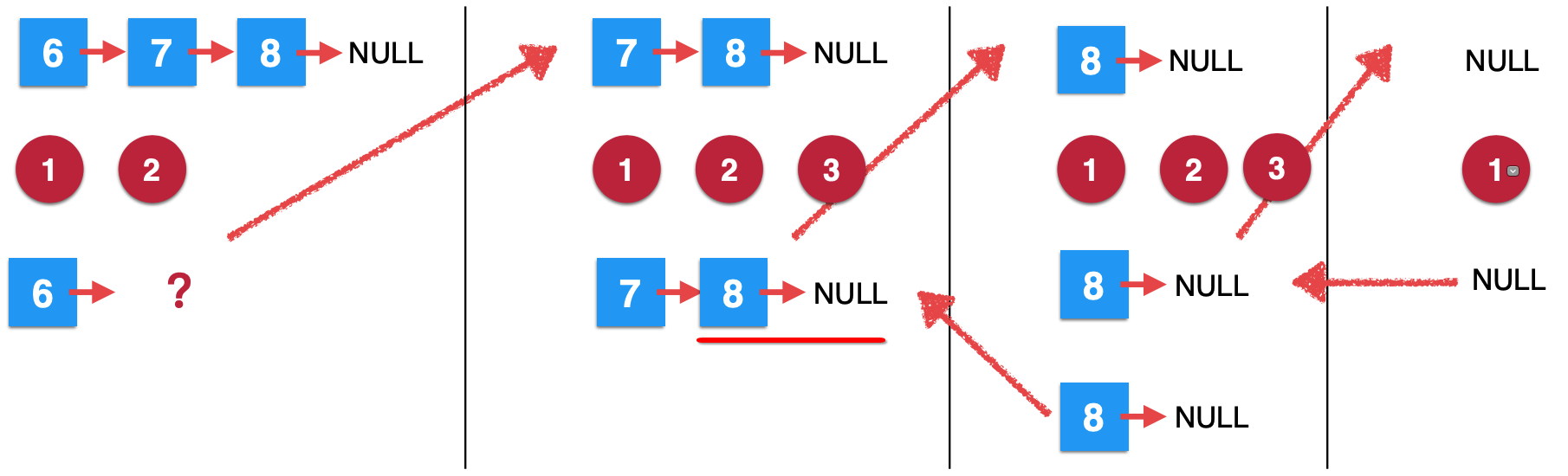
然后接着继续往下执行第三步,很明显由于此时的head就刚好等于待删除的元素7,所以返回它的next,所以如下:

7、第一次removeElements调用继续往下:
同样的逻辑,第一次的调用就可以继续往下执行,最终整个递归算法就可以结束了,如下:
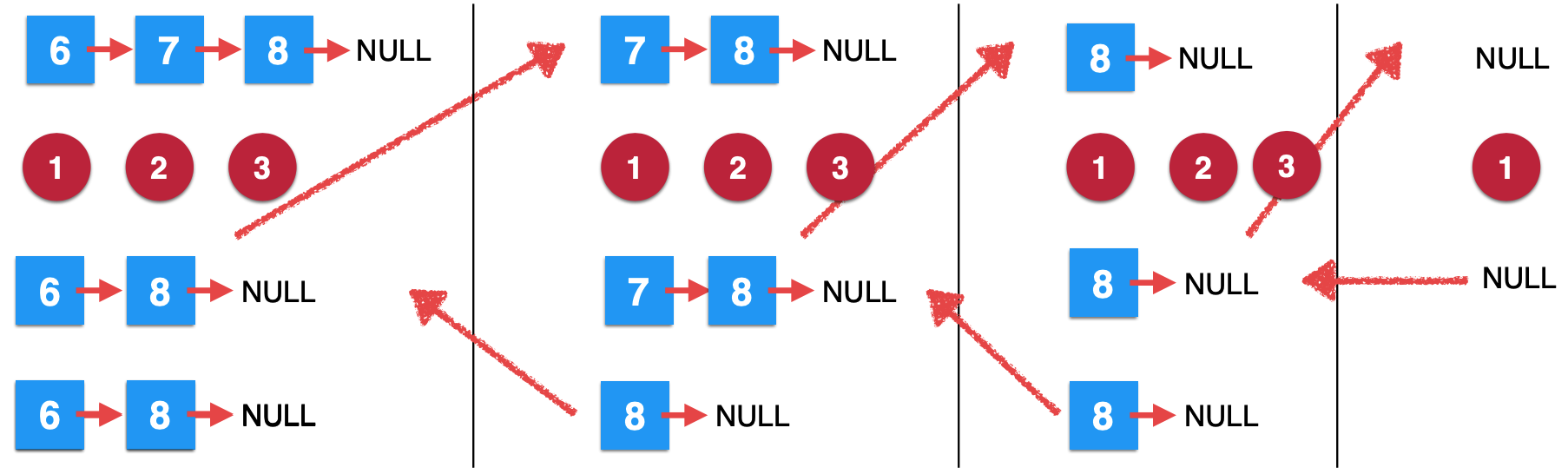
最终的结果就为6 -> 8 -> NULL。
递归调用的代价:
当然对于递归调用其实我们都知道它是有系统性能问题的,主要表现在:
1、函数调用是有时间开销的,比如当前的函数逻辑执行到哪了等等。
2、递归调用的过程是会消耗系统栈空间的,最典型的异常就是StackOverFlow对吧。
既然有这些代价存在,那递归存在的价值在哪呢?其实是对于非线性的数据结构【树、 图】逻辑实现会更加的简单,在线性结构上其实看得不是很明显,另外递归在逻辑输写上也显得比较清晰。
递归算法的调试:
在上面咱们是通过一步步递归函数的拆解的过程来理解咱们的递归程序对吧, 但是这种梳理的成本有点高,其实还有一个比较能看出整个递归内部机制的方式,那就是日志打印,通过给咱们的递归程序加上一定的日志输出最终呈现出整个递归过程,下面咱们以链表删除的程序为例:
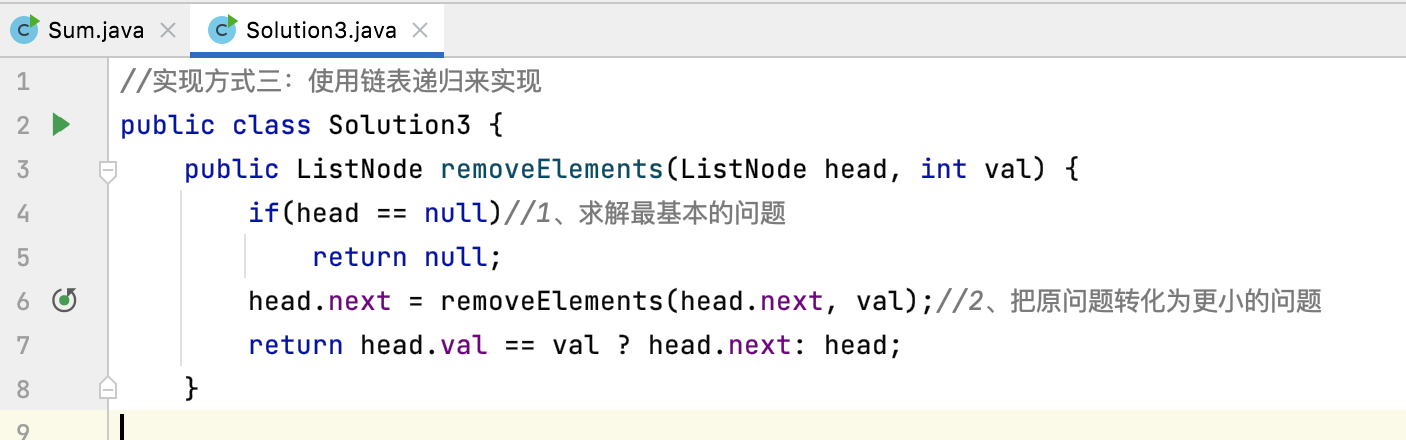
下面咱们来修改一下。
增加日志:
在递归调用中,很明显存在尝试的问题,所以为了能在日志输出中更加可读,这里加一个深度的参数:
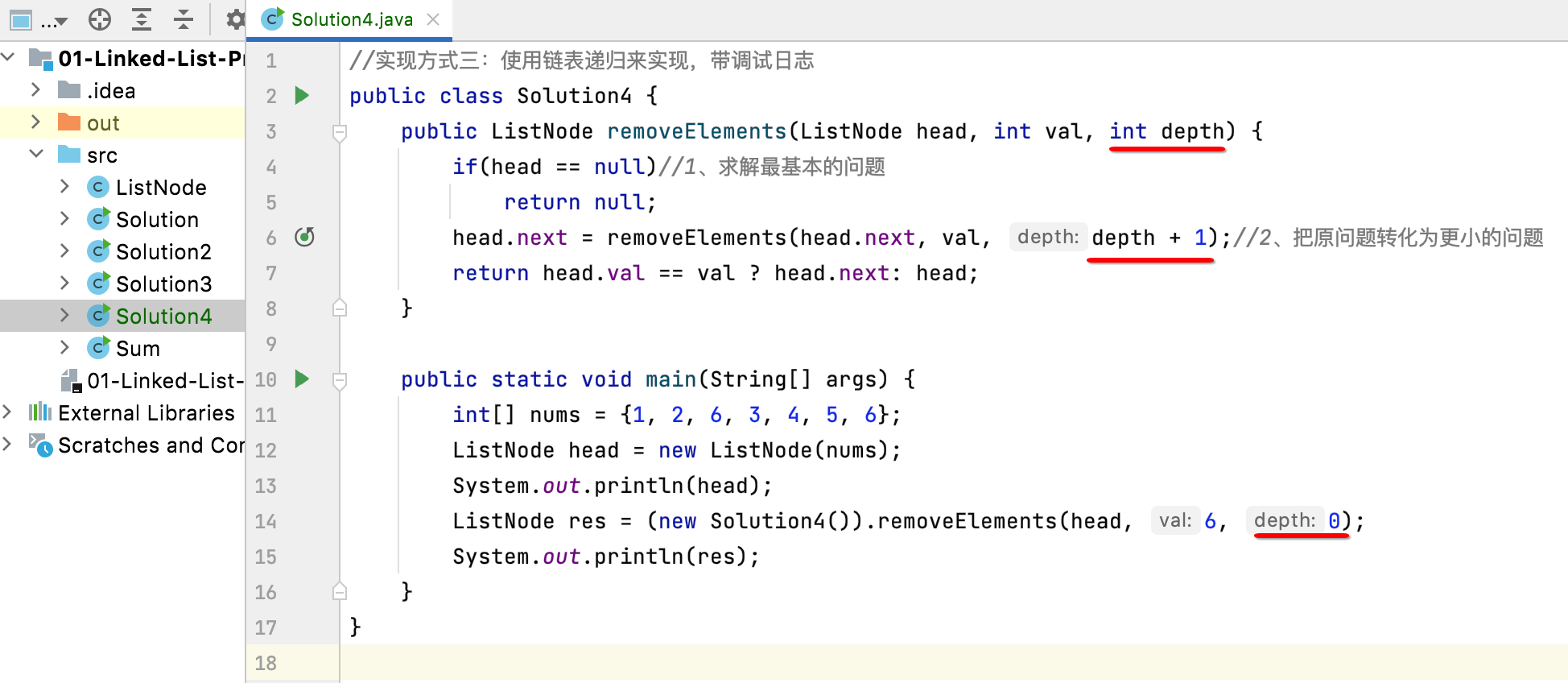
所以此时就可以先来打印一下调用深度:
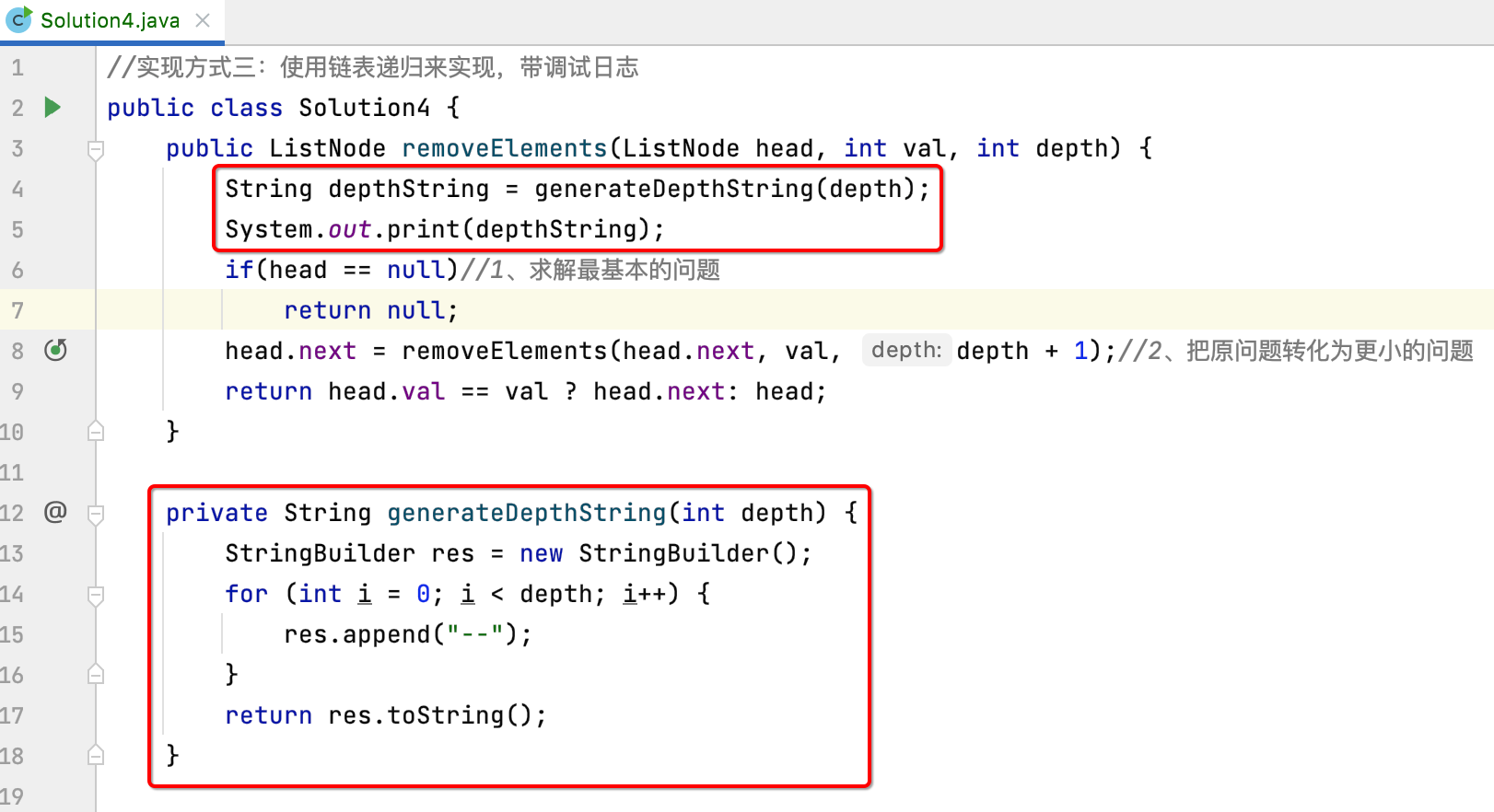
接着来再输出这么一句话:
然后在这个条件中加些打印:
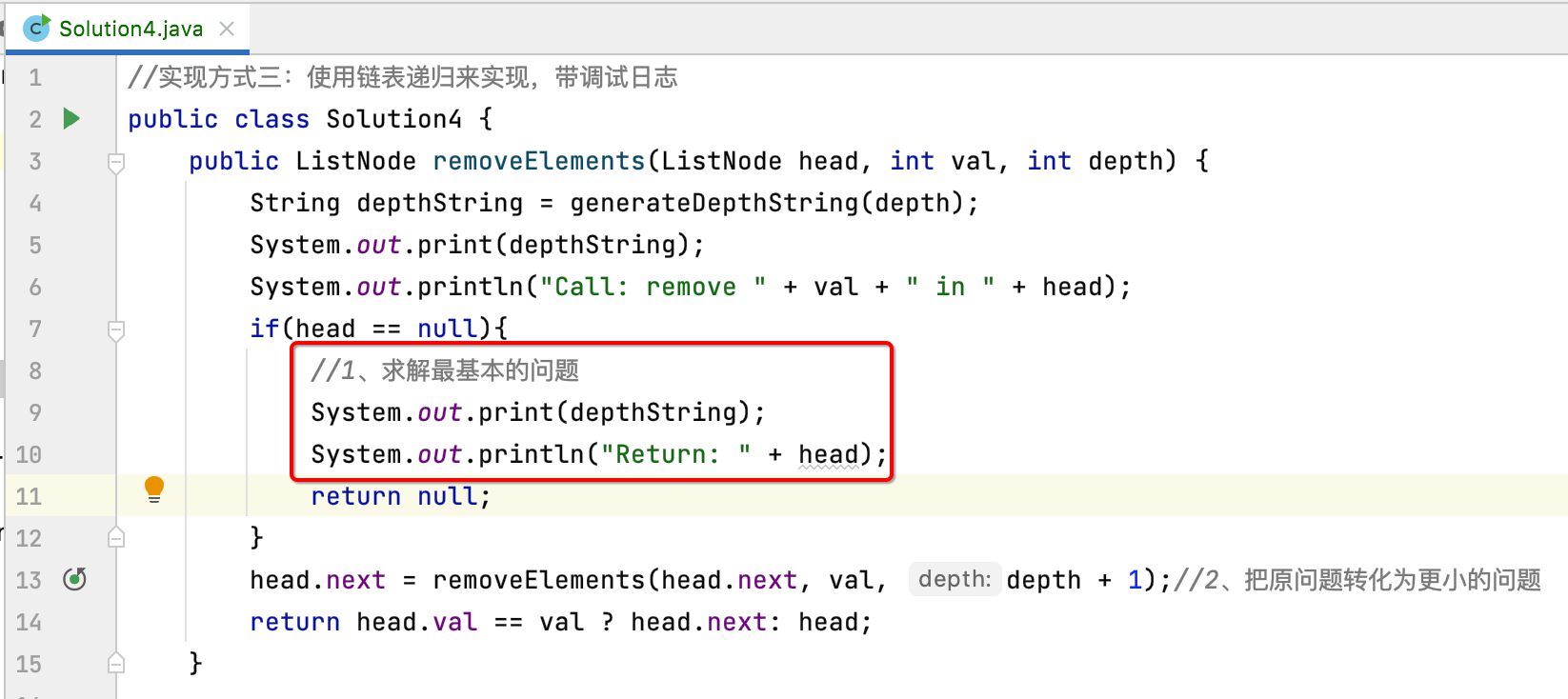
接下来则需要给这块的代码增加日志了:

为了打印这里需要改造一下:
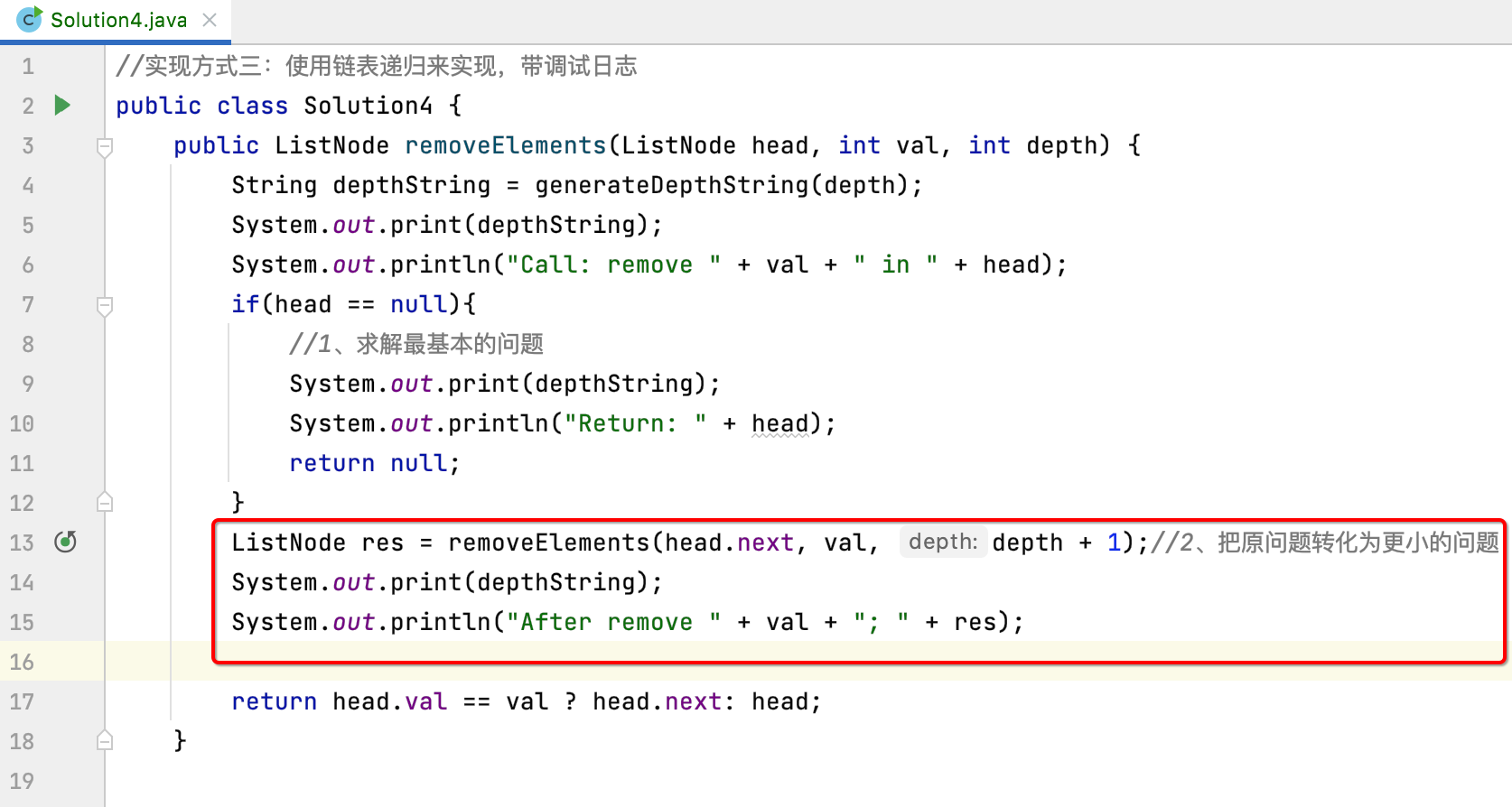
最后结果返回处也改造一下:
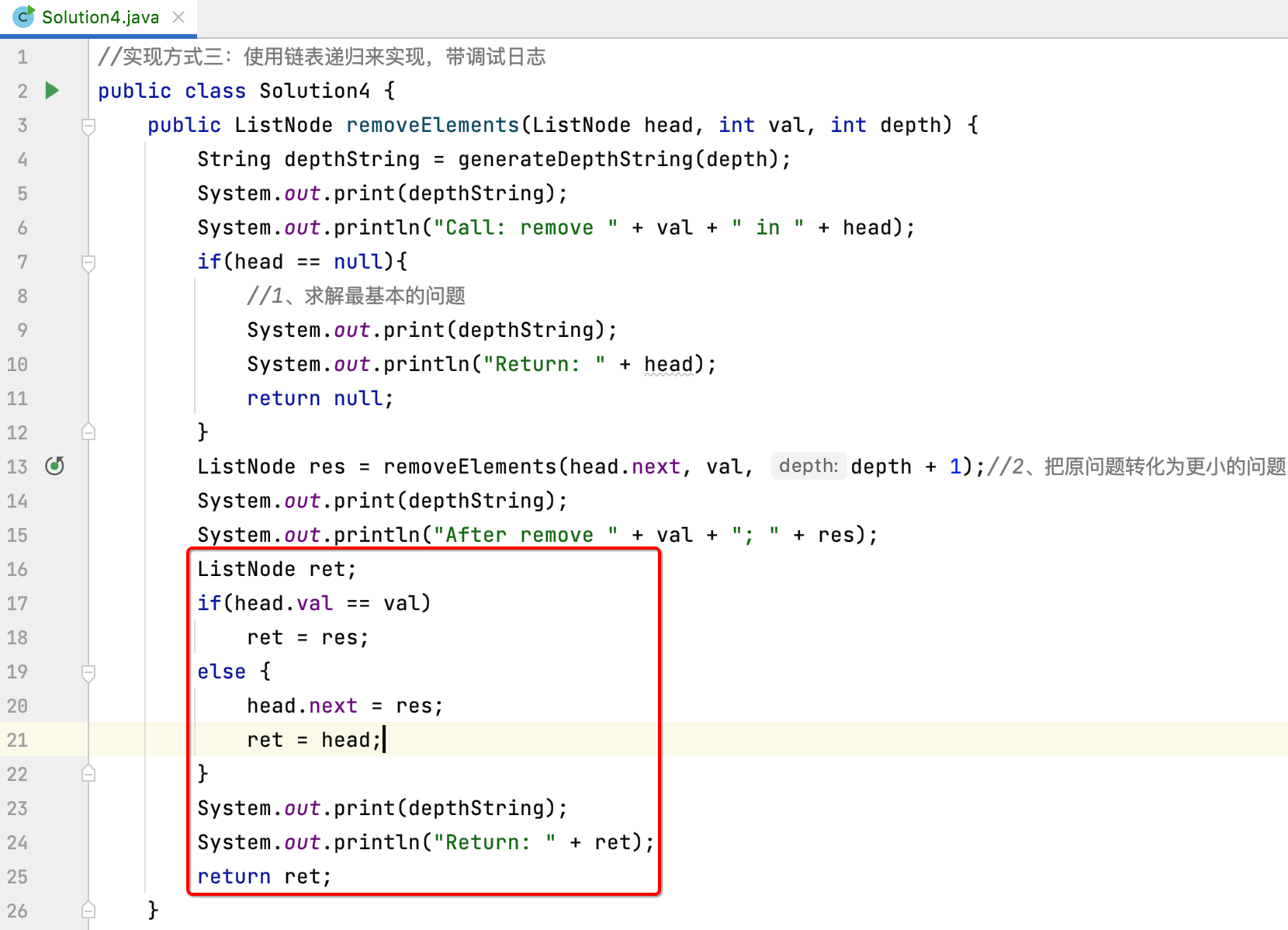
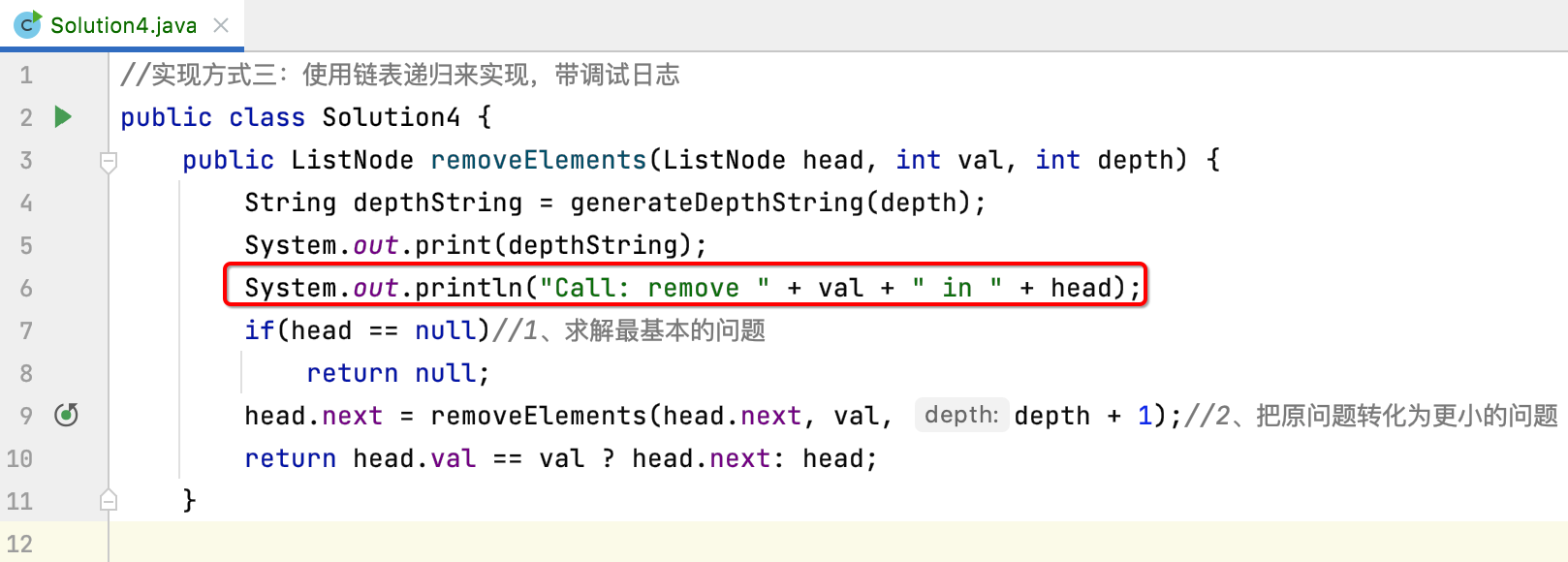
运行:
接下来运行看一下:
/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/bin/java -Dfile.encoding=UTF-8 -classpath /Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/charsets.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/deploy.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/ext/cldrdata.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/ext/dnsns.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/ext/jaccess.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/ext/jfxrt.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/ext/localedata.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/ext/nashorn.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/ext/sunec.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/ext/sunjce_provider.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/ext/sunpkcs11.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/ext/zipfs.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/javaws.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/jce.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/jfr.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/jfxswt.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/jsse.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/management-agent.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/plugin.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/resources.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/jre/lib/rt.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/lib/ant-javafx.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/lib/dt.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/lib/javafx-mx.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/lib/jconsole.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/lib/packager.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/lib/sa-jdi.jar:/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/lib/tools.jar:/Users/xiongwei/Documents/workspace/IntelliJSpace/algorithm_system_sudy/08-Recursion/01-Linked-List-Problems-in-Leetcode/out/production/01-Linked-List-Problems-in-Leetcode Solution4 1->2->6->3->4->5->6->NULL Call: remove 6 in 1->2->6->3->4->5->6->NULL --Call: remove 6 in 2->6->3->4->5->6->NULL ----Call: remove 6 in 6->3->4->5->6->NULL ------Call: remove 6 in 3->4->5->6->NULL --------Call: remove 6 in 4->5->6->NULL ----------Call: remove 6 in 5->6->NULL ------------Call: remove 6 in 6->NULL --------------Call: remove 6 in null --------------Return: null ------------After remove 6; null ------------Return: null ----------After remove 6; null ----------Return: 5->NULL --------After remove 6; 5->NULL --------Return: 4->5->NULL ------After remove 6; 4->5->NULL ------Return: 3->4->5->NULL ----After remove 6; 3->4->5->NULL ----Return: 3->4->5->NULL --After remove 6; 3->4->5->NULL --Return: 2->3->4->5->NULL After remove 6; 2->3->4->5->NULL Return: 1->2->3->4->5->NULL 1->2->3->4->5->NULL Process finished with exit code 0
看着是不是还是有点晕,是的,但是这个输出有助于我们看到整个递归的过程,对于分析程序还是作用挺大的。
链表的递归实现:
既然链表具有天然的递归性,那么咱们在之前https://www.cnblogs.com/webor2006/p/15319904.html所实现的链表是不是都可以改为递归的方式来实现呢?答案是可以的是,其中对于链表的增、删、改、查都可以使用递归方式实现,虽说实际可能不会这么搞,但是为了加强递归的理解做这么一个练习还是有益无害滴。
先来回忆一下之前链表的实现,有两种方式,一种是不带虚拟头节点,另一种是带虚拟应结点:
//带虚拟头结点的版本 public class LinkedList<E> { private Node dummyHead;//虚拟头结点 private int size; public LinkedList() { dummyHead = new Node(); size = 0; } // 获取链表中的元素个数 public int getSize(){ return size; } // 返回链表是否为空 public boolean isEmpty(){ return size == 0; } // 在链表头添加新的元素e public void addFirst(E e){ add(0, e); } // 在链表末尾添加新的元素e public void addLast(E e){ add(size, e); } // 在链表的index(0-based)位置添加新的元素e // 在链表中不是一个常用的操作,练习用:) public void add(int index, E e){ if(index < 0 || index > size) throw new IllegalArgumentException("Add failed. Illegal index."); Node prev = dummyHead; for(int i = 0 ; i < index ; i ++) prev = prev.next; // Node node = new Node(e); // node.next = prev.next; // prev.next = node; prev.next = new Node(e, prev.next);//更优雅的写法 size++; } // 获得链表的第一个元素 public E getFirst(){ return get(0); } // 获得链表的最后一个元素 public E getLast(){ return get(size - 1); } // 获得链表的第index(0-based)个位置的元素 // 在链表中不是一个常用的操作,练习用:) public E get(int index){ if(index < 0 || index >= size) throw new IllegalArgumentException("Get failed. Illegal index."); Node cur = dummyHead.next; for(int i = 0 ; i < index ; i ++) cur = cur.next; return cur.e; } // 修改链表的第index(0-based)个位置的元素为e // 在链表中不是一个常用的操作,练习用:) public void set(int index, E e){ if(index < 0 || index >= size) throw new IllegalArgumentException("Set failed. Illegal index."); Node cur = dummyHead.next; for(int i = 0 ; i < index ; i ++) cur = cur.next; cur.e = e; } // 查找链表中是否有元素e public boolean contains(E e){ Node cur = dummyHead.next; while(cur != null){ if(cur.e.equals(e)) return true; cur = cur.next; } return false; } // 从链表中删除第一个元素, 返回删除的元素 public E removeFirst(){ return remove(0); } // 从链表中删除最后一个元素, 返回删除的元素 public E removeLast(){ return remove(size - 1); } // 从链表中删除index(0-based)位置的元素, 返回删除的元素 // 在链表中不是一个常用的操作,练习用:) public E remove(int index){ if(index < 0 || index >= size) throw new IllegalArgumentException("Remove failed. Index is illegal."); Node prev = dummyHead; for(int i = 0 ; i < index ; i ++) prev = prev.next; Node retNode = prev.next; prev.next = retNode.next; retNode.next = null; size --; return retNode.e; } // 从链表中删除元素e public void removeElement(E e){ Node prev = dummyHead; while(prev.next != null){ if(prev.next.e.equals(e)) break; prev = prev.next; } if(prev.next != null){ Node delNode = prev.next; prev.next = delNode.next; delNode.next = null; size --; } } private class Node{ public E e; public Node next; public Node() { this(null, null); } public Node(E e) { this(e, null); } public Node(E e, Node next) { this.e = e; this.next = next; } @Override public String toString() { return e.toString(); } } @Override public String toString(){ StringBuilder res = new StringBuilder(); //第一种遍历方法 // Node cur = dummyHead.next; // while(cur != null){ // res.append(cur + "->"); // cur = cur.next; // } //第二种遍历方法 for(Node cur = dummyHead.next ; cur != null ; cur = cur.next) res.append(cur + "->"); res.append("NULL"); return res.toString(); } }
//没有带虚拟头结点的版本 public class LinkedList2<E> { private Node head; private int size; public LinkedList2() { head = null; size = 0; } // 获取链表中的元素个数 public int getSize(){ return size; } // 返回链表是否为空 public boolean isEmpty(){ return size == 0; } // 在链表头添加新的元素e public void addFirst(E e){ // Node node = new Node(e); // node.next = head; // head = node; head = new Node(e,head);//更优雅的写法 size ++; } // 在链表的index(0-based)位置添加新的元素e // 在链表中不是一个常用的操作,练习用:) public void add(int index, E e){ if(index < 0 || index > size) throw new IllegalArgumentException("Add failed. Illegal index."); if(index == 0) addFirst(e); else{ //往中间进行元素添加 Node prev = head; for(int i = 0 ; i < index - 1 ; i ++) prev = prev.next; // Node node = new Node(e); // node.next = prev.next; // prev.next = node; prev.next = new Node(e, prev.next);//更优雅的写法 size++; } } // 在链表末尾添加新的元素e public void addLast(E e){ add(size, e); } private class Node{ public E e; public Node next; public Node() { this(null, null); } public Node(E e) { this(e, null); } public Node(E e, Node next) { this.e = e; this.next = next; } @Override public String toString() { return e.toString(); } } }
1、新建文件:
这里还是回到之前链表的工程中,新建一个文件:

2、把不变的代码拷过来:
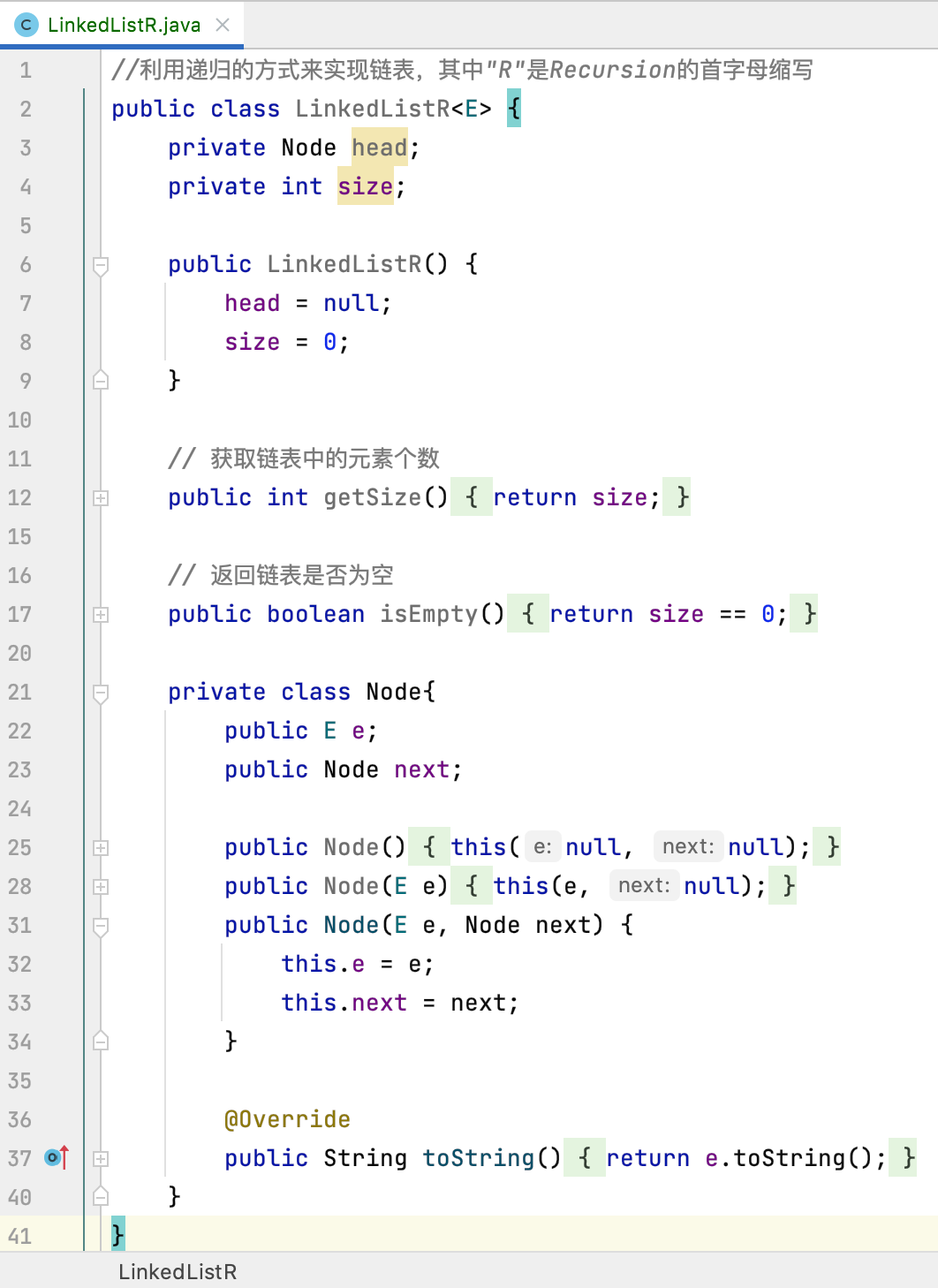
2、add、addFirst、addLast:
先回忆一下之前非递归方式跟添加相关的方法定义:

其核心就是add()这个逻辑的实现,因为addFirst和addLast其实都调用了它,那先来定义一下:
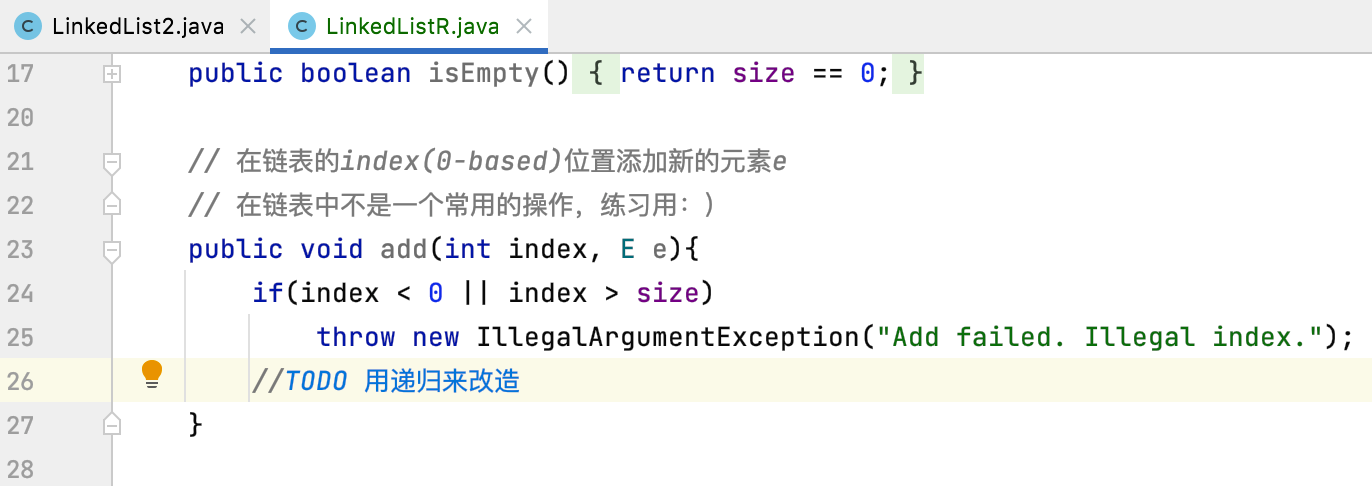
add():
那如何用递归来改造呢?根据链表递归的天然性质:

很明显需要单独再定义一个方法用来进行递归调用,如下:
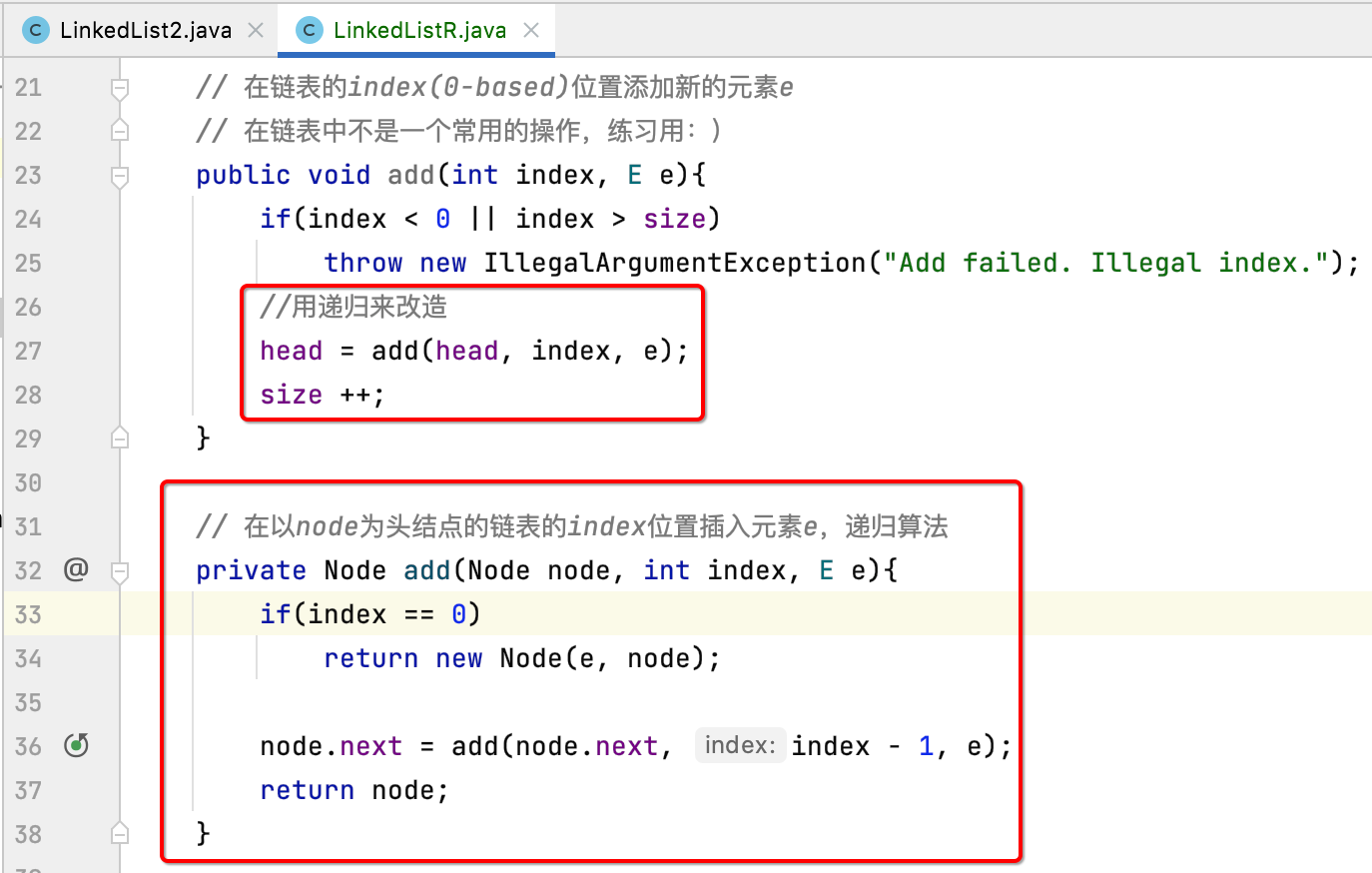
关于这个递归的写法不太清楚的同样可以利用上面所讲的调试方法来进行调试理解,这里就不过多说明了,注意一个小细节,对于递归函数的设计咱们是用的private的,而真正调用的add()方法是public的,这样设计的目的是递归函数需要使用 "Node"类,而对于外界用户来说,是感知不到 "Node" 类的存在的,所以将递归函数声明成private。
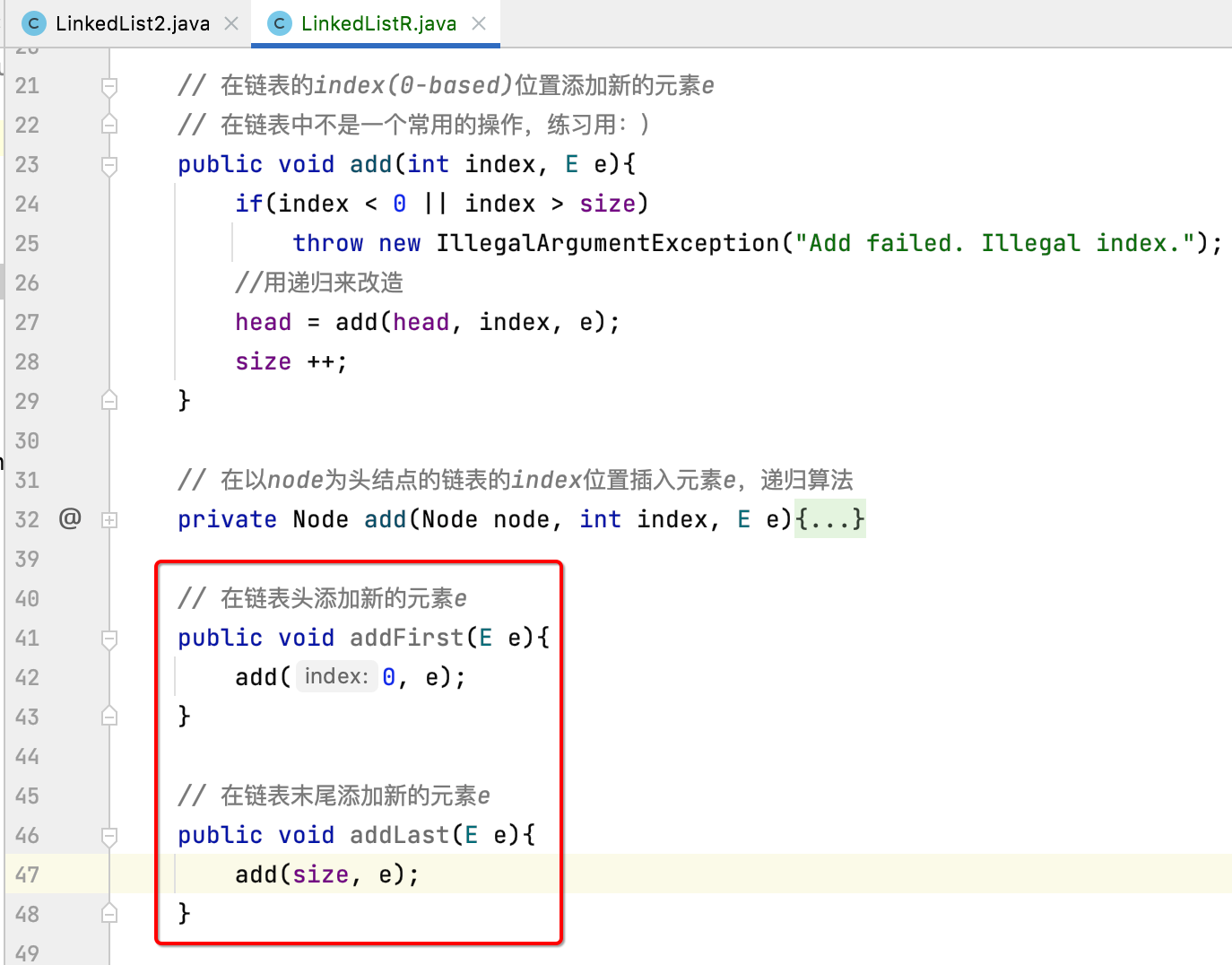
addFirst()、addLast():
对于这两个方法实现就比较简单了:
3、get、getFirst、getLast:
同样的先来回忆一下用非递归方式实现跟get相关的方法:
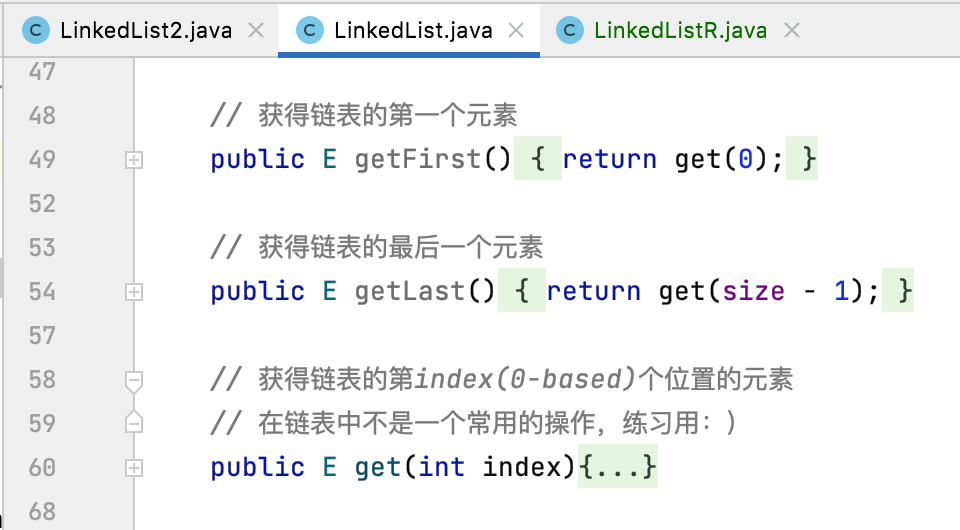
同样核心是get()这个方法的实现。
get():
既然要用递归,肯定要设计一下递归函数对吧,所以整体改造如下:
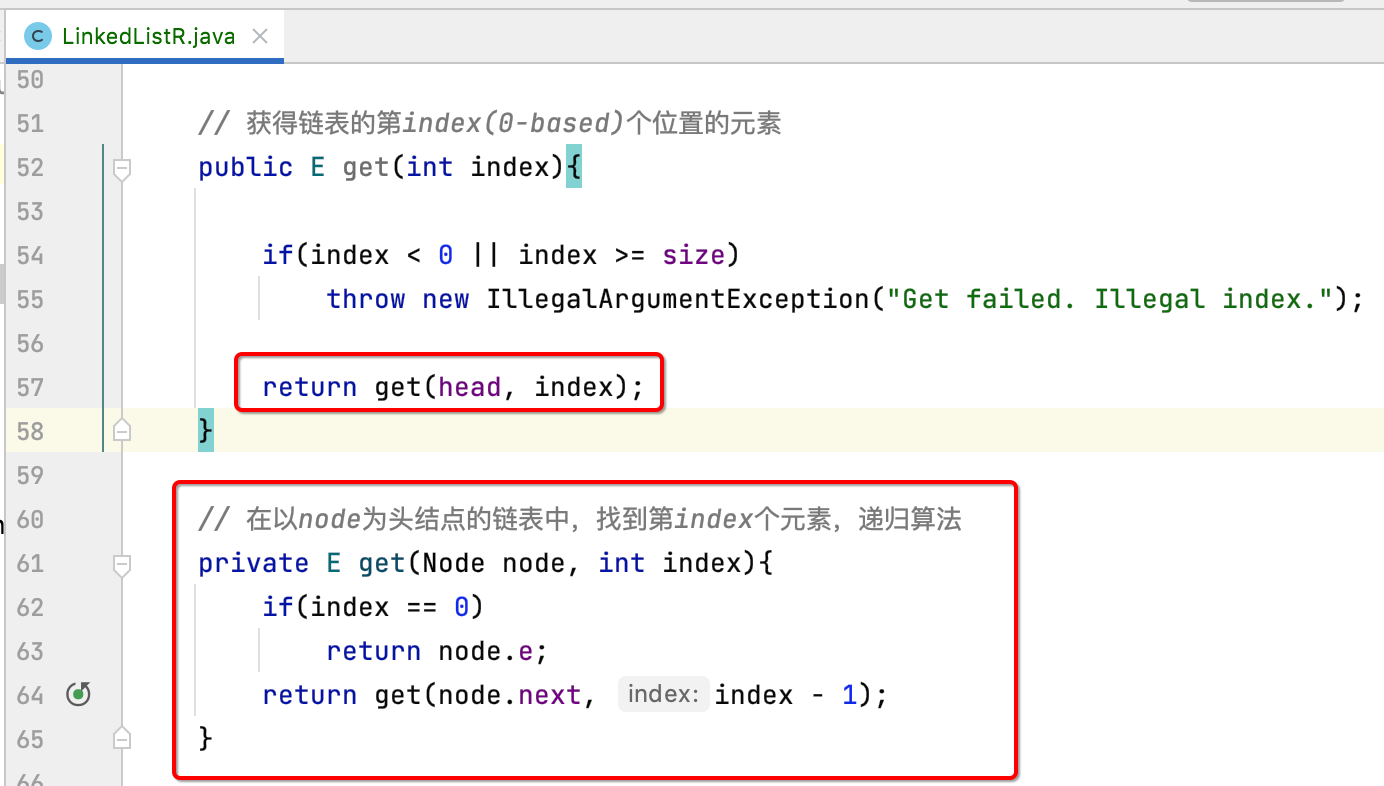
有木有发现,关于链表的递归函数的设计都会有一个Node参数,一个是index参数。
getFirst()、getLast():
对于这俩就简单了:
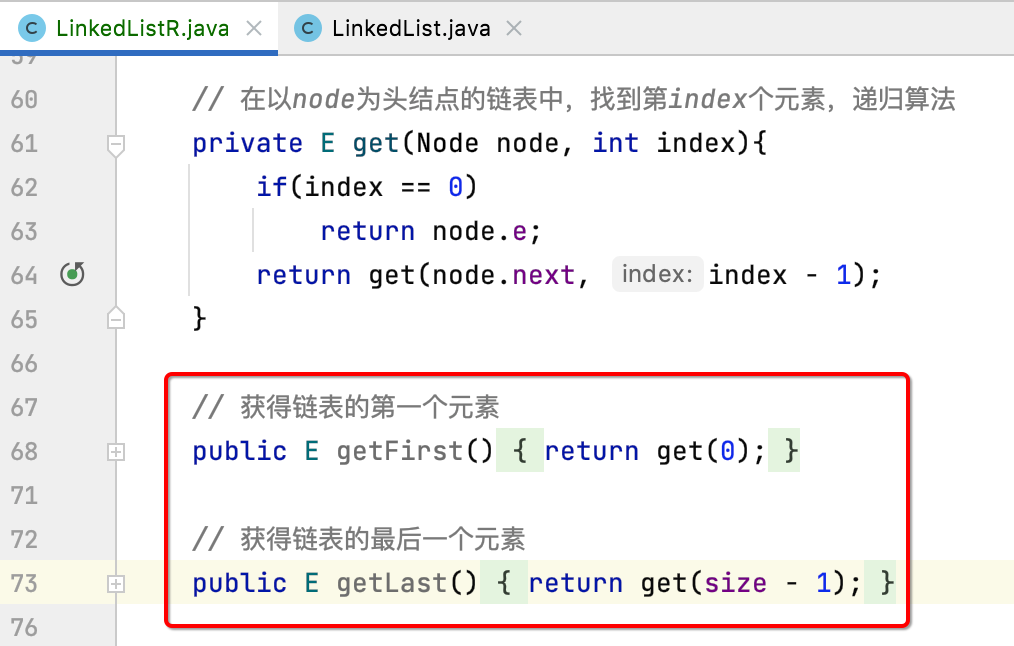
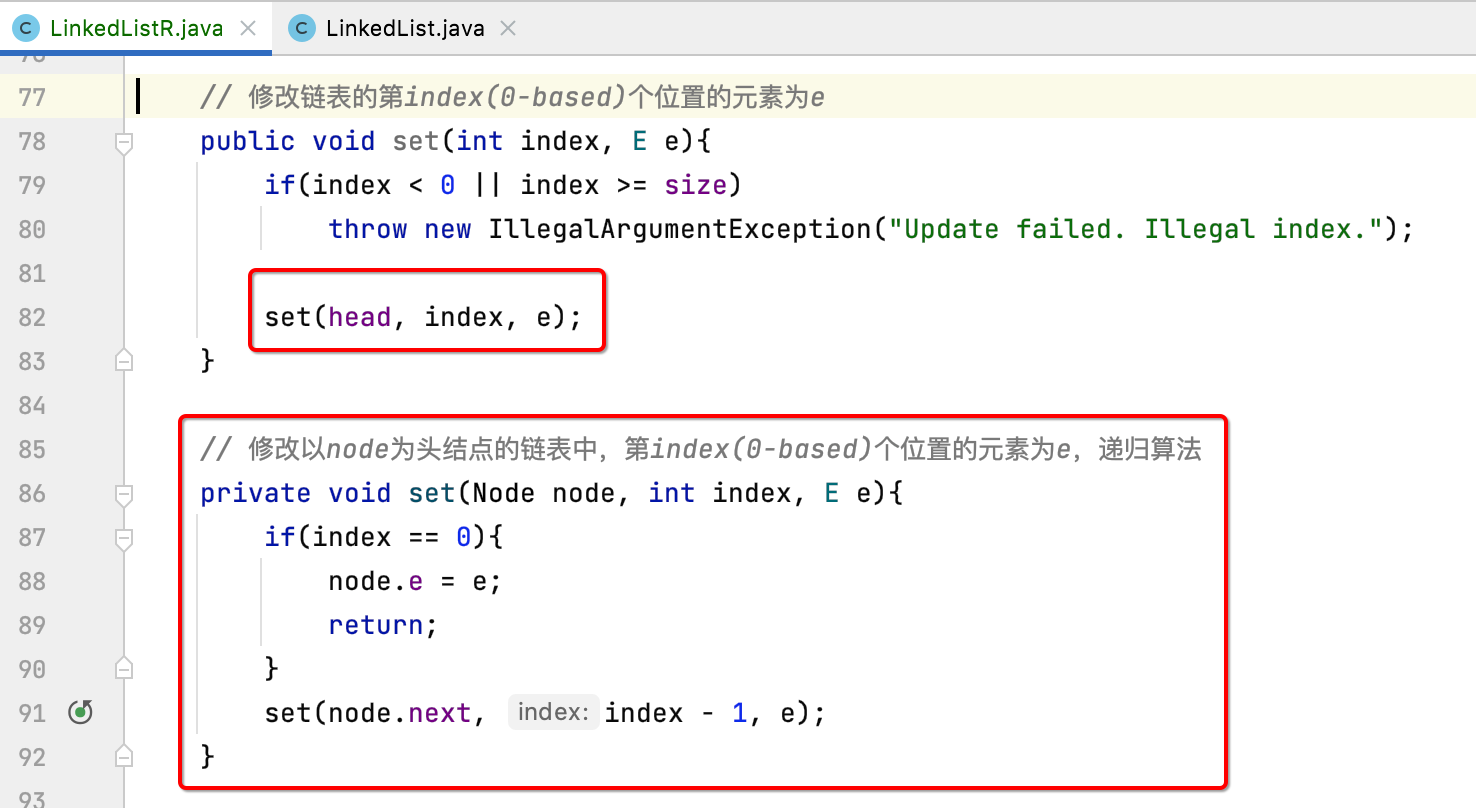
4、set:
接下来则是修改链表中指定位置的元素了,递归改造如下:
5、contains:
这里也需要改成递归,如下:
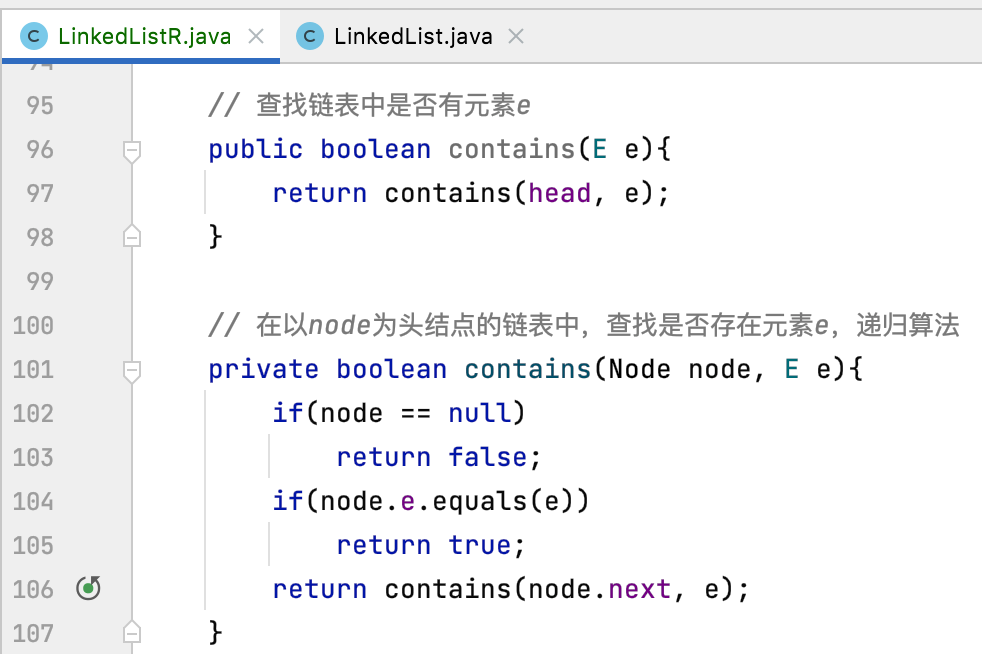
6、remove、removeFirst、removeLast:
回忆一下之前非递归方式相关的定义:
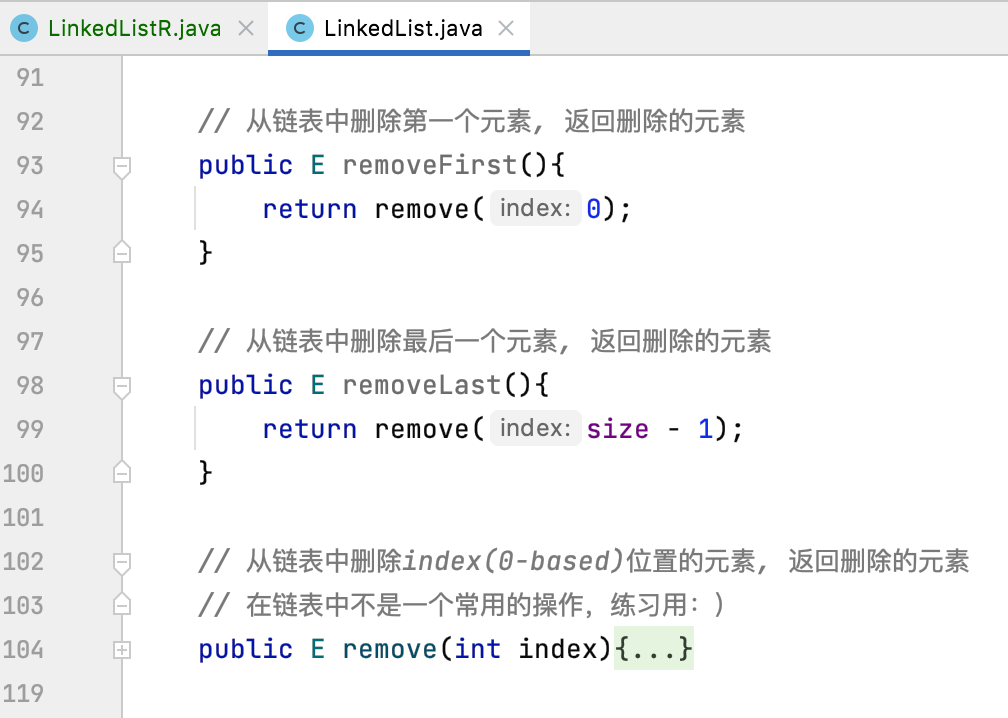
其核心是remove()这个方法。
remove():
改成递归如下:
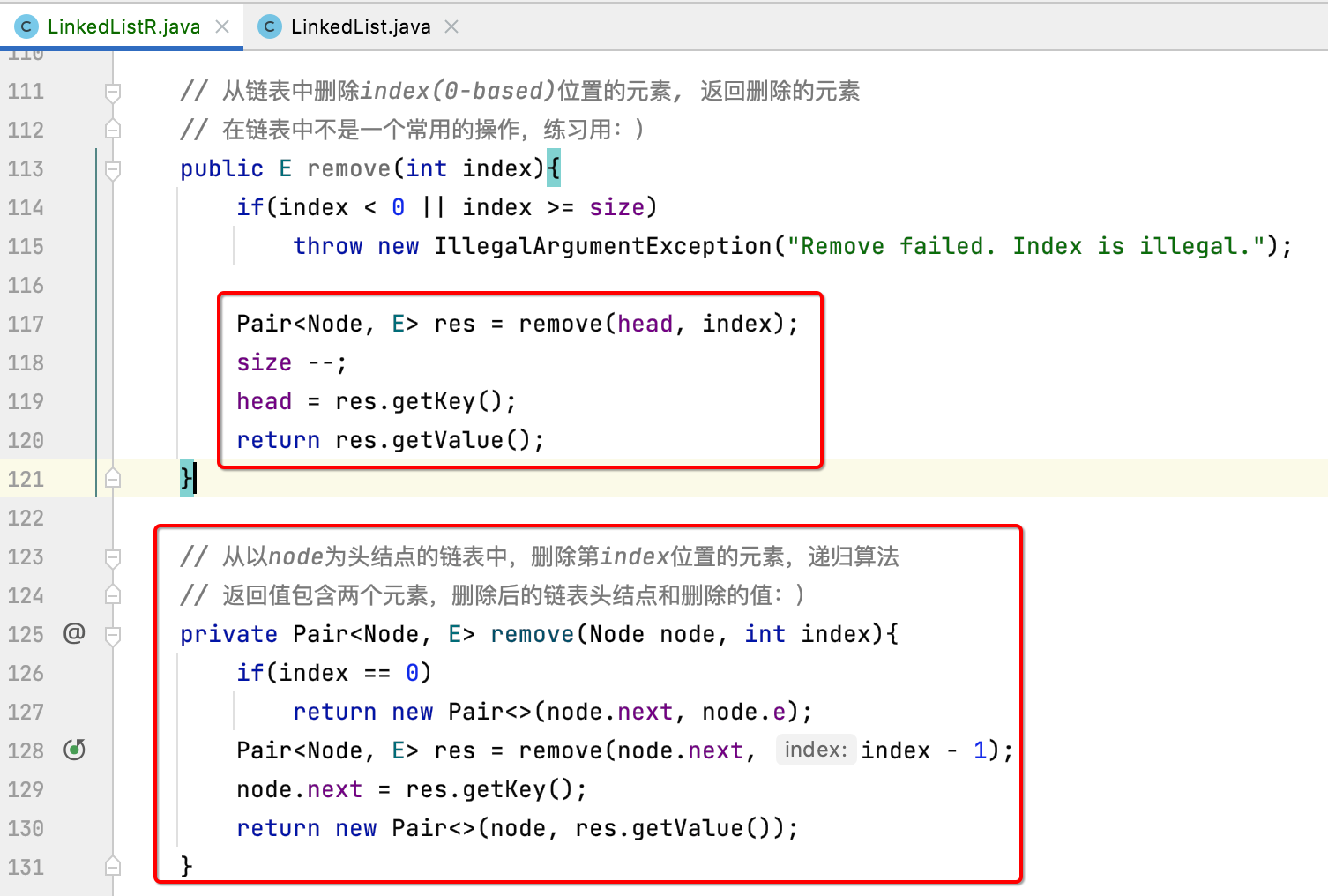
关于这块可能也不是很好理解,同样,可以去调试跟踪一下。
removeFirst()、removeLast():
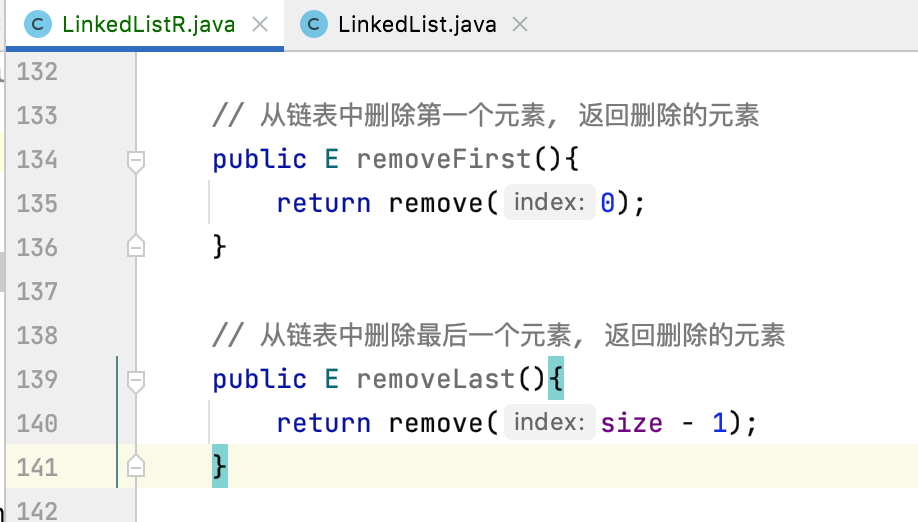
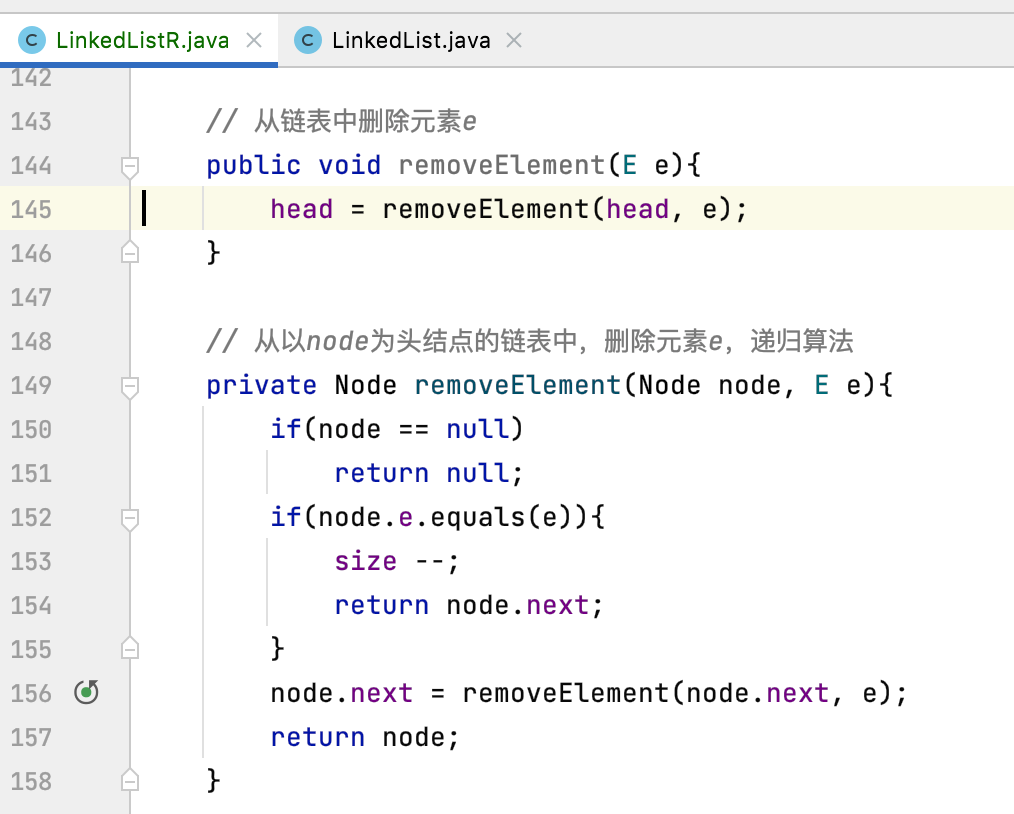
7、removeElement:
关于这个我们在之前已经用递归实现过了,这里就不过多说明了:
8、测试:
最后来测试一下:
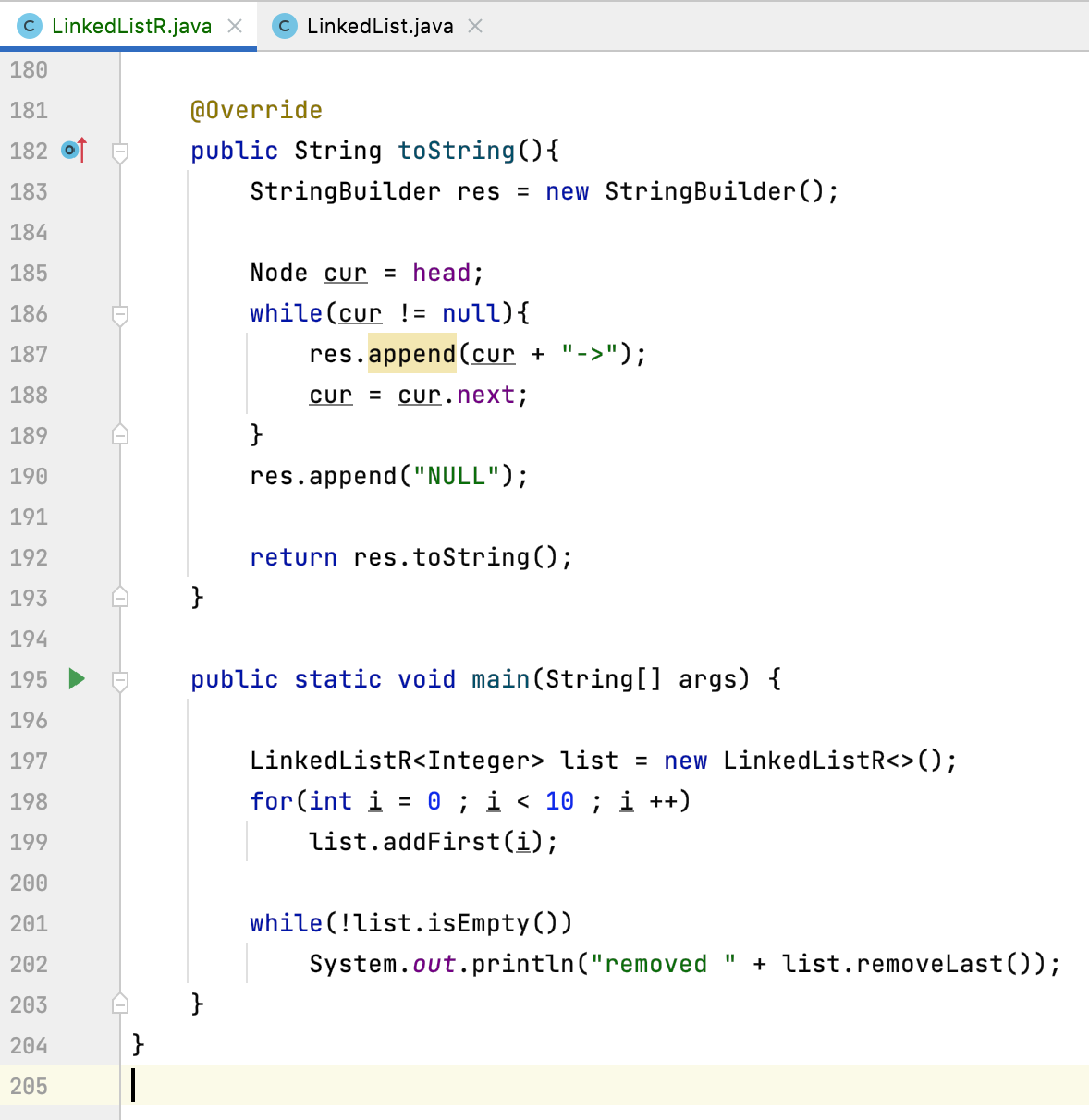
运行:
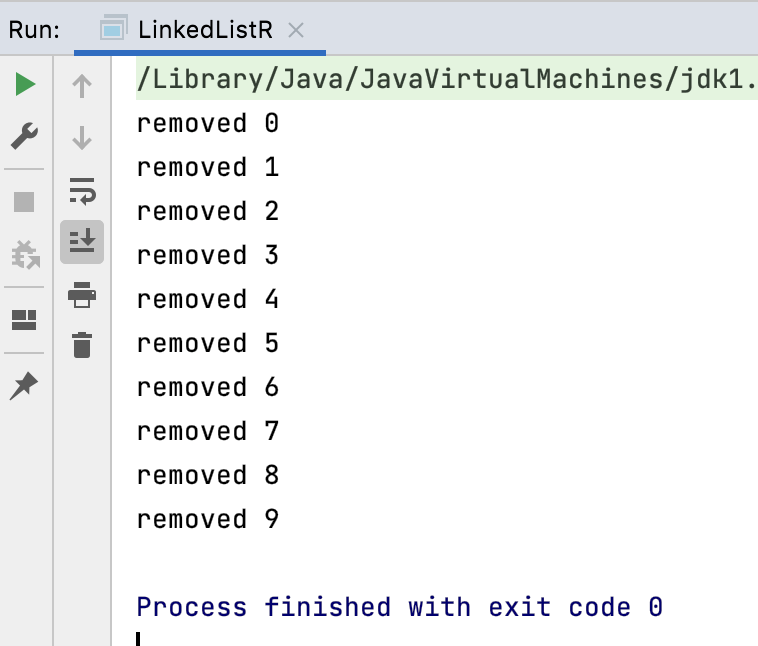
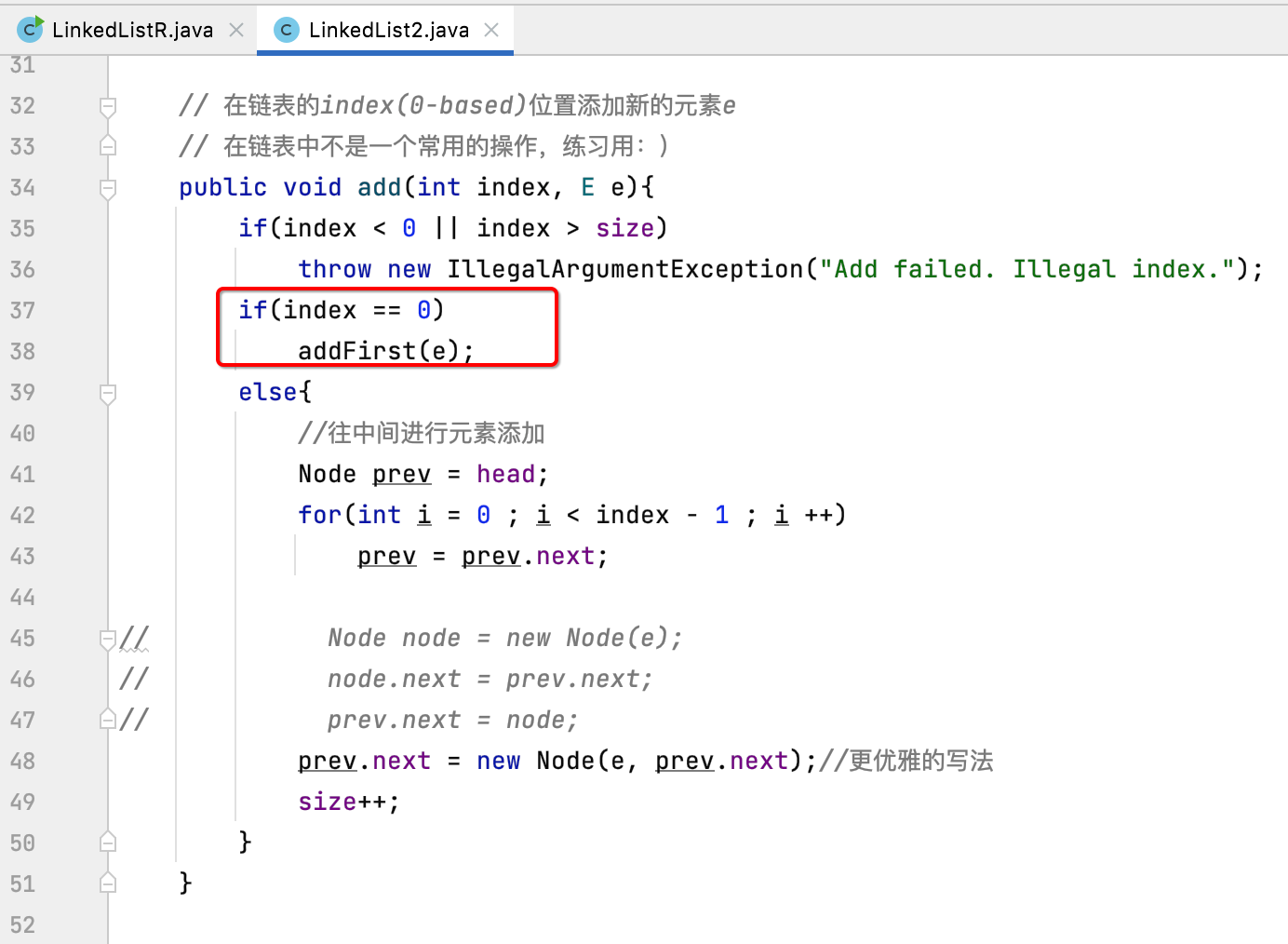
其中有个细节你有木有发现,使用递归之后,完全不用使用虚拟头节点,在处理位置0的问题上也是统一的行为,比如我们之前不使用虚拟头节点进行元素的添加时多了一些位置为0的判断:
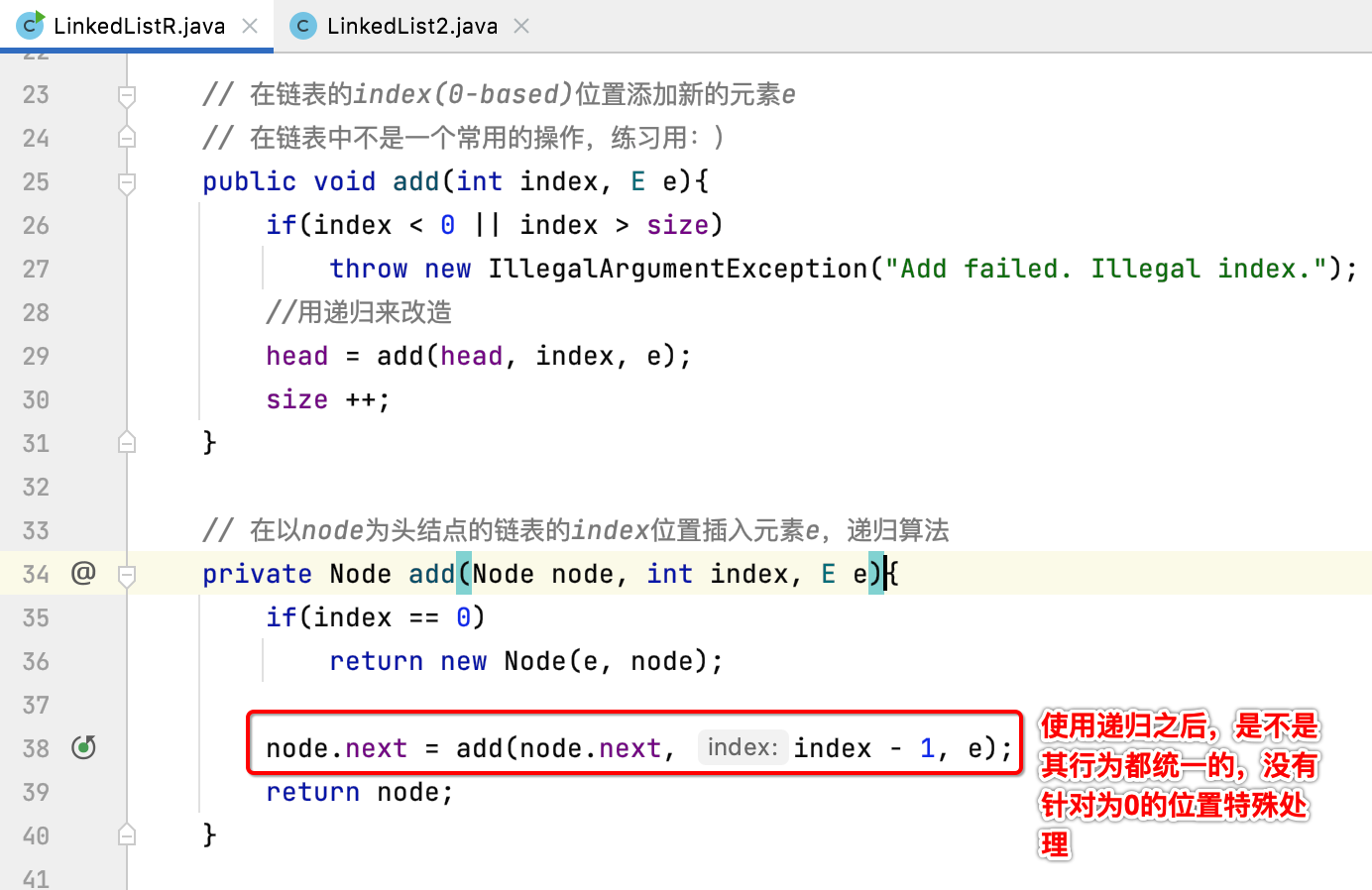
链表递归算法返回值问题探讨:
关于链表的递归实现说实话要改造并不是那么轻松的,在实际改造时可能或多或少会遇到如下两个问题,这里针对性解析一下这俩问题。
问题一:removeElements递归函数能否不返回值?
对于咱们之前实现的删除链表中指定元素的程序:

那如果咱们在这个递归函数不返回ListNode,你觉得还能完成同样的递归删除元素的效果么?答案是否,因为每次递归的结果是需要跟前面的链表再次链接起来的,何以见得?因为有这句话:

如果在递归函数中不返回值,你说还能跟之前的链表挂接起来么?
问题二: add递归函数能否不返回值?
还记得咱们在实现链表递归中的add的代码么?

其中对于add这个递归方法,能否也不要返回值Node呢?也就是这样写:

很明显是不可以的,同样存在递归处理的链表需要跟之前的链表进行连接的问题对吧,那,接下来就具体来看一下为啥这样写是不行的:
不返回Node分析:
比如这么一个链表:
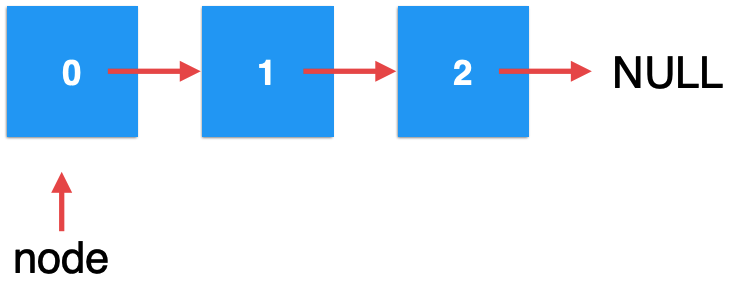
我们想往1的位置上插入一个元素e,其e具体值是多少不关心,此时是从第0个位置进行递归,很明显此时的node不是我们想要插入的位置 ,递归函数就会执行这块:
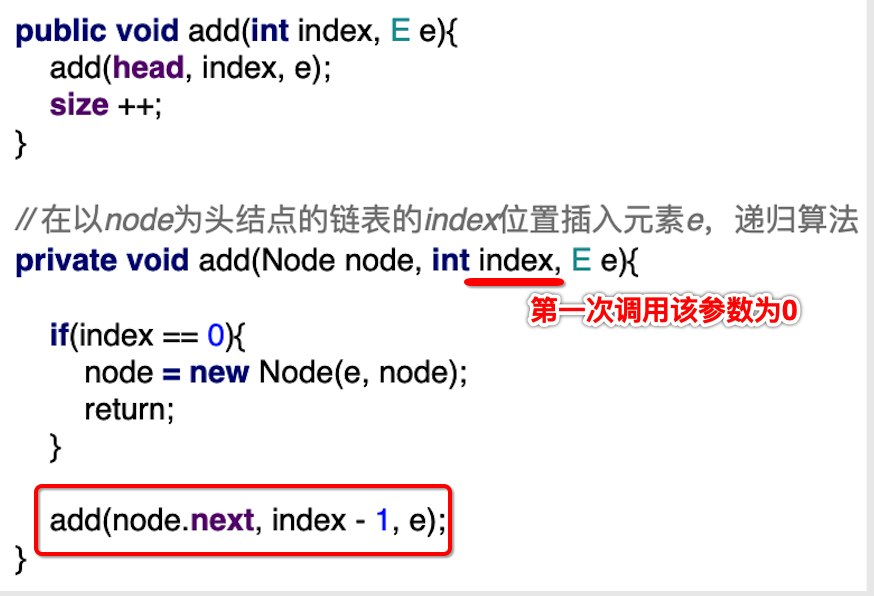
此时再次递归,此时的node就在这个位置上了:

此时index=0了,则会进入这个条件:
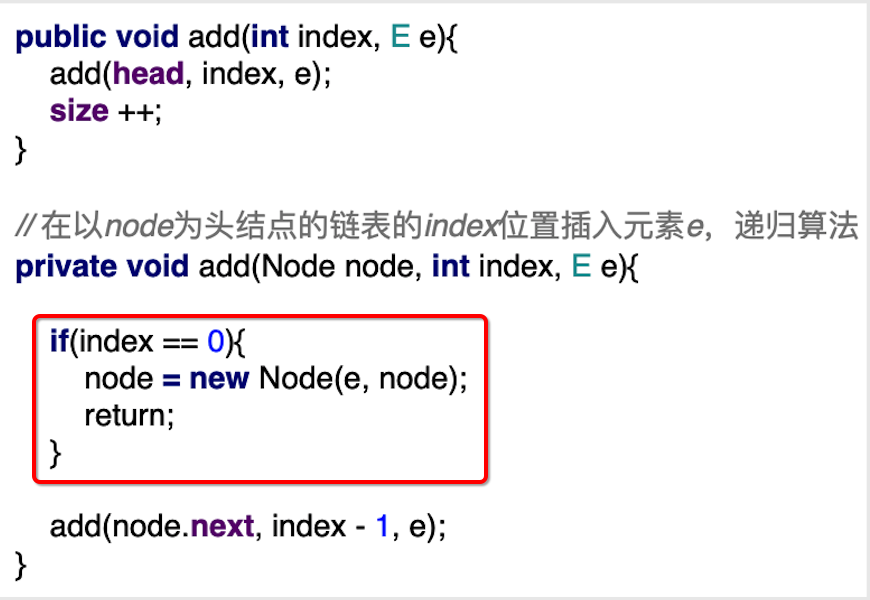
此时内存就变化为:

其中由于对node参数进行了赋值,所以此时的node就指向了:
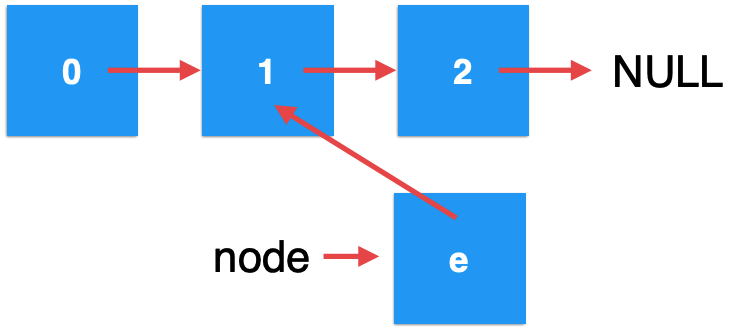
好,接着我们return了:

由于node参数是一个形参,也就是一个临时变量,当函数返回时其生命周期也就消失了,所以,此时node的指向就没了,回到上一层递归函数调用中,形态就转为:

关键点来了,由于我们新开辟的元素e木有被任何引用所引用,根据JVM垃圾回收机制,很明显会将它给回收掉,所以最终你会发现经过了add操作之后:
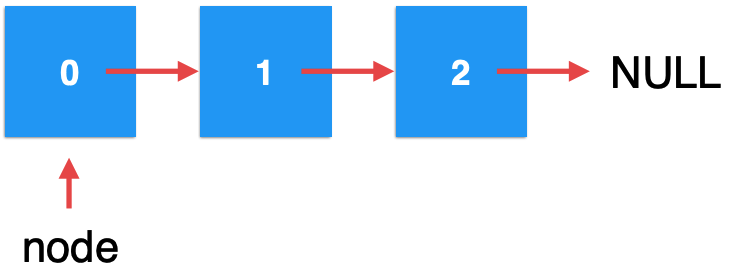
其实并没有成功将元素添加到链表中,这也就是为啥这里不能返回void的原因。
返回Node分析:
接下来再对比的分析咱们正确的代码,看为啥给递归设计成返回Node,在添加元素就能正常呢?
同样是以这个链表为例:
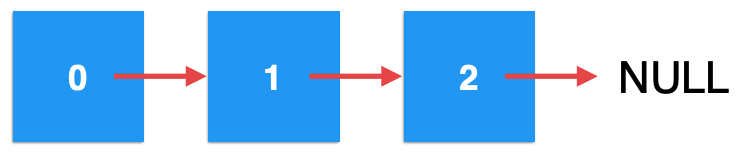
第一次调用,index=0,所以形态为:
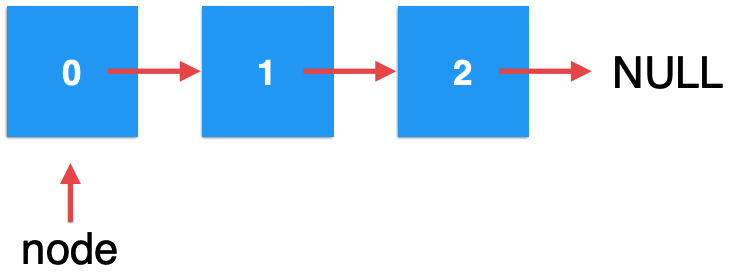
接着调用第二次递归,此时的index=0了,所以:
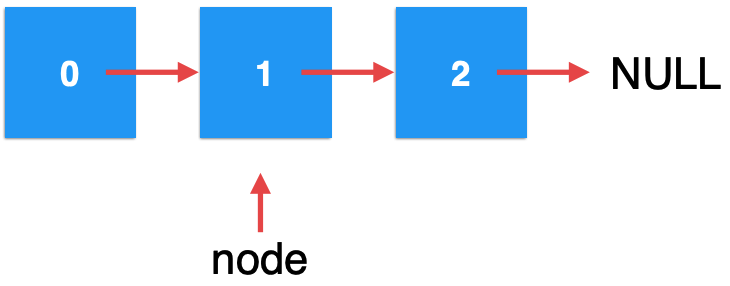
此时就会进入递归方法的这个条件:

所以此时新创建的元素就指向上当前的node,所以为:

而比较关键的是将它返回了,此时就会回到上一次递归的这句代码:

返回之后的形态就变为了:

而由于node.next指向了咱们刚创建的e元素的链表,那很明显形态最终就变为了:

最终程序执行到这:

最终看到的链表就是:

总结:
通过这么一对比,是不是对于链表递归的理解就更进一步了?返回值的意义这块一定需要明确。
更多和链表相关的话题:
斯坦福文档说明:
各种其它形态的链表:
双链表:

循环链表:
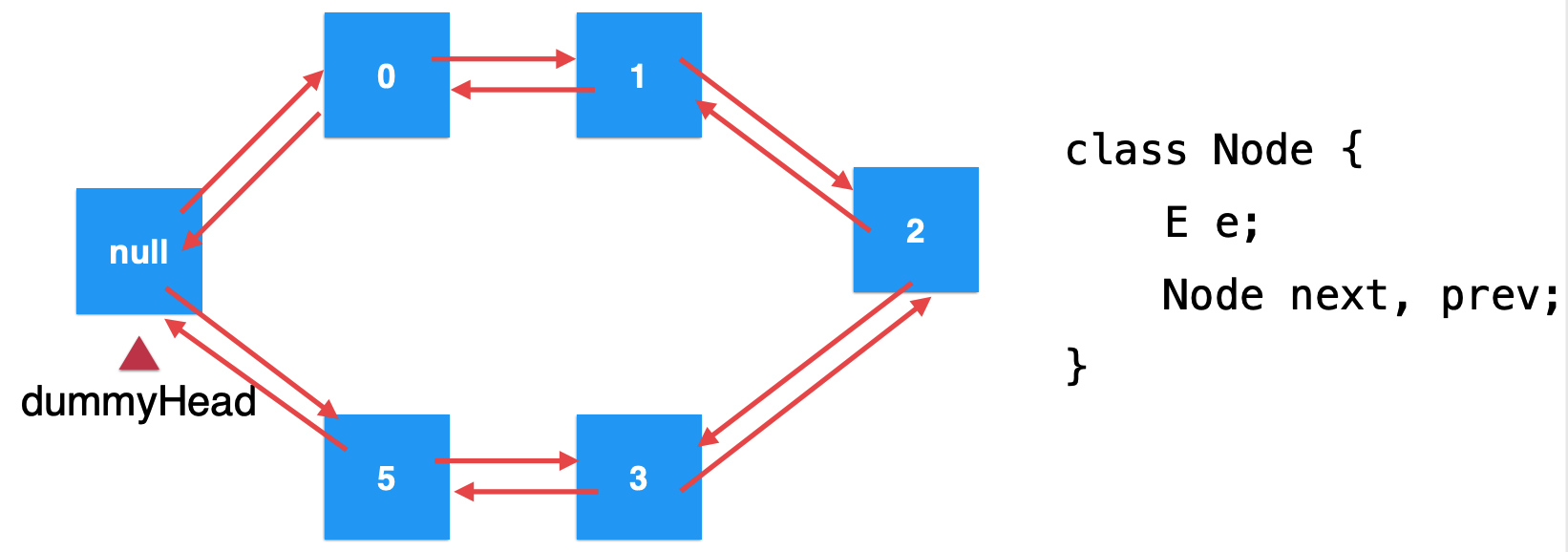
数组链表:
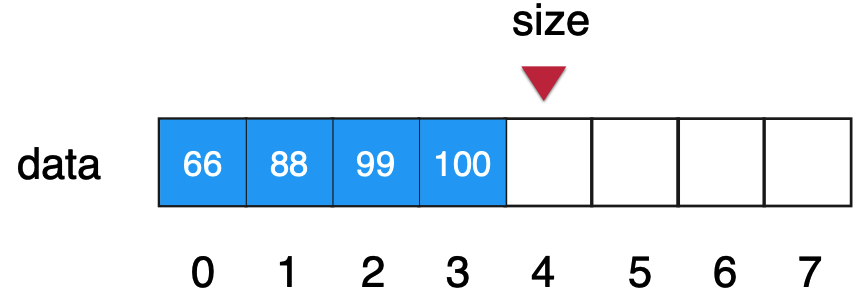
而如果我们在存储元素时,再多加一个索引属性,那么就可以构建链表这种数据结构了,比如: