算法与数据结构基础<三>----数据结构基础之栈和队列加强之用栈实现队列
在上一次https://www.cnblogs.com/webor2006/p/15134809.html针对栈和队列这俩非常基础又非常重要的数据结构进行了一个加强练习,其中用队列实现了一个栈,但是还差反转的实现,也就是用栈来实现队列,上篇中发现有个小标写错了~~
错了就错了吧,不改了,这篇之后,就木错了~~
目标:
对于这次所编写的程序,最终也是会copy到LeetCode的这一个题上来进行验证:https://leetcode-cn.com/problems/implement-queue-using-stacks/
这里把官方的题目再贴一下:
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty): 实现 MyQueue 类: void push(int x) 将元素 x 推到队列的末尾 int pop() 从队列的开头移除并返回元素 int peek() 返回队列开头的元素 boolean empty() 如果队列为空,返回 true ;否则,返回 false 说明: 你只能使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。 你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。 进阶: 你能否实现每个操作均摊时间复杂度为 O(1) 的队列?换句话说,执行 n 个操作的总时间复杂度为 O(n) ,即使其中一个操作可能花费较长时间。 示例: 输入: ["MyQueue", "push", "push", "peek", "pop", "empty"] [[], [1], [2], [], [], []] 输出: [null, null, null, 1, 1, false] 解释: MyQueue myQueue = new MyQueue(); myQueue.push(1); // queue is: [1] myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue) myQueue.peek(); // return 1 myQueue.pop(); // return 1, queue is [2] myQueue.empty(); // return false 提示: 1 <= x <= 9 最多调用 100 次 push、pop、peek 和 empty 假设所有操作都是有效的 (例如,一个空的队列不会调用 pop 或者 peek 操作) 来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/implement-queue-using-stacks 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
而其中给的模板代码如下:
class MyQueue { /** Initialize your data structure here. */ public MyQueue() { } /** Push element x to the back of queue. */ public void push(int x) { } /** Removes the element from in front of queue and returns that element. */ public int pop() { } /** Get the front element. */ public int peek() { } /** Returns whether the queue is empty. */ public boolean empty() { } } /** * Your MyQueue object will be instantiated and called as such: * MyQueue obj = new MyQueue(); * obj.push(x); * int param_2 = obj.pop(); * int param_3 = obj.peek(); * boolean param_4 = obj.empty(); */
具体实现:
初步实现:
1、新建文件,拷贝模板代码:
新建个类,然后把LeetCode的模板代码拷过来:
2、定义一个栈变量:
既然是要使用到栈来实现队列,当然得先定义一个栈喽,跟上次一样,这里还是使用JDK系统自带的类来实现:
3、pop():从队列的开头移除并返回元素
这个pop()不是栈的方法么?回忆一下:

嗯,是的,但是此刻它的意义不一样了,这一点必须先明白,不然比较容易晕,在Stack中,pop是指弹出“栈顶”的元素对吧,是不是此刻对“栈顶”的概念有些模糊了?回忆一下,这个千万不要模糊,不然代码就不好编写了:
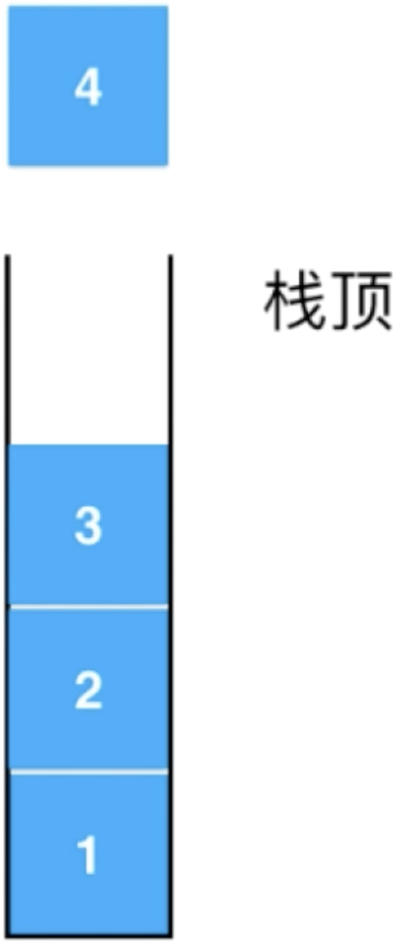
但是!!!此时的pop在队列的里面指的是弹出“队首”的元素,此时可以有对“队首”可能也有点模糊了对吧,复习一下:
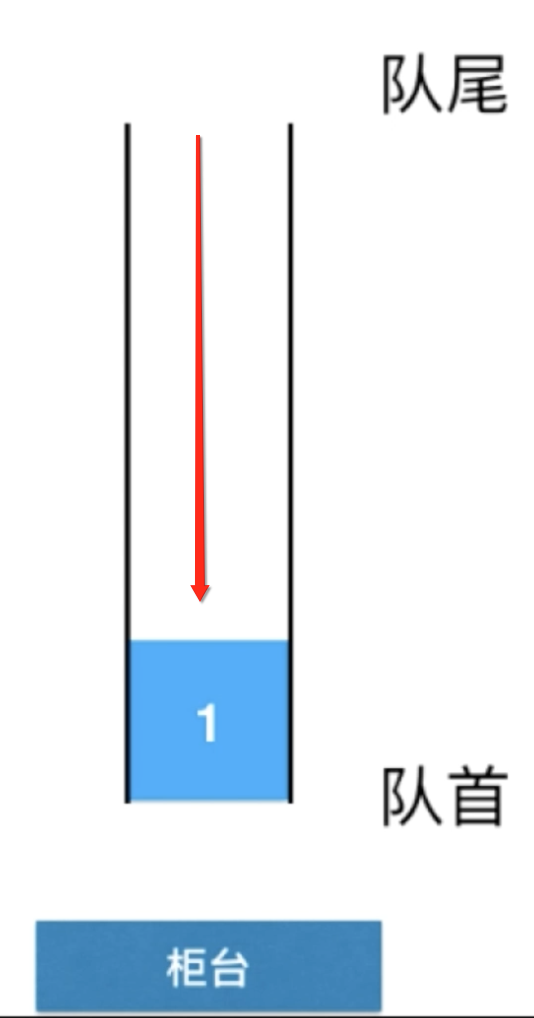
那,为了实现的方便,我们可以假设“栈顶就是队首” ,那么是不是实现就变得非常之简单了,因为其实行为已经统一了,如下:
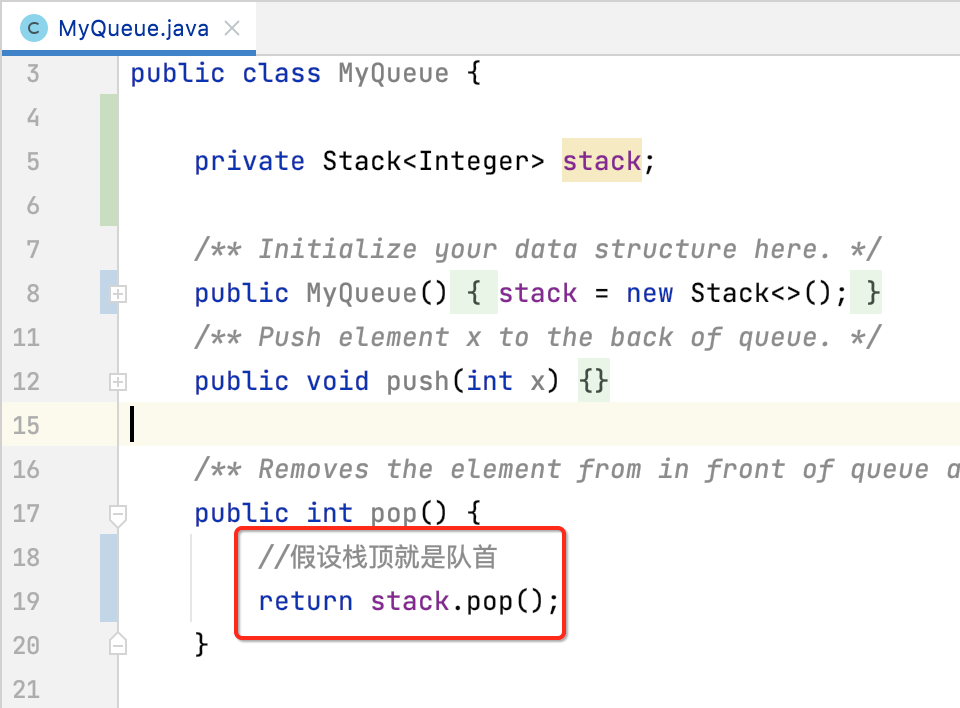
4、peek():返回队列开头的元素
对于它当然也简单了,直接返回队头的元素既可,也是得意于假设“栈顶就是队首”:

5、empty():
直接贴代码:

6、push():
思路:
接下来,核心的核心就是它的实现了,这里需要稍加挼一下逻辑了,不然很容易晕,正常往队列添加元素是不是从“队尾”来添加?看图理解:
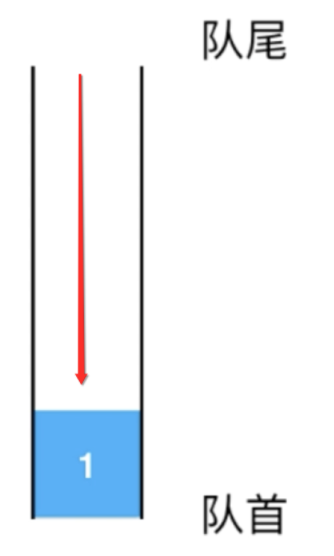
那由于我们已经假设“栈顶就是队首【一定要时刻记住它,是理解程序的关键】”了,那很明显这个push就是往栈底来添加元素了,这个可能有点绕,这里简单再啰嗦一下,因为现在是要从“队尾”来添加元素,而“栈顶”是队首,是不是“栈底”是队尾?
现在的问题就回到了如何让我们添加的元素变成栈底的元素呢?其实也很简单,可以借助另一个临时栈,如下操作就可以了:“使用另外一个 stack2 暂存现在 stack 的元素,然后,在 stack 中添加新元素后,再把 stack2 的元素放回来。”
实现:
下面具体来实现一下:
而它的逻辑用图来说明一下:
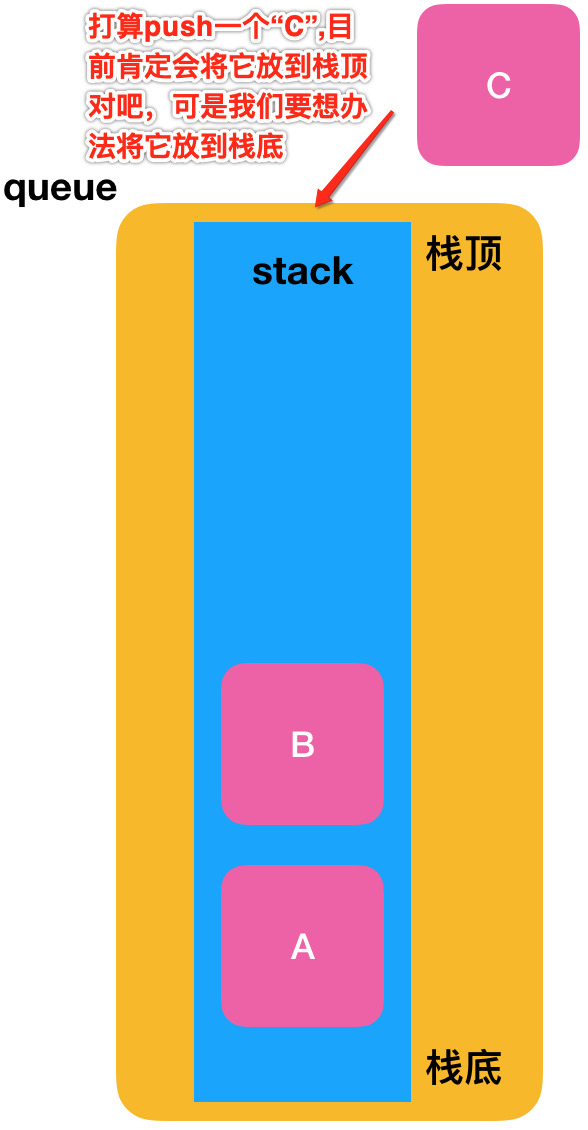
也就是这是最终预期的样式:
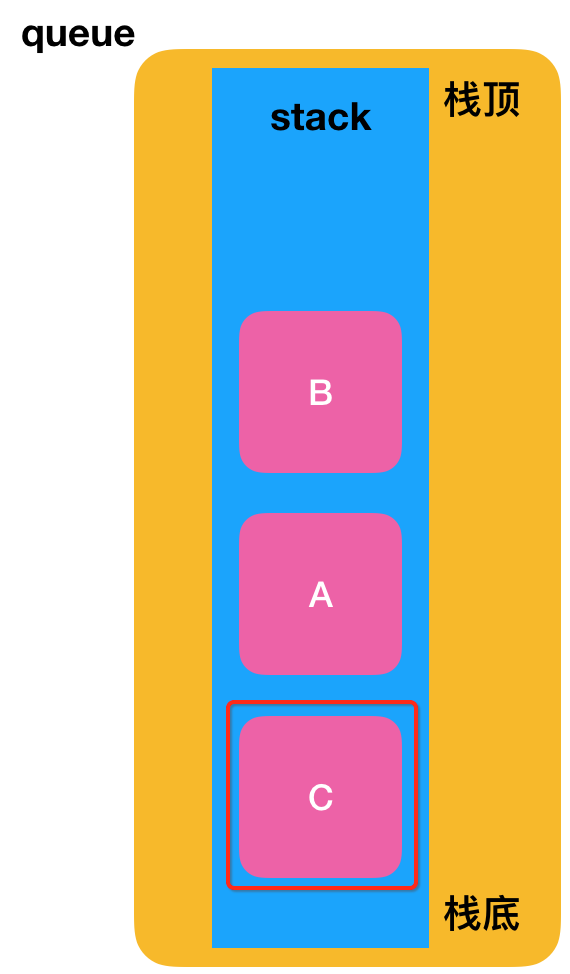
很明显目前按栈的后进先出的特性是办不到这点的对吧,此时借助一个临时的栈就可以办到了,具体过程如下:
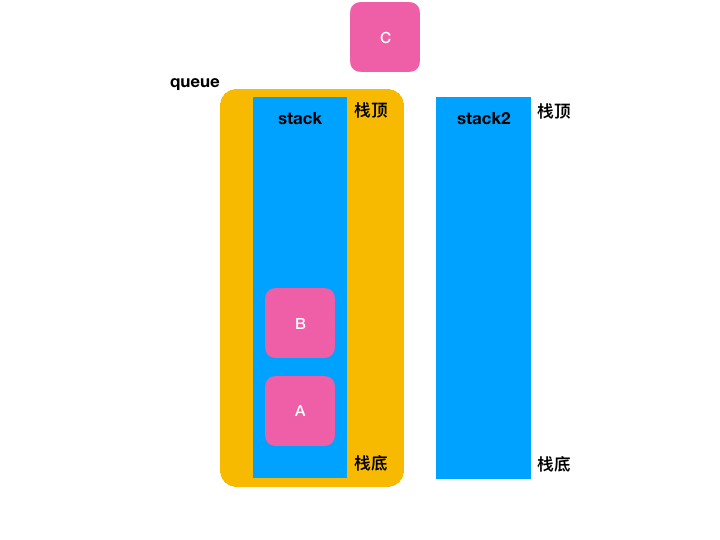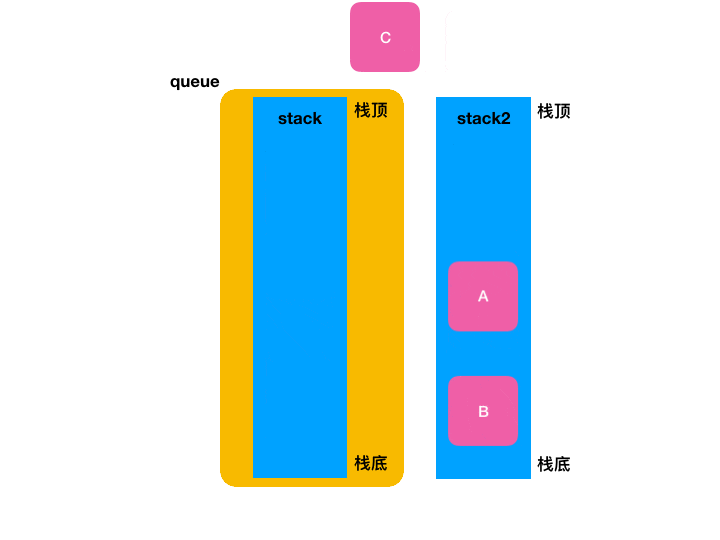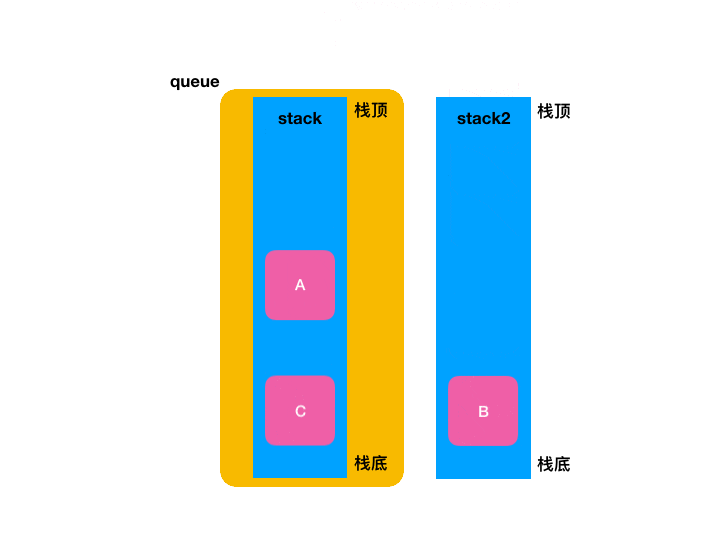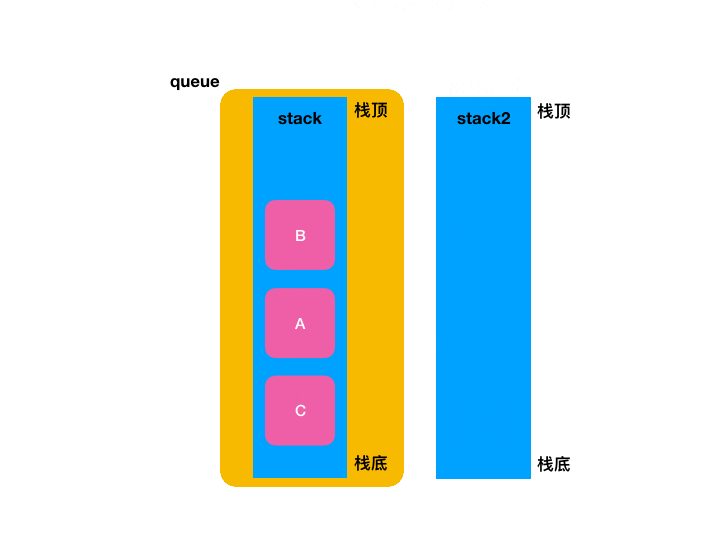
7、LeetCode进行验证:
接下来把编写的代码拷到LeetCode中进行验证,看是否能通过:
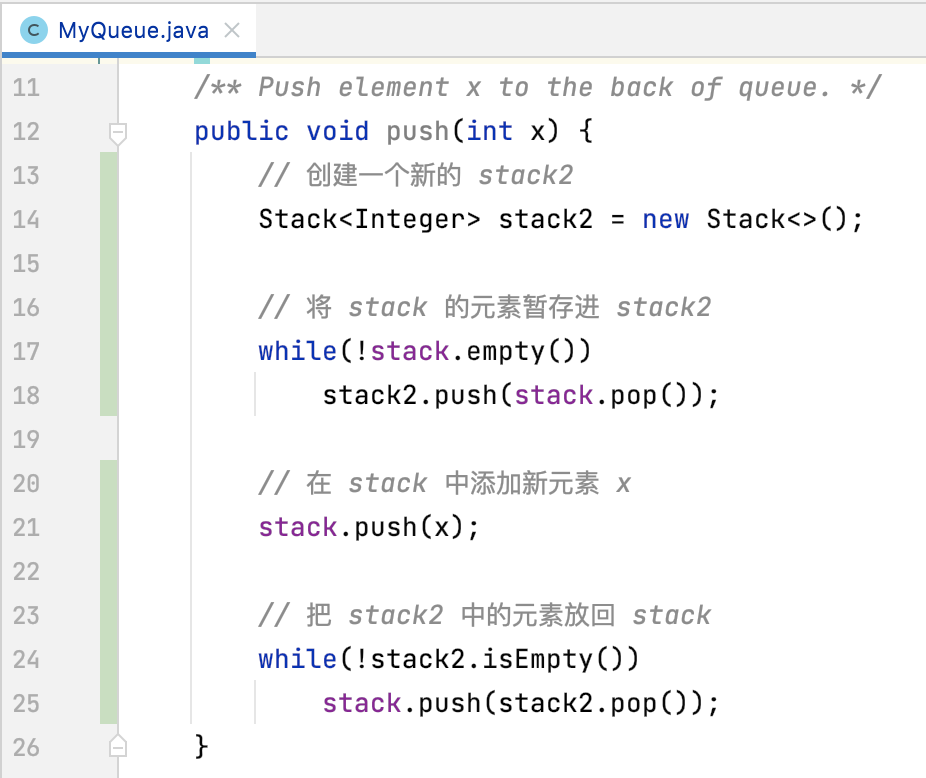
public class MyQueue { private Stack<Integer> stack; /** Initialize your data structure here. */ public MyQueue() { stack = new Stack<>(); } /** Push element x to the back of queue. */ public void push(int x) { // 创建一个新的 stack2 Stack<Integer> stack2 = new Stack<>(); // 将 stack 的元素暂存进 stack2 while(!stack.empty()) stack2.push(stack.pop()); // 在 stack 中添加新元素 x stack.push(x); // 把 stack2 中的元素放回 stack while(!stack2.isEmpty()) stack.push(stack2.pop()); } /** Removes the element from in front of queue and returns that element. */ public int pop() { //假设栈顶就是队首 return stack.pop(); } /** Get the front element. */ public int peek() { //假设栈顶就是队首 return stack.peek(); } /** Returns whether the queue is empty. */ public boolean empty() { return stack.isEmpty(); } }
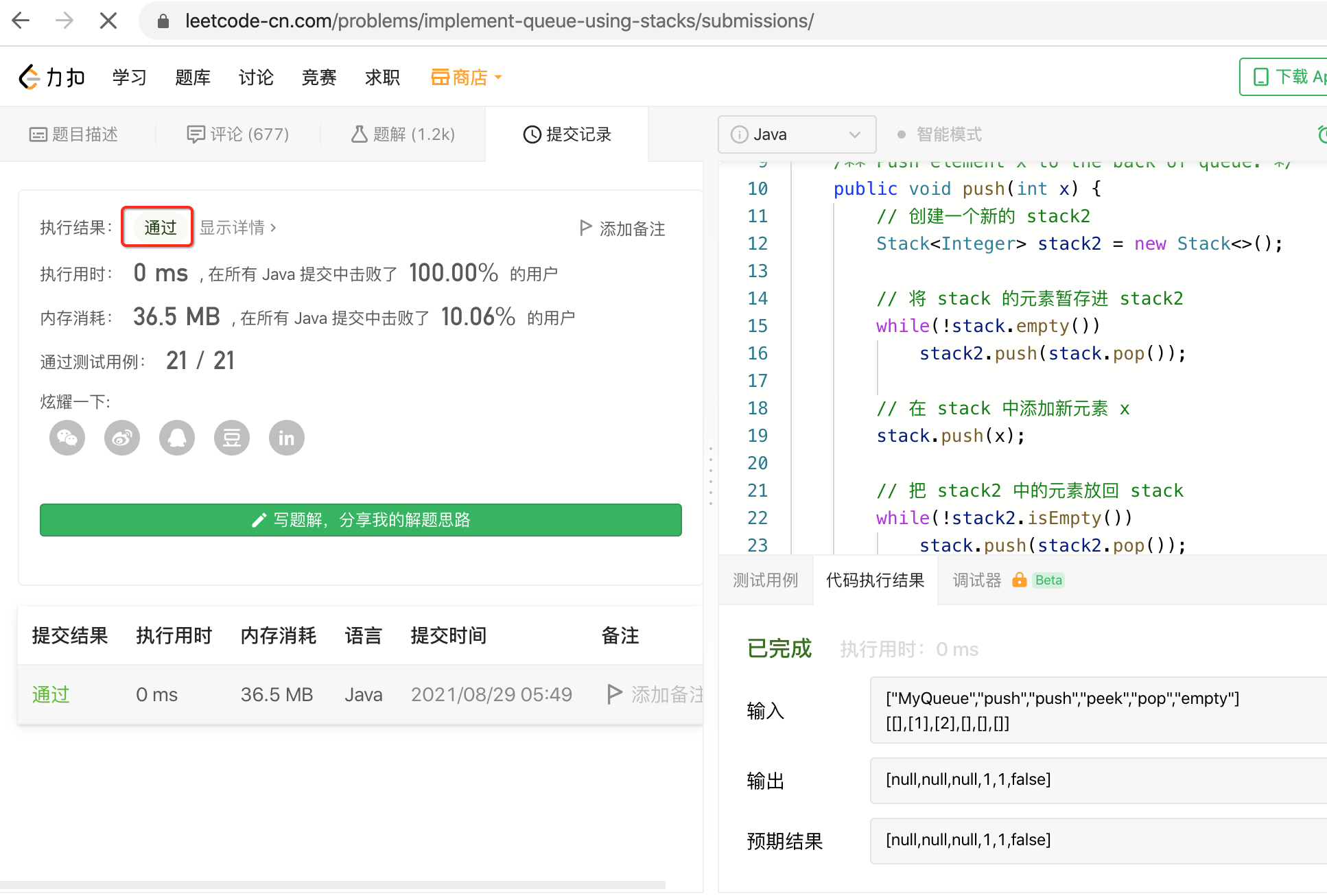
8、时间复杂度计算:
接下来分析一下里面各方法实现的复杂度,也是比较简单的,不多解释:
1、初始化的构造函数复杂度,是 O(1) 的;
2、判断队列是否为空的 empty,复杂度,是 O(1) 的;
3、出队的 pop,复杂度是 O(1) 的;
4、入队的 push,因为需要把队列中所有元素都拿出来一趟,所以复杂度是 O(n) 的;
实现方式二:
目前咱们实现的push复杂度是O(n)、pop复杂度是O(1),那能否实现一个push复杂度是O(1)、pop复杂度是O(n)的呢?当然可以,下面来改造一下,通过换一种方式实现,进一步拓展自己的思维。
思路:
其实思路也比较容易理解,就是把我们之前的假设条件“栈顶就是队首” 更改为“栈顶就是队尾”就能达到,我们知道栈是从“栈顶”存元素【当然也是从栈顶取元素的】的对吧,而队列是从“队尾”存元素的,有了“栈顶就是队尾”的假设,是不是push就直接往栈中添加元素既可,此时自然它的时间复杂度就变成O(1)了;而pop时就是取出栈底的元素了,当然你要想取出栈顶的元素肯定又得借助于一个临时的栈对吧,这种思路已经运用好几次了,就不过多解释了。
实现:
1、新建文件,准备模板代码:
import java.util.Stack; /** * 用栈实现队列实现方式二:假设"栈顶是队尾" */ public class MyQueue2 { private Stack<Integer> stack; /** Initialize your data structure here. */ public MyQueue2() { stack = new Stack<>(); } /** Push element x to the back of queue. */ public void push(int x) { //TODO } /** Removes the element from in front of queue and returns that element. */ public int pop() { //TODO return 0; } /** Get the front element. */ public int peek() { //TODO return 0; } /** Returns whether the queue is empty. */ public boolean empty() { return stack.isEmpty(); } }
其中需要改写的方法就是push()、peek()、pop(),其它的不变。
2、push():
如思路分析所述,如今的push变得非常简单了,因为是O(1)的嘛,如下:
3、peek():返回队列开头的元素
它是要取出队首的元素,而由于“栈顶是队尾”,那么很明显是要取出栈底的元素对吧,很显然又是一个O(n)的操作了:
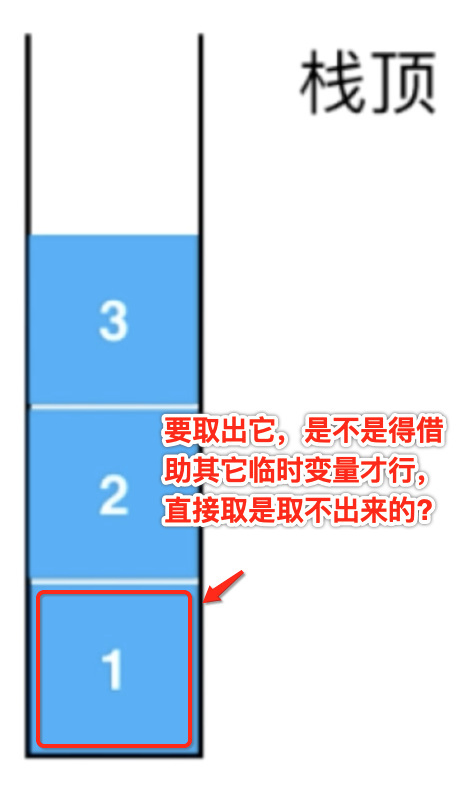
但是呢,这里有办法让它的时间复杂度还是为O(1),那就是增加一个追踪存储队首元素的变量front,当然维护它是在push时,这样我们在peek时直接返回这个front变量既可,代码如下:
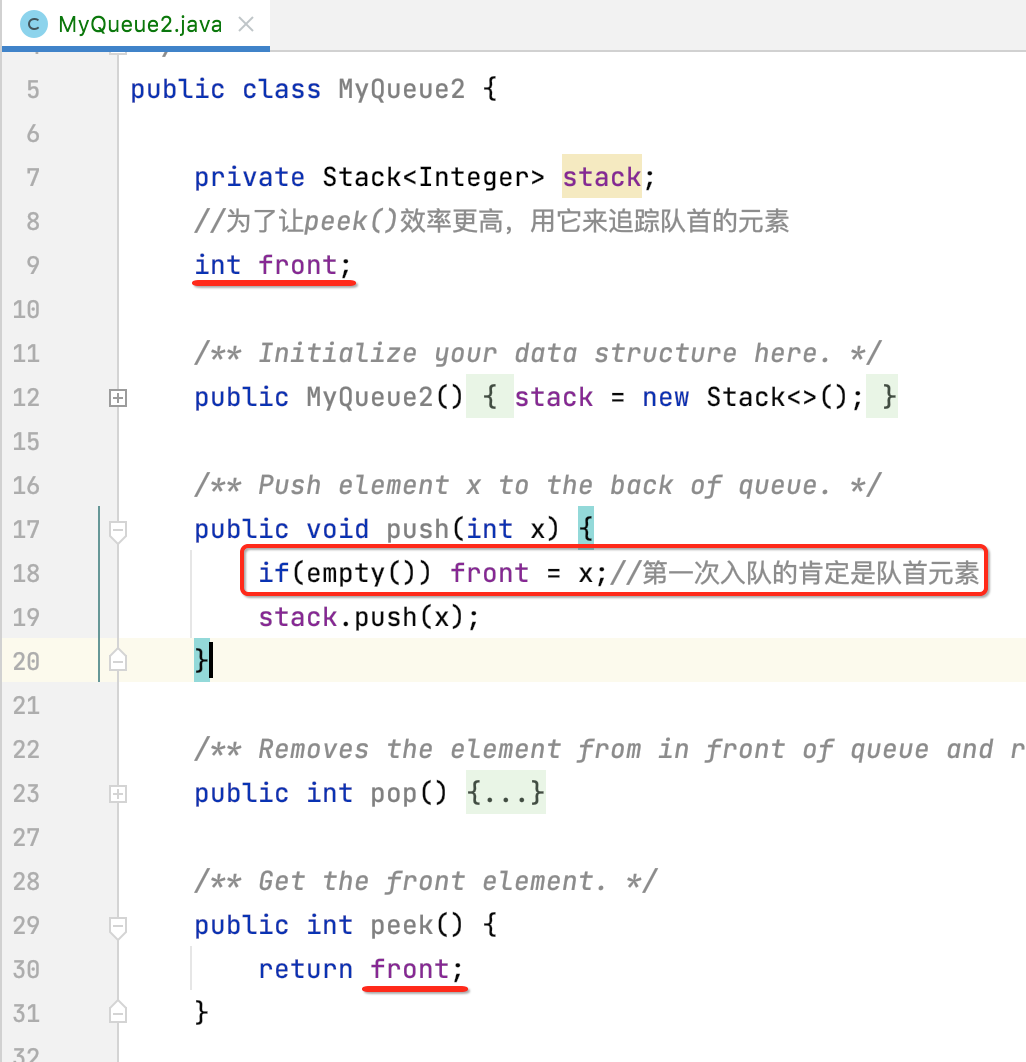
4、pop():
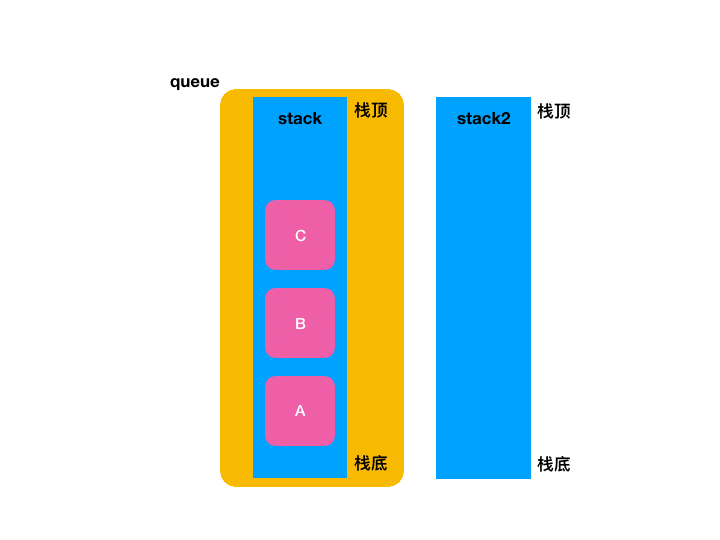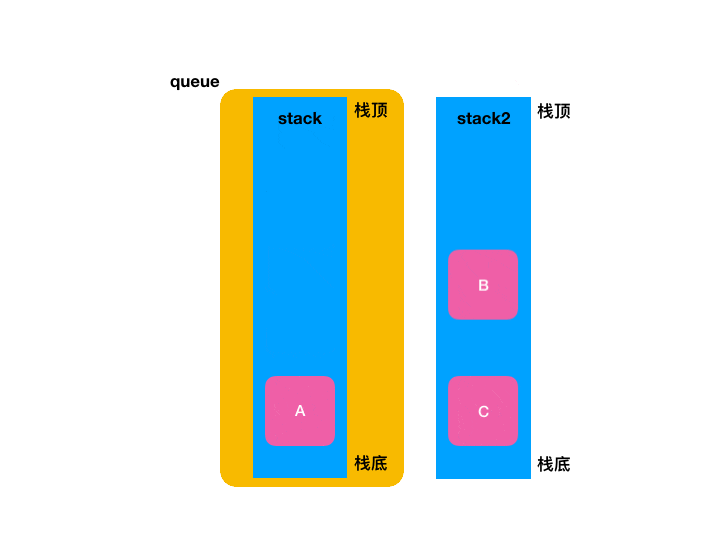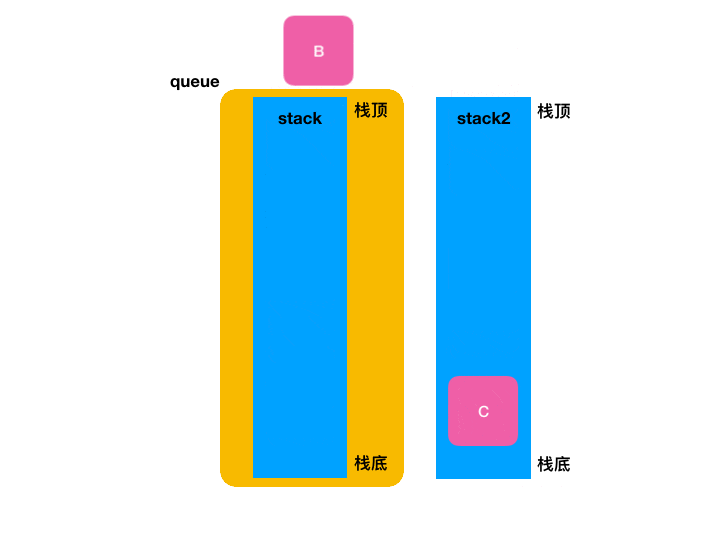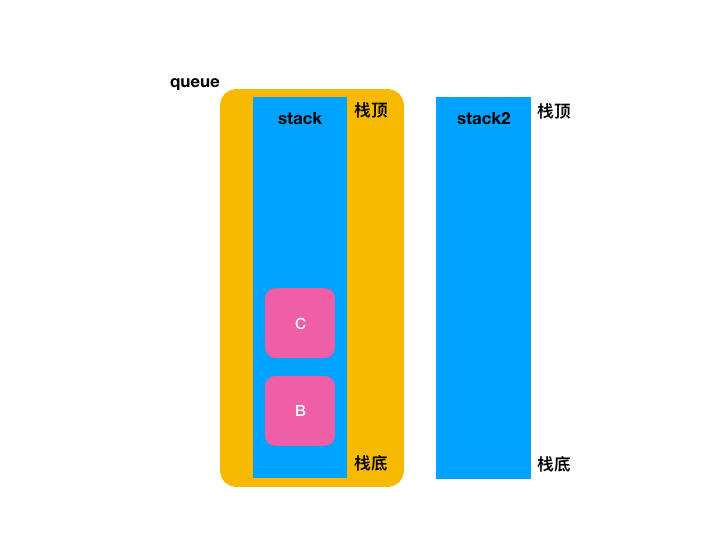
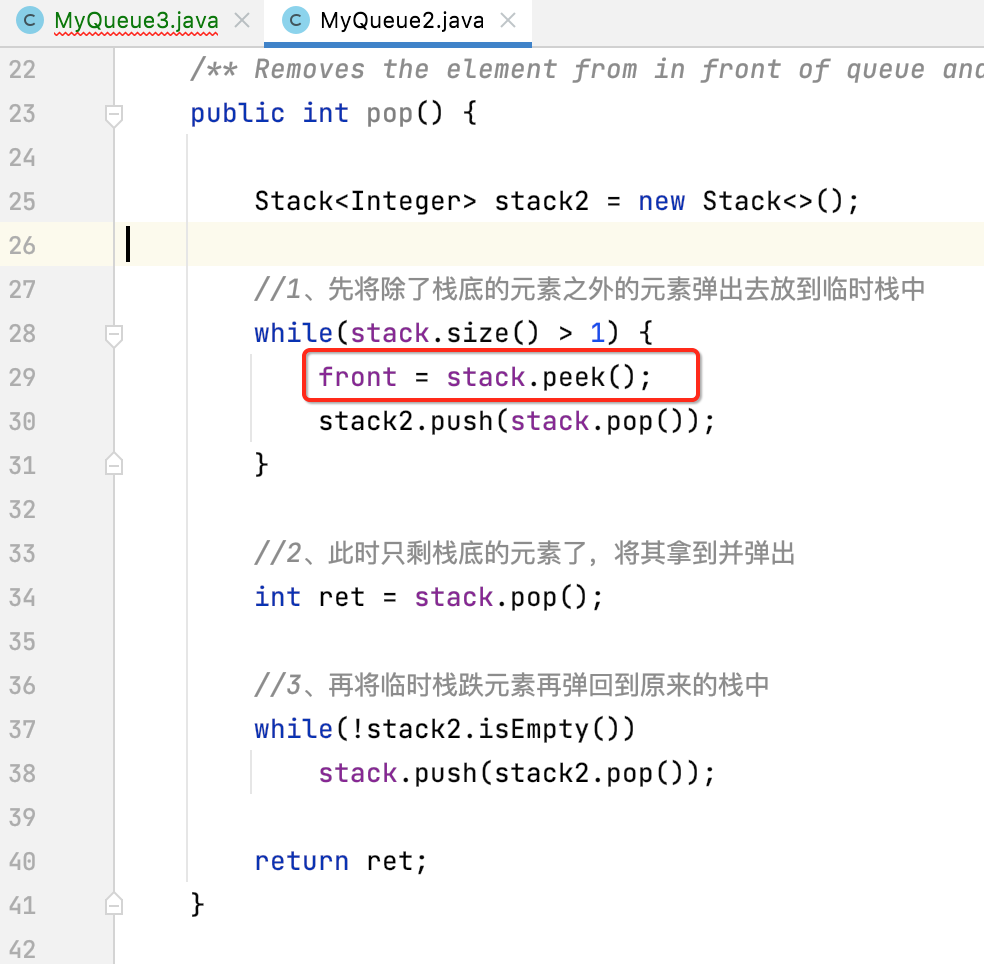
接下来核心的核心就是它了,很显然它一定是O(n),因为要想办法把栈底的元素弹出栈,直接拿是拿不到的,其思路也跟之前的push类似:依然是,我们使用另外一个栈 stack2 暂存除了最后一个元素以外的所有元素。在取出栈底元素以后,再把 stack2 的所有元素放回 stack 中。这个过程要注意对 front 的维护。代码如下:
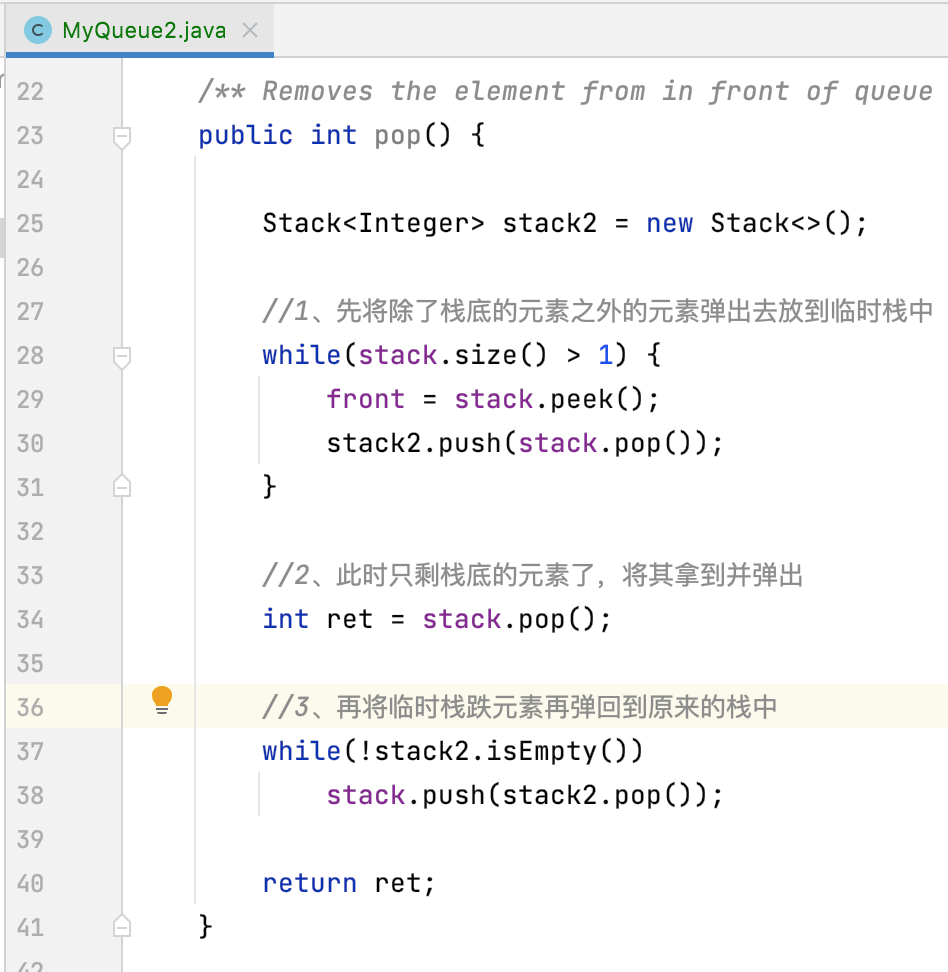
对于这段代码的逻辑可以看如下图:
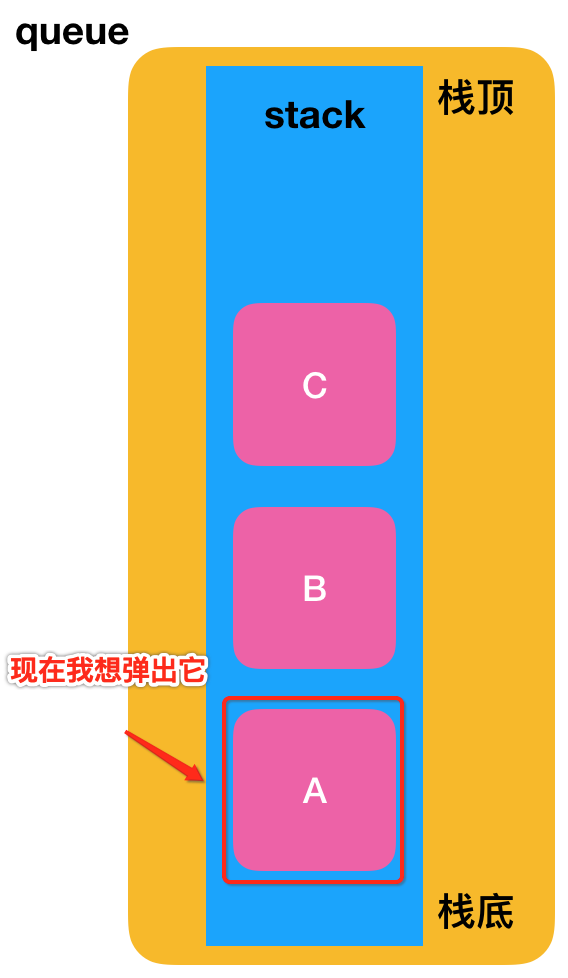
整个过程如下:
5、拷贝到LeetCode验证:
import java.util.Stack; /** * 用栈实现队列实现方式二:假设"栈顶是队尾" */ public class MyQueue2 { private Stack<Integer> stack; //为了让peek()效率更高,用它来追踪队首的元素 int front; /** Initialize your data structure here. */ public MyQueue2() { stack = new Stack<>(); } /** Push element x to the back of queue. */ public void push(int x) { if(empty()) front = x;//第一次入队的肯定是队首元素 stack.push(x); } /** Removes the element from in front of queue and returns that element. */ public int pop() { Stack<Integer> stack2 = new Stack<>(); //1、先将除了栈底的元素之外的元素弹出去放到临时栈中 while(stack.size() > 1) { front = stack.peek(); stack2.push(stack.pop()); } //2、此时只剩栈底的元素了,将其拿到并弹出 int ret = stack.pop(); //3、再将临时栈跌元素再弹回到原来的栈中 while(!stack2.isEmpty()) stack.push(stack2.pop()); return ret; } /** Get the front element. */ public int peek() { return front; } /** Returns whether the queue is empty. */ public boolean empty() { return stack.isEmpty(); } }
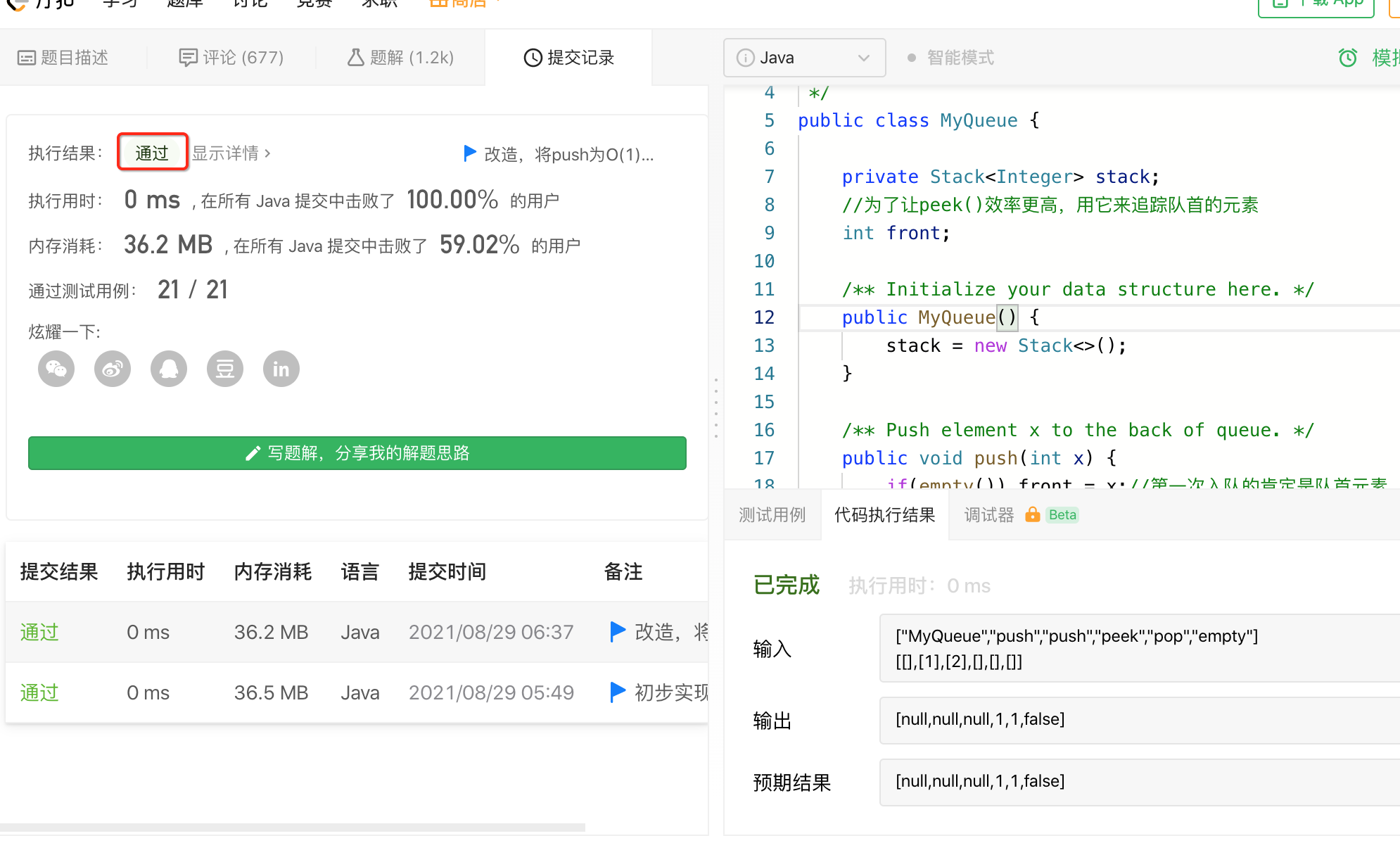
拷的时候注意将MyQueue2改为MyQueue哟~~
实现方式三:
思考:
对于方式二的这种实现有一个很大的问题在于:每次,我们 pop 的过程,都将 stack 的元素放进 stack2,再从 stack2 挪回来:
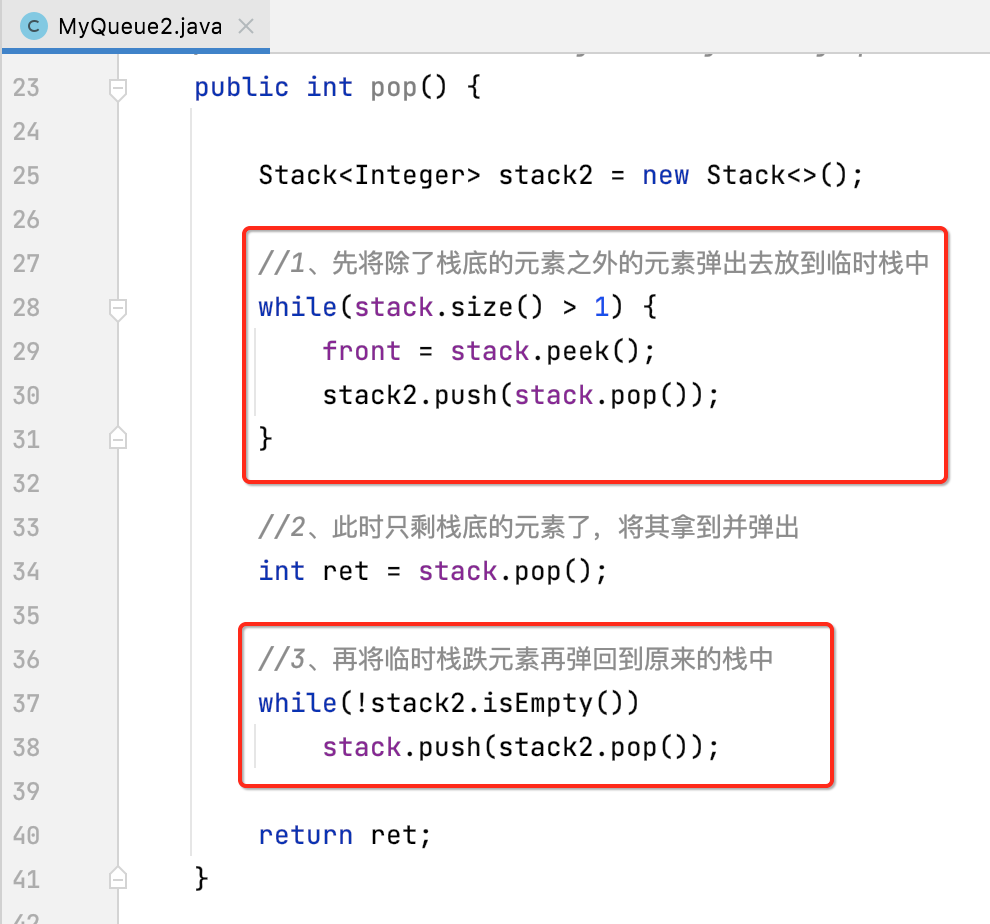
实际上,如果用户连续调用 pop 的话,这个过程相当于重复了。我们完全可以只把 stack 的元素扔到 stack2 一次。下次再调用 pop,如果发现 stack2 不为空,就直接拿 stack2 栈顶的元素就好了。比如对于这样的一个结构:
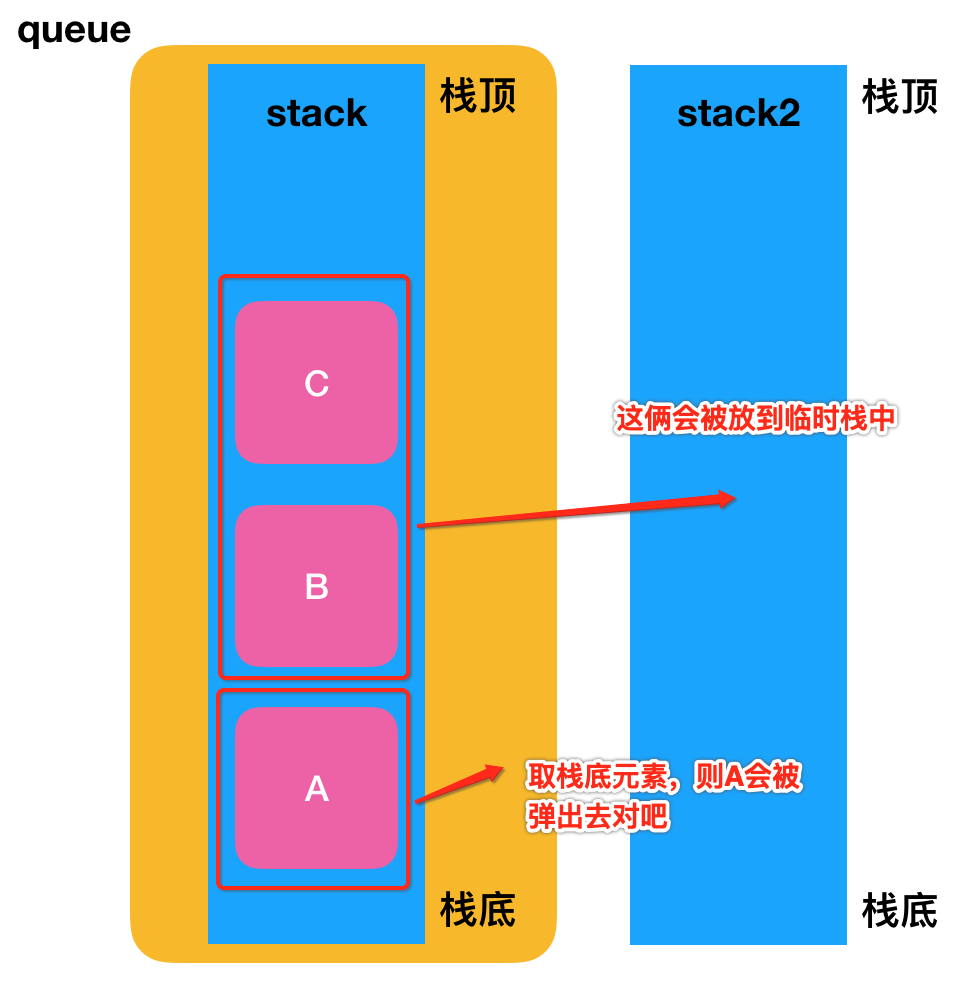
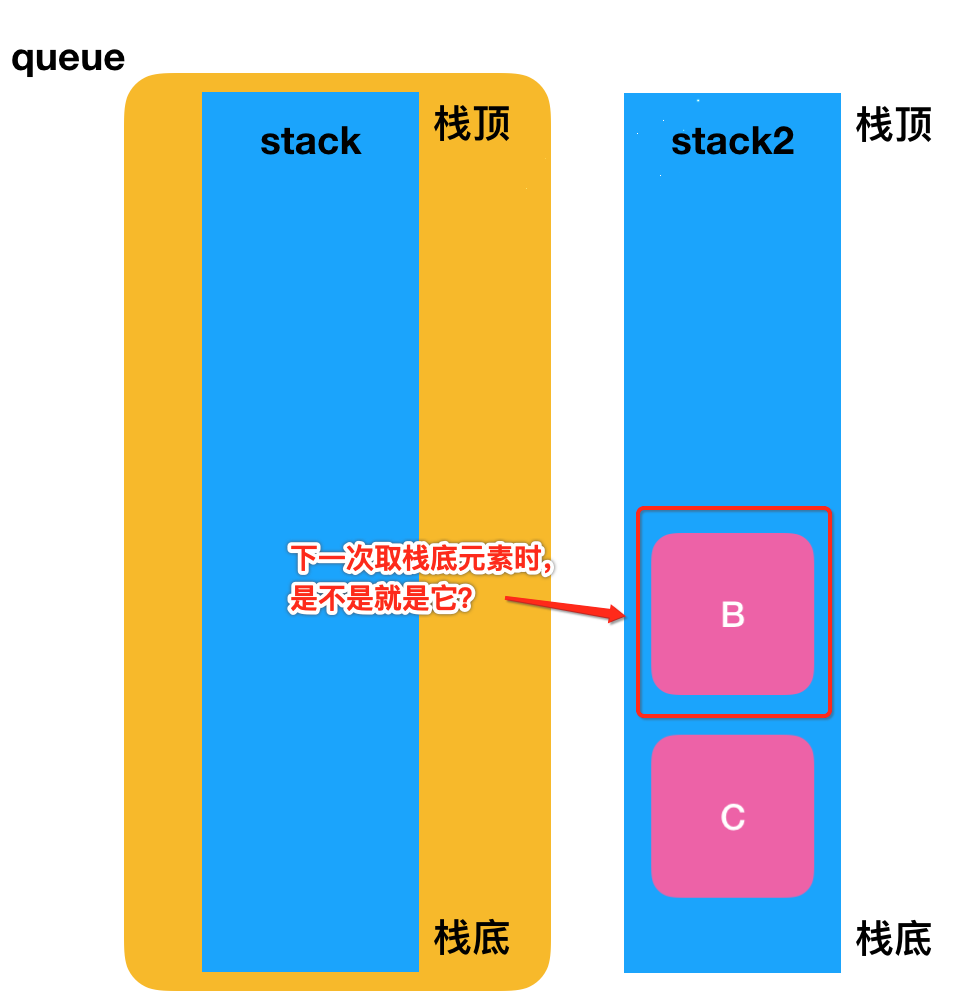
而没必要非得将stack2中的元素再拿回stack当中了,所以接下来可以进一步优化咱们的实现逻辑。
改造:
1、定义两个statck:
其实改造起来也比较简单,就是此时我们的 stack2 不能是 pop 里的一个临时变量了,而需要成为整个 MyQueue 的成员变量:
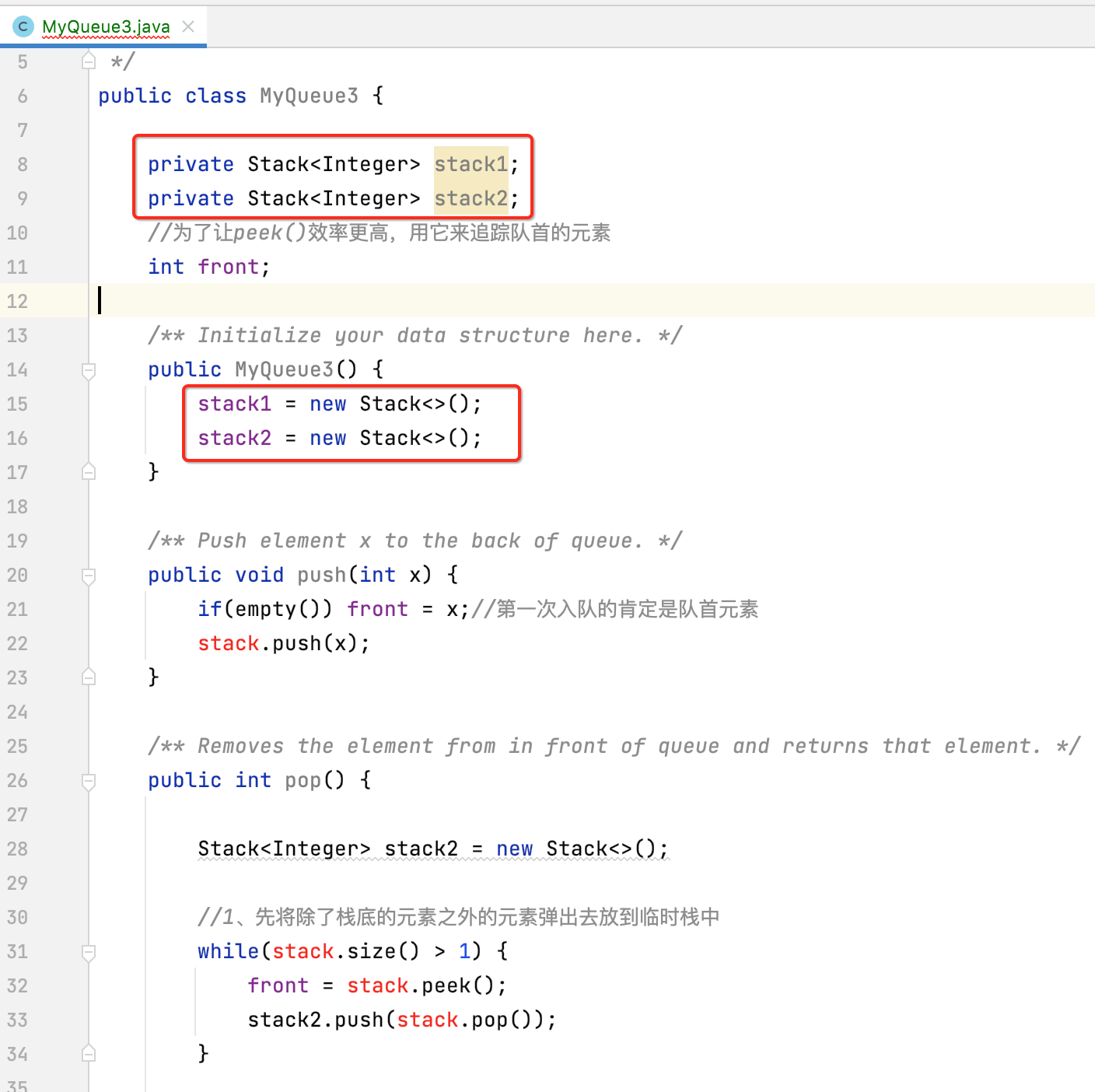
当然此时会报错,接下来则来进行相关改造。
2、pop():
这样一来,咱们的pop逻辑就可以简化为:
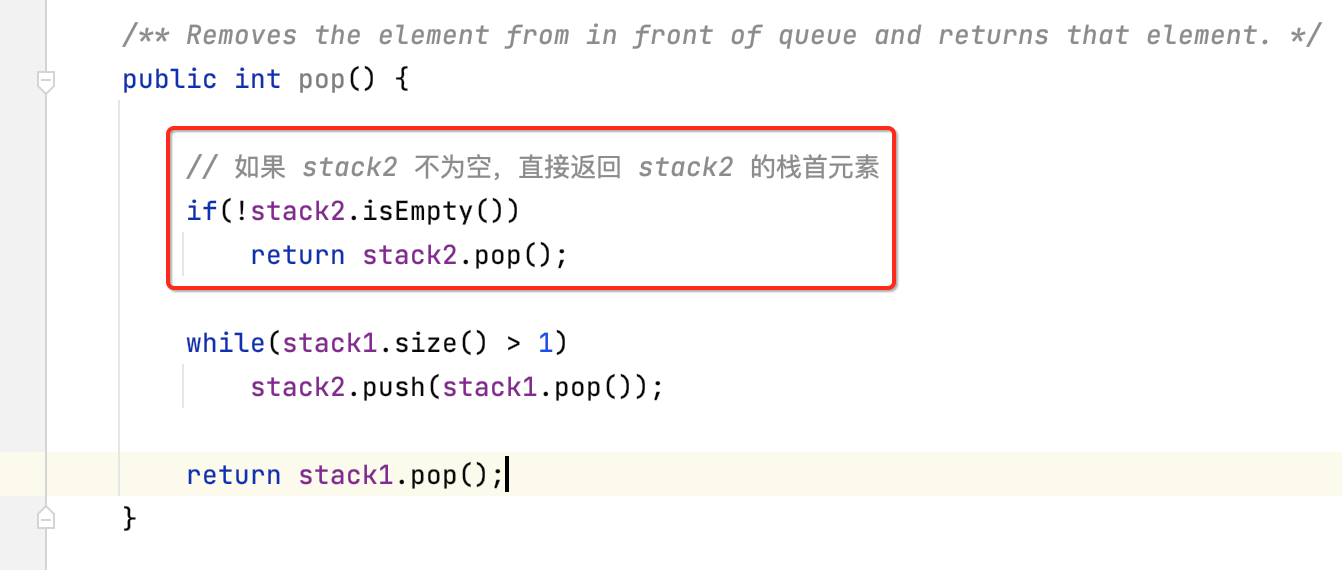
这里有一个注意点,原来咱们的实现为了peek()效率更高会维护front这个变量的,回忆一下:
这是因为peek()也得改造了。
3、peek():
其实改造也不难:当 stack2 不为空的时候,peek 的结果就是 stack2.peek(),否则的话,我们取我们在 push 的过程中更新的 front 的值。如下:

因为我们在push时维护了front了。
4、push、empty:
因为现在,stack1 和 stack2 中都可能存储元素,所以,我们在判断整个队列是否为空的时候,stack1 和 stack2 都要看一下:

对于push此时的逻辑也得发生一点小变化了:

改成stack1既可:
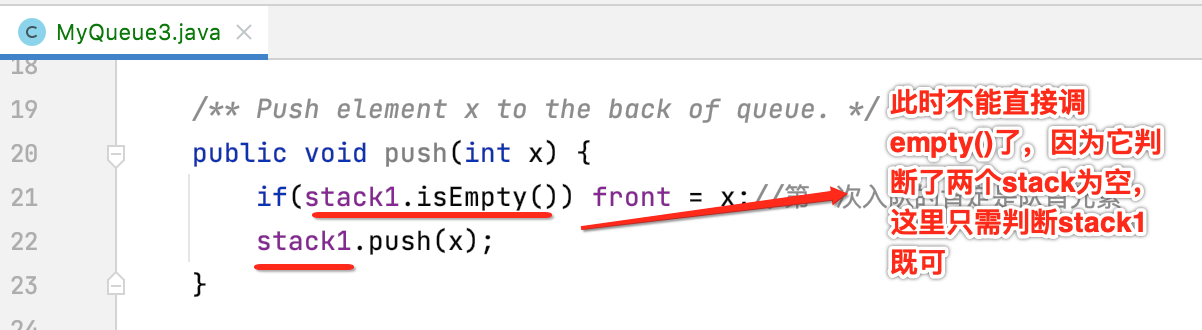
整体的代码如下:
import java.util.Stack; /** * 用栈实现队列实现方式三:pop优化 */ public class MyQueue3 { private Stack<Integer> stack1; private Stack<Integer> stack2; //为了让peek()效率更高,用它来追踪队首的元素 int front; /** Initialize your data structure here. */ public MyQueue3() { stack1 = new Stack<>(); stack2 = new Stack<>(); } /** Push element x to the back of queue. */ public void push(int x) { if(stack1.isEmpty()) front = x;//第一次入队的肯定是队首元素 stack1.push(x); } /** Removes the element from in front of queue and returns that element. */ public int pop() { // 如果 stack2 不为空,直接返回 stack2 的栈首元素 if(!stack2.isEmpty()) return stack2.pop(); while(stack1.size() > 1) stack2.push(stack1.pop()); return stack1.pop(); } /** Get the front element. */ public int peek() { if(!stack2.isEmpty()) return stack2.peek(); return front; } /** Returns whether the queue is empty. */ public boolean empty() { return stack1.isEmpty() && stack2.isEmpty(); } }
5、拷贝到LeetCode验证:
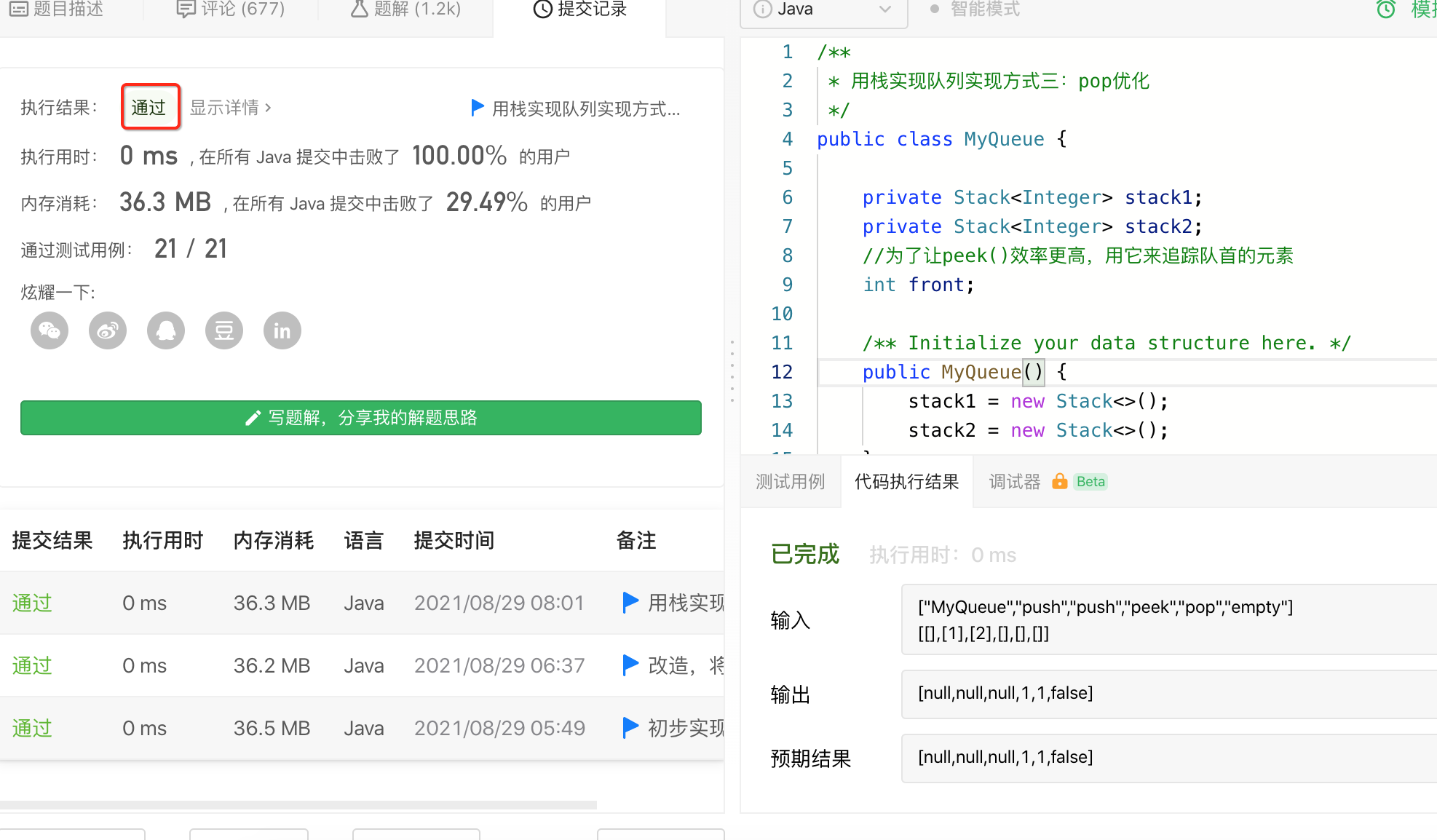
时间复杂度:
这个代码,相比第二种方式,其实整体的复杂度是没有变的,pop 的最差时间【注意是最差,而不是所有情况】复杂度依然是 O(n) 的。但是!!!平均对于每一个元素来说,都只有一次机会进 stack1,也只有一次机会进 stack2。所以,这样实现,pop 的均摊复杂度【关于它的概念不太清楚的可以参考https://www.cnblogs.com/webor2006/p/14092866.html,有详细说明】,变成了 O(1) 的,所以,此时的性能就达到最佳了。
总结:
至此, 对于栈和队列的概念通过最近的两次练习,应该对它们的认识会更加的深刻,也为后续学习其它更为复杂的算法与数据结构打下了扎实的基础,加油~~



