算法与数据结构基础<三>----数据结构基础之栈和队列加强之实现双端队列
在上一次https://www.cnblogs.com/webor2006/p/14216904.html咱们学习了栈和队列这俩基本数据结构了,接下来则会进一步深入加强,以加深对于它们的了解,也是面试时很有可能会被提到的~~
实现双端队列:
理论:
接下来准备实现一个全新的数据结构---双端队列,其实跟我们之前所学的队列关系紧密,我们知道,对于普通队列来说“只能从一端(队尾)添加元素,只能从另一端(队首)取出元素”,也就是先进先出对吧,但是!!!对于双端队列就不一样了,它的特点是:
- 可以在队列的两端添加元素
- 可以在队列的两端删除元素
而在方法设计上,通常就会对应有这四个方法:
- addFront,addLast
- removeFront,removeLast
而通常对于双端队列的命名是Deque,百度一下:
思考:
在正式实现它之前,先来挼一下实现思路,由于它其实也是建立在咱们之前实现的队列基础之上的,而对于双端队列主要就是涉及到如下四个方法:
- addFront,addLast
- removeFront,removeLast
而对于普通队列来说,“添加是从队尾开始的,而移除是从队首的”,可能有些人看到这句话有点歧义,对照着图来理解就对了:

队首是在下面,而队尾是在上面,不要理解反了,关于这块还有问题的可以参考它https://www.cnblogs.com/webor2006/p/14216904.html,那么回到我们这边要实现的双端队列的四个方法,很明显有两个完全跟我们之前实现的队列的是一模一样的逻辑,那就是:
- addLast,其实就是咱们之前普通队列的enqueue
- removeFront,其实就是咱们之前普通队列的dequeue
那么,咱们的关键就是只需要实现如下两个方法了:
- addFront
- removeLast
而要实现这两个方法,关键在于正确地计算出经过队列元素的添加和删除之后的front和tail,所以经过这么一分析双端队列貌似也没那么难,在正式实现之前,先把之前实现的队列的代码贴出来供回忆参考:
// 在这一版LoopQueue的实现中,我们将不浪费那1个空间 public class LoopQueue2<E> implements Queue<E> { private E[] data; private int front, tail; private int size; public LoopQueue2(int capacity) { data = (E[]) new Object[capacity]; // 由于不浪费空间,所以data静态数组的大小是capacity,而不是capacity + 1 front = 0; tail = 0; size = 0; } public LoopQueue2() { this(10); } public int getCapacity() { return data.length; } @Override public boolean isEmpty() { // 注意,我们不再使用front和tail之间的关系来判断队列是否为空,而直接使用size return size == 0; } @Override public int getSize() { return size; } @Override public void enqueue(E e) { // 注意,我们不再使用front和tail之间的关系来判断队列是否为满,而直接使用size if (size == getCapacity()) resize(getCapacity() * 2); data[tail] = e; tail = (tail + 1) % data.length; size++; } @Override public E dequeue() { if (isEmpty()) throw new IllegalArgumentException("Cannot dequeue from an empty queue."); E ret = data[front]; data[front] = null; front = (front + 1) % data.length; size--; if (size == getCapacity() / 4 && getCapacity() / 2 != 0) resize(getCapacity() / 2); return ret; } @Override public E getFront() { if (isEmpty()) throw new IllegalArgumentException("Queue is empty."); return data[front]; } private void resize(int newCapacity) { E[] newData = (E[]) new Object[newCapacity]; for (int i = 0; i < size; i++) newData[i] = data[(i + front) % data.length]; data = newData; front = 0; tail = size; } @Override public String toString() { StringBuilder res = new StringBuilder(); res.append(String.format("Queue: size = %d , capacity = %d\n", size, getCapacity())); res.append("front ["); // 注意,我们的循环遍历打印队列的逻辑也有相应的更改 for (int i = 0; i < size; i++) { res.append(data[(front + i) % data.length]); if ((i + front + 1) % data.length != tail) res.append(", "); } res.append("] tail"); return res.toString(); } public static void main(String[] args) { LoopQueue<Integer> queue = new LoopQueue<>(); for (int i = 0; i < 10; i++) { queue.enqueue(i); System.out.println(queue); if (i % 3 == 2) { queue.dequeue(); System.out.println(queue); } } } }
实践:
1、新建文件,拷贝原来队列复用的代码:
既然跟我们之前实现的队列逻辑基本差不多,所以可以把用得到的代码拷贝过来,这里就不重复解释了:
/** * 双端队列 */ public class Deque<E> { private E[] data; private int front, tail; private int size; // 方便起见,我们的 Deque 实现,将使用 size 记录 deque 中存储的元素数量 public Deque(int capacity){ data = (E[])new Object[capacity]; // 由于使用 size,我们的 Deque 实现不浪费空间 front = 0; tail = 0; size = 0; } public Deque(){ this(10); } public int getCapacity(){ return data.length; } public boolean isEmpty(){ return size == 0; } public int getSize(){ return size; } // addLast 的逻辑和我们之前实现的队列中的 enqueue 的逻辑是一样的 public void addLast(E e){ if(size == getCapacity()) resize(getCapacity() * 2); data[tail] = e; tail = (tail + 1) % data.length; size ++; } // addFront 是新的方法,请大家注意 public void addFront(E e){ //TODO } // removeFront 的逻辑和我们之前实现的队列中的 dequeue 的逻辑是一样的 public E removeFront(){ if(isEmpty()) throw new IllegalArgumentException("Cannot dequeue from an empty queue."); E ret = data[front]; data[front] = null; front = (front + 1) % data.length; size --; if(getSize() == getCapacity() / 4 && getCapacity() / 2 != 0) resize(getCapacity() / 2); return ret; } // removeLast 是新的方法,请大家注意 public E removeLast(){ //TODO return null; } public E getFront(){ if(isEmpty()) throw new IllegalArgumentException("Queue is empty."); return data[front]; } // 因为是双端队列,我们也有一个 getLast 的方法,来获取队尾元素的值 public E getLast(){ if(isEmpty()) throw new IllegalArgumentException("Queue is empty."); //TODO,这块需要调整逻辑 return null; } private void resize(int newCapacity){ E[] newData = (E[])new Object[newCapacity]; for(int i = 0 ; i < size ; i ++) newData[i] = data[(i + front) % data.length]; data = newData; front = 0; tail = size; } @Override public String toString(){ StringBuilder res = new StringBuilder(); res.append(String.format("Queue: size = %d , capacity = %d\n", getSize(), getCapacity())); res.append("front ["); for(int i = 0 ; i < size ; i ++){ res.append(data[(i + front) % data.length]); if(i != size - 1) res.append(", "); } res.append("] tail"); return res.toString(); } }
2、addFont()方法实现:
它的实现代码也不难,如下:
// addFront 是新的方法,请大家注意 public void addFront(E e){ if(size == getCapacity()) resize(getCapacity() * 2); // 我们首先需要确定添加新元素的索引位置 // 这个位置是 front - 1 的地方 // 但是要注意,如果 front == 0,新的位置是 data.length - 1 的位置 front = front == 0 ? data.length - 1 : front - 1; data[front] = e; size ++; }
其中当front==0的时候,其要添加的位置是data.length-1呢?看图说话:
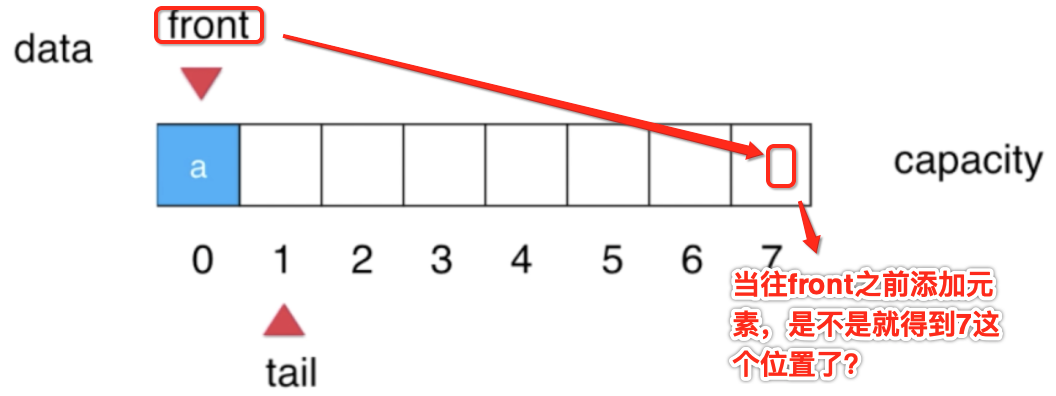
而如果front!=0的情况,当然就是插入到front-1的位置了喽。
3、removeLast():
// removeLast 是新的方法,请大家注意 public E removeLast(){ if(isEmpty()) throw new IllegalArgumentException("Cannot dequeue from an empty queue."); // 计算删除掉队尾元素以后,新的 tail 位置 tail = tail == 0 ? data.length - 1 : tail - 1; E ret = data[tail]; data[tail] = null; size --; if(getSize() == getCapacity() / 4 && getCapacity() / 2 != 0) resize(getCapacity() / 2); return ret; }
理解一下,当tail==0时:
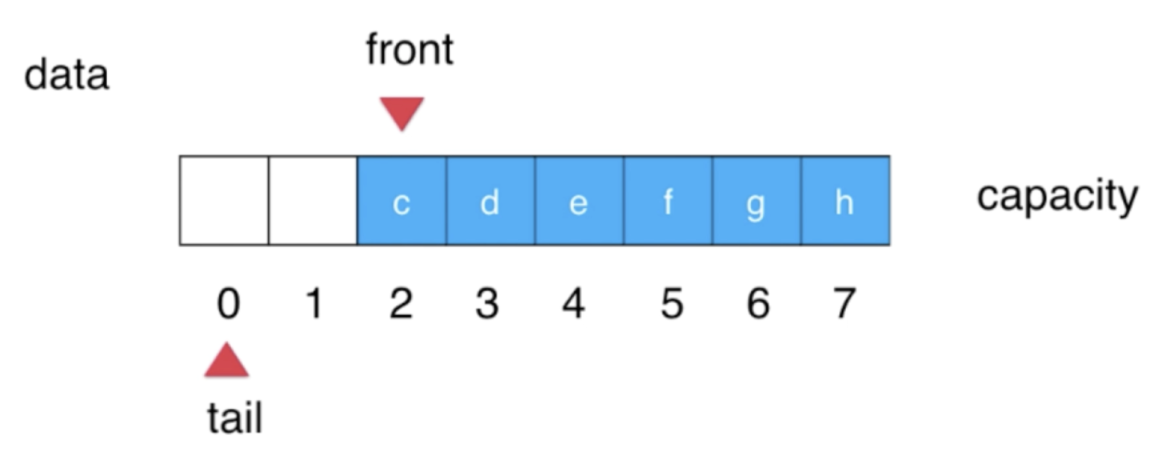
此时removeLast是不是得回到第7个位置的“h”元素需要被删除了?而如果tail!=0,那当然移除的是tail-1个元素了。
4、getLast():
队尾的元素直接根据tail指向的前一个位置来获取,如下:

5、测试:
/** * 双端队列 */ public class Deque<E> { private E[] data; private int front, tail; private int size; // 方便起见,我们的 Deque 实现,将使用 size 记录 deque 中存储的元素数量 public Deque(int capacity){ data = (E[])new Object[capacity]; // 由于使用 size,我们的 Deque 实现不浪费空间 front = 0; tail = 0; size = 0; } public Deque(){ this(10); } public int getCapacity(){ return data.length; } public boolean isEmpty(){ return size == 0; } public int getSize(){ return size; } // addLast 的逻辑和我们之前实现的队列中的 enqueue 的逻辑是一样的 public void addLast(E e){ if(size == getCapacity()) resize(getCapacity() * 2); data[tail] = e; tail = (tail + 1) % data.length; size ++; } // addFront 是新的方法,请大家注意 public void addFront(E e){ if(size == getCapacity()) resize(getCapacity() * 2); // 我们首先需要确定添加新元素的索引位置 // 这个位置是 front - 1 的地方 // 但是要注意,如果 front == 0,新的位置是 data.length - 1 的位置 front = front == 0 ? data.length - 1 : front - 1; data[front] = e; size ++; } // removeFront 的逻辑和我们之前实现的队列中的 dequeue 的逻辑是一样的 public E removeFront(){ if(isEmpty()) throw new IllegalArgumentException("Cannot dequeue from an empty queue."); E ret = data[front]; data[front] = null; front = (front + 1) % data.length; size --; if(getSize() == getCapacity() / 4 && getCapacity() / 2 != 0) resize(getCapacity() / 2); return ret; } // removeLast 是新的方法,请大家注意 public E removeLast(){ if(isEmpty()) throw new IllegalArgumentException("Cannot dequeue from an empty queue."); // 计算删除掉队尾元素以后,新的 tail 位置 tail = tail == 0 ? data.length - 1 : tail - 1; E ret = data[tail]; data[tail] = null; size --; if(getSize() == getCapacity() / 4 && getCapacity() / 2 != 0) resize(getCapacity() / 2); return ret; } public E getFront(){ if(isEmpty()) throw new IllegalArgumentException("Queue is empty."); return data[front]; } // 因为是双端队列,我们也有一个 getLast 的方法,来获取队尾元素的值 public E getLast(){ if(isEmpty()) throw new IllegalArgumentException("Queue is empty."); //TODO,这块需要调整逻辑 return null; } private void resize(int newCapacity){ E[] newData = (E[])new Object[newCapacity]; for(int i = 0 ; i < size ; i ++) newData[i] = data[(i + front) % data.length]; data = newData; front = 0; tail = size; } @Override public String toString(){ StringBuilder res = new StringBuilder(); res.append(String.format("Queue: size = %d , capacity = %d\n", getSize(), getCapacity())); res.append("front ["); for(int i = 0 ; i < size ; i ++){ res.append(data[(i + front) % data.length]); if(i != size - 1) res.append(", "); } res.append("] tail"); return res.toString(); } public static void main(String[] args){ // 在下面的双端队列的测试中,偶数从队尾加入;奇数从队首加入 Deque<Integer> dq = new Deque<>(); for(int i = 0 ; i < 16 ; i ++){ if(i % 2 == 0) dq.addLast(i); else dq.addFront(i); System.out.println(dq); } // 之后,我们依次从队首和队尾轮流删除元素 System.out.println(); for(int i = 0; !dq.isEmpty(); i ++){ if(i % 2 == 0) dq.removeFront(); else dq.removeLast(); System.out.println(dq); } } }
运行看一下:
Queue: size = 1 , capacity = 10 front [0] tail Queue: size = 2 , capacity = 10 front [1, 0] tail Queue: size = 3 , capacity = 10 front [1, 0, 2] tail Queue: size = 4 , capacity = 10 front [3, 1, 0, 2] tail Queue: size = 5 , capacity = 10 front [3, 1, 0, 2, 4] tail Queue: size = 6 , capacity = 10 front [5, 3, 1, 0, 2, 4] tail Queue: size = 7 , capacity = 10 front [5, 3, 1, 0, 2, 4, 6] tail Queue: size = 8 , capacity = 10 front [7, 5, 3, 1, 0, 2, 4, 6] tail Queue: size = 9 , capacity = 10 front [7, 5, 3, 1, 0, 2, 4, 6, 8] tail Queue: size = 10 , capacity = 10 front [9, 7, 5, 3, 1, 0, 2, 4, 6, 8] tail Queue: size = 11 , capacity = 20 front [9, 7, 5, 3, 1, 0, 2, 4, 6, 8, 10] tail Queue: size = 12 , capacity = 20 front [11, 9, 7, 5, 3, 1, 0, 2, 4, 6, 8, 10] tail Queue: size = 13 , capacity = 20 front [11, 9, 7, 5, 3, 1, 0, 2, 4, 6, 8, 10, 12] tail Queue: size = 14 , capacity = 20 front [13, 11, 9, 7, 5, 3, 1, 0, 2, 4, 6, 8, 10, 12] tail Queue: size = 15 , capacity = 20 front [13, 11, 9, 7, 5, 3, 1, 0, 2, 4, 6, 8, 10, 12, 14] tail Queue: size = 16 , capacity = 20 front [15, 13, 11, 9, 7, 5, 3, 1, 0, 2, 4, 6, 8, 10, 12, 14] tail Queue: size = 15 , capacity = 20 front [13, 11, 9, 7, 5, 3, 1, 0, 2, 4, 6, 8, 10, 12, 14] tail Queue: size = 14 , capacity = 20 front [13, 11, 9, 7, 5, 3, 1, 0, 2, 4, 6, 8, 10, 12] tail Queue: size = 13 , capacity = 20 front [11, 9, 7, 5, 3, 1, 0, 2, 4, 6, 8, 10, 12] tail Queue: size = 12 , capacity = 20 front [11, 9, 7, 5, 3, 1, 0, 2, 4, 6, 8, 10] tail Queue: size = 11 , capacity = 20 front [9, 7, 5, 3, 1, 0, 2, 4, 6, 8, 10] tail Queue: size = 10 , capacity = 20 front [9, 7, 5, 3, 1, 0, 2, 4, 6, 8] tail Queue: size = 9 , capacity = 20 front [7, 5, 3, 1, 0, 2, 4, 6, 8] tail Queue: size = 8 , capacity = 20 front [7, 5, 3, 1, 0, 2, 4, 6] tail Queue: size = 7 , capacity = 20 front [5, 3, 1, 0, 2, 4, 6] tail Queue: size = 6 , capacity = 20 front [5, 3, 1, 0, 2, 4] tail Queue: size = 5 , capacity = 10 front [3, 1, 0, 2, 4] tail Queue: size = 4 , capacity = 10 front [3, 1, 0, 2] tail Queue: size = 3 , capacity = 10 front [1, 0, 2] tail Queue: size = 2 , capacity = 5 front [1, 0] tail Queue: size = 1 , capacity = 2 front [0] tail Queue: size = 0 , capacity = 1 front [] tail
其中可以稍加说明一下测试结果:

没有size成员变量的循环队列:
理论:
在上面实现中,咱们使用了一个size变量来记录队列元素的个数,跟之前学习队列数据结构实现的一样,也可以用另一种方式来实现,那就是不浪费这个size变量的空间,用front和tail来算出元素总数,所以接下来基于这个优化思想再用另一种方式来实现一下双端队列,同样是浪费一个空间,但是这里不会用到size了。
实践:
/** * 双端队列:还是浪费一个空间,但是不使用size */ public class Deque2<E> { private E[] data; private int front, tail; public Deque2(int capacity){ data = (E[])new Object[capacity+1]; front = 0; tail = 0; } public Deque2(){ this(10); } public int getCapacity(){ return data.length - 1; } public boolean isEmpty(){ return front == tail; } public int getSize(){ //此时需要注意它的逻辑为: //如果tail >= front,很简单,队列中的元素个数就是tail-front; //如果tail < front,说明循环队列"循环"起来了,此时,队列中的元素个数为:tail-front+data.length //这个式子也可以理解为,data中没有元素的数目为front-tail,整体元素个数就是:data.length-(front-tail) //=data.length-front+tail return tail >= front ? tail - front : tail - front + data.length; } // addLast 的逻辑和我们之前实现的队列中的 enqueue 的逻辑是一样的 public void addLast(E e){ if ((tail + 1) % data.length == front) resize(getCapacity() * 2); data[tail] = e; tail = (tail + 1) % data.length; } // addFront 是新的方法,请大家注意 public void addFront(E e){ if ((tail + 1) % data.length == front) resize(getCapacity() * 2); // 我们首先需要确定添加新元素的索引位置 // 这个位置是 front - 1 的地方 // 但是要注意,如果 front == 0,新的位置是 data.length - 1 的位置 front = front == 0 ? data.length - 1 : front - 1; data[front] = e; } // removeFront 的逻辑和我们之前实现的队列中的 dequeue 的逻辑是一样的 public E removeFront(){ if(isEmpty()) throw new IllegalArgumentException("Cannot dequeue from an empty queue."); E ret = data[front]; data[front] = null; front = (front + 1) % data.length; if(getSize() == getCapacity() / 4 && getCapacity() / 2 != 0) resize(getCapacity() / 2); return ret; } // removeLast 是新的方法,请大家注意 public E removeLast(){ if(isEmpty()) throw new IllegalArgumentException("Cannot dequeue from an empty queue."); // 计算删除掉队尾元素以后,新的 tail 位置 tail = tail == 0 ? data.length - 1 : tail - 1; E ret = data[tail]; data[tail] = null; if(getSize() == getCapacity() / 4 && getCapacity() / 2 != 0) resize(getCapacity() / 2); return ret; } public E getFront(){ if(isEmpty()) throw new IllegalArgumentException("Queue is empty."); return data[front]; } // 因为是双端队列,我们也有一个 getLast 的方法,来获取队尾元素的值 public E getLast(){ if(isEmpty()) throw new IllegalArgumentException("Queue is empty."); //TODO,这块需要调整逻辑 return null; } private void resize(int newCapacity){ E[] newData = (E[]) new Object[newCapacity + 1]; int sz = getSize(); for (int i = 0; i < sz; i++) newData[i] = data[(i + front) % data.length]; data = newData; front = 0; tail = sz; } @Override public String toString(){ StringBuilder res = new StringBuilder(); res.append(String.format("Queue: size = %d , capacity = %d\n", getSize(), getCapacity())); res.append("front ["); for (int i = front; i != tail; i = (i + 1) % data.length) { res.append(data[i]); if ((i + 1) % data.length != tail) res.append(", "); } res.append("] tail"); return res.toString(); } public static void main(String[] args){ // 在下面的双端队列的测试中,偶数从队尾加入;奇数从队首加入 Deque2<Integer> dq = new Deque2<>(); for(int i = 0 ; i < 16 ; i ++){ if(i % 2 == 0) dq.addLast(i); else dq.addFront(i); System.out.println(dq); } // 之后,我们依次从队首和队尾轮流删除元素 System.out.println(); for(int i = 0; !dq.isEmpty(); i ++){ if(i % 2 == 0) dq.removeFront(); else dq.removeLast(); System.out.println(dq); } } }
其运行结果跟第一版的是一样的。
用队列实现栈&用栈实现队列
在之前我们实现栈和队列,底层全是使用的动态数组对吧,那。。如果没有动态数组,而只有队列这么一个数据结构,你能用它来实现栈么?类似的如果只有栈这么一个数据结构,你能用它来实现一个队列么?而这两个经典算法题也出现在了leetcode中了,具体可以点击下面两个链接来查看:
用队列实现栈
用栈实现队列
当然,咱们的目标就是把实现的代码拷到Leetcode中来进行验证,且用多种方式来实现。
用队列实现栈:
基本实现:
1、定义一个队列的成员变量:

其中直接使用 Java 内置的 Queue。Java 中的 Queue 是一个接口,具体实例化它,需要选择一个数据结构。在这里,我们选择使用 LinkedList。LinkedList 是链表,关于链表,在下一次就会学习到。
2、push():
对于一个栈来说,关键是栈顶在哪里。栈是一端入,同一端出;而队列是一端入,另一端出。那如果只给出一个队列,我们先假设入队的一端是栈顶,那么,对于这个push方法就非常简单了,直接将元素放入队列中就好了,如下:
3、pop():移除栈顶的元素并返回
分析:
接下来的问题就来了,我们想要获得栈顶的元素,但是呢底层的数据存储在一个队列中,也就是需要获得队列中的队尾的那个元素移除并返回才对,那么问题来了:
我们只能取出队首的元素【因为是先进先出】,所以,要想拿到队尾的元素,我们就必须先把现在队列中的 n - 1 个元素都取出来。剩下的那一个元素,就是队尾的元素。
关于上面这一段,可能有点抽象,这边简单画一个图辅助理解:

目前是这么一个形态,Stack的底层是用Queue来实现的。好,接下来入栈几个元素:
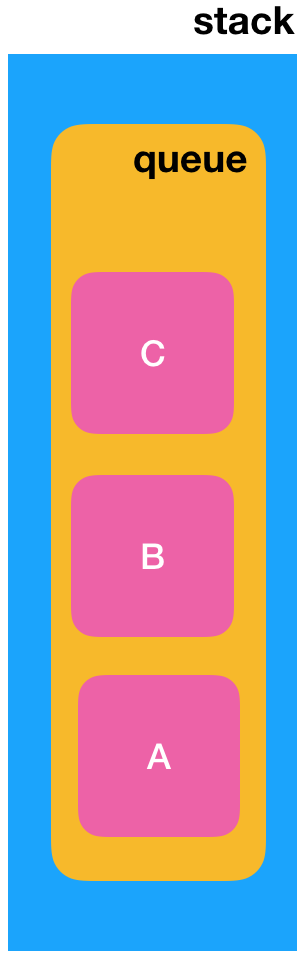
此时,我想pop()取栈顶的元素的话,就应该是“C”的对吧,但是!!!请注意,此时C是在队列的队尾哟,而队列出是从队首拿的,就形成了矛盾了不是?如下:

对于上面的这段文字应该就容易理解说的啥了吧?这里一定得要搞清楚“栈顶、栈底、队首、队尾”它们之间的概念才能不会晕,这里用图再说明一下:

好,接下来核心的问题就回到了如何才能取到"C"这个栈顶的元素, 无它法:我们就必须先把现在队列中的 n - 1 个元素都取出来。剩下的那一个元素,就是队尾的元素。
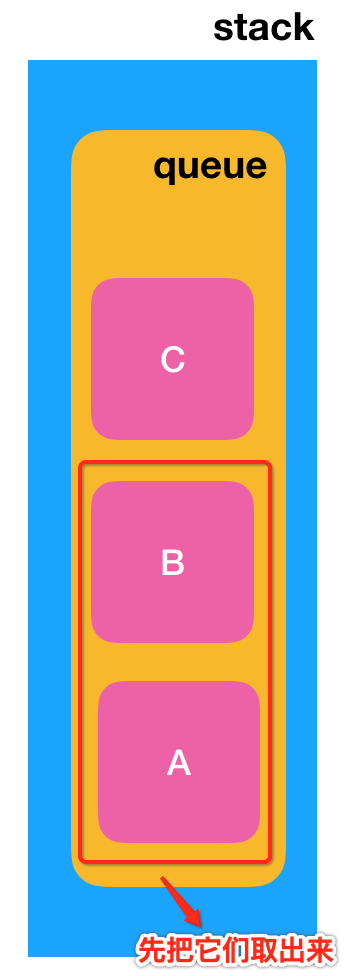
但是!!!取出来是不能丢掉的,得将其保存起来,而由于这题限制了我们必须使用队列这个数据结构。所以,此时,我们可以使用另外一个队列 比如叫q2【临时保存的队列】,来存储从 q 【原队列】中取出的所有元素。最后,q 里只剩下一个元素,就是我们要拿出的“栈顶元素”。将这个元素删除后,q2 里的数据就是原始的数据,我们用 q2 覆盖 q 就好,所以这么一来,实现思路就已经明确下,下面就可以来实现了。
实现:
/** Removes the element on top of the stack and returns that element. */ public int pop() { // 创建另外一个队列 q2 Queue<Integer> q2 = new LinkedList<>(); // 除了最后一个元素,将 q 中的所有元素放入 q2 while (q.size() > 1) q2.add(q.remove()); // q 中剩下的最后一个元素就是“栈顶”元素 int ret = q.remove(); // 此时 q2 是整个数据结构存储的所有其他数据,赋值给 q q = q2; // 返回“栈顶元素” return ret; }
4、top():
一旦我们实现了 pop,实现 top 就简单了。我们可以复用我们已经实现的 pop,将栈顶元素拿出来,记录下来,作为返回值。然后因为 top 不会删除元素,我们再将这个值放进队列就好了。如下:
/** Get the top element. */ public int top() { int ret = pop(); push(ret); return ret; }
5、empty():
/** Returns whether the stack is empty. */ public boolean empty() { return q.isEmpty(); }
6、将整个代码拷到Leetcode中进行验证:
import java.util.LinkedList; import java.util.Queue; public class MyStack { private Queue<Integer> q; public MyStack() { q = new LinkedList<>(); } /** Push element x onto stack. */ public void push(int x) { q.add(x); } /** Removes the element on top of the stack and returns that element. */ public int pop() { // 创建另外一个队列 q2 Queue<Integer> q2 = new LinkedList<>(); // 除了最后一个元素,将 q 中的所有元素放入 q2 while (q.size() > 1) q2.add(q.remove()); // q 中剩下的最后一个元素就是“栈顶”元素 int ret = q.remove(); // 此时 q2 是整个数据结构存储的所有其他数据,赋值给 q q = q2; // 返回“栈顶元素” return ret; } /** Get the top element. */ public int top() { int ret = pop(); push(ret); return ret; } }

7、复杂度分析:
- 初始化的构造函数复杂度,是 O(1) 的;

- 判断栈是否为空的
empty,复杂度,是 O(1) 的;
- 入栈的
push,复杂度是 O(1) 的;
- 出栈的
pop,因为需要把队列中所有元素都拿出来一趟,所以复杂度是 O(n) 的;
- 而
top,因为使用了pop,复杂度也是 O(n) 的。
思考:我们可不可能将 top 的复杂度降至 O(1)?
答案是可能的!
其实,我们没有必要每次取出栈顶元素的时候,都把所有元素再拿出来一趟。
在整个类中,我们可以使用一个变量,假设就叫 top,来追踪记录栈顶元素:
import java.util.LinkedList; import java.util.Queue; // 小优化,使用一个变量记录栈顶元素 // 注意,提交给 Leetcode 的时候,需要将 MyStack2 改成是 MyStack public class MyStack2 { private Queue<Integer> q; private int top; public MyStack2() { q = new LinkedList<>(); } /** Push element x onto stack. */ public void push(int x) { q.add(x); top = x; } /** Removes the element on top of the stack and returns that element. */ public int pop() { // 创建另外一个队列 q2 Queue<Integer> q2 = new LinkedList<>(); // 除了最后一个元素,将 q 中的所有元素放入 q2 while (q.size() > 1) { // 每从 q 中取出一个元素,都给 top 赋值 // top 最后存储的就是 q 中除了队尾元素以外的最后一个元素 // 即新的栈顶元素 top = q.peek(); q2.add(q.remove()); } // q 中剩下的最后一个元素就是“栈顶”元素 int ret = q.remove(); // 此时 q2 是整个数据结构存储的所有其他数据,赋值给 q q = q2; // 返回“栈顶元素” return ret; } /** Get the top element. */ public int top() { return top; } /** Returns whether the stack is empty. */ public boolean empty() { return q.isEmpty(); } }
将其拷到leetcode中验证一下正确性:
思考:上面的方式,push 是 O(1) 的,pop 是 O(n) 的。能不能写出一个实现,push 是 O(n) 的,pop 是 O(1) 的?
当然可以,就是想办法把栈顶的元素放到队首,也就是在push时需要对元素进行一个排序,也就是pop时直接从队列中取出就是栈顶的元素,如下:
核心的核心就是如何来改造这个push()方法了,怎么放呢?一样的思路,我们使用另外一个队列暂存所有的元素。我们可以先把 q 的所有元素放到 q2中,然后把新的元素入队给 q,之后,再把 q2 中暂存的元素放到 q 中,就好了:
public void push(int x) { Queue<Integer> q2 = new LinkedList<>(); while(!q.isEmpty()) q2.add(q.remove()); q.add(x); while (!q2.isEmpty()) q.add(q2.remove()); }
这个容易理解么?下面简单用图说明一下:
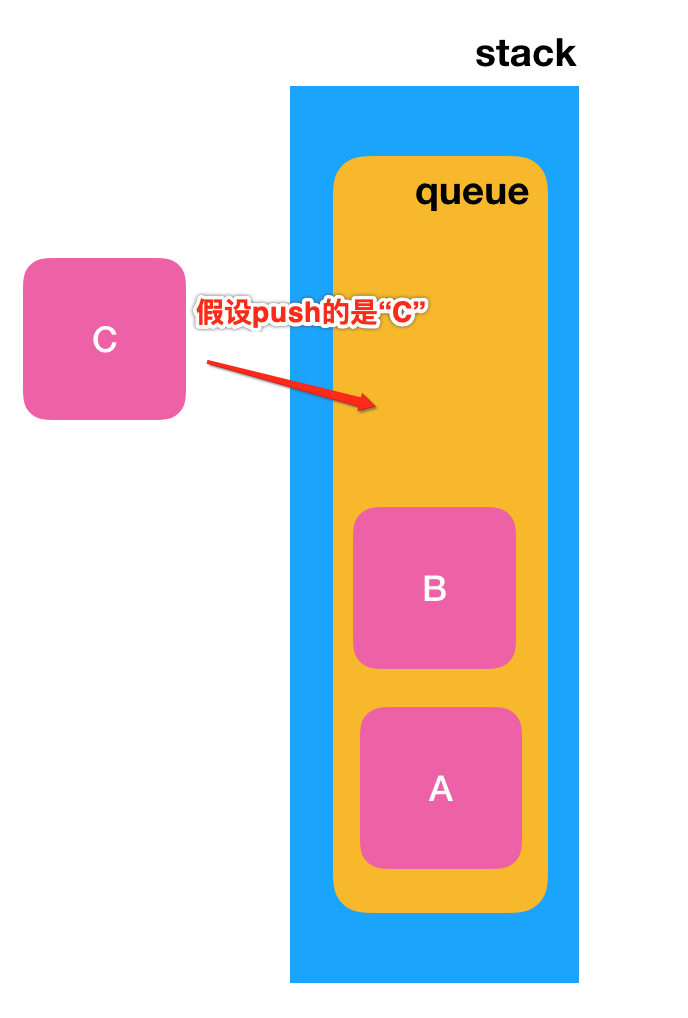
此时先不着急直接入队,而是在执行它之前,先将队列中的所有元素都添加到一个临时队列中,如下:
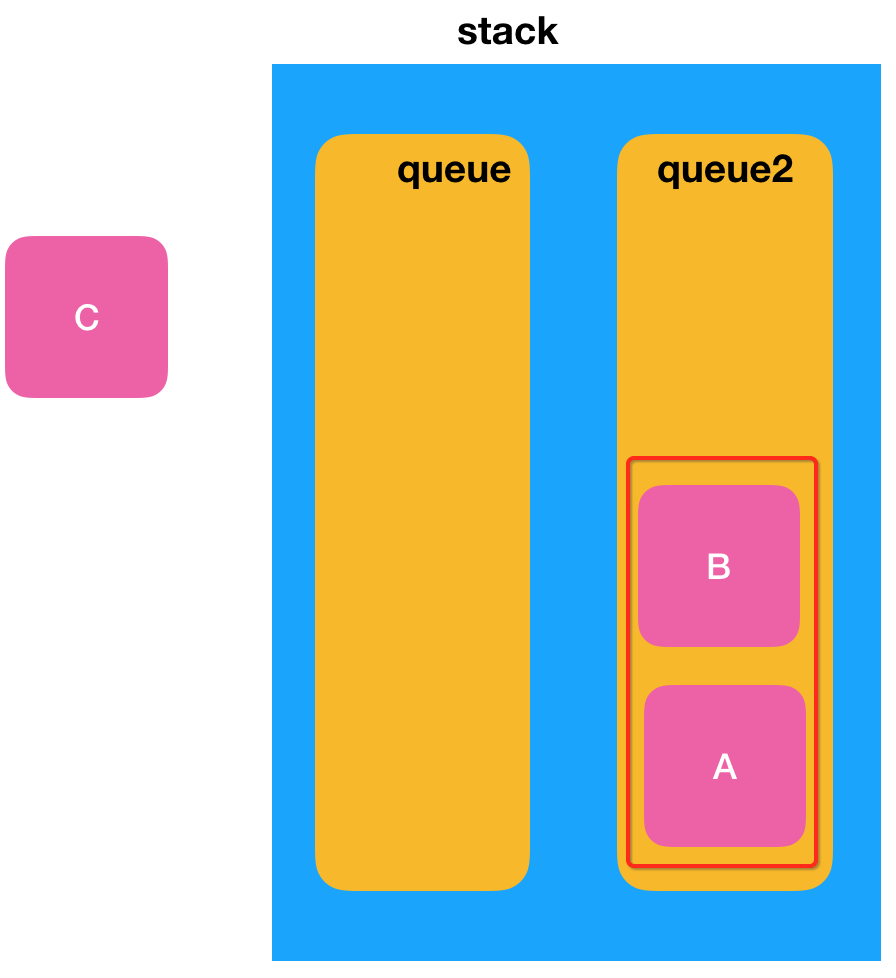
也就是对应代码的这一段:
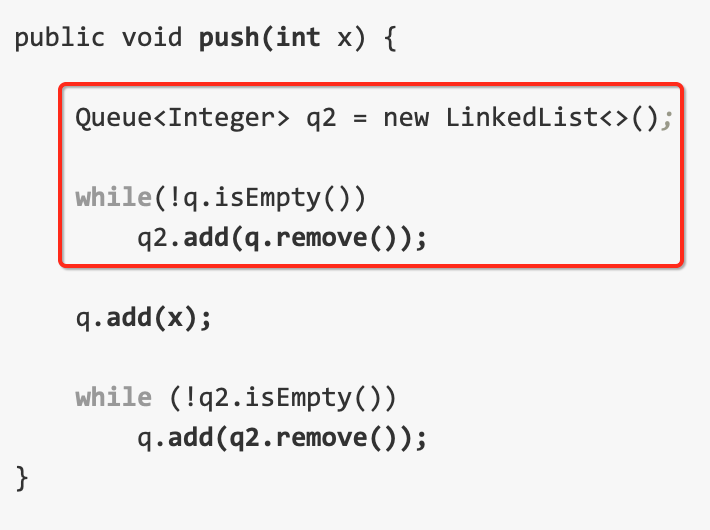
接着再将新添加的元素添加到第一个真正的队列中,此时的情况为:
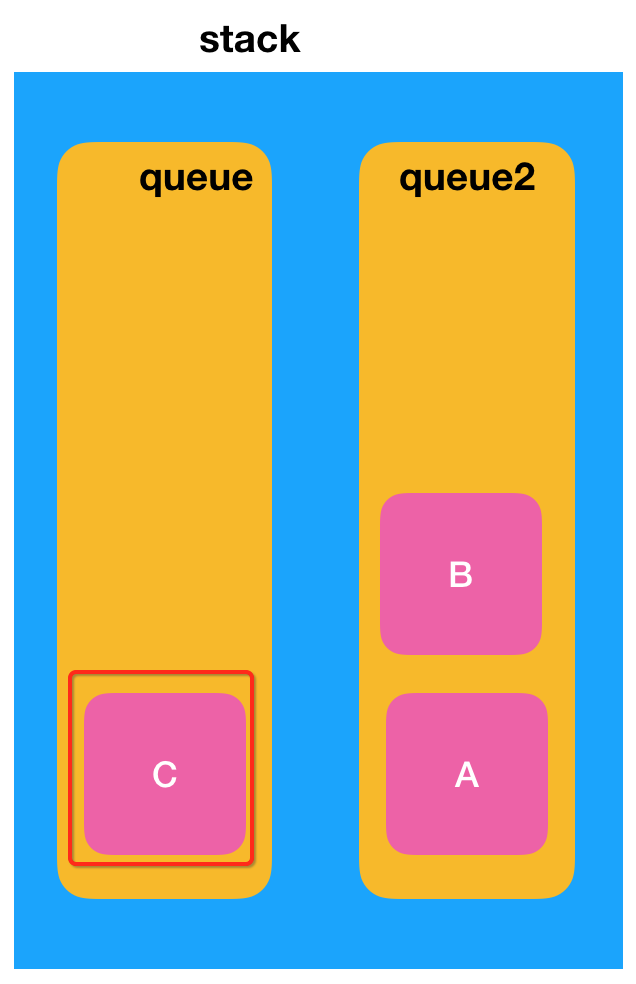
此时再将备份的queue2中的所有元素再挪回到queue中,那么最终的形态就为:
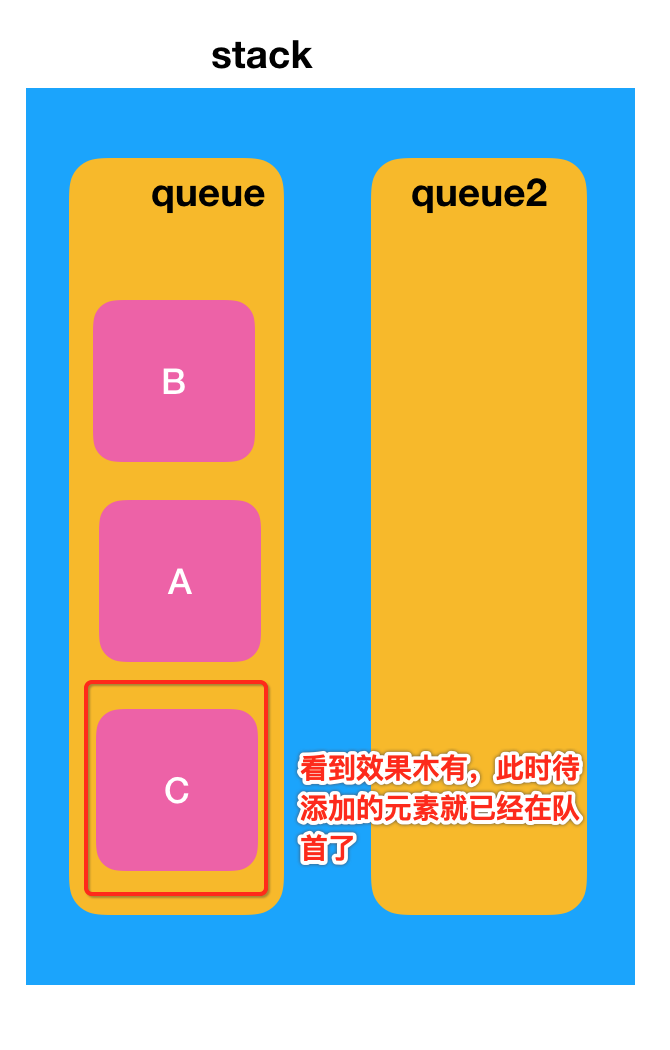
那queue2呢?不浪费空间了么,不会的,因为它是方法的局部变量,方法执行完就会销毁的。
还有一种更加容易理解的实现方式:
public void push(int x) { Queue<Integer> q2 = new LinkedList<>(); q2.add(x); while(!q.isEmpty()) q2.add(q.remove()); q = q2; }
也就是直接给 q2 里添加新的 x,然后把 q 中所有元素再添加到 q2 中。最后,让 q 指向新的 q2就好了。
整个代码如下:
import java.util.LinkedList; import java.util.Queue; // 写出一个实现,push 是 O(n) 的,pop 是 O(1) 的? public class MyStack3 { private Queue<Integer> q; public MyStack3() { q = new LinkedList<>(); } /** Push element x onto stack. */ public void push(int x) { //想办法让栈顶的元素放到队列的队首 Queue<Integer> q2 = new LinkedList<>(); q2.add(x); while(!q.isEmpty()) q2.add(q.remove()); q = q2; } public int pop() { return q.remove(); } public int top() { return q.peek(); } /** Returns whether the stack is empty. */ public boolean empty() { return q.isEmpty(); } }
此时我们的 pop,时间复杂度是 O(1) 的;push,时间复杂度是 O(n) 了。
同样放到Leetcode中进行验证看是不是同样好使:
思考:对于上面O(n)的push我们可不可能只是用一个队列,而不使用第二个队列解决这个问题?
对于上面咱们不是已经将push变为O(n)复杂度了么?其中它里面用了一个临时的队列来存放队首元素除外的那些元素:
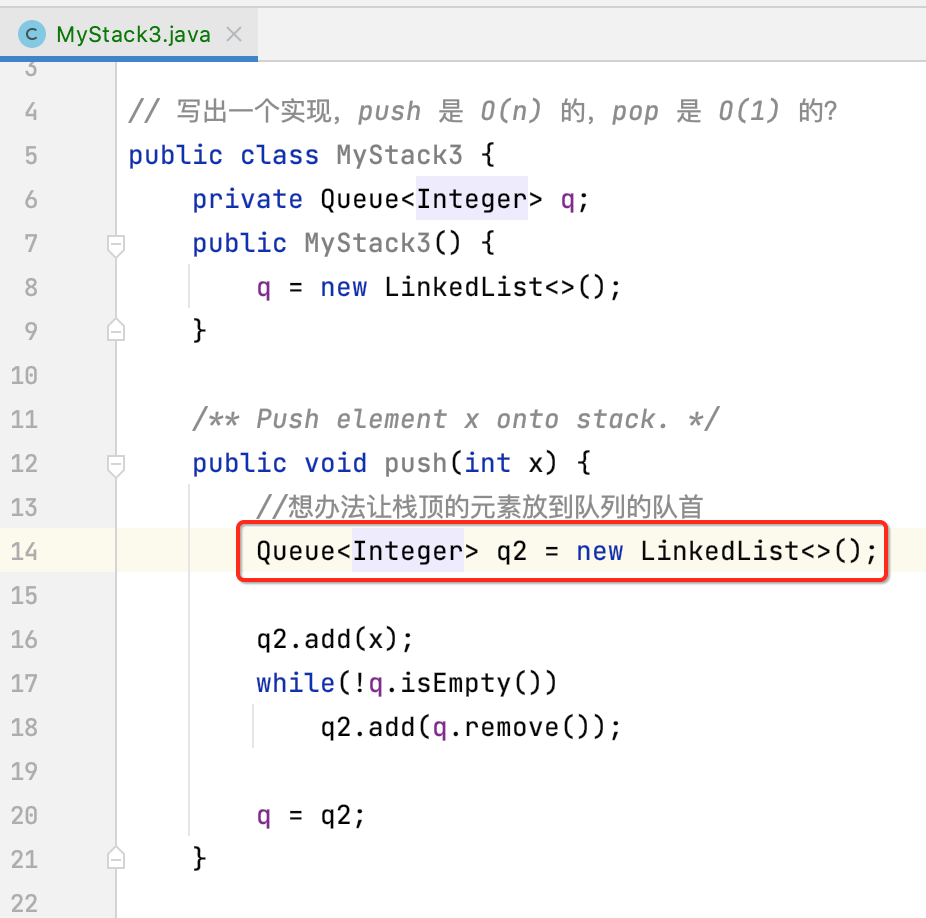
那有没有可能,不借助这第二个临时的队列来达到同样的效果呢?有的,代码如下:

这个应该很容易理解,先文字描述一下:
比如,我们的队列中,元素是 1, 2, 3。对于栈来来说,添加元素 4 以后,我们希望得到 4, 1, 2, 3
可是因为 q 是队列,我们将 4 入队,得到的是 1, 2, 3, 4
现在,队列中有 4 个元素,我们只需要执行 3 次出队再入队。
第一次,出队 1 再入队 1,得到:2, 3, 4, 1
第二次,出队 2 再入队 2,得到:3, 4, 1, 2
第三次,出队 3 再入队 3,得到:4, 1, 2, 3
至此,就是我们想要的结果了。
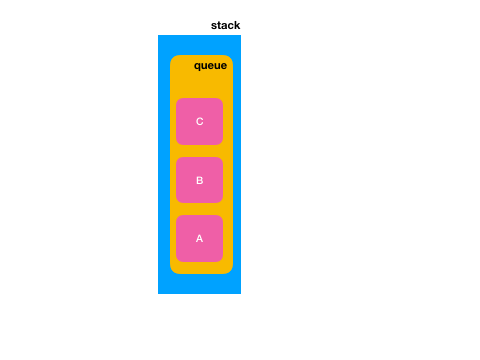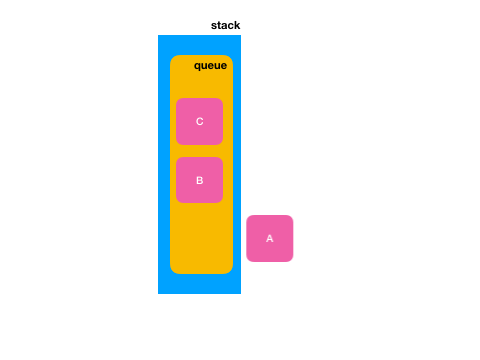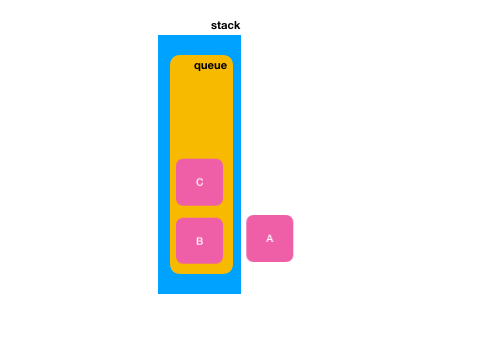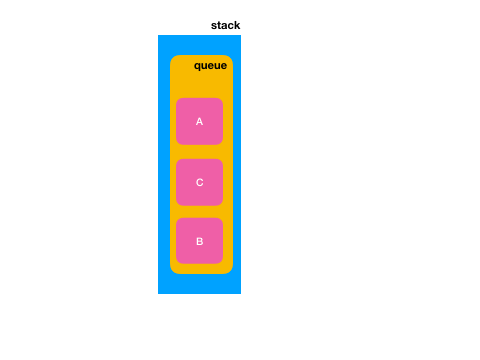
可能文字有点抽象对吧,下面再用图解一下就清楚了:
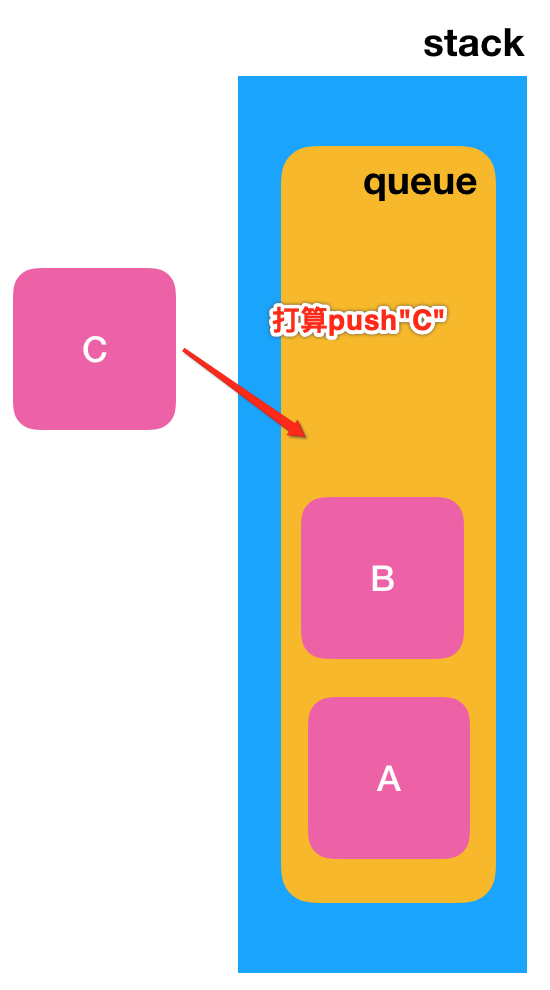
直接将它添加到队尾中如下:
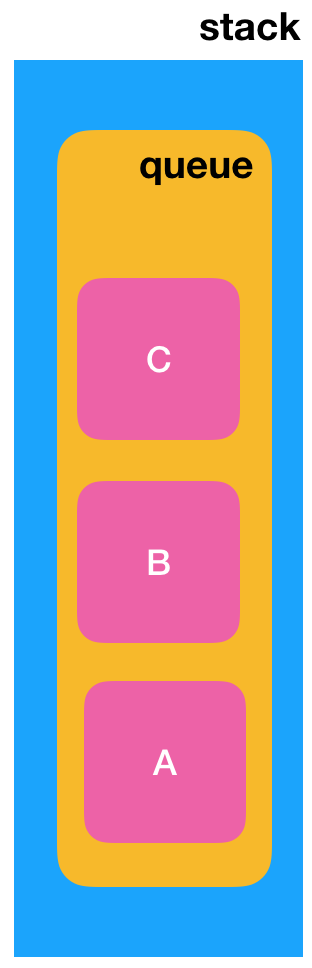
但是很明显我们是想把“C”要放到队首中,也就是“A”的位置对吧,此时再执行n-1次先出队再入队的操作,也就是针对这俩元素:
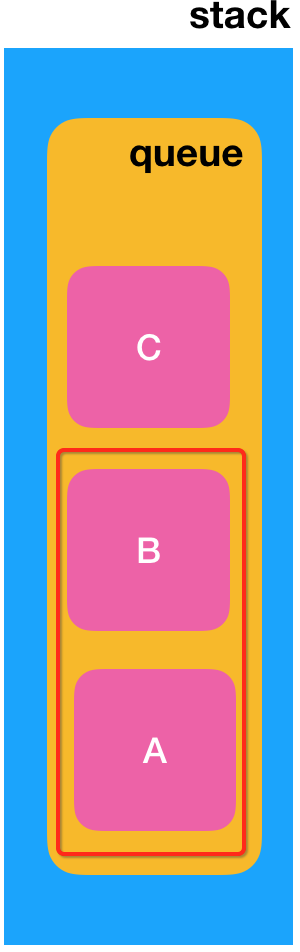
先将“A”出队,然后此时再将它添加入队,此时“A”元素是不是就跑到队尾了?
此时再出队一个再放队,那么结果就是:
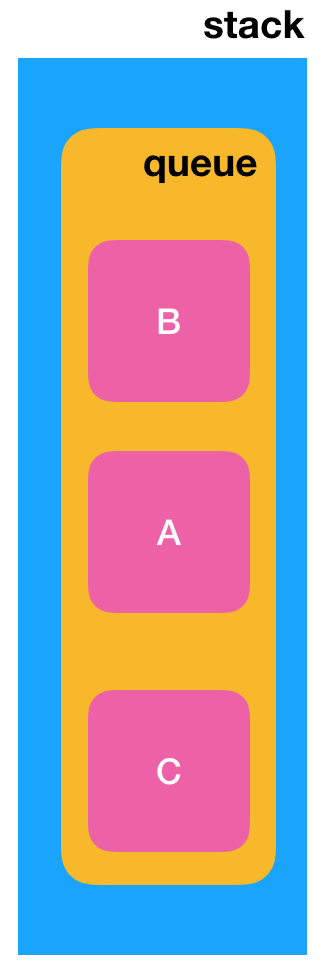
是不是要入队的元素就已经放到了队首了?所以整个代码如下:
import java.util.LinkedList; import java.util.Queue; // push 的过程只使用一个 queue // 注意,提交给 Leetcode 的时候,需要将 MyStack4 改成是 MyStack public class MyStack4 { private Queue<Integer> q; public MyStack4() { q = new LinkedList<>(); } /** Push element x onto stack. */ public void push(int x) { //想办法让栈顶的元素放到队列的队首 // 首先,将 x 入队 q.add(x); // 执行 n - 1 次出队再入队的操作 for(int i = 1; i < q.size(); i ++) q.add(q.remove()); } public int pop() { return q.remove(); } public int top() { return q.peek(); } /** Returns whether the stack is empty. */ public boolean empty() { return q.isEmpty(); } }
同样将其拷到Leetcode中进行验证:

总结:
至此,关于用队列实现栈的多种实现就已经学会了,那如果反过来,让你用栈来实现队列呢?这也是非常经典的面试题之一,关于它下回继续。



