线性代数学习之坐标转换和线性变换
空间的基和坐标系:
继续接着上一次https://www.cnblogs.com/webor2006/p/14376460.html往下学习,前面已经详细的学习了什么是空间、什么是向量空间、什么是子空间,在此基础上又知道了对于一个空间来说基是很重要的属性,并且对于一个空间来说其实是有无数组基的,而我们比较感兴趣的通常是正交基和标准正交基,当然这不是所有的情况,在不同的领域中会对不同的基感兴趣,既然一个空间存在这么多种不同的基,就会涉及到空间中的一组基跟另外一组基是怎样变换的,这也是此次所要研究的话题,具体就是要了解坐标转换和线性变换两个概念,而这里先来从坐标转换相关的概念开始了解。
在之前线性代数的学习中,在理解空间的基的一个视角就是坐标系,其实坐标系跟空间的基是一一对应的关系的,当有了一组空间的基时就可以说有了空间的一个坐标系,反过来也成立,举个之前举过的二维空间的例子:
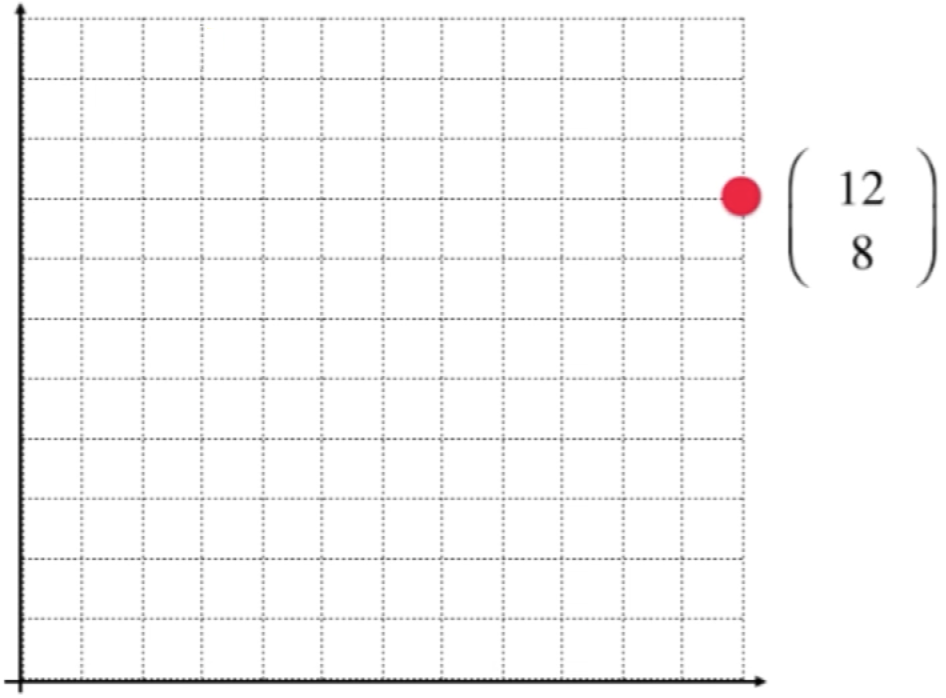
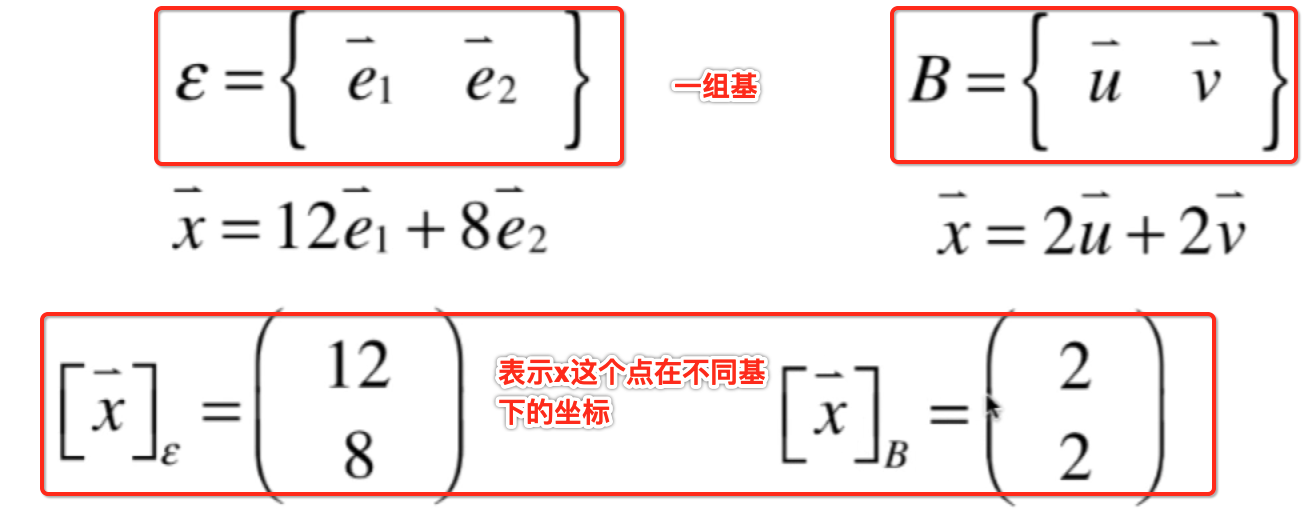
其中在这个坐标系上取一点(12,8),之所以这个点是(12,8)是建立在一个标准坐标上的,标准就包括水平向上和垂直向上的坐标轴以及定义了什么是一个单位,如下:
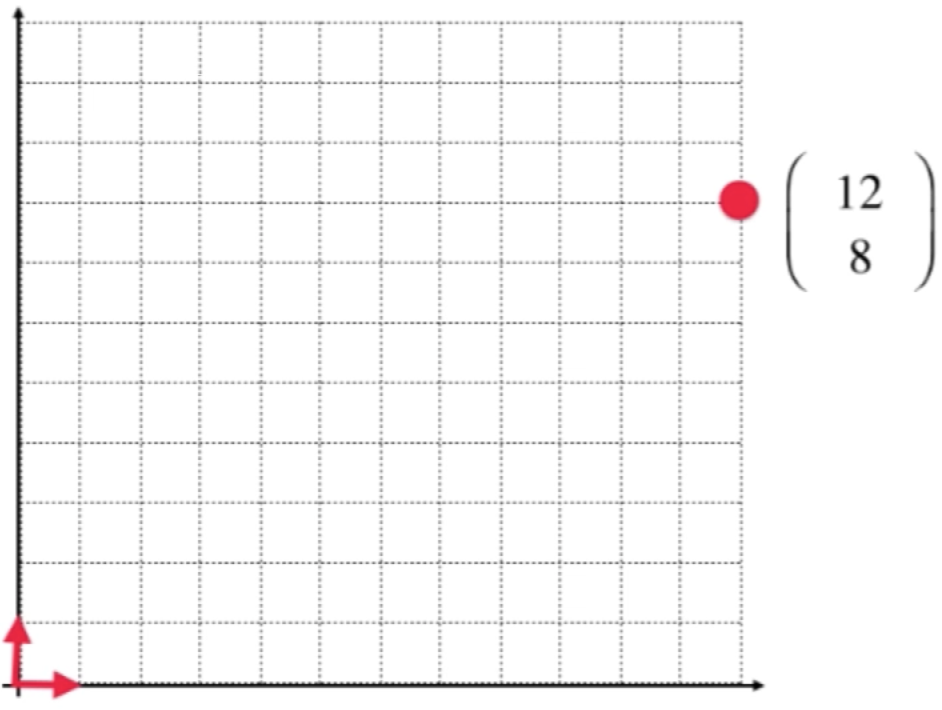
而红色的两个单位箭头其实就是定义了二维平面的一组基,当然二维平面可以有无数组基,比如这样:
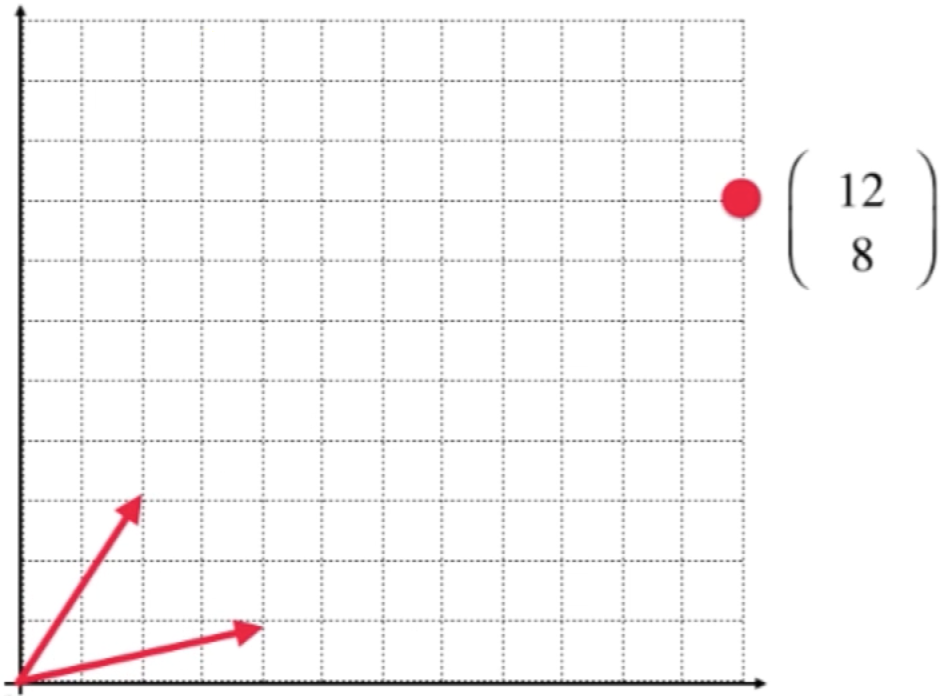
如果定义好了这么一个基的话,可以以这两个基的向量所对应的方向当作二维平面两个轴的方向,而两个向量的模当作是两个方向上的一个单位是多少,这样这组基又定义了这么一个坐标系:
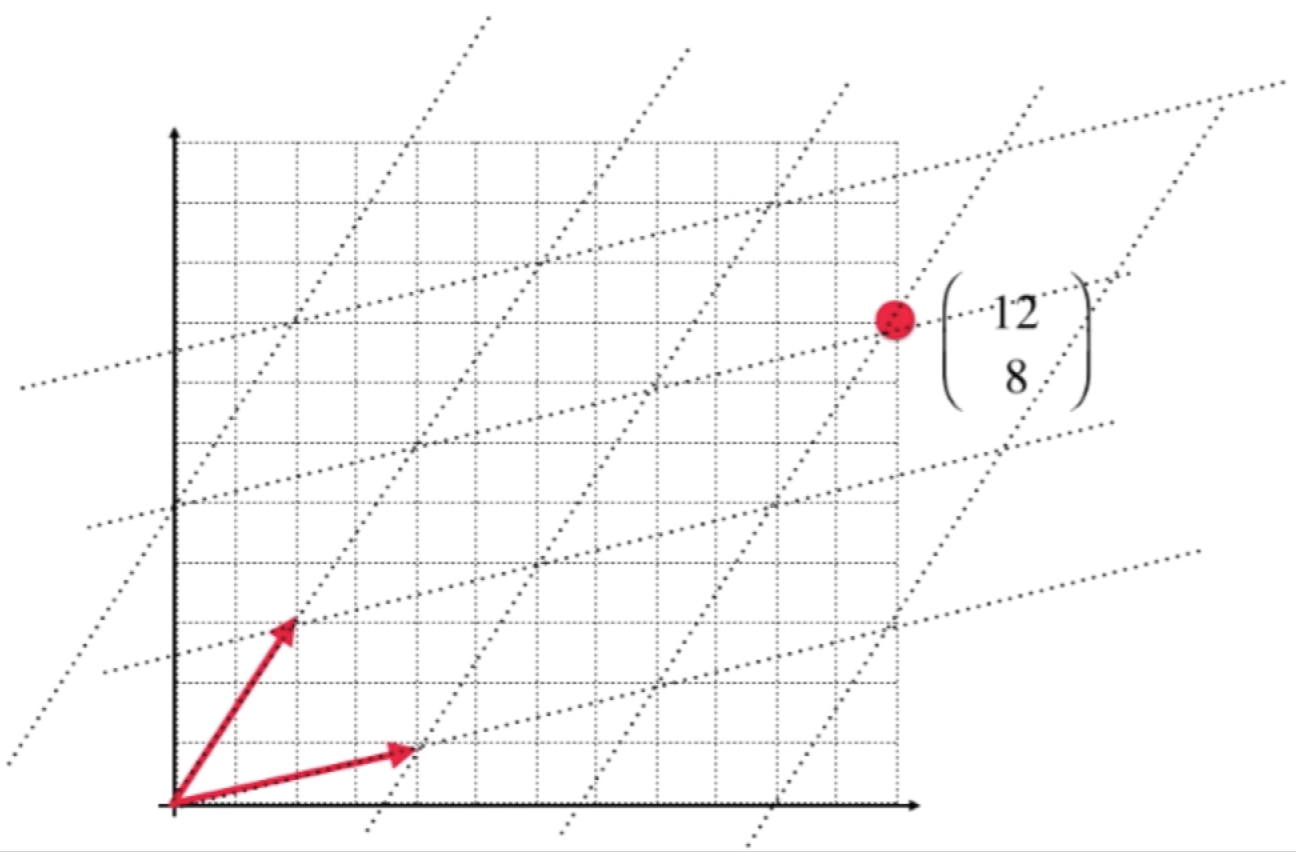
此时这个点的坐标就变成了(2,2)了:
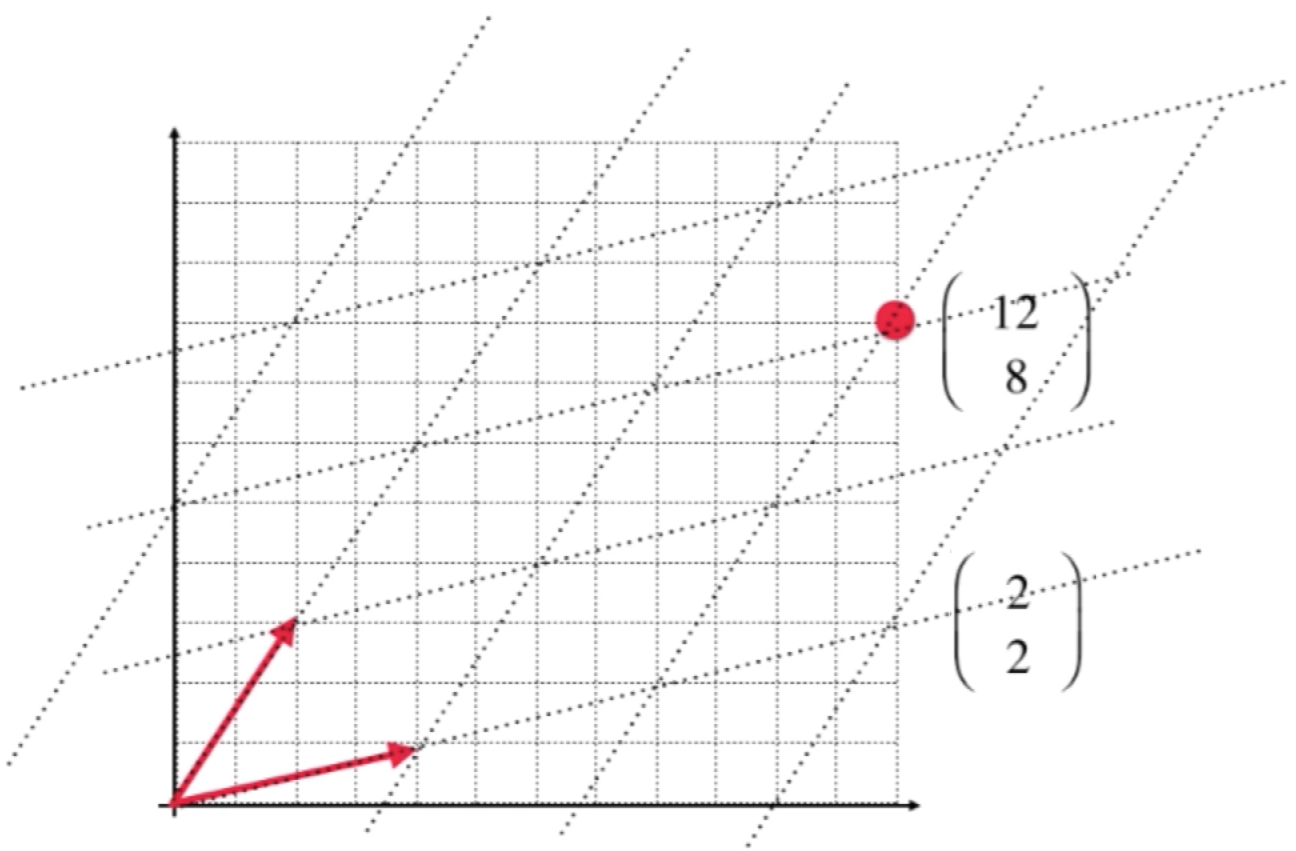
可见同样一个点就对应了两个表示法:
第一组基如果以列排列的话这个点表示的是:
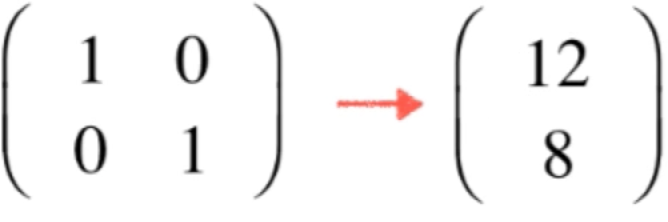
而第二组基也是列排列的话这个点表示的是:
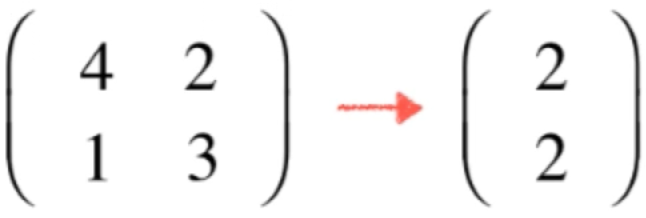
这就是空间的基和坐标系之间的关系,它们是一一对应的,而关于空间的基更严谨的有这么一个结论,之前https://www.cnblogs.com/webor2006/p/14306046.html已经证明过:
在n维空间,如果给定一组基,任何一个向量(或者是点)都可以表示成这组基的线性组合,且表示方法唯一!
下面再来对这两种空间对应的坐标系的情况进行一个总结:

所以对于n维空间的一个点或者向量,我们定义为x,那么给定任何一组基都可以表示成这组基的线性组合,且表示方法唯一,所以:
![]()
前面的式子是在e1、e2这组基下,后面的式子是在u、v的这组基下,而相应的每一组基都对应着一个坐标系,如下:

发现规律木有,实际上我们说的坐标的值就是把这个向量x表示成这组基所对应的线性组合,相应的线性组合中每一个基向量前面的那个系数,所以就可以给下面的一个定义啦:
如果给定向量空间V中的一组基B,B定义为:
以及V中的一个向量x:则x一定可以被这组基线性表示。假设:
则称x在这组基B下的坐标,为:
而由于不同的坐标对应的是同一个x点,所以为了区分起见,也可以记做:
也就是这一组坐标(c1,c2,...,cn)在大B这组基下相应的坐标,有点晕,回到具体的例子来看:
其中这个符号怎么读的呀:
关于数学符号的读法在网上搜了个表,可以参考一下:
大写 小写 英文注音 国际音标注音 中文注音 Α α alpha alfa 阿耳法 Β β beta beta 贝塔 Γ γ gamma gamma 伽马 Δ δ deta delta 德耳塔 Ε ε epsilon epsilon 艾普西隆 Ζ ζ zeta zeta 截塔 Η η eta eta 艾塔 Θ θ theta θita 西塔 Ι ι iota iota 约塔 Κ κ kappa kappa 卡帕 ∧ λ lambda lambda 兰姆达 Μ μ mu miu 缪 Ν ν nu niu 纽 Ξ ξ xi ksi 可塞 Ο ο omicron omikron 奥密可戎 ∏ π pi pai 派 Ρ ρ rho rou 柔 ∑ σ sigma sigma 西格马 Τ τ tau tau 套 Υ υ upsilon jupsilon 衣普西隆 Φ φ phi fai 斐 Χ χ chi khai 喜 Ψ ψ psi psai 普西 Ω ω omega omiga 欧米伽 其中咱们的这个就读epsilon【艾普西隆】
而通常我们说到的坐标系都是在这组基下:

所以称之为“标准基(Standard Basis)” 而标准基所对应的坐标系就称为“标准坐标系”。但是!!!这里说的“标准基(Standard Basis)”很容易跟之前所学的“标准正交基(Orthonormal Basis)”搞混,这里一定要分清楚!!!!
所以对于n维标准基(n维标准坐标系),就是:
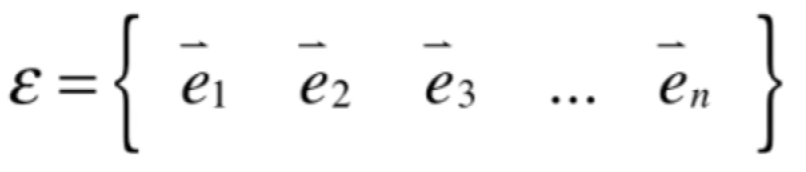
其他坐标系与标准坐标系的转换:
上面已经了解了空间的基与坐标系之间的关系,空间中有几数组基,而每一组基都对应着一个坐标系,与此同时也知道了标准基的概念,相应的坐标系就叫标准坐标系,那对于标准坐标系与非标准的坐标系之间是如何转换的呢?下面来探讨这个它:
还是回到之前的那个二维平面坐标系的例子:

第一组基如果以列排列的话这个点表示的是:

而第二组基也是列排列的话这个点表示的是:

用符号来表示的话:
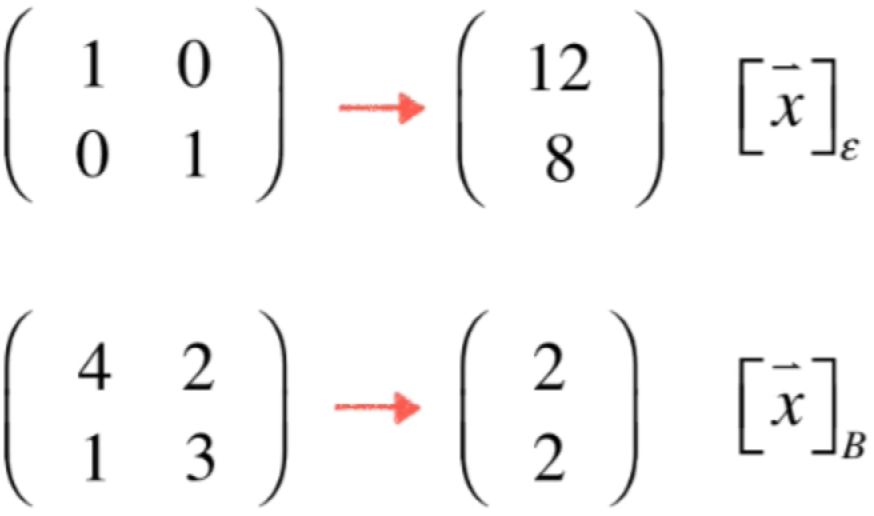
那这两个坐标之间有啥联系呢?其实这个问题在之前学习看待矩阵视角时有学过,这里再来整理一下:
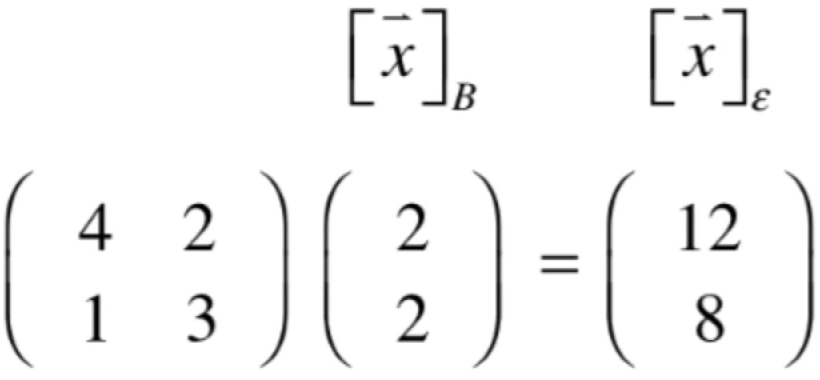
也就是可以用矩阵的乘法来描述,可以用列视角来看就是:
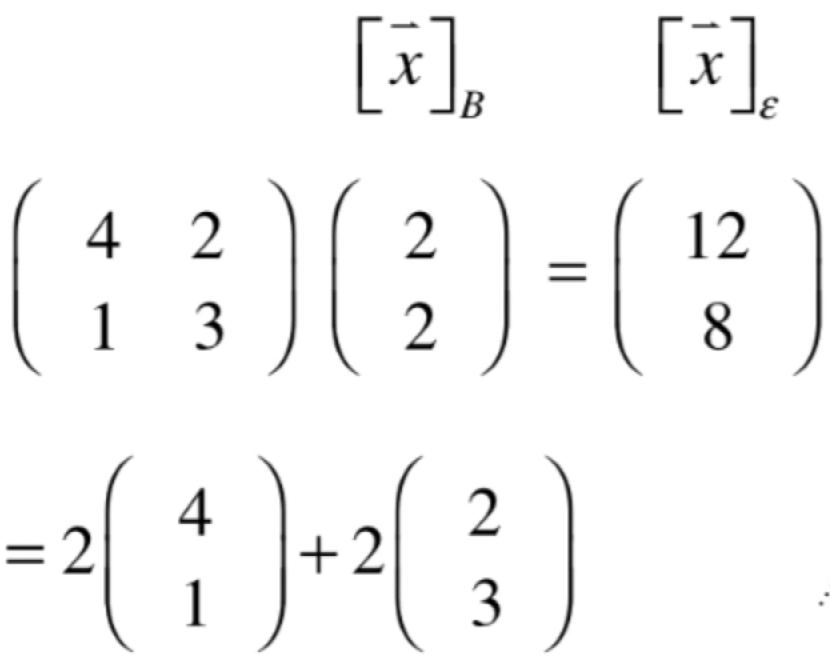
而其中的(4,1)和(2,3)是在标准坐标系下来衡量的,所以可以总结一下【比较抽象】:
假设有一组基B:
设立矩阵,它里面的元素就是由n个向量逐列排开:
这个矩阵看似像1xn的矩阵,其实是nxn的,有了这个矩阵之后,在这组基下的一个向量:
就有:
这个有点抽象,得结合上面举到的具体例子来理解,如下:
其中:
称之为坐标转换矩阵,
那为啥会有这么个转换关系呢,下面来证明一下:
其中B中的基的两个向量可以表示为:
也就是这两个向量都是基于标准基中来描述的,而:
然后将u、v代入式子:
而标红的式子恰恰就是矩阵的乘法展开的样子:
所以就得证了。
在上面我们已经从B这样的坐标系转换到了标准坐标系:
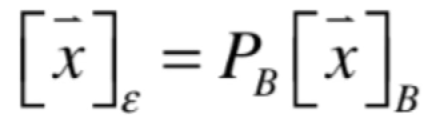
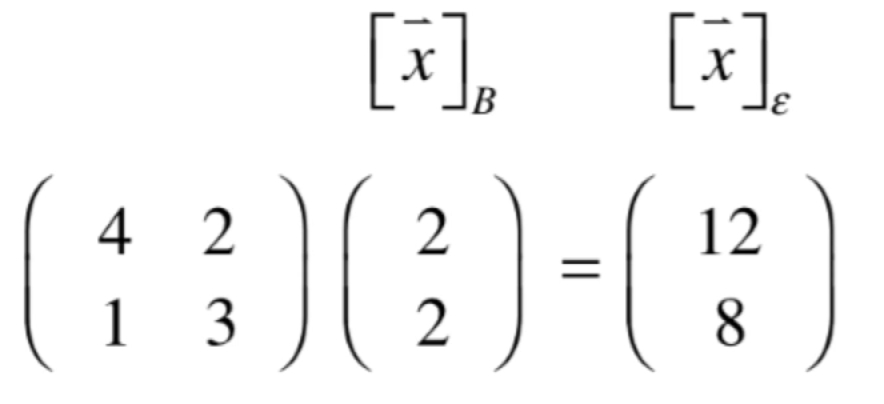
那怎么反过来转换呢,也就是从标准坐标系转换到B这样的坐标系中,其实很简单:
等式两边同时乘以Pb的逆,如下:

那为啥Pb这个矩阵是一定可逆的呢?因为它首先是一个方阵,另外它里面列向量一定是线性无关的,也是生成空间的,就可以根据方阵的那N多命题中推出它一定是可逆的,这里具体就不看了,因此,对于坐标转换相互的式子总结就是:
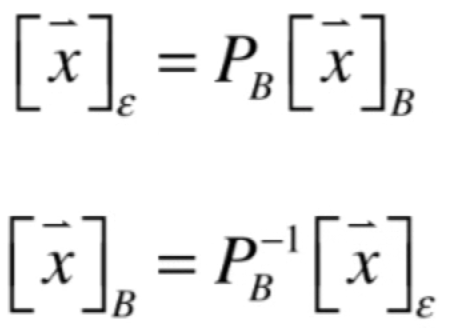
这里千万不要搞混Pb和Pb的逆的使用,Pb所乘的坐标一定是B这组基下所对应的坐标,而如果不是B这组基下所对应的坐标而是标准坐标系所对应的坐标,就应该用Pb的逆矩阵来乘。
任意坐标系转换:
在上面已经对于任意坐标系与标准坐标系之间的转换进行了阐述,那如果两个坐标系都是任意坐标系它们之间该如何转换呢?
假设有一组基:
另一组基:
在B这组基下的一个向量:
求C这组基下的一向量:
其实求解方法以标准坐标系为桥梁既可,首先求出B这组基下的向量在标准基下所对应的坐标,根据上面的公式既可:
![]()
然后只要用C这组基构造成Pc矩阵,再用Pc的逆矩阵乘以在标准坐标基下所表示的坐标既为在C这组基下所表示的值,如下:
![]()
而将标准基下的坐标的值代入,可以合成一个式子为:
![]()
进一步还可以把它表示成:
![]()
那如果反过来呢?也就是在C这组基下的一个向量:
![]()
求在B这组基下的一个向量:
![]()
此时就可以用它进行推导:
![]()
左右两边都乘以Pc,如下:
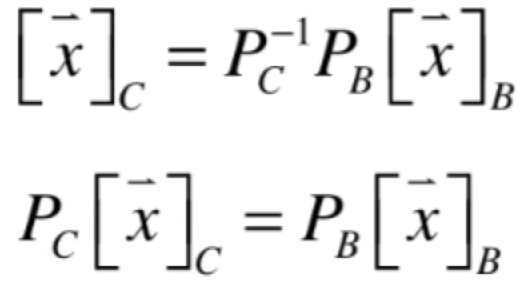
然后左右两边再乘以Pb的逆就有:
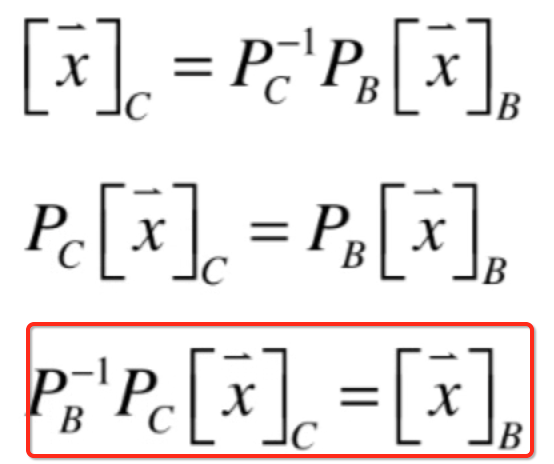
同样的也可以表示为:
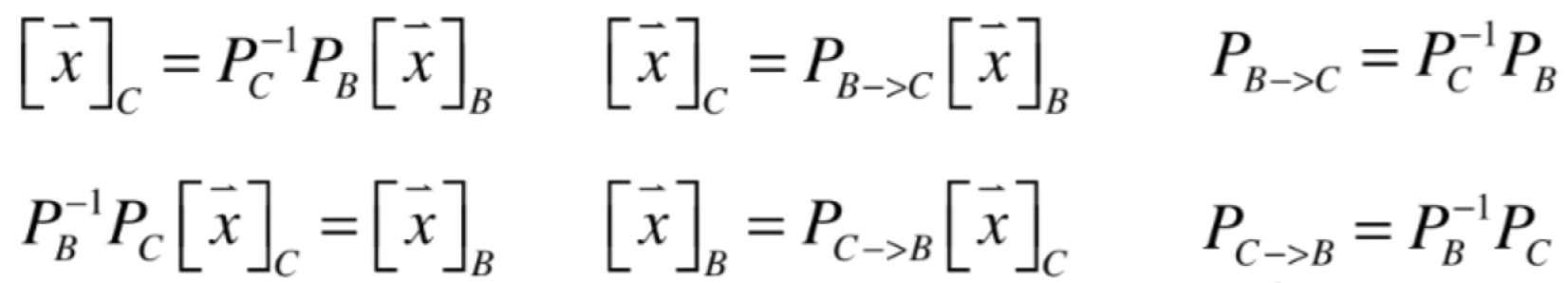
而这两矩阵其实是互为逆矩阵的:
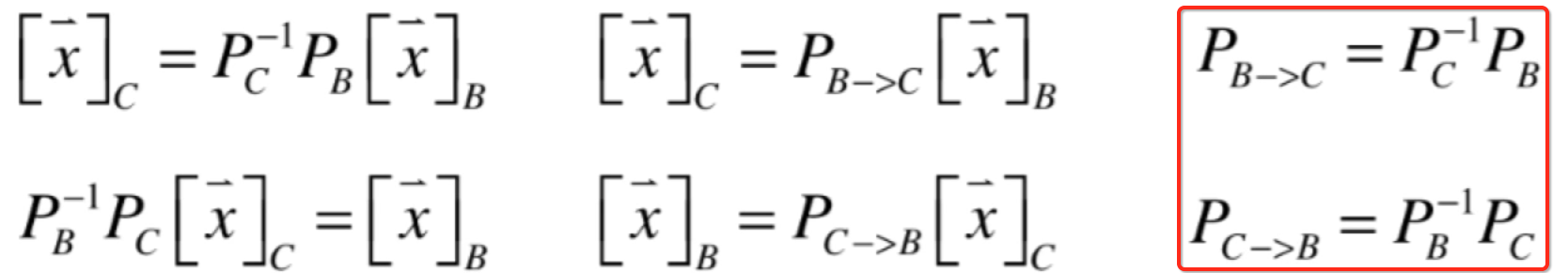
证明方法也很简单,如下:
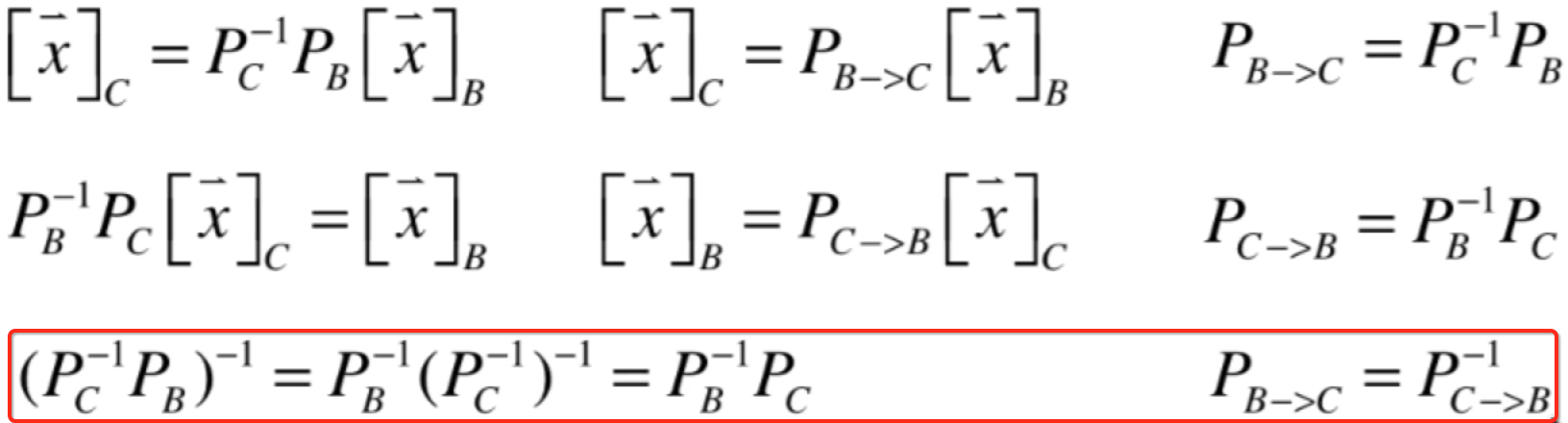
这里再回到之前所学任意坐标系与标准坐标系之间的转换:
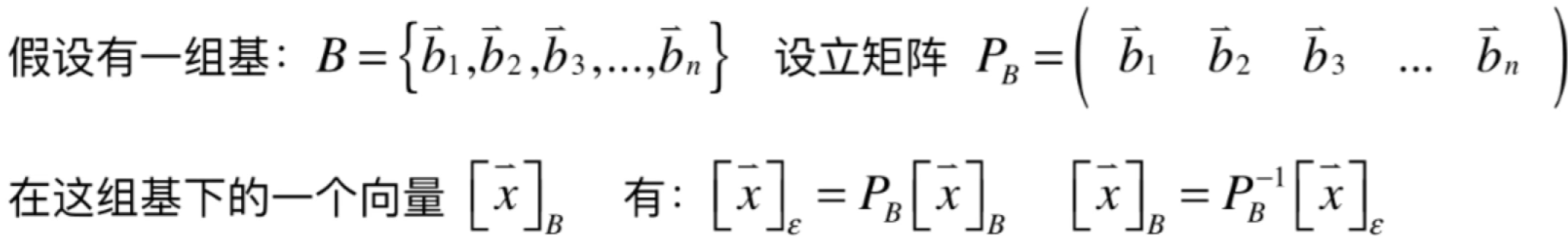
其中标准坐标系也是一个坐标系,得到的结论应该跟咱们目前所学的两个任意坐标系之间的转换结果是一样的才行,下面来以这次所学的视角理解一下,对于标准坐标系其实可以这样表示:
![]()
其中Pc就是单位矩阵:
![]()
此时看一下B到C之间的转换,以任意两个坐标系的视角来看待就有:
![]()
同样的反过来:
![]()
跟之前所述的任意坐标系与标准坐标系之间的转换是刚好吻合的,其实它是两个任意坐标系之间的转换的一个特例。
其实对于标准坐标系还可以看成这样:

这样再来看两个任意坐标系之间的转换:

而如果我们知道了B这组基向量在C坐标系下的表示:
![]()
此时就可以直接拿到坐标系之间转换的结果:
![]()
所以就有:
![]()
说实话这个说得有点抽象,下面以具体的例子再来理解一下这个结论:
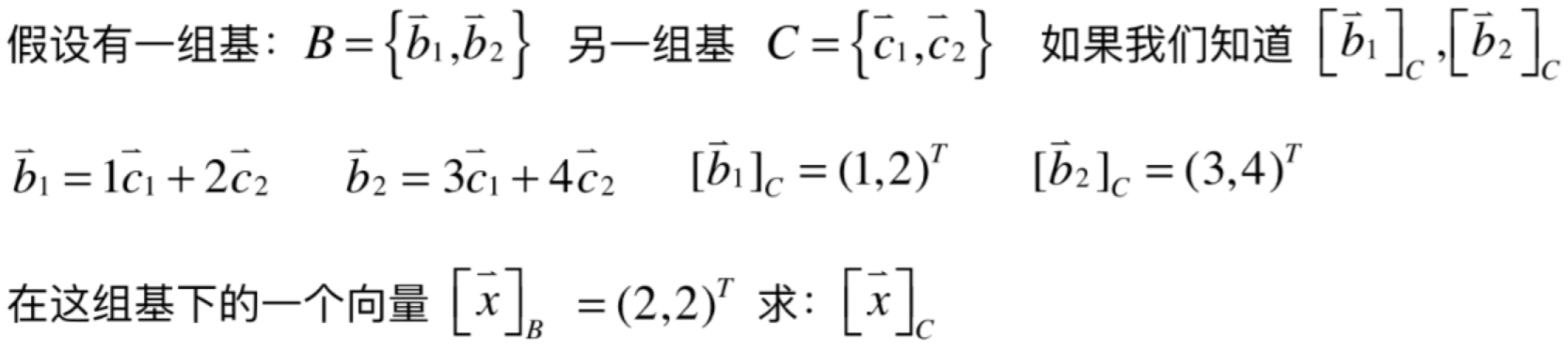
首先求这个矩阵:
![]()
也就是向量按列排列成矩阵:
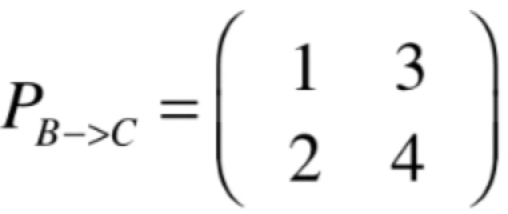
此时要求x在C坐标系下的坐标就可以用这个公式:
![]()
如下:
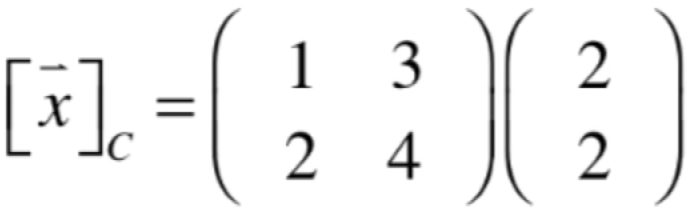
也就是如果知道了一组基到另一个坐标系下的表示的话,就可以不以单位矩阵做为桥梁来进行坐标转换的计算了,其证明为:
![]()
而b1向量和b2向量为:
![]()
将其代入进来就有:
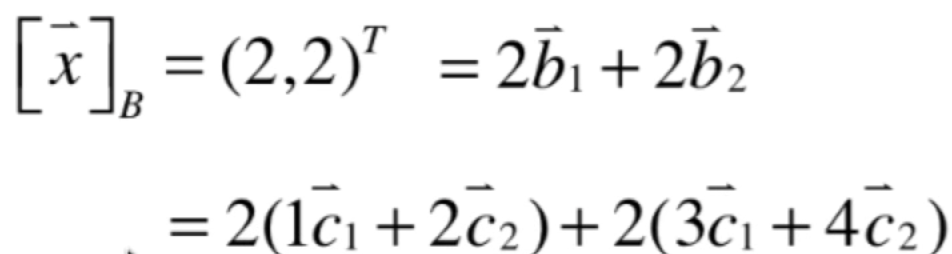
而它其实就是:
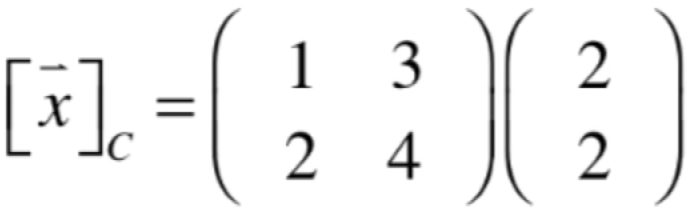
反之,如果已知C坐标系下的坐标,求B坐标系下的坐标,如下:
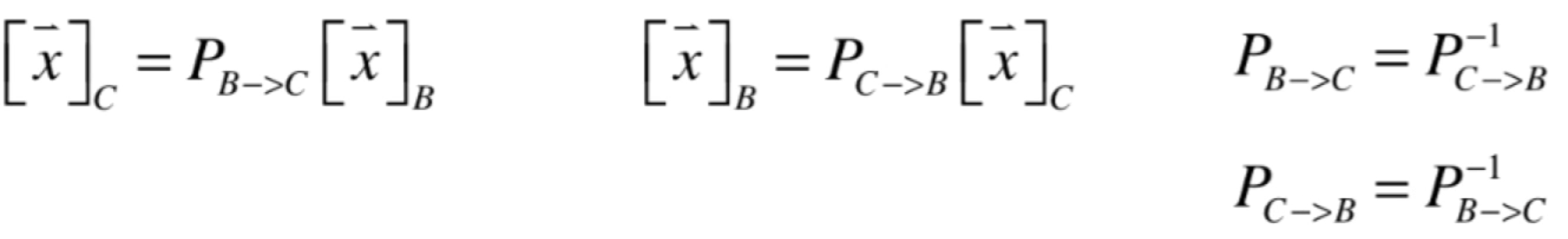
最后总结一下:
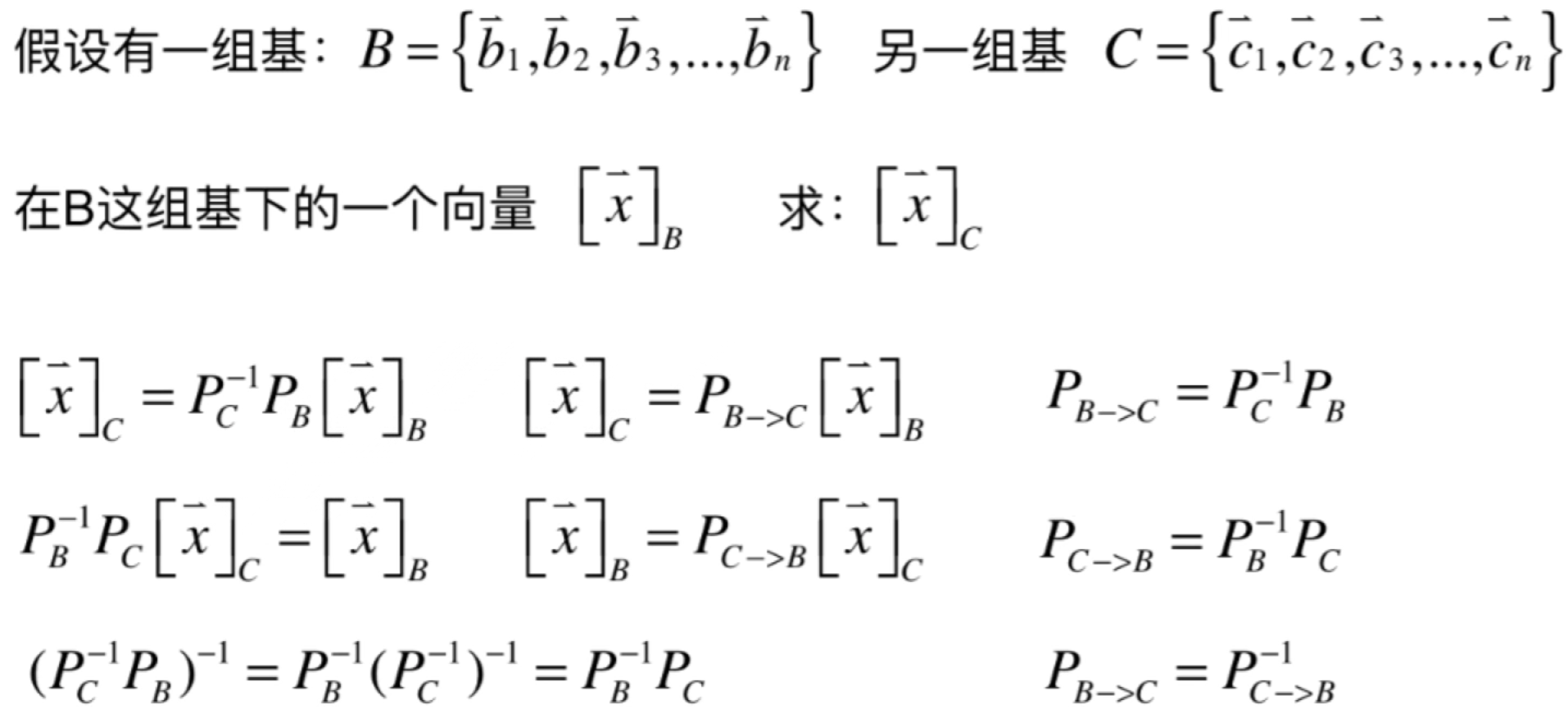
对于这些还是比较容易晕的,需要好好挼挼。
线性变换:
在上面一直探讨的是关于坐标系的转换,其实在线性代数领域关于变换这个话题会关注一个更加宏观更加庞大的定义,称为线性变换,而对于之前学习的坐标系转换其实是线性变换其中的一种。
什么是变换?
先来了解什么是变换,通常在数学的世界中一说变换就意味着是一个函数, 而在线性代数领域只对线性变换感兴趣,对于非线性变换是不感兴趣的【就像之前学习空间一样,在线性代数中只对向量空间感觉兴趣,对非向量空间不感兴趣】,先来看一下变换的定义:
一个变换T(x)称为线性变化,必须满足以下两个性质:
性质一:
两个向量之和的变换就等于两个向量分别做变换。
性质二:
其中c属于实数集,它说明给向量u进行常数c相乘之后再做变换就等于先对向量进行一个变换然后再乘以常数c。
以上性质再一次说明了当时在学习向量时的两个基本运算:向量的加法和数量乘法,这两个运算是贯穿整个线性代数从始至终的,
线性变换:
上面对于变换有了基本了解之后,那啥是线性变换呢,回忆一下之前学习矩阵时我们可以所矩阵看做是向量的函数:
![]()
所以矩阵所表示的变换,均为线性变换。那为啥它是属于线性变换呢?当然得要从它需要满足的两条性质来证明喽:

![]()
下面来证明第一条性质:
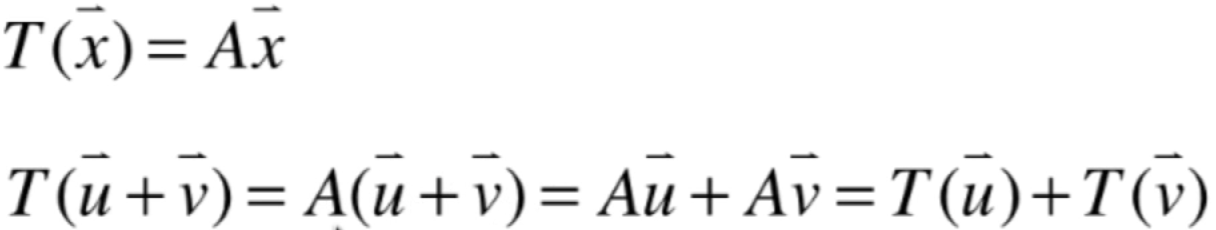
木问题,接下来再来看第二条性质,也比较简单:
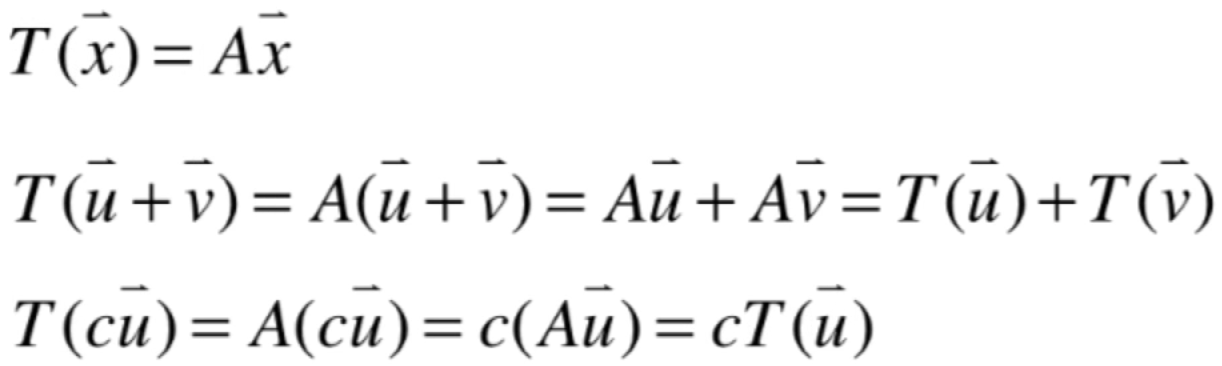
是不是就证明矩阵表示的变换均为线性变换了?有了这样的一个视角,回到矩阵上来,它既可以看成空间,也可以看做是变换,这两个视角其实是一致的,还是用之前举的例子:

它可以看作是空间,比如:
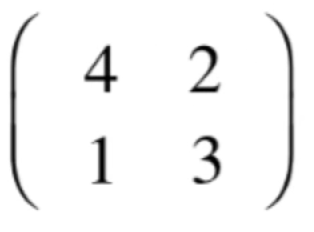
它是一组基构成的空间,但是!!根据上面学习的坐标系转换的知识,它又可以看成是从B这个坐标系转换成ξ标准坐标系的坐标变换矩阵【其中看到变换一词木有,也就是矩阵也可以看成变换】!所以这两个视角是等价的,也就是空间既变换,变换既空间。不同的空间对应着不同的基,对应着不同的坐标系,所以对于这个矩阵的乘法就可以看作是不同的基的变换或是不同的坐标系之间的变换,反过来一个变换也就对应着不同的基和不同的坐标系,下面来看一下这个反过来的情况,其实也是之前学习矩阵变换时接触过的,比如让每个点关于x轴翻转:


那从空间的基的角度来想这个问题:
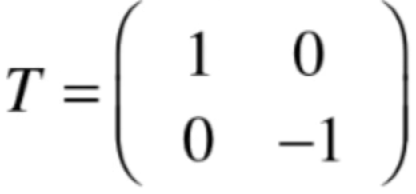
这个变换矩阵其实就是表示(1,0),(0,-1)这样一组基,这个变换就会将这组基下的(x,y)看它在标准基下就是(x,-y),这样就完成了x轴的翻转。所以可以看出对于这个变换矩阵T本质就是对应另外一组基另外一个坐标系,同理再看一个关于y轴翻转的例子:
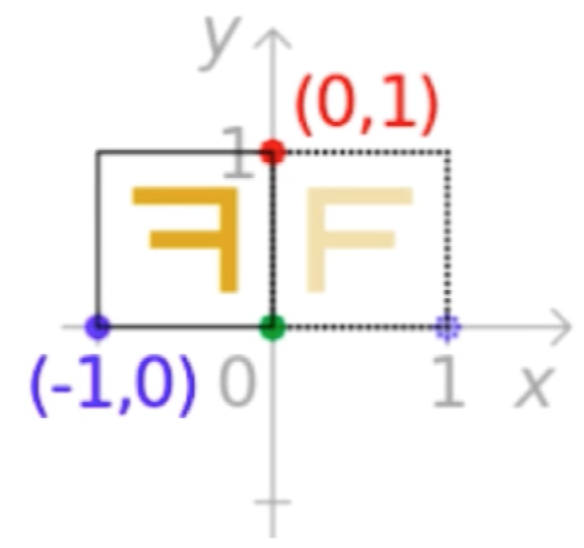
它对应的变换矩阵为:
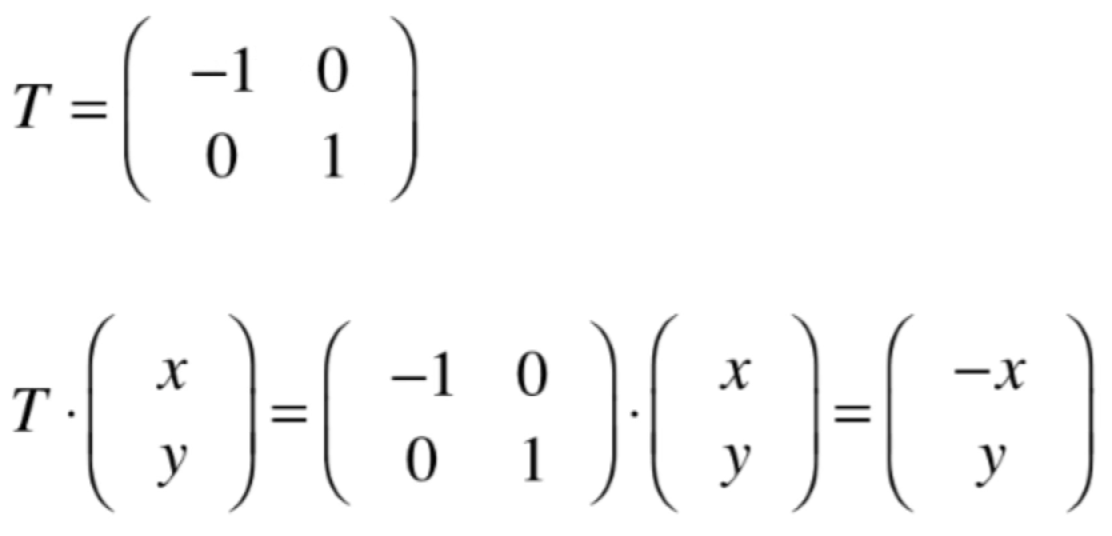
这样对于T中的(-1,0)、(0,1)这样坐标系的x,y就成为了所看到的(-x,y)。这样的视角可以再来看一下变换:让每个点关于原点翻转(x轴,y轴均翻转)
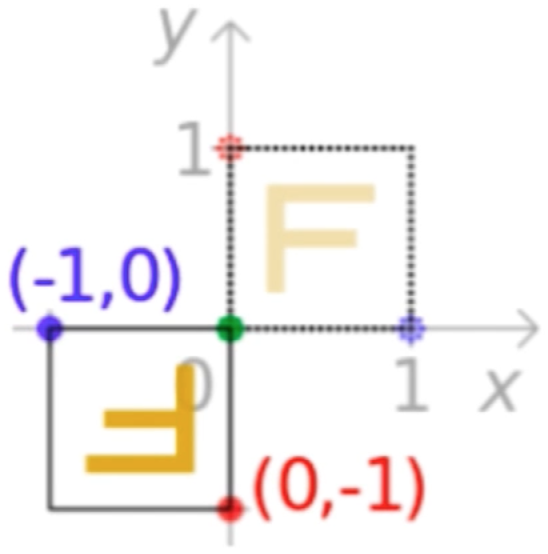
它对应的变换矩阵为:
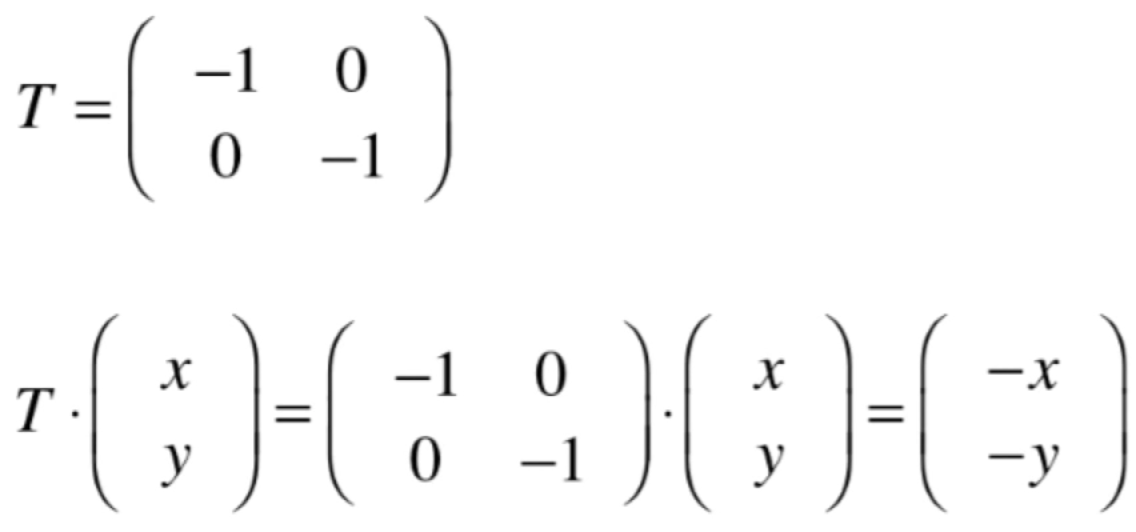
基中T就是另外一组基,我们做这个坐标系的转换就达到图中的变换效果。再回忆一下沿x方向错切效果:

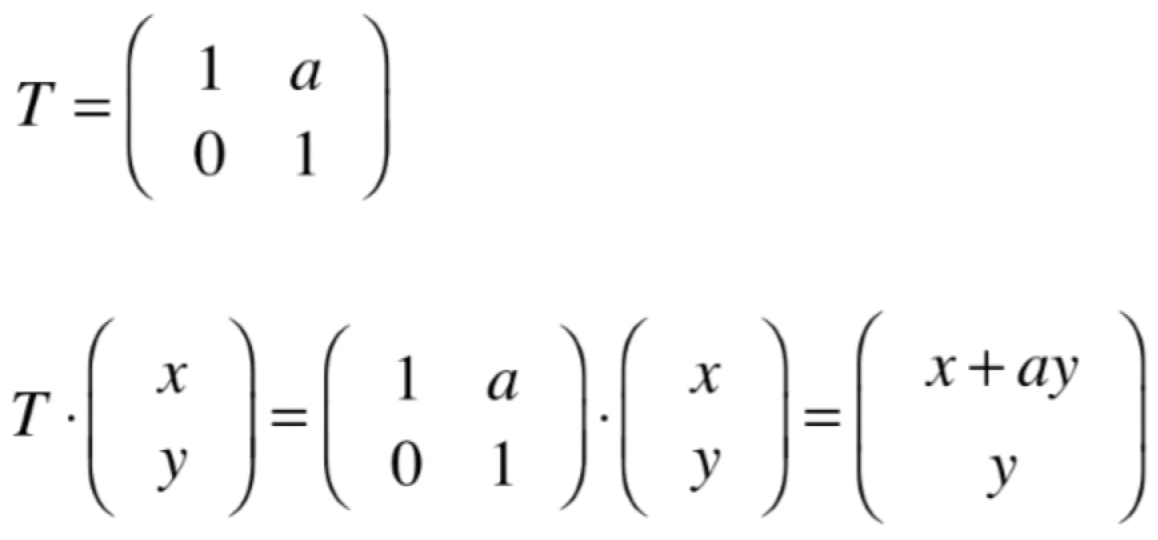
其中变换矩阵中是另外一组基,在这样的一个坐标系下(x,y)在标准坐标系下就是(x+ay,y)。
再看沿y方向错切:
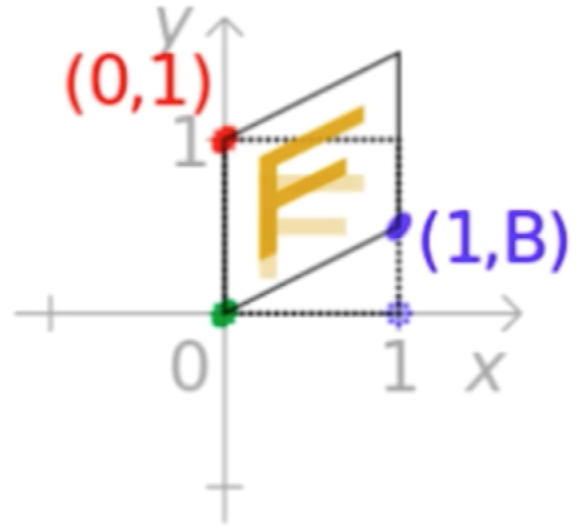

其实就是看(x,y)这个点的坐标在(1,b)、(0,1)这样的坐标系下对应在标准坐标系的位置为(x,bx + y)。
最后再看一下旋转的效果:

它对应的变换矩阵为:
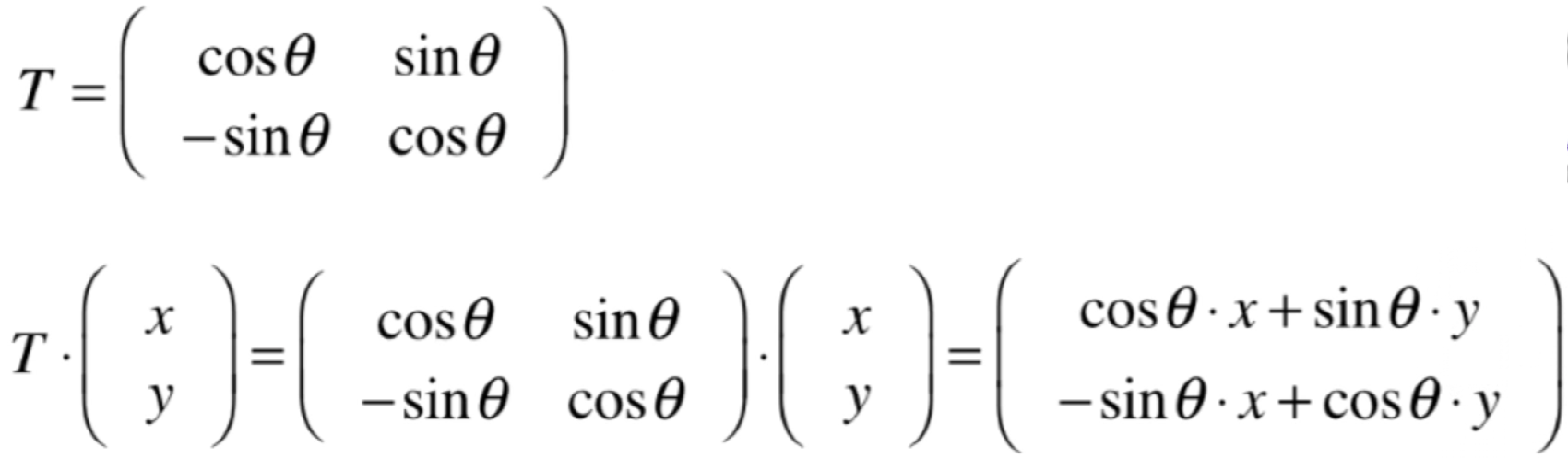
也同样可以将T看成一组坐标系,然后看(x,y)在这组坐标系下对应标准坐标系下的位置。
而之前学习矩阵表示空间和矩阵表示变换联系起来举了这么个例子:

也就是要想让正F向左倒的效果,它对应的变换矩阵就可以从空间的基或坐标系的视角来想这个问题,其实深色的F的x轴就是原来坐标系的y轴,而它的y轴就是原来坐标系的x反向方,所以把这两个坐标轴按列排列起来就形成了一个坐标转换矩阵就为:

最后关于线性变换总结一下:
所有的矩阵都可以用来表示一个线性变换;
用矩阵表示空间的视角和用矩阵表示变换的视角是等价的;
更多和坐标转换和线性变换相关的话题:
对于这次的学习首先是介绍了坐标转换,在此基础之上又了解了线性变换,而不管是坐标转换还是线性变换都可以看成是理解矩阵的一个视角,这也就是之前所说的可以把矩阵看作是一个空间,也可以看成是一种变换。而这次所举的所有的例子其实都是在同等维度的空间中进行转换的:

都是在二维平面中从一点转换到另一点,其实这样的变换有很多实际的应用,下面来举例说明一下:
1、最典型的是二维动画、三维动画,比如:
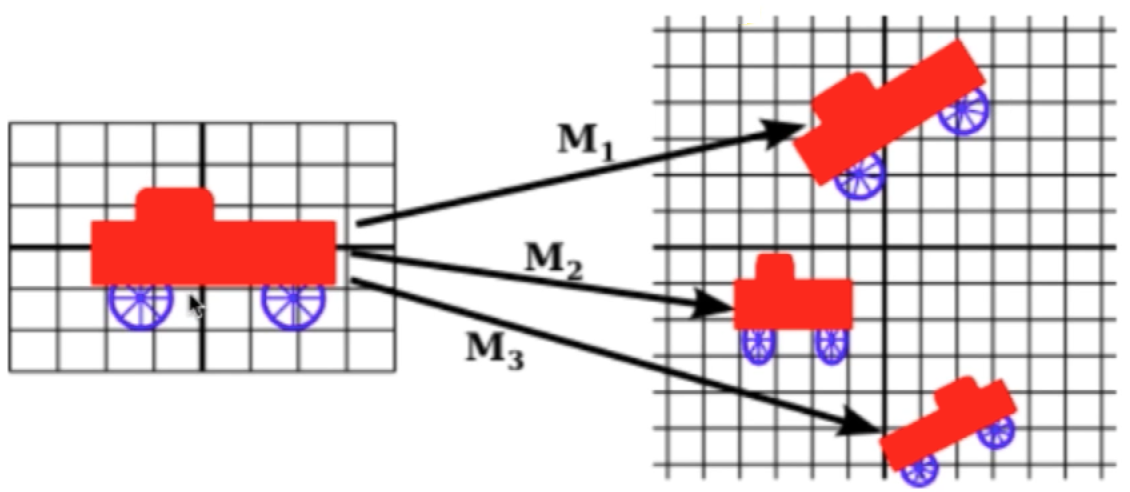
这种都是同维度空间的转换例子.
2、不同维度之间的转换:
实际当然也有不同维度空间的转换,比如看3D动画的静态图像,就需要用到3D空间转到了2D空间的过程,比如:
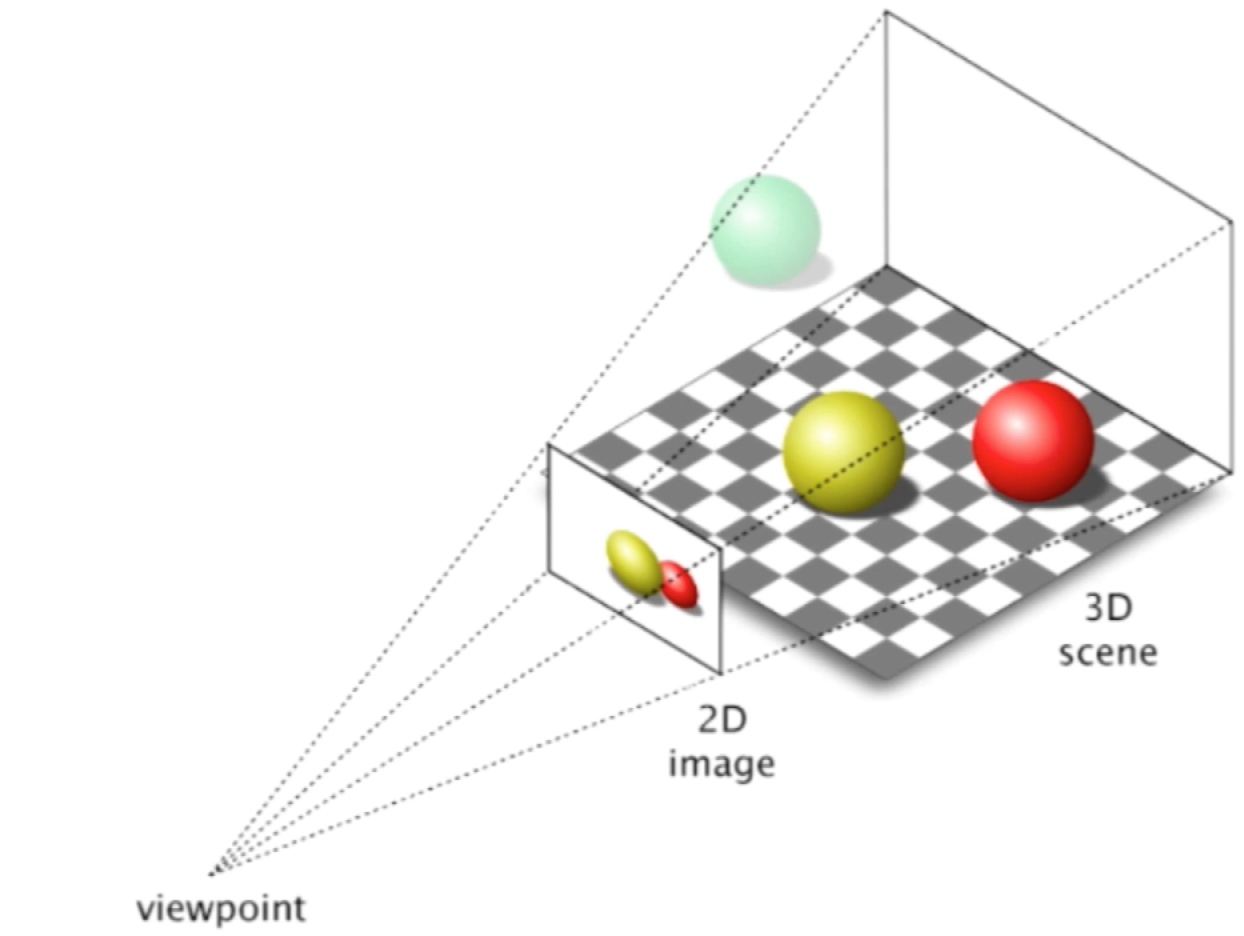
由于屏幕是一个二维空间,所以对于三维空间的物品要展现在屏幕中就需要从3维转换到2维,这是从高维空间向低维空间的转换的例子,反过来也有从低维向高维空间进行转换的应用,最典型的就是计算机视觉,其实就是通过机器可以看到我们的世界从而提取出一些信息,而机器是通过摄像头来看到的信息,而摄像头拍下来的图片是一个二维的,但是二维的照片中蕴含着三维的信息,所以计算机世界就需要通过这个二维的照片恢复在三维世界中的信息,从而理解一些问题,比如看下图:

照片是二维的,但是哪个更高,更个离白球更近就涉及到三维的信息,此时就需要从二维转换成三维坐标系了。
3、同维度空间转换的应用:
最典型的就是压缩,这里以二维坐标为例,比如:

有五个数据点,每个数据点都需要2个数据来表示,但是!!!如果坐标轴长这样呢?
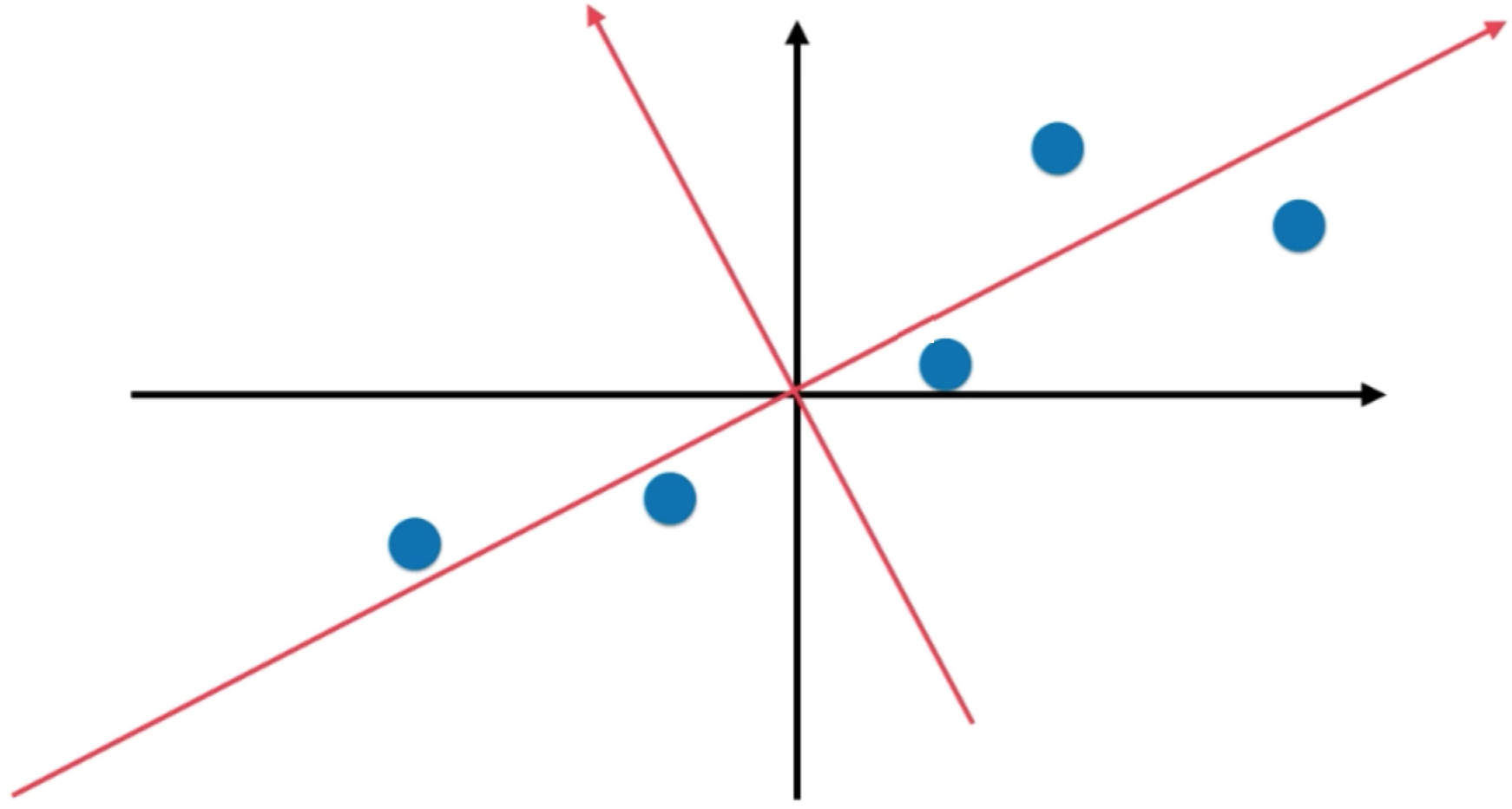
此时这两个红色的基来说,这些点所对应的y轴的值都非常小,而所有信息都集中的红色的x轴上了,是不是就可以做压缩处理了,假如计算出了这么一组基,只需要记x轴的信息,y轴的可以扔掉,这样对于这些点的数据表示瞬间就可以压缩一倍,这其实就是坐标系之间的一个转换的应用,很多压缩算法的本质,就是找一组基!!!像JEPG就是典型的这种压缩算法的应用,像傅里叶变换、小波变换其实就是找一组基。
总而言之,上面举的这些例子就了解下既可,重点是知道在线性代数中的空间变换有很多实际的使用场景,所以好好学习它们的基础是有利无害的。

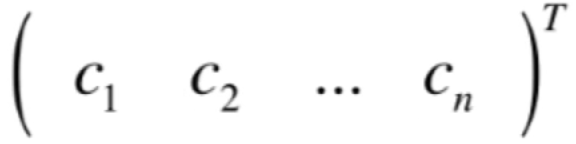
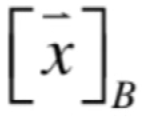
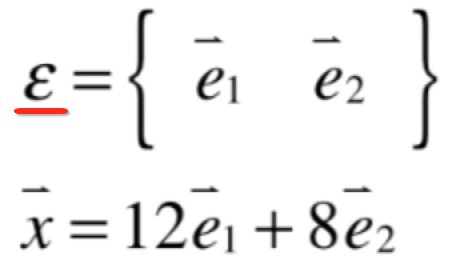

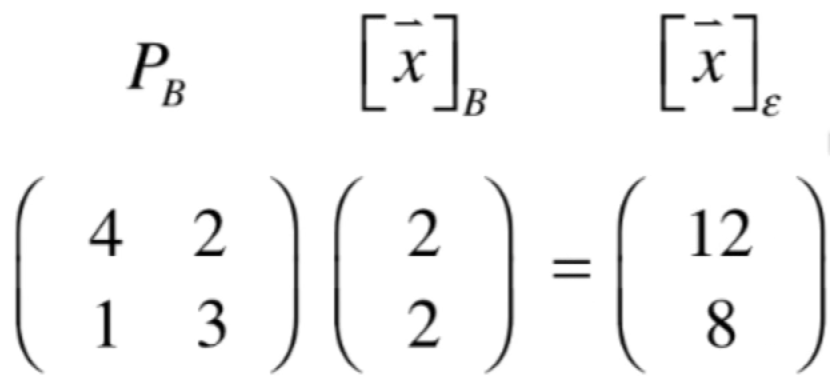
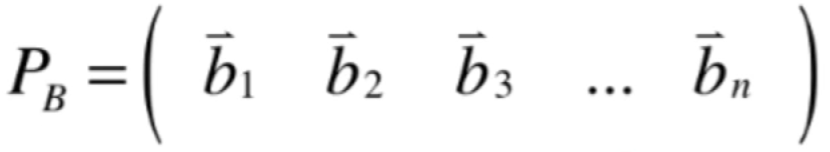
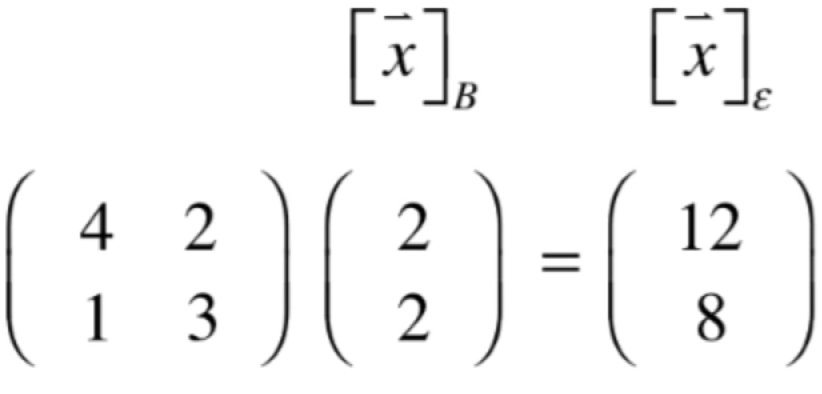
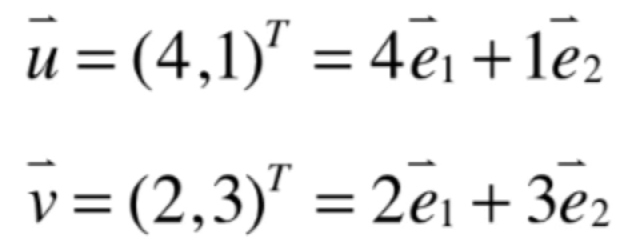
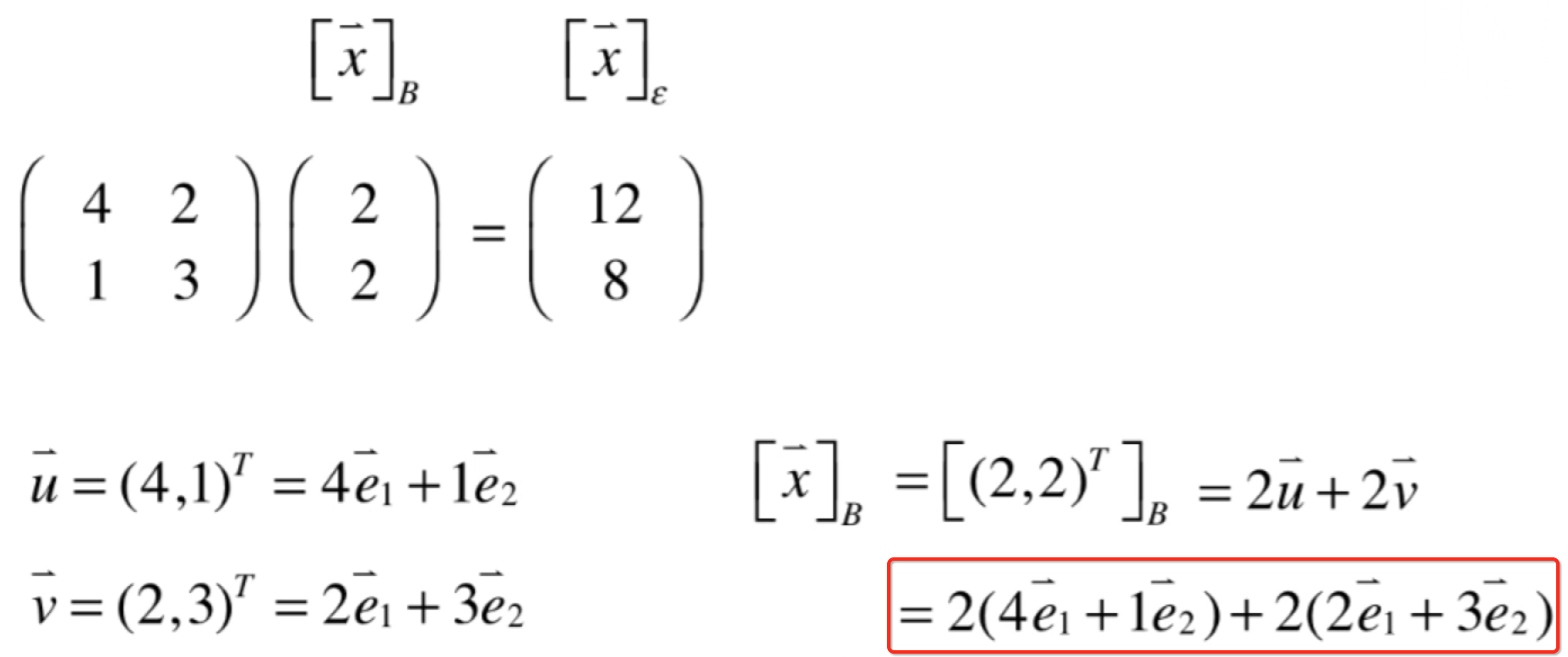
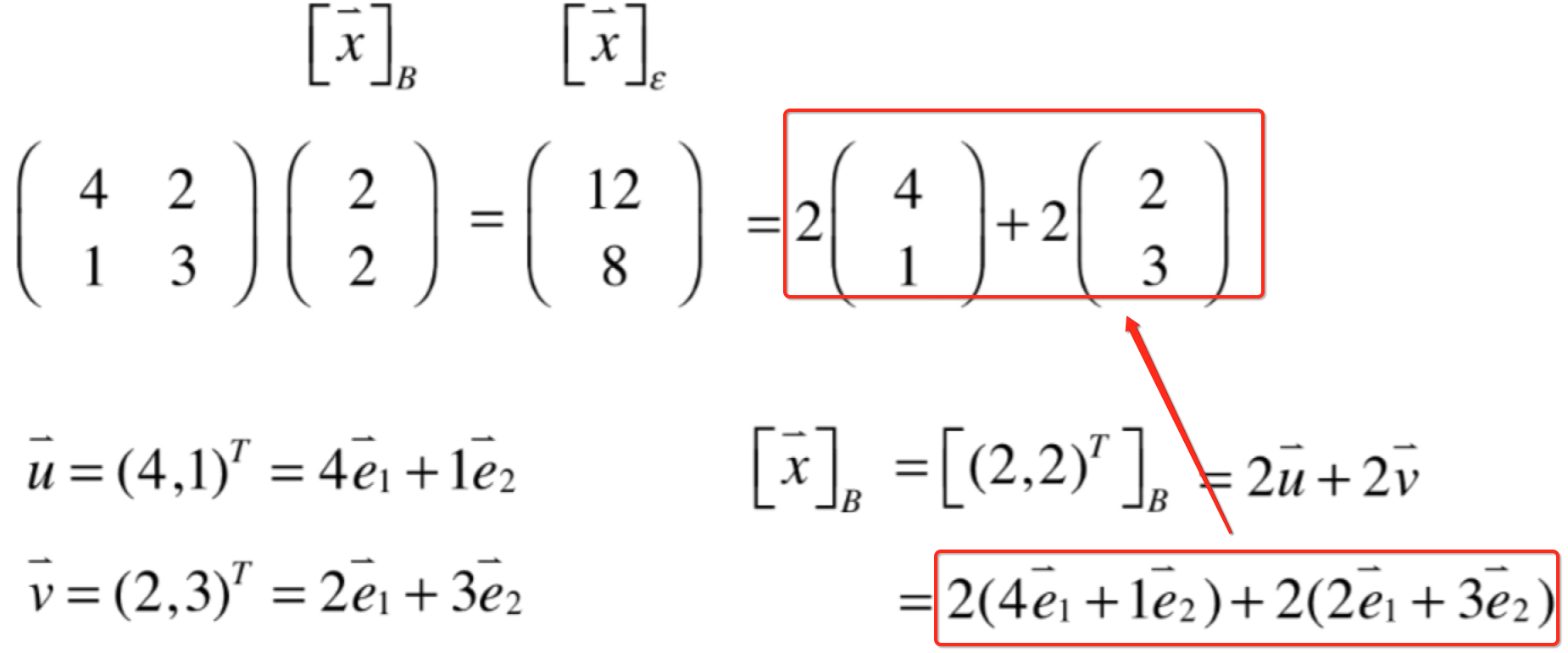




【推荐】还在用 ECharts 开发大屏?试试这款永久免费的开源 BI 工具!
【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步