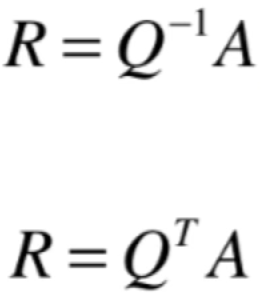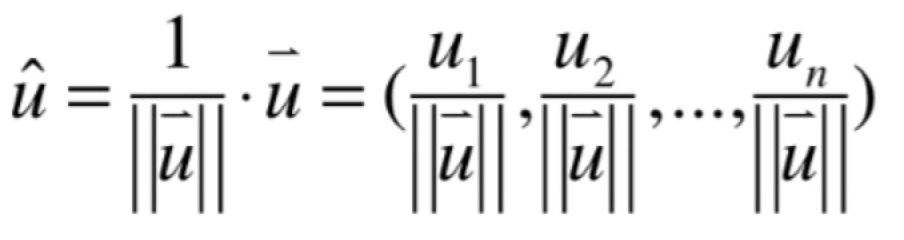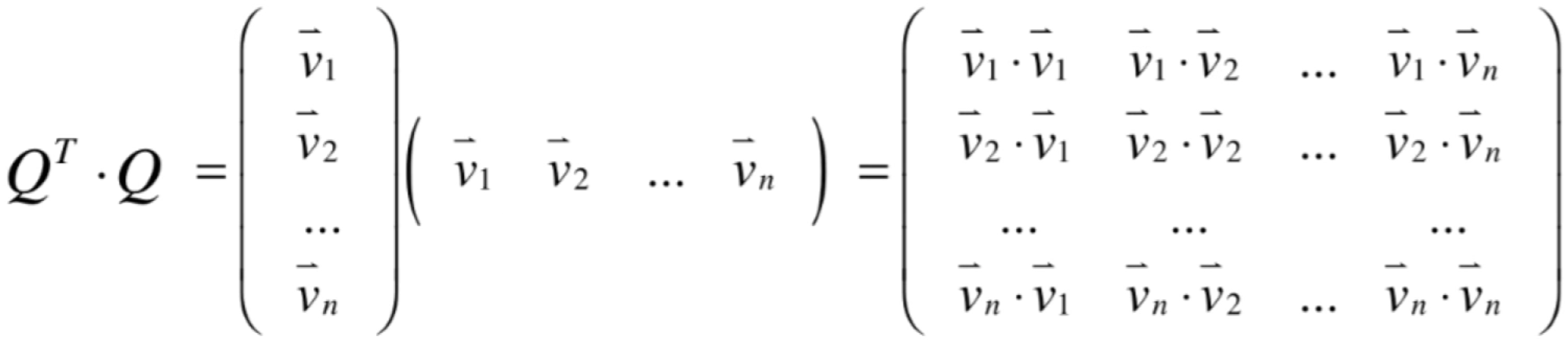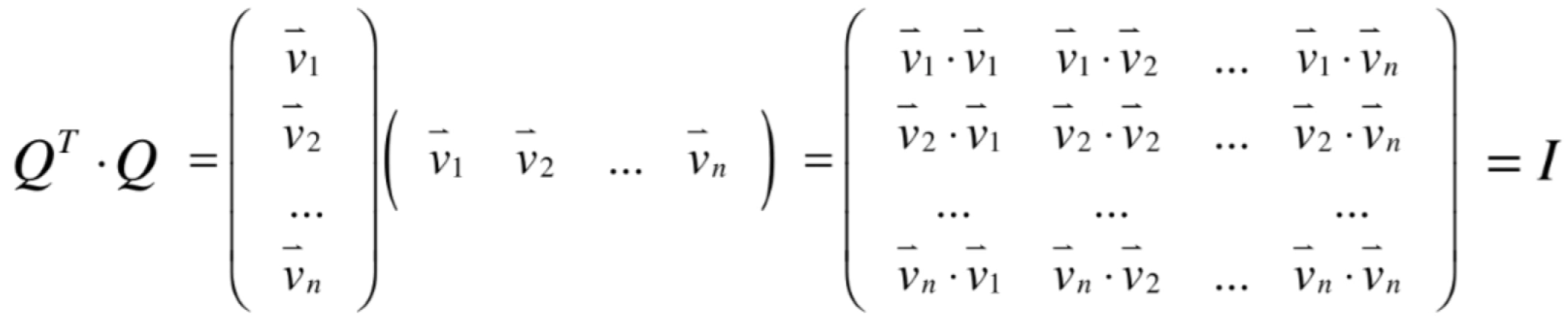线性代数学习之正交性，标准正交矩阵和投影

正交基和标准正交基：

前言：

经过上一次https://www.cnblogs.com/webor2006/p/14352737.html的学习，对于空间的概念已经有了非常深刻的认识了，而描述空间很重要的方式除了维度以外，那就是空间的基了，而如小标题所示就是跟空间的基相关，所以先来回忆一下空间基的相关概念：

“一个n维空间任何一组线性无关的向量，都是这个n维空间的一组基”，比如之前举的二维平面的例子：

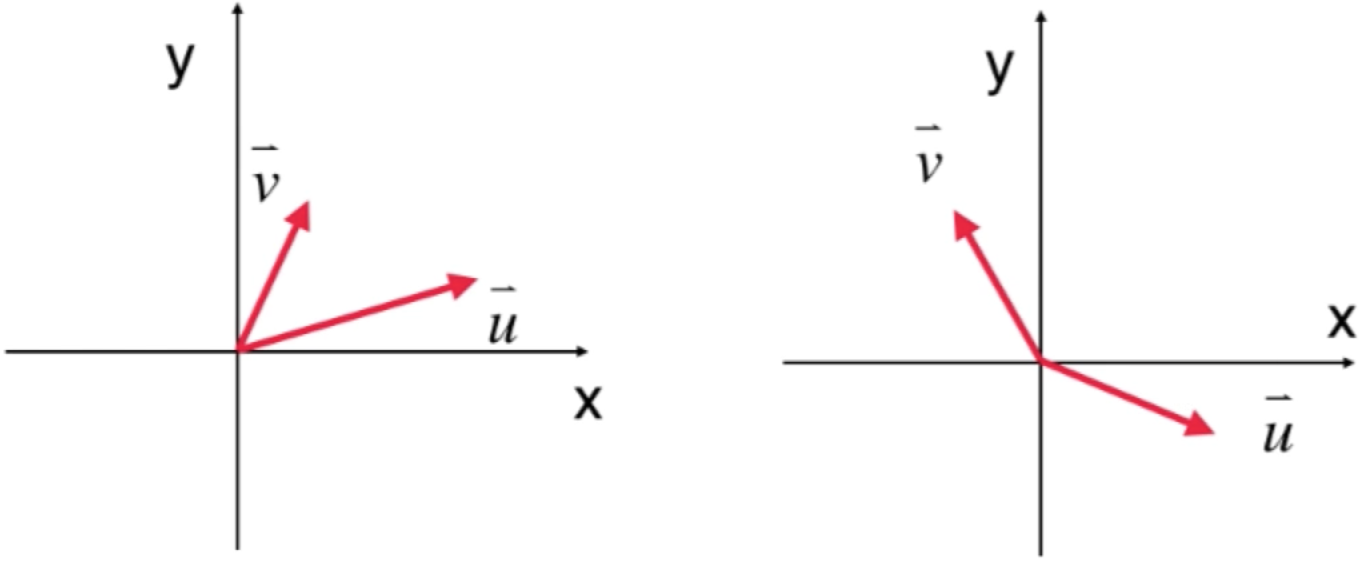
但是！！实际为了研究方面还是喜欢这样的一组基，也就是咱们此次要研究的正交基：

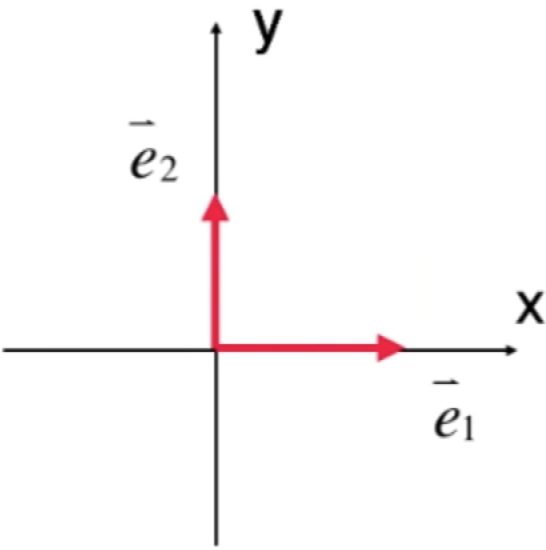
这是因为在空间中任意取出一个点的话：

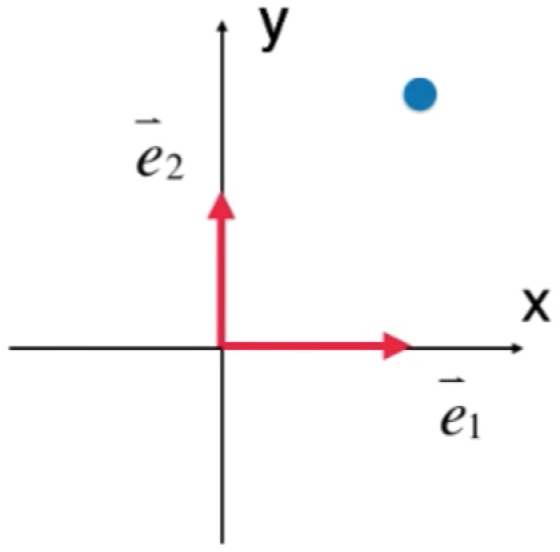
很容易通过正交基来描述这个点的位置，只需要看它所在的横纵坐标就成了，如下：

而如果不是正交基，要找到点所在的位置就相对困难很多，比如：

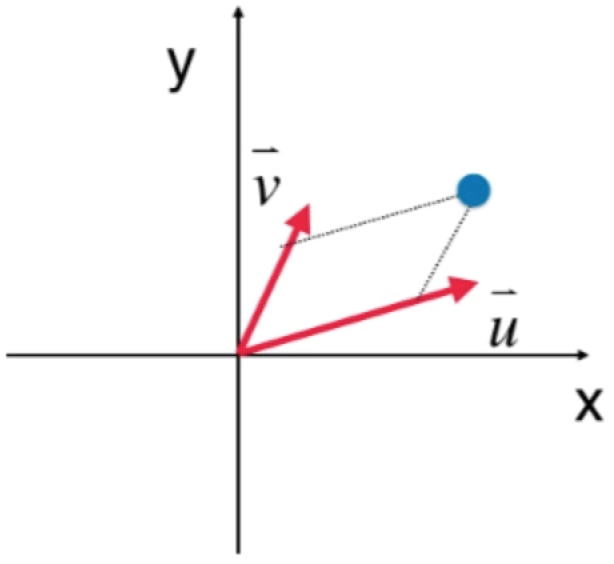
正交基【Orthonormal Basis】：

什么是正交？

接下来则正儿八经的什么是“正交”，这个在之前已经被多次使用过了，先来回忆一下之前https://www.cnblogs.com/webor2006/p/14257300.html学习的向量的点乘：

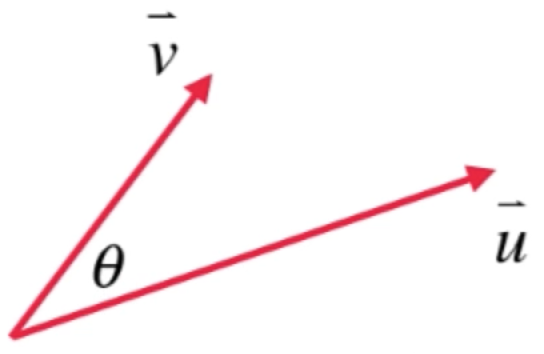
如果说当θ=90度的时候，此时：

所以对于向量的点乘就为：

在线性代数领域，如果两个向量点乘的结果为0，就说明两个向量垂直，也就是两个向量正交。

正交向量组：

它是指：一组向量，如果两两正交，则成为正交向量组。

对于正交向量组它有一个非常优美的性质：正交非零向量组一定线性无关，其中它要求不能有零向量，这是因为零向量点乘任何一个向量结果都为0【而根据正交的定义也能说明零向量跟任何向量都垂直的】，另外也能说明：正交向量组一旦存在零向量，那么这组向量一定是线性相关的，因为在0零量前头可以取任何非0的数，也就可以找到一组非全零的k乘以向量的结果为0。不过这里还是关注正交非零向量的性质，其实为啥它们一定是线性无关的其实很容易想明白，因为都是垂直独立的呀，不过下面还是严谨的证明一下这个结论：

正交非零向量组一定线性无关：

证明：假设：

是一组正交向量组，要想证明线性无关，只需要证明下面这个式子只有零解：

关于线性无关的定义回忆一下：

此时等式两边可以乘以一个vi向量，就为：

此时就可以用分配率进行变换：

而由于它们都是正交向量组，所以：

点乘的结果都为0 ，除了没有标红的，所以式子又变为：

而对于向量点乘向量又可以变为：

对于这个式子不太明白的也可以根据它很容易的推导出来：

由于θ=90度，所以v.v = v的模 * v的模=v的模的平方，此时就可以分析一下发现：

因为已知了这个向量是非零向量，当然它的模一定是大于0的，而要让等式成立，此时ki就只能是0，此时就得证了。

接下来再来回忆一下空间的基的概念：

n维空间中，任意n个线性无关的向量，一定是这个n维空间的基。

再结合咱们目前的这个概念：“正交非零向量组一定线性无关”，就有如下结论了：

n个非零正交向量一定是n维空间的基！【因为里面已经包含线性无关的概念了】

那有了这个概念就可以忘记之前所学的线性无关，线性相关，生成空间了，转而来看正交，而判断两个向量正交是非常容易的，点乘一下得0就可以了，n维空间中只要给出两两互相垂直的非零向量，它们就是n维空间的基。

正交基：

此时对于什么是正交基的概念就很容易理解了，定义如下：

如果一个空间的一组基两两正交，则称这组基为一组正交基。

在这里注意此时不用限定向量要非零了，因为正交基首先要是一组基，而对于一组基来说一定是线性无关的，如果线性无关肯定是没有零向量。

标准正交基【Orthogonal Basis】：

先来看一下它的定义：

如果一个空间的一组正交基，模均为1，则称这组基是一组标准正交基。

也就是它是一种特殊的正交基，它有无数组，比如二维坐标中：

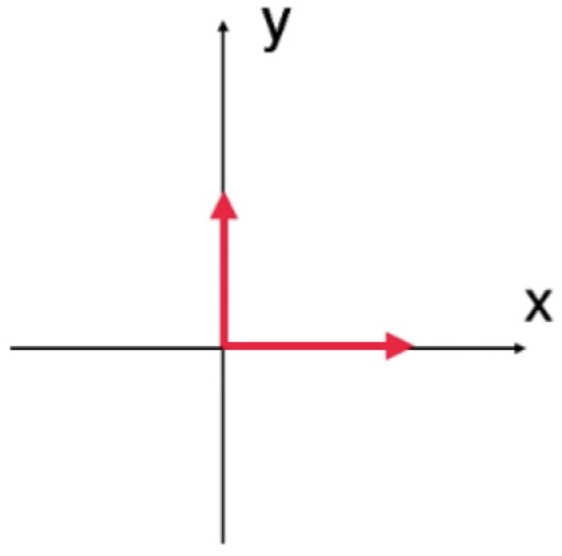
还比如：

虽说它的概念比基或正交基还要缩小，但是要知道一个空间的标准正交基也有无数组。

关于这个小节中，“n个非零正交向量一定是n维空间的基！”这个概念是比较有意义的，使得我们求解空间的基的时候变得更加简单了。

一维投影：

接下来学习一个新的概念---一维投影，貌似它跟上面所学的正交没啥关系，其实它们俩的关系是巨大的，而其实这里是将一个复杂的过程给进行拆解，先来看复杂过程的一小部分，那么这个“复杂的过程”是指什么呢？在上面咱们学习了什么是正交基，什么是标准正交基，但是通常我们只能得到空间中随便的一组正交基，在上一次https://www.cnblogs.com/webor2006/p/14352737.html学习了四大子空间【行空间、列空间、零空间、左零空间【暂且它不用看】】，学习了如何得到它们的维度，如何得到它们的一组基，但是得到的这组基我们绝对不给保证它们是正交的，我们得到这组基是什么样子跟给定的矩阵是什么样子是密切相关的，可是我们又是这么的喜欢正交基，所以：我们希望进一步找到这空间的一组正交基，从而进一步找到标准正交基就比较容易了【只需要将其归一化，因为标准正交基的定义就是它们的模均为1】，也就是只要求出单位向量既可，关于这个可以回忆https://www.cnblogs.com/webor2006/p/14257300.html：

所以接下来先从最简单的二维情况出发，看一下是如何查找空间的正交基的，比如给出任意两个向量【不共线的两个向量】：

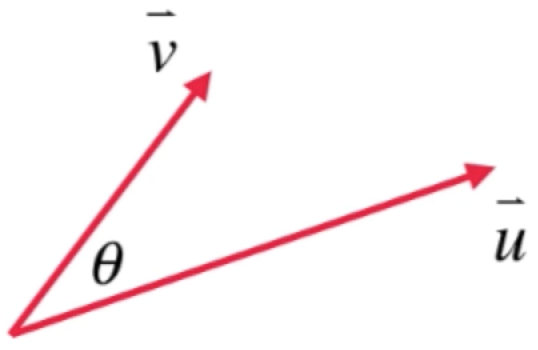
其实是给出了二维平面的一组基，那怎么通过这两个向量来求出二维平面的一组正交基呢？答案就是需要借助投影，过程如下：

1、从v向量的末端往u向量上做一个垂线：

2、以垂足的位置做为另外一个向量的末端，下面蓝色的向量其实就是v向量在u向量的投影：

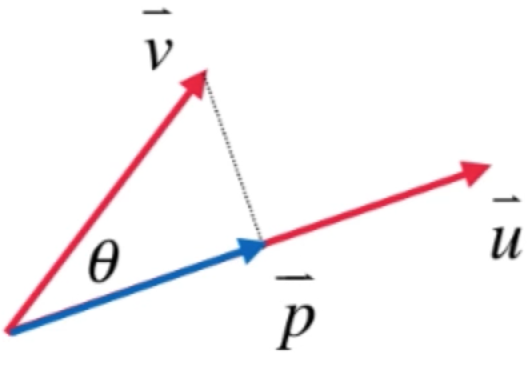
3、如果已知p向量的话，那么想要求出跟u向量垂直的向量就非常简单了，如下做个辅助线：

其中整理一下思路：

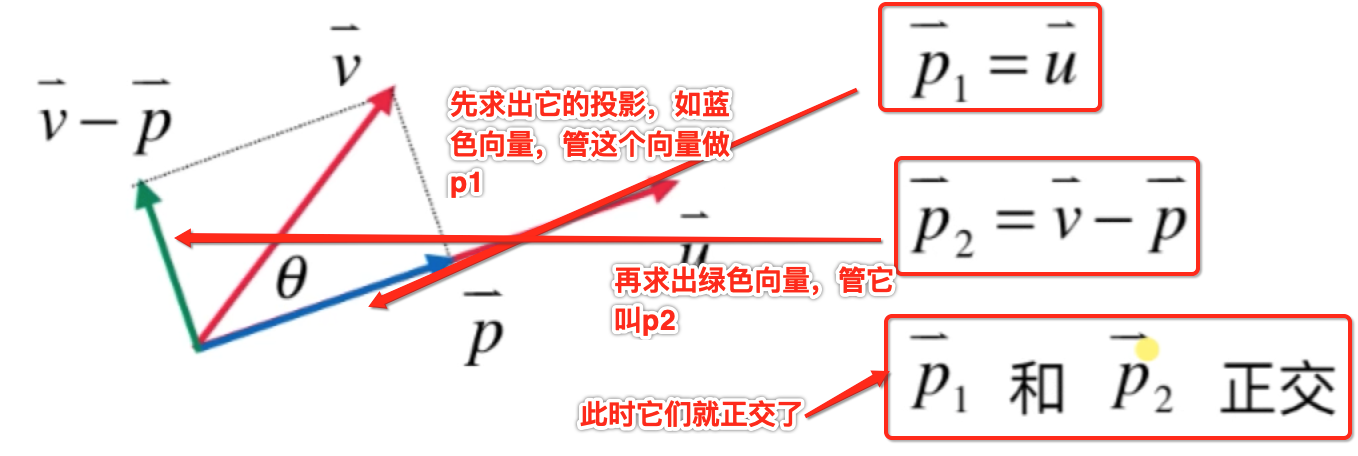
4、关键就是求出投影向量p了，此时就需要使用三角函数的知识了，也就是：

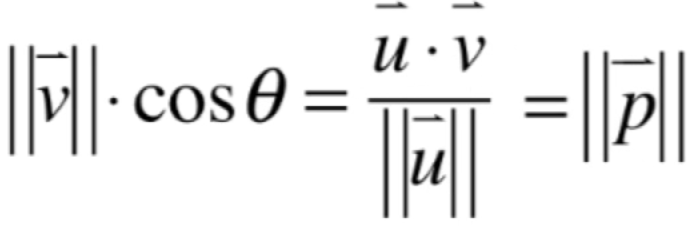
也就是p向量的模已经知道了，接下来则来求p这个向量的方向了，从图中可以看到求p的方向其实也就是u向量的方向对吧？如何求方向呢？如下：

知道了p向量的模和方向之后，就可以算出p这个向量是多少了，如下：

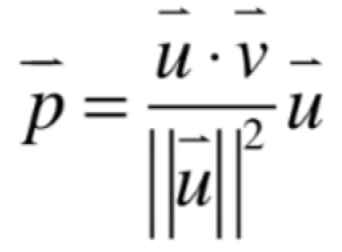
而由于对于分母来说又有一个等式展开：

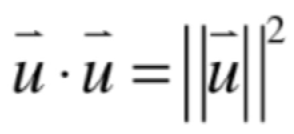
所以此时对于向量p也可以写成这样：

但是！！！这里需要注意：

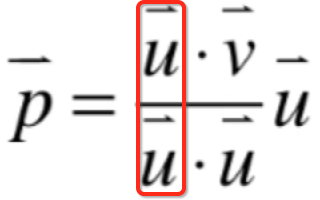
这俩是不能约分的，因为这是向量的点乘，而不是两个数，所以为了避免用户觉得可以约分，所以通常也可以表示成它：

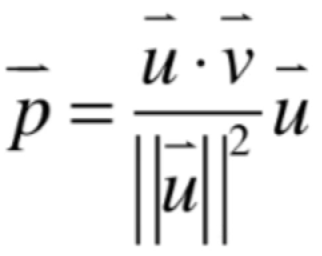
既然能求出一维投影的p，进而就可以求出它：

这样就解决了在二维空间中找出了一组正交基了。

高维投影：

接下来则来看一下更多维度的投影问题，然后最后将求正交基的过程总结成一个非常严谨的算法过程，还是先回忆求二维平面投影当时的情况：

投影P的求解公式为：

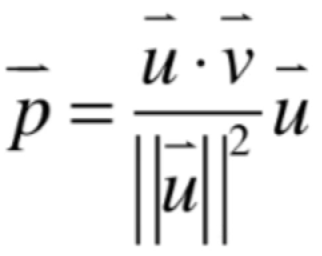
而：

所以将上面p向量的等式代入到这个p2等式中就有：

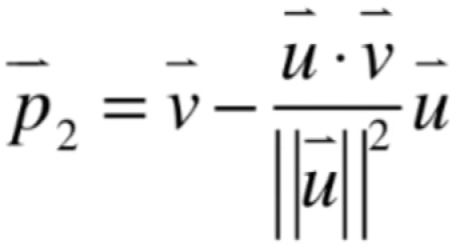
此时p和p2正交，那如果是在三维空间中呢，比如这三个向量：

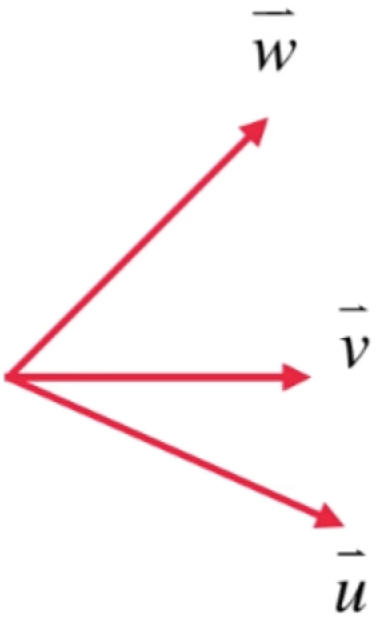
首先先处理两个向量的正交情况，比如处理u和v为：

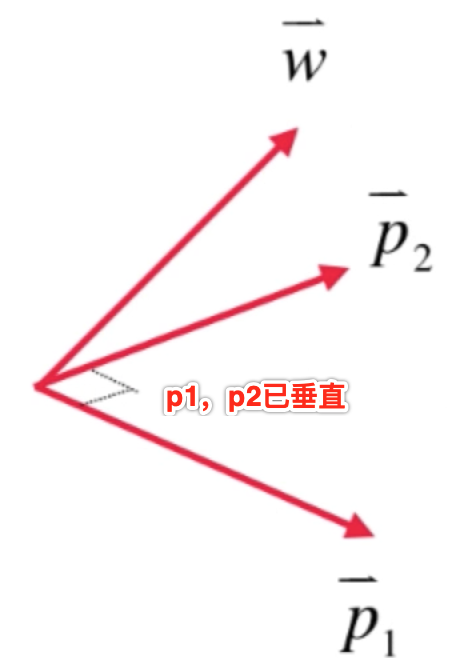
接下来再让第三个向量w让其跟p1和p2向量垂直既可，其实只要找到w向量分量跟p1、p2所在的平面垂直既可，根据高中立体几何的求解，可以很容易算出来，先向平面引一下垂直线：

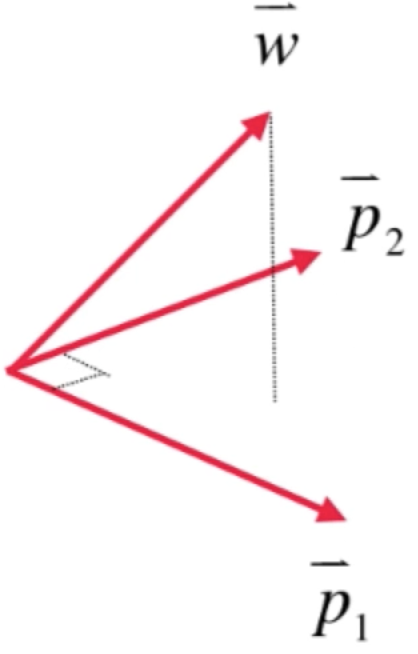
然后再以w向量的末端跟垂足做一个向量，如蓝色所示：

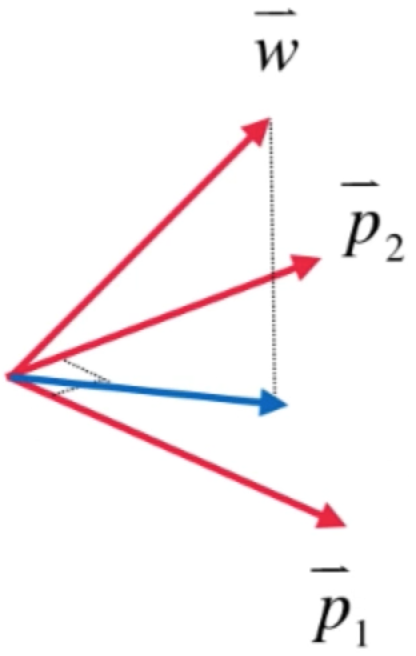
如果假设这个蓝色的向量叫p：

此时咱们要想找的跟p1、p2向量都垂直的其实是绿色向量这根：

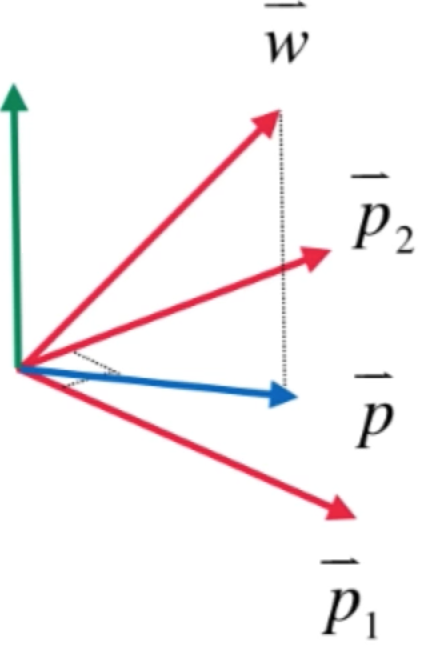
而它是多少呢？再做个引用就知道了：

此时发现木有是不是跟一维的投影很类似，只是这里是向二维的平面进行一个投影，而要想求解这根绿色的向量，就得要求出p这个向量，也就是求w向量在p1、p2向量所组成的平面上的投影，而由于p1、p2已经是垂直的了，所以它们已经是它们所组成的二维空间这样的一个子空间的一组正交基了，所以此时可以有此等式：

也就是p可以写成是p1和p2的线性组合，所以关键就是要求解出这个系数k1和k2了，或者可以在p向量末端向p1和p2向量做垂线，然后形成两个标黄线的分向量a、b：

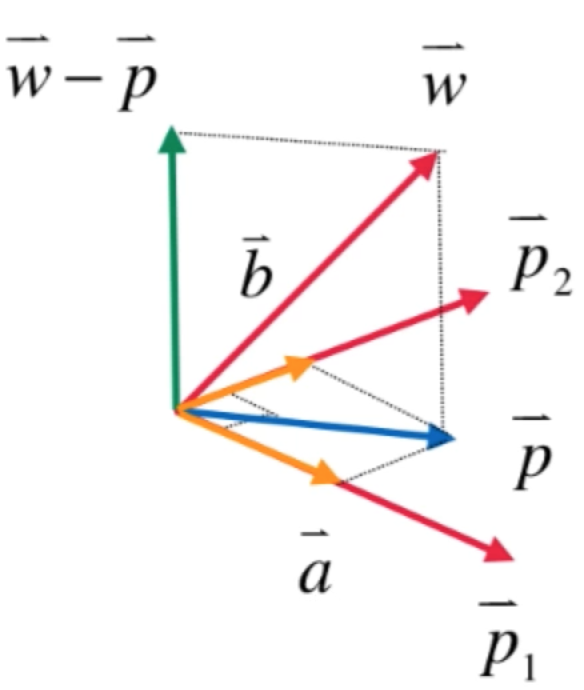
是不是又有如下等式了：

而问题的焦点就是怎么求出a和b两根向量呢？此时就需要让w向量跟p1和p2向量建立联系，此时需要将w向量的末点和p这个向量在p1和p2上的垂足进行一个连接，就会成这样了：

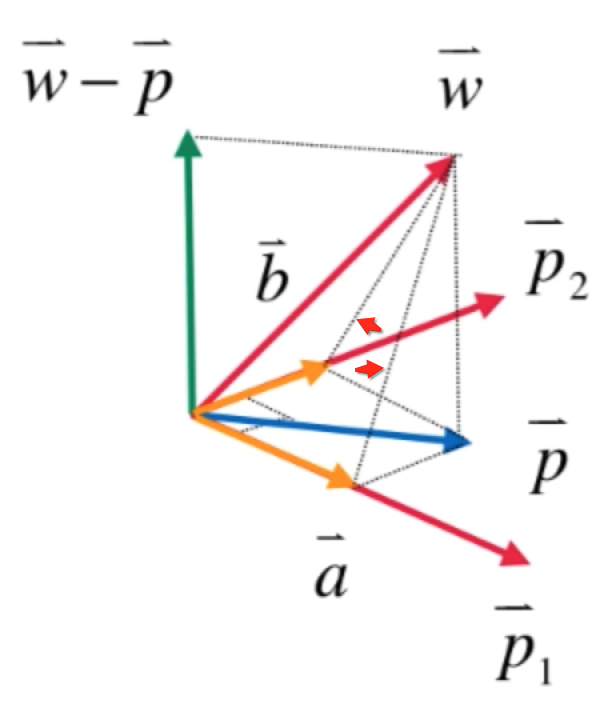
其实这两根线都是垂直于p1和p2的，那么就是说：

换言之，对于第三个向量w而言其实就是在已经做出来的正交基p1和p2上做投影a和b的加和，就是w向量在由p1和p2组成的子空间的投影，而a和b是多少呢？如下：

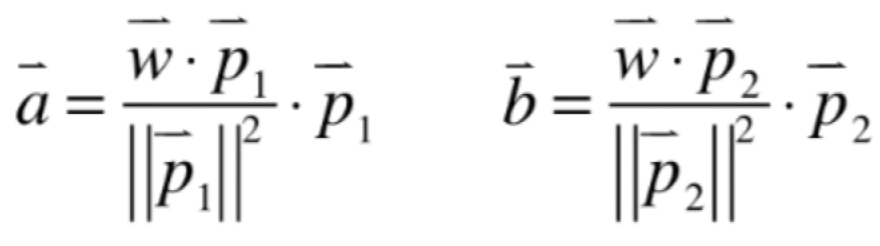
所以此时P向量就可以求出来了，将a和b的结果代入：

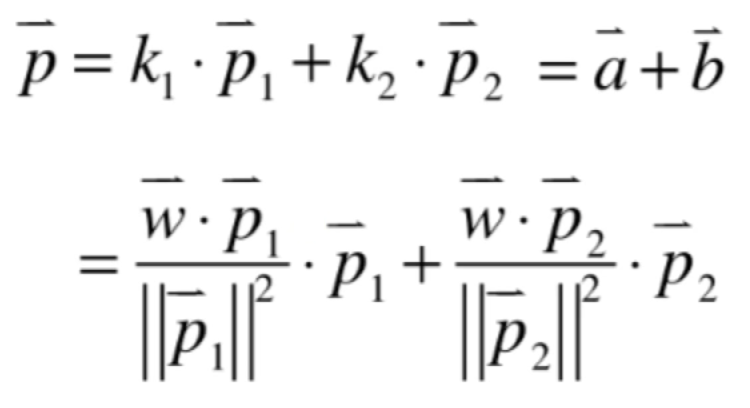
p求出来了，那对于第三个正交基绿色的向量就可以求出来了，如下：

对于上面的求解正交基的过程进行一个规律总结，比如已知u，v，w三个不共面的向量，本身它们三个形成了空间的一组基，那如果想要找到这三个向量的一组正交基，可以按如下步骤来求：

1、先将u不动，也就是做为正交基的结果p1。

2、按v这个向量跟p1垂直，也就是求第二个正交基向量，根据之前在二维正交基的求角公式：

很显然此时的这个正交基为：

而由于u向量已经用p1来表示了，所以此时式子就可以变为：

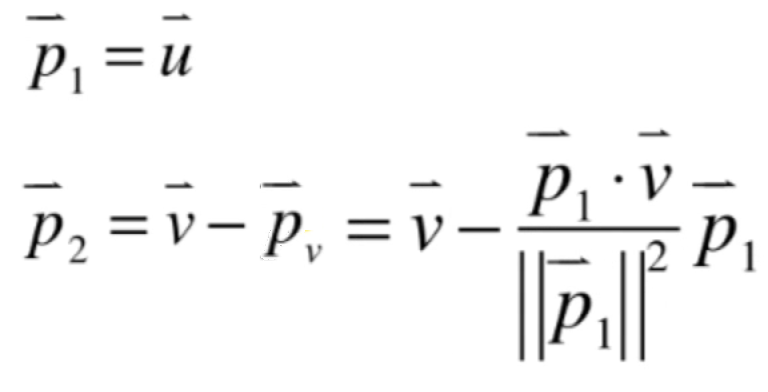
3、求第三个正交基向量，其实就是：

现在对于三维空间的正交基的求解过程已经清楚了，那如果上升到四维呢？假设有第四根向量x，其实同样的道理，对于第四根正交基的求解如下：

也就是用x去减去它在p1、p2、p3上的投影，得到的结果就是第四个正交基的向量。

格拉姆-施密特过程：

所以，接下来就可以抽象总结求正交基的方法了：

如果已知一组基：

求一组正交基，方法就是：

此过程就叫格拉姆-施密特过程（Gram-Schmidt过程），注意：算法的输入必须是一组基，也就是它们线性无关的，下面回到二维空间中来看一下假设存在线性相关会怎么样：

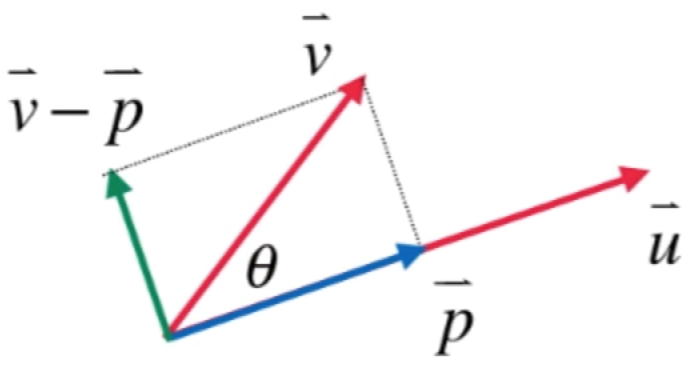
假设v和u是线性相关的，也就是v和p是共线的，v在u上投影蓝色的向量就是v自身，而相应的v-p绿色的向量就是v-v=0向量，很显然正交基中是不可能有0向量的。

进一步的，如果找到了一组正交基之后，想要得到它们的标准正交基，则相当的简单，直接把所有的正交基向量每一个按下面的式子进行归一化的处理既可，如下：

实现格拉姆-施密特过程：

接下来则回到python的世界当中实现格拉姆-施密特过程。

新建文件：

定义函数：

其中basis是代表一组基。

验证基：

首先来验证一下咱们传进来就真的是一组基，此时就需要看它们是否是线性无关了，而怎么看它们是线性无关呢？此时就可以利用上一次https://www.cnblogs.com/webor2006/p/14352737.html学习矩阵的秩的知识了，我们可以将这组基的向量用行的方式将其排列起来，开成一个矩阵，如下：

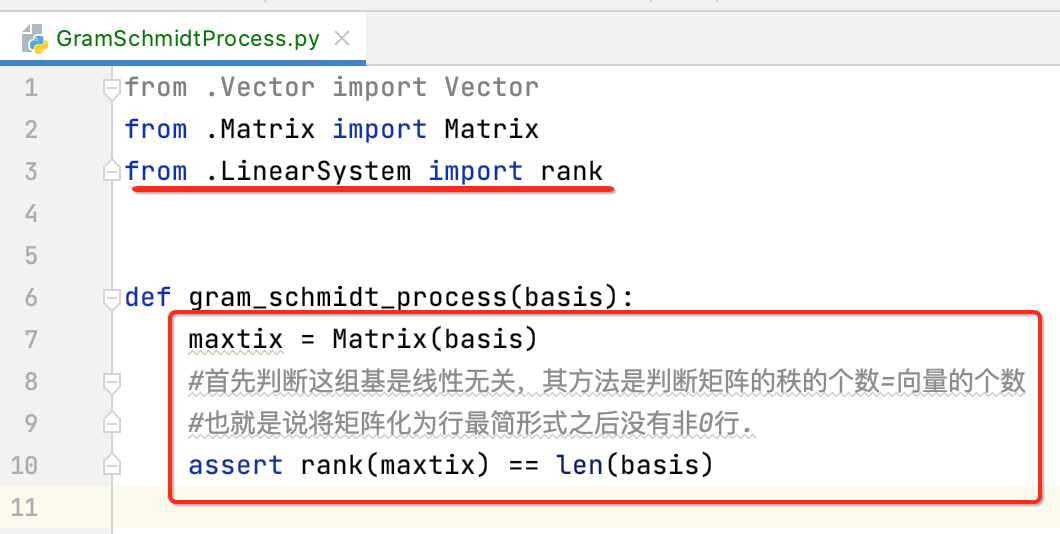
修改Matrix构造：

先来看一下目前Matrix构造的封装：

也就是目前还不支持传向量列表的形式，所以需要兼容一下，也很简单：

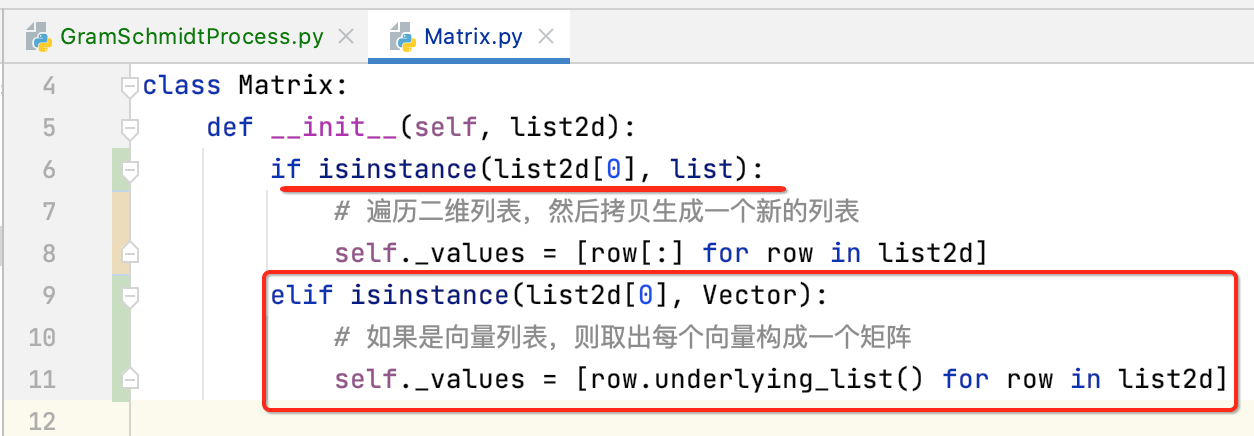
实现过程：

接下来则真正实现求解过程，首先根据咱们上面所述的求解过程，先将一个向量不动作为第一个正交基，所以：

接下来就需要每次用当前的向量减去之前已经求出来的正交基空间中的投影，回忆一下过程：

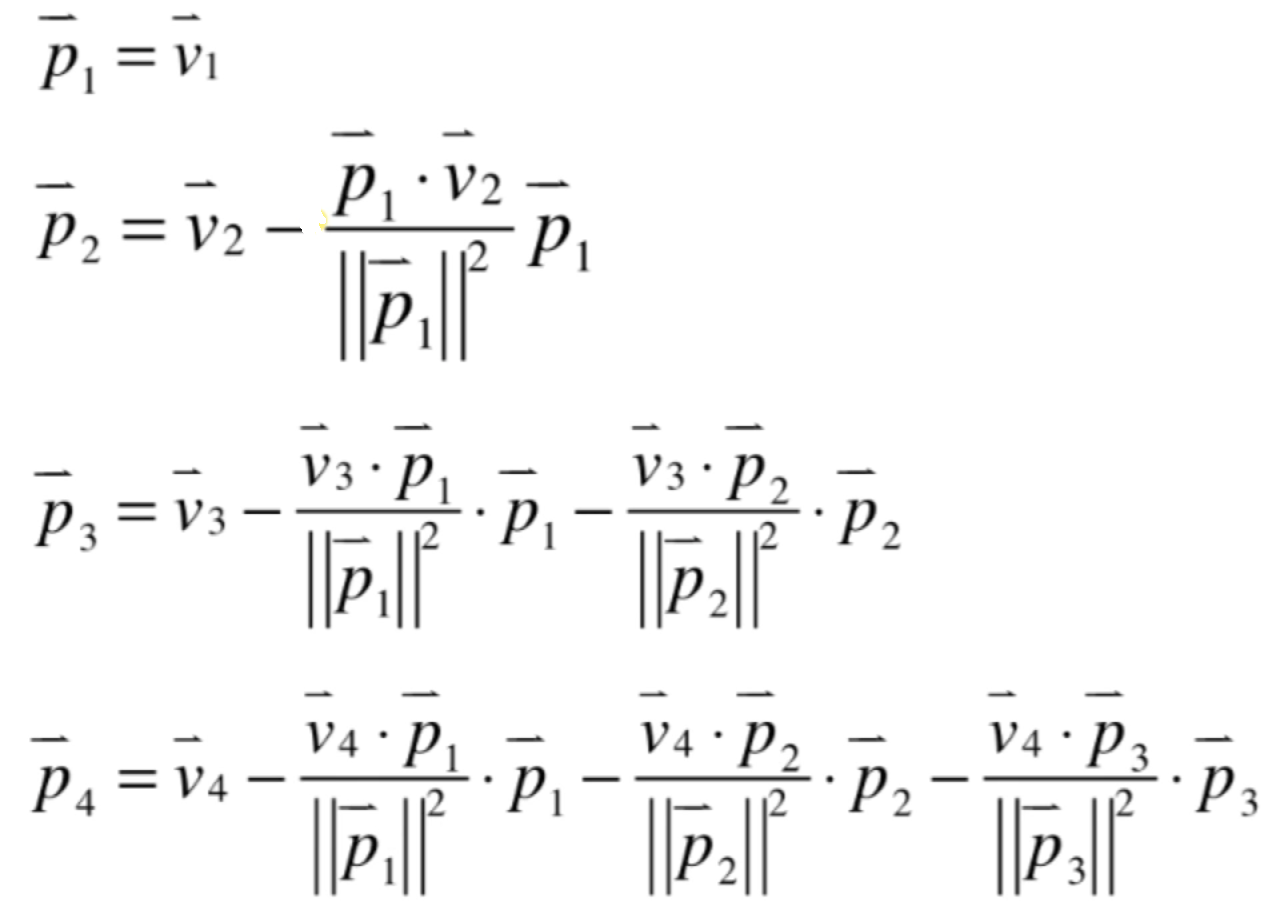
所以需要有循环了，如下：

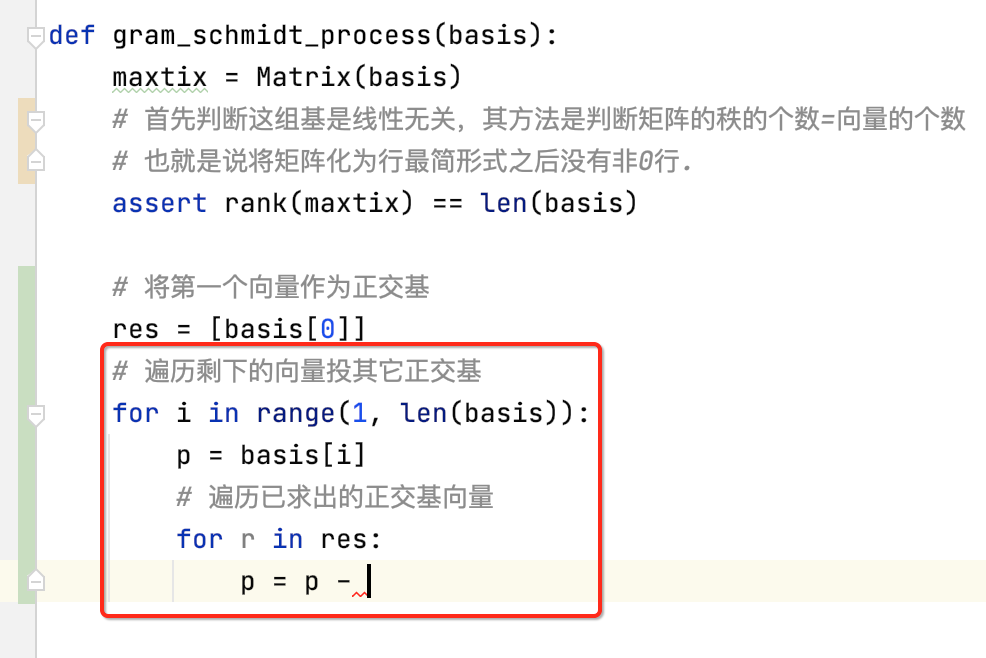
其中减去的就是当前向量向之前已知求解出来的所有正交基向量的投影，这块式子稍复杂一些，注意小心编写，严重按照之前的推出的公式来，所以可以写为：

注意：这里有一个需要修正的地方，就是对于分母的写法：

也就是向量模的平方，但是！！！这里有精度缺失，因为在求向量的模时使用了开根号：

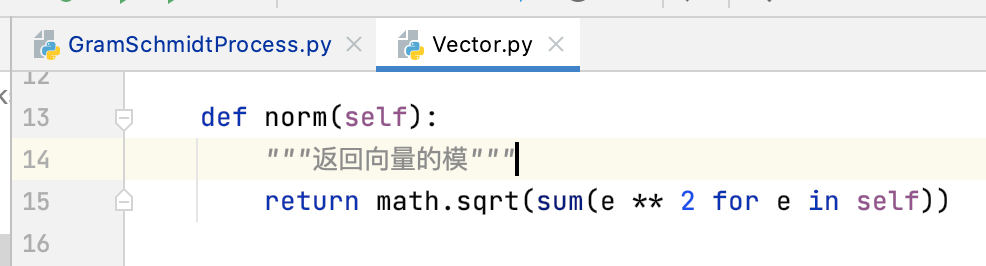
因为在计算机世界中开根本身就是一个近似的计算，所以为了避免这个误差，改为这样的写法：

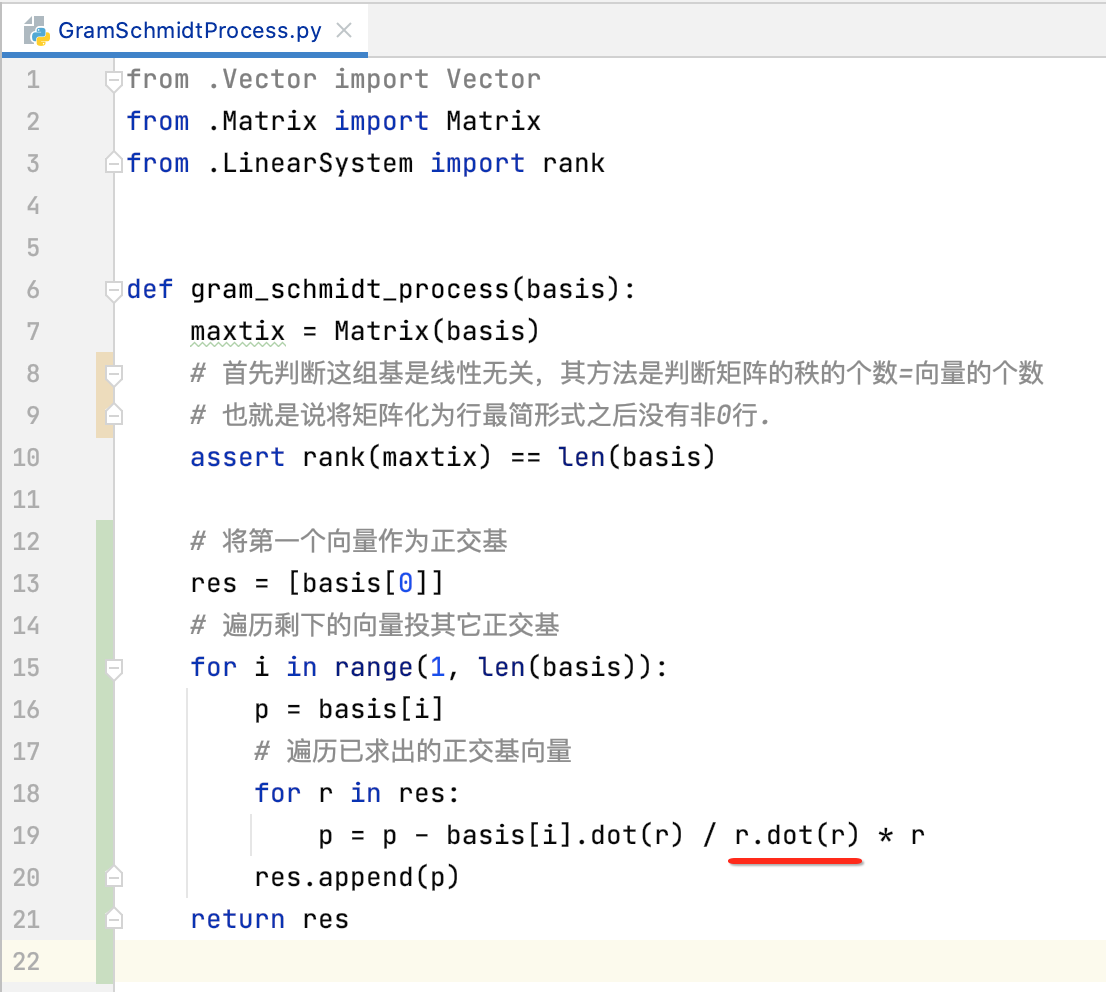
为啥可以写成点乘呢？回忆一下之前https://www.cnblogs.com/webor2006/p/14257300.html所学：

其中同一个向量的夹角为0 ，所以就能看就是该向量模的平方啦。

测试：

接下来做下测试：

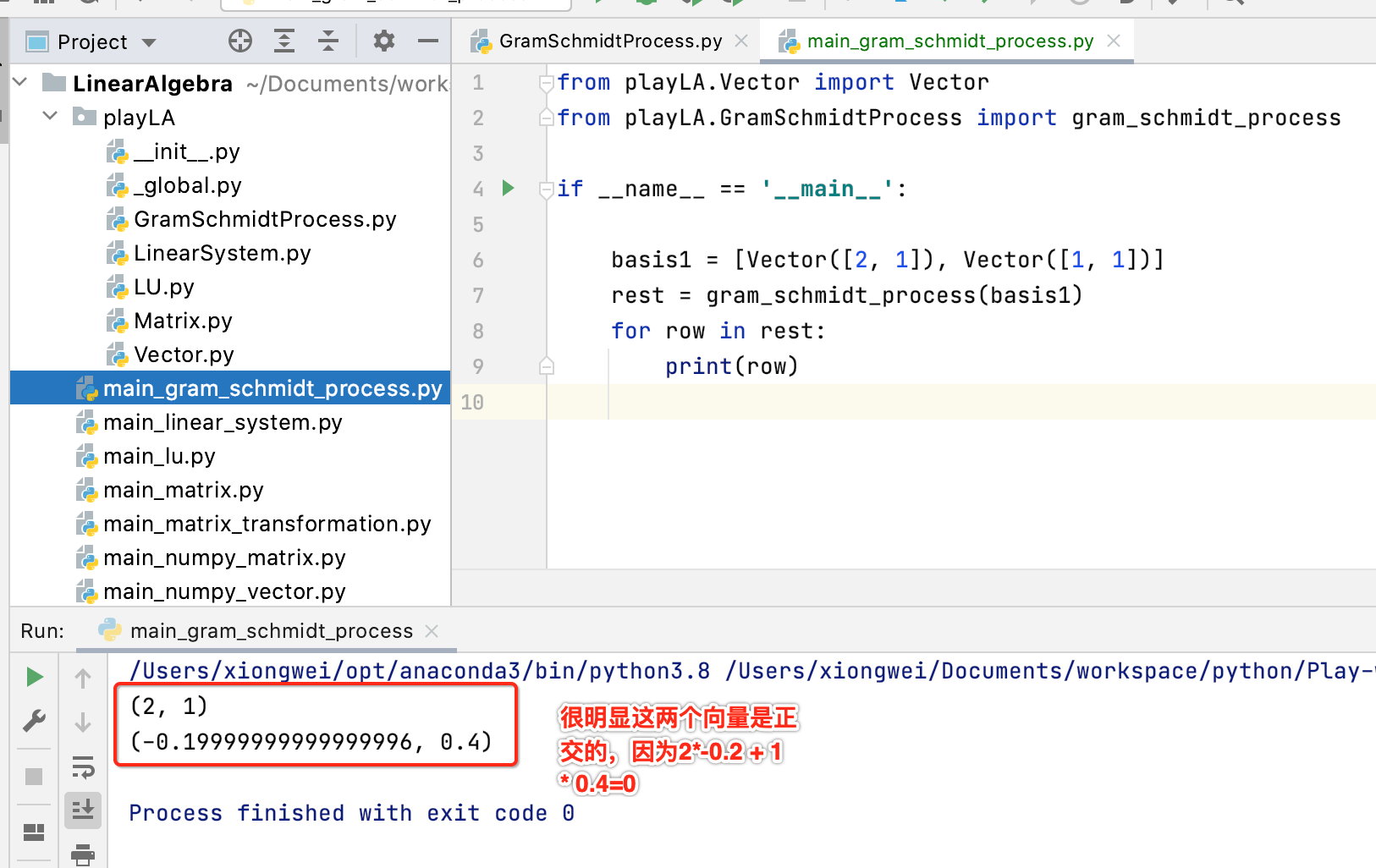
接下来要得到标准正交基就很简单了，如下：

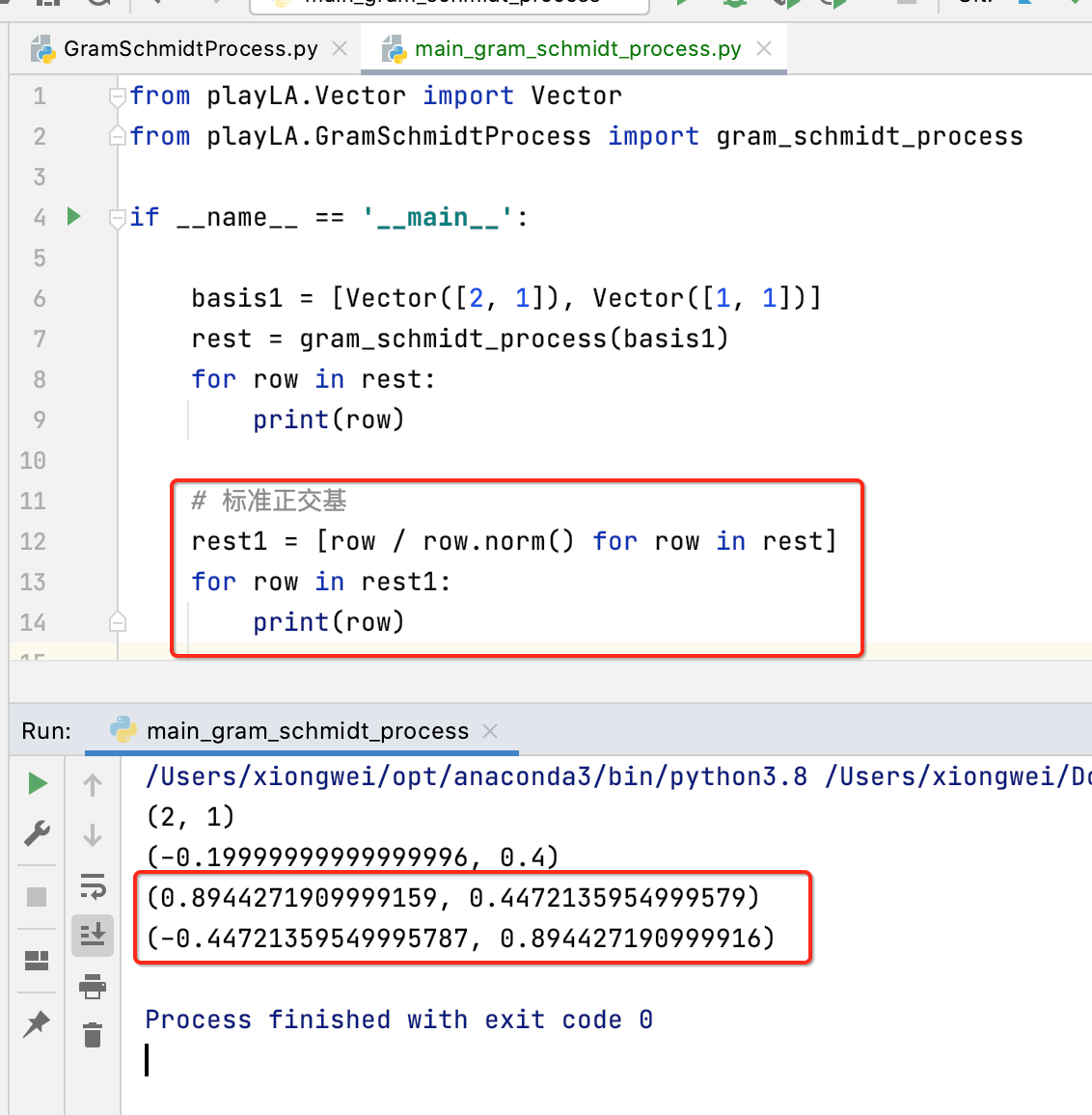
而为了这两个向量相垂直，只需要两个向量点乘为0既可，验证一下：

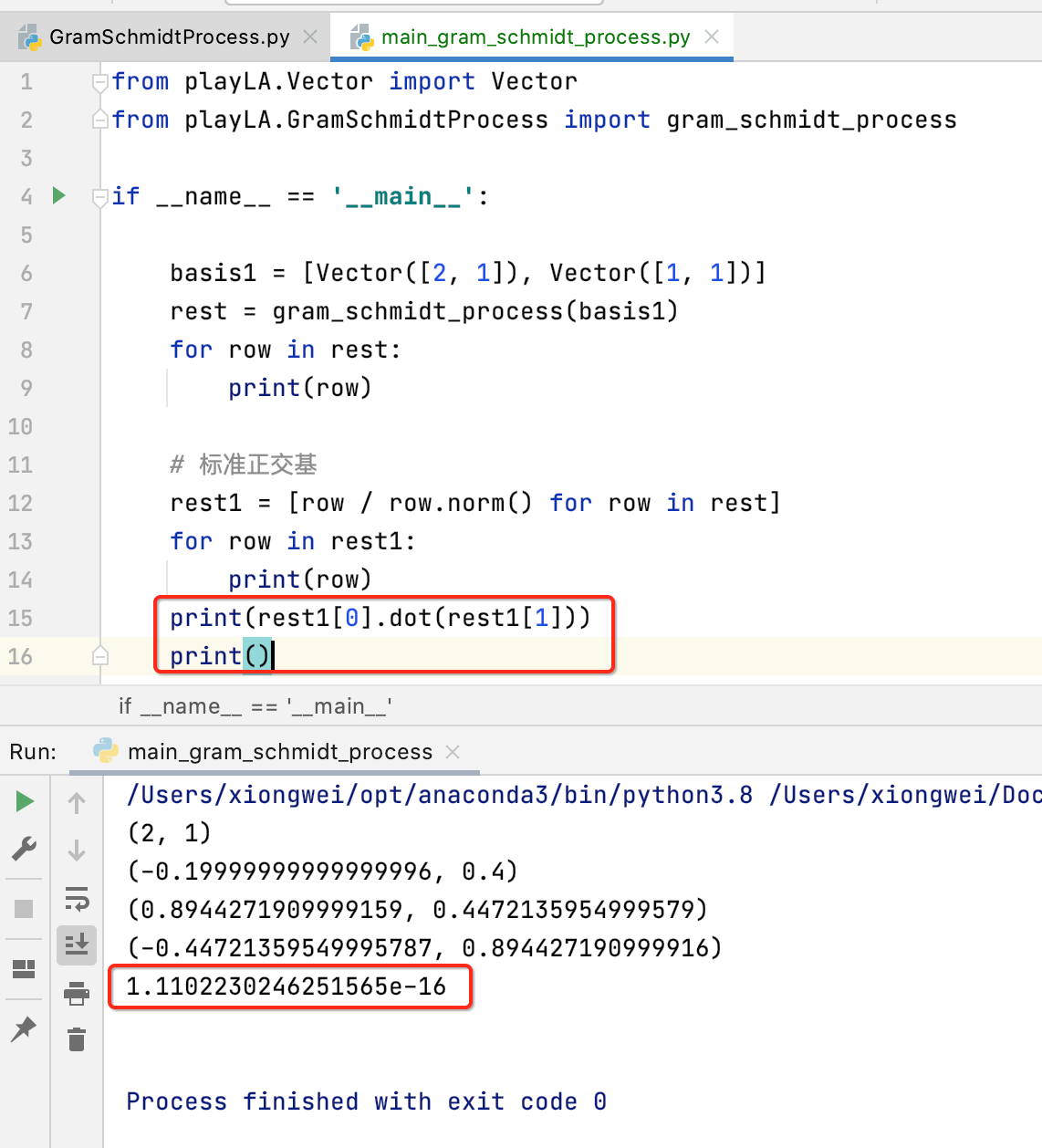
接下来再来测试一组向量：

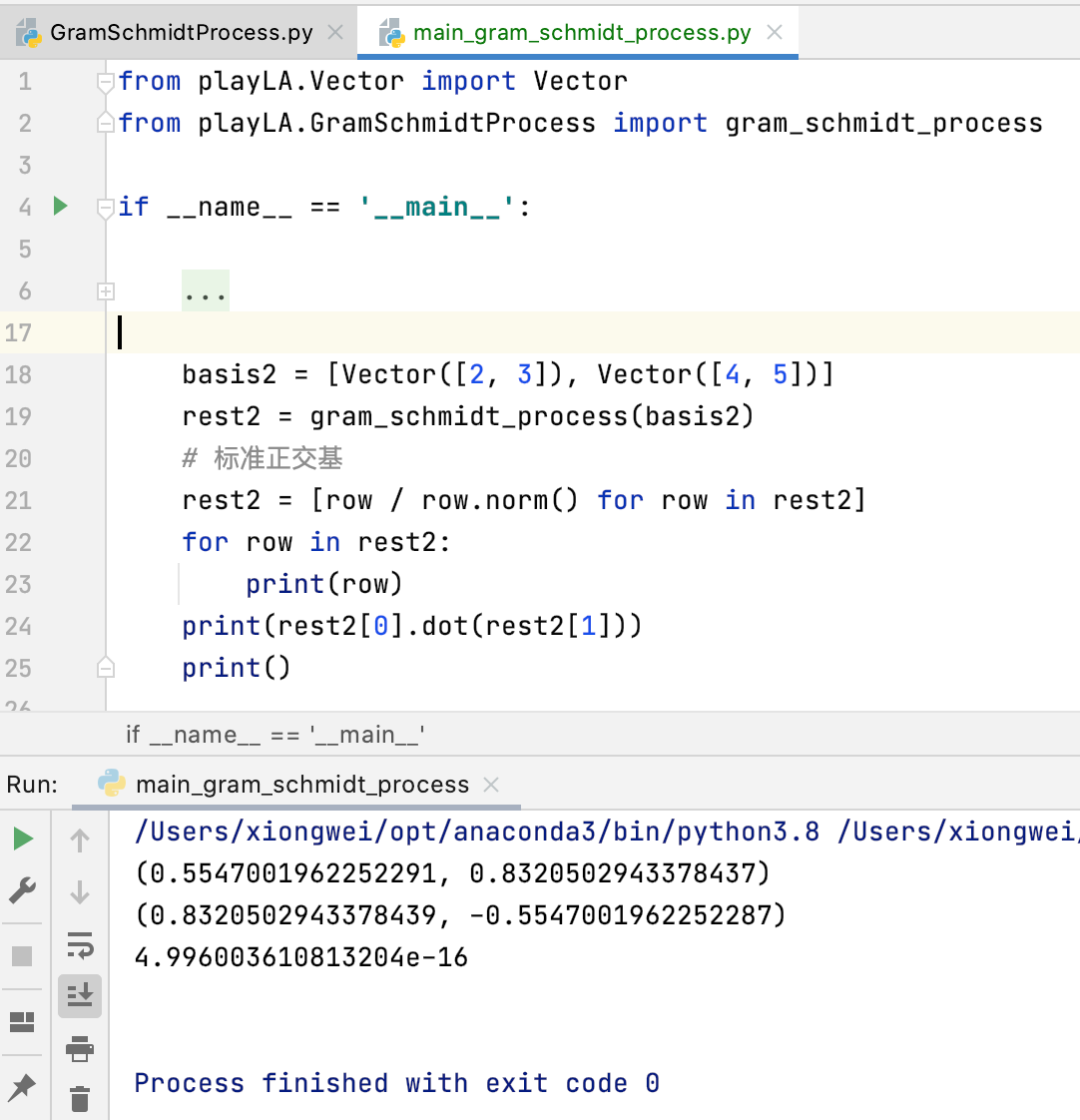
再来看一下三维向量的情况：

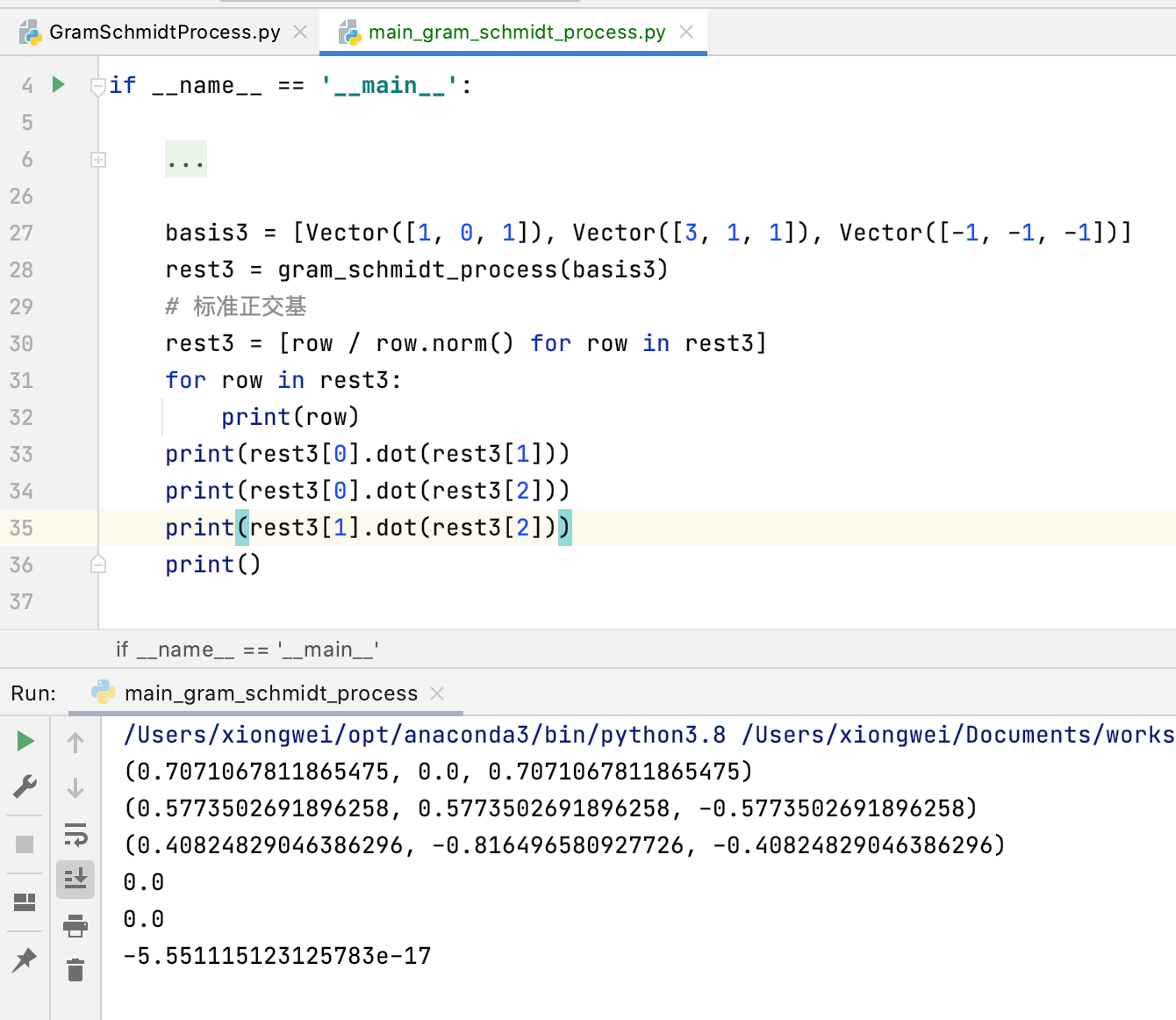
不多解释了，下面再来看一组用例：

为了证明求出的标准正交基是正确的，依然两两点乘看下是否为0：

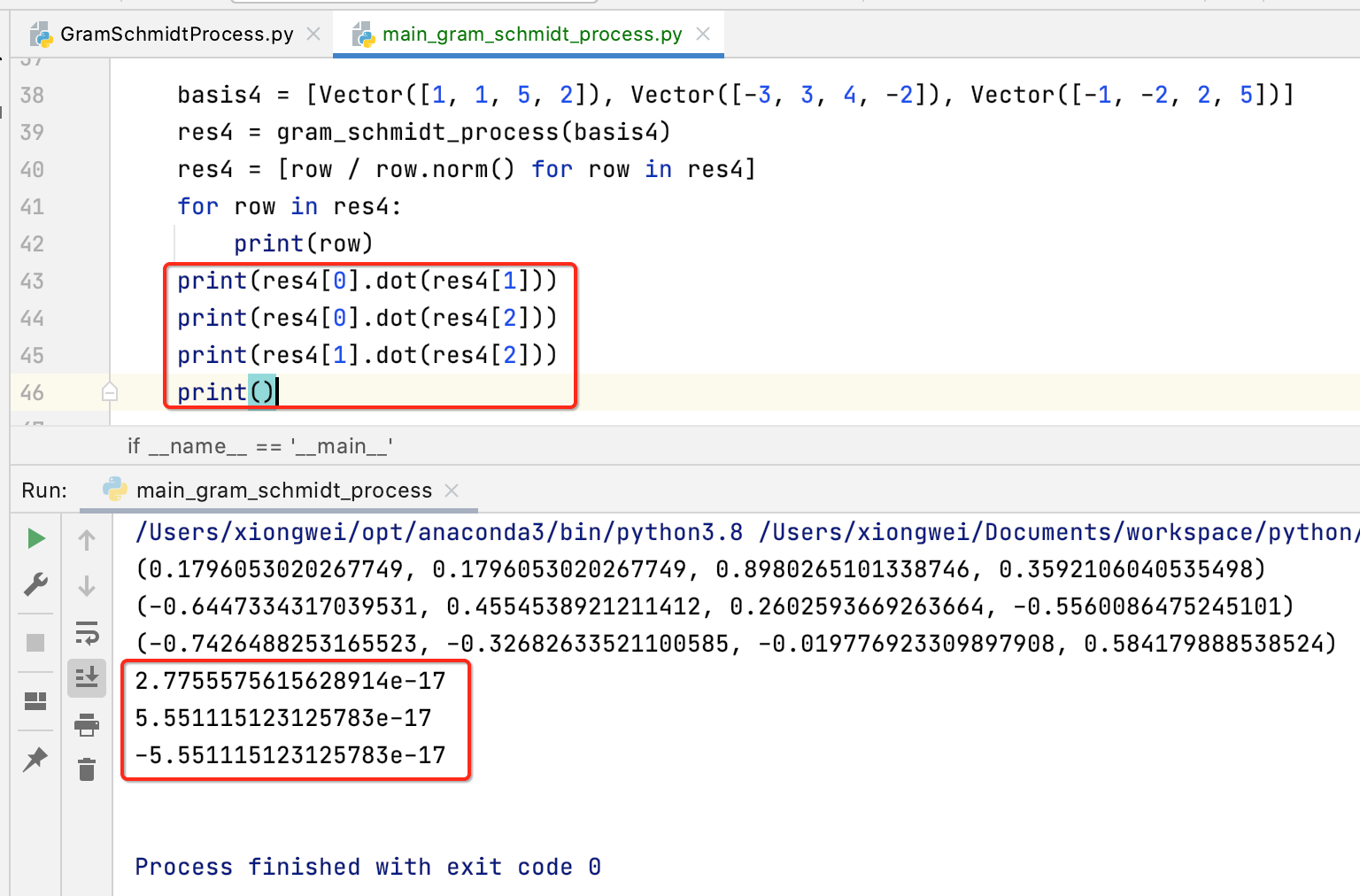
也就是利用Gram-Schmidt过程可以求出高维空间嵌套的子空间它的一组标准正交基。

标准正交矩阵的重要性质：

什么是标准正交矩阵：

目前我们已经知道如何求一组基的正交基，进而求出标准正交基，这里则来探讨一下标准正交矩阵的概念，先来回忆一下矩阵表示空间的情况：

而其实是把矩阵的一组基一列列的排列起来形成一个矩阵，然后再跟向量进行相乘得到的点的结果。对于标准正交基它是有多个向量，而如果也按照列的方式排成矩阵，此时这个矩阵就叫标准正交矩阵，用正式一点的定义就是如下：

一组n维标准正交基：

如果把它们按照列的方式排成一个n阶方阵Q【为啥是n阶方阵呢，因为有n个向量，每个向量的无数个数也为n】，称Q就为标准正交矩阵。

重要性质：

性质一：

那对于标准正交矩阵，它有一个非常重要的性质，如下：

也就是标准正交矩阵的转置乘以它自身结果等于单位矩阵，下面来证明一下这个式子：

证明：

假设：

上面这看起来像一个向量，其实它是一个矩阵，本质长这样的：

而此时我们要论证的式子就可以变为：

其中前面的矩阵是用行向量来表示的，而后面的是以列向量来表示的，两者相乘得到：

而由于每一个向量全是标准正交基，两两相乘，主对角上的是自身乘以自身为1，其它的都为0，所以这不很显然就是单位矩阵的样子么？

性质二：

根据上面的性质一，就可以得到标准正交矩阵Q的各列是线性无关的，而根据方阵的若干等价命题再往下推：

也就是说标准正交矩阵Q是可逆的，根据之前https://www.cnblogs.com/webor2006/p/14271706.html的矩阵左逆和右逆概念：

，那么：

那下面一个非常漂亮的结论就出来了：

也就是对于标准正交矩阵，如果要求它的逆真的太easy了，用这个结论，直接是这个矩阵的转置就成了，而不用像之前求矩阵的逆用那么复杂的方式了，具体可以回忆https://www.cnblogs.com/webor2006/p/14306045.html。

矩阵的QR分解：

什么是QR分解：

在上面说的性质二：

它有啥用呢？接下来就来研究一下它的应用---矩阵的QR分解。还记得之前https://www.cnblogs.com/webor2006/p/14306045.html已经学习过了一种矩阵的分解法么？简单回忆一下：

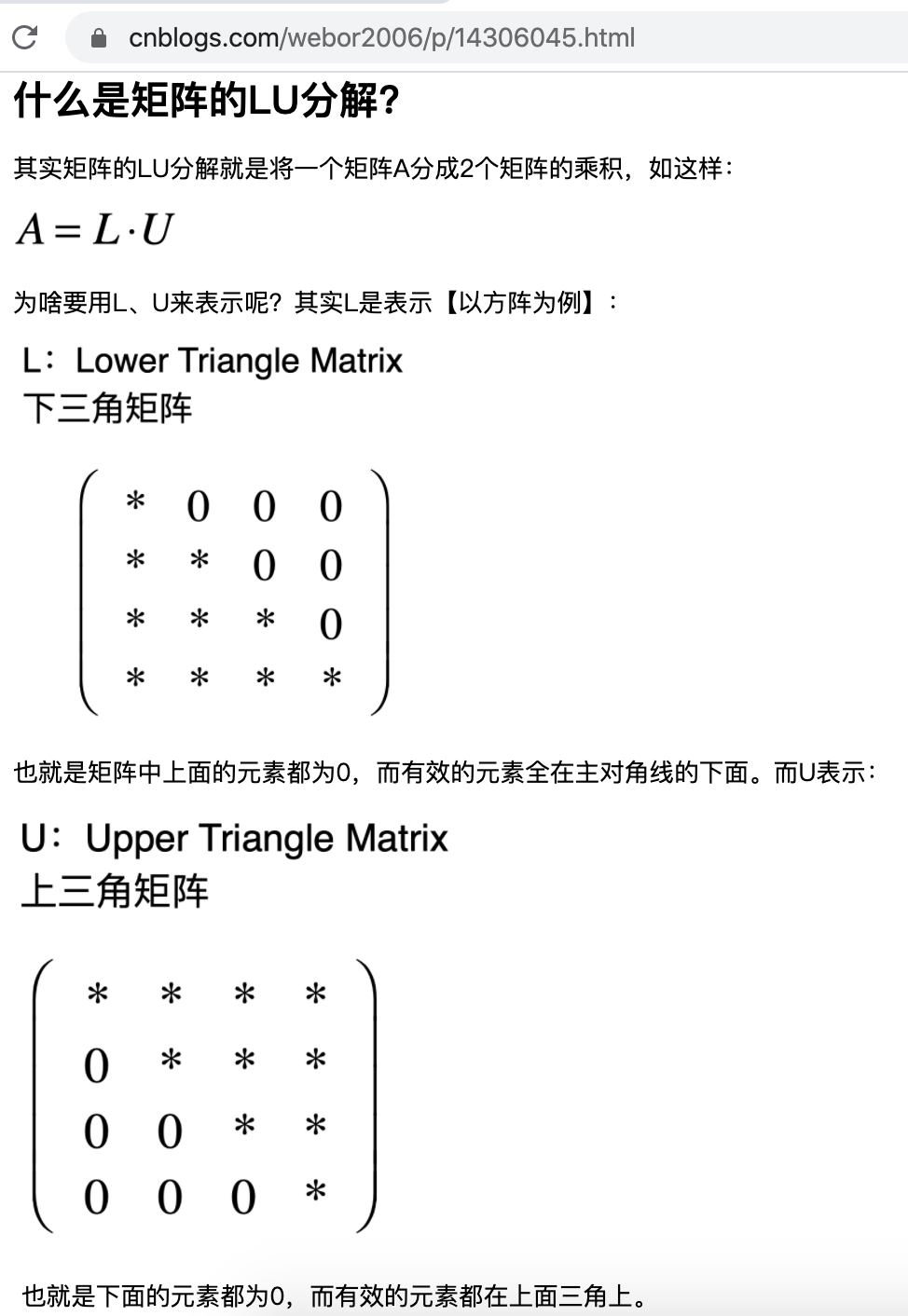
同样的，对于矩阵的QR分解也类似：

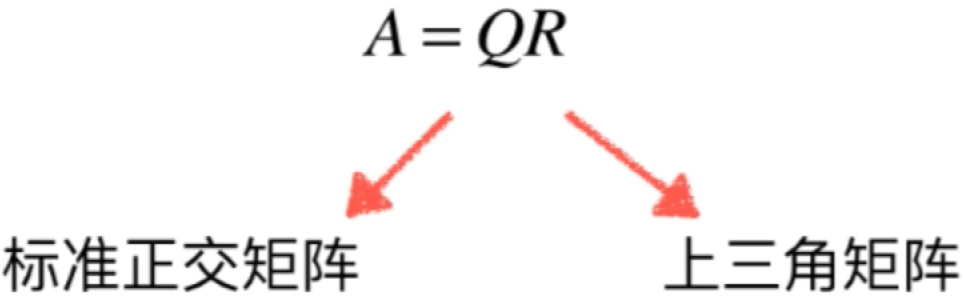
接下来看一下为啥可以这样分解，很多真实世界的问题本质都是Ax=b的线性系统，而如果说A可以分解成QR两部分的话，式子又可以变为：

此时等式两边都可以乘以Q的逆：

而由于Q是标准正交矩阵，所以它的转置就等于Q的逆，所以此时等式又可以变化为：

而由于R是一个上三角矩阵，此时由于是已经做完了高斯消元的过程了，所以就可以倒着推依次将各个未知数求解出来，所以此时就可以非常快的将方程给求解出来了，这也是为啥把一个矩阵A可以进行QR分解的原因，可以让Ax=b这样的线性系统更快地得到求解。

对于Q这个标准正交矩阵肯定是需要对矩阵A进行一个Gram-Schmidt过程，所以其A一定是要求各个列向量是线性无关的，对于QR分解来说其实并不只局限于方阵上，但是这里只针对方阵的QR分解进行一下学习。

QR分解过程【复杂，需要耐心】：

下面来看一下整个的分解过程，假设A的形态为：

然后对它执行Gram-Schmidt过程【其中A中的列向量之间都是线性无关的，这是个大前提】，就得到一组正交基：

具体怎么算的这里再贴一下，上面也已经提及过了：

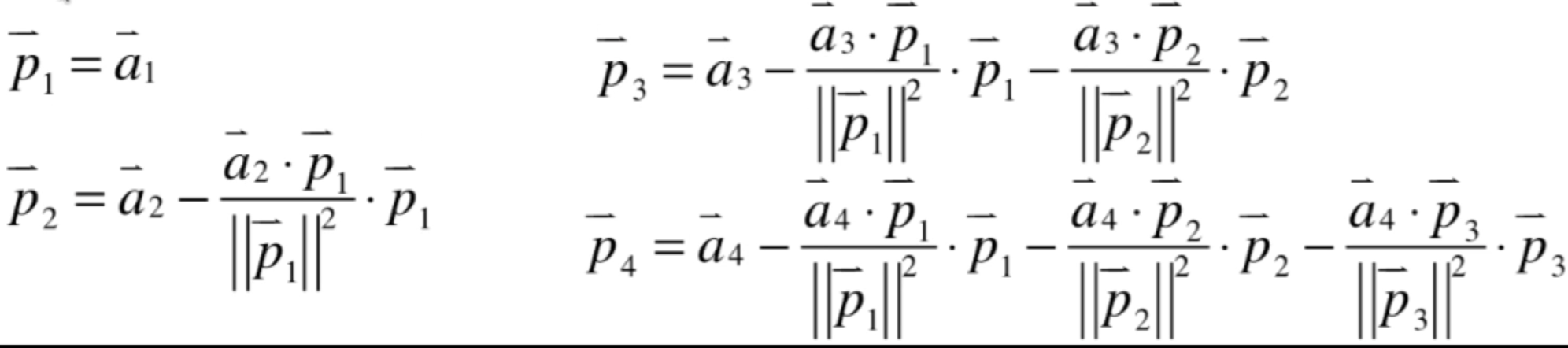
然后再将其规范化得到标准正交基，如下：

下面来看一下A、p向量、q向量之间的关系：

首先：

而由于q1就是p1的单位向量，所以此时等式又可以变为：

这里其实是想关注a向量和q向量之间的关系，其中a向量是A矩阵的一个列向量，而q是标准正交基Q中的一个列向量，而QR分解描述的就是A矩阵和标准正交矩阵之间存在着关系：

那往这个关系上靠，咱们是不是可以把p1的模当成一个系数来对待：

如下：

同样的，对于p2向量来说也有类似的等式：

此时又将这个式子往rq上靠，变换如下：

再来看一个p3正交基向量，是不是同样也可以将其化为rq相关的式子：

依照这个规律，是不是就可以有：

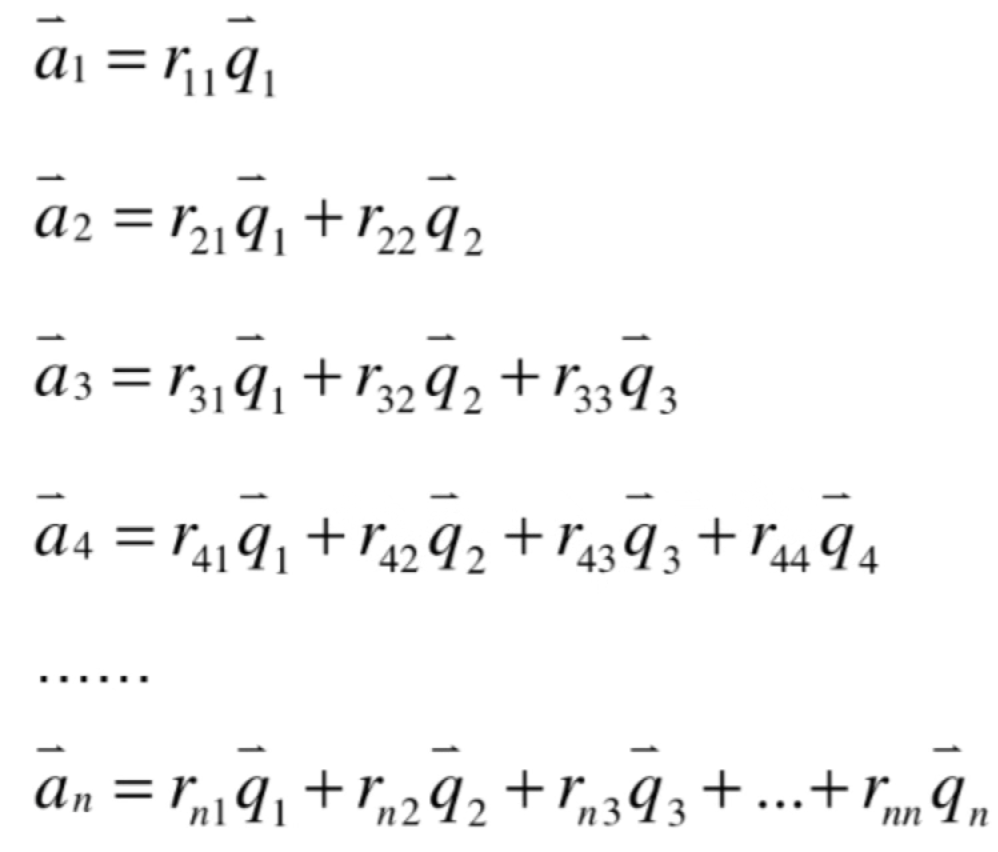
也就是根据标准正交基，就可以反推出矩阵A中的列向量，也就是：

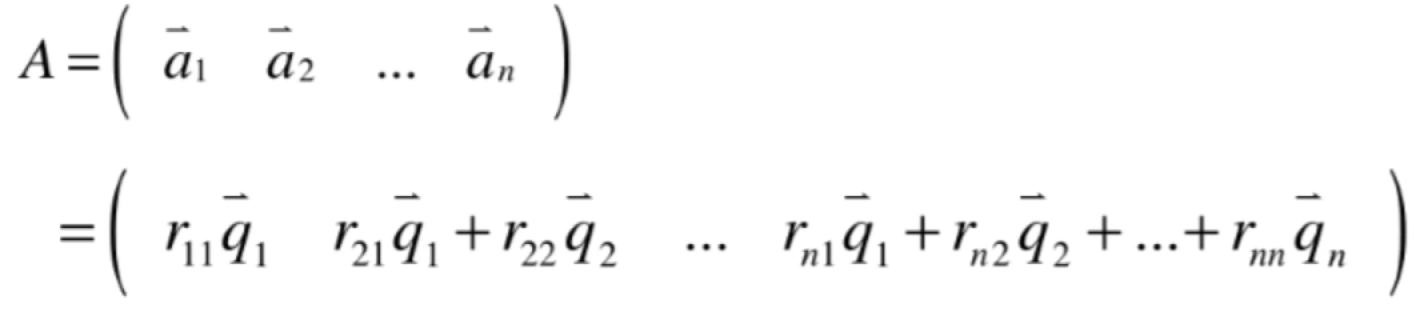
而对于这个矩阵，其实是可以写成n个矩阵相加的形式，如下：

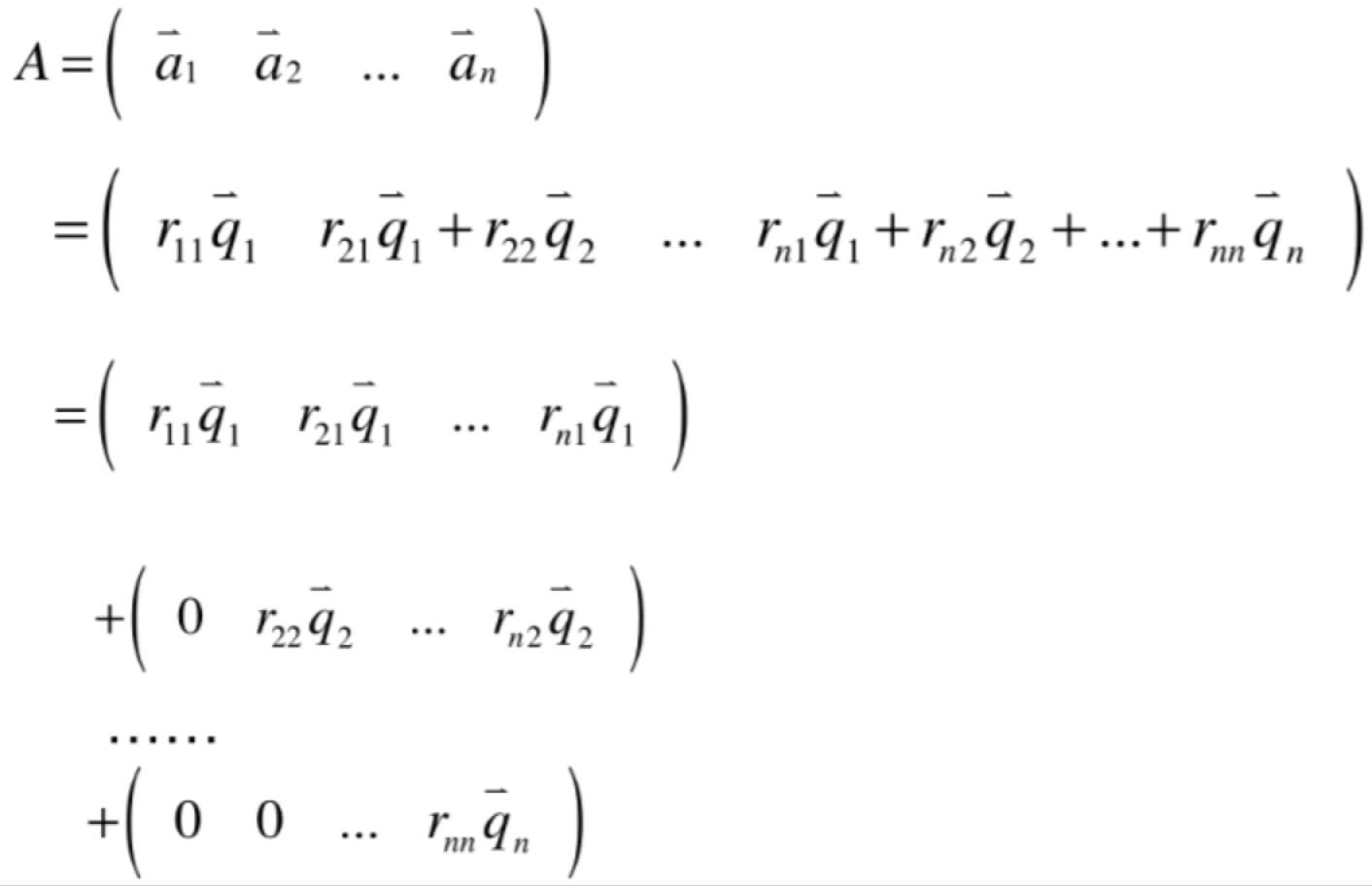
而回忆一个之前学习矩阵乘法以列视角的形式看待会有如下等式：

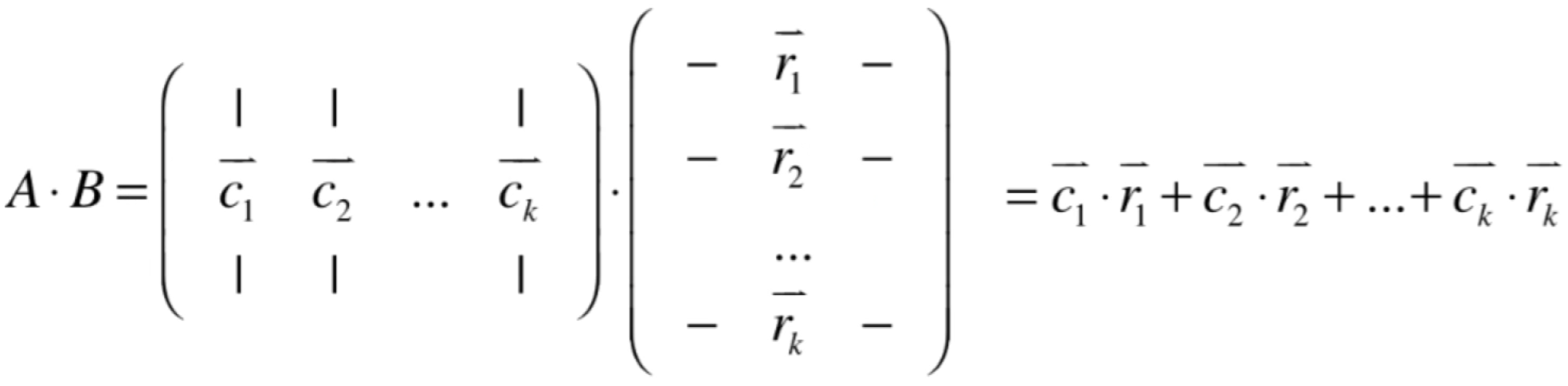
而目前咱们已经把A化成了n个矩阵相加的结果，所以用这个列视角的相乘就可以进一步化为：

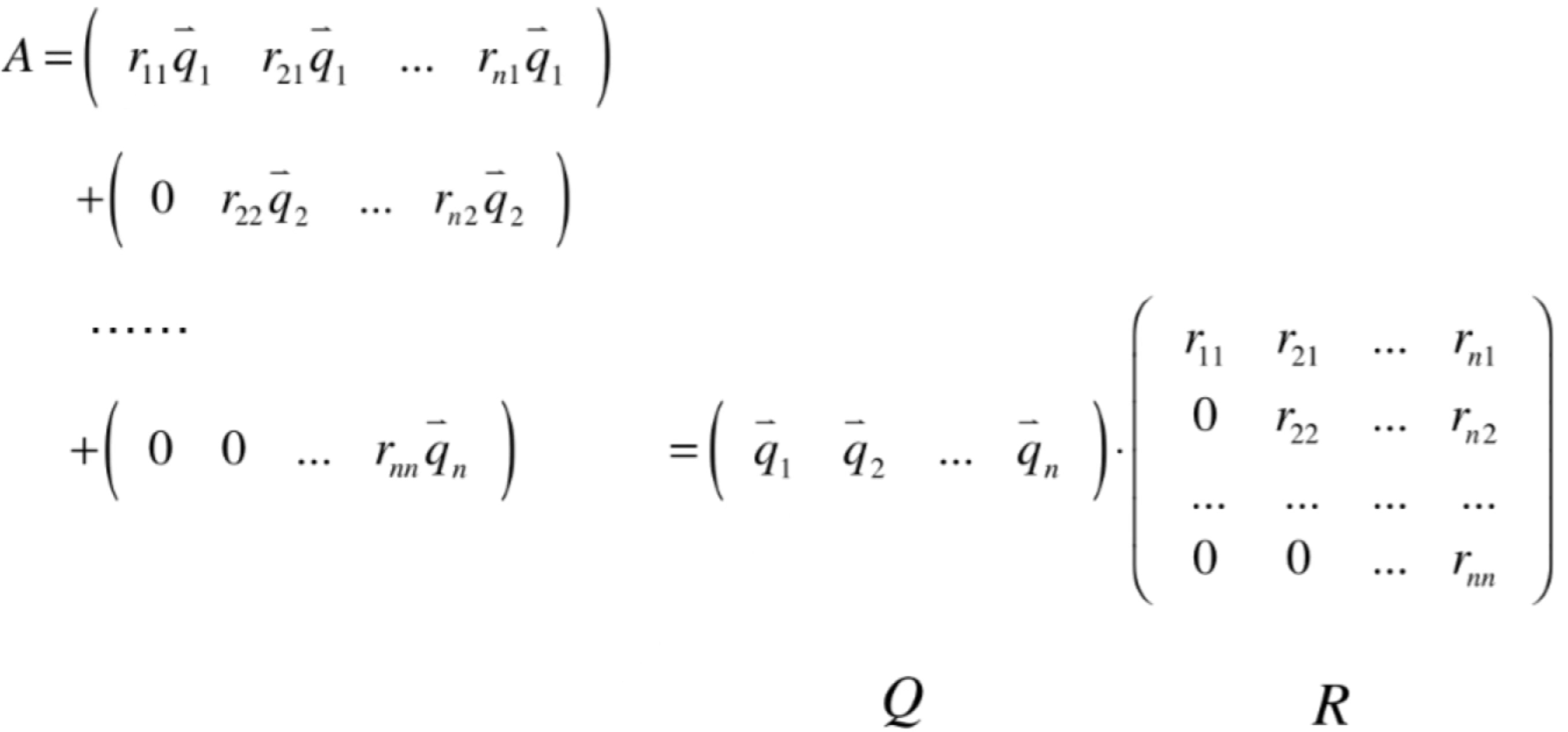
这就化成了QR分解的样子了，其桥梁就是执行Gram-Schmidt过程，其中Q就是标准正交基的向量，而R这个矩阵怎么求呢？其实很简单，回归到QR的式子中：

其中已知了A和Q了，求R还难么？如下：

而Q的逆矩阵又可以根据上面标准正交矩阵的性质：

进一步推出R的求解式子为：

所以对于一个列向量是线性无关的矩阵A的QR分解求解方法就已经搞定了。

实现矩阵的QR分解：

最后咱们回到Python世界中实现一下矩阵的QR分解：

断言方阵：

由于这里只考虑方阵的QR分解，所以这里做一个断言：

对矩阵执行Gram-Schmidt过程：

首先将矩阵的列向量放到一个列表中，因为执行gram-schmidt过程的函数是要求一个列表，如下：

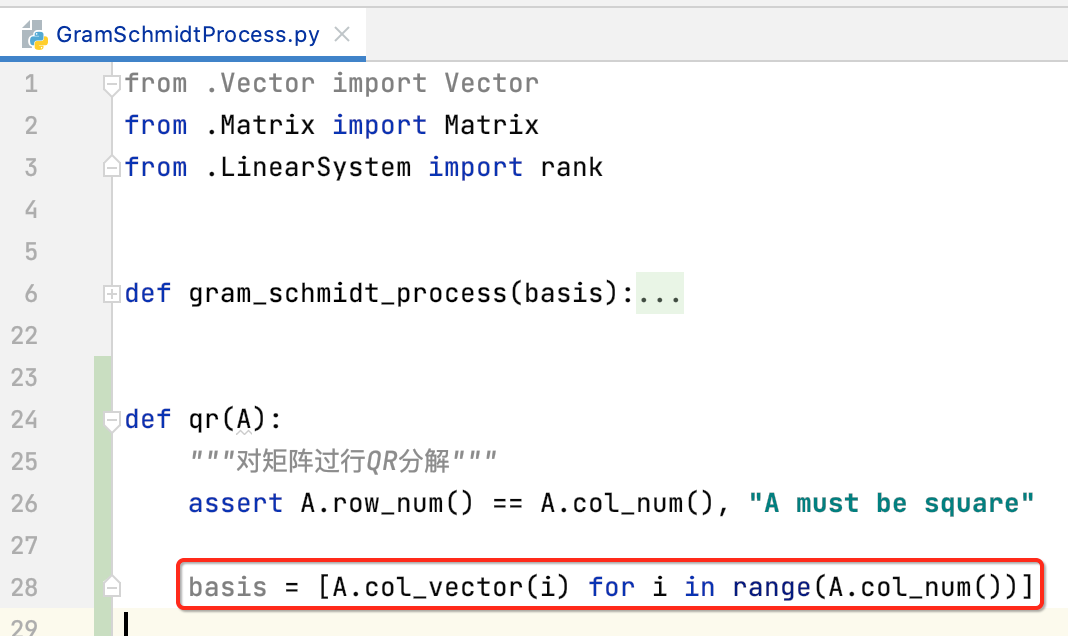
然后执行gram-schmidt过程，求这些向量空间的一组正交基：

求Q：

而QR分解是对标准正交基感兴趣，所以接下来将这组正交基都归一化，如下：

不过，这里有个注意点，要Matrix构造时取出的是它每行的向量进行构造的：

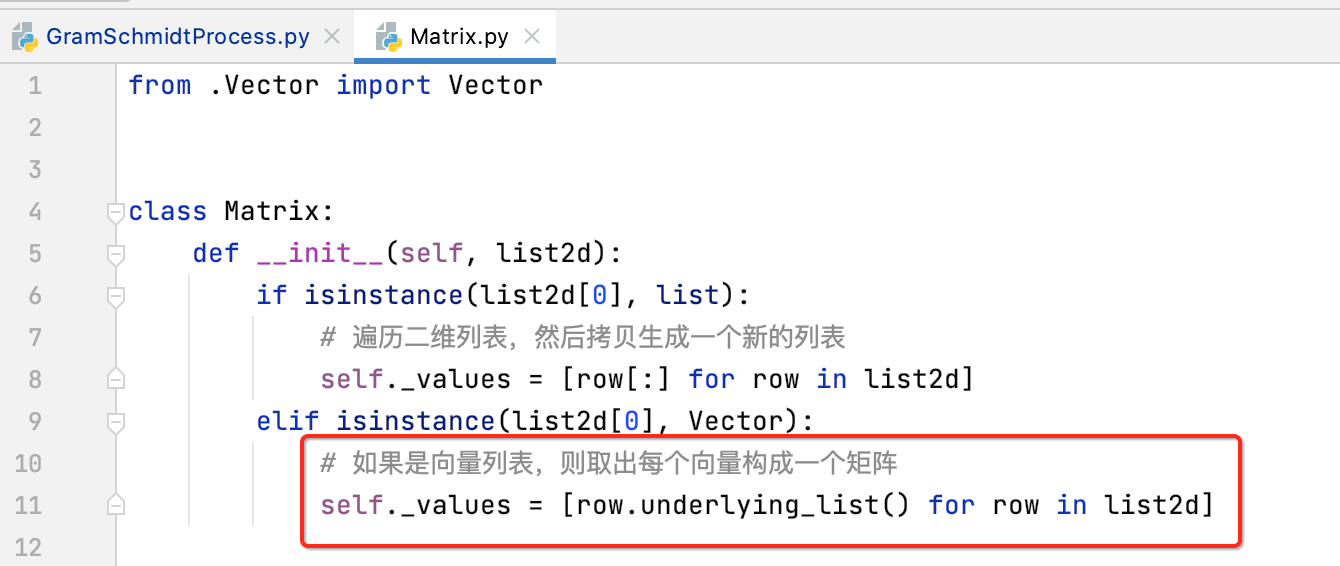
但是！！QR分解的Q是要求以每一列是标准正交向量，所以很简单，咱们来个矩阵的转置既可，如下：

求R：

根据QR分解的公式：

所以求R很简单：

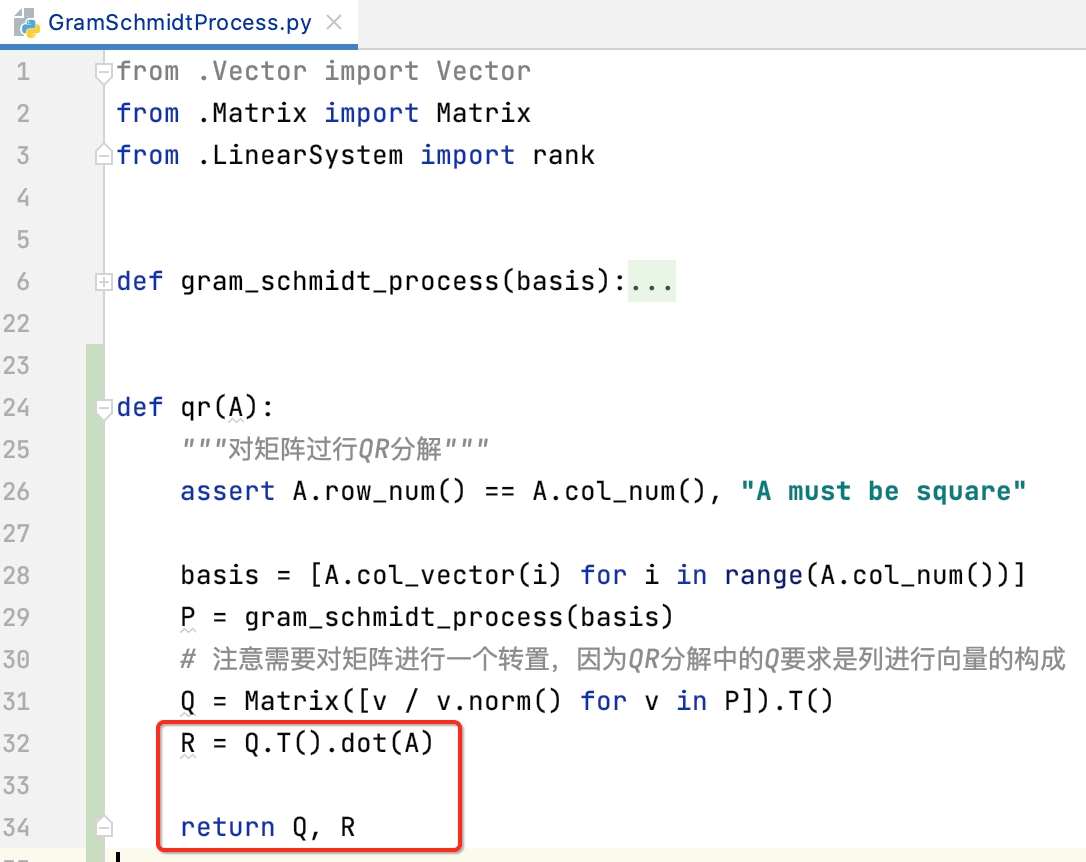
测试：

运行：

/Users/xiongwei/opt/anaconda3/bin/python3.8 /Users/xiongwei/Documents/workspace/python/Play-with-Linear-Algebra/LinearAlgebra/main_qr.py
Matrix([[0.5773502691896258, 0.408248290463863, 0.7071067811865475], [0.5773502691896258, 0.408248290463863, -0.7071067811865475], [0.5773502691896258, -0.8164965809277259, 0.0]])
Matrix([[1.7320508075688776, 1.1547005383792517, 1.1547005383792517], [1.1102230246251565e-16, 0.816496580927726, 0.816496580927726], [0.0, 0.0, 1.414213562373095]])
Matrix([[1.0000000000000002, 1.0000000000000002, 2.0], [1.0000000000000002, 1.0000000000000002, 4.440892098500626e-16], [1.0000000000000002, 2.220446049250313e-16, 2.220446049250313e-16]])


Process finished with exit code 0

木有问题，其中看到R的结果，第一行不是0，第二行为0，第三行的前2行为0等等，刚好跟咱们分析的是一致的，另外Q点乘R的结果就是A，也进一步证明咱们的分解是完美的。

再来测试一个用例：

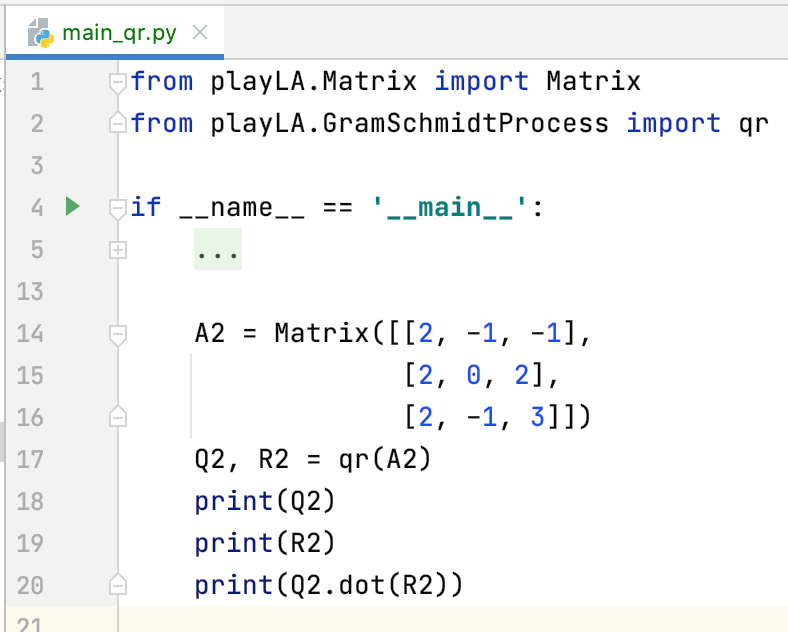
运行结果：

/Users/xiongwei/opt/anaconda3/bin/python3.8 /Users/xiongwei/Documents/workspace/python/Play-with-Linear-Algebra/LinearAlgebra/main_qr.py
Matrix([[0.5773502691896258, -0.408248290463863, -0.7071067811865475], [0.5773502691896258, 0.8164965809277259, 1.1775693440128314e-16], [0.5773502691896258, -0.408248290463863, 0.7071067811865476]])
Matrix([[3.4641016151377553, -1.1547005383792517, 2.3094010767585034], [-2.220446049250313e-16, 0.816496580927726, 0.8164965809277258], [4.440892098500626e-16, -1.1102230246251565e-16, 2.8284271247461907]])
Matrix([[2.0, -1.0000000000000002, -1.0], [2.0000000000000004, -2.220446049250313e-16, 2.0000000000000004], [2.000000000000001, -1.0000000000000002, 3.000000000000001]])

Process finished with exit code 0

木问题。

总结：

最后对咱们这次所学重点进行一个归纳总结：

正交基。
标准正交基。
正交非零向量组一定线性无关。
n个非零正交向量一定是n维空间的基！
如果给定一个空间的一组基，通过格拉姆-施密特过程，就能找到这个空间的一组正交基。
通过正交基，又可以得到标准正交基,其求解很简单：
一维投影
高维投影
标准正交矩阵的重要性质：
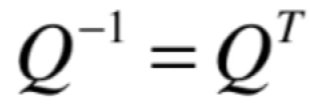
QR分解：

，其中R有求解可以进一步进化：

posted on 2021-02-05 10:47 cexo 阅读(3010) 评论(0) 编辑收藏举报

刷新页面返回顶部

cexo