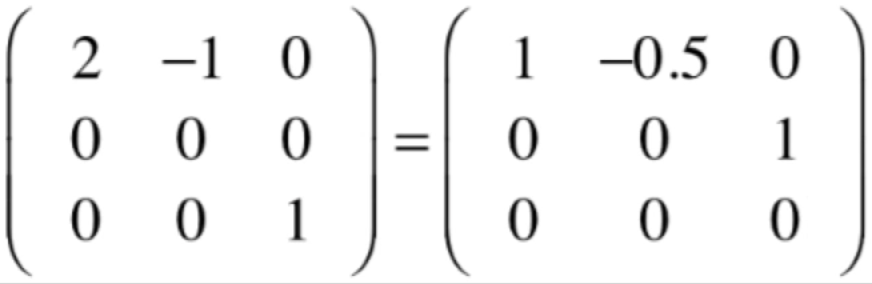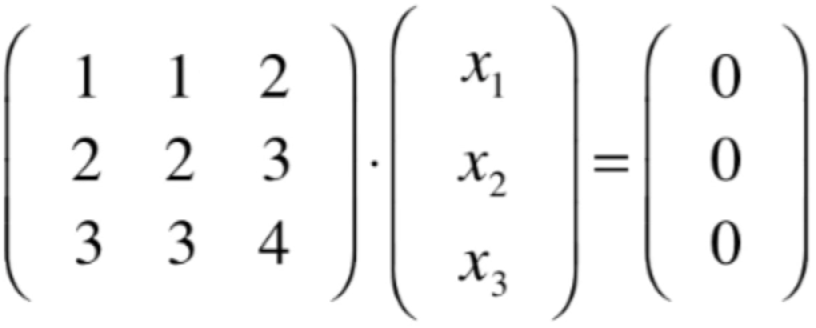线性代数学习之向量空间,维度,和四大子空间
空间:
在上一次https://www.cnblogs.com/webor2006/p/14306046.html学习了诸多在线性代数中非常核心的概念(线性组合、线性相关、线性无关、生成空间,空间的基...),这次则继续学习重要的核心概念(空间、维度、四大子空间)。在之前的学习中用到了很多的“空间”这俩词,比如二维空间、三维空间,n维空间,但是一直还木有严谨的对它进行定义,而数学又是一门非常讲究严谨的学科,所以这次专门针对“空间”的概念进行一个学习。
什么是空间?
空间是一个集合,通常叫这些空间为欧几里得空间,它是有序实数元组的集合,比如:
(6,666)属于二维欧几里得空间【对于上面的”有序“这个修饰词也很好理解,因为(666,6)表示的是二维空间的另一个点】,其中用这个符合来表示:![]()
(3.14,0,sqrt(2))属于三维欧几里得空间,其中用这个符合来表示:
![]()
如果是n维欧几里得空间,则表示为:
![]()
其中对于欧几里得空间概念中的"有序实数元组"有点绕,所以也可以简单说欧几里得空间是点集;而以向量的视角来理解又可以说欧几里得空间是起点到原点的向量集合;
什么是向量空间?
由于空间【为了叙述方便,通常将欧几里得这四个字给省略掉】是一个集合,对于线性代数而言不关心杂乱无章的集合,而只关心具有某些特殊性质的空间---向量空间。向量空间就是指空间中的元素是"向量",关于向量咱们已经非常熟悉了,不过这里还是以严谨的态度对它再做出一个定义【当然是数学科学家们给出的】,对于向量而言:
我们必须定义两种运算:加法和数量乘法,回忆一下之前所学向量基本运算:
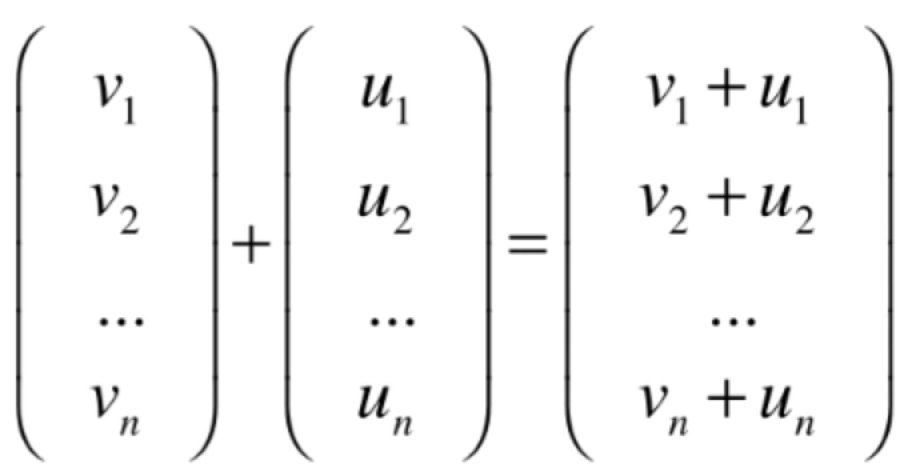
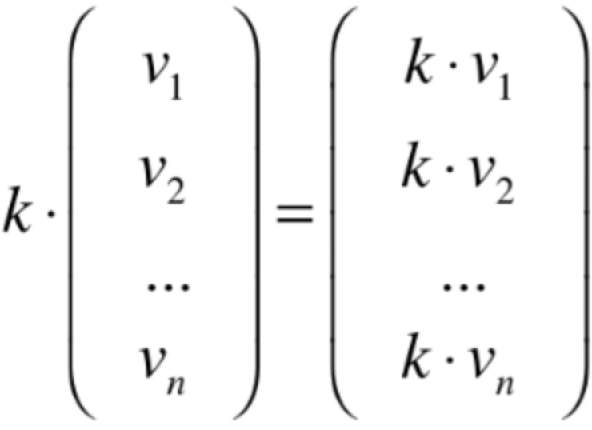
另外只定义这俩运算还不够,因为有可能胡乱定义的对吧,所以还必须满足十条性质【不需要记,有个了解既可,因为本身我们在线性代数中所学的向量本身就具备有这十条性质了】:
1、如果u,v都属于v,则u+v属于v;
2、如果u属于v,k是一个实数,则ku属于v;
这两条是向量的核心性质,通常在数学上又被称为封闭(closure),对于这个封闭也很好理解,也就是对于上面两个操作之后的向量还是在该空间中,不管怎么算都逃不过这个空间。举一个简单不满足封闭性的空间例子,比如对于一个整数集合的加法是满足封闭性的,因为整数+整数一定还是整数,但是对于除法是不满足的封闭性,整数/整数可能会是小数。
在此基础上,其它剩余的性质就比较好理解了:
3、加法交换律:u + v = v + u;
4、加法结合律:(u + v) + w = u + (v + w);
5、存在O【零向量】属于向量空间,使得u + O = u;
6、对于每一个u存在-u,使得u + (-u) = O;
7、如果u属于V,k是一个整数,则ku属于V;
8、数量乘结合律:(kc)u = k (cu);
9、数量乘分配律:k(u + v) = ku + kv;
10、1 * u = u;
而对于我们所说的欧几里得空间:
![]()
就是向量空间,因为它满足向量空间的定义,因为本身对于向量的两个基本运算【向量的加法和数量乘法】就已经满足了,对于剩下的8条性质也可以由这俩基本运算推导出来,其实在之前向量的学习过程中已经推导过的,其中对于十条性质中有两个稍特殊一点,第一个是在欧几里得空间中一定是有一个零向量,如下:

有序实数元组中每一个元素都为0,另一条性质中的第6条【对于每一个u存在-u,使得u + (-u) = O】,它长这样:
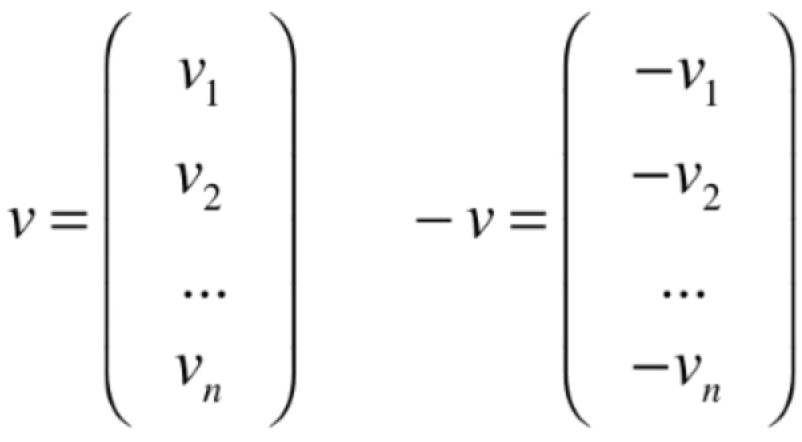
这里要注意:向量空间不仅仅只有欧几里得空间,世界上有无数的向量空间,每一个不同的向量空间其中所对应的元素也是不一样的,所以对于不同的向量空间的基本运算其实也是不一样的,所以下面来对非欧几里得空间进行一个了解。
广义向量空间【了解】:
先来回忆一下向量空间的定义:
向量空间是指一个集合,集合中的元素可以定义两种运算:加法和数量乘法,使得满足十条性质。
其中欧几里得空间就是向量空间,我们通常说起向量,就是指欧几里得空间中的元素。为了区别,通常把非欧几里得空间的向量空间,称为广义向量空间。那这些广义的向量空间长啥样呢?下面举个例子:
方阵:
对于所有的2*2方阵,其实就构成了一个向量空间,因为它的加法就是满足矩阵加法,而数量乘法就是矩阵的数量乘法, 另外还遵行另外的8个向量空间的性质的,所以说这个向量空间中的元素不再是向量了,而是一个2*2的方阵了,同样的可以上升到n阶也是满足的,也就是所有的n阶方阵其实都可以构成一个向量空间,注意:这个向量空间中的n阶的n必须是一样的,如果像2*2和方阵和3*3的方阵构成的空间就不是向量空间了。
矩阵:
其实进一步的,像所有的2*3的矩阵,也可以构成一个向量空间。同样的对于所有的n*m的矩阵也可以构成一个向量空间。
多项式:
所有的多项式,也可以构成一个向量空间,如:
![]()
其中加法就是多项式的加法;而乘法就是多项式乘以一个数。其中要注意这里对阶数没有要求,上面式子是一个p阶的多项式,而它可以跟非p阶的一起构成向量空间的。
函数:
所有的某类函数,也可以构成一个向量空间,这块就不举例子了,了解一下。
那有木有不能形成一个向量空间的例子呢?有!!!看下面:

很显然这样的矩阵【主对角线之外都是0】可以形成一个向量空间。但是!!
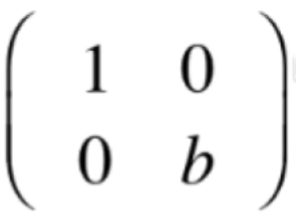
它形成不了向量空间的,因为如果这样的矩阵相加第一个元素就变为2了,也就是不在是同一个空间上了,所以就不满足向量空间的定义了。
子空间:
先来看一下子空间的定义:假设V是一个向量空间,如果S是V的子集,且S还是一个向量空间,则称S是V的一个子空间。 比如:
所有的2阶方阵都形成了一个向量空间,我们用V表示,而所有如下形式的方阵也可以形成一个向量空间,我们用S来表示:
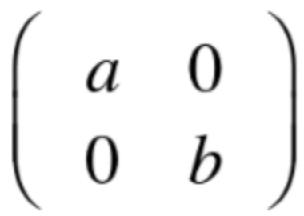
很明显S就是V的子空间。但是!!在上面也举了一个这样的方阵是构成不了向量空间的,将其记为S:
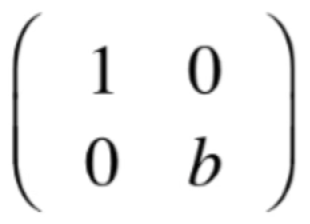
此时S就不是V的子空间了。所以对于子空间的定义可以是如下:
假设V是一个向量空间,如果S是V的子集,且S还是一个向量空间,则称S是V的一个子空间;
但是标红的S要判断它是否是向量空间则需要看向量空间的十条性质啊,其实不用这么麻烦,可以简化成下面这个定义:
假设V是一个向量空间,如果S是V的子集,且S对加法和数量乘法封闭【满足这两条就一定满足向量空间的十大性质】,则称S是V的子空间;
那为啥只要S对加法和数量乘法封闭满足就能说明这个S就能满足向量空间的十大性质呢?下面证明一下,目前对于十大性质已经满足了这两条:

其中根据2个基本运算其实是可以很自然的推出其它6个性质,因为本身V是一个向量空间就已经满足各个加法和数量乘法的各个运算的性质了,而由于S是V的子集,所以对于S上的加法和数量乘法是没有变化的,依然是满足剩下的6个性质,所以最后只剩下对于5、6条进行证明就可以说S这个子集就满足向量空间的十大特性了,不过要来证明最后的这俩特性得先绕一下小弯,先来看下面的东东。
向量空间的性质:
这里先回到向量空间的性质上来,若V是一个向量空间,则满足:
- 存在O零向量属于向量空间,使得u + O = u;
- 如果向量u属于V,k是一个实数,则ku属于V;
那如果k=0,是不是0u = O(零向量)?如果O零向量用欧几里得空间来理解就是向量里面的元素全为0,这个等式很容易推出来,但是!!!目前是站在更一般的空间角度来思考这个问题,所以下面来证明一下0u = O:若V是一个向量空间,则:0u = O:
证明:
1、0 = 0 + 0,这个没啥可说的;
2、此时等式两边同时乘以u,就有:0u = (0 + 0)u;
3、而根据分配率【向量空间十大性质第9点】,右边的又可以变为:0u = 0u + 0u;
4、根据向量空间的第6条性质:向量空间V中的每一个向量u,都存在-u,使得u + (-u) = O,所以可以假设对于0u,存在-0u,使得0u + (-0u) = 0,所以等式两边都可以加上-0u,如下:0u + (-0u) = 0u + 0u + (-0u),之前的要这么绕,就是为了往0u = O这个待论证的等式上靠,所以此时就可以变为: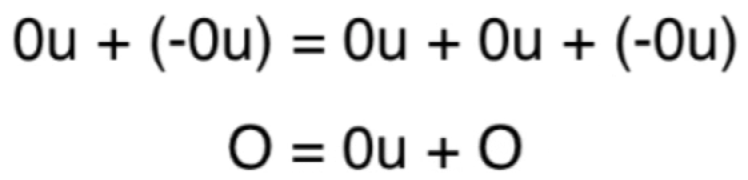
5、而等于右边的(0u + O)= 0u,所以等式就可以化为O = 0u,而左右交换一下,不就是0u = O了么?
这样求出来的这个等式有啥意义呢?就可以很轻松的求解出向量空间中的O零向量了,也就是用0乘以空间中的任何一个向量就可以得到O零向量了。
下面再来看一个性质,对于V是一个向量空间,则满足:
- 对于每一个u存在-u,使得u + (-u) = O;
- 如果向量u属于V,k是一个实数,则ku属于V;
其中有一个新的性质,就是-u = -1u,下面来证明一下:
若V是一个向量空间,则:-u = -1u:
证明:
1、这里看u + (-1u)它的结果,根据向量空间的最后一条性质就可以变成:1u + (-1u)。
2、根据分配率又可以变为:(1 - 1)u。
3、此时就变为0u。4、而根据上面所证明的0u=O,所以就可以得到u + (-1u) = O,而根据十大性质的第6条u + (-u) = O,是不是此时就可以证明-u = -1u了?
这样求出来的这个等式有何意义呢?同样的根据这个等式就可以很轻松的求解出向量空间中负向量是多少了,也就用-1*向量既可。
好,知道了上面标红的两条性质之后,接下来就可以回到子空间的概念待证明的地方了:

此时需要根据S对加法和数量乘法封闭来证明向量空间的最后两个性质也能成立,下面来证明一下【这块比较绕,一定要结合上面论证的两个红色的关于向量空间的新性质来进行理解】:
对于u属于S,
5、存在O【零向量】属于向量空间S,使得u + O = u;
由于u属于S,很明显0u也属于S,而根据上面的新的性质0u=O,是不是说明O零向量属于S。此性质就得证了。
6、对于每一个u存在-u属于S,使得u + (-u) = O;
同样的,由于u属于S,那-1u也是属于S,而根据上面的新的物质-1u=-u,那也说明-u也属于S。此性质就得证了。
此时S已经就满足向量空间的十大特性了,而由于S是V的子集,V本身也是一个向量空间,那么S就是V的子空间了。这里用了一些论证的过程,其实不用太过在意推论过程,这里记住如果S是V的子集,然后对于S不用一一来验证它的向量空间的十大特性,只需要满足对加法和数量乘法封闭这两条特性,就可以很安全的说S是V的子空间【子空间的意思就是它也是一个向量空间】。另外还要知道这么个结论:
“如果V是一个向量空间,那么V的任何子空间都一定包含O(零向量);对于V的子空间S,如果u属于S,则-u也一定属于S。”
直观理解欧几里得空间的子空间:
上面咱们已经对于子空间有了一定的理论上的了解之后,下面回到二维坐标平面直观的感受一下子空间,对于欧几里得空间的零向量为x轴和y轴所交叉的位置:
而在这空间中任意拿到一个向量u:
就一定能找到和它反向的向量-u,如下:
接下来看一下什么是子空间:
过原点画一条直线,所以落在这直线上的点所对应的向量都在这条直线所表示的子空间中,比如:
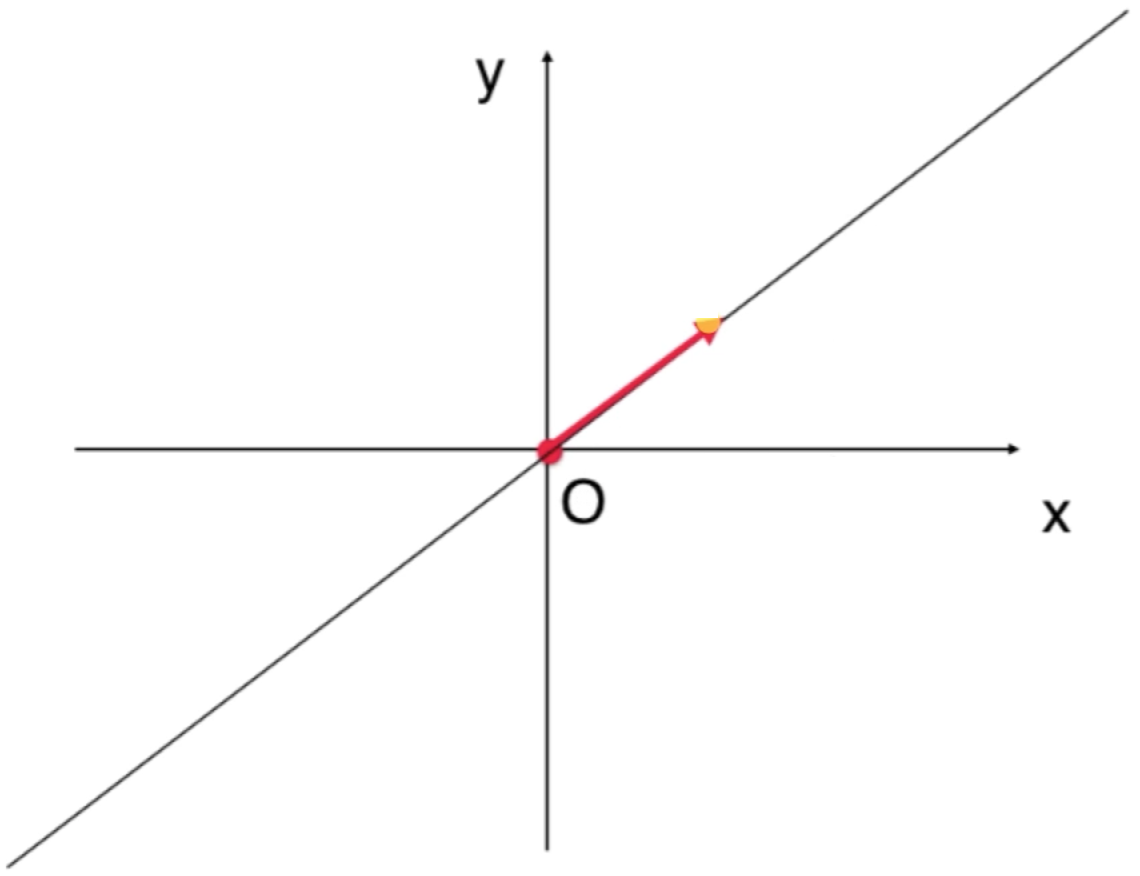
很显然对于在这直线上的所有向量都是对加法和乘法封闭的,因为在这直线上任意取一个向量对其进行加法或者一个数量乘法肯定也还是在这条直线上,因此!!我们就可以说这条直线是整个二维欧几里得空间的子空间。
问题一:那是不是二维平面上所有的直线都是欧几里得空间的子空间呢?
答案是不是的,比较咱们让这条直线稍稍挪动一下位置让其不过原点了:
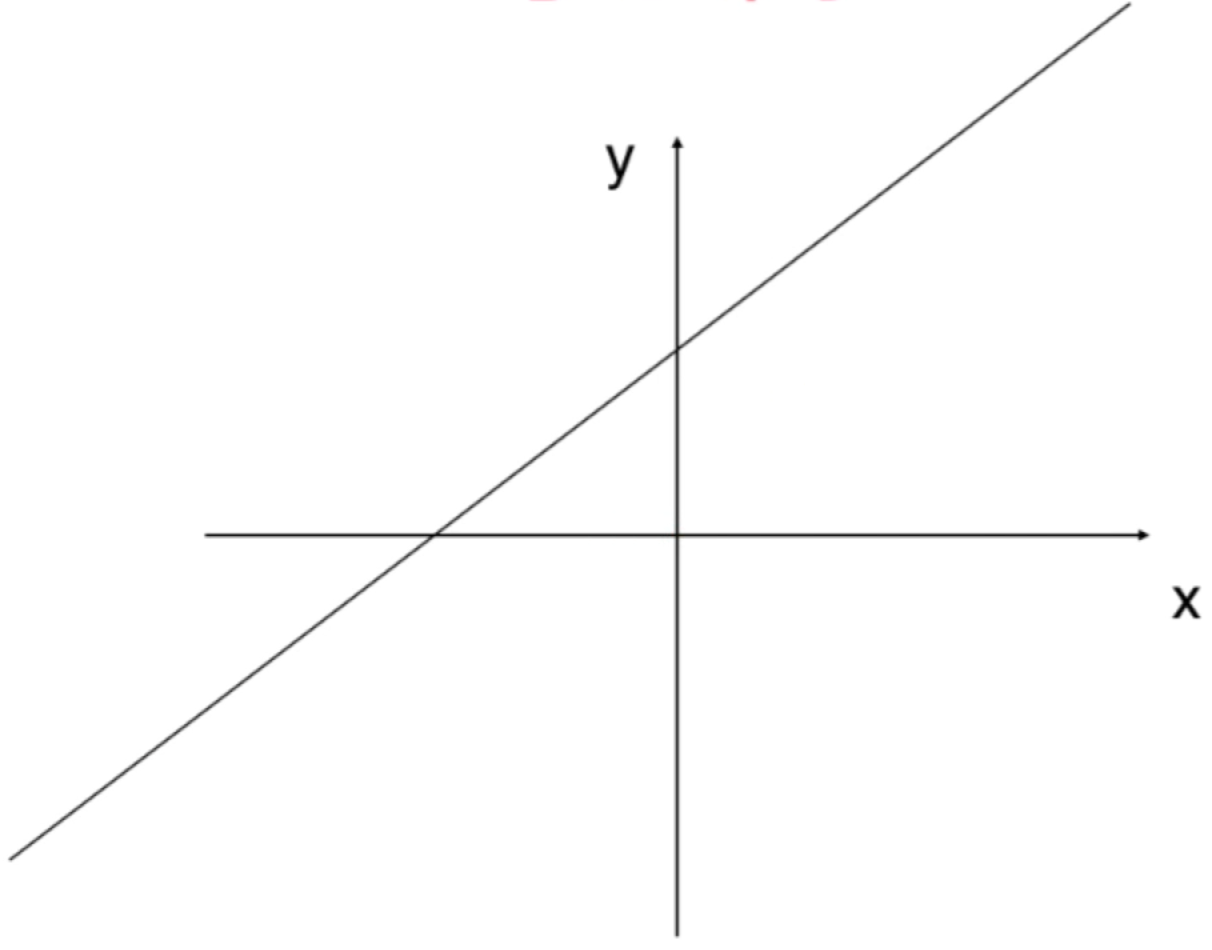
很显然这根直线也是二维平面的一个子集【注意:此时还不知道它是不是它的子空间】,也就是这根直线上所有的向量也都在这个平面上,注意加粗的这句话,此时在欧几里得空间中对于该直线上所有的向量是指从原点到这根直接上的点的有向的线段,比如以下两个向量:
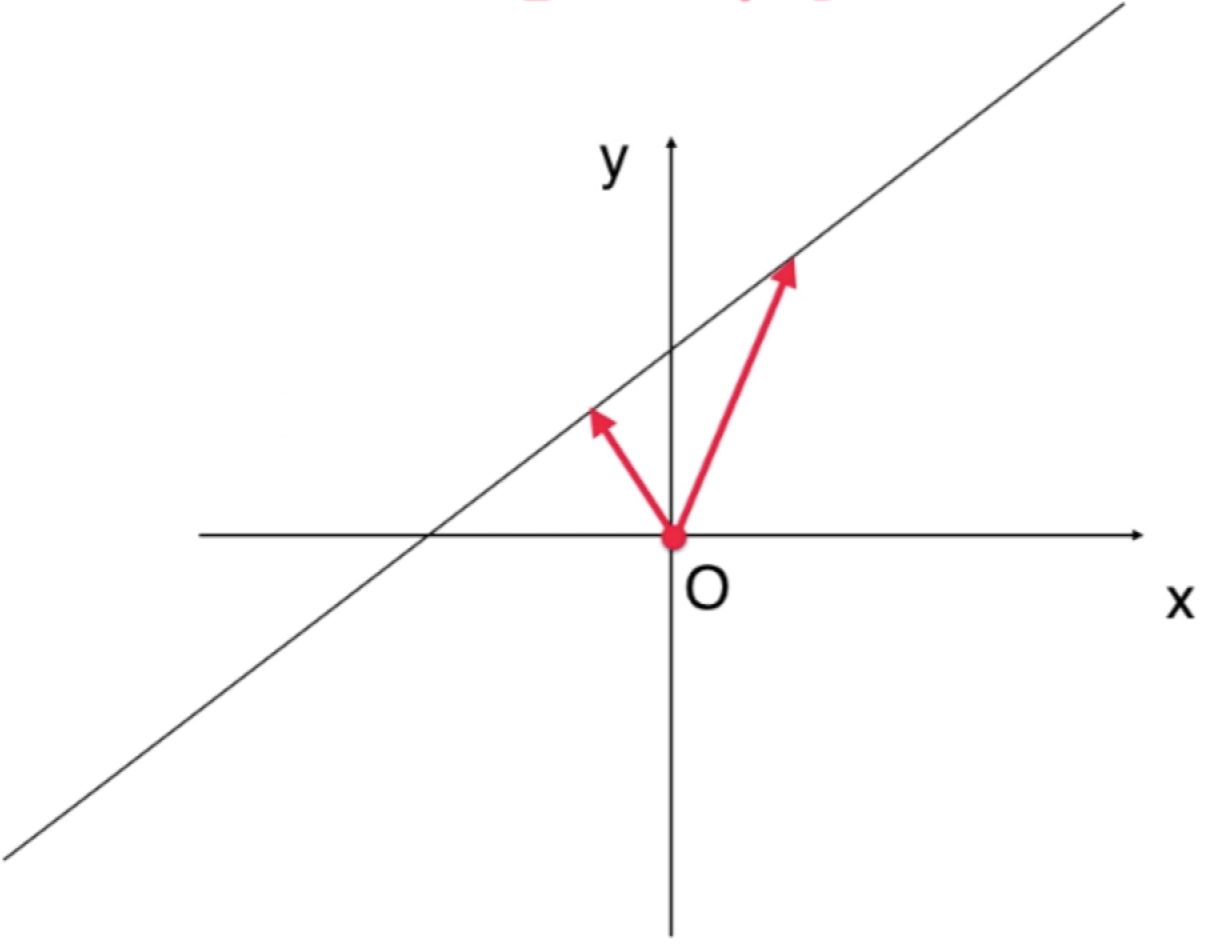
这样一画出来是不是就可以看出这两个向量对于加法是不封闭的,因为这两个向量加法之后的向量是长这样:
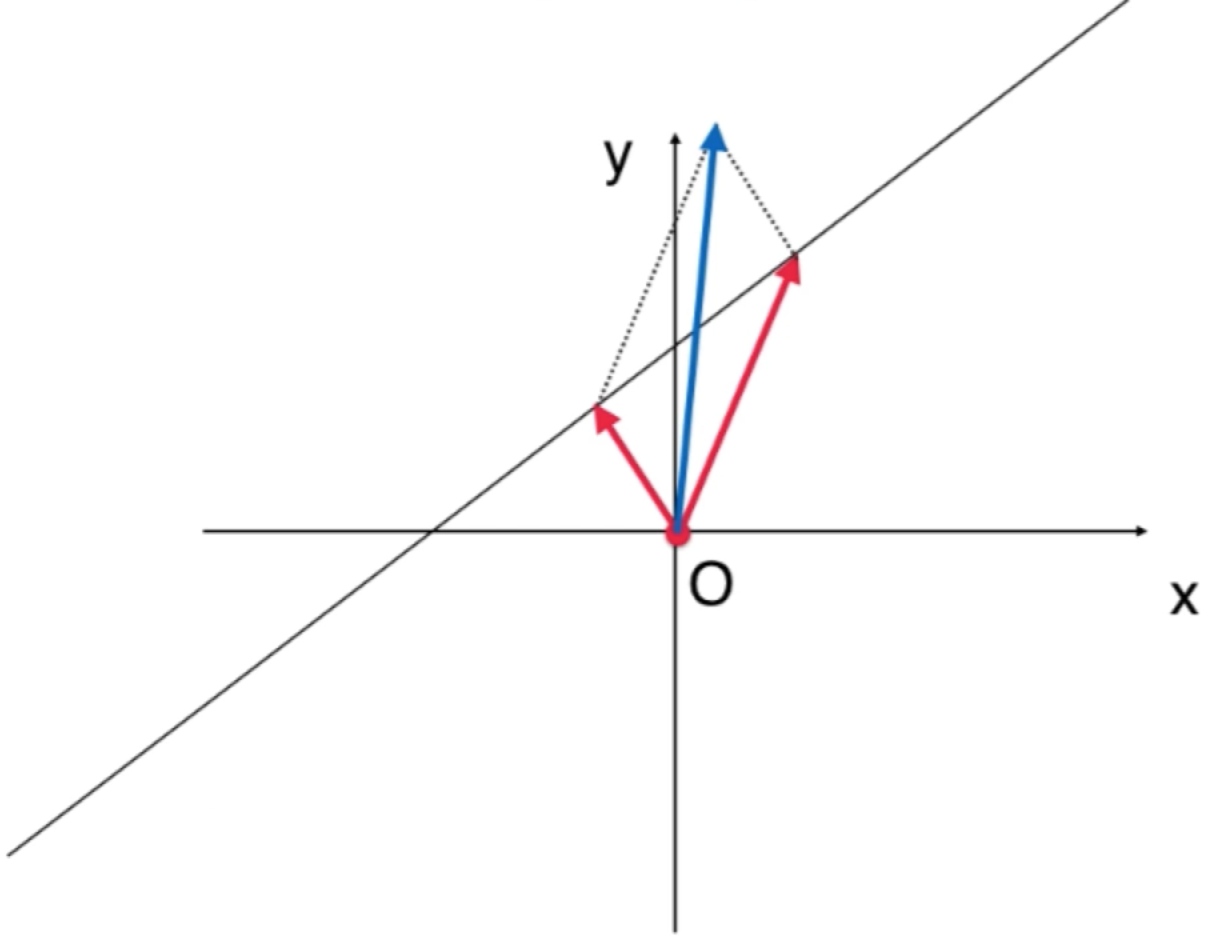
所以很显然这根直线确实是一个空间,并且这个空间上所有的元素确实是欧几里得空间所对应的一个“子集”,但是!!!我们不能说这根直线是欧几里得的一个子空间,因为这个空间根本不是一个向量空间,对于加法根本不封闭,同样的对于向量的数量乘法也不封装,比如咱们对其中一个向量乘以一个负数,得到的结果如下【如绿色的向量】:
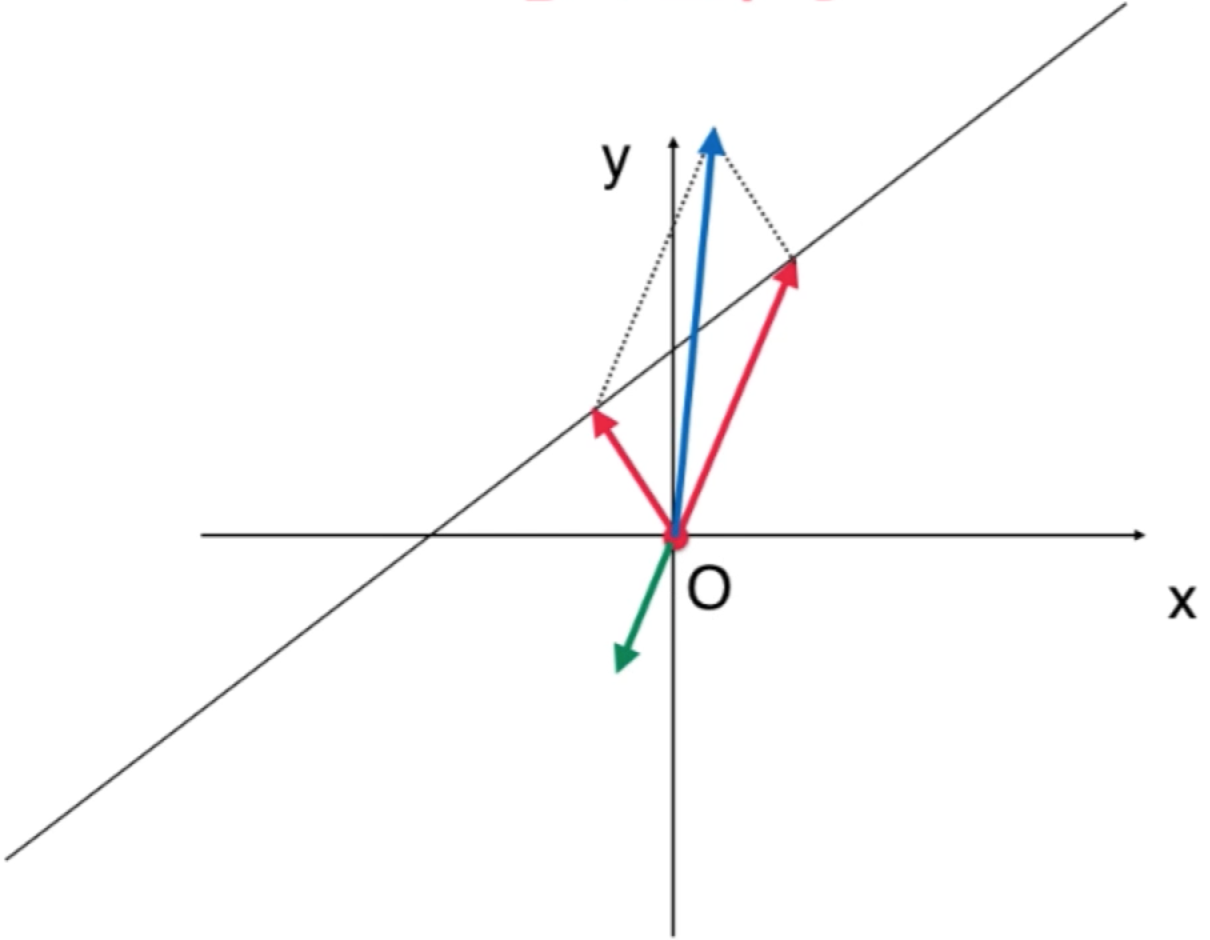
既然对于加法和数量乘法都不封闭,很显然足以说明该空间不是一个向量空间,就更别谈子空间啦~~另外从上面推出的一个向量空间的性质:
![]()
从图中可以看出,这根直线压根不包含O(零向量),所以也能证明出该直线空间不是整个欧几里得的子空间。
问题二:那是不是说只要包含O(零向量)的空间就一定是子空间呢?
答案也是不一定的,比如说这样子的:
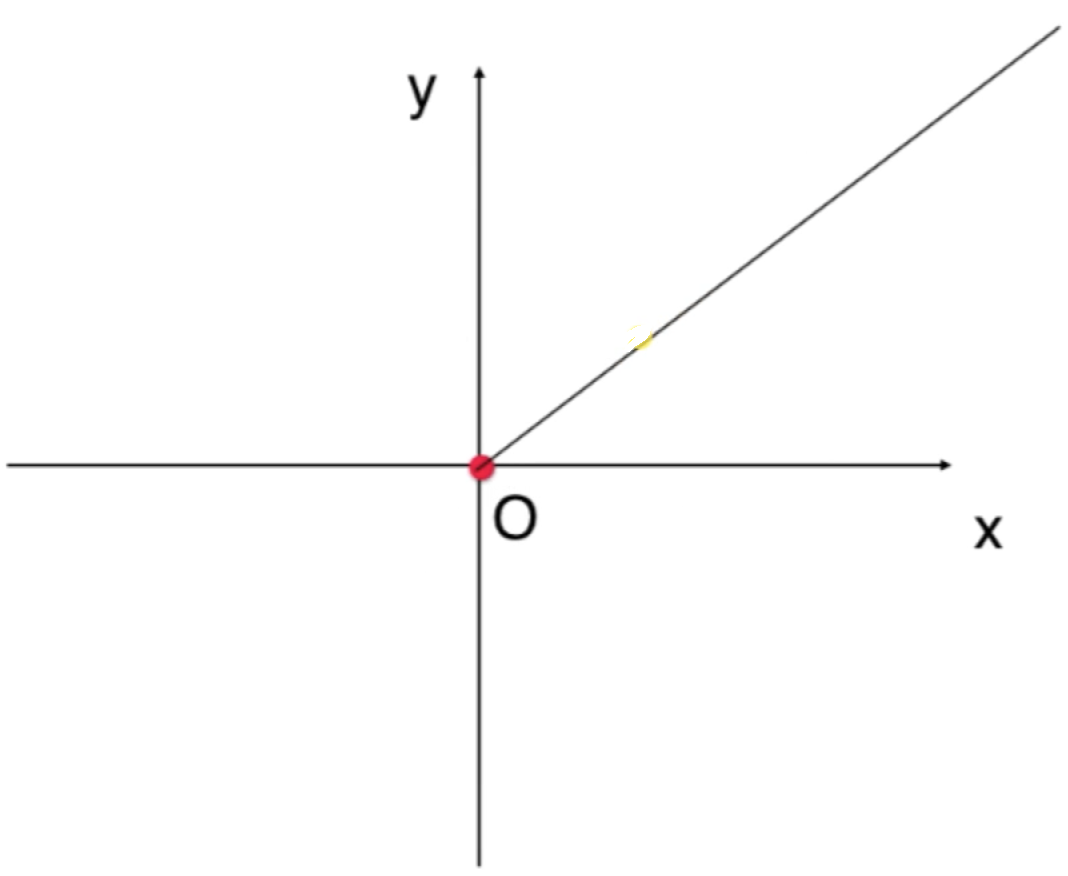
是从O为原点空间发射出去的一根射线,很显然它是二维空间中的一个“子集【一定要注意措辞,子集非子空间】”,那它是不是一个子空间呢?那下面来看一下它是不是对于加法和数量乘法封闭,很显然对于加法是封闭的,在这根射线上任取一个向量:
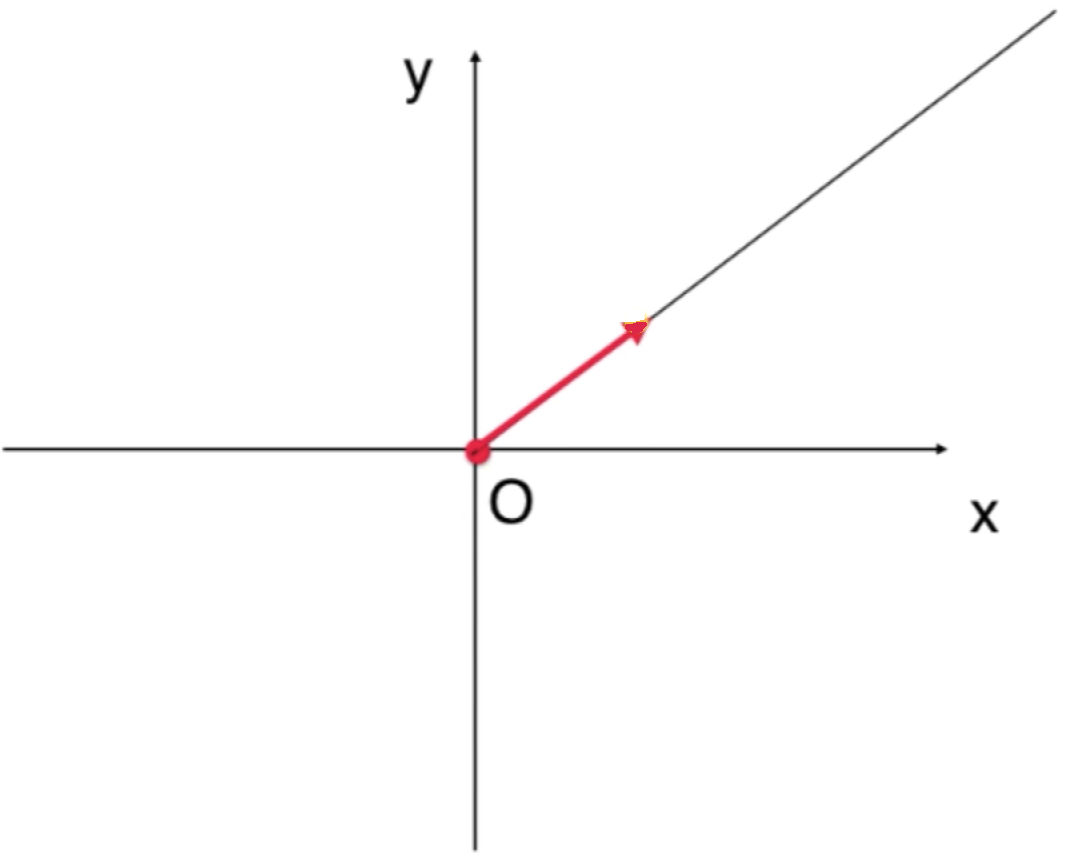
随便取2个向量相加还是在这个射线上,但是!!!数量乘法就不满足封闭性了,乘以负数就可以看出了【蓝色向量】:
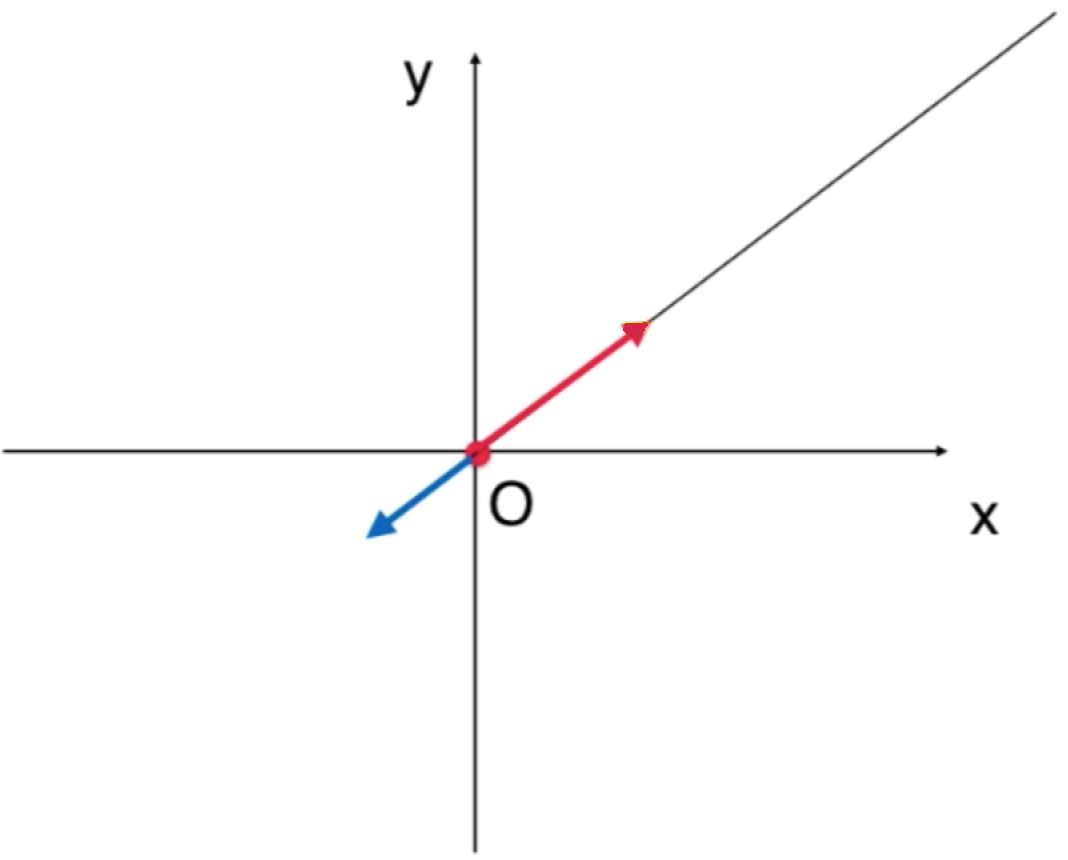
所以从这点就可以看出这根直线所代表的空间不是子空间,不过从上面所推出向量空间性质的这点也能看出来:
![]()
很显然咱们的-u不属于这根直线所代表的空间中,这样就对咱们上面推出的向量空间的性质有了一个更加直观的认识,另外对于过原点的子空间从维度角度也可以进一步直观理解:

很显然这根直线是一个一维平面的,而整个欧几里得是一个二维平面,很显然一维平面是二维平面的一个子平面,也能对于这个“子”有一个直观的认识。
那对于三维空间呢?其实是过原点的一个平面就是三维空间中的一个子空间,对于平面上所有的向量一定是满足加法和数量乘法的封闭性的【二维的平面】;同样的对于过原点的一条直线也是三维空间的一个子空间,因为直线上的向量对于加法和数量乘法也是封闭的【一维的直线】;甚至对于原点本身也是三维空间的一个子空间,因为原点本身就是由(0,0,0)构成的,而它里面取出一个元素也还是(0,0,0),那很显然对于加法和数量乘法也都是在这个(0,0,0)的集合本身中,所以原点也是三维空间的一个子空间【原点】;从这个阐述可以看到,对于三维空间来说,它的子空间可以是二维的平面 、一维的直线,原点,那么对于N维空间也可以推出:
过原点的一个m维空间(m < n),是n维空间的一个子空间。
对于子空间由于它也是一个向量空间, 这使得在向量空间中的所有性质都适用于子空间,而对于子空间最典型的应用就是机器学习的算法【关于机器学习未来有时间一定要学习学习,逼格好高的样子】,因为在机器学习时有可能面对数据的维度太高了,通常需要做一步降维操作,而这个降维操作通常就是高维数据所代表的空间找到一个子空间,这些数据在子空间也能很好的找到它们的位置 ,同时信息也没有丢失,这样很多时候就只需要研究子空间就可以了,而不用管复杂的高维空间,因为子空间维度低相对而言也要简单很多,计算速度也会更快性能也更好。
维度:
在之前线性代数的学习中通常都是以二维空间,三维空间或者是n维空间视角来进行研究,但是到底啥是维度呢目前一直木有严谨数学上的定义,所以这里从线性代数更加广义向量空间的角度来定义一下维度。
先给一个大前提说明:以后说到“空间”一词记得就是指的“向量空间”,而向量空间最常用的一种就是我们一直在用的“欧几里得空间”,所以以后线性代数的学习一说到“向量空间”如果没特殊说明也是指的“欧几里得空间”。
还记得之前https://www.cnblogs.com/webor2006/p/14306046.html学习时谈到了空间的基的概念么?回忆一下:

也就是一组向量要能:
1、生成空间;
2、线性无关;
有了空间的基我们就可以用来描述整个空间了,而对于空间的基是有一组向量,而一个空间的基中,向量的个数,称为维度。所以下面具体看一下:
1、二维欧几里得空间的维度是2,而它的基中的向量其实就是标准正交基:![]()
而对于维度可以用这样的符号来表示:
![]()
其中dim是dimension的缩写,表示维度的意思,R的平方表示二维欧几里得空间。
2、三维欧几里得空间的维度为3,而它的基中的向量也是三个标准正交基:
![]()
用符号表示就是:
![]()
3、n维的欧几里得空间的维度为n,所以它用符号表示就为:![]()
根据上面的几种情况可以汇总一下:一个(欧几里得)空间的任何一组基,其中的向量个数都是相同的,这个比较好理解,拿二维的基来看:
![]()
每个基的向量个数都是跟维度2个数是相同的对吧。所以对于上面关于维度的概念的描述:“一个空间的基中,向量的个数,称为维度”也更加好理解了,也就是从空间中找到一组基,看这一组基的向量个数为多少,此数量就是空间的维度,注意,这个就是看向量里面的元数个数【如果在子空间这一点就有问题了】。
子空间和维度:
对于看一个空间的维度其实就是看它的基中向量的元数的个数,但是!!如果涉及到子空间的情况此时就得要小心了,再这样看待维度可能就是有问题的,
比如还是回到之前举的二维空间的子空间的例子:

而这条直线为二维欧几里得空间的子空间对吧,在这条直线上所有的向量其实都是包含有两个数字的,比如这根直线是跟x,y轴成45度的直线,那么这根直线上的每一个点其实就是(1,1)、(2,2)、(3,3)...这样子的点,向量的个数是2,而从空间的角度来看待这根直线,先来找这个子空间的基,其实任何一个这条直线上的非零向量,都可以生成这条直线(子空间)上的所有向量,所以这个非零向量就是这根直线子空间的一组基,而根据维度的定义,这根直线所代表的子空间的维度却是为1的。
再拿三维空间的子空间来举例,如之前关于子空间的说明:
对于三维空间来说,它的维度为:
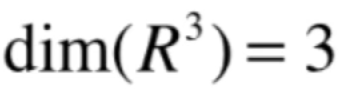
而下面来看一下它的子空间的几条说明:
1、过原点的一个平面,是三维空间的一个子空间,这个子空间用它来表示:
那么它的维度其实是为2的:
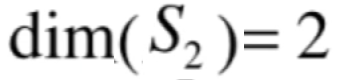
但是!!!它的基中的向量里面的元数个数是3。
2、过原点的一条直线,是三维空间的一个子空间,这个子空间用它来表示:
而它的基只能有一个,所以它的维度是1:
但是!!!它的基中的向量里面的元数个数是3。
3、原点本身,是三维空间的一个子空间,这种情况很特殊,对于原点本身来说它没有无数组基,它只有唯一的O向量这组基,对于这种情况我们认为它是没有任何自由度的,被压缩到只有一个唯一的位置,所以它的维度为0,所以子空间用它来表示:
由于它的基虽说有一个O向量,但是维度为0,可以表示为:
但是!!!它的基中的向量里面的元数个数是3。
好,下面先来对欧几里得空间的维度再来复习一下:
一个欧几里得空间的任何一组基,其中的向量个数是相同的。
一个欧几里得空间的维度是固定的。
那么对于下面这句话看描述对么?
一个欧几里得空间中的每一个有序实数元组包含n个元素,这个空间的维度就为n?
很明显在子空间的情况下这句话就不对了,在上面的证明中也可以看到了,所以,在面对下面这个问题时回答就不是那么简单了:
![]()
此时就得看被这三个向量所生成的空间的基中有多少个向量,这里先回忆一下之前https://www.cnblogs.com/webor2006/p/14306046.html对于生成空间的一个性质:

而其中还有这么一个性质:

回到咱们要解答的这个问题上,很显然对于u和v这两个向量是线性相关的【因为v*-2 = u;u * -1/2 = v,所以u可以表示v和w的一个线性组合,同理v也可以表示u和w的一个线性组合】,所以可以删除u(或v),那咱们选择把u给删去,那看一下v和w之间的关系,显示它们俩是线性无关的,所以这个生成空间的维度就为2,用三维空间来直观看一下也能清晰的感受到是一个2维平面:
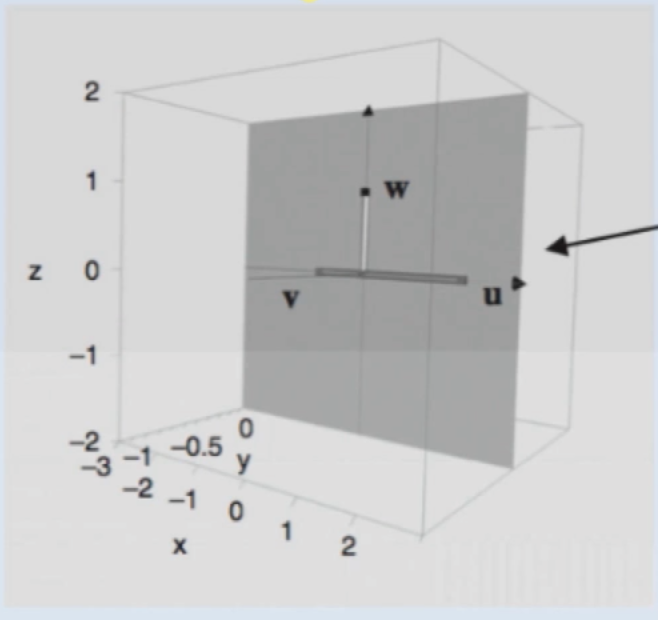
其中标灰的那个区域显示就是个二维平面,也就是整个生成空间的维度为2。所以对于维度的计算不能以“一个欧几里得空间中的每一个有序实数元组包含n个元素,这个空间的维度就为n”它做为标准进行计算,而应该是:
一组n维向量:
它们的生成空间,是n维空间的子空间。
拿咱们举例的u,v,w这三个向量生成空间来理解,u,v,w是三维向量,其生成空间是三维空间的子空间,但是不能说这三个向量组成的空间的维度就是3,而实际它们生成的空间维度是2。
对于上面所说的结论都是针对欧几里得空间而言的,实际上这们也可以扩展到更加广义的向量空间,只是对于线性代数的学习一般是基于欧几里得空间来进行探究的,具体如下:
一组向量:
属于空间V,则它们的生成空间是V的子空间。
一组n维向量:这们的生成空间,是n维空间的子空间,换言之如果这组向量生成空间的维度是m的话,那么m肯定是<= n的。
最后总的来说:“一个空间的基中,向量的个数,称为维度”,千万不要把向量中有多少个元素就认为是空间的维度了就成~~
行空间和矩阵的行秩:
行空间:
在上面我们对于这样的问题进行了一个剖析:
显然:u 和 v 是线性相关的,所以可以删除u (或v);而又由于u 和 w 线性无关,所以这个生成空间的维度为2。
用上面的这种方式我们就可以扩展到n维向量:
给出一组n维向量:
其生成空间的维度是多少?其实就归结为找到这组向量有多少和其他向量线性相关,然后将其给删除掉,直到剩下的向量它们是线性无关。
那么问题来了,对于上面举的三个向量你用肉眼一看不知道哪些向量是线性相关的,但是如果向量的数量更多一些,维度更大一些的话,这种肉眼判断的方式肯定就很难了,那有木有一种系统性的方法能得到这个问题的答案呢?当然有,而且这方法是之前已经学过了的,之前https://www.cnblogs.com/webor2006/p/14306046.html在学习线性相关时就举过例子:
而对于上面增广矩阵消元的过程可以抽象为:
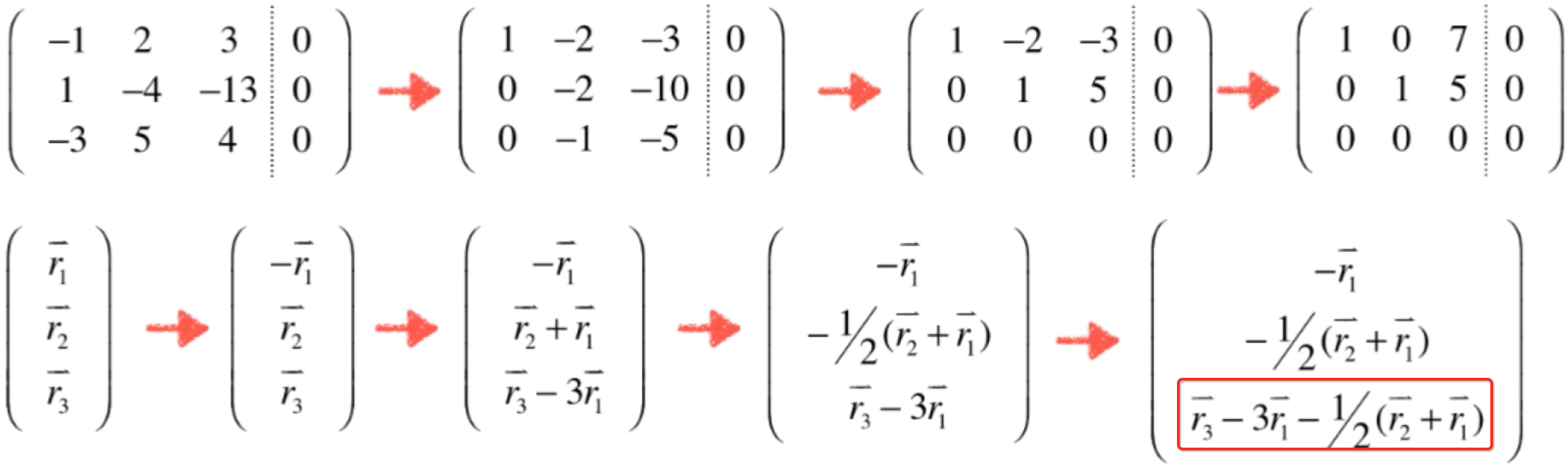
其中对于标红的这个式子归一处理之后,就可以发现:
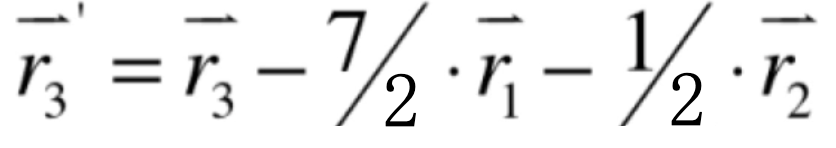
其实它就等于原来矩阵行向量的一个线性组合,而由于咱们这个例子当上面高斯约旦消元之后最后一行是一个0行,所以此时就有如下等式:
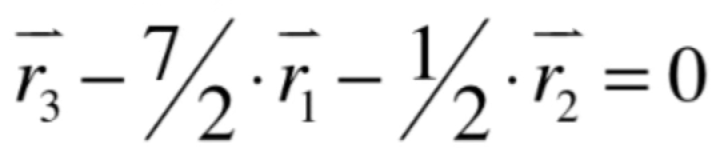
这就意味着r1、r2、r3向量存在非0的系数,使得线性结果的组合为0,换言之就是这三个向量是线性相关的,因为线性相关的定义如下:

而对于r3这个向量很显然就是由r1和r2的行向量进行加加减减的操作,所以就可以变换成这样的一个式子:
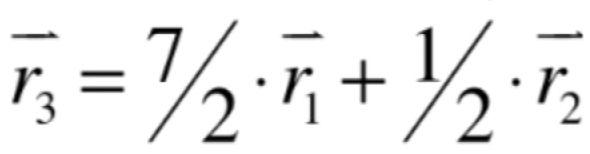
也就是r3可以写成是r1和r2的线性组合,那么此时就可以把r3这个向量给删除掉了,好!!!基于这样的一个结论,假如说对于一个有m行的增广矩阵进行高斯约旦消元法后如果有x行都为0的话,那么这x行所对应的行向量可以表示成m-x行的线性组合,所以这x行的向量全都可以删除掉,所以,对于咱们的问题就可以定结论了:
给出一组n维向量:
其生成空间的维度是多少?其实就归结为找到这组向量有多少和其他向量线性相关,然后将其给删除掉,直到剩下的向量它们是线性无关。
其方法是:将这组向量按照行排列成一个矩阵,执行Gauss-Jordan消元法(化为RREF行最简形式),非零行的个数既为其生成空间的维度。
下面以这样的方式再对这个简单的例子进行一个维度的求解:
![]()
将这三个向量一行行的罗列起来就形成这样的一个矩阵:
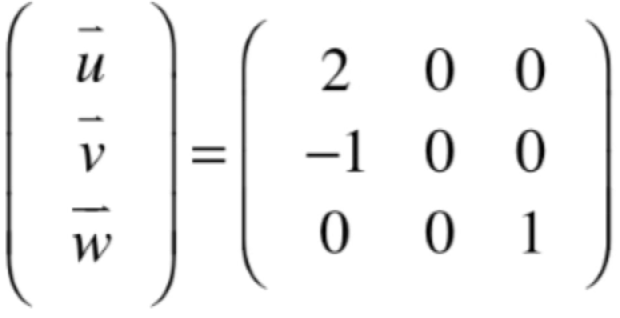
将其执行Gauss-Jordan消元法,过程如下:
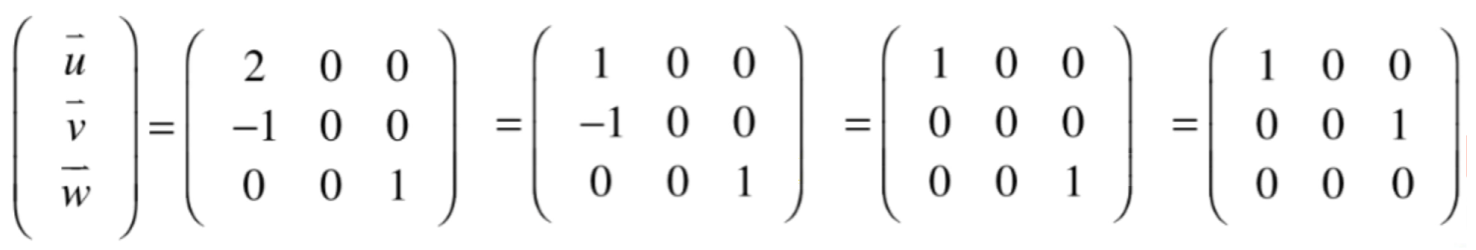
其中可以看到非0行为2,所以就可以根据这种方法很轻松地算出来向量生成空间的维度了。
那此时就可以回到主题上来,如小标题所示---行空间,其实很容易理解,对于一个矩阵我们知道:

其中行向量生成的空间,称之为行空间(Row Space);
其中列向量生成的空间,称之为列空间(Column Space);
对于这个定义不仅仅只对于咱们举的这个方阵有效,对于一个长方阵一样有效,比如有一个3行4列的矩阵:
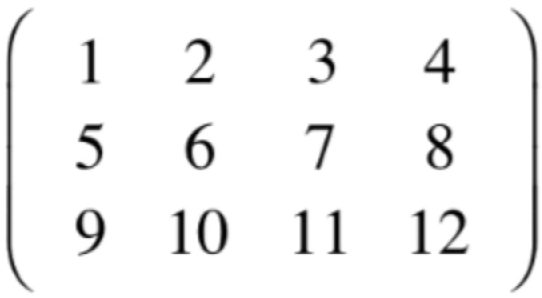
其中行空间是一个4维空间的子集【因为向量是由4个元素组成,也就是4维向量】。而扩展到m行n列的矩阵,行空间则是n维空间的子集;
而列空间是一个3维空间的子集【因为向量是由3个元素组成,也就是3维向量】,而扩展到m行n列的矩阵,列空间则是m维空间的子集;
矩阵的行铁:
其中对于求解空间的维度看的是矩阵化为行最简形式的非零行的个数,由于对于行最简形式的非零行是非常重要,所有一个高大上的名词又出现了:
一个矩阵的行最简形式的非零行数量称为矩阵的行秩(Row Rank)。
所以,我们就可以说:
行空间的维度,为矩阵的行秩。
注意:对于维度和行秩作用的对象是不一样的,维度作用于空间,而行秩作用于矩阵,但是它们俩可以产生关联。
另外再来探究一个话题:既然现在已经知道了行空间的维度是多少了,那能否进一步地找到行空间的一组基?毕竟只有找到了空间的一组基才能更好地理解这个空间,同时对于空间中的任何一个点就可以用这一组基表示它。其实结论很简单,还是拿之前举的三个简单的三维向量为例,化为行最简形式为:
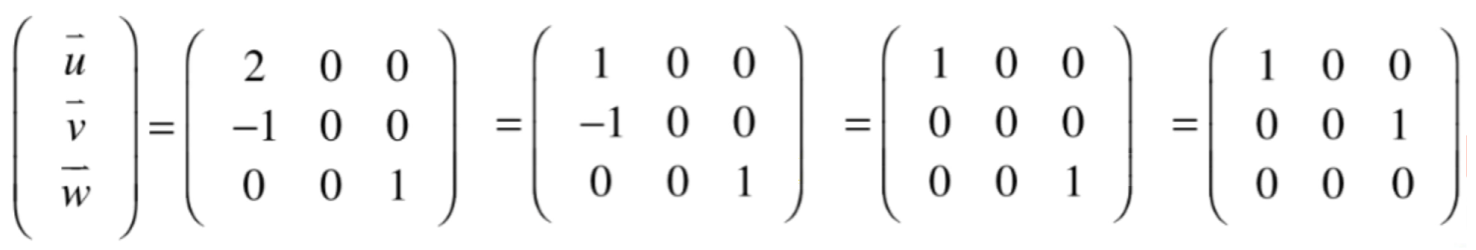
其实最终行最简形式的非零行就是行空间的一组基,下面来证明一下,为了证明方便,先来对于原矩阵和行最简形式的矩阵用字母代替一下:
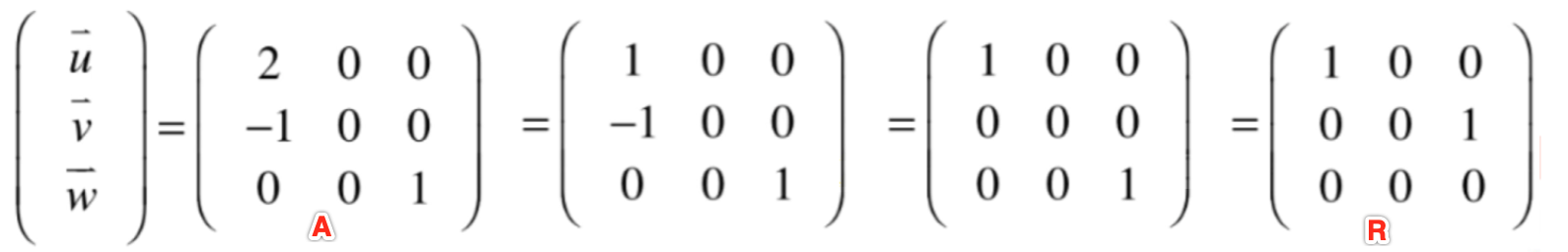
证明的关键就是A的行空间其实就是R的行空间,而怎么证明呢?其实有点像集合论中的证明方式,想一下如果想证明两个集合A,B相等的话,只需要证明A是B的子集,B又是A的子集就行了,也就是证明A集合中的任一一个元素都属于B,B集合中任一一个元素又都属于A,同理,咱们只要分别证明以下结论就成,具体如下:
A的行空间的每一个向量,都在R的行空间中;
B的行空间的每一个向量,都在A的行空间中;
很显然这条证明是成立的,因为A的行空间的每一个向量其实就是A的行向量的线性组合,而根据高斯消元法从A通过矩阵的基本行变换得到的R,而R中的每一行也是原来A中每一行的线性组合,所以就可以证明“A的行空间的每一个向量,都在R的行空间中”,反之也能推出A的每一行也是R中每一行的线性组合,所以也能证明“B的行空间的每一个向量,都在A的行空间中”,不管这证明是多么的抽象,最终结论是:“A的行空间就等于R的行空间”,所以也可以说:
R的行空间的基就是A的行空间的基,反之也成立,最后关于行空间的又一结论就出来了:“一个矩阵的行最简形式的非零行向量,就是A的行空间的基【注意:此时不是拿原矩阵的非零行作为A的行空间的基,而是化为最简形式矩阵的非零行向量,因为在之后的列空间的基学习中是有区别的,之后可以对比】”,所以回到咱们的这个简单例子,其中A的行空间的基就为R中的非零行的2个向量,用三维图来看的话就是一个平面,之前也看过:

列空间:
上面已经对于矩阵的行空间进行了一个详细学习,接下来则来看一下对应的列空间了, 还是回到这个话题:
![]()
这个问题的解答关键之处就是看这组向量是否线性无关对吧?而上面已经道出了怎么求解这组向量线性无关了,但是这里可以回到线性组合中来直观的观察出来,也就是:
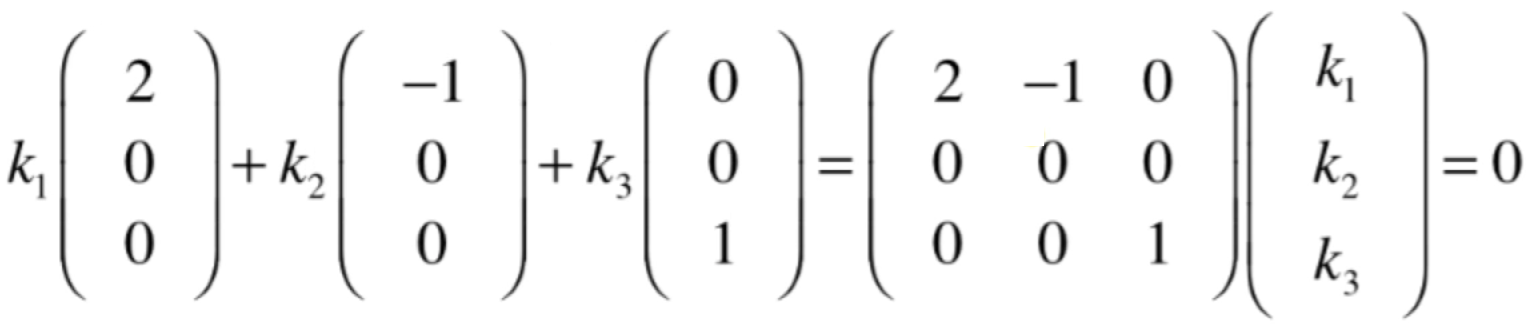
看这个线性方程组只有唯一解?又回到了求解线性系统的问题了,很显然要求的这个是一个齐次线性组,所以只需要看系统矩阵就好了:
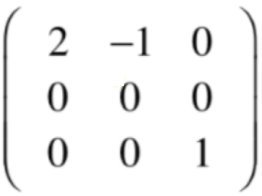
将其化为行最简形式,过程如下:

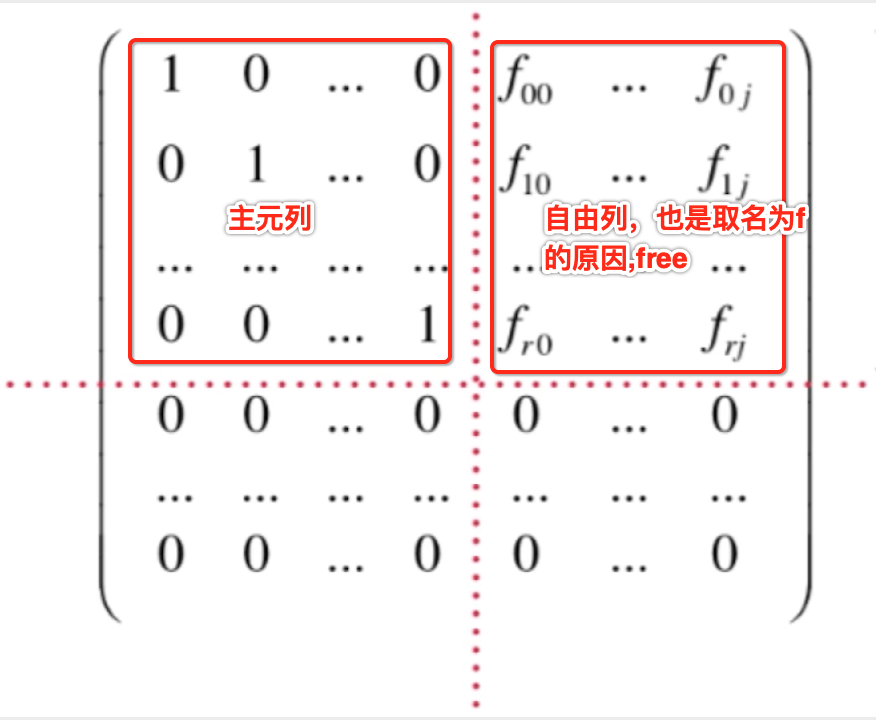
其中以列视角来看待的话,可以有主元列和自由列,回忆一下这块的概念https://www.cnblogs.com/webor2006/p/14280299.html:
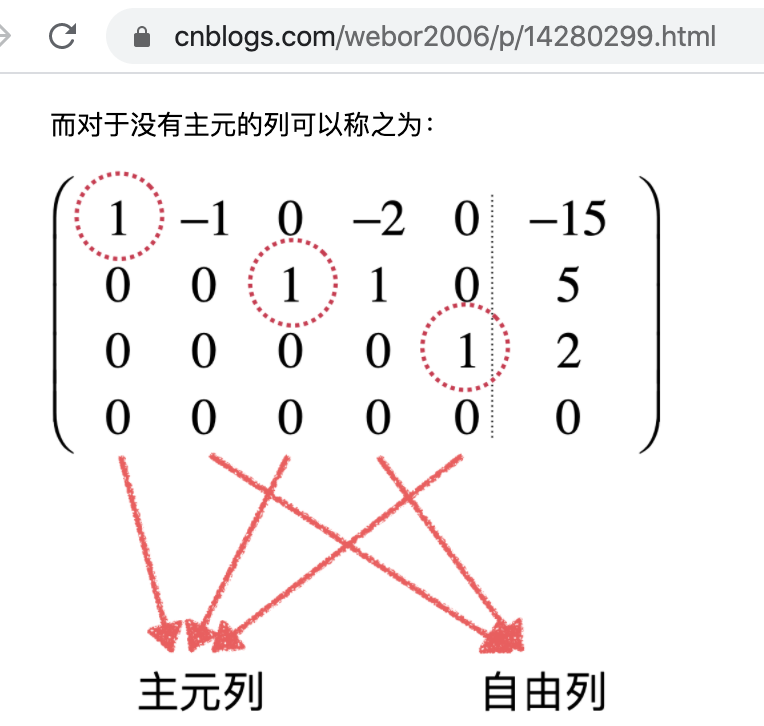
而自由列上的元素意味着可以随便取值,当然也可以取非零值!拿第一行来说:
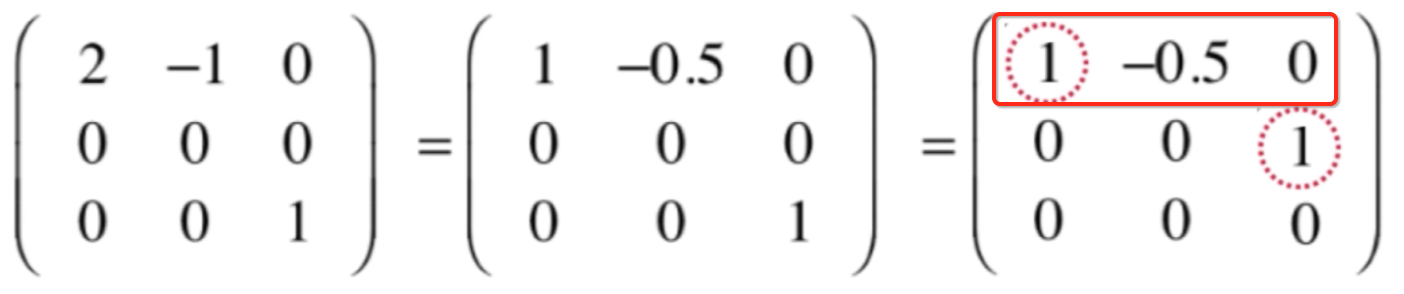
它所对应的方程可以表示为:k1-0.5*k2 = 0,也就是k1 = 0.5*k2,是不是k2可以随便取一个值都有一个对应的k1?而k1取非零值是是不是就意味着咱们的向量是线性相关的,所以对于自由列的个数,为可以表示为其他向量线性组合的向量个数,也就是可以删掉的,回到咱们这个例子来看:
![]()
这个向量就可以删掉了,而主元列的个数,为线性无关的向量个数,所以可以看出主元列的个数既为向量生成空间的维度!另外一个专列名词又出现了:
主元列的个数,为列秩(Column Ranke),跟行秩对应的。
所以与行秩之对应的就有如下结论了:
m行n列,列空间是m维空间的子空间;
一个矩阵的行最简形式的主元列数量称为矩阵的列秩;
列空间的维度,为矩阵的列秩;
那既然能求出列空间的维度了,那能否求出列空间的一组基【注意这个是跟行空间有区别的地方】?其实就是将其系数矩阵化为行最简形式:

由于自由列可以表示其它列的线性组合,所以可以很放心的将其删除掉,剩下的主元列则全是线性无关的,所以:
主元列的对应原矩阵的列,是列空间的一组基。一定要注意:
这里一定要跟行空间求基的进行对比,回忆一下:

这是因为行最简形式本身就是原矩阵的行进行行操作得来的,所以在上面也证明了行最简形式的行空间跟原矩阵的行空间是一个空间,但是!!这个性质在列空间中是不存在的,由于列矩阵在化为行最简形式时是对行进行变换,而非列,所以最终化为行最简形式的列已经跟原来矩阵的列没有关系了,这点一定要清楚。
所以总结列空间基的求法就是:行最简形式主元列的对应原矩阵的列,是列空间的一组基。最后为了区别行空间和列空间下面对其对比总结一下【重要】:
对于一个m行n列的矩阵:
行空间:
1、行空间是n维空间的子空间;2、行最简形式的非零行个数为矩阵的行秩;
3、行空间的维度,为矩阵的行秩;
4、行最简形式的非零行,是行空间的一组基;
列空间:
1、列空间是m维空间的子空间;2、行最简形式的主元列数就是矩阵的列秩;
3、列空间的维度,为矩阵的列秩;4、主元列的对应原矩阵的列,是列空间的一组基;
矩阵的秩和矩阵的逆:
矩阵的秩:
先来回忆一下上面所讲的矩阵的行秩和列秩:

矩阵的列秩是看化为行最简形式的主元列的个数,为2;而对于它的行秩是看化为行最简形式后的非零行的个数:
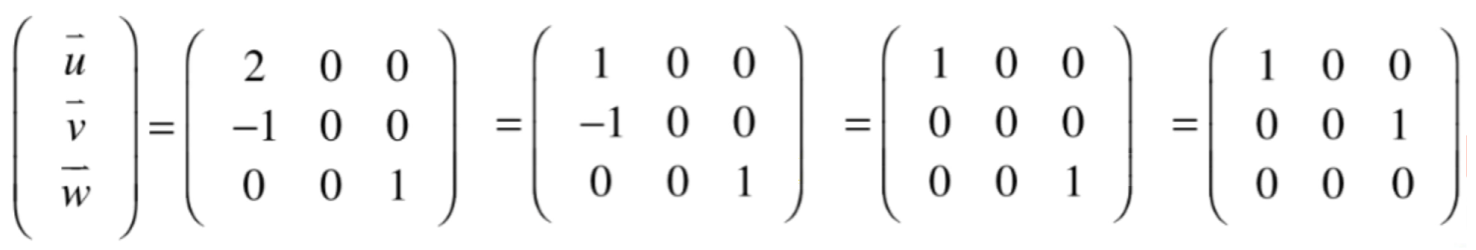
很显然该矩阵的行秩也为2,也就是矩阵的行秩=矩阵的列秩,这是不是一个巧合呢?其实不是巧合,任何矩阵的行秩跟列秩都相等,下面咱们来证明一下为啥相等:
矩阵的行秩 = 矩阵的列秩
证明:对于任何一个矩阵: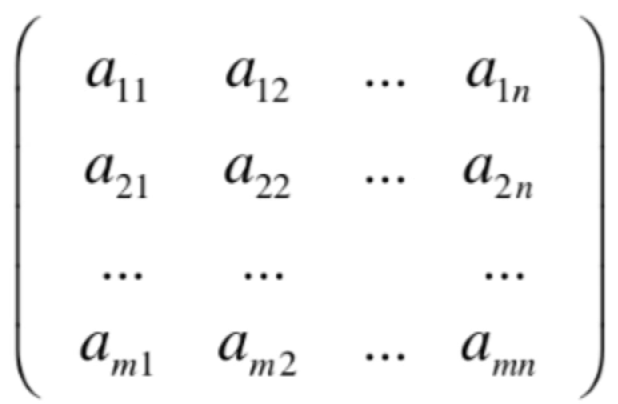
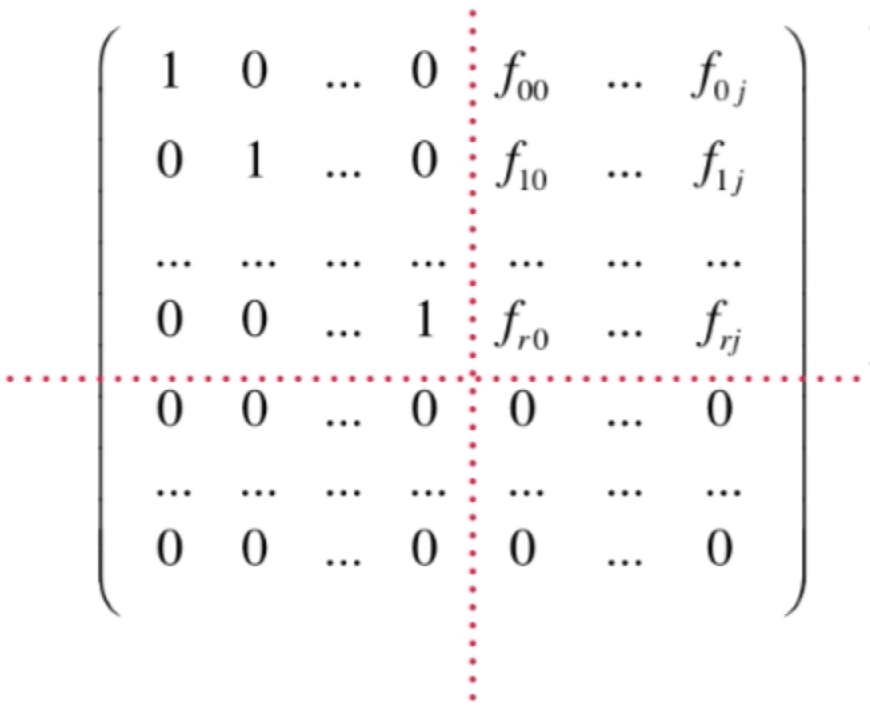
经过高斯约旦消元法,其实最终会化成这样的一个形式:
对于这个矩阵看起来有些晕,下面来解读一下它,对于行最简形式如果有0行一定是在行最简形式的最下面对吧?所以可以在零行与非零行之间画一条分隔线,像这样:
另外对于非零行还可以绘制一条竖线,像这样:
经过这么一个辅助线之后,有啥新发现么?其实是:
其中主元列是一个方阵,但好像咱们之前举的矩阵化为行最简形式之后貌似不是上面的这个样子呀,回忆一下:
很显然不是咱们预期要的那个形式,其实可以做一个变换让其变成预期的行最简形式,也就是让第二列和第三列交换一下位置就行了:
其中左上角主元列的单位矩阵有r行r列:
通过这样的视角通过将矩阵化为行最简形式后它的非0行一定等于主元列数,这不就证明了矩阵的行秩=矩阵的列秩,而且都排在了这个单位矩阵中,抽象来表达上面的矩阵形式,其实也就是:

当然并不是所有的行最简形式都可以化成上面这种形式,可能是没有全0行,这点需要明白。
既然矩阵的行秩=矩阵的列秩,那么可以统一把它们叫为“矩阵的秩(Rank)”,而秩又可以跟空间挂上勾,也就是矩阵的秩既是行空间的维度,又是列空间的维度,也能进一步推导出“一个矩阵的行空间和列空间维度相等!【注意:并没有说行空间跟列空间相等,而是说维度相等】”,其中对于这个结论“矩阵的秩=矩阵的行秩=矩阵的列秩”有啥用呢?非常有意义,在很多时候就可以快速地做出一些基本判断,比如看下面这个问题:
u = (1, 1, 2),v = (2, 2, 3),w = (3, 3, 4)的生成空间的维度?
很明显肉眼直观很难看出来,需要进行一番计算,但是!!!如果将这三个向量写成矩阵的形式【用行的形式还是列的形式组成都无所谓】,这里以行的方式吧,如下:

以列视角一看,第一列和第二列很明显是线性相关了,所以它的列秩肯定<=2,不可能为3,而由于行秩=列秩,所以它生成空间的维度一定是<=2,而你如果以行视角来看很难看出u,v是线性相关对不?所以如果你知道了列秩就很轻松地能知道行秩了,大大加快计算速度。
到目前为止,我们来梳理一下关于行空间与列空间的结论:
对于一个m行m列的矩阵:
行空间是n维空间的子空间;列空间是m维空间的子空间;对于一个n阶方阵(n行n列):
行空间是n维空间的子空间;列空间是n维空间的子空间;
其中关于标红的n阶方阵有个问题来了:“何时行空间和列空间都是n维空间?”,其实也就是说矩阵的行秩和矩阵的列秩都为n,那不就是矩阵的秩r = n,此时又有一个新概念来了,称这样的n阶方阵为满秩(Full Rank),也就是对于这个矩阵来说每一行都是非0行,每一列都是主元列,没有自由列和0行,所以有如下结论:
对于一个n阶方阵,矩阵的秩r = n是满秩(Full Rank),而它的行最简形式的非零行个数为n,行最简形式的主元列个数也为n,此时可以推出:
也就是行最简形式是单位矩阵,因为对于方阵的行最简形式在之前的N多命题中已经明确给出结论了,回忆一下:
而经过矩阵的秩的学习,对于方阵的N多特性此时又可以进行相关的扩展了,如下:

实现矩阵的秩:
接下来则回到python中对于矩阵的秩的求角进行一下实现,对于求矩阵的秩可以用行秩也要以用列秩,这里采用行秩的方式来求,因为它相对而言较简单,只需要化为行最简形式之后数非0行的个数既可。
修改LinearSystem:
由于求矩阵的秩也是要对它进行线性系统的求解,所以还是在LinearSystem中定义一个方法:
而由于当时这个类在设计化为行最简形式时是一定要指定b的,回忆一下:
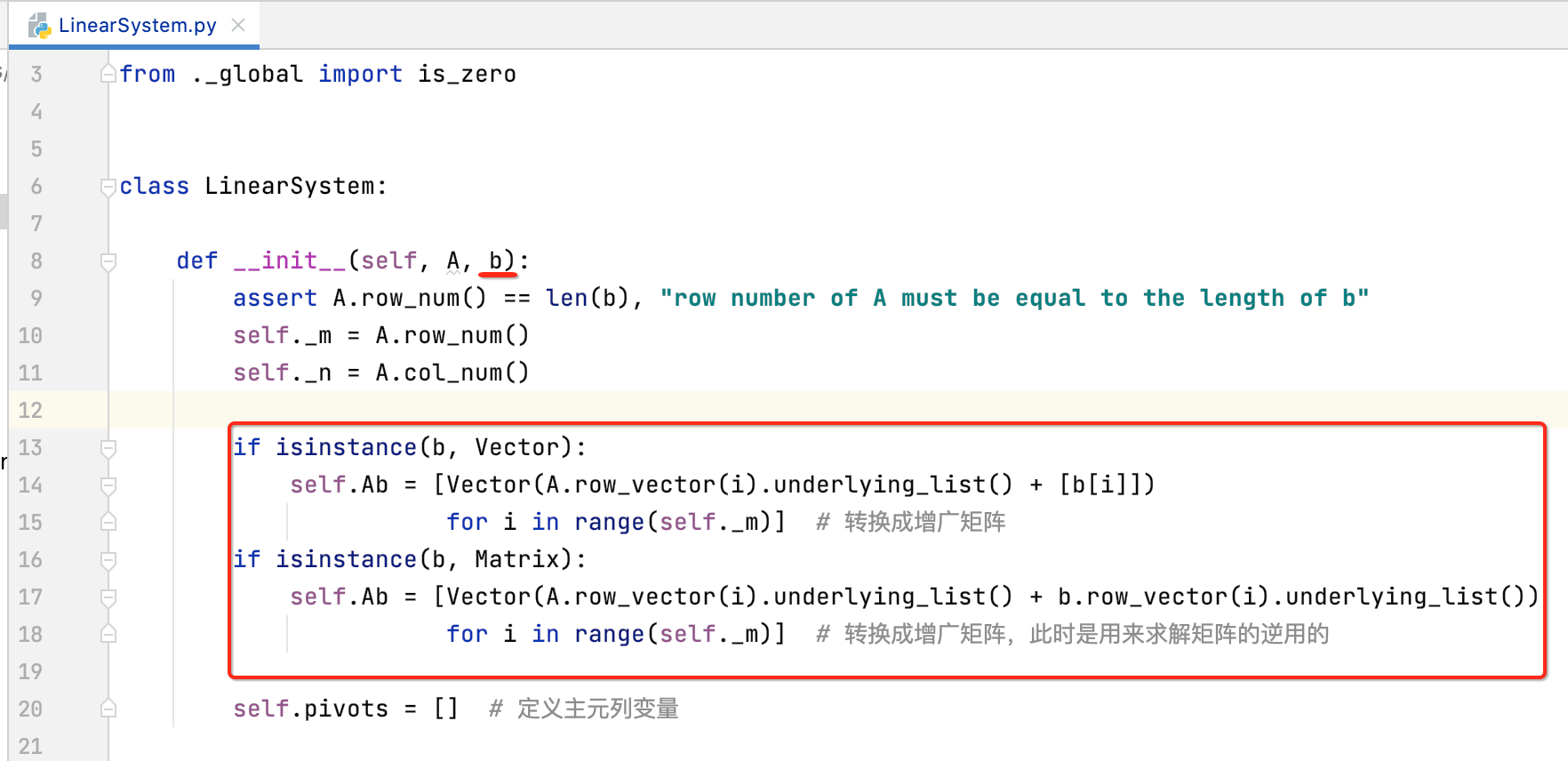
而对于矩阵秩的求解是不需要传这个b的,所以修改一下代码,让其可以为空,修改如下:
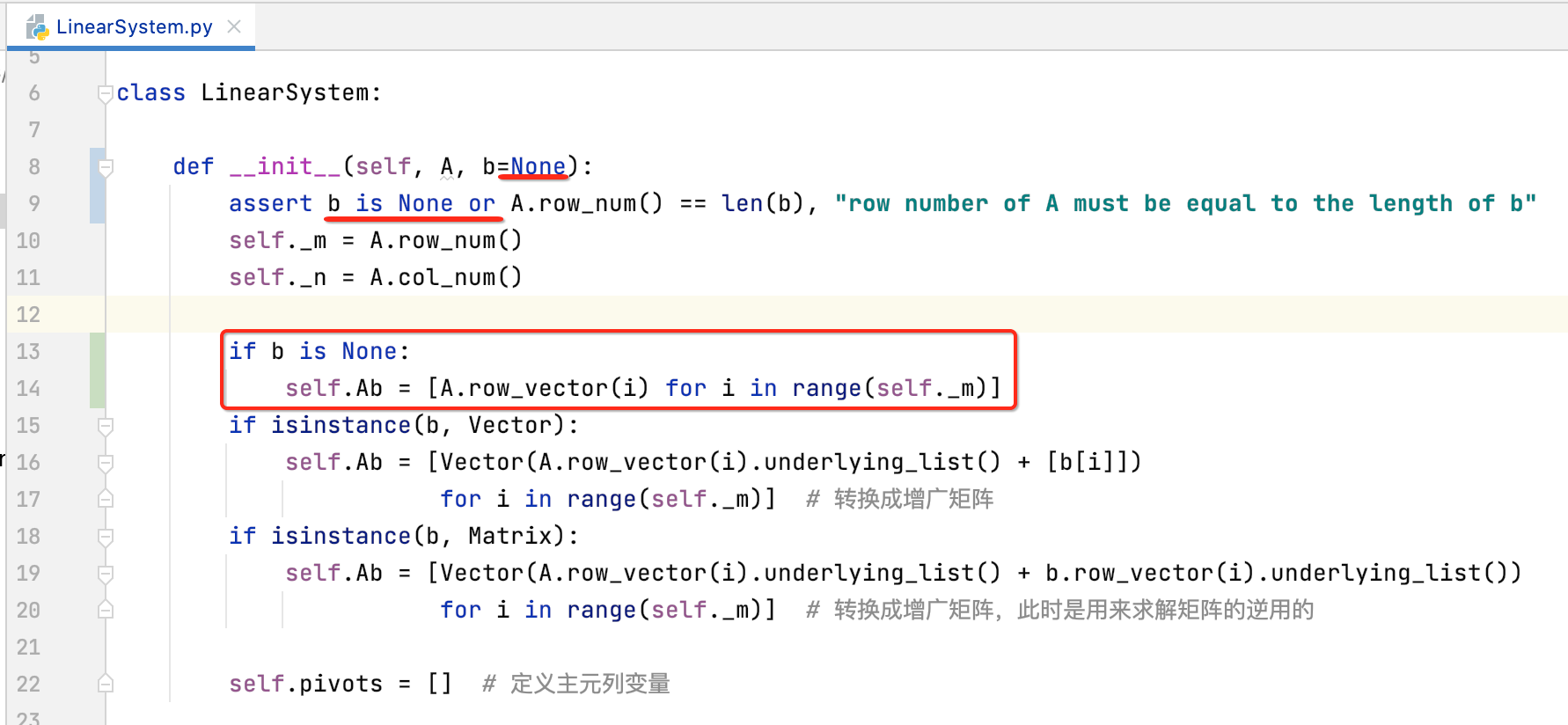
进行矩阵的高斯消元:
这块就比较简单了,由于高斯消元方法已经封装好了,如下:

判断行最简形式的非0行的个数:
其实就是行最简形式矩阵中的每一行是否是0向量,如果不是则+1既可,所以先生成一个零向量:

然后再来进行每行的判断,如下:
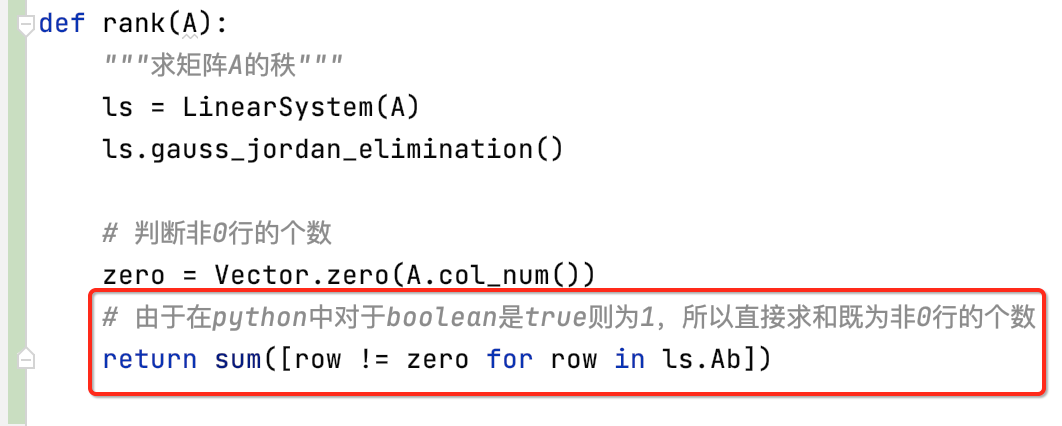
重载Vector的不等号:
由于咱们在计算非0行时用到了向量的不等号运算符,如下:
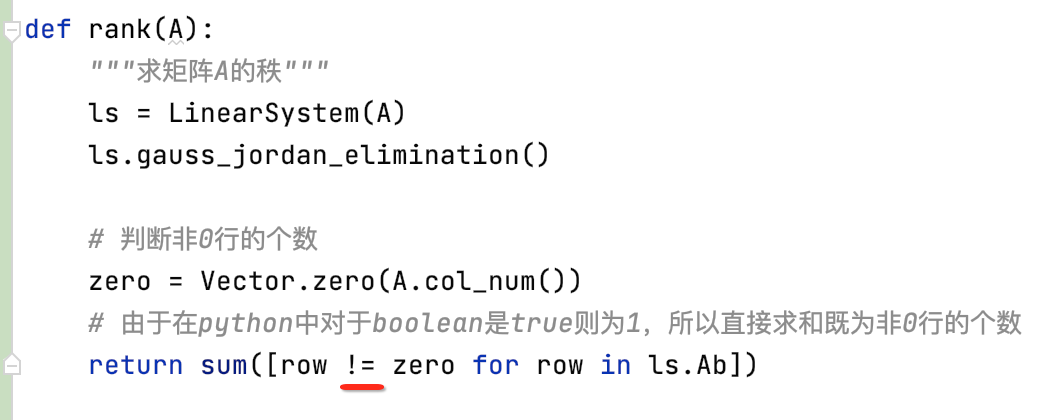
而目前Vector类中并没有重载此符号,所以重载一下:
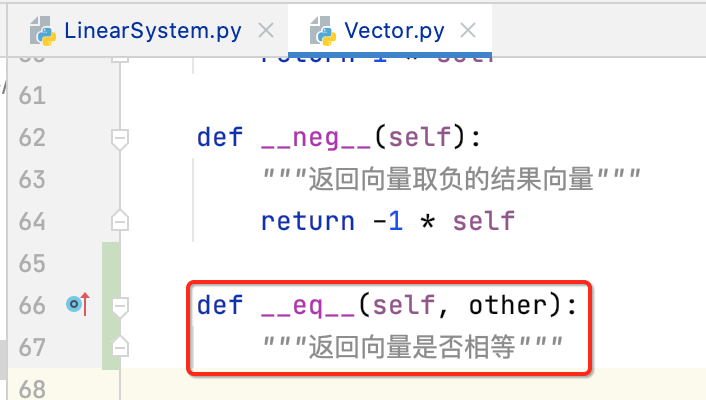
判断两个向量是否相等其实也就是判断向量中每个元素是否相等,那程序如何实现呢,如下:
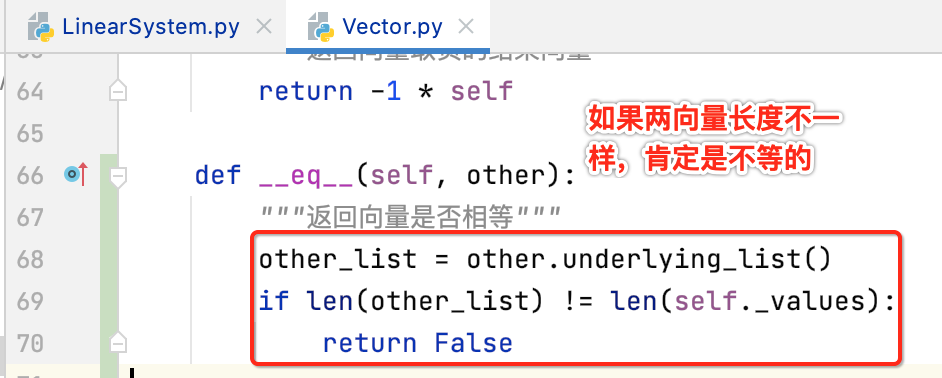
接下来在元素相等的情况下则需要一个个元素进行比较,此时python的写法就需要用到zip将两个向量列表打包,具体写法如下:
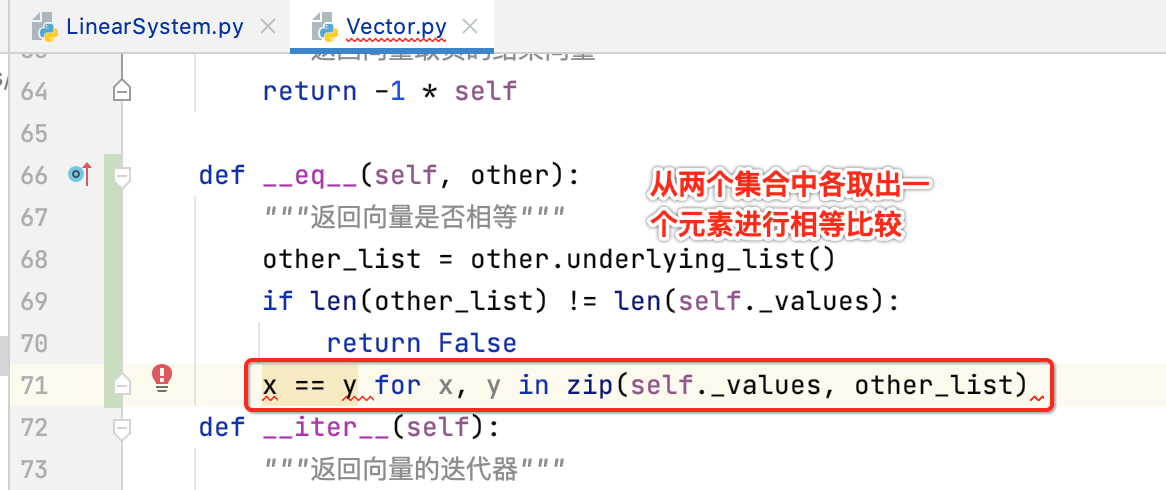
此时由于元素有可能是浮点,所以对于元素的相等得要用之前咱们封装好的这个相等判断:
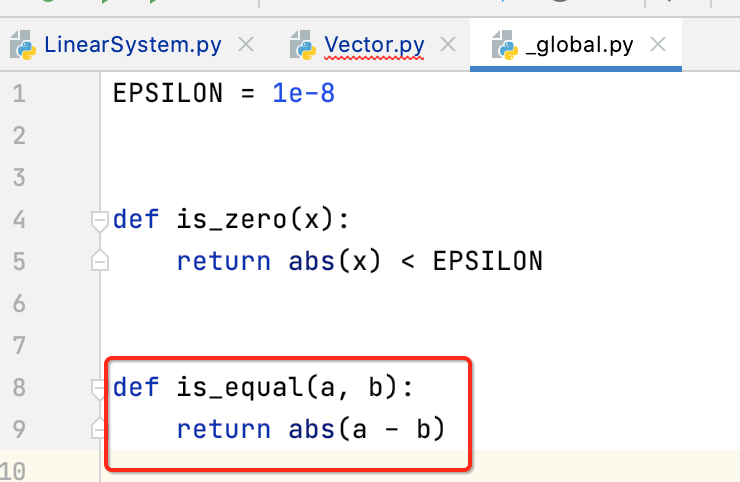
所以修改一下:
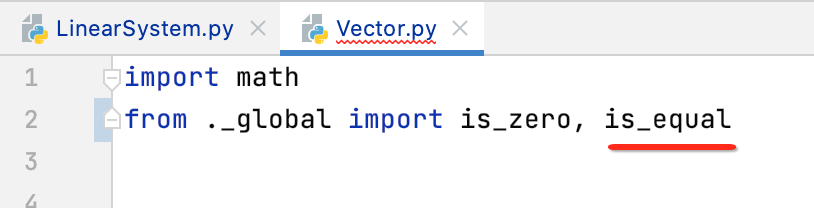
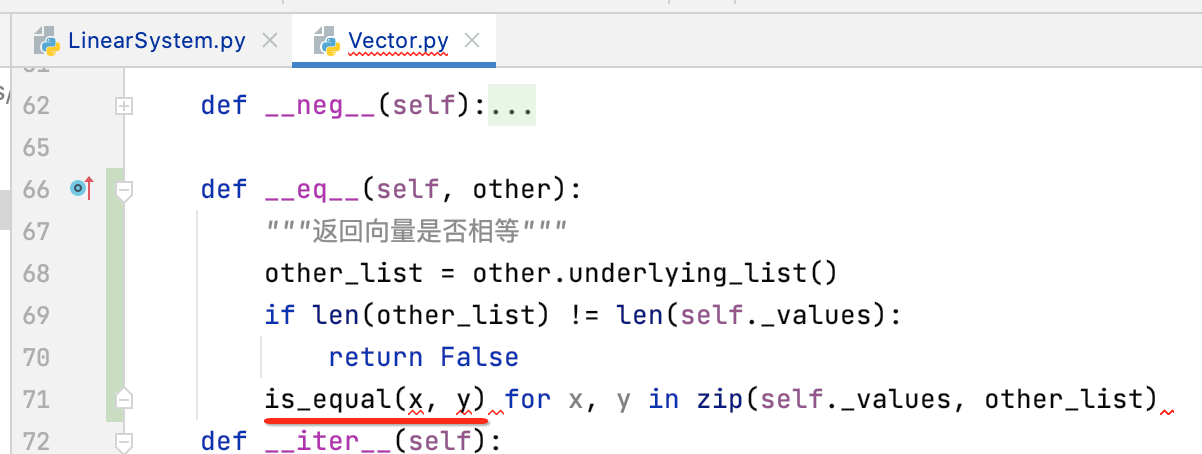
而咱们需要所有的元素两两相等,此时就需要这样办了:
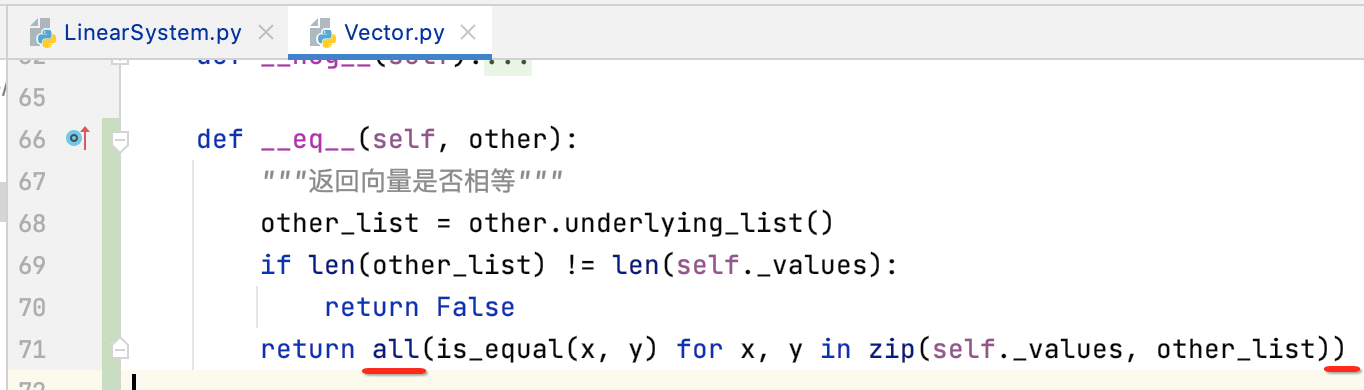
有了等于号的实现,对于不等号就可以很轻松的实现了,如下:
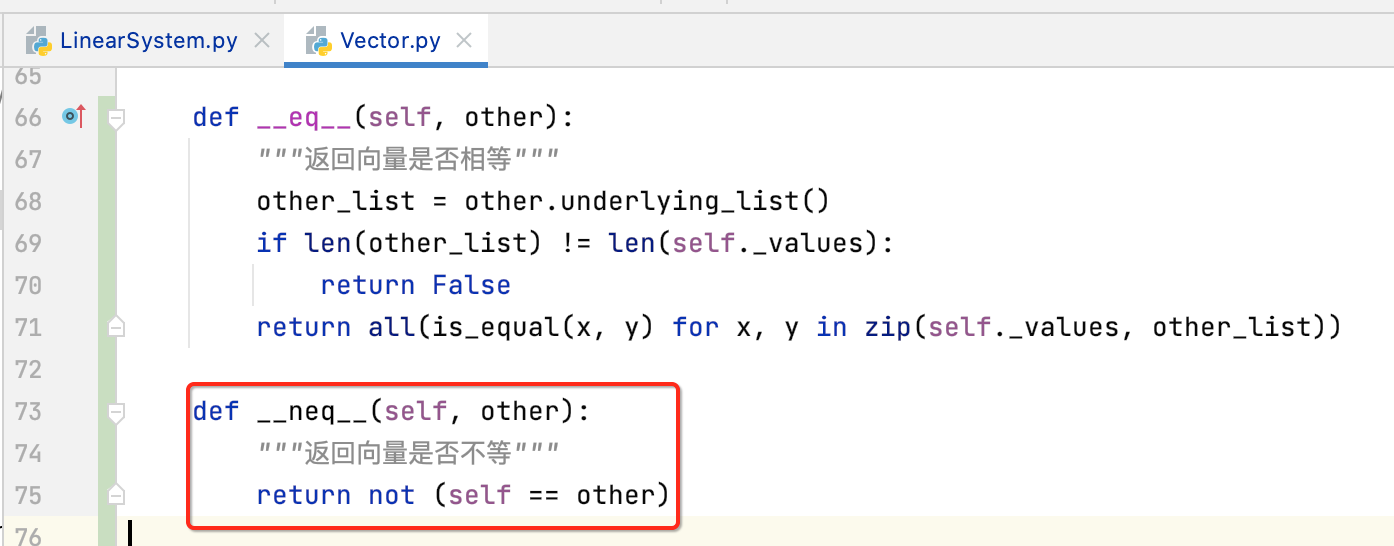
测试:
先来验证一下向量的等于与不等于的逻辑:

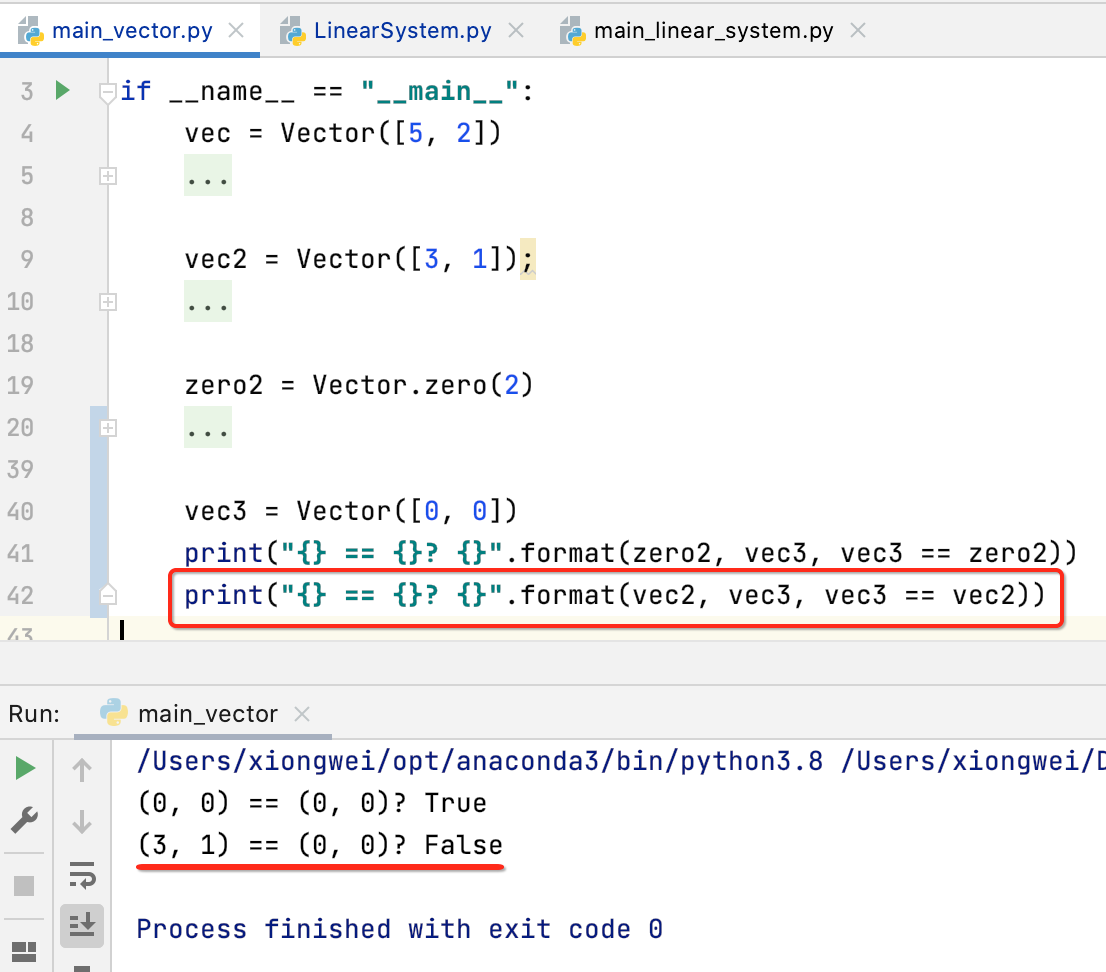
接下来再测试一下不等:
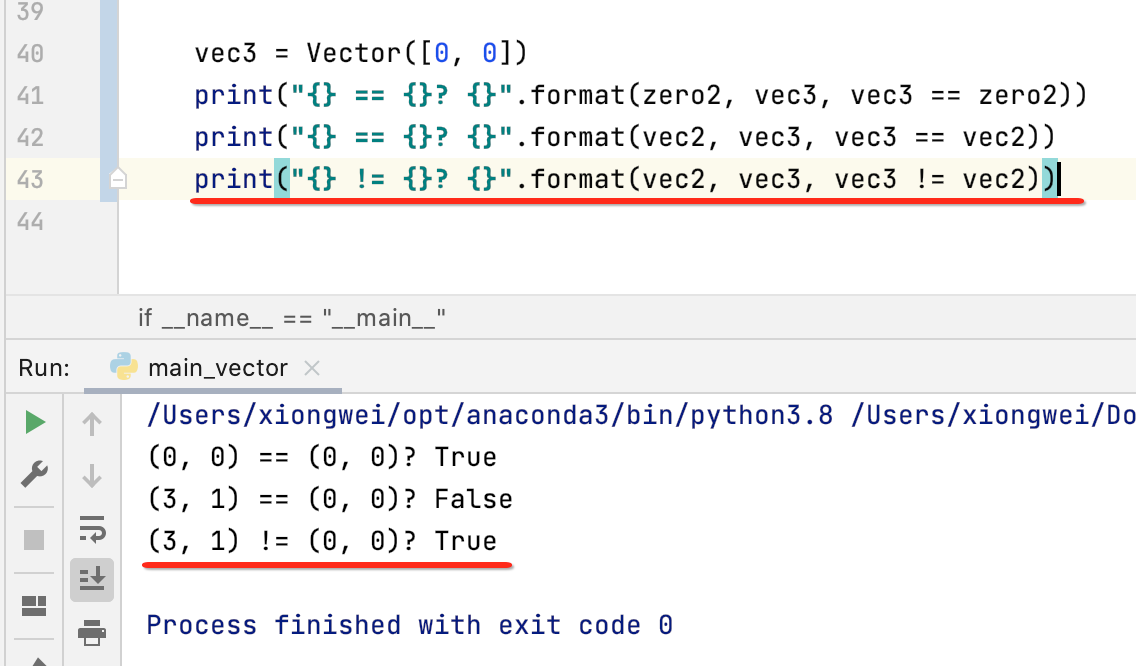
接下来就可以测试矩阵秩的方法了:
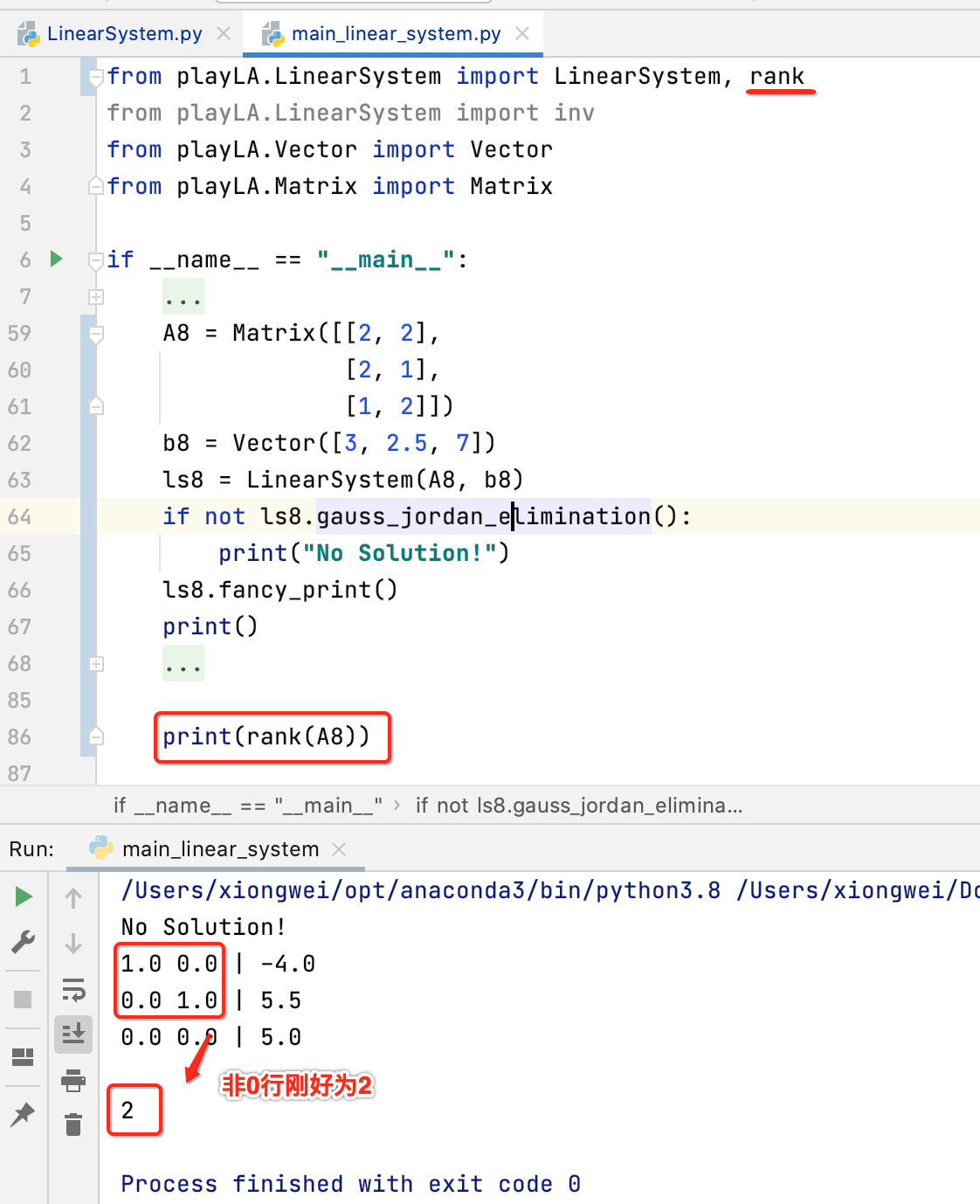
再来看一个:
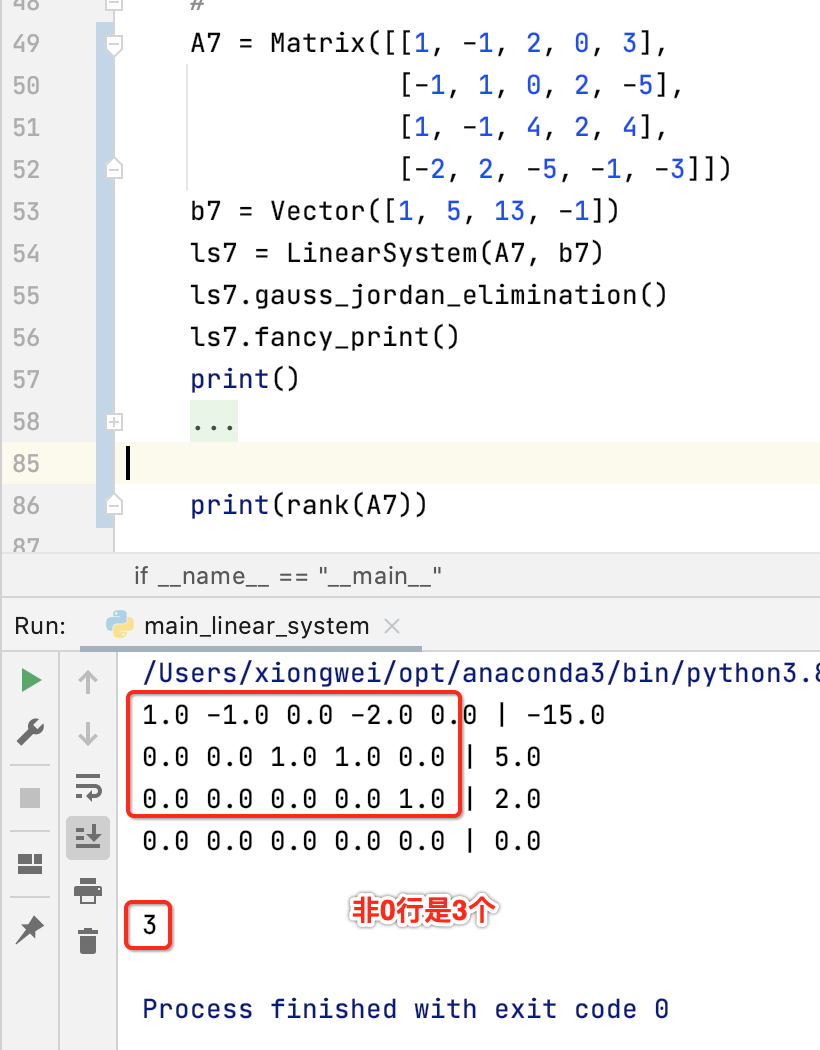
再来瞅一个:
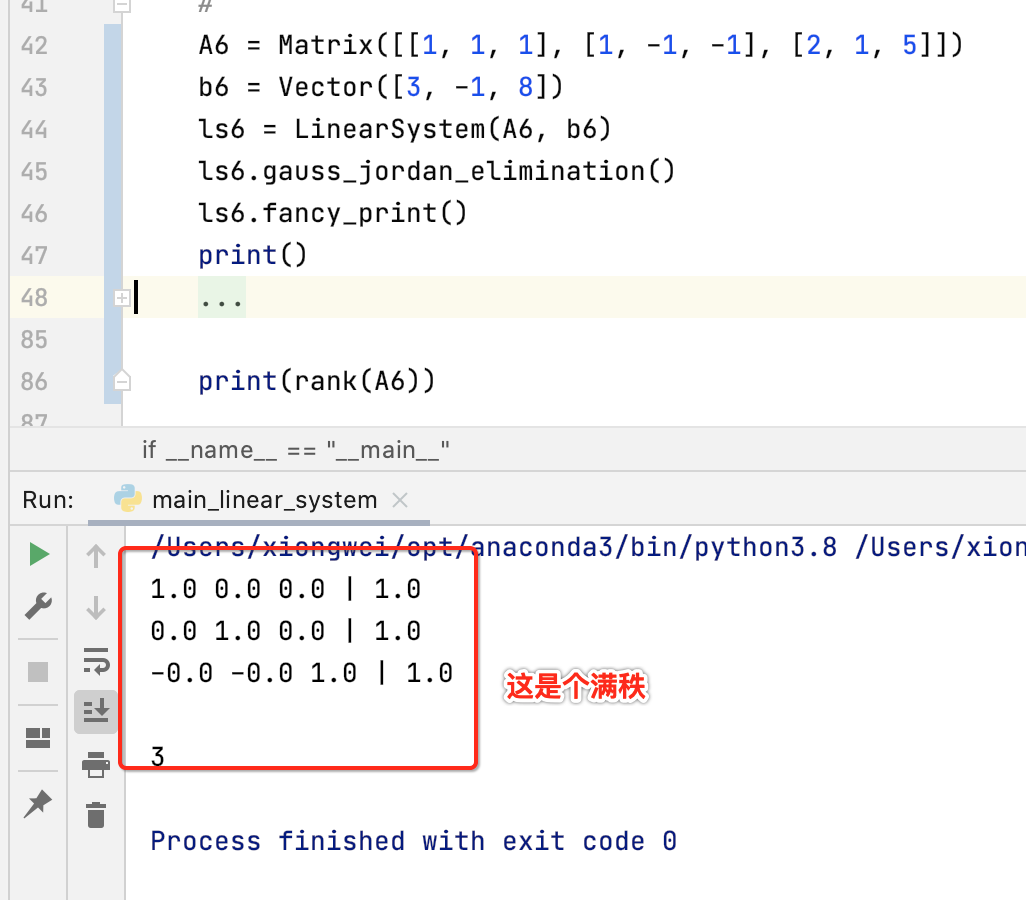
零空间与看待零空间的三个视角:
零空间:
接下来则学习一下另外一个根据矩阵而得出的重要的子空间----零空间, 它相对于行空间和列空间要稍微抽象一点,这是因为对于行空间和列空间我们可以直接看到生成子空间中的所有向量就是这个矩阵的行向量或者是列向量,但是!!!生成一个零空间所对应的那些向量并不能通过一个矩阵获得,那么什么是零空间呢?先来证明一个非常重要的结论:
一个齐次线性方程组的所有解,形成一个向量空间。
证明:
先来看一个例子:其中矩阵有3列,对应的未知数就有3个(x1,x2,x3),上面待证明的结论的意思是所有满足这个奇次线性方程组解的向量就形成了一个向量空间, 下面来看证明过程:
1、一个齐次线性方程组一定是有解的。
2、而有解就有可能是唯一零解,也就是空间中只有0这一个向量,很显然这种情况这个线性方程的解就是一个向量空间,这个向量的维度为0;
3、而如果有无数解的情况,就稍复杂一些了,接下来就得证明无数解也能构成向量空间:如果系数矩阵为m*n的矩阵,解为n维向量,如果解形成向量空间,则该向量空间是n维欧几里得空间的一个子空间,其中为啥n维空间就是欧几里得空间呢?因为每一个解都是有序的实数元组,而回忆一下欧几里得空间的定义:
而要想证明“解形成向量空间,则该向量空间是n维欧几里得空间的一个子空间”,此时在前面已经花了很大的篇幅对于子空间的证明只需要满足:
所以:我们只需要证明解所组成的空间对向量的加法和数量乘法封闭就好了,而证明就如下:
a、证明空间对向量的加法封闭:
假设系数矩阵为A,而向量u和v都是解,很明显就有:
然后此时就可以将这两式子加起来:
然后根据分配率就可以变为:
这个变化又说明啥呢?说明u+v也是解呀,此时就说明了该空间对向量加法是封闭的?所以此时a这个就得证了。
b、证明空间对向量的数量乘法封闭:
还是假设系数矩阵为A,假设u是解,就有:
然后此时可以乘以k,式子就变为:
然后它又可以变为:

此时就又可以说明问题了,很显然k*向量u和向量u都是在同一空间中,那ku也是解,该空间也就对数量乘法封闭了。
此时“一个齐次线性方程组的所有解,形成一个向量空间,称这个空间就为零空间(Null Space)。”
也就是说A的零空间,就是Ax = 0中,所有x组成的空间。
深入理解零空间:
说实话零空间还是有些难理解,下面则从另外几个视角对其进行一个巩固理解。
视角1:从代数角度
对于“A的零空间,就是Ax = 0中,所有x组成的空间”这句话是从代数角度来理解的,也就是求解这个方程组的解组成的空间既为零空间。
视角2: 把矩阵看作是向量的转换函数
还是从回忆开始【可以看到,对于新的概念完全是来自于之前所学,所以对于数学的学习每个概率的理解都不能马虎】:我们可以把矩阵看作是向量的函数(转换函数),拿旋转矩阵来说:
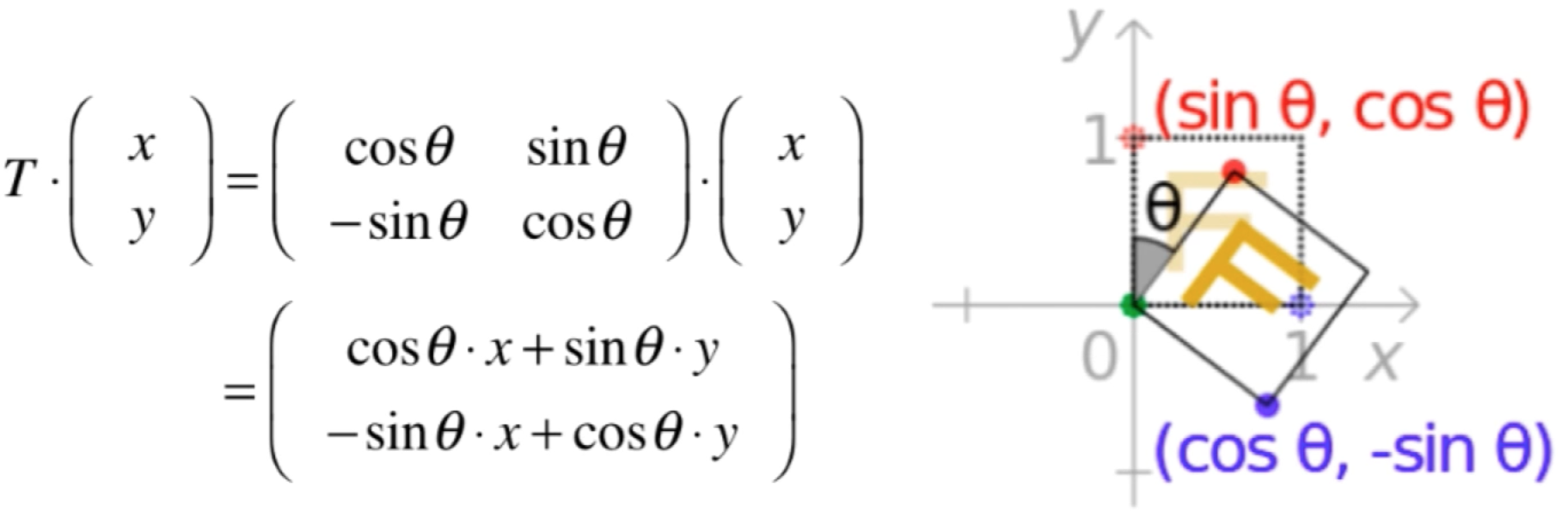
如果以这种视角来看待的话,其实可以把Ax=0中的系数矩阵A看成是一个转换函数,此时零空间x它就是这么一个空间:零空间是一个集合,集合中的所有的向量,在A的变换下,都将映射到零点!
视角3: 把矩阵看作是空间
对于矩阵还可以将其看作是一个空间,比如:
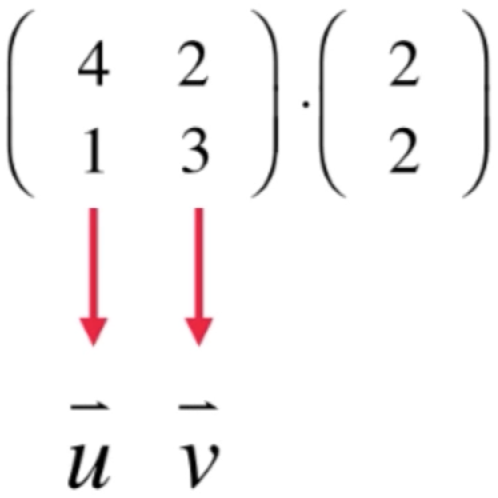
它对应的空间为:
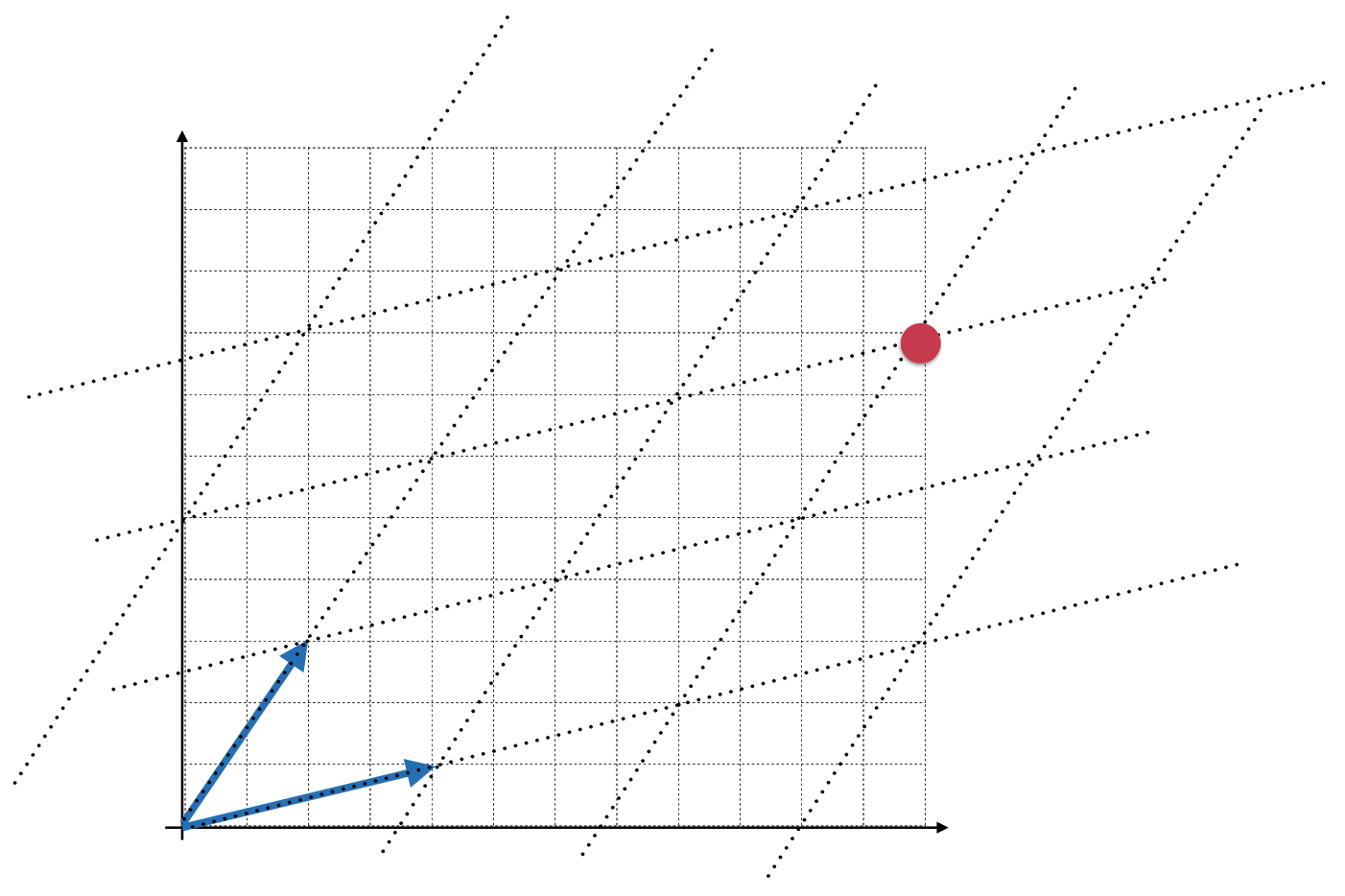
此时看零空间x就可以为:零空间是一个集合,这个集合中的所有的向量,和A的行向量点乘结果为0! 其实也很好理解,根据矩阵和向量的乘法的定义:
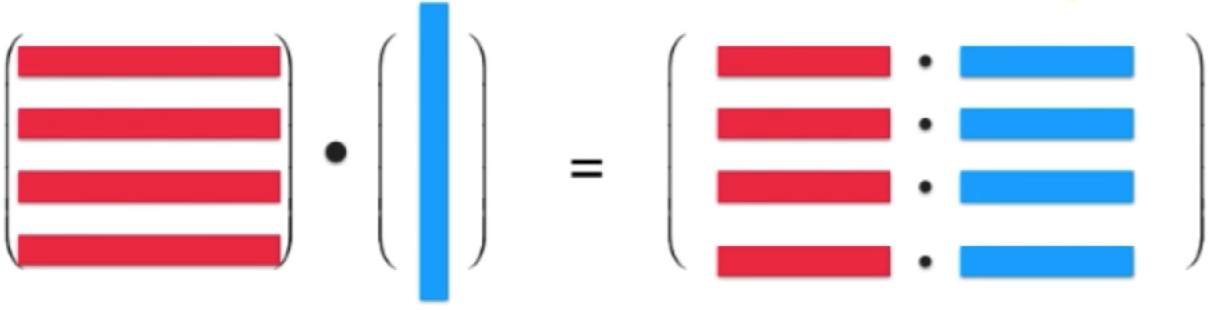
套到咱们的式子中:

根据这个进一步又能推出:“这个集合中的所有的向量,和A的行空间【注意跟上面的区别,A的行空间指的是 A的行向量通过线性组合方式可以生成的那些向量,这个集合比A的行向量要大得多,一个mxn的矩阵,它的行向量只有m个,但是它的行空间的向量可以有无数个的,m个向量任意线性组合那个k值随便取所得到的结果都在A的行空间中】中所有向量点乘结果为0。”,这是为什么呢?这是因为零空间的每一个向量和A的每一个行向量的点乘结果为0,而行空间的向量不过就是这些向量的线性组合,这些线性组合再点乘零空间的每一个向量,很显然结果还是为0,因为就是多了些系数嘛,可以稍抽象,不能理解的记住结论就好。
既然有“零空间的所有向量和A的行空间中的所有向量点乘结果为0”,又根据之前所学能推出:
“这个集合中的所有向量,和A的行空间中所有向量垂直(正交)。”,进而又能说明,“这个集合和A的行空间正交,换言之就是A的零空间和A的行空间正交【这个结论就能更加生动的理解零空间了】”,也就是说:“A的零空间中所有的向量,和A的行空间中所有向量垂直”,下面以图来说明:

对于这两个平面空间虽说是垂直,但是它不满足咱们要说的零空间的性质,典型的看相交的那一个直线就不是相垂直的,那对应于咱们所述的零空间的空间形态又是怎么样的呢?其实下面这个就满足:

也就是一个二维平面【二维空间】和一根直线【一维空间】相垂直,把这俩空间当成子空间的话,那么在直线上的任何一个向量和在平面上的任何一个向量都是垂直的,也就说明这两个空间的正交的,同理,对于由两根直线组成的坐标轴也就满足这个性质:
把直线看成是空间的话,从直线上任取两个向量一定是正交的。那从上面举的三种形态,是不是就可以说两个二维平面就不可以正交呢?

答案不是的,其实它在三维平面上是不可能正交,但是!!!在四维空间中是可以正交的,但由于四维我们大脑想象不到,所以对于零空间的理解依然还是很抽象的,不过上面的方方面面的各种视角的阐述一定是比直接给出一个零空间的定义在理解上要强很多倍的。
总结:
有木有发现,上面举了三个视角来看待零空间,其实之前学习矩阵的三个视角是一模一样的,这就是神奇之处,下面对零空间的三个视角再归纳总结一下:
矩阵A的零空间:
1、把A看作是系统:A的零空间,就是Ax=0中,所有x组成的空间;
2、把A看作是函数(变换):A的零空间,所有被A变化为0的空间;
3、把A看作是空间:A的零空间,是和A的行空间正交的向量空间;
零空间基与秩-零化度定理:
零空间基:
先来抛出一个问题:零空间的维度是多少?能否给出一组基?
由于零空间是齐次线性方程组所有的解构成的空间,所以从解齐次线性方程组开始,比如对下面这个矩阵进行求解,也就是将其化为行最简形式:
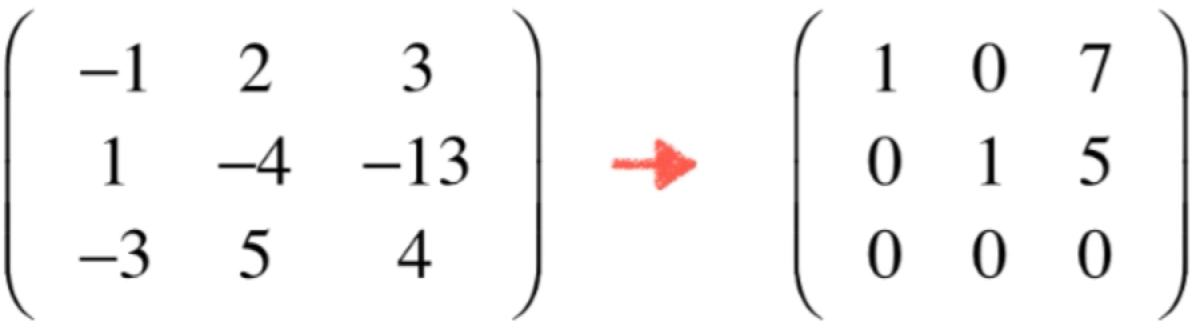
根据行最简形式此时就可以写成如下线性方程组:
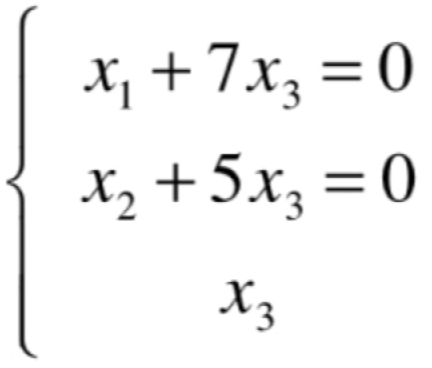
进一步的:
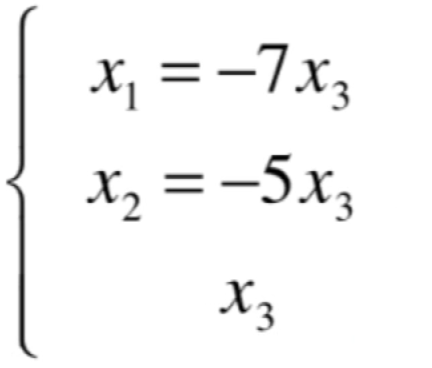
其中x3可以取任意值,都可以求解出x1和x2了,对于线性方程组的解就已经求出来了,但是!!面对零空间的话,还需要进一步,因为零空间所有解所构成的空间,每一个解其实都是一个向量,面对咱们这个解也就是对应于:
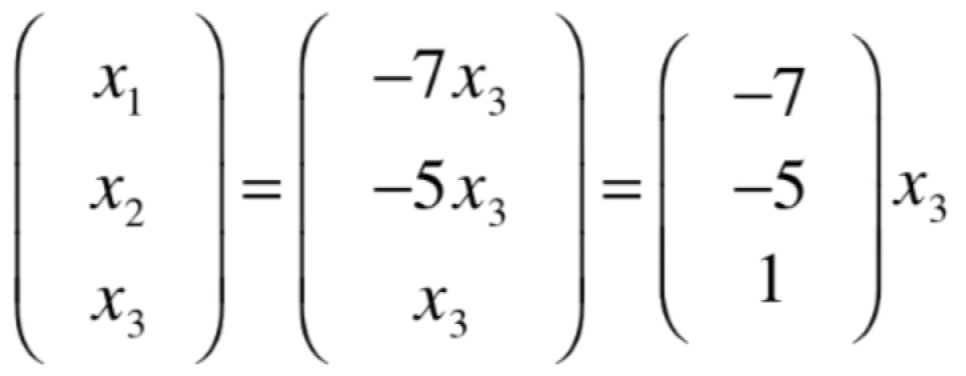
这样的形式就可以表示这个齐次线性方程组所有的解向量,也就是(-7,-5,1)这个向量所有的线性组合,也就是X3可以随便取,此时就可以得出这个矩阵A的零空间的维度为1,对应的一组基就为(-7、-5、1)。
下面再来举一个更复杂5x6矩阵的例子加深对于零空间维度的理解:

依然将其化为行最简形式,如下:

其中有两个非0行,对应的齐次线性方程的解为:
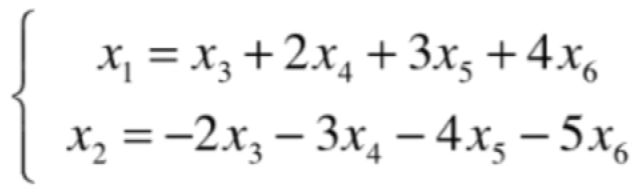
而由于x3...x6都处于自由列的位置,所以可以随便取值:

同样的可以将它写成解向量的形式,如下:
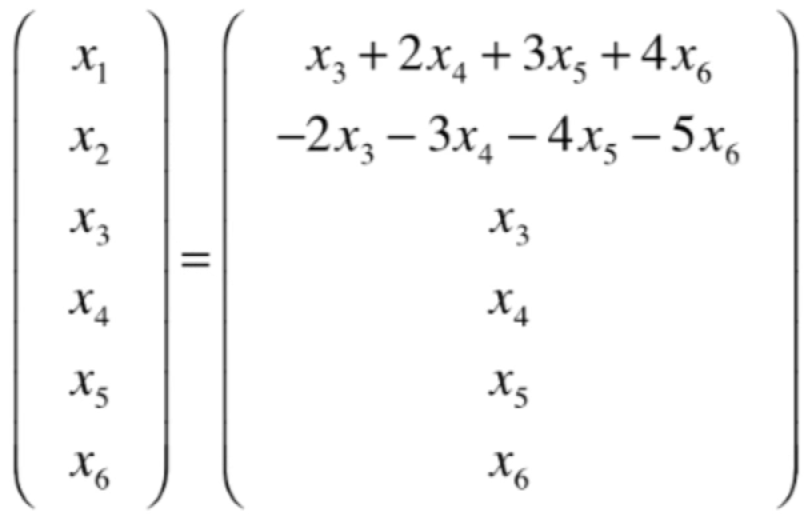
此时再将其拆解一下,每一部分只包含一个未知数,如下:
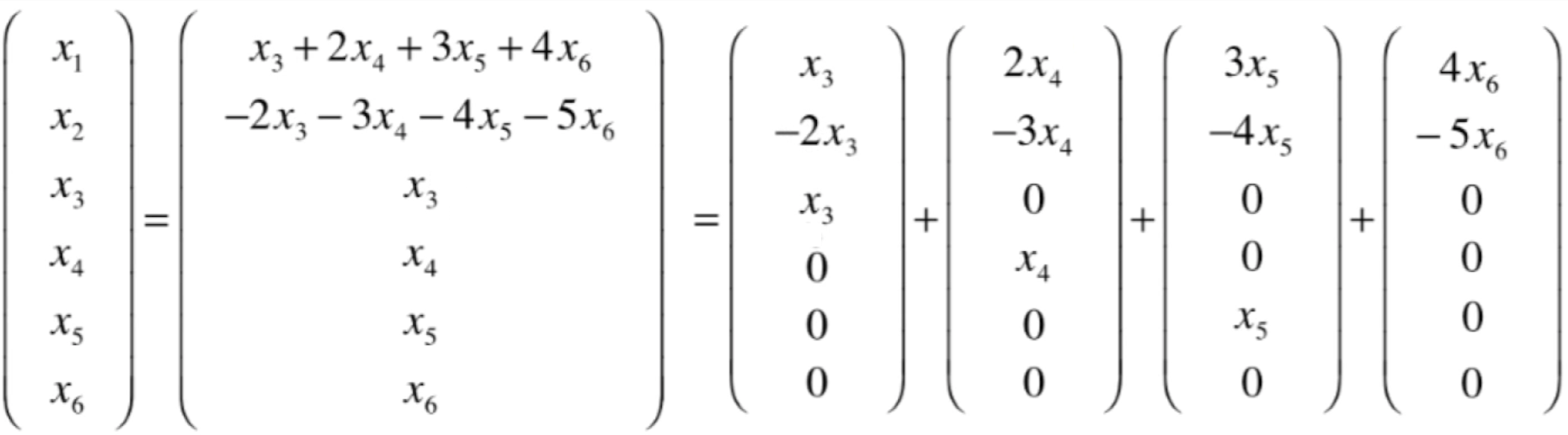
然后再进一步,将未知数给提出来: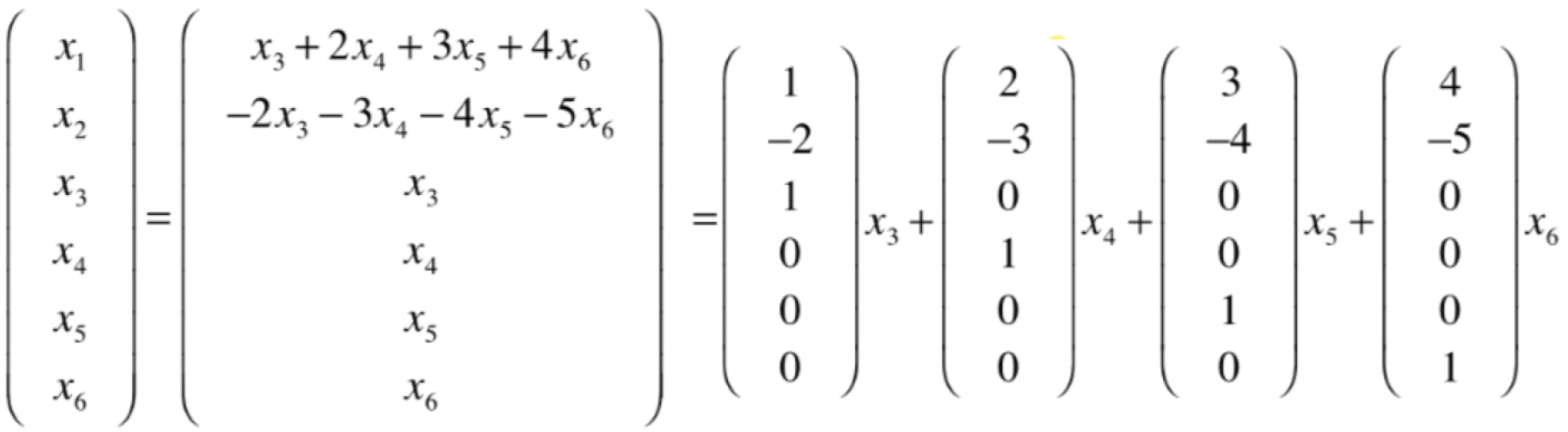
这形式是不是就是这四个向量的生成空间,也就是这四个向量的线性组合所能表示出来的所有的向量就是这个齐次线性方程组的解,换言之这个齐次线性方程组的角就是这个生成空间,进一步这个生成空间就是矩阵的零空间,所以此时对于这个矩阵A的零空间的维度就为4,因为这四个向量肯定是线性无关的:

下面来回忆一下上面的过程,将系数矩阵化为行最简形式,其中主元列是2个,自由列是4个:
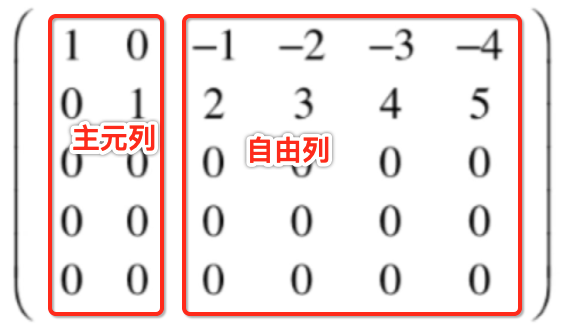
而自由列对应的就是这些未知数:
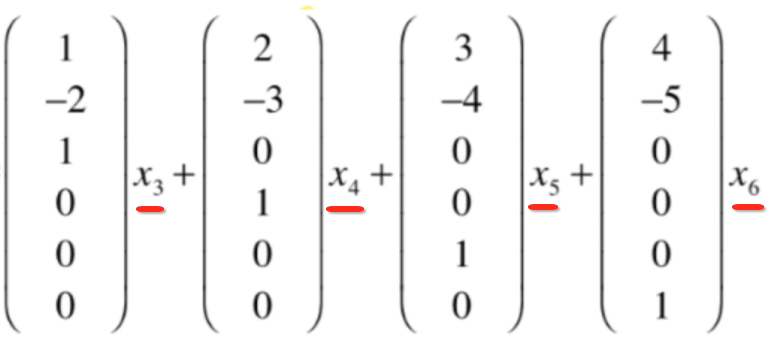
而其中对于这四个矩阵的元素是分为了两部分,看一下:
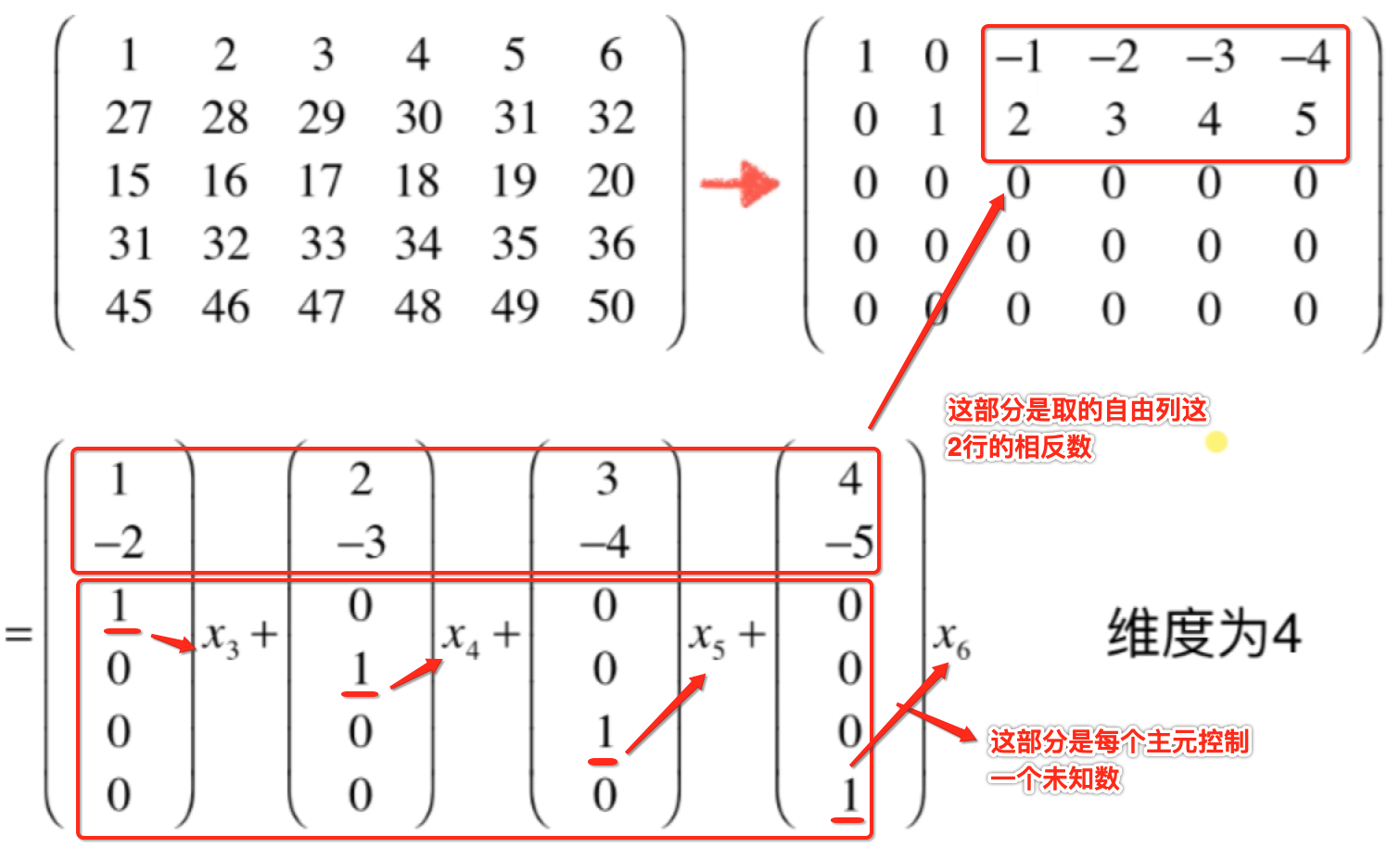
所以零空间的一组基就是上面的这四个向量。总结一下,其实零空间的基就是看化为行最简形式的自由列的个数就好了,而基的话就需要计算生成解空间中未知数的向量。
秩-零化度定理:
回忆一下上面举的复杂矩阵化为行最简形式的例子:
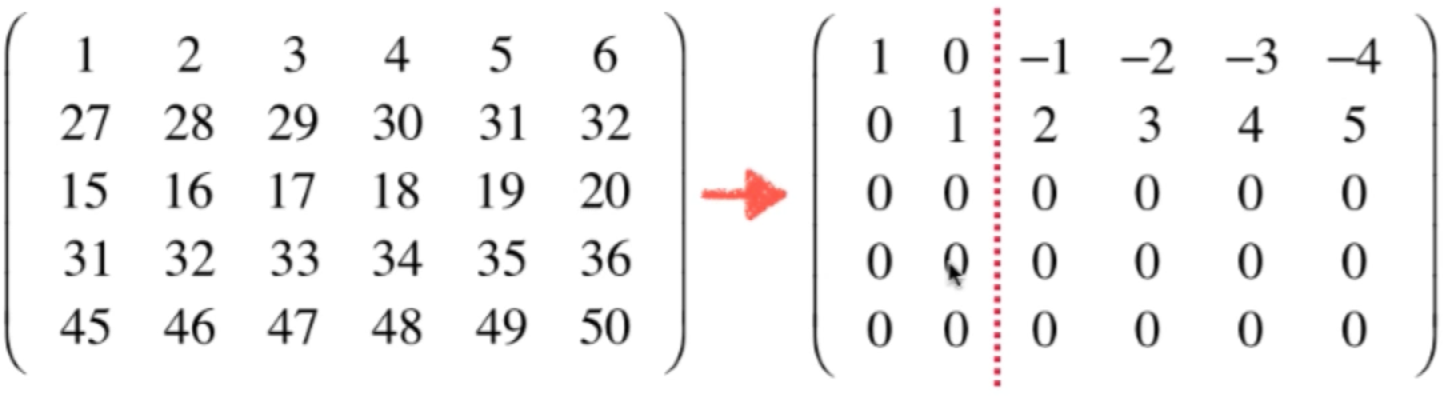
抽象一下来说:对于一个m*n的矩阵,将其化为行最简形式,主元列数就是列空间的维度,而自由列数就是零空间的维度,很显然又有一个结论:
列空间的维度+零空间的维度=n,好,小标题的概念要出现:
秩(rank)【列空间的维度】 + 零化度(Nullity)【零空间的维度】 = n,所以这就是 秩-零化度 定理。
列空间和零空间总结:
关于零空间的概念至此就学得差不多了,接下来对于列空间和零空间进行一下总结:
对于一个m行n列的矩阵:
列空间:
1、Ax=V(x任取);表示x可以随便取,相应所能得到的所有的v所组成的空间。
2、列空间是m维空间的子空间。这是因为mxn的矩阵,每一个列向量都有m个元素,所以是m维空间的子空间。
3、列空间的维度,为行最简形式中主元列数。
4、主元列的对应原矩阵的列,是列空间的一组基。
零空间:
1、Av=0;能让这个等式成立的所有v组成的空间。
2、零空间是n维空间的子空间。这是因为零空间中的所有的向量都是Av=0的一个解,对于A来说它有n个未知数,所以相应的解就有n个元素。
3、零空间的维度,为行最简形式中自由列数。
4、求零空间的基需要求解Av=0,求出来的角再进行一下变形,把它化为几个线性无关的向量,每一个向量控制一个自由元,它们的一个线性组合,这些向量就是零空间的基。
最后再来看一个问题:何时零空间的维度为0?由于零空间的维度就是自由列的个数,换言之也就是对于矩阵的行最简形式木有自由列,全是主元列,也就是列空间的维度为n,此时零空间的维度就为0,那对于方阵呢?既为满秩的时候,零空间的维度为0,其中又绕回到了方阵,是不是又想扩充等价命题,是的,如下:

左零空间,四大子空间和研究子空间的原因:
左零空间和四大子空间:
到目前为止已经学习了N多概念了,如向量空间、子空间、维度、行空间、列空间、矩阵的秩、零空间。 接下来先对这次所学习的若干个子空间以及它们之间的关系,进而引出一个左零空间这样的概念:

其中注意列空间和零空间符合表示法,在一些教材中可能会这样描述的,看到得要有印象,而根据“秩-零化度 定理”,我们就可以知道它们维度,如下:
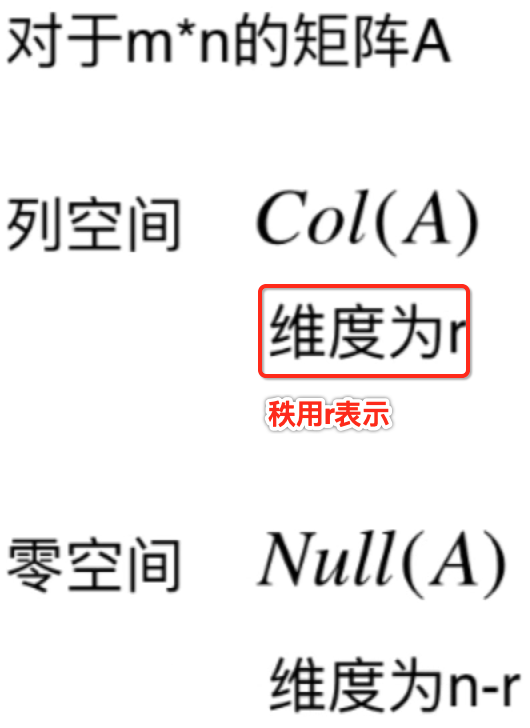
接下来再来回忆一下行空间,但是它不是用row这个符号来表示的哟,在学习向量时通常更喜欢用列向量,同时在学习矩阵时把它用一列列来排列能证明很多问题,所以也是更倾向于用列向量,所以,对于行空间也用列的符号来表示,如下:

稍加理解一下:行空间是由所有矩阵的行向量的线性组合组成的空间,将A转置过来,A的行向量就是A转置的列向量,所以A的行空间就是A转置的列空间,接下来分析一这三者的关系,其中对于行空间和列空间之间的联系就是它们的秩是一样的,而对于行空间跟零空间也存在关系,如下:

关于为啥正交,可以回忆上面的总结:

目前从关系图上看,明显缺了一个右下角的,也就是跟列空间对应的零空间一样,这块缺失的区域应该是A的转置的零空间,叫A的左零空间,
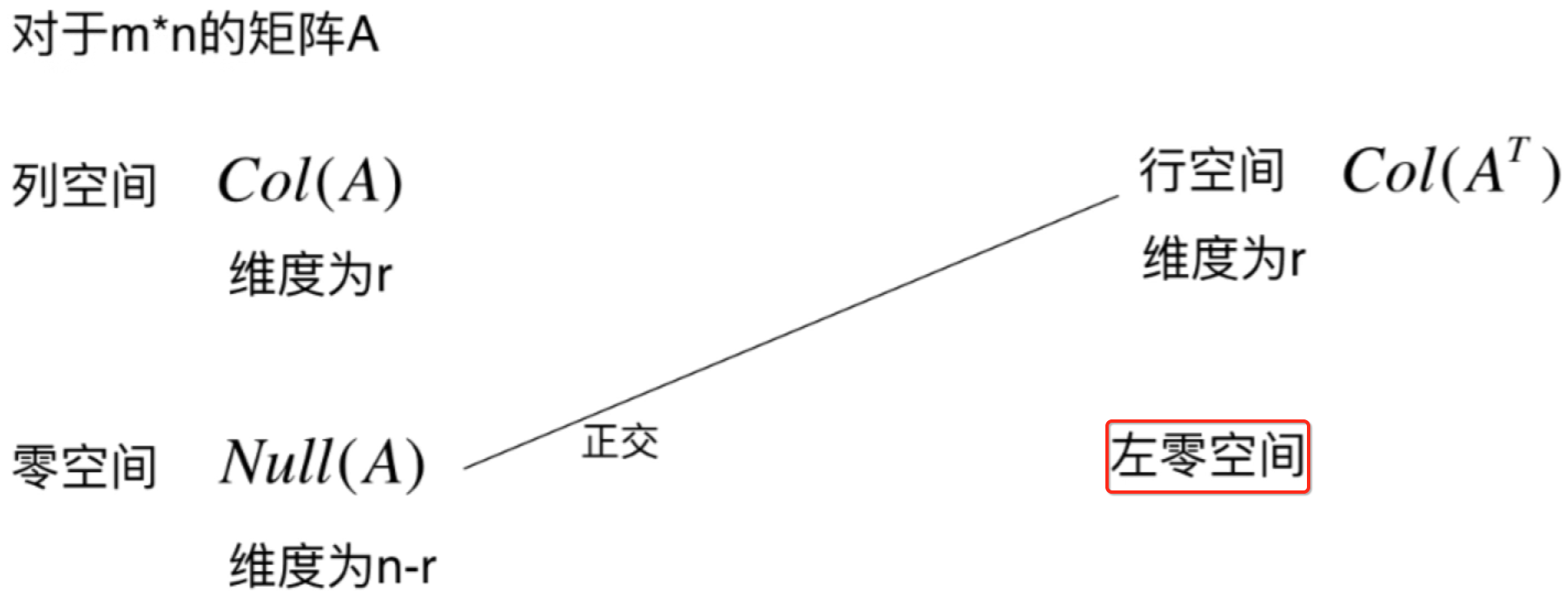
而对于它的维度可以很空间看出来,为:
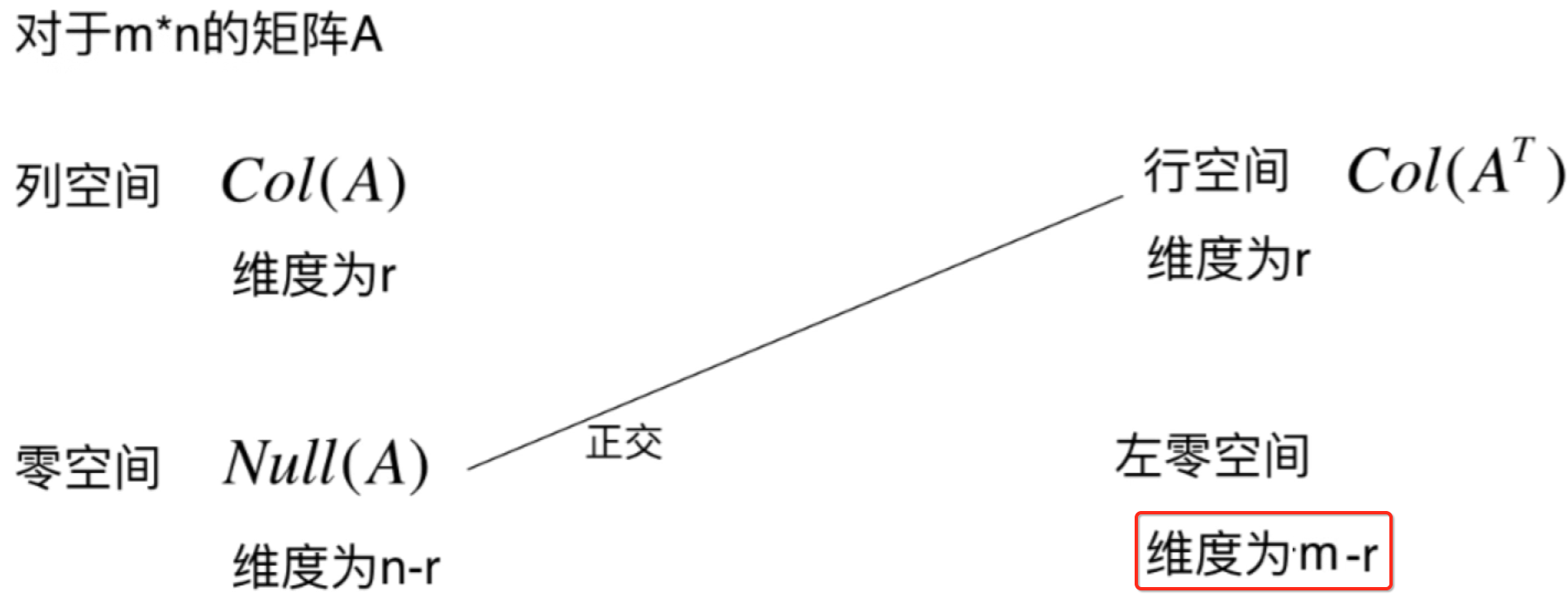
这是因为m*n的矩阵A的转置是n*m的矩阵,有m个未知数m列,转置的列空间为r的话,意味着A的转置的行最简形式的r个主元列,相应的就有m-r个自由列,所以A的转置的零空间【也就是左零空间】的维度就为m-r,相应的,它跟列空间也是成正交关系,如下:
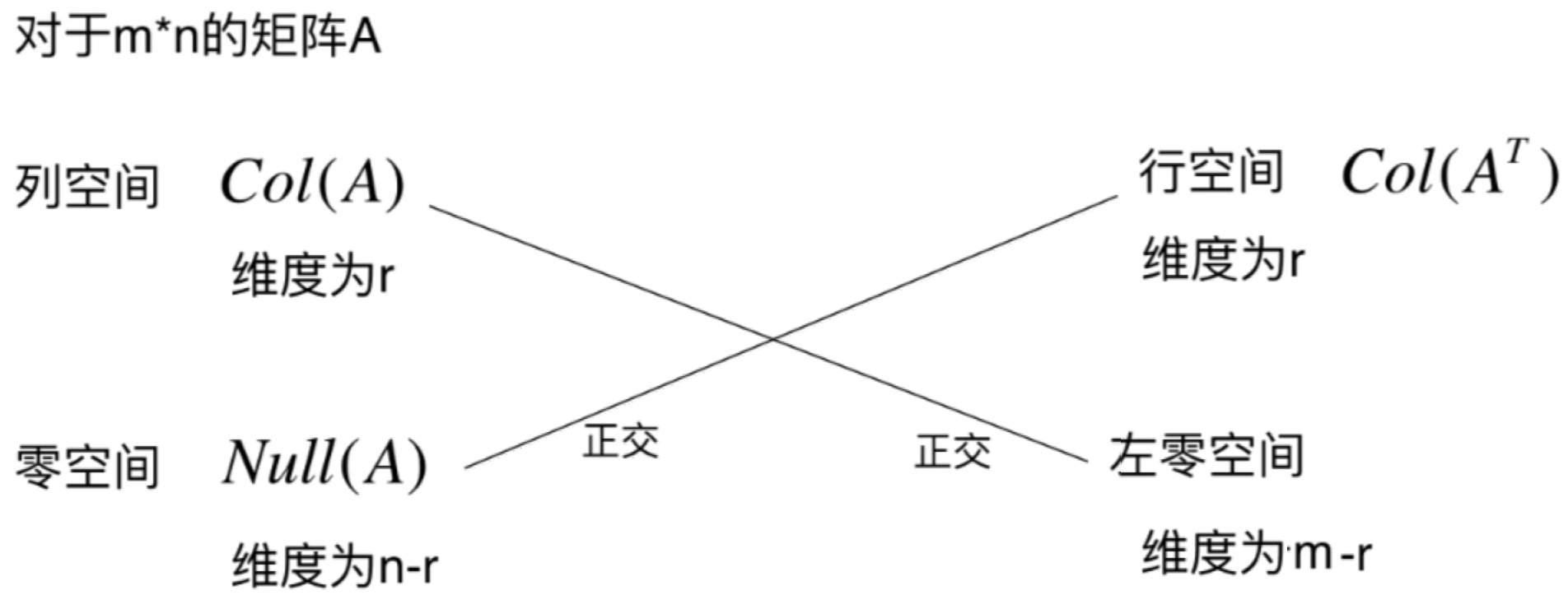
那接下来讨论一个问题:为啥A的转置的零空间叫做A的左零空间呢?其实可以从左零空间的定义来导出来,如下:
为啥A的转置的零空间叫做A的左零空间呢?
对于m*n的矩阵A,左零空间它的表示为:
而根据零空间就可以知道:
然后左右两边都取转置,式子就可以变换为:
此时就又可以变为:
这样来看,拿矩阵A来说是不是就推导出来左零空间是让x向量的转置乘以矩阵A=0满足这样条件的所有x所在的空间,其中x是左乘A【关键点】?此时就得跟零空间的进行一个对比了,它是满足Ax=0这样条件的x所组成的空间,x是右乘A对吧?所以一对比对于左零空间的概念理解起来就不模糊了。
研究子空间的原因:
最后来讨论一下为啥咱们要来研究子空间呢?
1、子空间维度大大降低,关于这块在上面有描述到,这里贴一下就不过多说明了:

而咱们学习的四大子空间就是构成更加复杂的降维子空间的一些基础。
2、子空间是其它一些应用的基础,这里举一个简单的例子:
很多真实世界的问题本质都是求解Ax=b的线性系统中的x是多少,但是!!在真实的世界中得到的这个知阵A可能是有很多行的,所以大概率的A的行数是大于列数的,也就意味着方程的个数远远大于未知数的个数的,也就意味着大多数情况Ax=b是无解的,但是无解并不代表这个问题就真正无解,可以求它的近似解也可以描述该问题, 此时就可以使用子空间来求解了,如何求呢?
先不考虑等号右边的b,只看Ax, 其实它就是矩阵A的列空间,矩阵x向量,以列视角来看的话,它等于向量的每一个未知数跟矩阵A中的每一列相乘最终再相加对吧?所以Ax就是矩阵A的列空间【不太理解的记得回看列空间的概念,列空间就是矩阵列向量所生成的空间】,只是过目前就是要找一个向量正好就是b这个向量呢?但目前A的行数大于列数,很显然大概率是找不到这个向量的,那怎么办?其实只要让b这个向量在A的列空间中, 只要在肯定是有解了,对于A的行最简形式的非0行的个数一定是小于等于n的,所以解决思路就是找A的列空间中离b最近的b',也就是求解:Ax = b',找到近似值最终此问题就有解了,而要找到b'看到木有就需要知道矩阵A的列空间,也就是四大子空间的一个,这也就是学习子空间的另一大意义。
对于上面的一大堆“费话”如果没理解也不要紧,言而总之,知道学习子空间是有“意义”的就成。
tips:这次学的真的概念太多了,也太抽象了,需要好好消化,为未来更加进一步打下坚实的基础。