线性代数学习之矩阵的应用和更多矩阵相关的高级话题
矩阵变换和矩阵在图形学中的应用:
前言:
在上一次https://www.cnblogs.com/webor2006/p/14265708.html中已经对于矩阵有了比较详细的了解了,这里则来看一下矩阵的一些具体应用,主要是在图形变换中的应用。其实之前在介绍矩阵其实就是向量的函数时就举了一个转换的应用了,回忆一下:
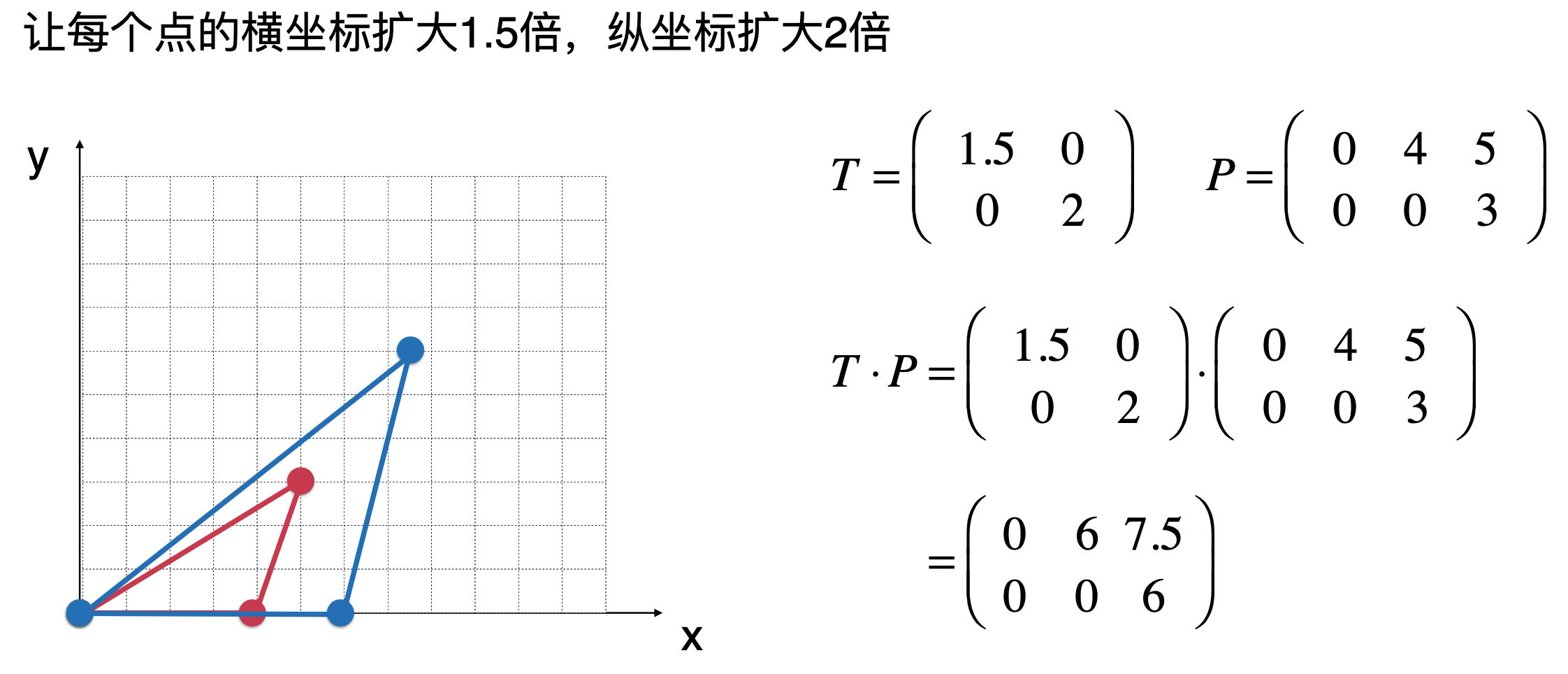
其中矩阵T就是transform的意思,这里就可以用一个抽象视角来看的话:
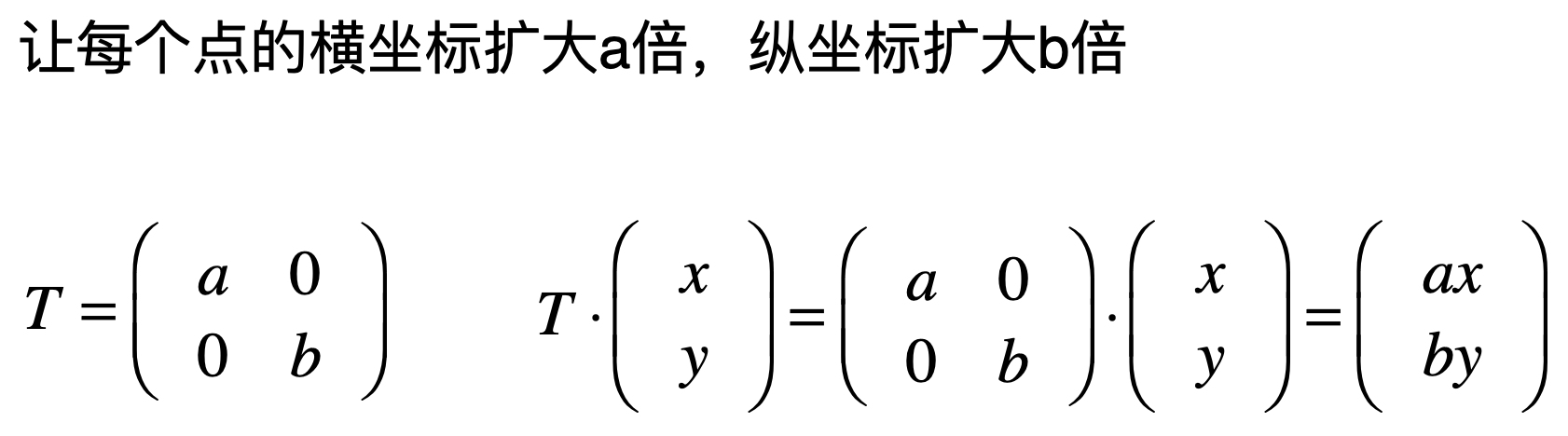
其中这种T的矩阵就是一种变换矩阵,其实对于变换矩阵可以有N多种,而一般的这种变换矩阵的应用通常是出现在图形学当中,所以下面从图形学的角度来学习更多的一个转换矩阵,当然图形里面的转换是非常复杂的,这里只是学习几种比较简单的,目的是为了进一步加深对于矩阵的乘法操作,因为对于图形的各种转换都需要用到矩阵的乘法。
更多变换矩阵:
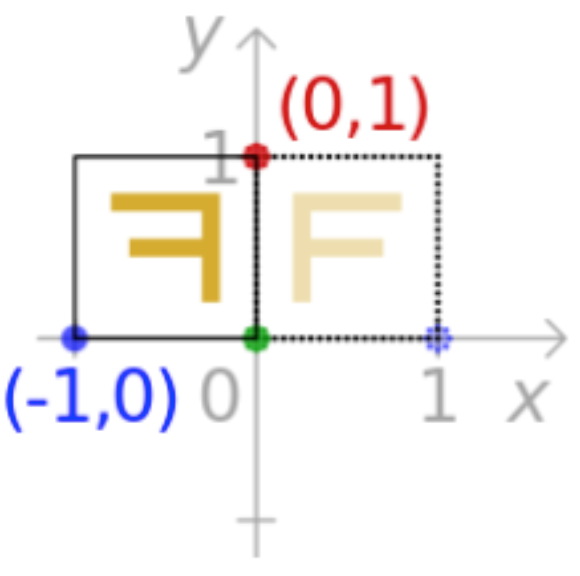
让每个点关于x轴翻转:
比如说这样的一个效果:
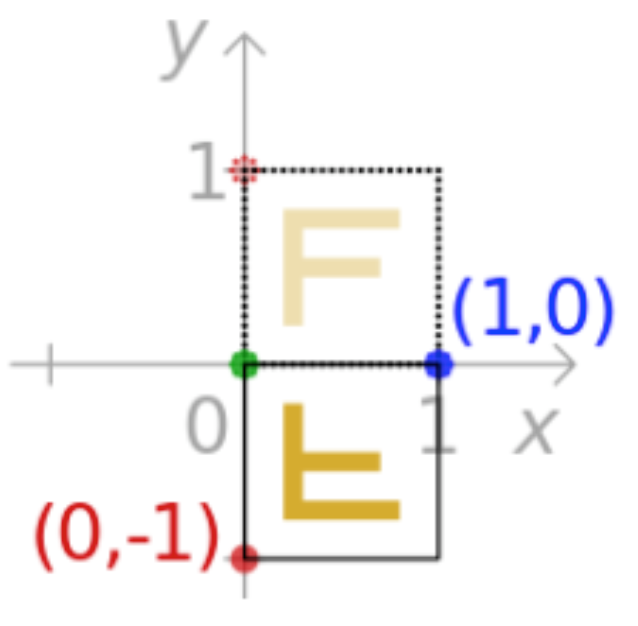
那怎么能办到这种效果呢?其实也就是要完成这样的一个式子:
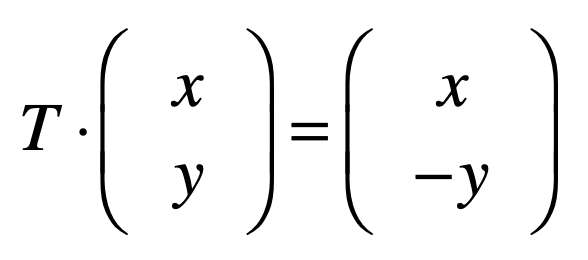
其中关键是这个T矩阵的求解了,首先先确定这个T矩阵的形状,由于矩阵x向量需要满足矩阵的列跟向量的行一样,所以很明显此时矩阵T的列是2列,而根据等号的向量结果是2行的,说明矩阵T的行是2行,所以它的形状是(2,2)的,所以此时T就可以假设是它:

这样的话,是不是就可以进一步进行计算成这样:
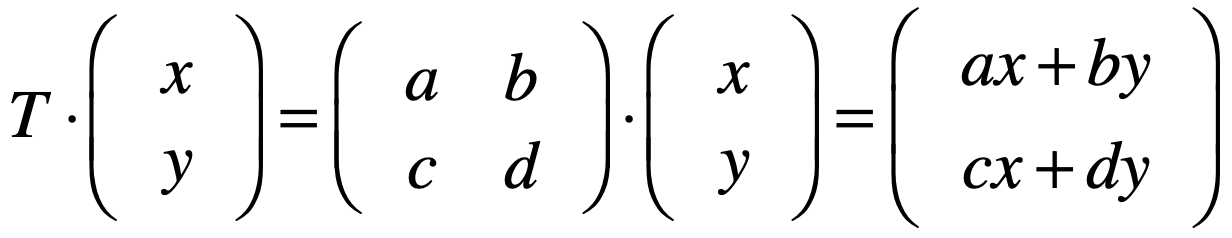
而根据最终的结果向量很容易就能求解出此矩形T的元素为:
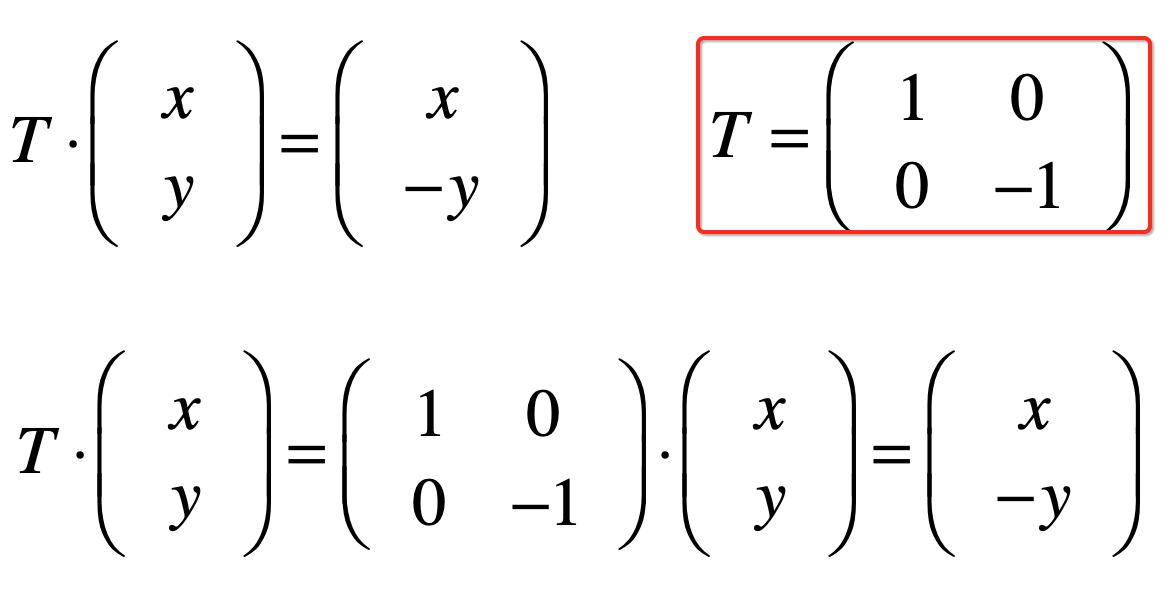
让每个点关于y轴翻转:
知道了让每个点关于x轴翻转后,换y转翻转就变得非常简单了,先看一下最终的样子:
这里直接给出结果:
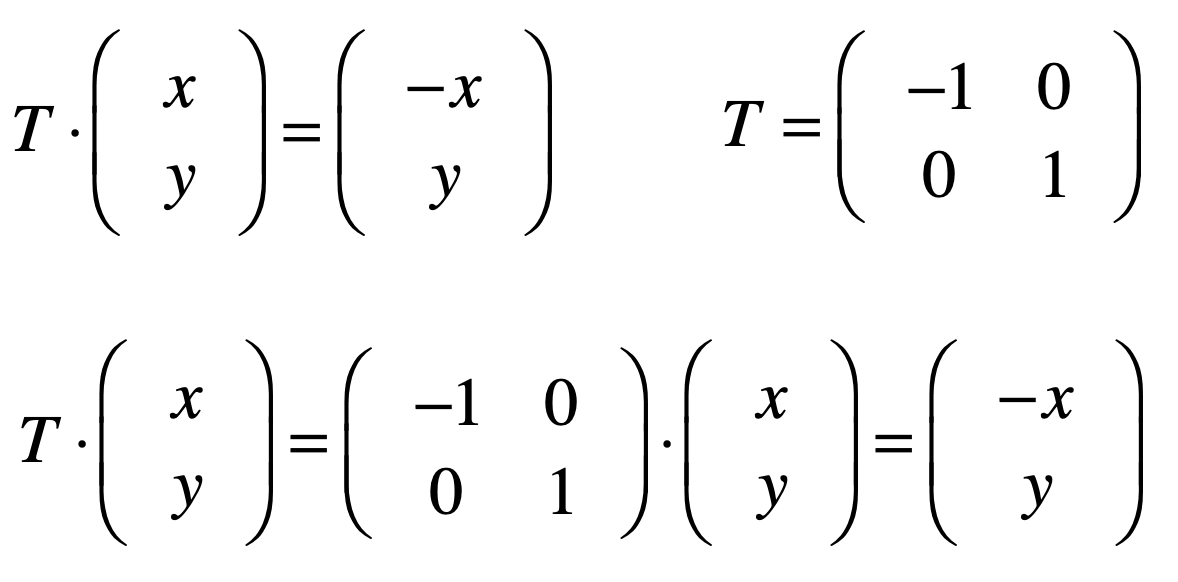
让每个点关于原点翻转(x轴,y轴均翻转):
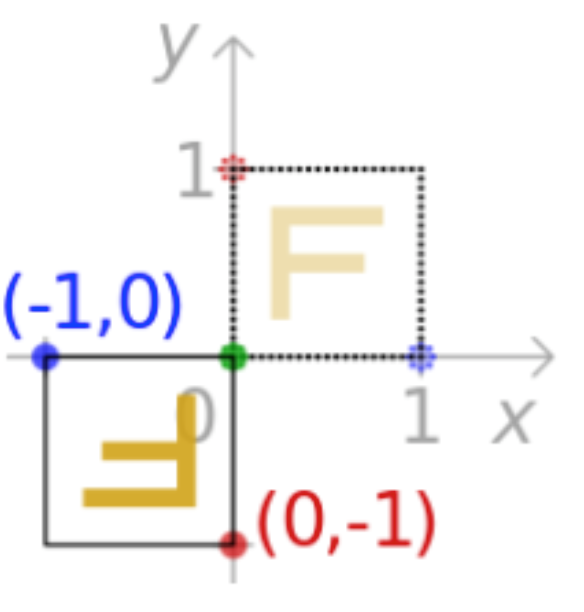

其实有一个更加直观的计算方式,既然我们已经知道向X轴翻转和向Y轴翻转的矩阵了:
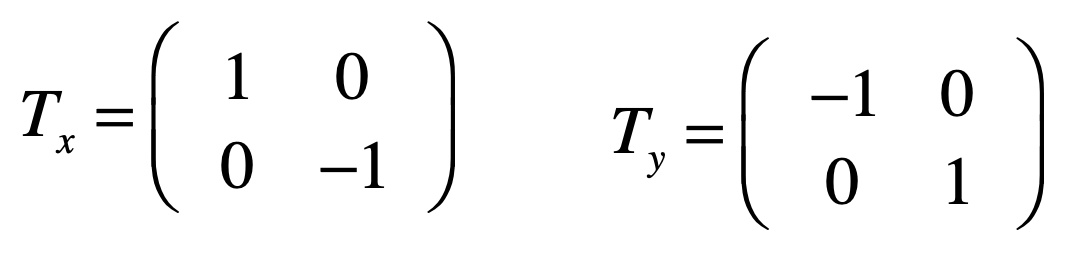
那么先让咱们的点进行x轴翻转,完了之后再让其进行y轴进行翻转,是不是就是这样的一个运算?
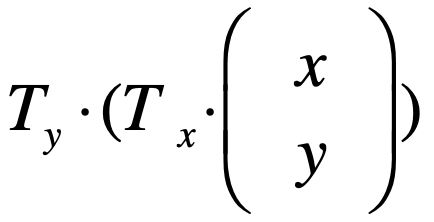
而根据矩阵乘法的结合率来说,变换一下也可以求出这个变换矩阵:
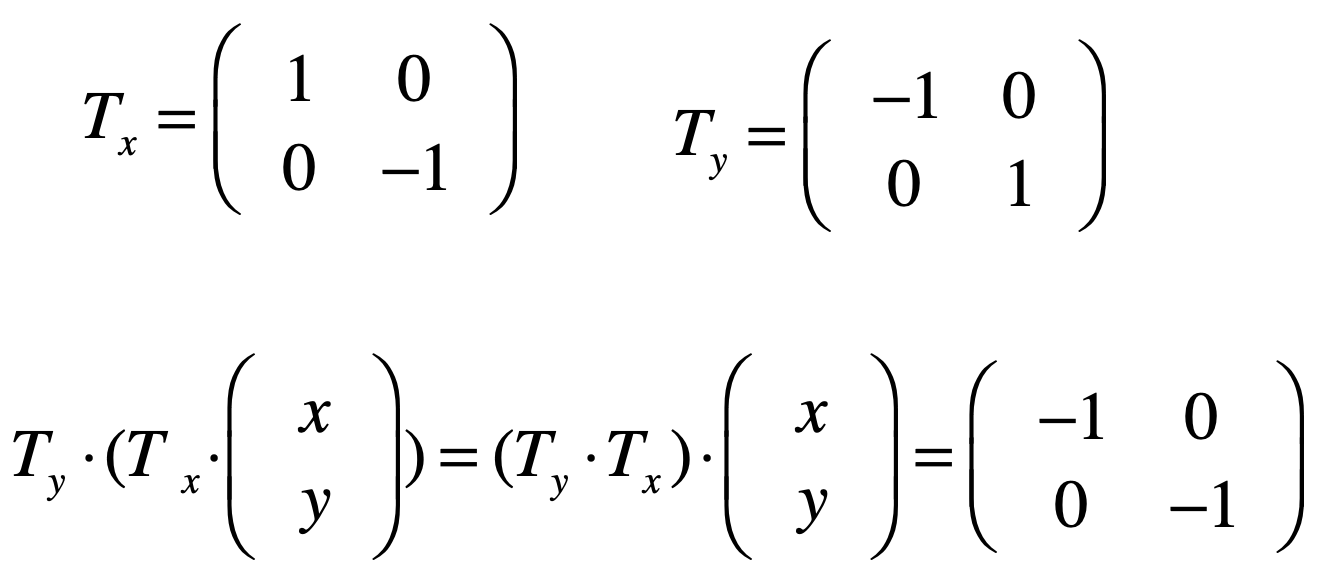
沿x方向错切:
在图形变换中还有一种比较常见的效果,如下:
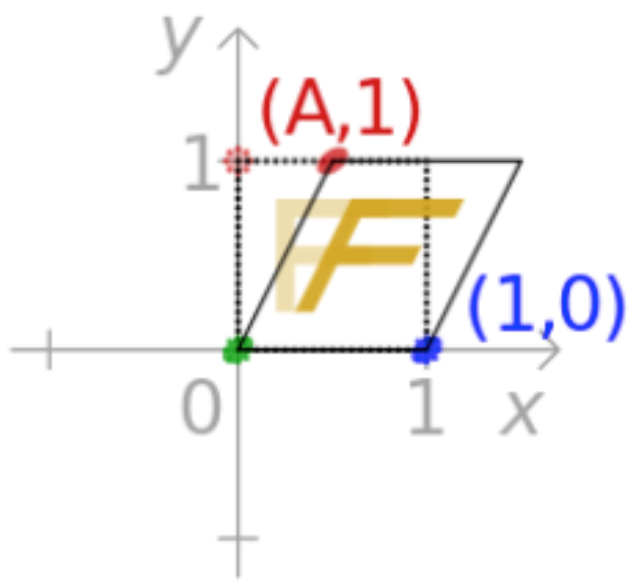
其中y值不变,只是让x进行一定的变化,其中x坐标的变化让其跟y坐标成一定的比例,具体就不推导了,直接给出结论:
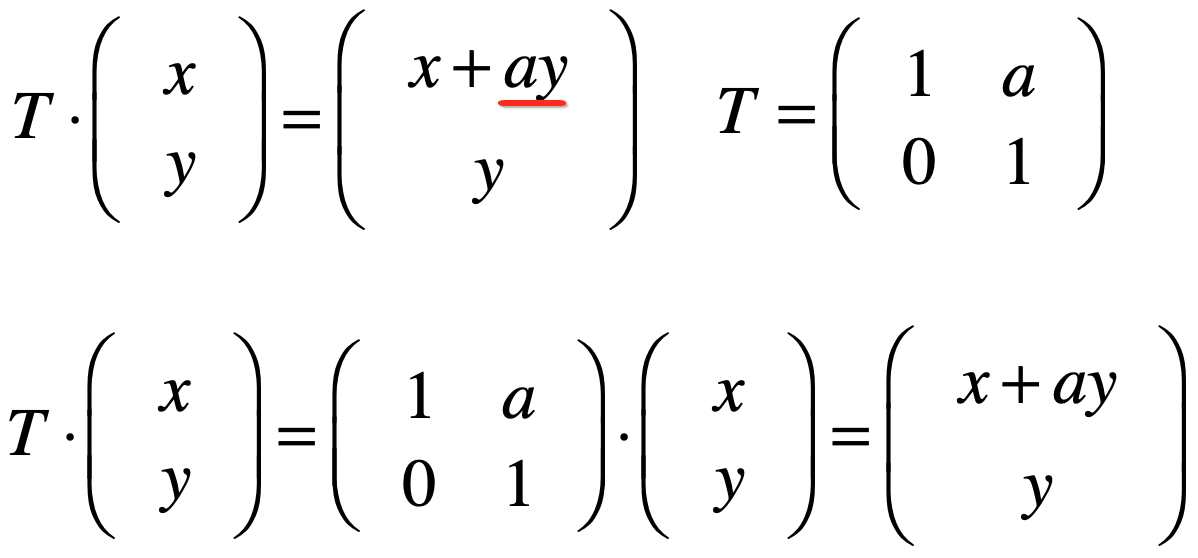
其中错切的幅度是可以自由定义的。
沿y方向错切:
类似的,也可以沿y方向进行错切,如下:

其变换矩阵为:
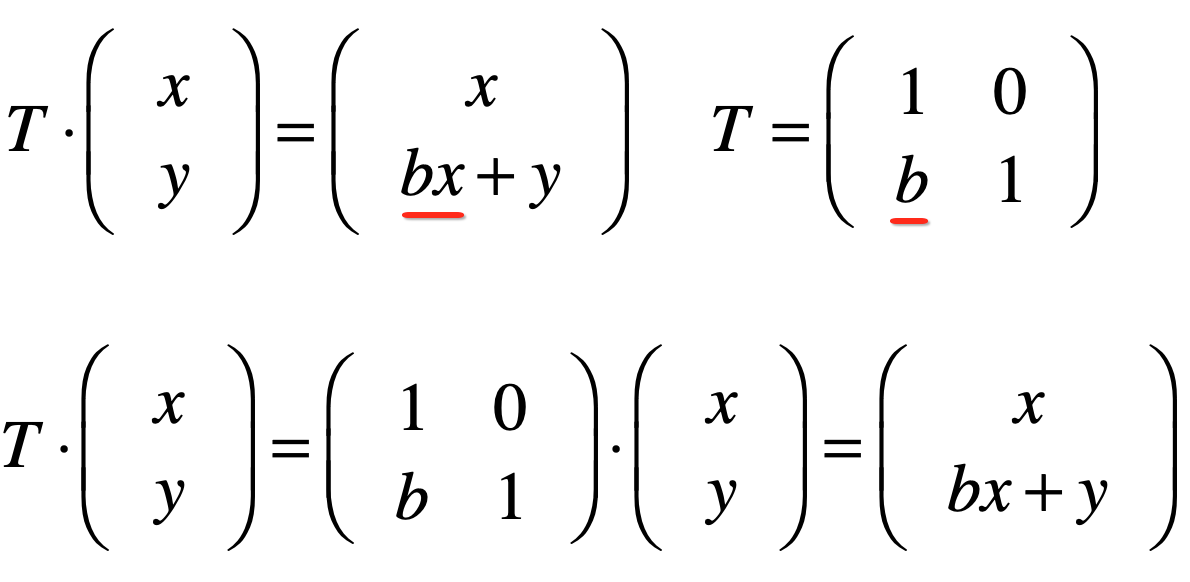
矩阵旋转变换:
接下来在图形中还有一个非常之常见的矩阵变换,那就是旋转变换,如下:
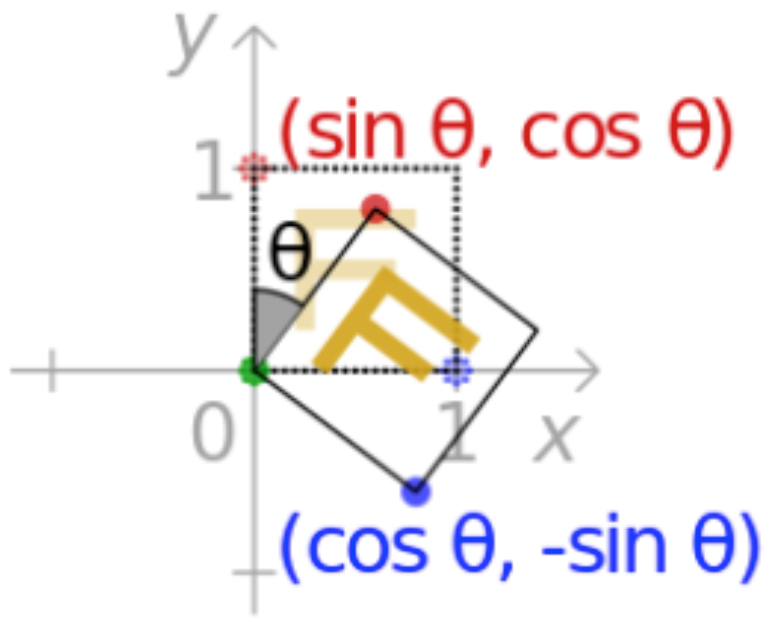
为啥要单独起一个大标题呢?因为这里要来见证一下它的推导过程,这块的变换是比较麻烦的,如图所示需要用到三角函数的知识,不过也不难,下面一点点来看一下是一个什么变换矩阵能达到此效果:

其实也就要找到一个矩阵T,但是呢由于最终转换的坐标咱们也不知道,所以说这个旋转的核心是要确定等号右边的这个结果坐标的计算,那如何确定结果坐标点呢?这里回到二维坐标上来:
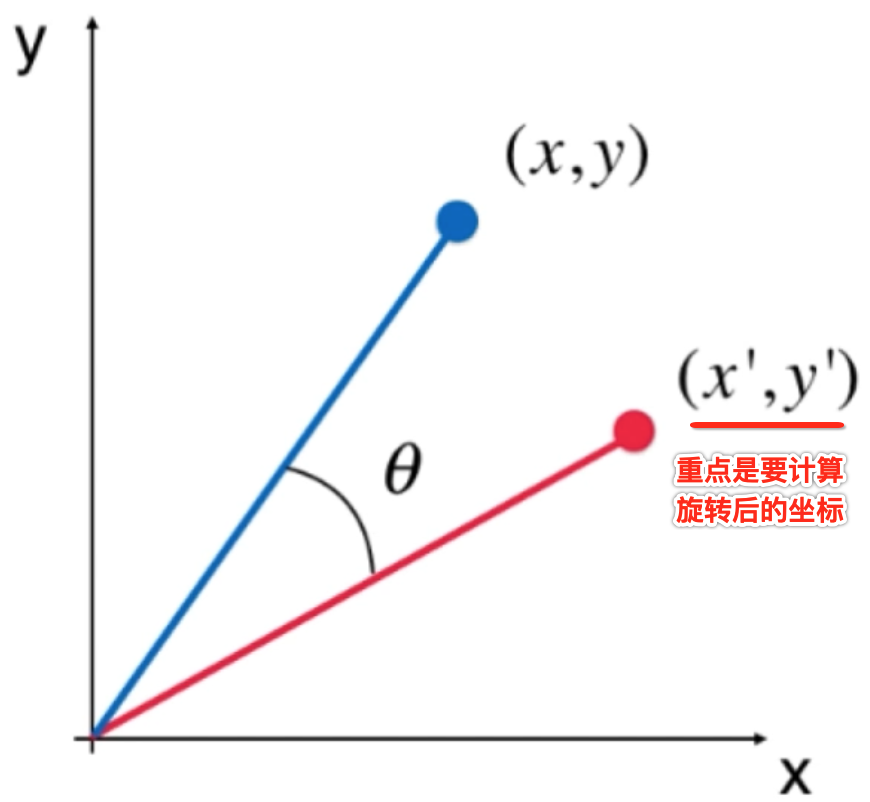
此时需要假设啦,假设(x,y)跟x成这样的一个角度:
然后假设向量(x,y)的模是d,关于向量的模这里回忆一下:

也就是:

此时可以列一个等式了:
![]()
此时d就等于:
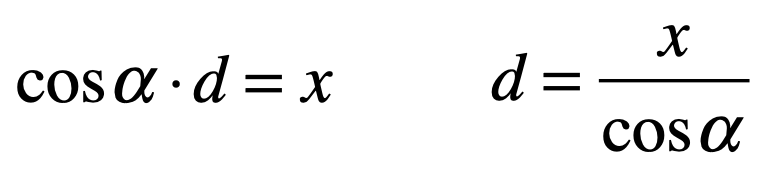
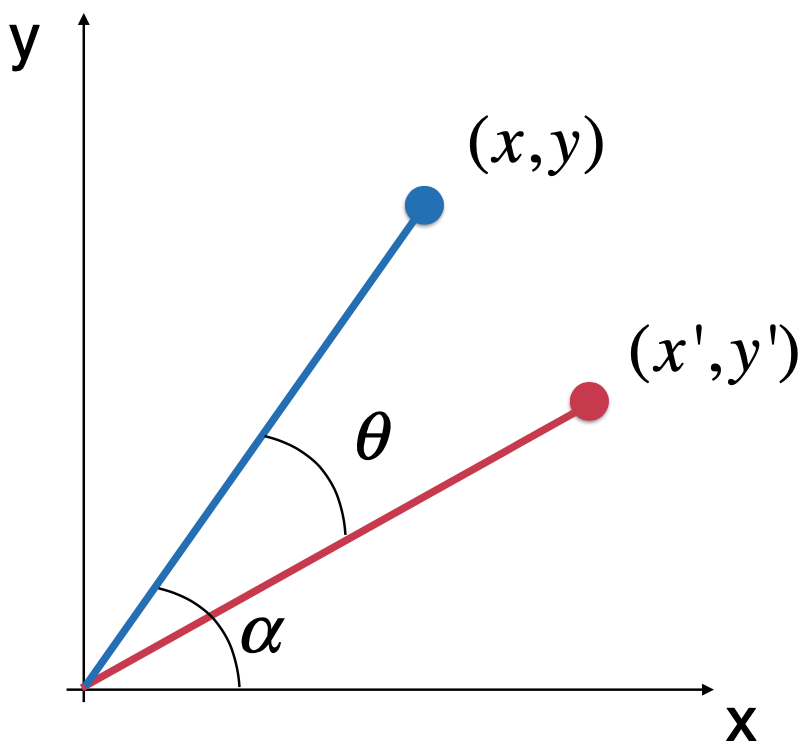
同样的对于y,也有类似的等式出现,如下:
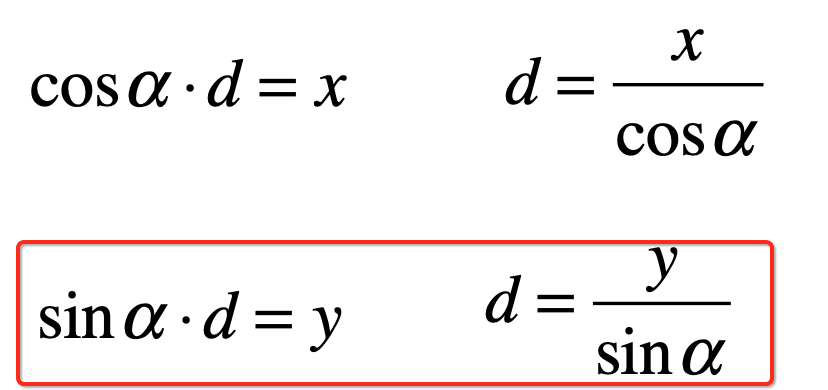
而对于旋转后的坐标来说,由于它的模跟(x,y)的模是一模一样的,也就是向量的长度没变,此时又会出现如下等式啦:
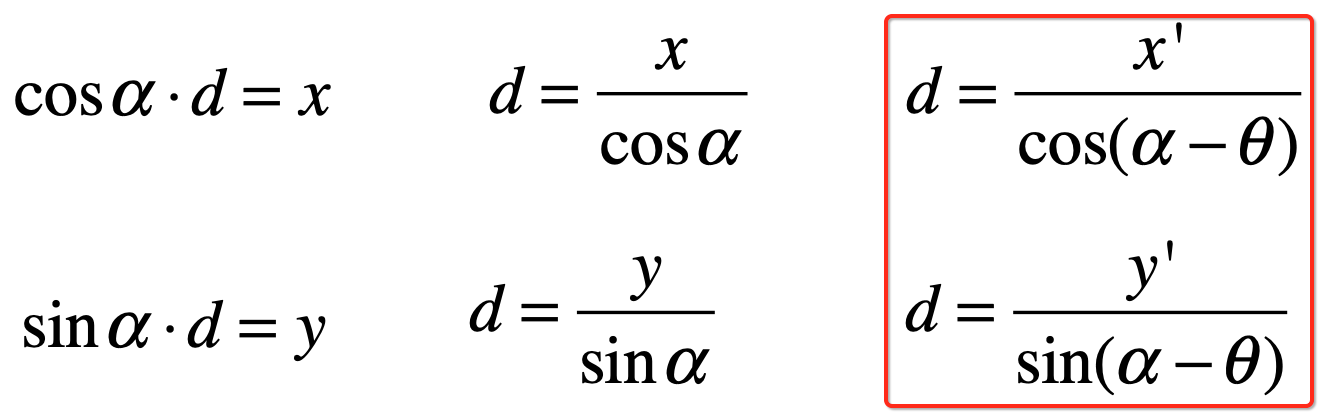
那既然都等于d,就可以形成一个方程式了呀:
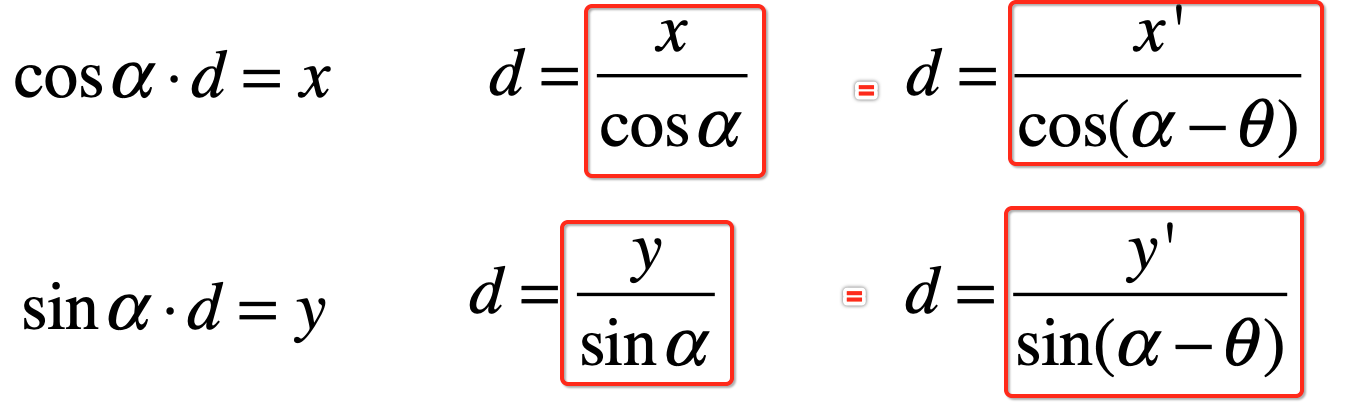
此时就可以算出x'y'啦,如下:
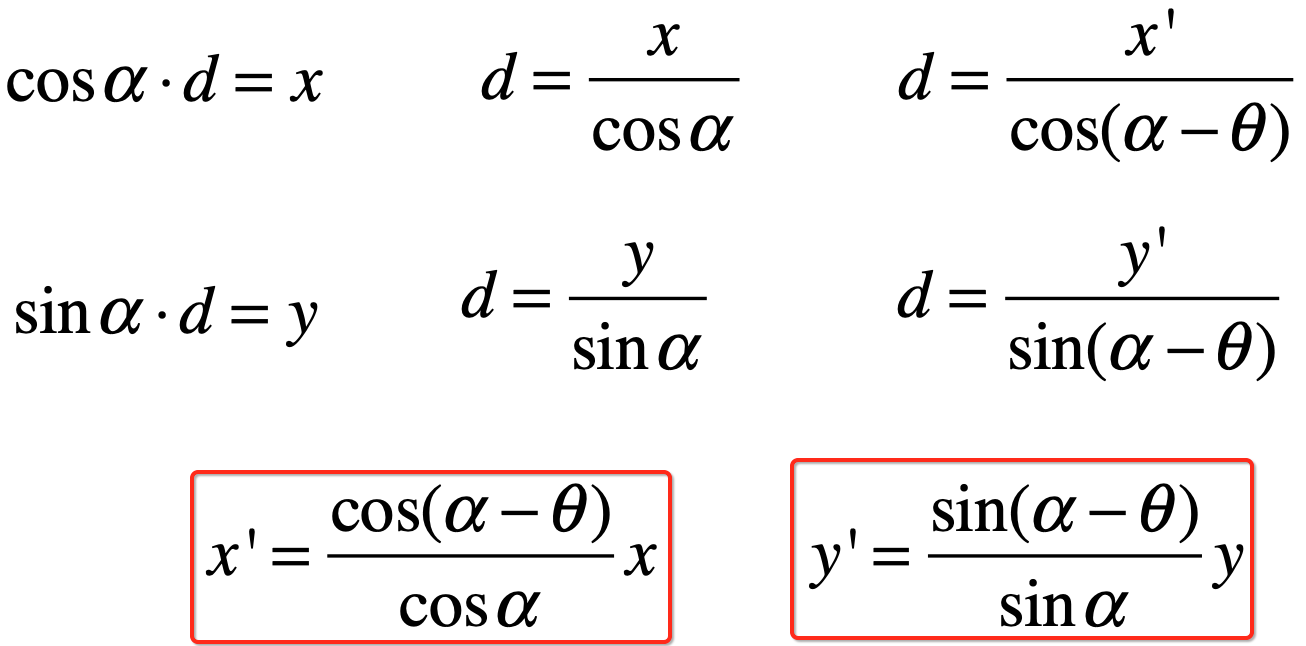
接下来就可以进一步演化啦,先来看x'的进一步演化,不过这里得先用到两角和差的公式了,先来回忆一下这公式:

此时就可以变换为:

此时再来分解为:
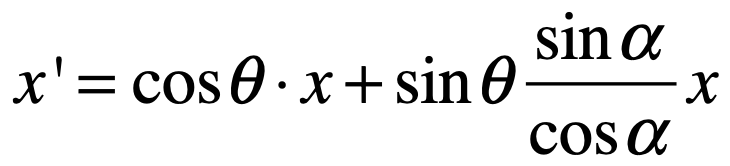
而sina/cosa就是tana,这又是啥依据呢?自己其实可以推出来,这里就不过多说明了,比较简单,而tan函数回忆一下:

所以:
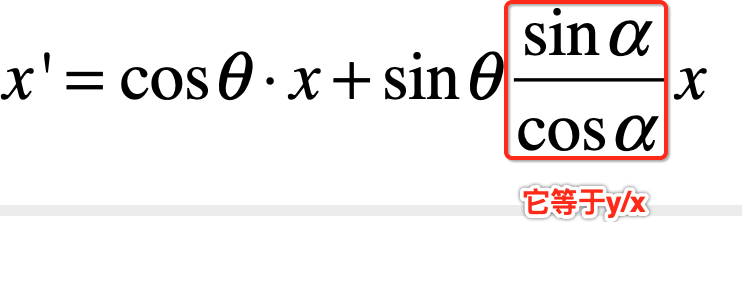
所以最终又可以变为:
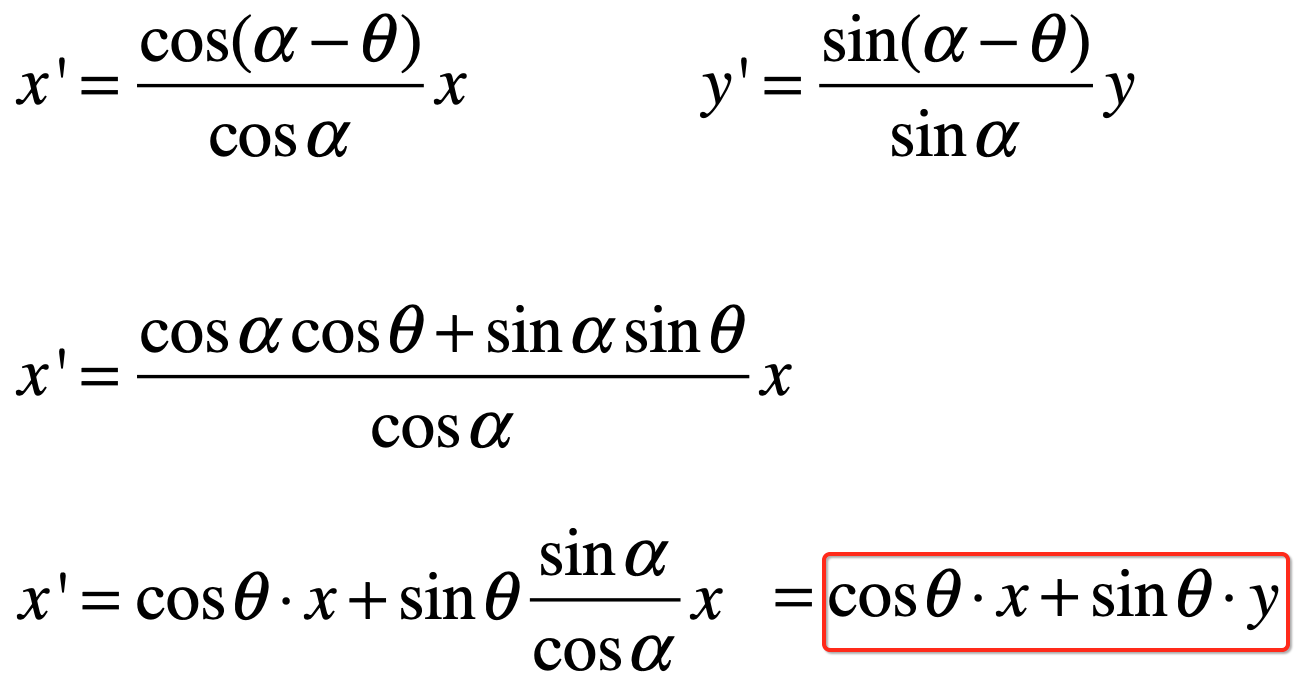
同理,对于y'也可以最终算成:
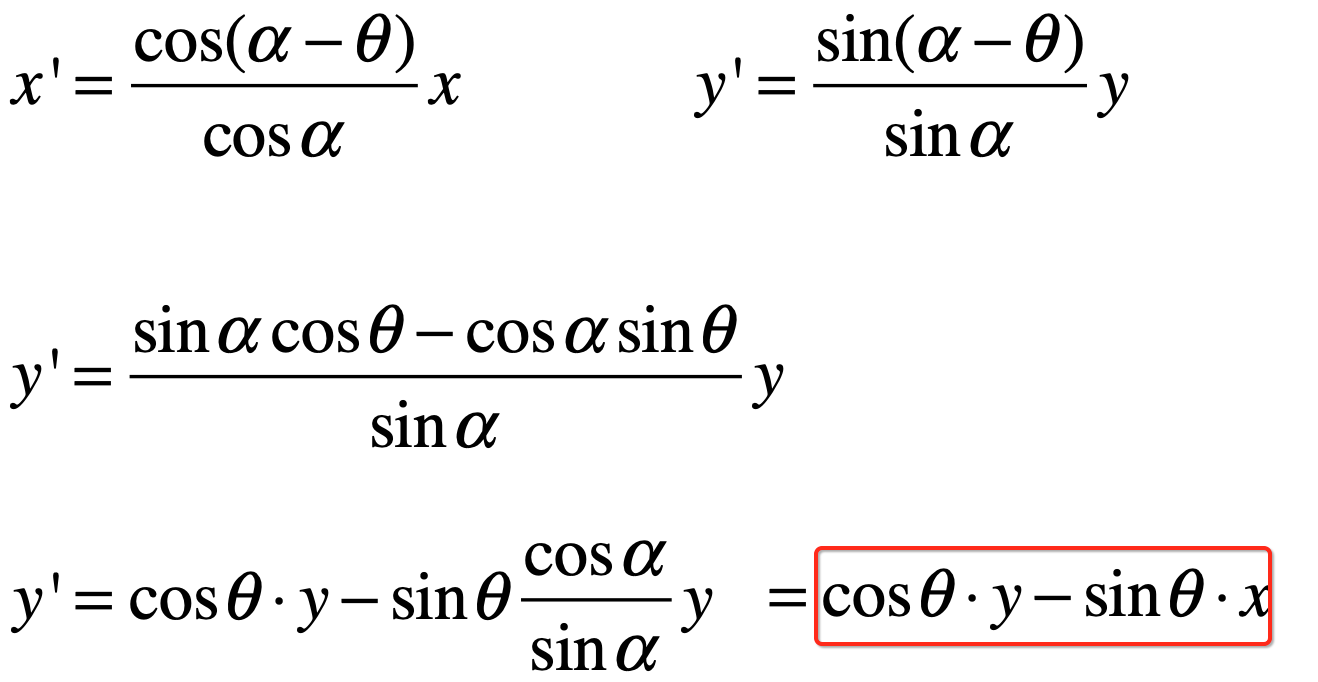
所以,此时再回到咱们的目标旋转式子来,=号右边的就可以确认了:

此时再算变换矩阵T就非常容易啦,如下:
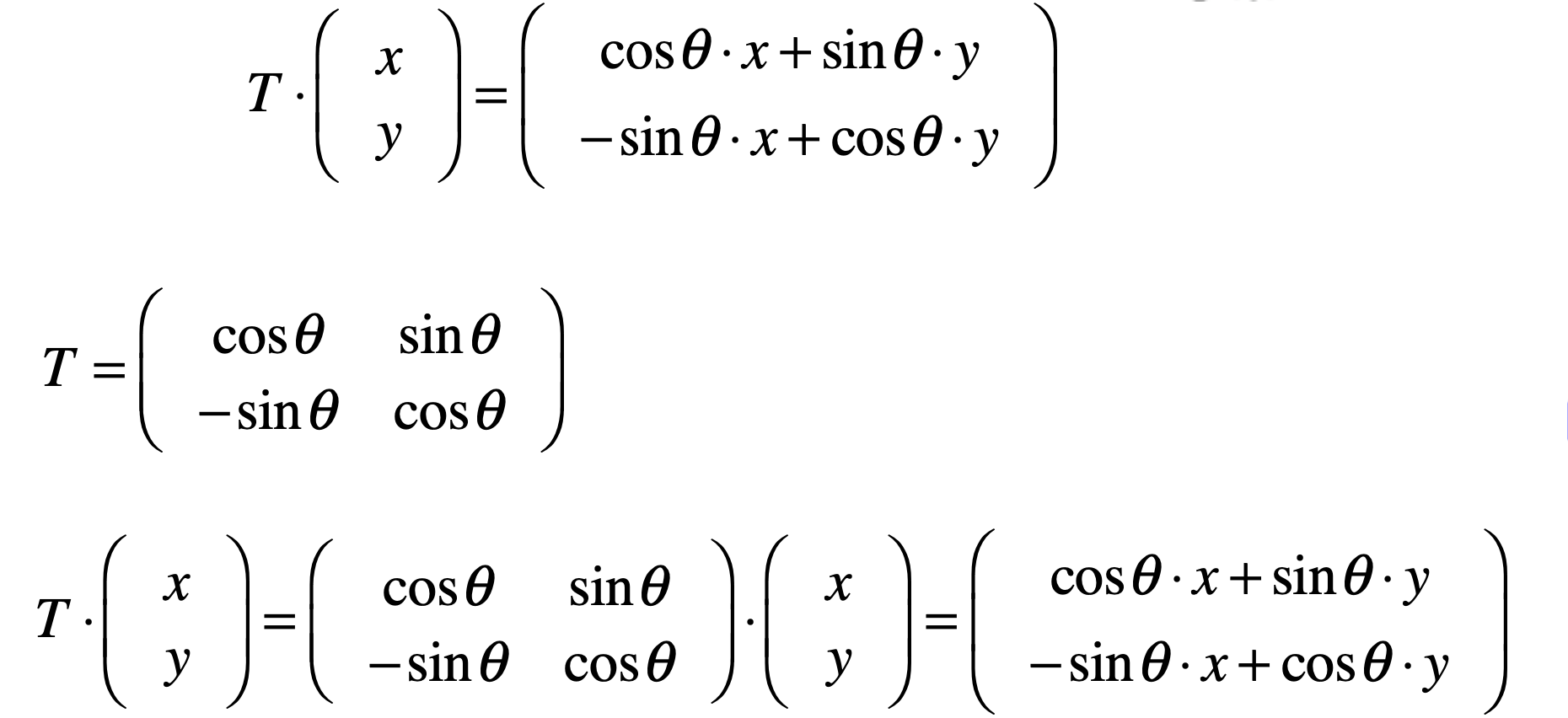
实现矩阵变换在图形学中的应用:
在上面说了这么我矩阵的变换效果,下面则回到python的世界中实际应用一把。
新建文件:
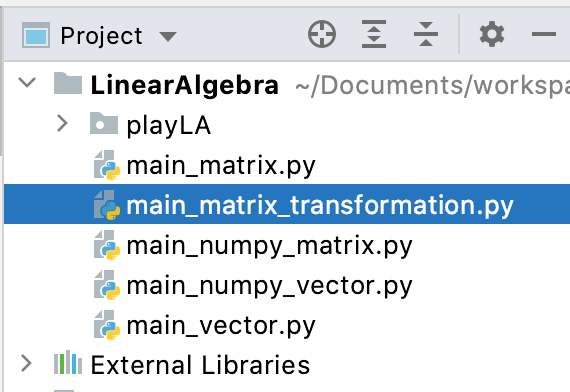
其中先定义一个F样子的坐标点,如下:
if __name__ == "__main__": points = [[0, 0], [0, 5], [3, 5], [3, 4], [1, 4], [1, 3], [2, 3], [2, 2], [1, 2], [1, 0]]
添加绘制相关的包:
由于需要进行图形的绘制,所以这里需要导这么一个库:

对于这个库如果安装了Anaconda会自动安装它的。
将坐标点绘制出来:
这里先将获取所有的x轴的点和y轴的点,如下:
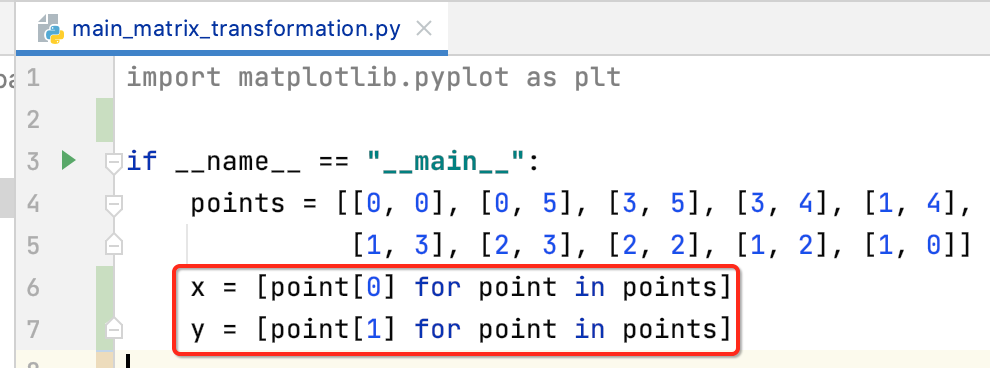
然后就可以调用绘制库将其显示出来了,如下:

运行:
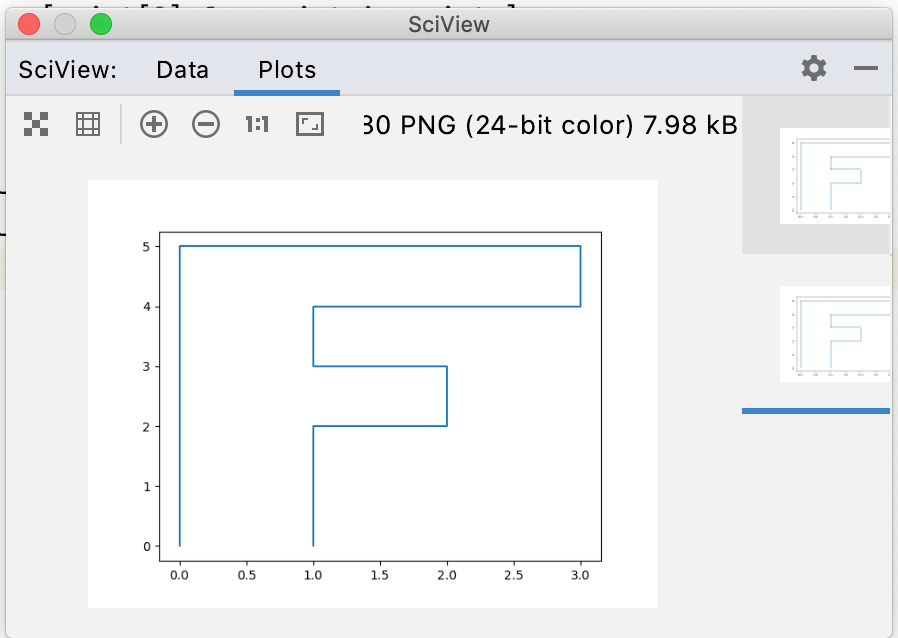
但是感觉这绘制出来的不太好看呀,这是因为看到x轴和y轴的单位都不一样,需要设置一下:
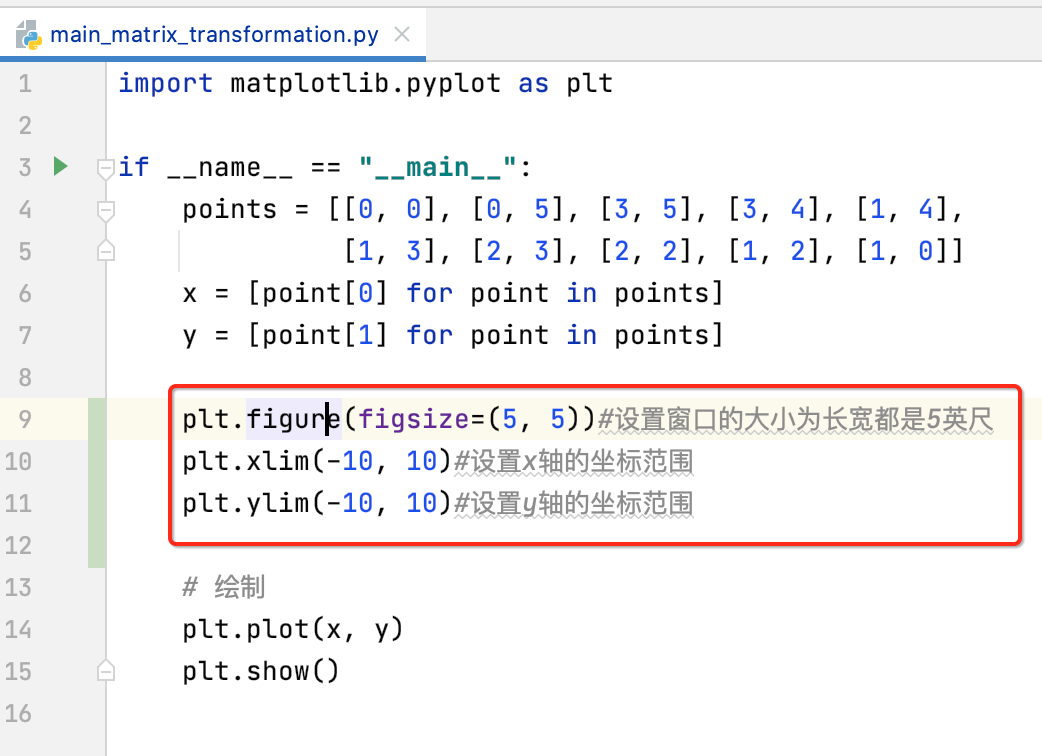
再运行:
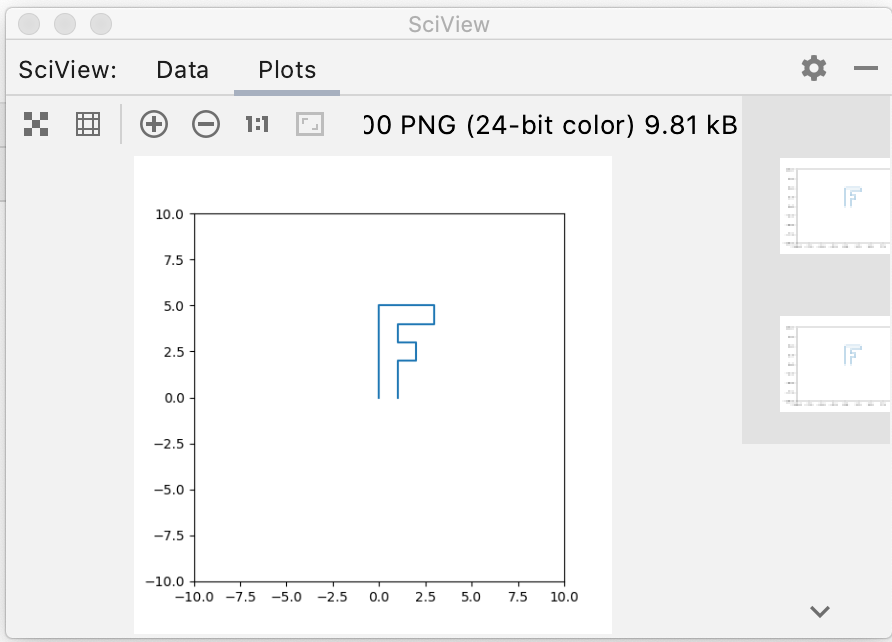
嗯,正常了,接下来就可以开始领略一下矩阵的各种变换效果啦。
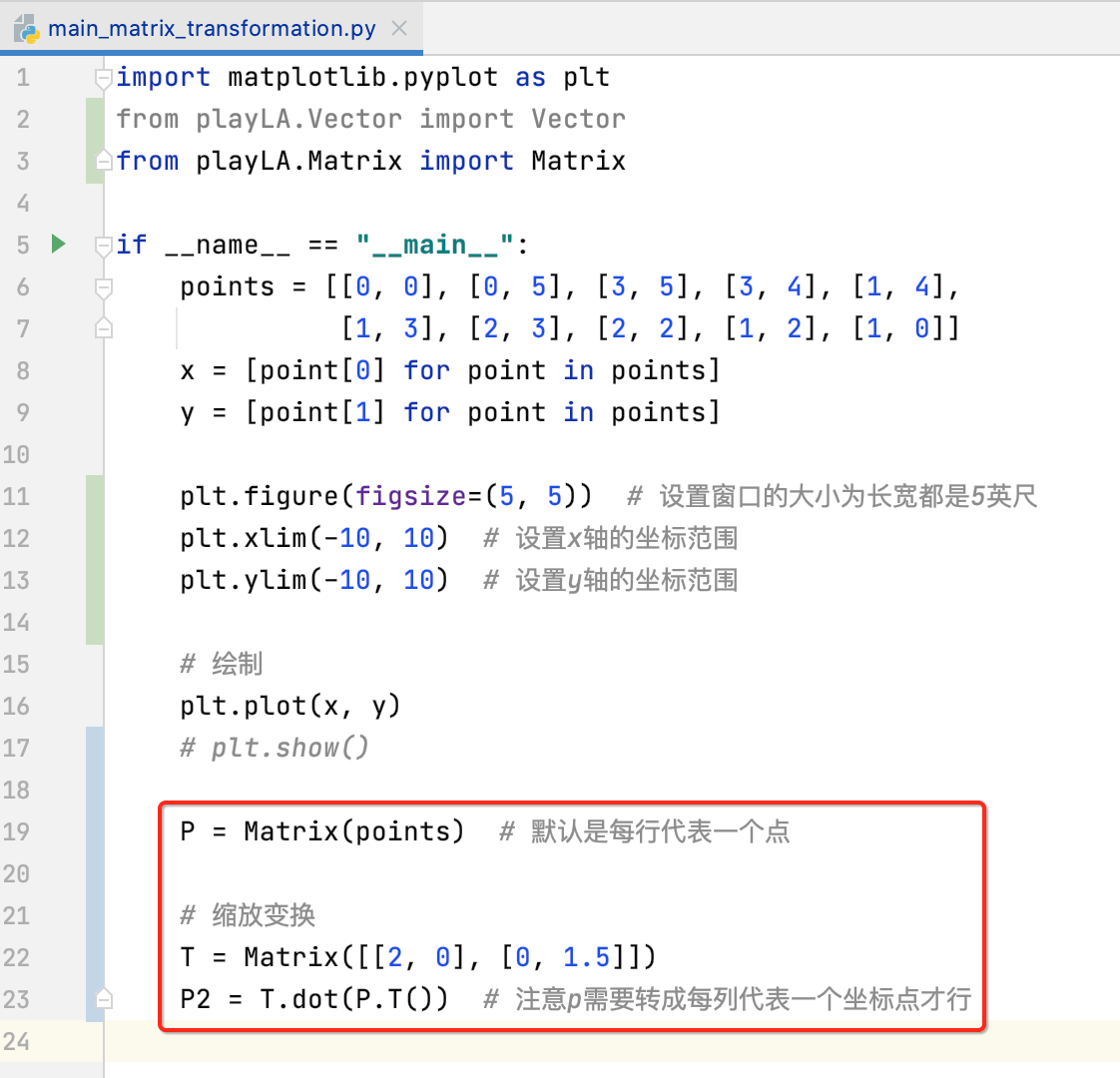
缩放变换:
先将绘制的点放到矩阵中:
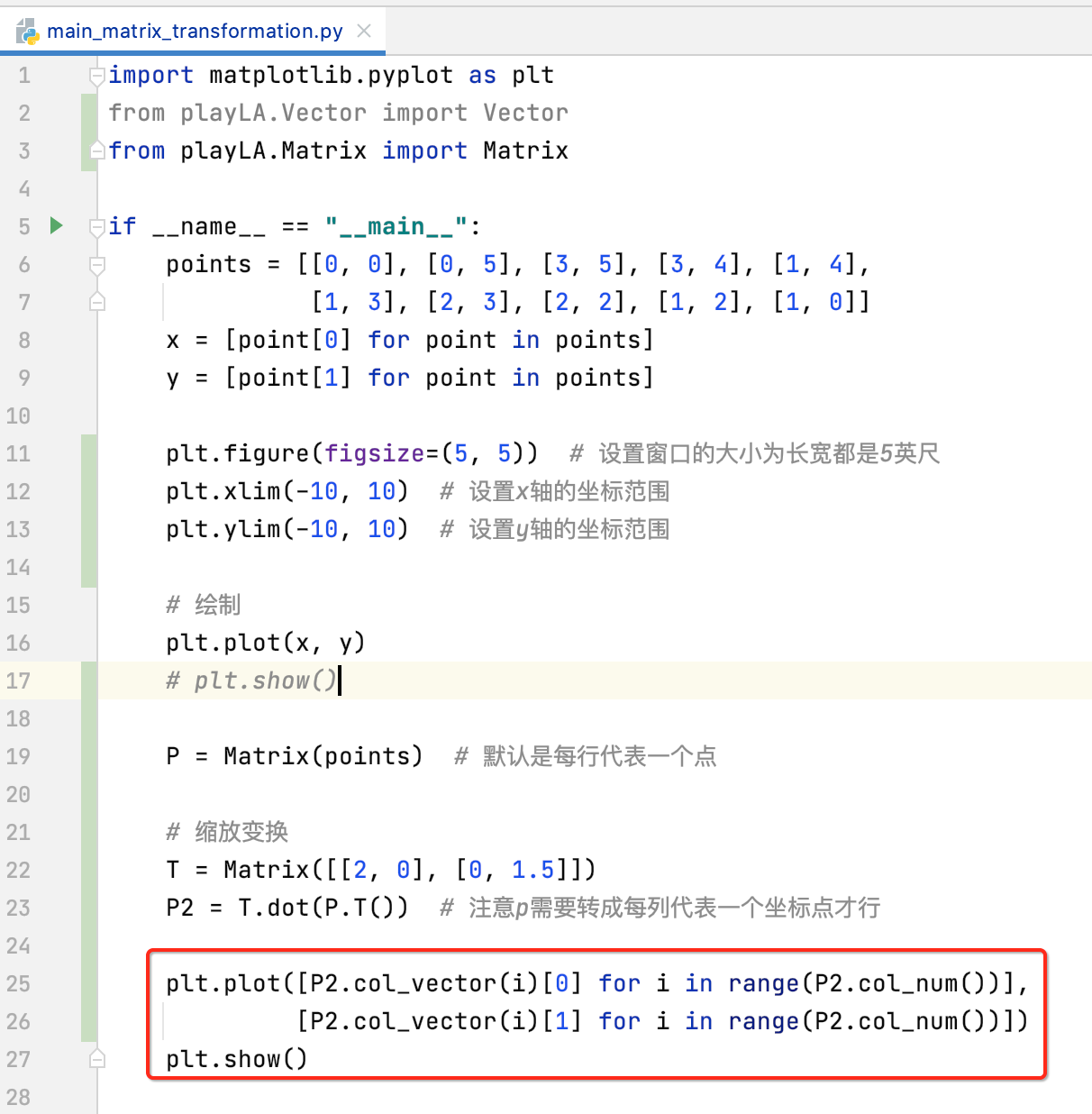
接下来则来绘制一下转换之后的坐标:
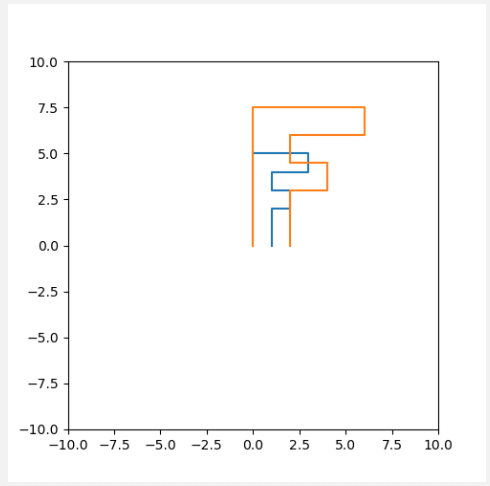
运行看一下效果:
x轴翻转:
有了上面的第一个转换效果之后,接下来只需要修改变换矩阵T的值既可,如下:
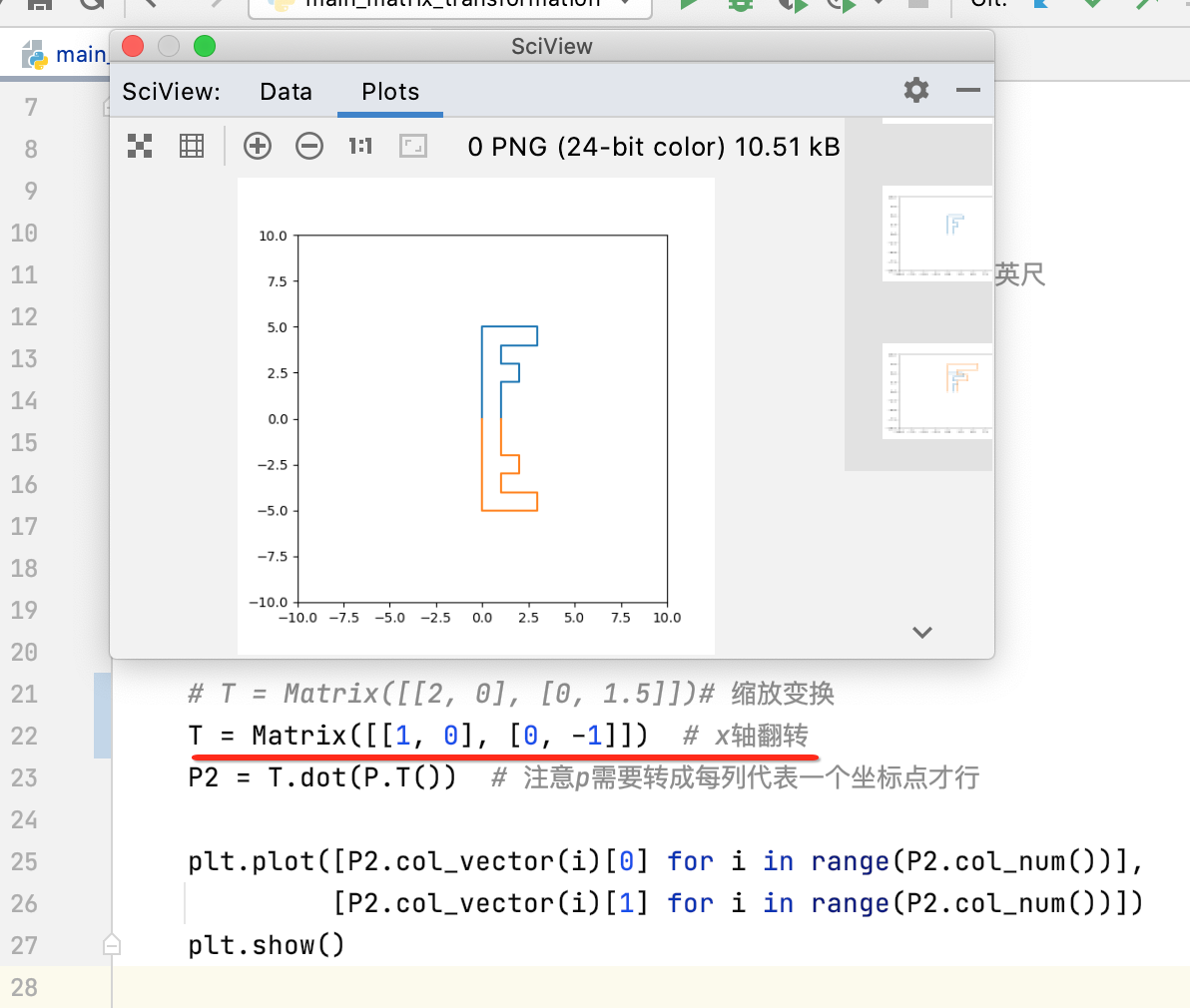
y轴翻转:

让每个点关于原点翻转(x轴,y轴均翻转):

沿x轴错切:
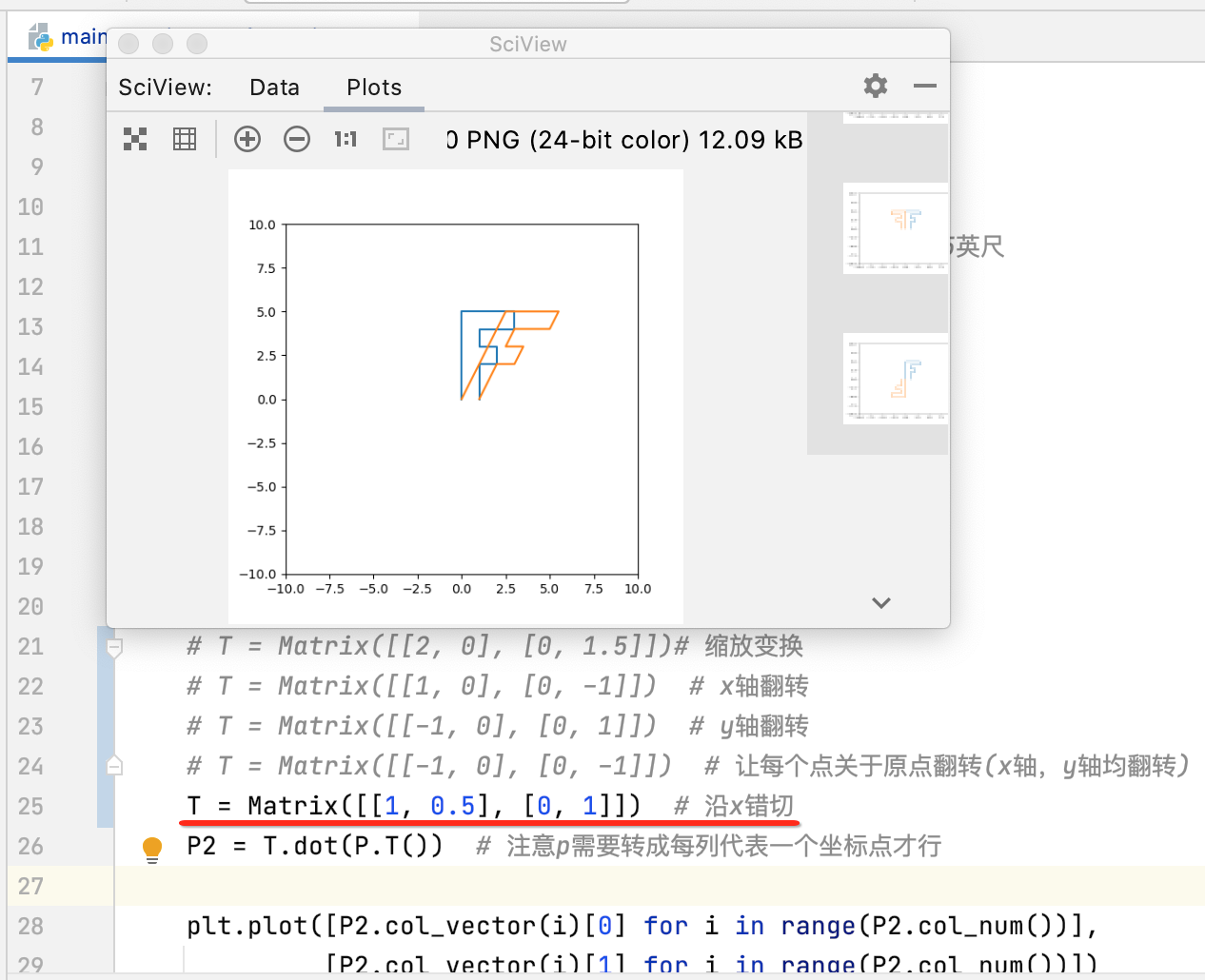
其实就是一个斜体字的效果~~
沿y轴错切:
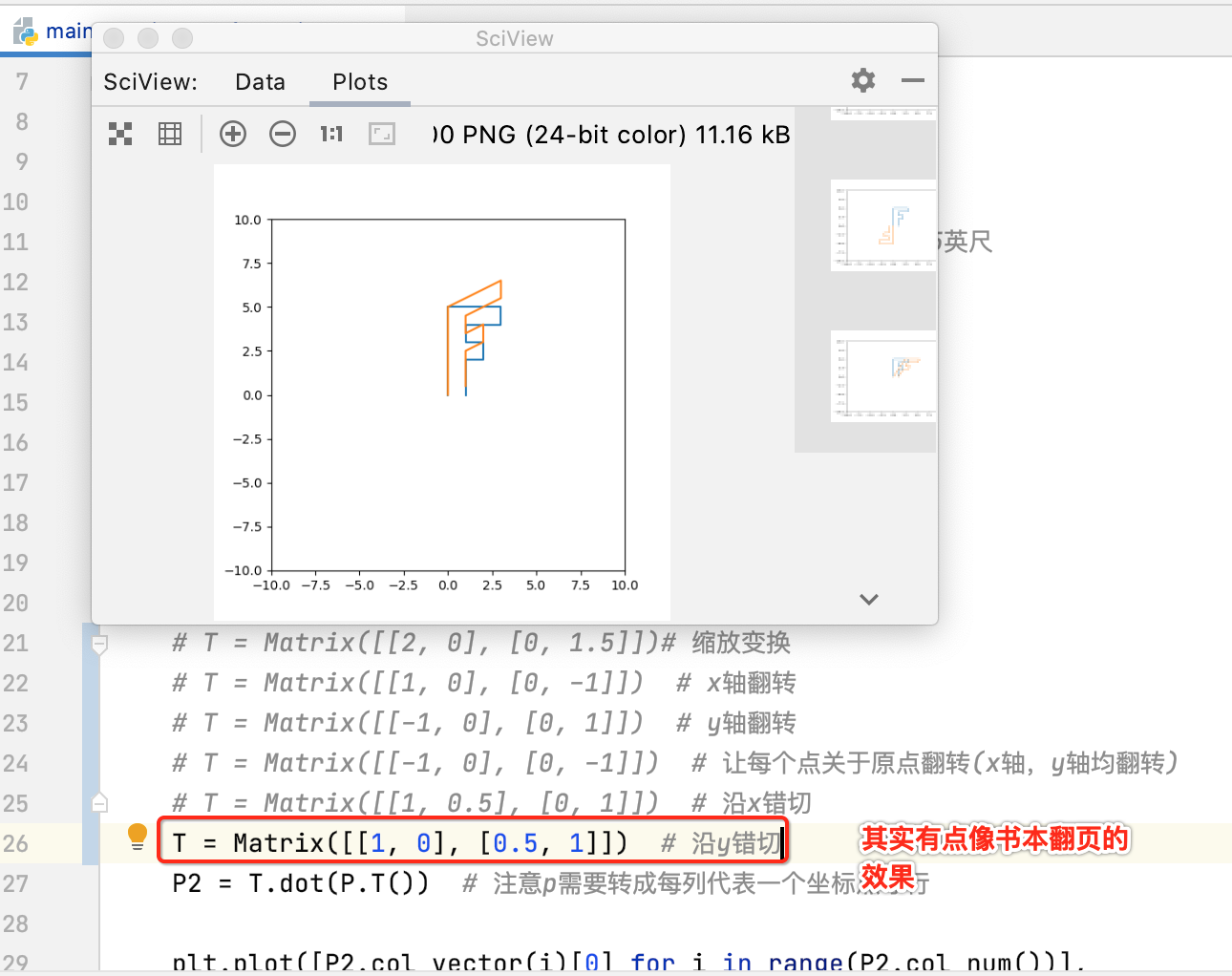
旋转:
先回忆一下它的转换矩阵:

所以先来定义旋转的角度,而通常在数学库中对于角度通常使用的是弧度制来表示的,所以平常比较要旋转60度则需要用pi/3来表示,如下:

其中需要用到数学库,记得导一下包:
从缩放变换到单位矩阵:
这里先回忆一下之前的缩放变换矩阵:

那如果让每个点的横坐标扩大1倍,纵坐标扩大1倍,是不是就有如下式子了?
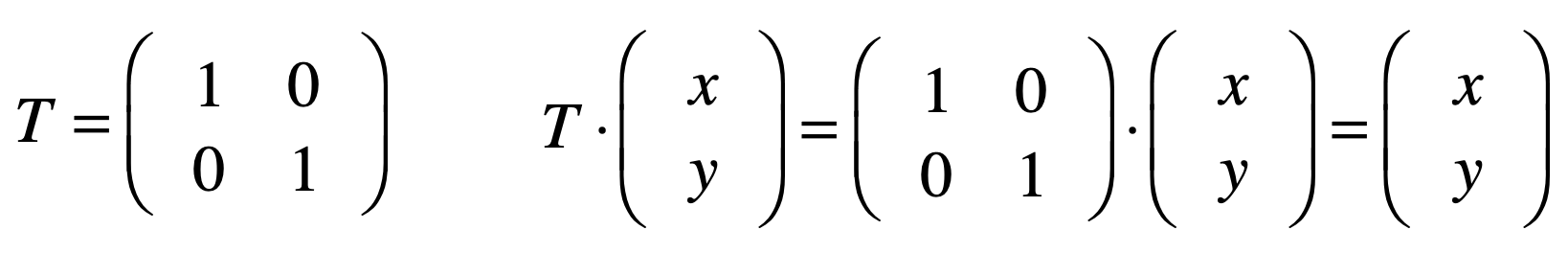
此时一个新的概念出来了,对于变换矩阵没有对向量对应的坐标产生任何的影响,此矩阵就称之为单位矩阵。通常用i来表示单位矩阵,其中i是指Identity:

上面表示2x2的单位矩阵,而对于矩阵它是有不同形状的,所以不同形状的单位矩阵如下:
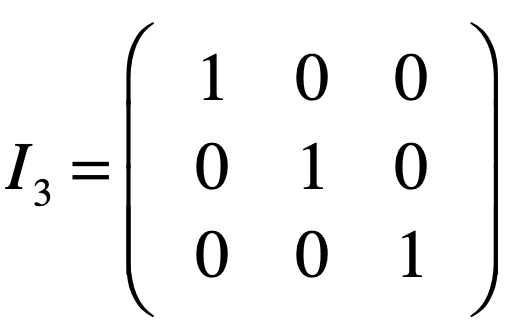
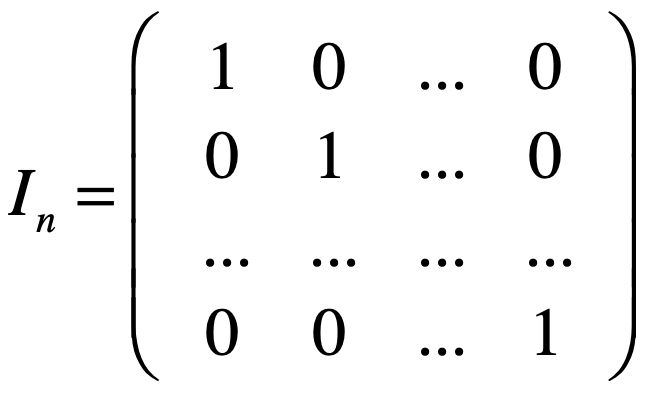
其中发现规律木有,单位矩阵都是从左上角到右下角的对角线【也称主对角线,这个概念对于未来的学习是有用的,对它有个印象】上的值都为1,而其它的都为0,抽象来归纳的话,其实就是:
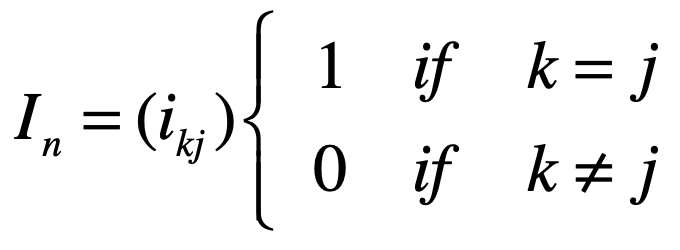
也就是行数等于列数的元素都是等于1,其它的都为0,另外一个重要的结论也出来了:单位矩阵一定是方阵!!。在之前也学过一个一定是方阵的情况,回忆一下:

所以对于方阵这个特殊矩阵是很有用的。
而单位矩阵有如下性质:
![]()
这里简单论证一下:
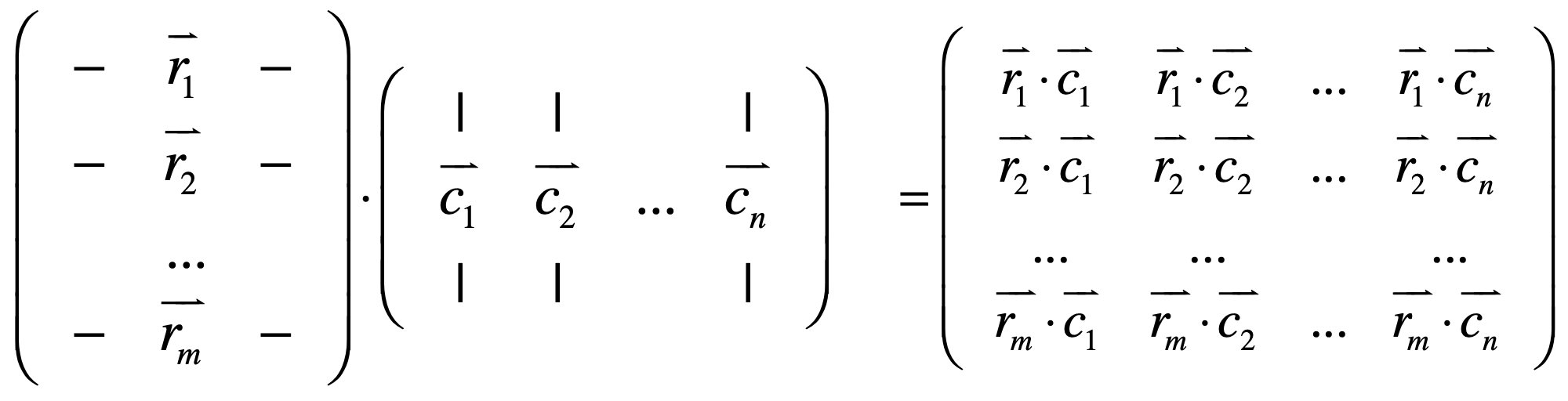
上面是矩阵与矩阵的乘法式子,所以如果对于结果矩阵中的元素记作是a的话,就有如下式子:
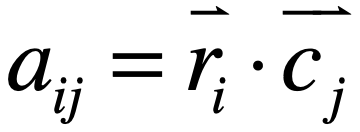
也就是ri这个向量点乘cj这个向量,而如果前面的这个矩阵是单位矩阵的话:
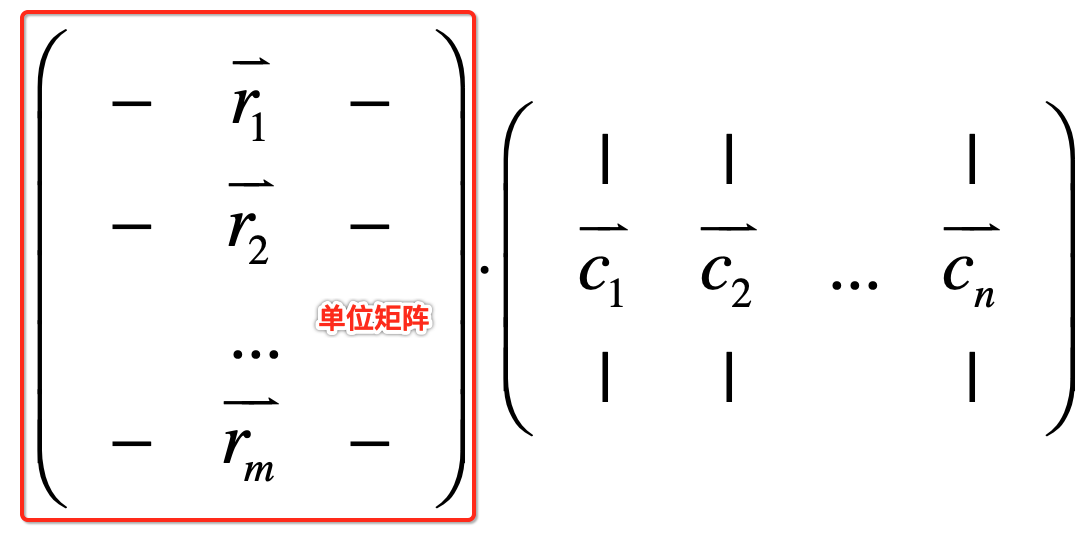
这就意味着ri这个向量中只有第i个元素等于1,其它的元素都为0,而根据向量的点乘就是各个元素进行相乘最后再相加,所以最终式子就变为:
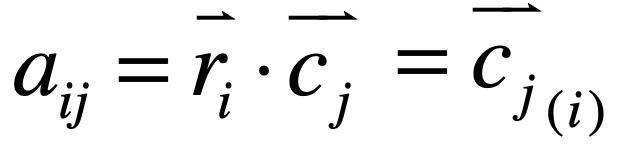
也就是从Cj这个列向量中取出了它的第i个元素,而由于Cj这个列向量是后一个矩阵的列向量,而它的第i个元素就是后一个矩阵的第i行第j列所对应的那个元素,其结果就是结果矩阵的第i行第j列的元素,所以:

同样还有如下两个结论:
![]()
![]()
对于上面的结论有点抽象,可以用实际数来算一下,然后再来回头看这结论就会踏实很多,如下:

而对于单位矩阵的这个性质,对于非方阵也是合适的,看一下下面的矩阵:
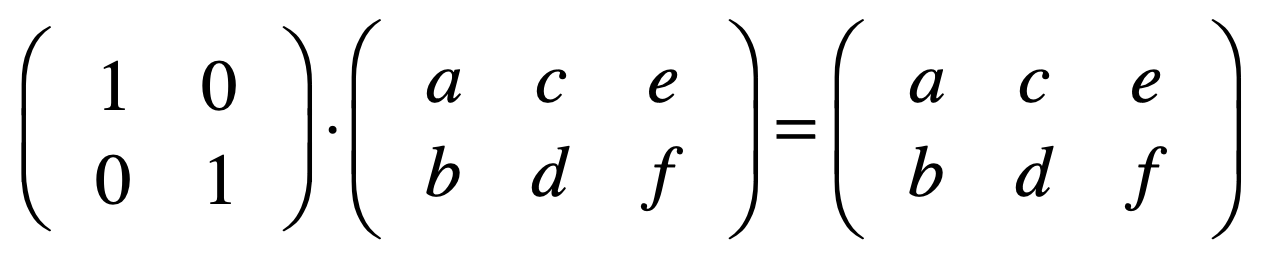
而如果将上面相乘的后面矩阵提前,此时的单位矩阵就是:

而对于单位矩阵跟数字系统中的1一样,非常的重要!!!
矩阵的逆【比较绕】:
在上面已经知道了单位矩阵,其实它就类似于数字1,回忆一下,对于数字有如下特性:
![]()
但是除0之外,同理对于矩阵而言,如果满足:
![]()
其中I为单位矩阵,则称B是A的逆矩阵,记作:
![]()
A称为可逆矩阵,或者叫非奇异矩阵(non - singular)【因为可逆的矩阵是居多的,所以是非奇异的】,但是!!有些矩阵是不可逆的!称为不可逆矩阵,或者奇异矩阵(singular)【因为不可逆的矩阵是居少的,所以是奇异的】
下面具体举一个可逆矩阵的例子:
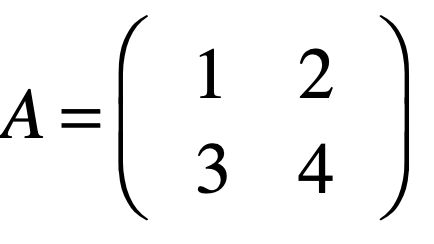
而它的逆矩阵为:
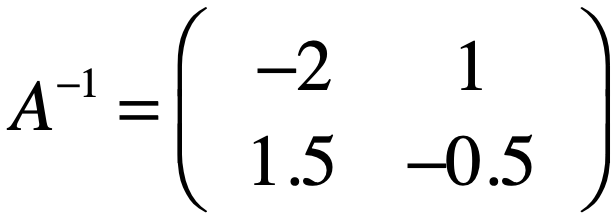
至此怎么求一个矩阵的逆矩阵以及判断矩阵是否可逆,之后再来探究。下面继续来看其它的一些概念(左逆矩阵、右逆矩阵):

也就是有一些矩阵只能找到它的左逆矩阵,还有一些矩阵只能找到它的右逆矩阵,因为矩阵是乘法是不遵守交换律的嘛,而对于代数的学习中,对于左逆矩阵和右逆矩阵倒不是很关心,其重点是要推出下面这个结论:
“如果一个矩阵A既存在左逆矩阵B,⼜又存在右逆矩阵C,则B = C。”
对于这个结论可以证明如下:
已知:
![]()
此时则从AC这个等式开始进行变换,如下:
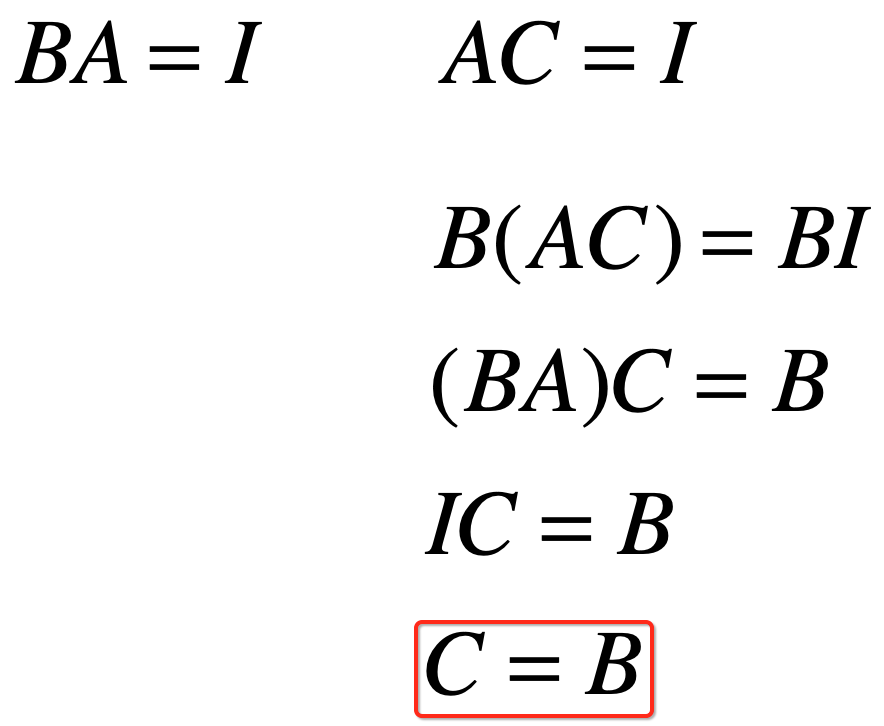
另外如果对于矩阵A,存在矩阵B,满足BA = AB = I,矩阵A可逆,所以可以得出一个很重要的结果:可逆矩阵一定为方阵!!而非方阵一定不可逆!!
有了逆矩阵的知识之后,接下来就可以回答在之前https://www.cnblogs.com/webor2006/p/14265708.html学习矩阵幂运算时的几个疑问了,回忆一下:
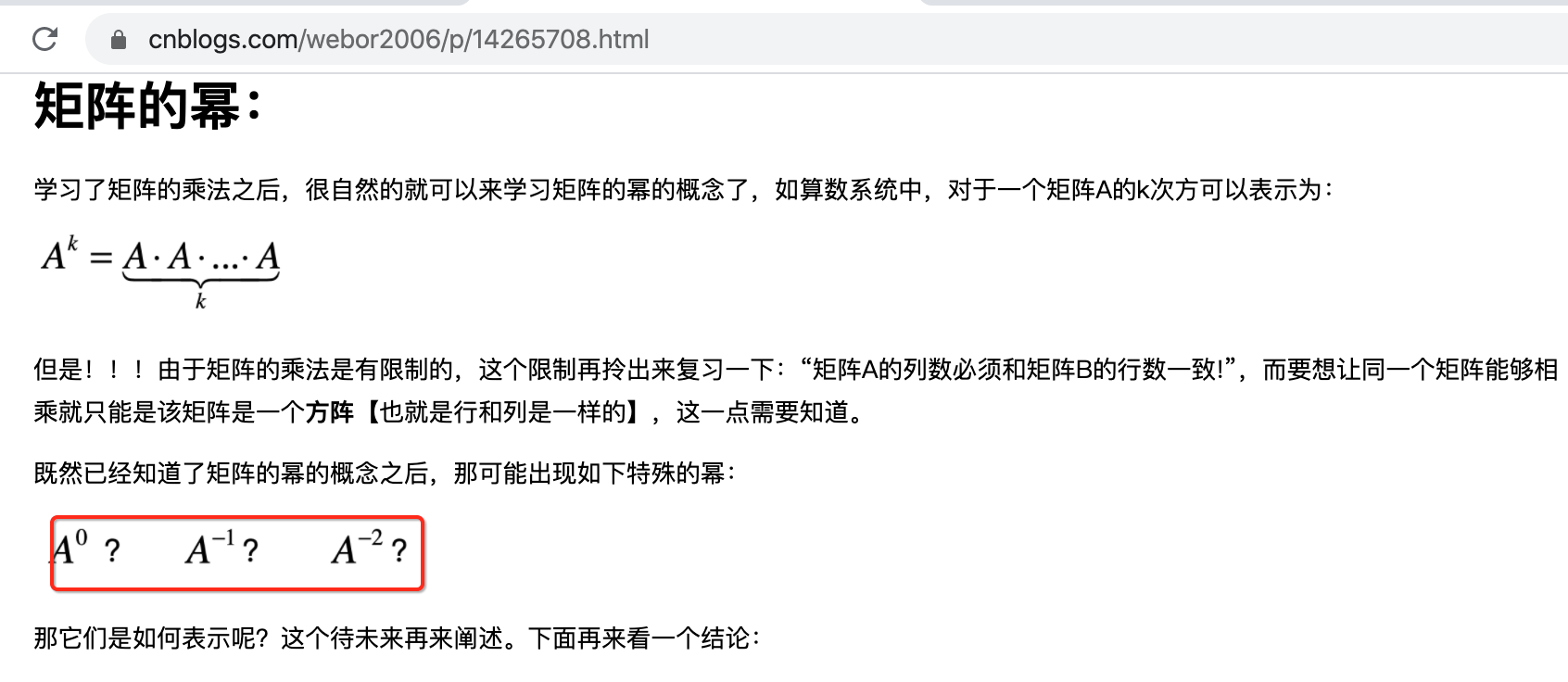
结论如下:
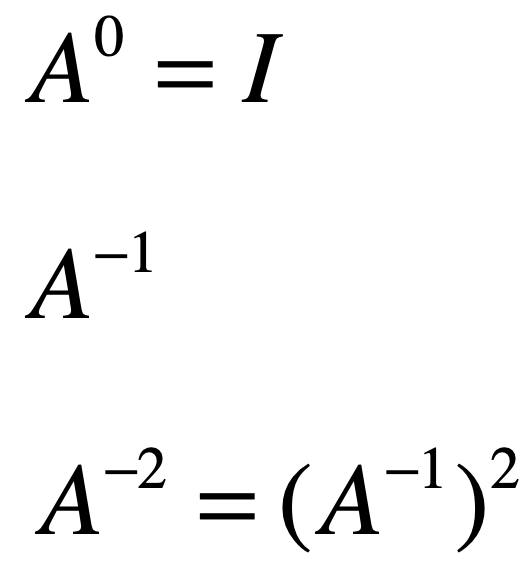
其中这里重点知道A的0次方是单位矩阵,而A的-1次方是逆矩阵,而对于A的-2次方其实不是太重要。
实现单位矩阵和Numpy中矩阵的逆:
实现单位矩阵:
接下来回到python中来实现一下单位矩阵:

然后调用一下:
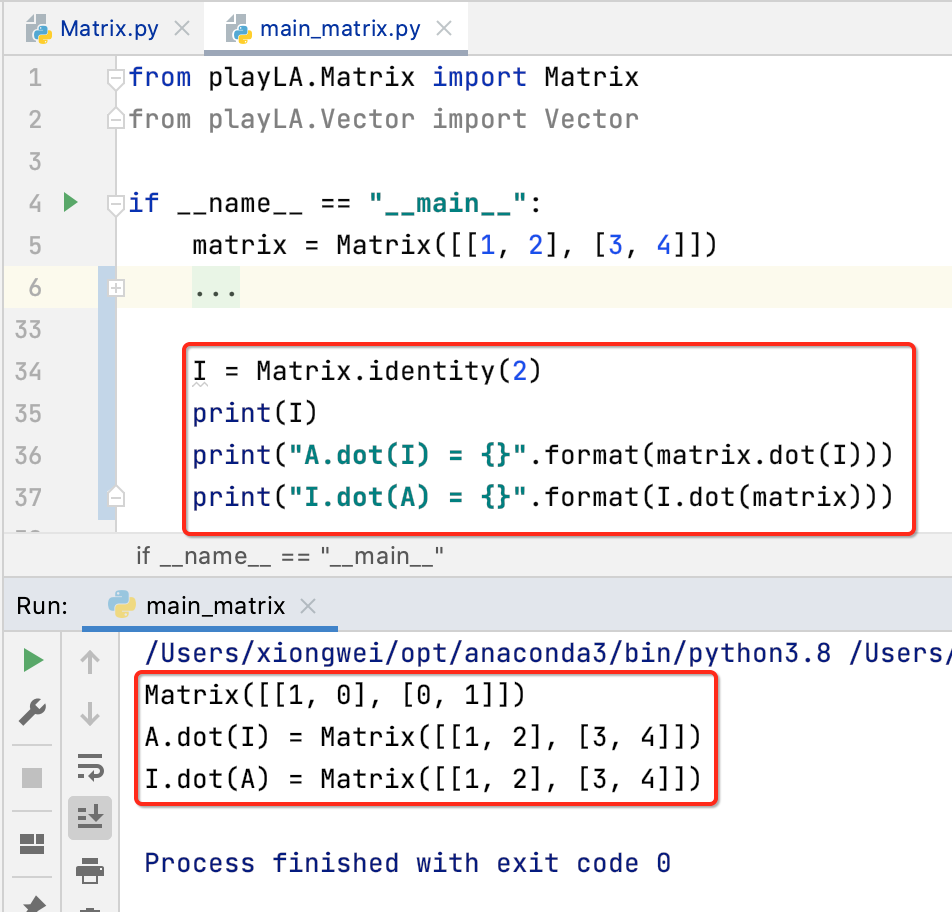
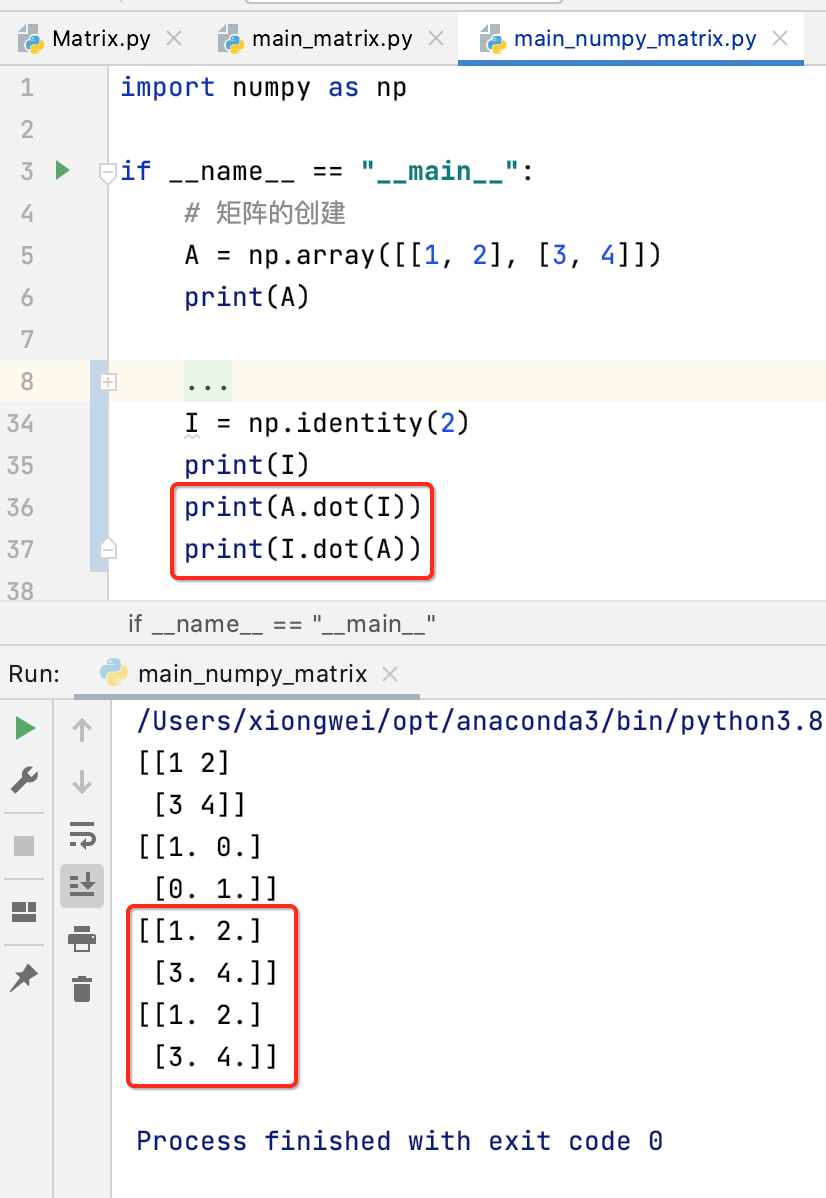
这里回到numpy库也来使用一下:
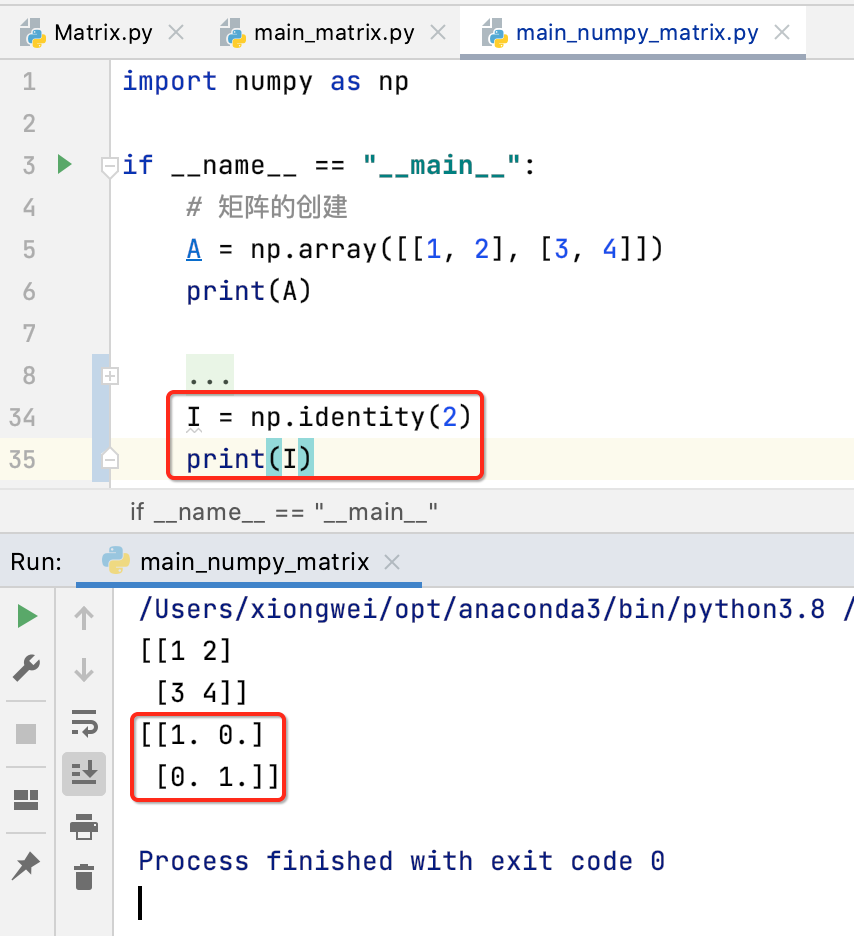
也来看一下单位矩阵的乘法的特性:
Numpy中矩阵的逆:
由于矩阵的逆咱们还没学怎么求:

所以咱们自己目前也没法实现,不过可以使用数学库numpy先来体会下:

对于求出的结果咱们可以用下面方式来验证一下,因为一个矩阵x逆矩阵有如下特性:
![]()
所以咱们调用一下:
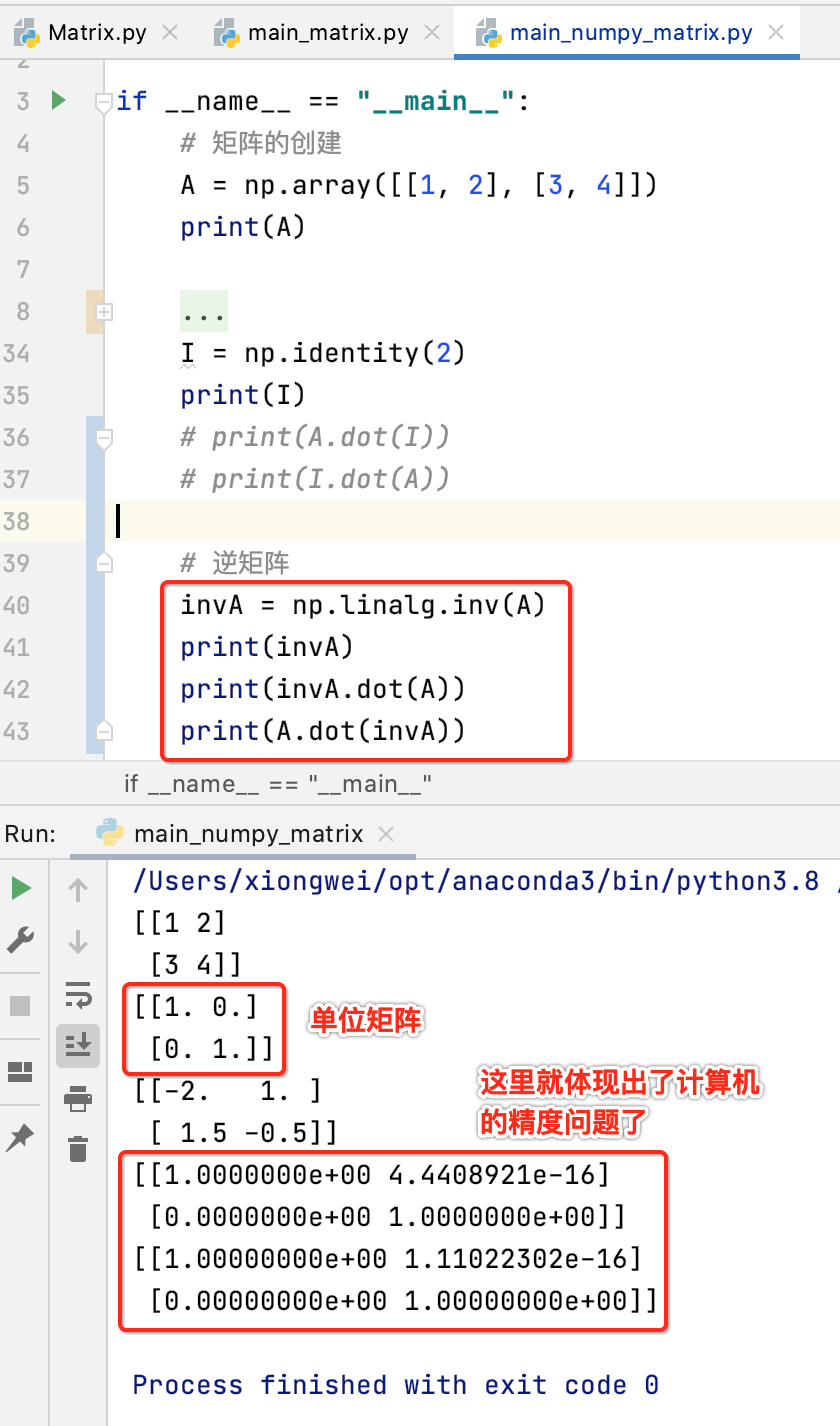
其中看一下精度问题:

对于浮点数,所以像之前我们设置了一个精度为:

也就是判断浮点数是否为0是这样判断的,只要小于这个精度就认为等于0:
另外对于逆矩阵还有这么一个规定:

所以,咱们来试验一下如果用numpy求非方阵的逆矩阵,看看有啥效果:

矩阵的逆的性质:
性质一:
由于矩阵的逆在后续的学习中是非常之重要的概念,如之前学习其它概念一样,下面来看一下矩阵的逆的基本性质,先来回忆一下逆矩阵的概念:
![]()
另外它其实还有这么一个结论:对于矩阵A,如果存在逆矩阵B,则B唯一。而对于这个结论可以采用反证法,如下:

结果发现B=C,跟咱们的假设矛盾了,所以就论证了上面的结论了。
所以以后如果求解出了一个矩阵的一个逆矩阵之后,就可以万事大吉了,因为一个矩阵的逆矩阵是唯一的。
性质二:
![]()
其实也就是要证明,一个矩阵X要满足它:
![]()
其实只要证明XA满足矩阵的逆的定义就成了,如下:
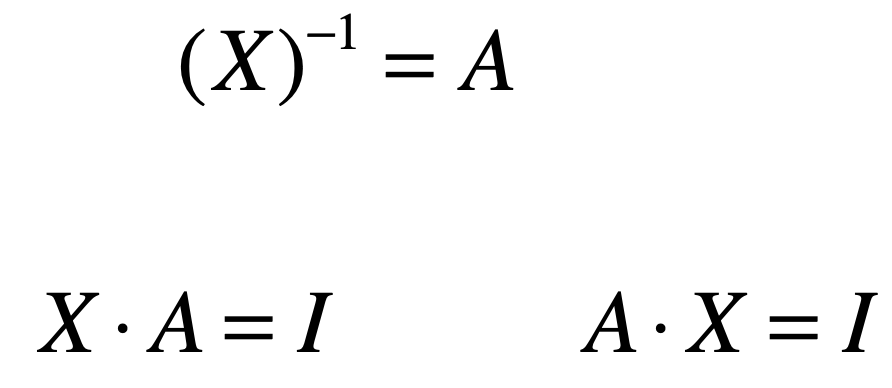
而此时对于X可以用下面式子代替:
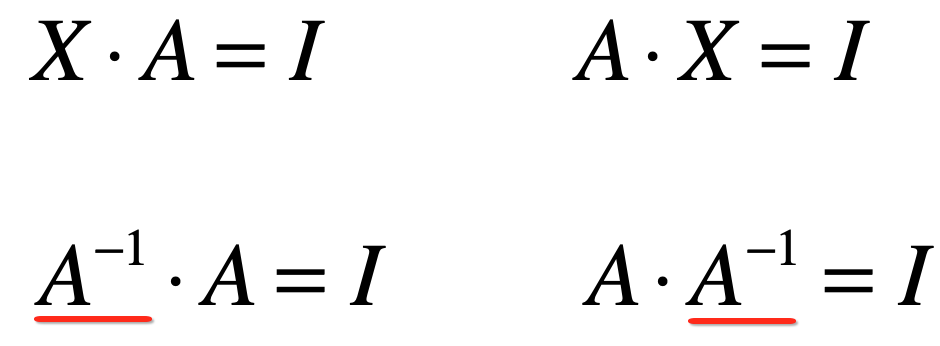
是不是可以看出A^-1就是矩阵A的逆矩阵,如结论所示。
性质三:
![]()
按照性质二的论证思路,其实只要证明:
![]()
论证也比较简单,如下:
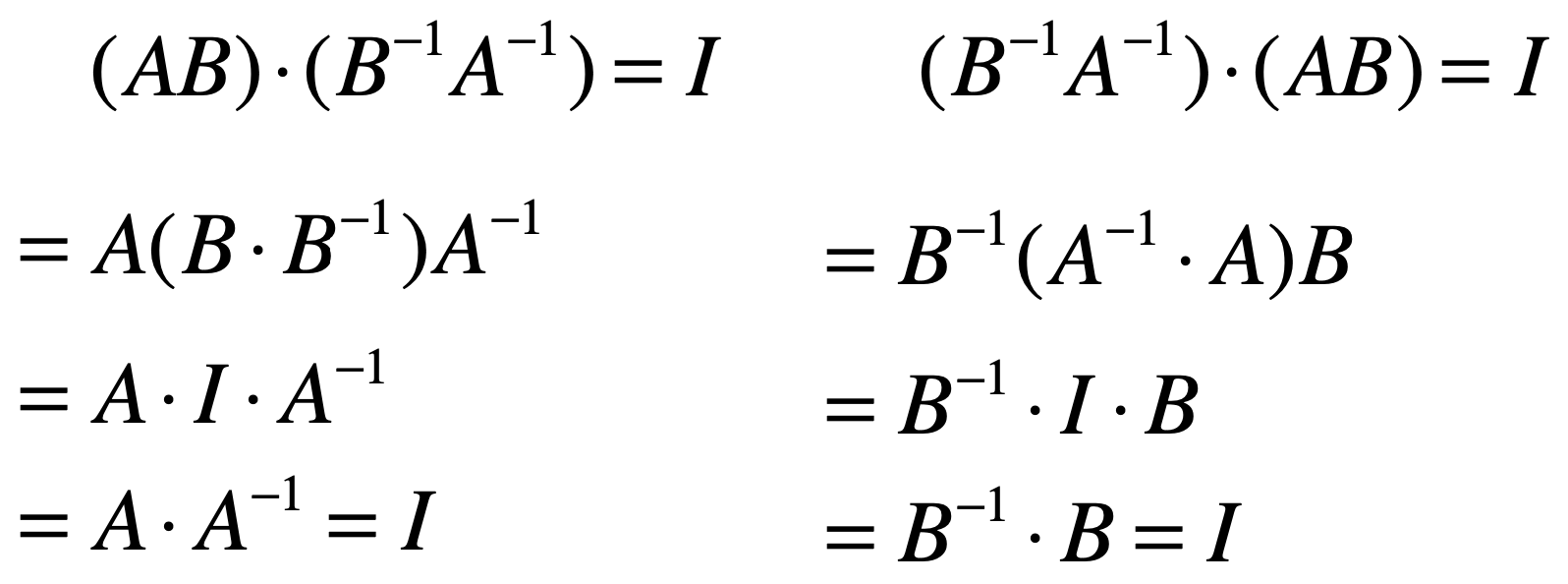
而它跟我们之前学习的矩阵的转置的特性非常像,如下:
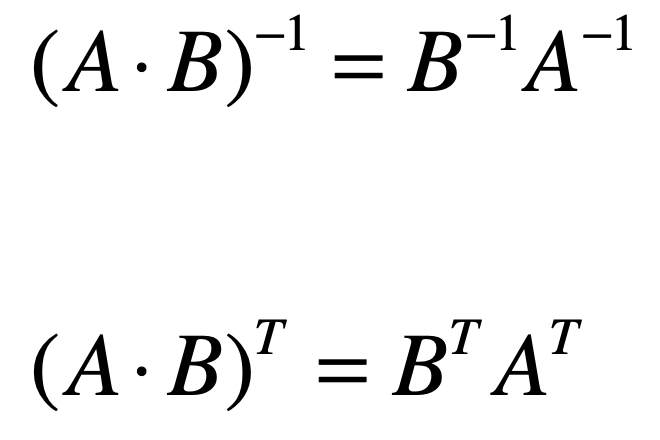
而事实上,矩阵的转置和矩阵的逆之间在某些特殊的情况下,也确实存在着非常重要的关系,这里先提前给出结论,待之后再来探讨,那就是:对某一类特殊的矩阵,它的转置其实就等于它的逆。
性质四:
![]()
同样的证明思路:
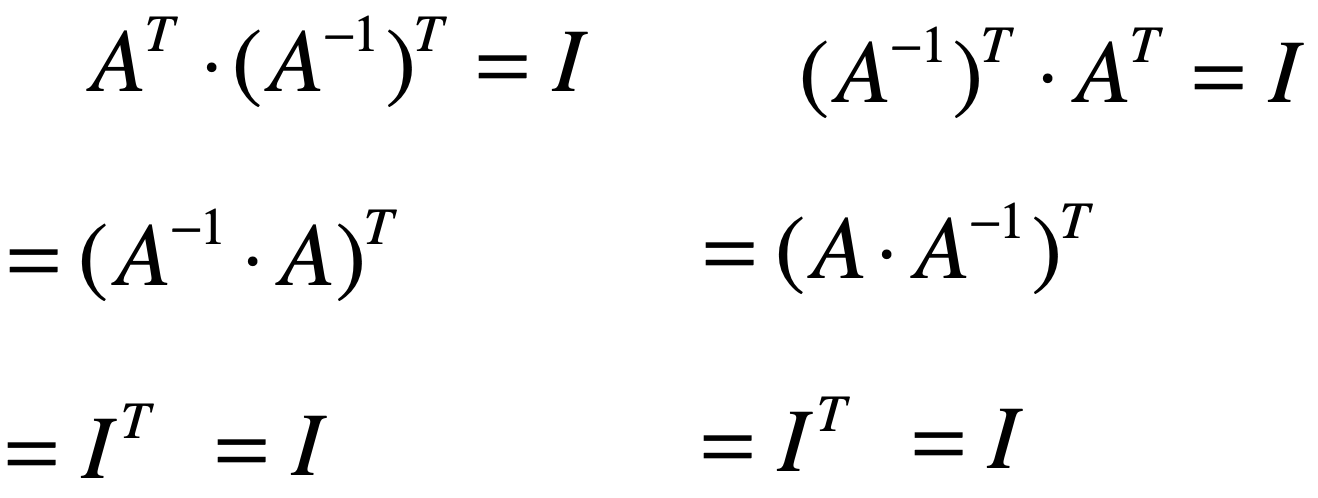
学到这,对于上述公式的证明已经不需要再用具体的矩阵来进行推导了,直接可以用矩阵的语言既可进行推导,这也是学习了足够多的线性代数的基础之后的结果。
看待矩阵的关键视角:用矩阵表示空间【非常重要】
对于矩阵还有另外一个视角:空间,而在之后的线性代数的学习中也能慢慢体会到它处理的很多问题都是把矩阵当作空间来看待,而空间也是线性代数的核心,所以下面来学习一下这个视角。
回忆:矩阵和向量相乘:
如下:
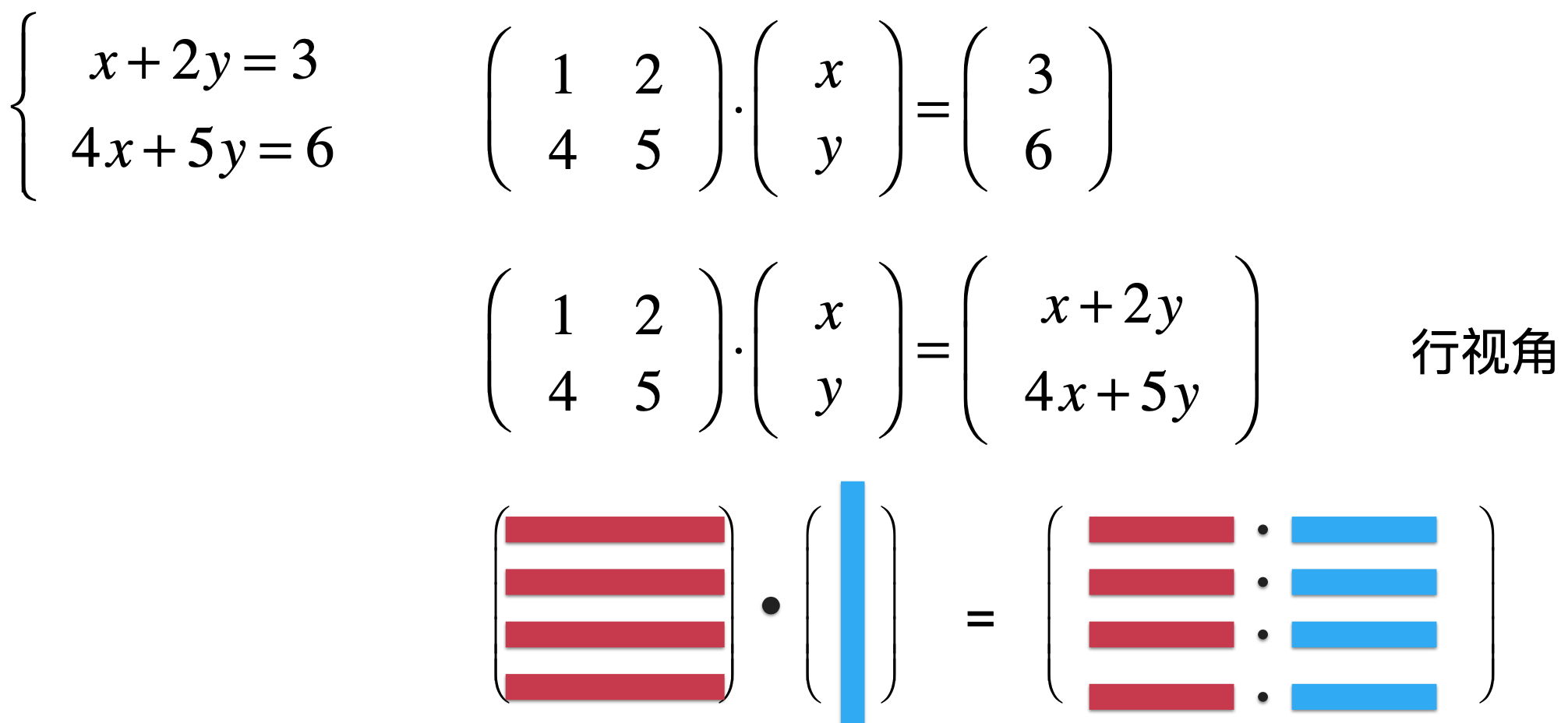
使用的是行视角来看的。
使用列视角:
既然有行视角,当然也有列视角对吧,对于同样的式子就会为:
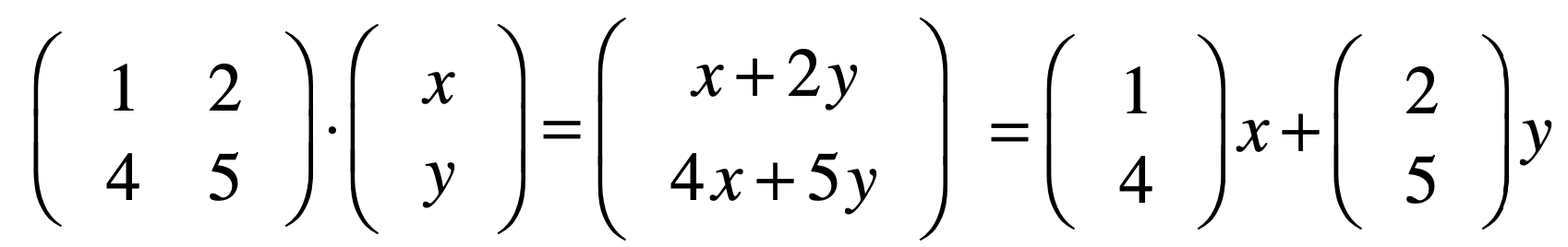
其中可以看到结果跟使用行视角使用的情况是一模一样的对吧,用抽象一点的思维来看,其实就是:
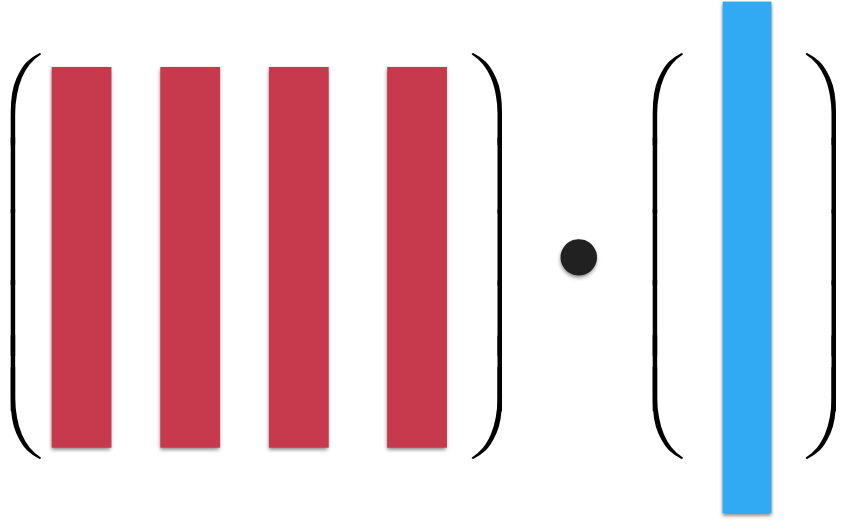
而更细的话就是:
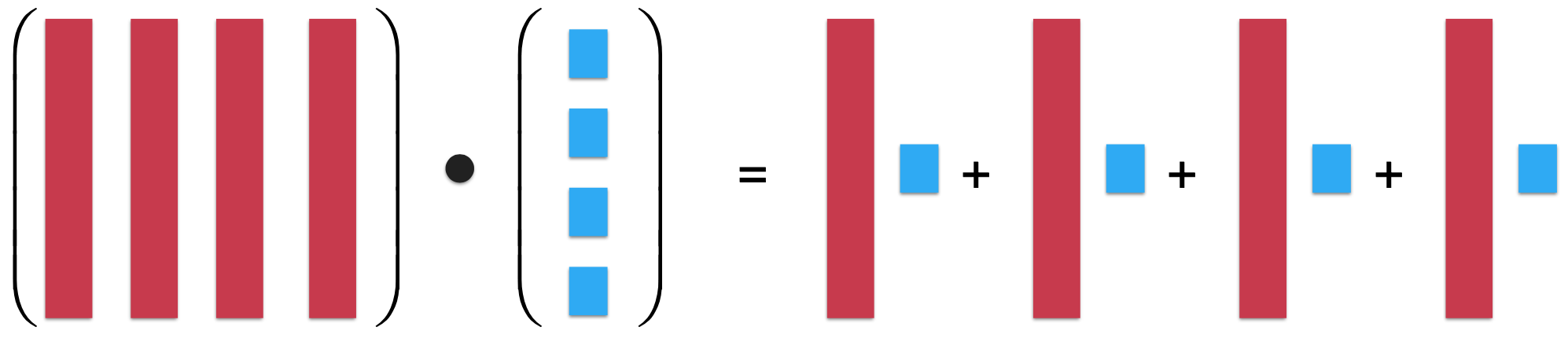
那,使用列视角来看待矩阵的话有啥意义呢?其实是很有意义的,下面再来看一下单位矩阵乘法:
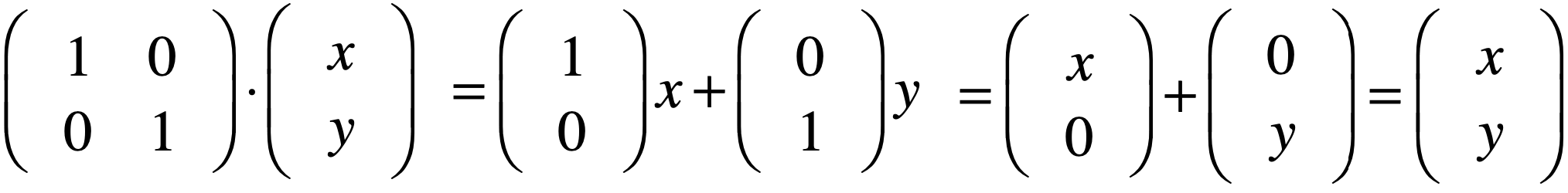
其结果跟我们之前学习的单位矩阵的性质是一样的。而重点看一下它:
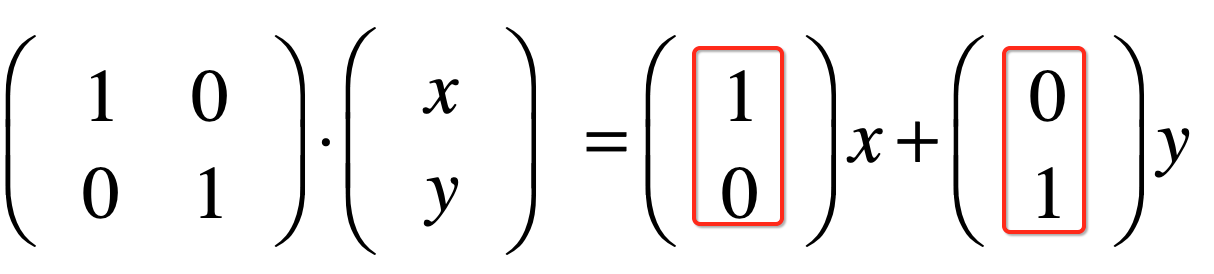
其中回忆一下之前https://www.cnblogs.com/webor2006/p/14257300.html提到过标准单位向量:

其实也就是对应二维坐标空间的这俩点:
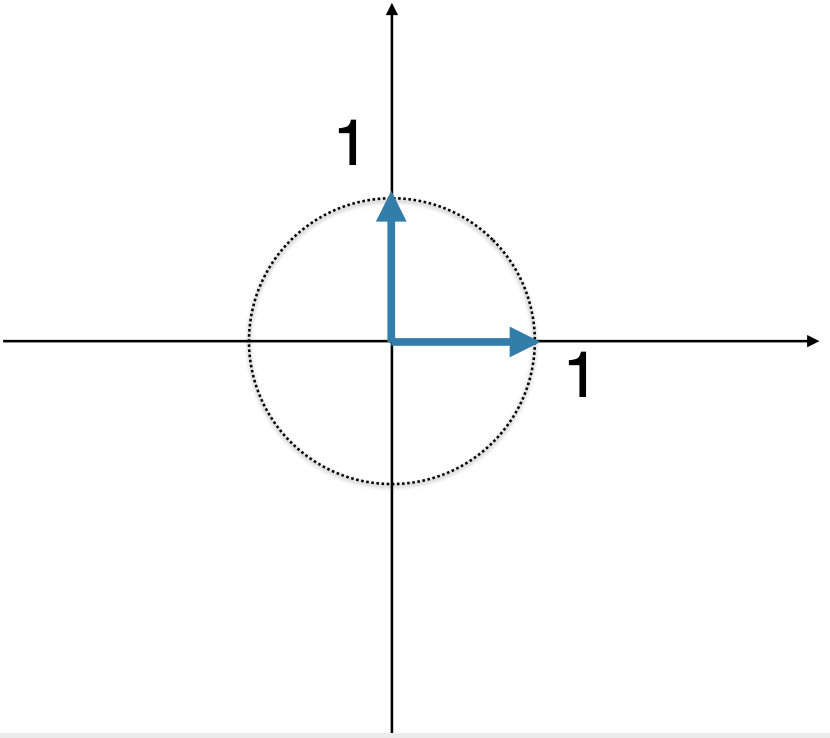
所以,此时式子又可以变化为:

那这样变化有啥意思呢?有意思,下面就可以理解是:
x.e1向量=往e1向量伸缩x倍;
y.e2向量=往e2向量伸缩y倍:
所以在二维坐标中就可以表示为:
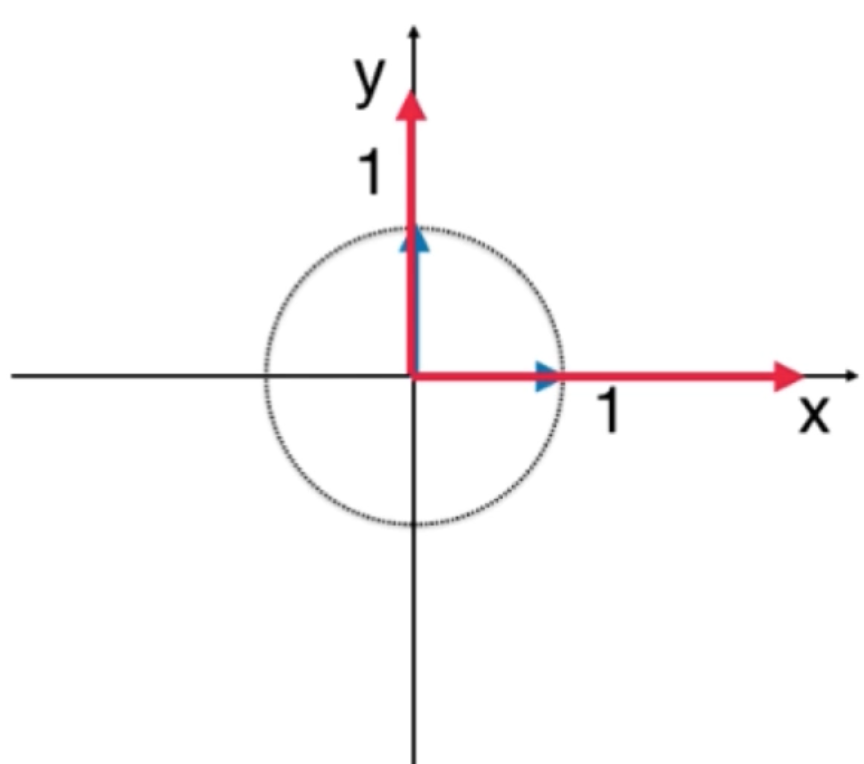
然后再结这两个向量求加法,不就是平行四边行的对角线么,所以:
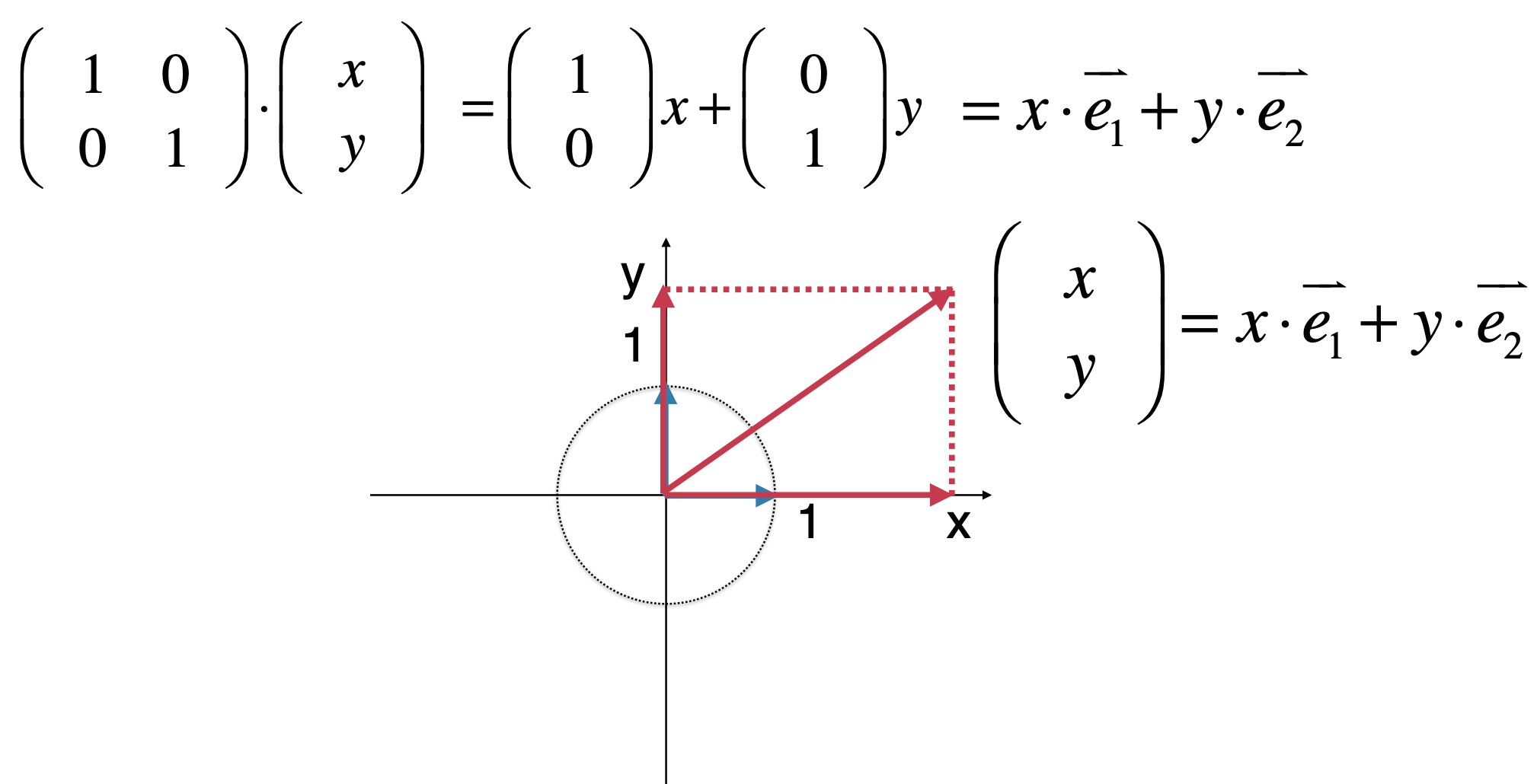
那这样看又有啥意义呢?如下。
矩阵表示空间:
这里就可以这样来看了:

也就是e1向量和e2向量分别表示轴的方向对吧?换言之,二维空间本身就需要由2个轴来定义,而该矩阵就定义了2个坐标轴,所以该矩阵就表示了整个二维空间了。其中又道出了一个非常重要的结论:"矩阵表示空间",那是不是对于任意一个矩阵都可以表示空间呢?比如下面这个矩阵:
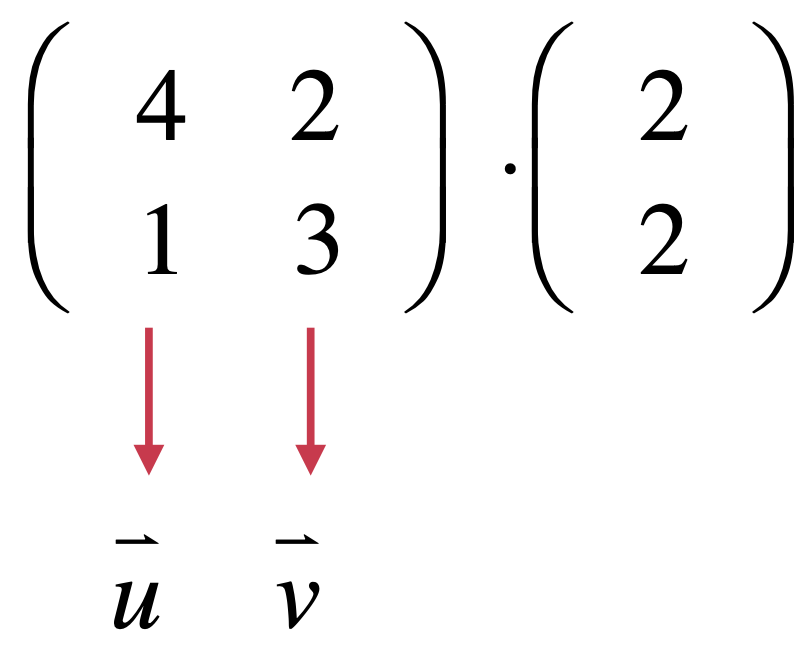
是不是这个矩阵就代表了一个由u向量和v向量这俩个向量所组成的空间呢?是的,这里还是回到二维坐标空间来表示这俩向量:
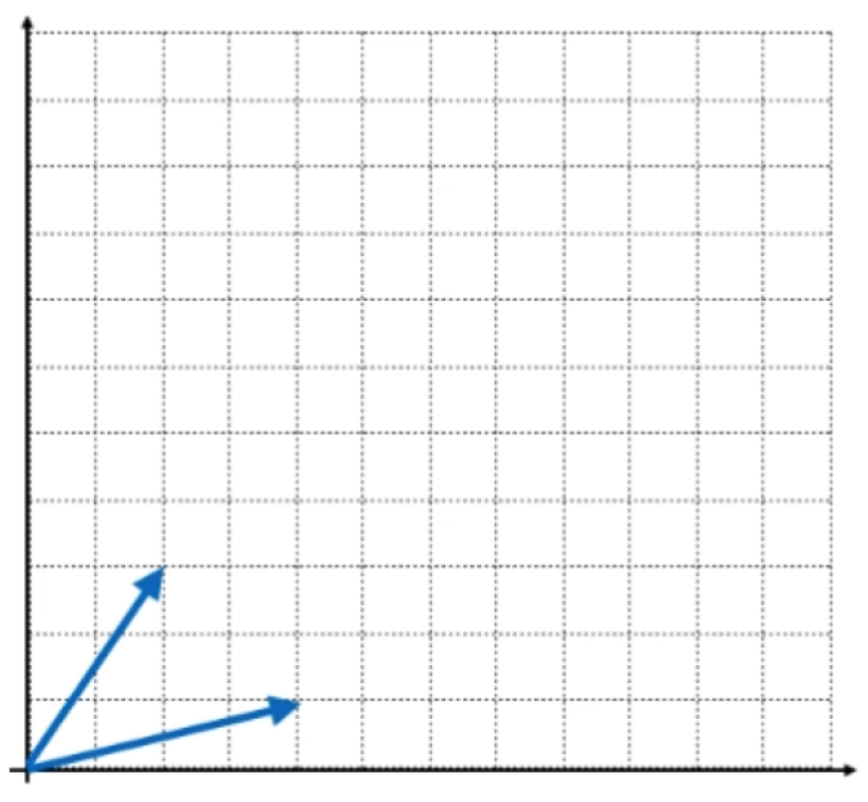
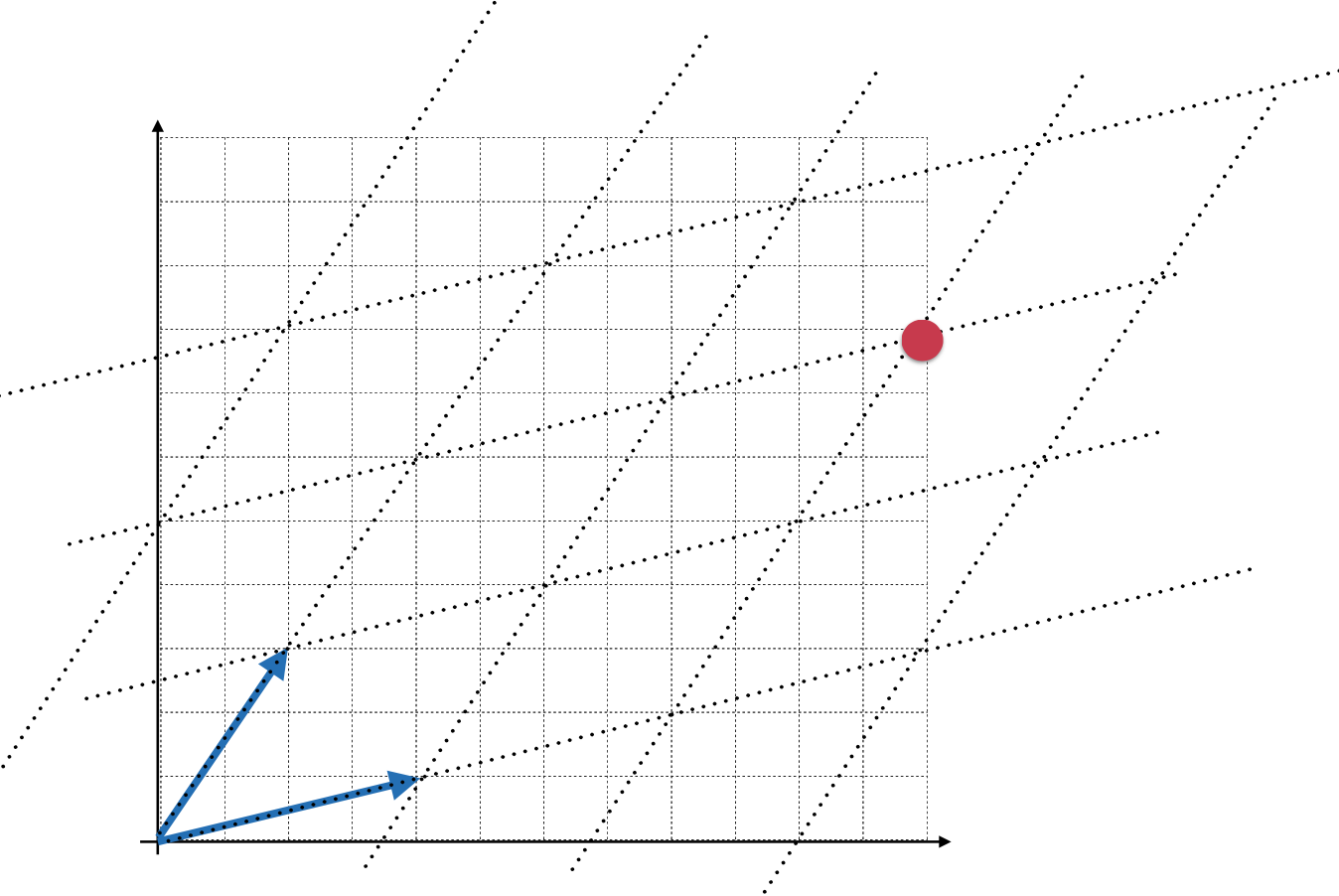
而对于这个空间(其实就是欧拉空间)中,对于这个点:
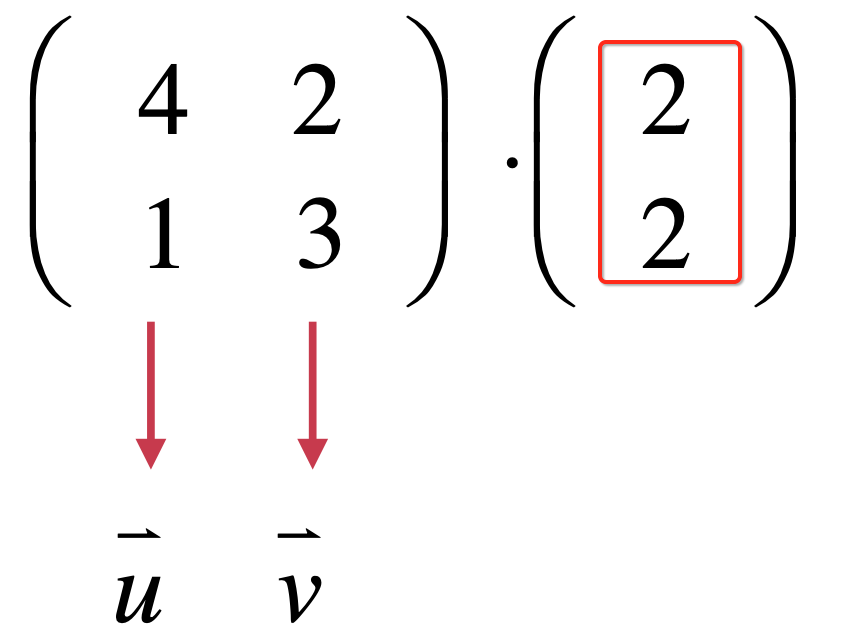
其实就是在u向量和v向量的空间中分别走2步,如下:
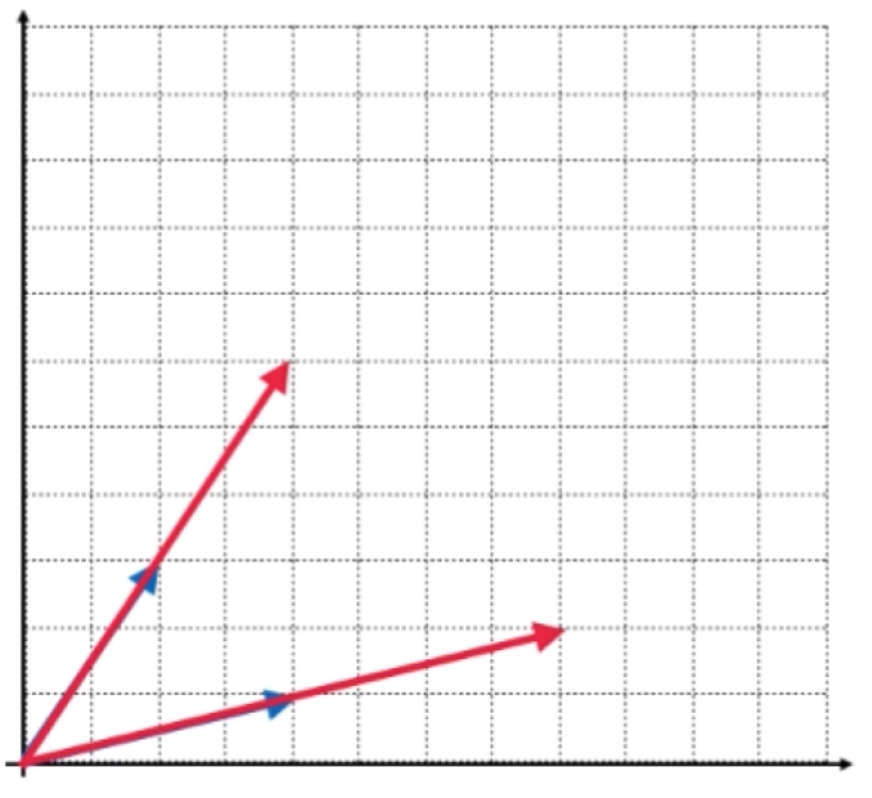
而最终的结果就是这俩个向量之和,所以结果为:
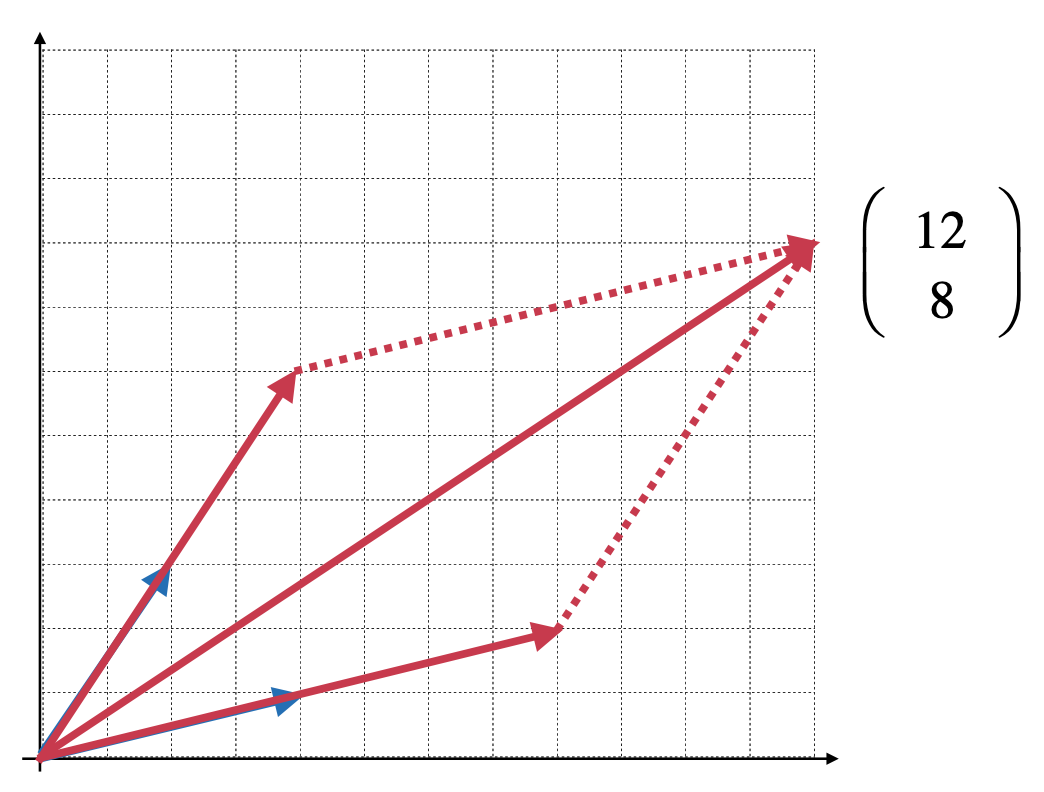
那此时可以发现就是这个矩阵定义了一个空间,然后空间*坐标点其实就是在这个空间中看该坐标点在空间的哪个位置,为了能更加清楚的认知到这个矩阵表示的是一个新的空间,可以在坐标轴上画上虚线来直观的体会一下矩阵表示空间这句话:
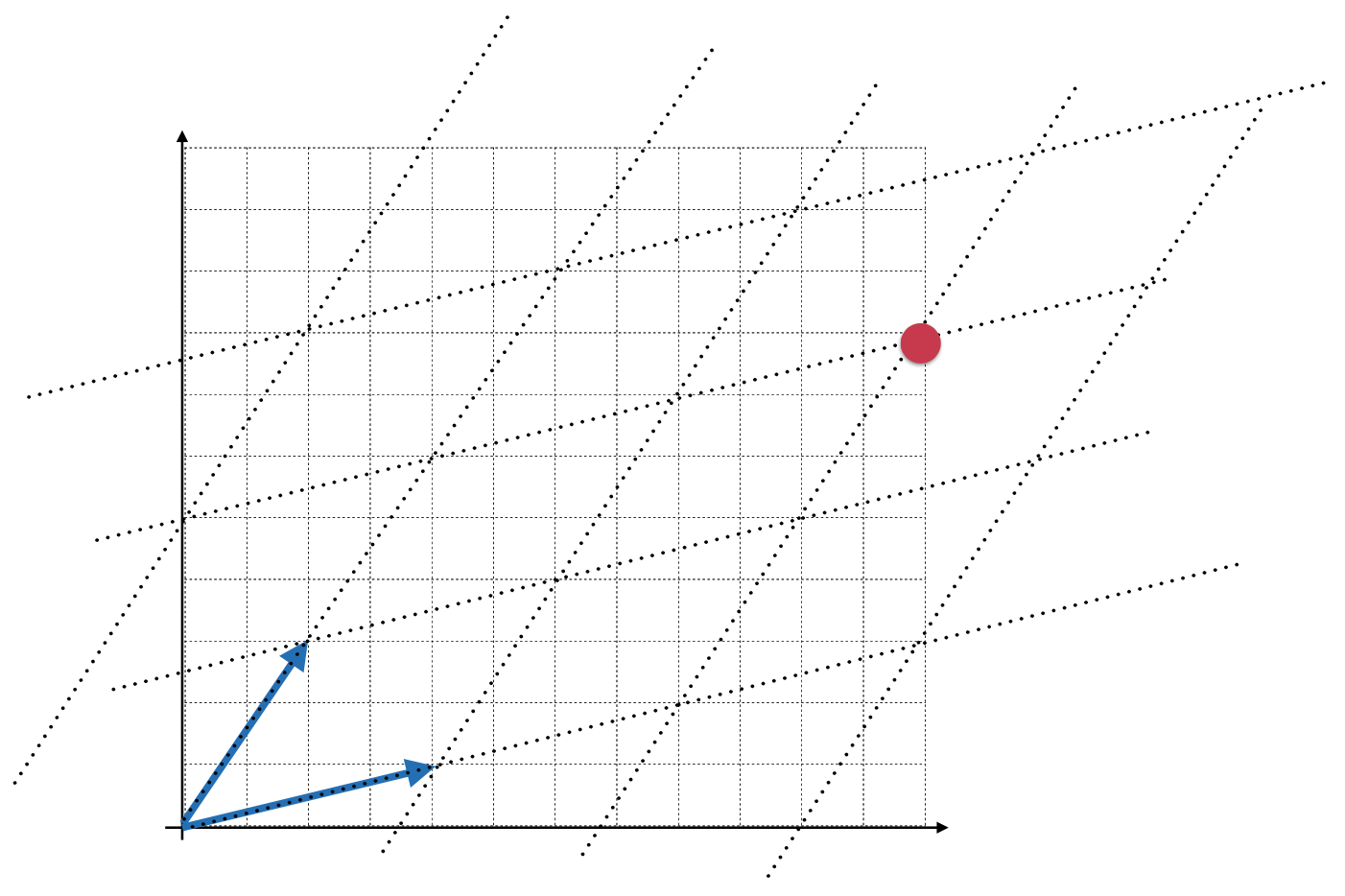
此时如果将二维坐标系去掉就长这个样子:

所以矩阵表示空间这个视角就应运而生。
回头看图形变换:
当有了空间的视角来看待矩阵之后,接下来再回头看一下之前在图形中的各种变换,其视角也不一样了,如下:
其实也可以将这个变换矩阵看成是在这个空间中的是怎么样的,这个新的空间就是:
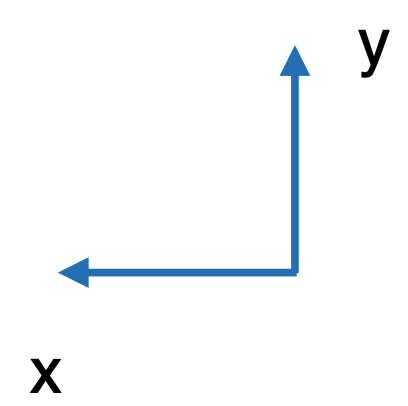
同理:

它就是在这个空间中的变化:
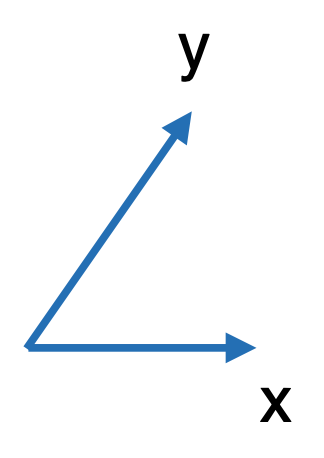
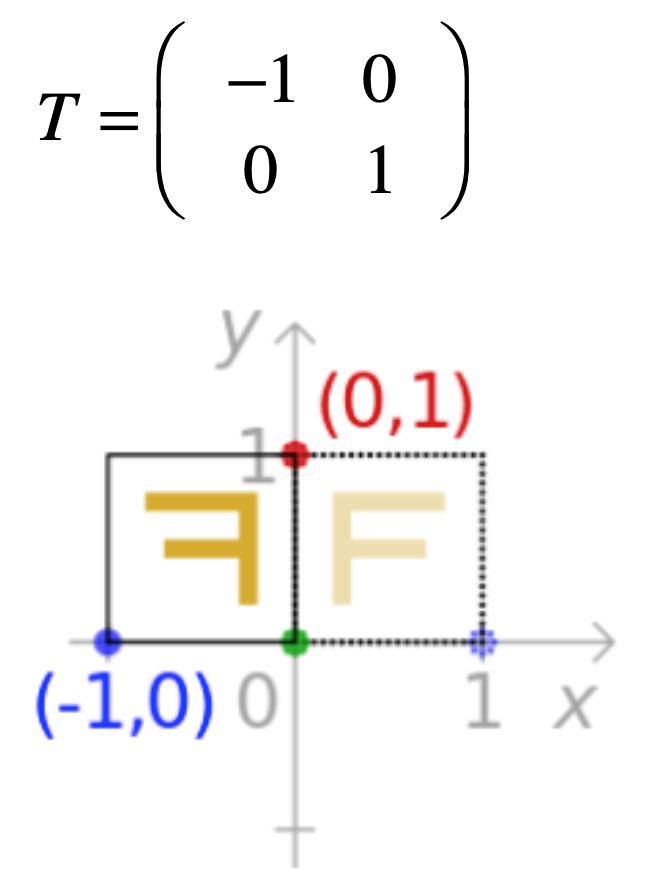
有了这样的一个视角之后,有一个非常酷的事,就是平常不需要过多的计算,根据效果就可以很容易的推导出变换的矩阵,比如对于这样的翻转效果:

其实就是要将F放到这样的坐标系中:

那不很容易的写出这个表示空间的矩阵了?如下:

而原来没有空间的视角对于图形的旋转推导是多么的复杂,回忆一下:

所以,对于三维的矩阵也可以这样看:
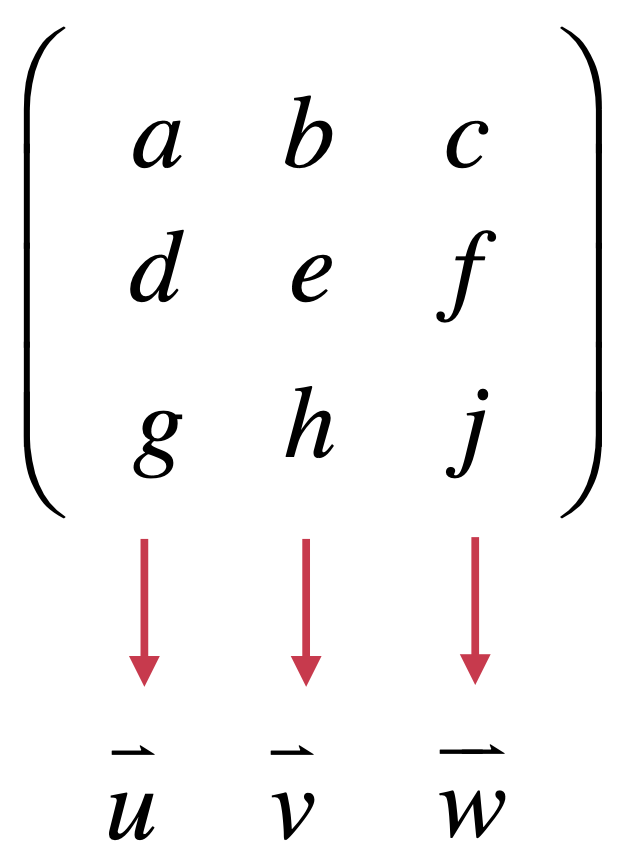
而如果对于n维则需要用n轴来定义,而每一个维度也应该是n个数,那不就是典型的方阵嘛,所以表示空间的矩阵一定是方阵!!!目前矩阵表示空间可能感觉不出它有很大的用处,待之后的慢慢深入会发现这个概念就非常非常重要了,这里先感性的对它有一个认识既可。
总结:看待矩阵的四个重要视角:
矩阵的运算:
下面来回忆一下对于矩阵的运算咱们都学了啥?
- 矩阵的加法
- 矩阵的乘法(和数字;和向量【这是最重要的】;和矩阵)
- 矩阵的幂
- 矩阵的转置
- 矩阵的逆,不过目前还没有学怎么求~~
四个重要视角:
而学习矩阵的一个非常有用的就是得要学会不同的视角来看待它,下面总结一下:
视角一:数据

但是这不是线性代数都要关心的视角。
视角二:系统
这个就是线性代数所关心的视角了,比如:
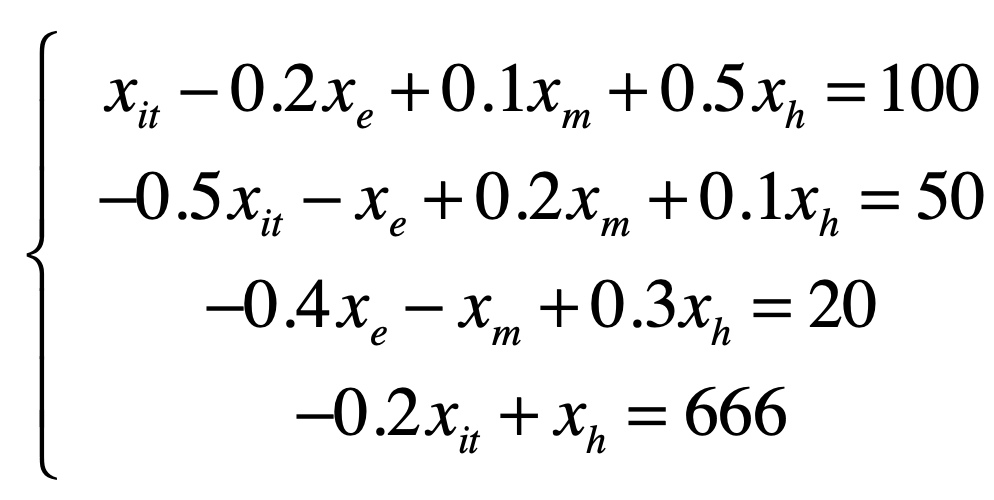
而它又可以用矩阵表示为:
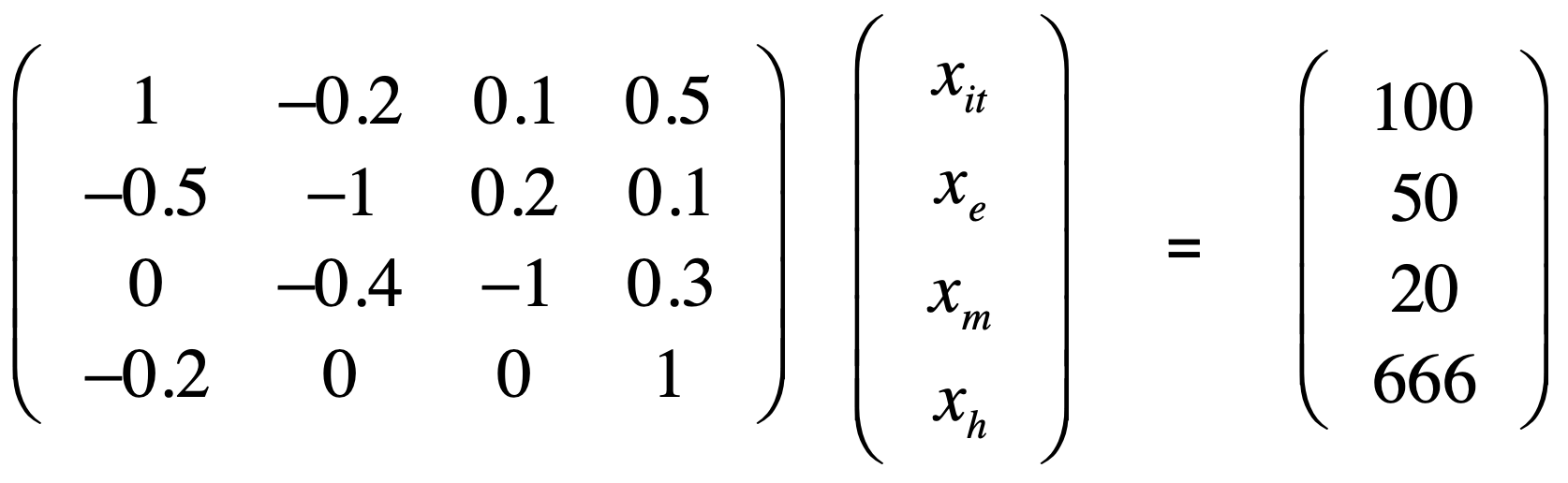
而其实对于未知数也可以不用再关心了,因为根据前面矩阵就可以推导出它有四个未知数,最终将结果向量和前面矩阵就可以合成这么一个矩阵,如下:

关于这块未知数可以忽略的这块会在未来再来学习。
视角三:变换(向量的函数)
关于这块主要是用在图形学当中,其式子是:
![]()
回忆一下几个变换效果:
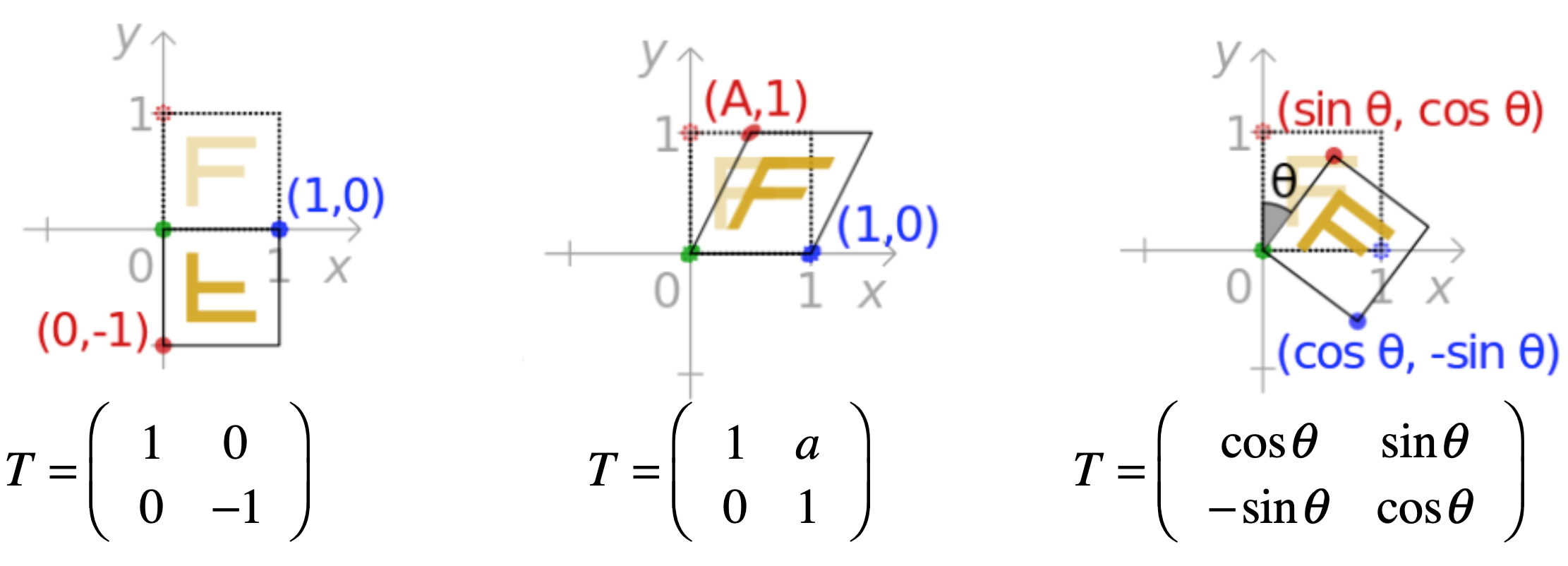
视角四:空间
当以列视角来看待矩阵时,就跟空间挂勾了,比如:
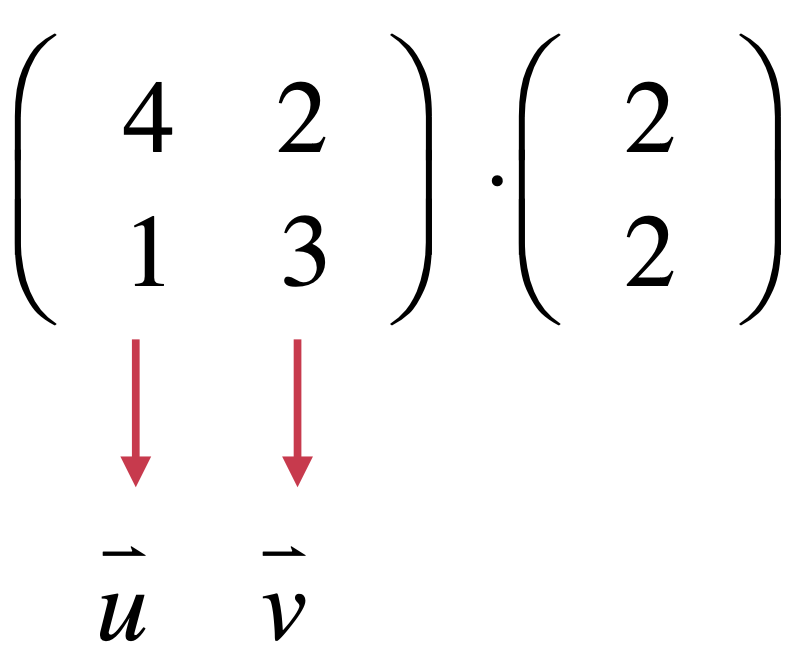
而可以把上面这个乘法看成是向量U和向量V所代表的空间中的某个点的位置 ,如下:
总的来说就是如下四个视角来看待矩阵:
- 二维数据
- 系统
- 变换
- 空间
而在下一次的学习就来解决当把矩阵看作是一个系统之后在线性系统中需要处理哪些问题,而它又是在未来学习将矩阵看成是变换和空间的一个非常扎实的基础。所以在数学这个领域真的是一环套一环的,需要认真谨慎对待每一个知识点。



