线性代数学习之向量的高级话题

继续跟着上一次https://www.cnblogs.com/webor2006/p/14245895.html的对线性代数进行恶补，最近这块的学习时间会分配多一些​，因为要被考了嘛不捉急一点，这里依然是对向量的一个探讨~~当然依然是概念很多，也很枯燥，但是理解这些基础也是在之后学习更深入的学习线性代数必经之路，数学本身是一个非常严谨的学科，中间落了任何环节对于后面的学习都会受到影响，所以切勿焦躁~~

规范化和单位向量：

向量的长度：

如上一次的学习一直在提到向量是具有“方向”的，但是既然它是一个有向的线段，除了方向肯定也是有大小的，所以对于向量来说除了在看待方向之外，通常也要看一下这个向量的大小是多少？对于这么一个向量：

它是个二维向量，直接在二维平面上绘制如下：

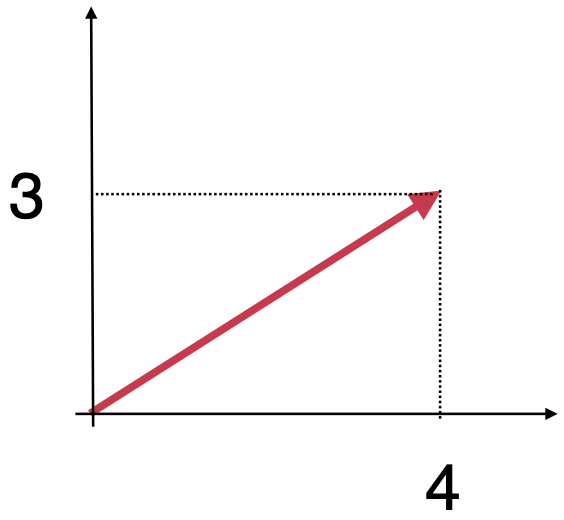
其实就是求这个直角三角形的斜边的大小对不？

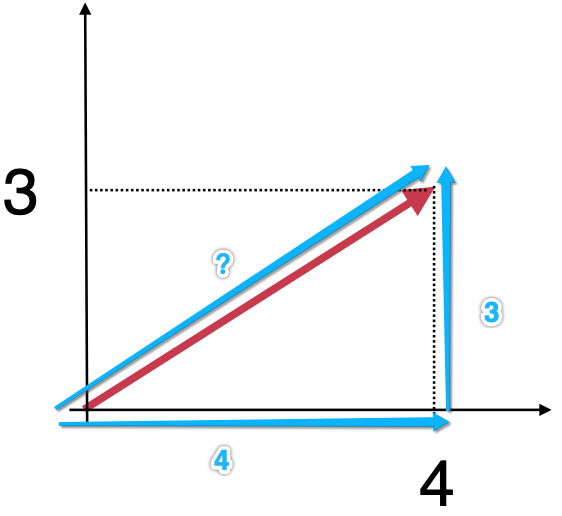
而其实根据初中所学的勾股定理就能算出其斜边的大小来，由于现在自己数学的水平可能停留在了小学。。所以用度娘上的一张图回忆一下：

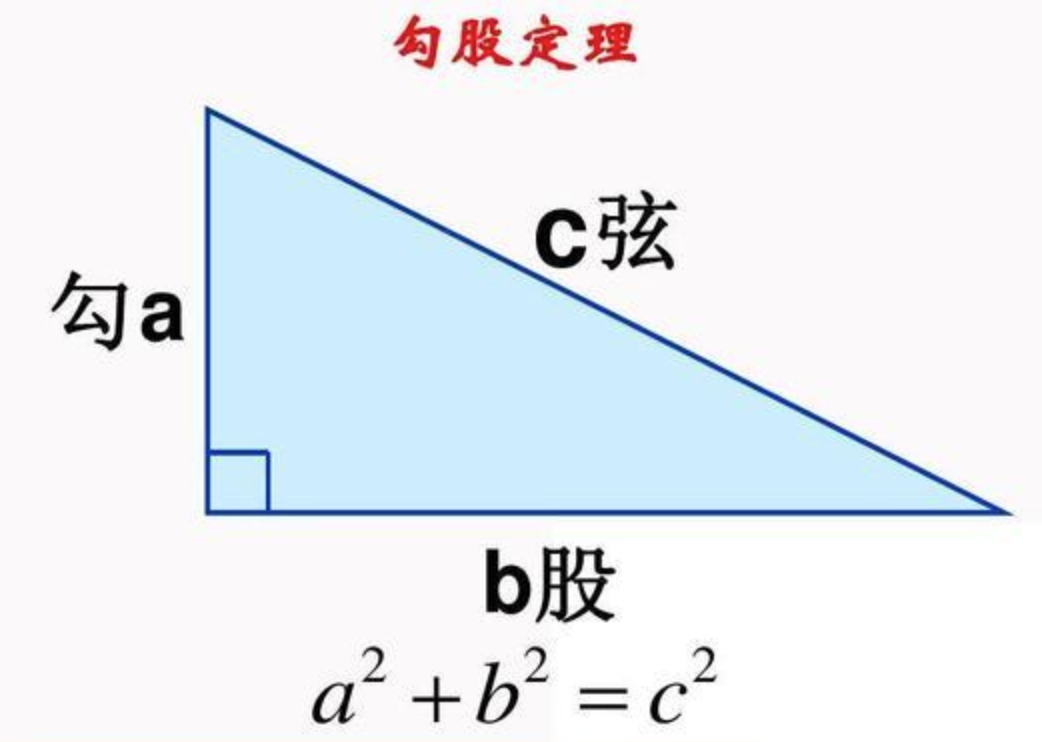
所以：

向量的模：

二维向量：

而在线性代数里，对于向量u的大小是用这样的双竖线来表示的，如下：

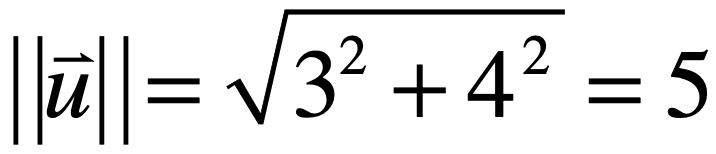
对于这个大小有一个专业的词来表示：向量的模。

思考：为啥要用双竖线来表示呢?【了解】

另外为啥在表示向量的模时是用的双竖线呢？

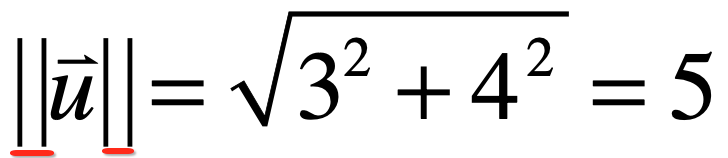
这是因为单竖线跟数学中求一个数的绝对值重合了，所以对于向量的取模用的是双竖线。换言之，单竖线和双竖线里面作用的对象是不一样的，单竖线里面作用的是一个个的数，而双竖线里面作用的是一个个的向量；另一个层面为啥使用双竖线是因为咱们目前的这种求解的方式是求的圆点到向量所代表点的欧拉距离，啥叫欧拉距离？百科一下：

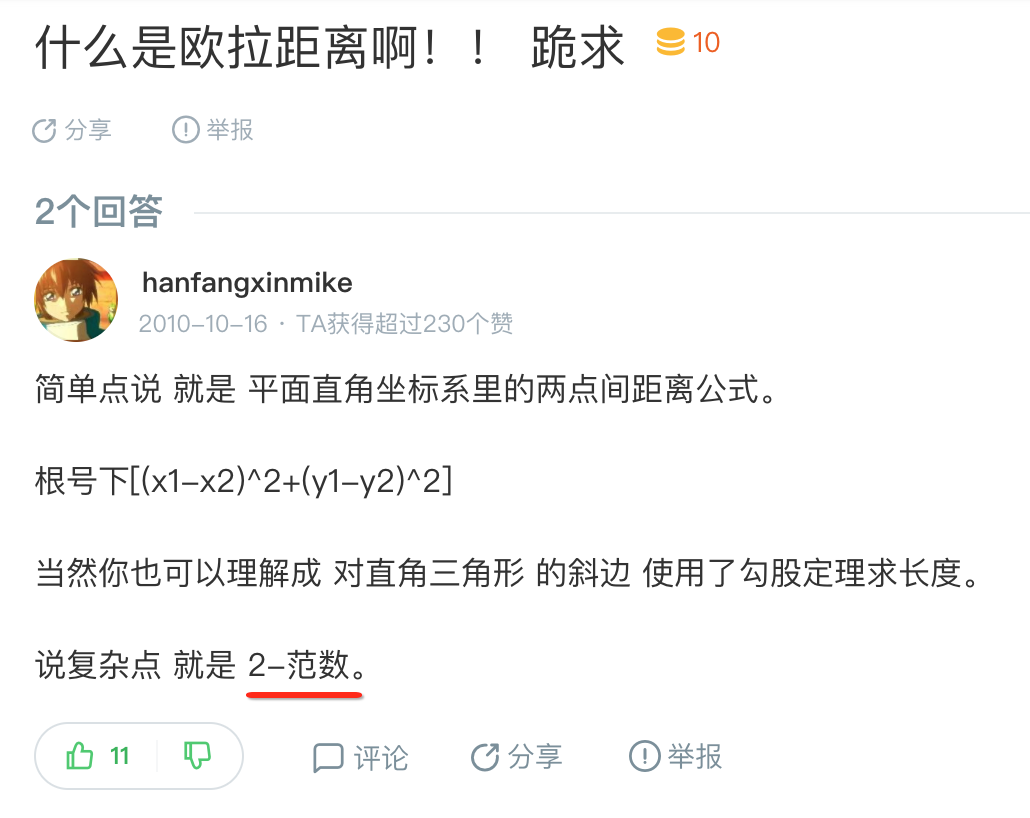
嗯，反正词挺高大上的，直观理解就是咱们目前的勾股定理求斜边，另外图中提到了一个更加高大上的词：“2范数”，它又是啥呢？

有些抽象，也不用过多纠结，看一下它的另一个定义：

其中看到木有，对于二范数的符号表示就是用的双竖线对不？

而它刚好就是对于咱们勾股定理中的求平方再开二次根是一种形态：

实际上把二范数这个概念作用在向量上跟欧拉距离是重合的，关于这块有个了解既可。

三维向量：

上面是针对二维向量的求解模的方式，那如果是三维的向量其模又是如何求解的呢？比如：

它所对应的三维坐标情况如下：

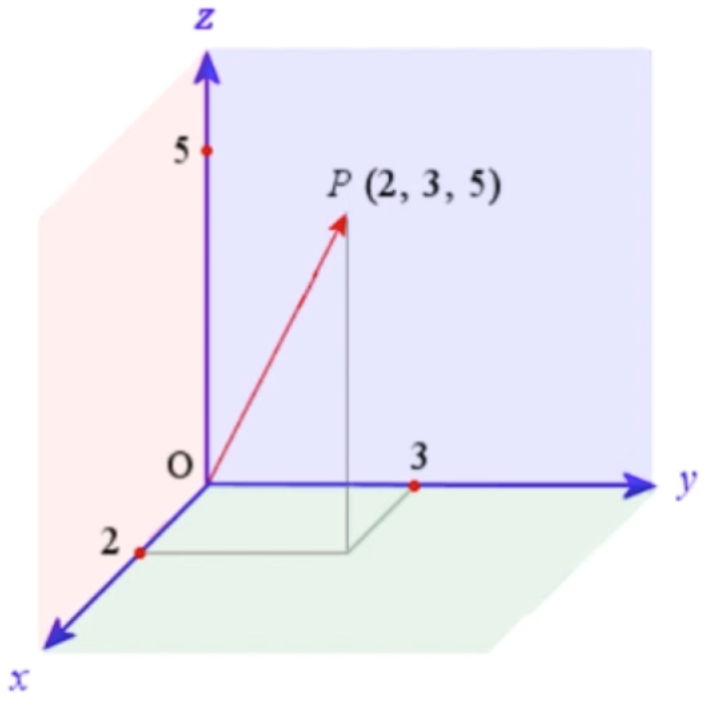
此时也就是在立体几何中计算OP这个线段的长度既可，此时就需要有立体几何的知识了，不过也不是太难，看一下：先做一个辅助线：

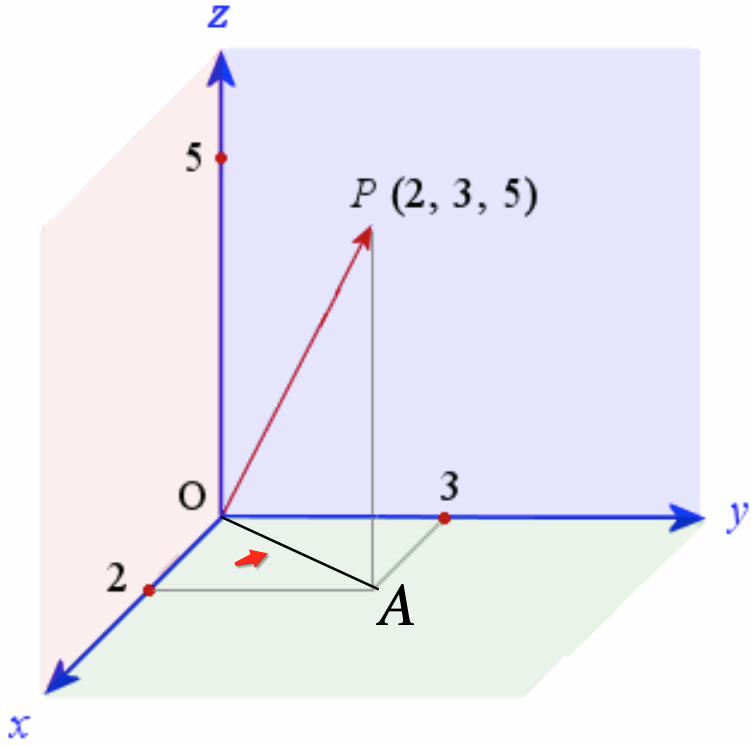
这样一看OP其实就是这个直角三角形的斜边的长度对么？

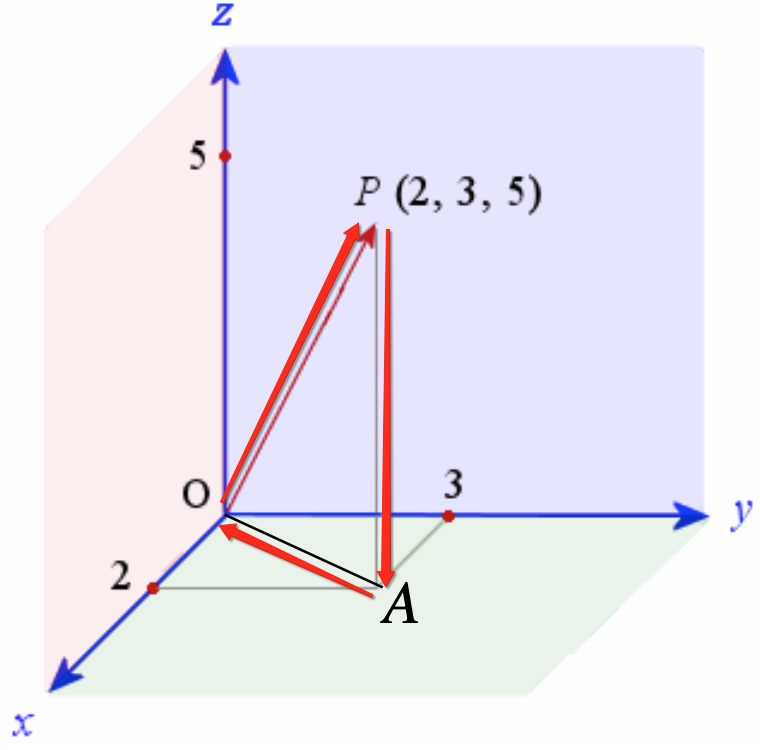
但是此时看一下这个直角三角形已知大小的边貌似只有它：

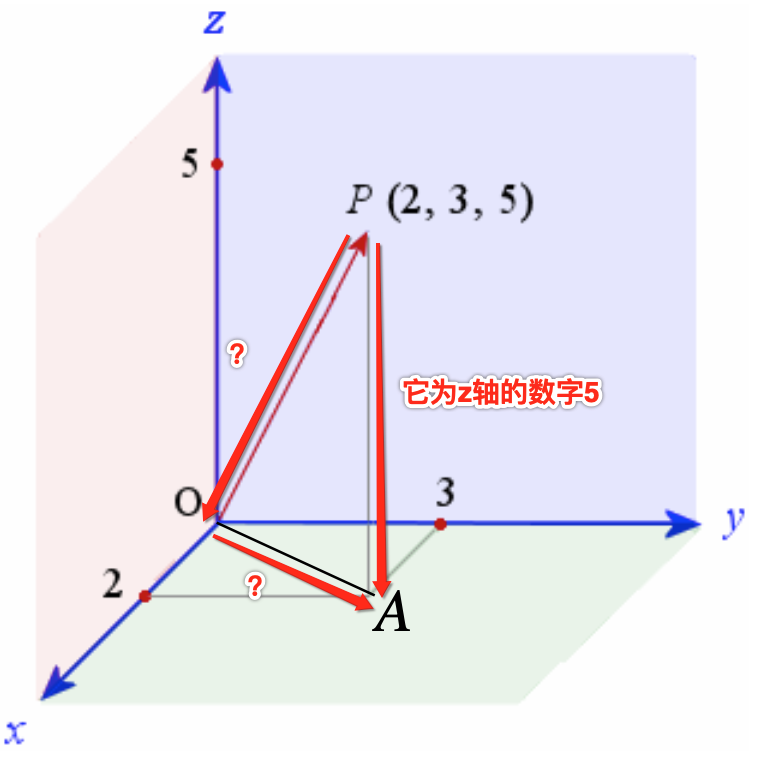
所以此时要能算出斜边OP还需要知道OA的大小，而它其实又是另一个直接三角形的斜边，如下：

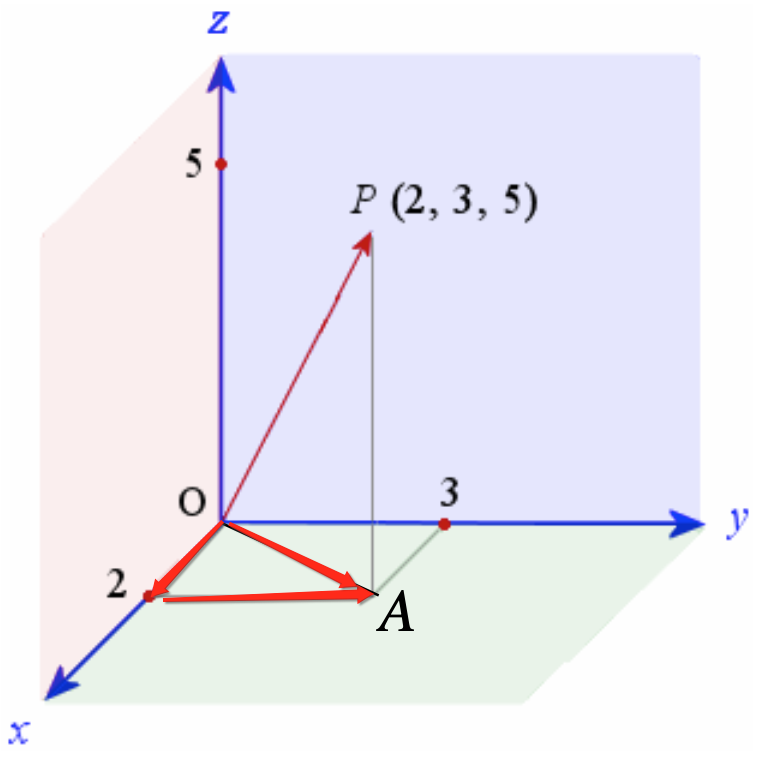
所以根据勾股定理此时就可以很方便地求出OA这个向量的大小，如下：

所以咱们就可以算出OP这个向量的模了，如下：

其实发现规律木有，对于三维的和二维的其计算模的最终都是取向量每个坐标轴分量的平方和再开根。

N维向量：

所以，对于N维向量：

它的U的长度或模的公式为：

 

单位向量 unit vector：

既然我们已经能算出向量的大小了，那么就可以算出它的单位了，如下：

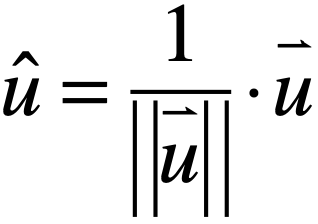
上面这啥意思，其实就是用向量除以向量的大小，最终得出来的就是单位向量，而将式子展开一下就变为：

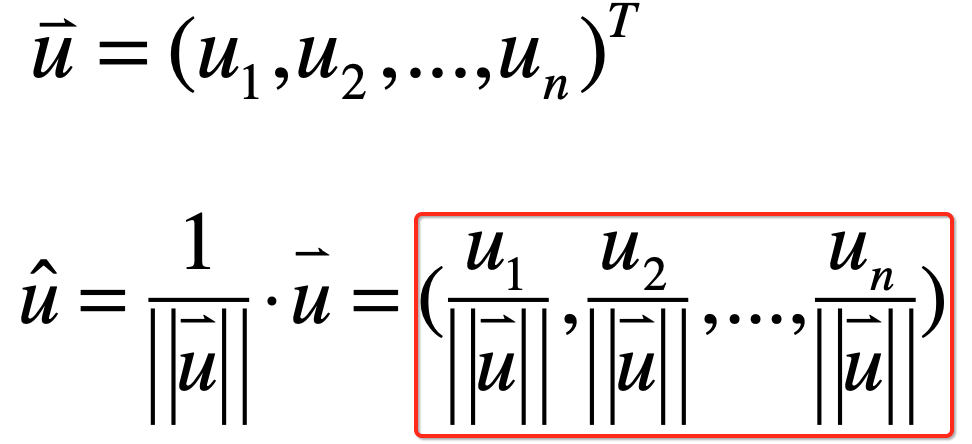
其中单位向量用这个字符来表示：

以平面坐标来理解单位向量：

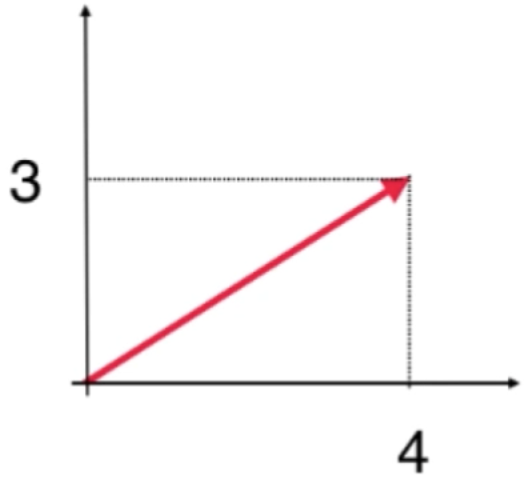
而这个向量的长度为5，然后它的单位向量就是整个向量的1/5对不？所以标蓝的就是单位向量：

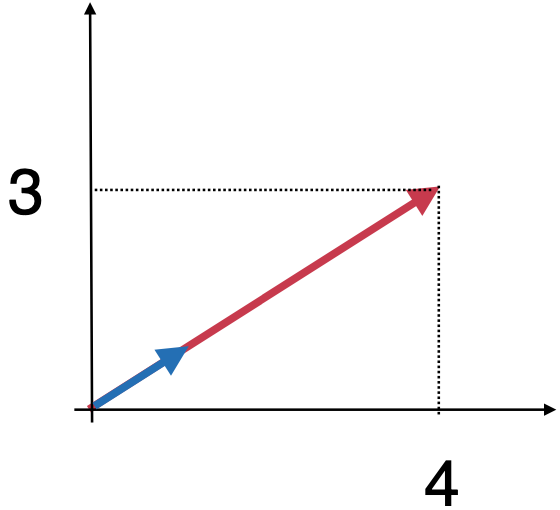
其中单位向量的方向依然是保持不变的。而单位向量的模记住永远等于1：

 

既然它的大小是固定的1，所以说对于单位向量来说大小已经不重要了，而重要的是指它的方向，所以总结如下：

如果只需要求得向量的方向可以使用单位向量既可；而如果只求向量的大小则直接求向量的模既可。

而根据U的向量求出U向量的单位向量的过程叫做：归一化、规范化（normalize）。

标准单位向量 standard unit vector：

另外单位向量其实是有无数个的，这里从坐标轴就可以得知：

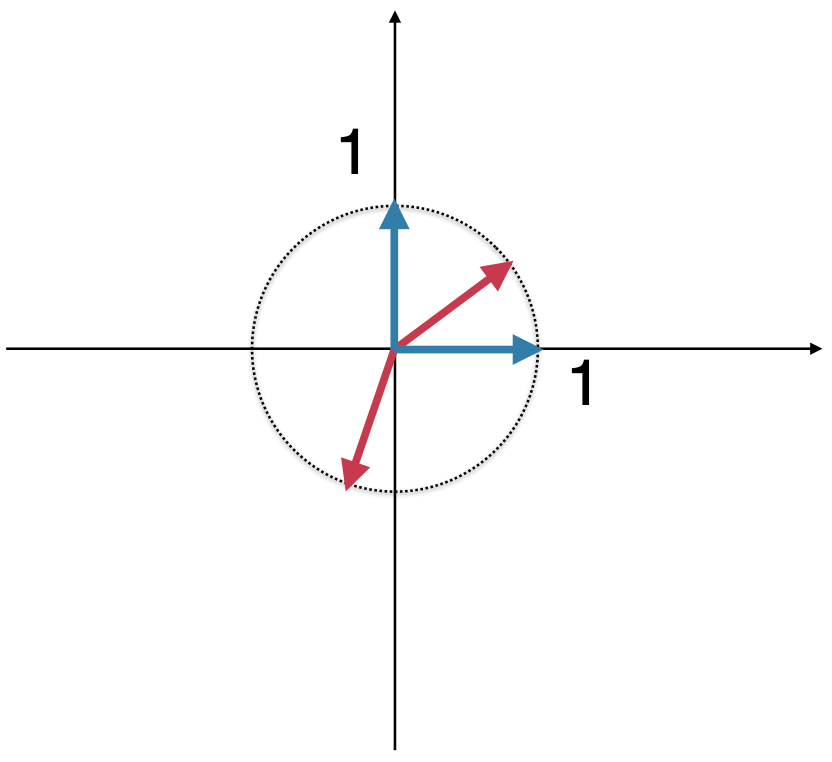
图中是以(0,0)为圆心，半径为1做一个圆，从坐标原点到圆上的任意一点所对应的向量都是一个单位向量， 那当然就是无数个喽，但是！！！在二维空间中，有两个非常特殊的单位向量：

 

也就是这俩单位向量只由0，1组成的，这样的单位向量就叫做：标准单位向量(Standard Unit Vector)。而标准单位向量是指向坐标轴的正方向，也就是图中标蓝的那两个。另外单位向量中只能有一个维度的值为1，其它维度的值都应该为0，比如：

二维空间中，有两个标准单位向量：

三维空间中，有三个标准单位向量：

对应三维坐标轴如下：

那n维空间中，则有n个标准单位向量：

那标准单位向量有啥用呢？很重要！！！在未来空间的学习中就可以看到了，待未来再来体会，目前先来了解它的概念。

实现向量规范化：

接下来则来编程实现一下上面理论所描述的求一个向量的模和求一个向量的单位向量。

求向量的模：

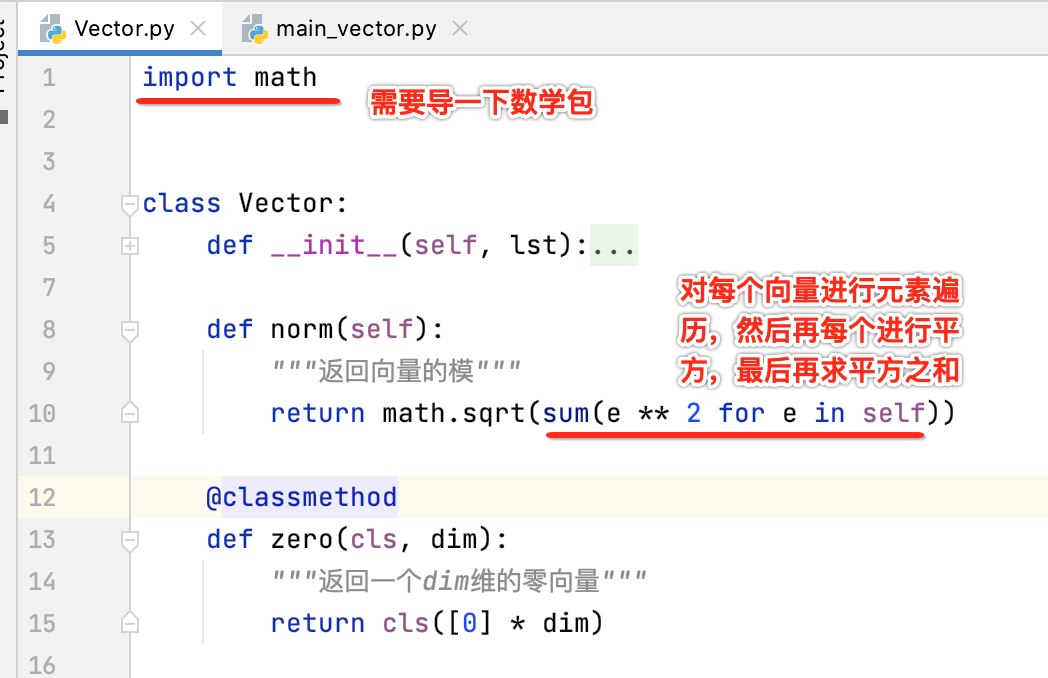
调用一下：

求向量的单位向量：

知道了单位向量的计算大小之后，就可以来算它的单位向量了，也就是规范化，如下：

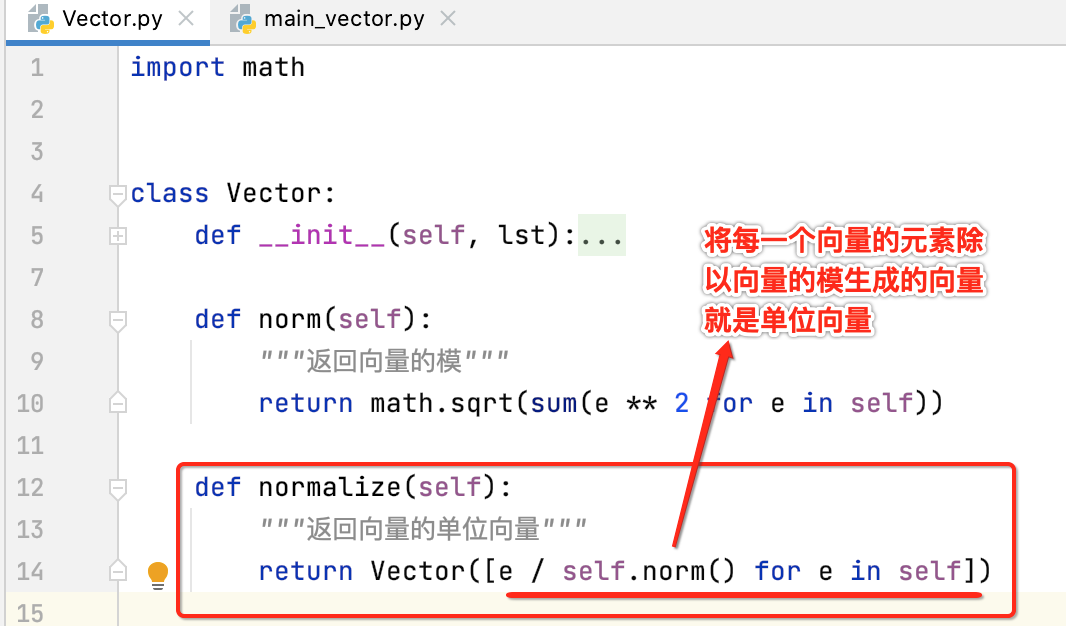
但是！！这种写法不够优，为啥？

所以可以提前一下：

下面来调用一下：

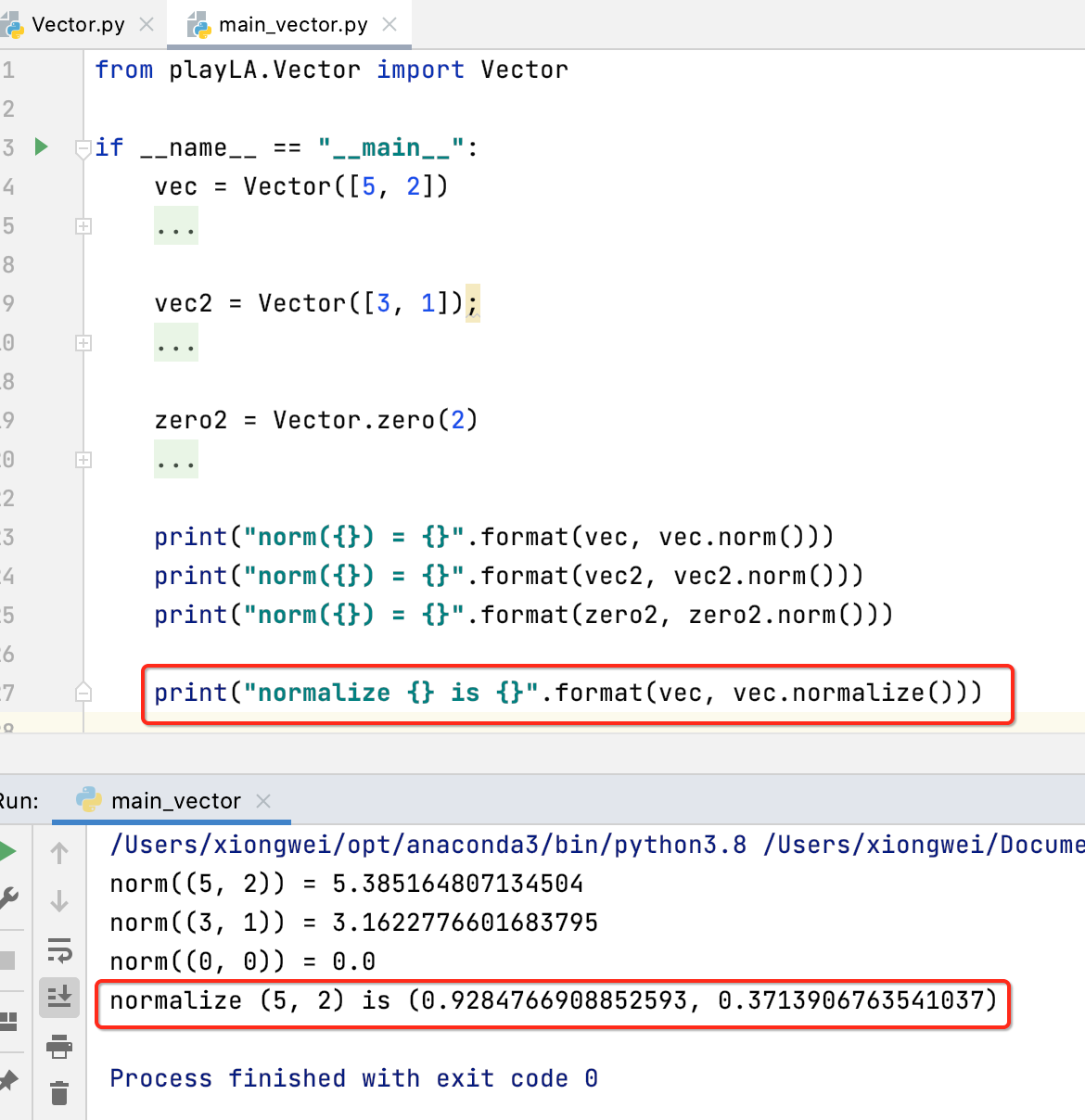
为了验证确实计算出来的是单位向量，咱们对它进行一下取模，因为所有的单位向量的长度都为1，如下：

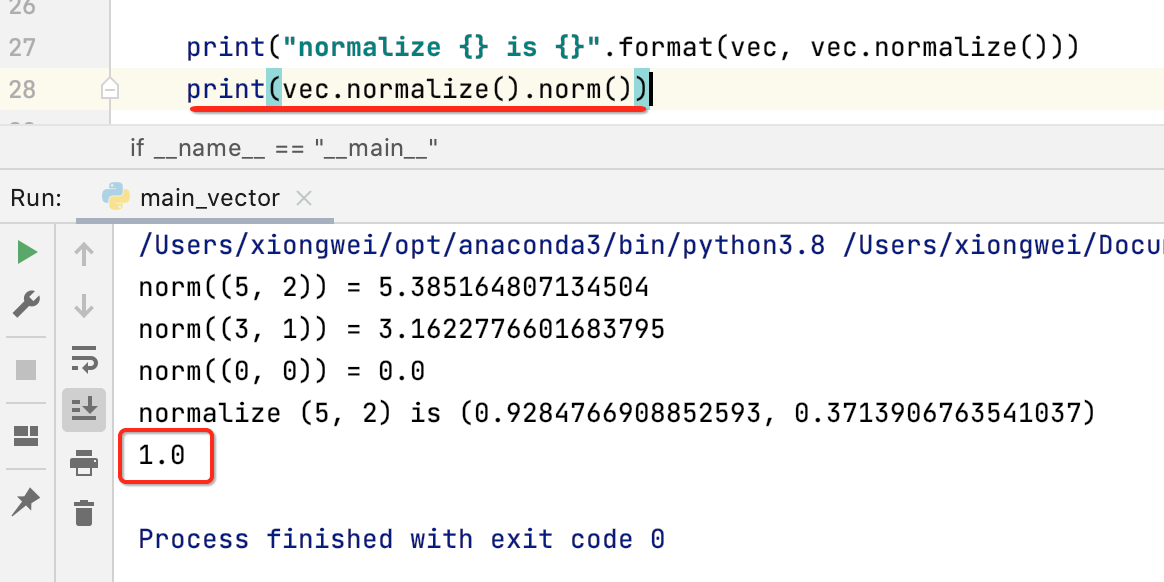
然后再换一个向量试一下：

优化：

目前对于求向量的单位向量写法还是有待加强的，目前咱们是用的乘：

 

貌似直接用向量除以向量的模不就可以了么，而且阅读性也更加的好，如下：

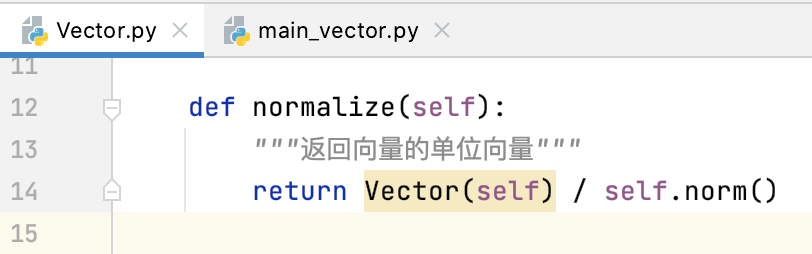
运行一下呗：

/Users/xiongwei/opt/anaconda3/bin/python3.8 /Users/xiongwei/Documents/workspace/python/Play-with-Linear-Algebra/02-Vectors/03-Implement-Our-Own-Vector/main_vector.py
Traceback (most recent call last):
  File "/Users/xiongwei/Documents/workspace/python/Play-with-Linear-Algebra/02-Vectors/03-Implement-Our-Own-Vector/main_vector.py", line 27, in <module>
    print("normalize {} is {}".format(vec, vec.normalize()))
  File "/Users/xiongwei/Documents/workspace/python/Play-with-Linear-Algebra/02-Vectors/03-Implement-Our-Own-Vector/playLA/Vector.py", line 14, in normalize
    return Vector(self) / self.norm()
TypeError: unsupported operand type(s) for /: 'Vector' and 'float'
norm((5, 2)) = 5.385164807134504
norm((3, 1)) = 3.1622776601683795
norm((0, 0)) = 0.0

Process finished with exit code 1

报错了，为啥呢？因为目前咱们的Vector还不支持除法操作，所以像Vector乘法一样，定义相关的魔法函数既可，如下：

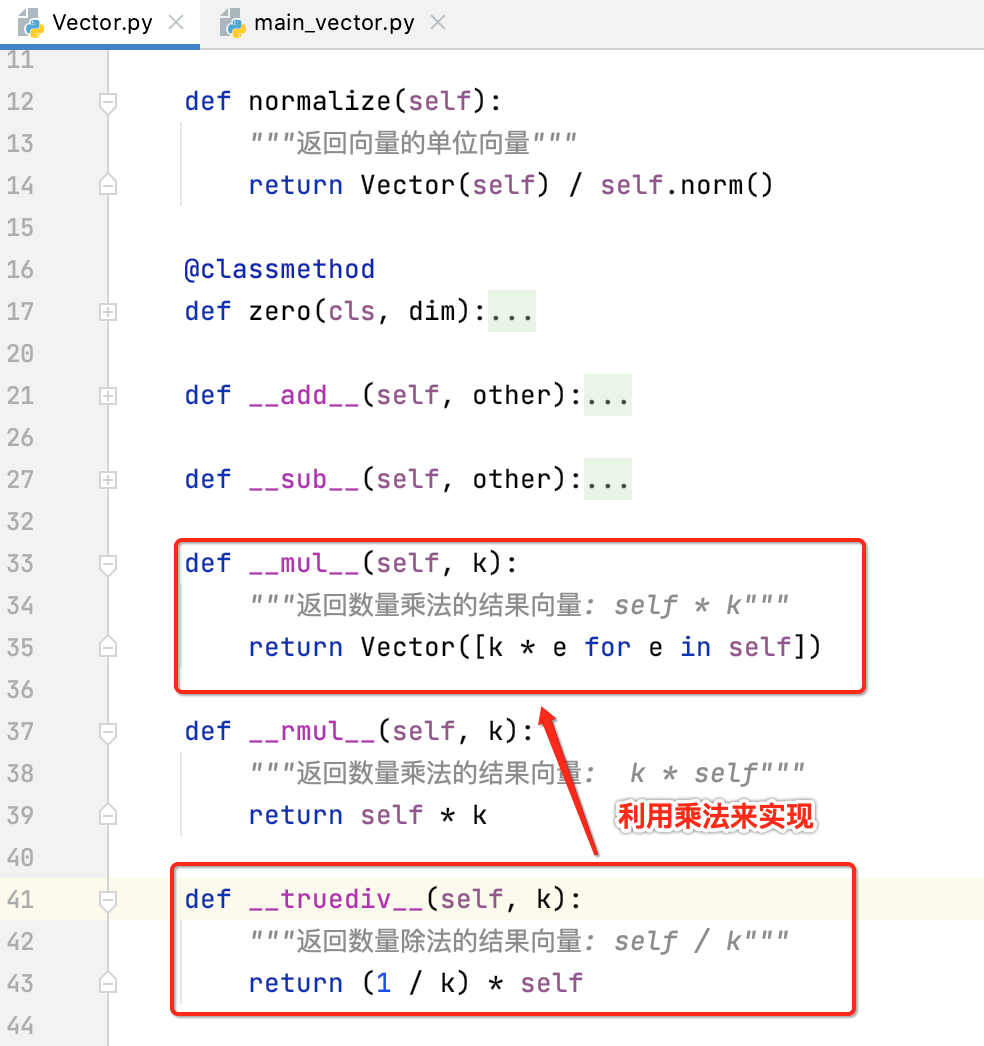
此时再运行就ok了。 但是此时还是有待完善之处，下面来算一下零向量的单位向量，看一下：

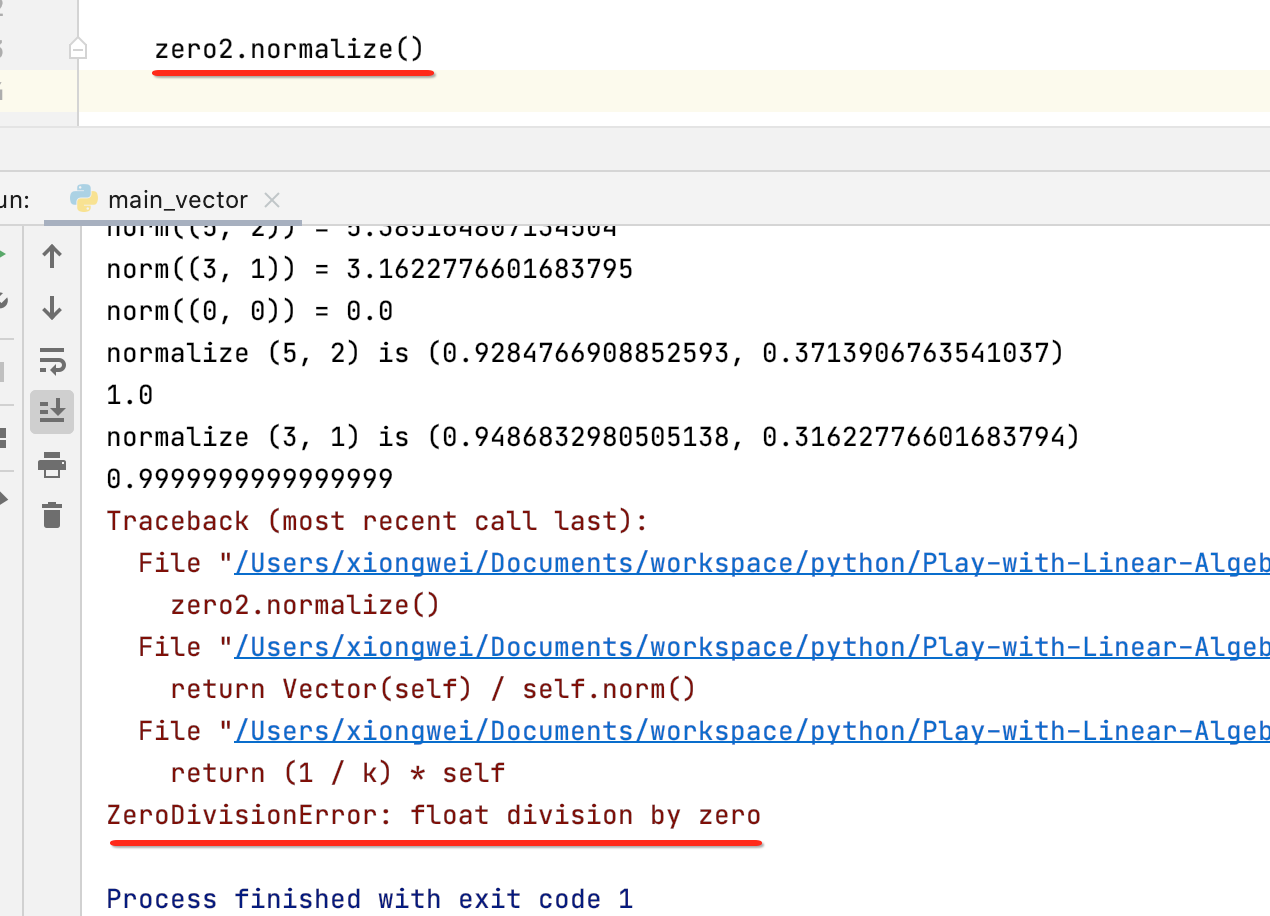
所以此时咱们可以加一个判断：

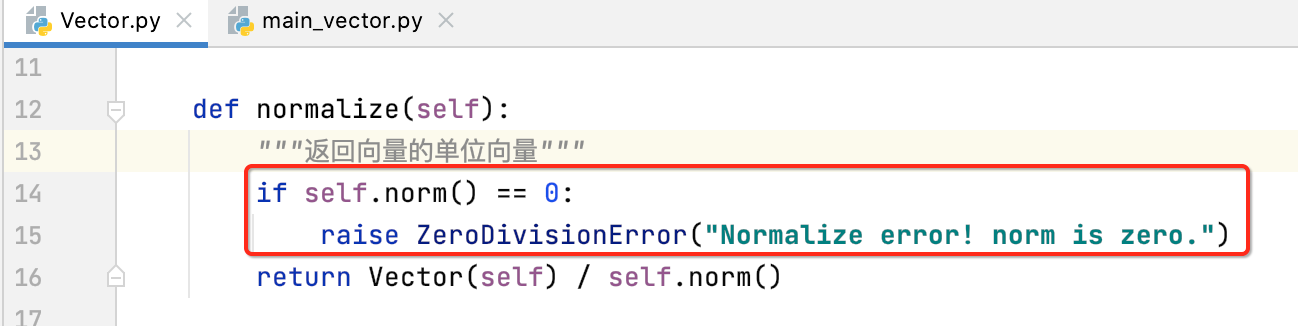
但是！！还是有些问题的，因为self.norm()返回的是浮点型，浮点型不能用==来进行判断，应该怎么判断呢？这里比较好的做法是判断两个浮点数之间的距离小于某一个非常小的数，比如0.00000000001之类的，则就认为这俩浮点数是相等的，所以可以这样：

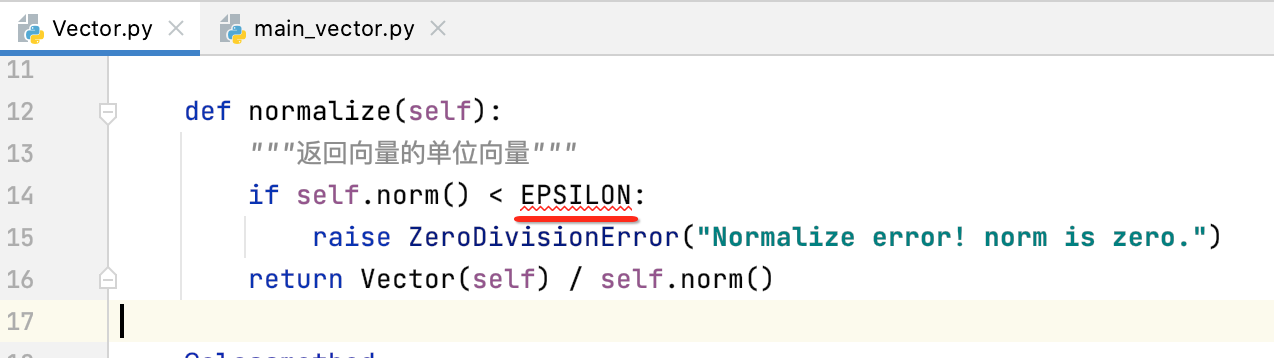
其中EPSILON是一个非常非常小的数，可以理解为0，这里看一下网上https://blog.csdn.net/norman_irsa/article/details/80630656对这个名词的解释：

由于这个精度值肯定在未来还会被其它的类使用，所以这里将其定义成一个公共的：

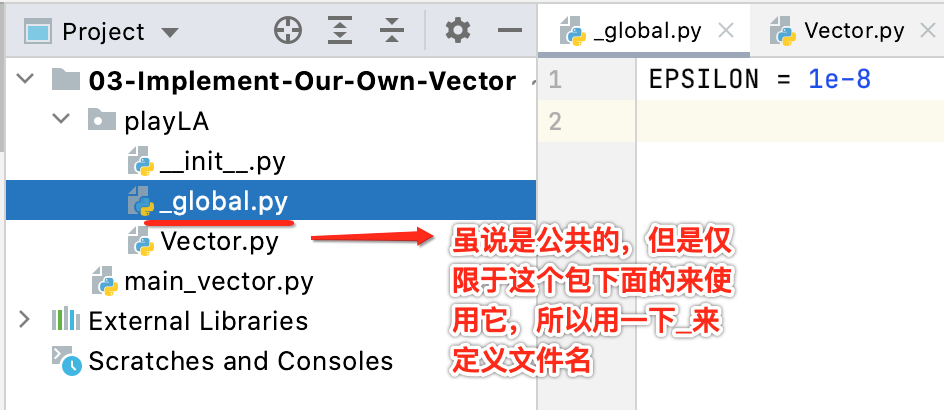
也就是1/（10^8），接下来咱们就可以在Vector中来引用它了：

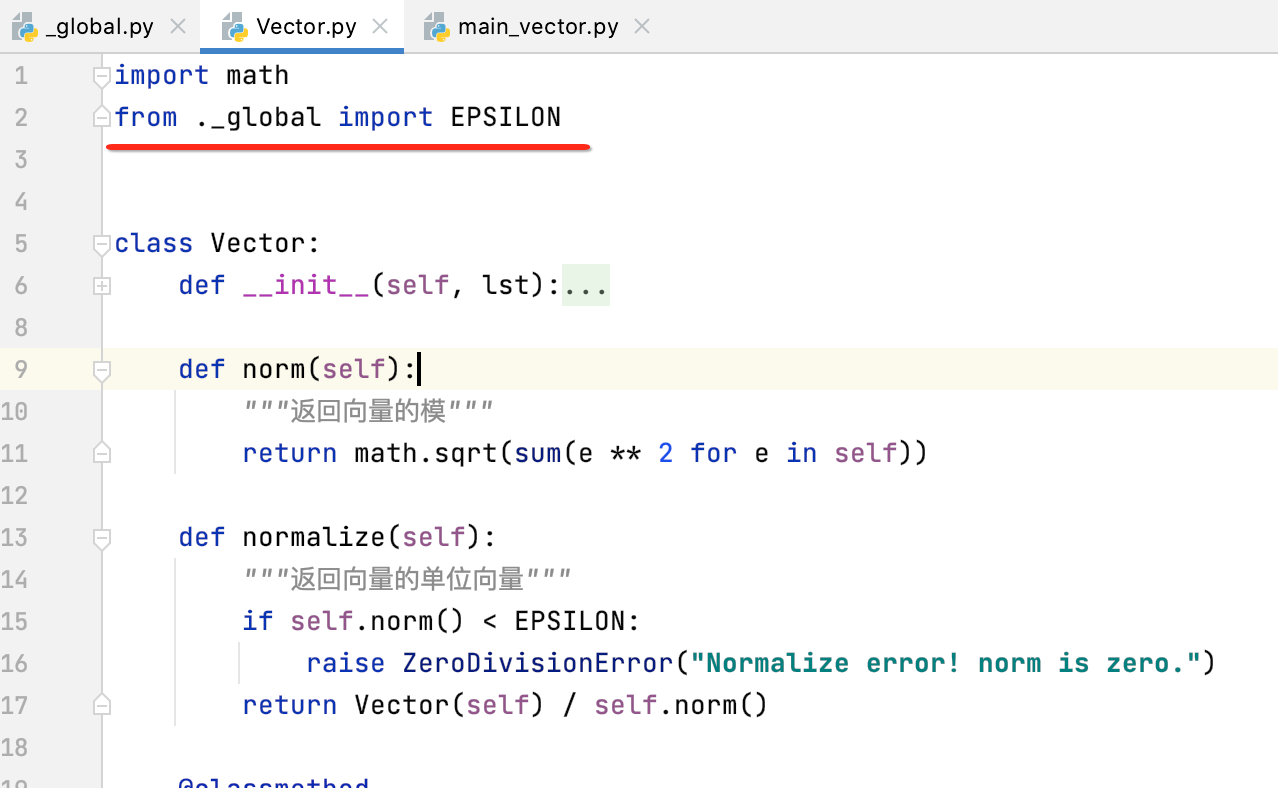
此时再运行当然也是会报错的，就是咱们自定义的异常：

 

咱们在调用时就可以捕获这个异常了：

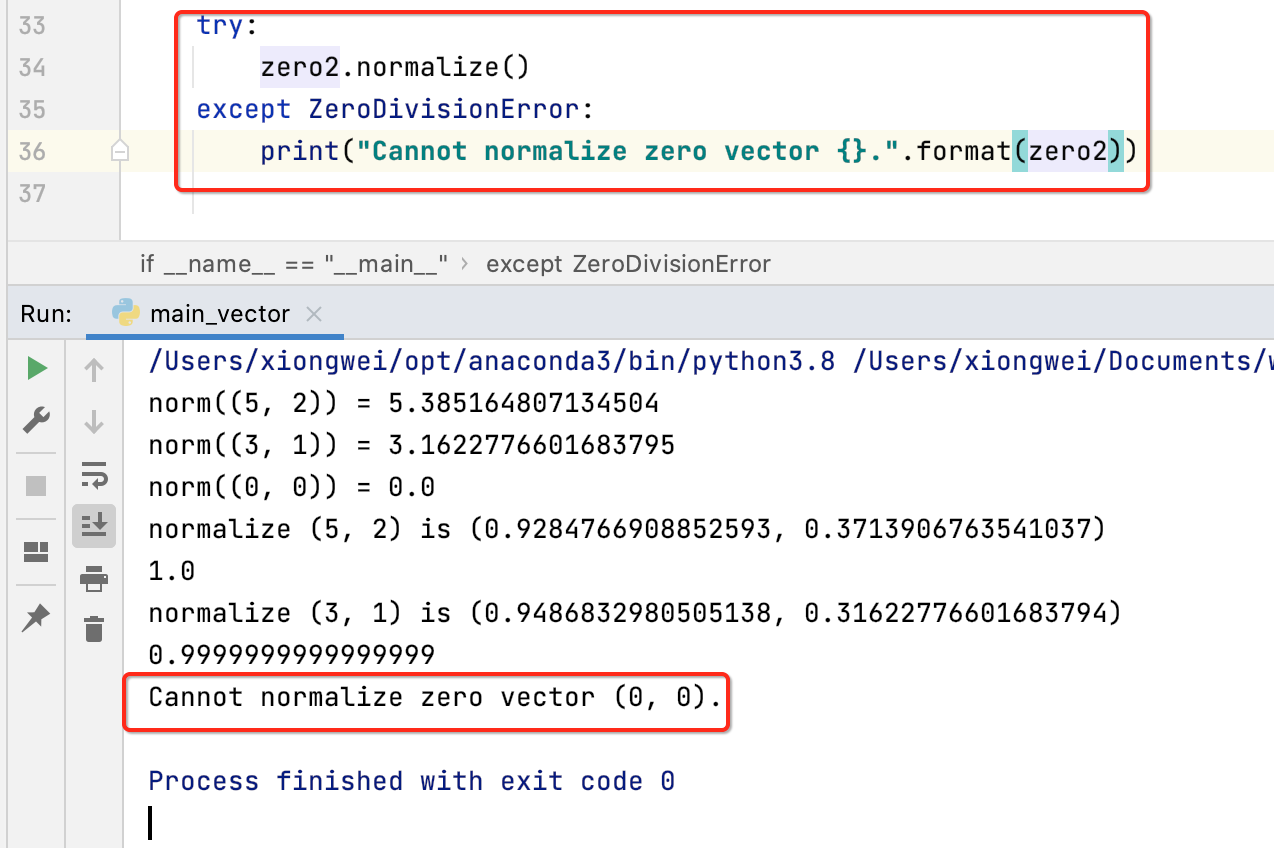
此时就比较完美了，当然这里又涉及到N多Python的语法，不懂的直接照抄就行~~重点是学习线性代数相当的知识。

向量的点乘与几何意义：

向量的点乘：

接下来学习一下非常非常重要的要领----向量的点乘，啥是向量的点乘呢，看下面：

也就是两个向量之间的乘法操作，在之前咱们已经介召了向量的数量乘法，那是向量与数之间的乘，而向量与向量之间的乘法又是如何定义的呢？像这样？

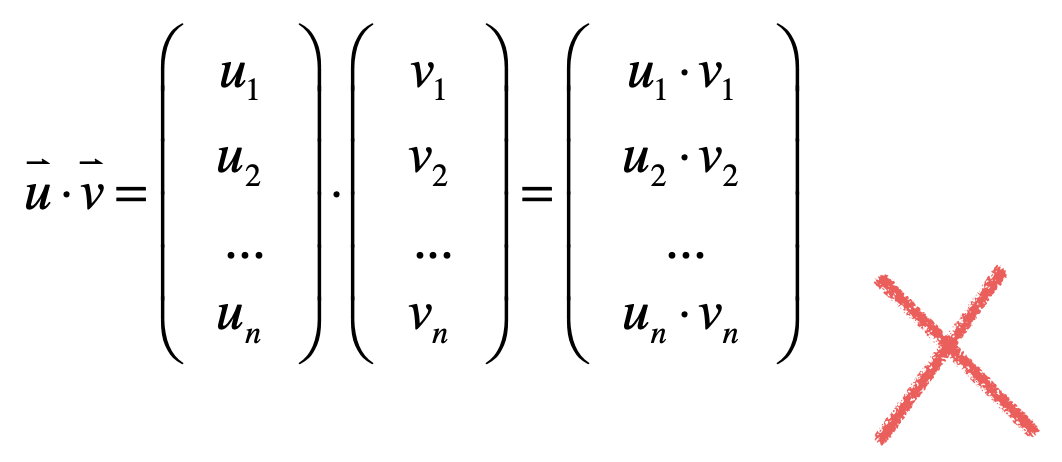
图中也看到了一个大红叉，肯定不是这样像向量的+那样直接将向量对应的元素相成再组成一个向量的，为什么？这块之后再来揭示，目前先保留这个疑问，其实对于向量之间的乘法定义是这样的：

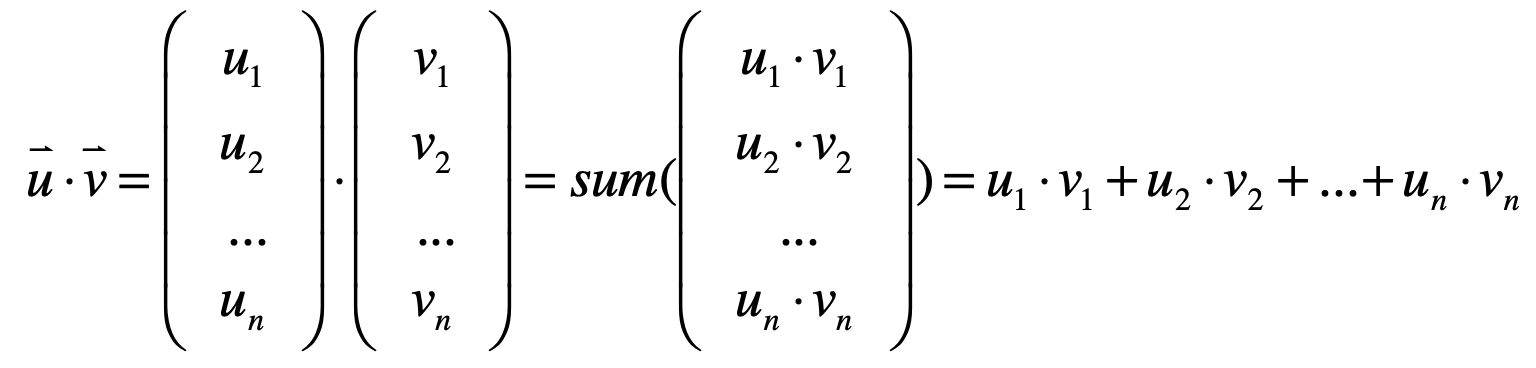
那为啥要这样定义呢？也是后续再来揭示，目前先记住它就成。

从上面这个公式可以看出一个重要的特性：两个向量“相乘”，结果是一个数【又称之为标量】！而非向量~~而更严格的说法：这叫两个向量的点乘(dot product)或者是两个向量的内积(inner product)。

而上面定义了相量的点乘之后，在几何意义上其实它正好等于这样的一个结果：

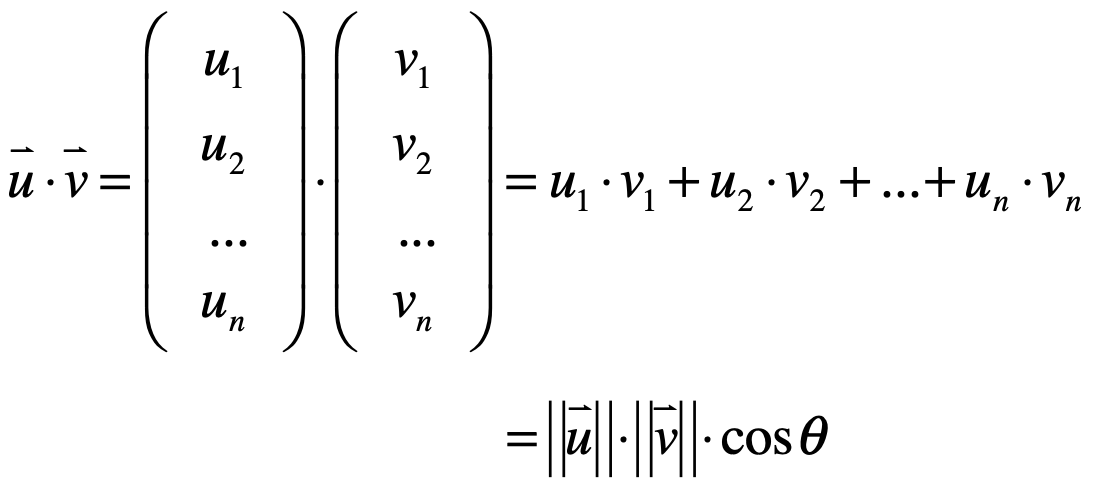
其中cosθ是指向量u和向量v之间的夹角，那为啥会有这样的一个结论呢？下面来证明一下：

还是以二维空间为例，有这么两个向量：

其中为啥那个绿色的那条是向量u-向量v？其实很简单，还记得向量的加法么？

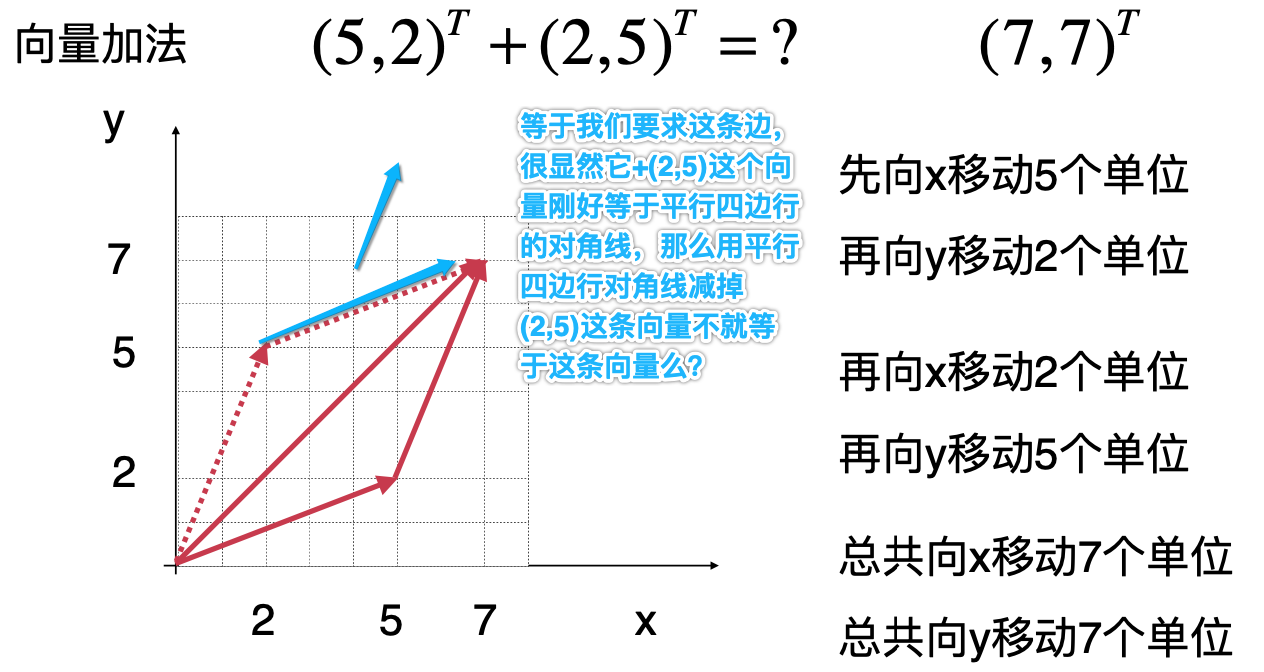
所以此时等式可以写成：

 而根据余弦定理：

又可以推导出：

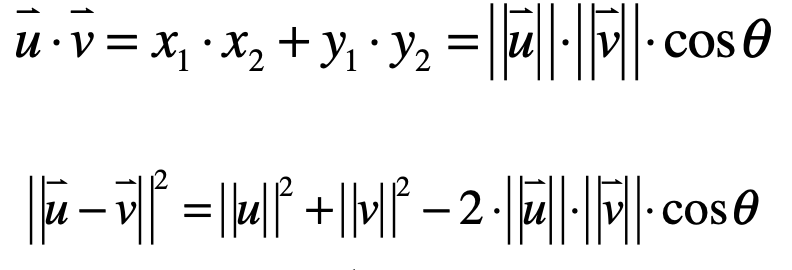
然后将2.||u||.||v||.cosθ挪到等式左边，形态为：

此时等号左边刚好等于我们要论证式子左边，接下来只要将等式右边证明成是它那么就可以了：

下面进一步推导，将坐标代入进去等式右边就为：

是不是就推导出了向量点乘的公式了？

向量点乘的直观理解：

为了进一步加深对于向量点乘的理解，这里以一种更加直观的视角进一步理解一下：

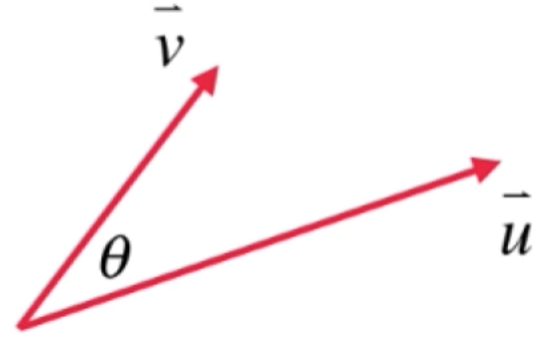
此时其实向量v可以向向量u做一个垂线：

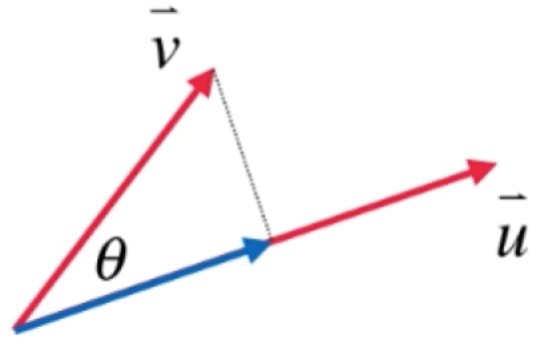
而此时根据余弦公式：

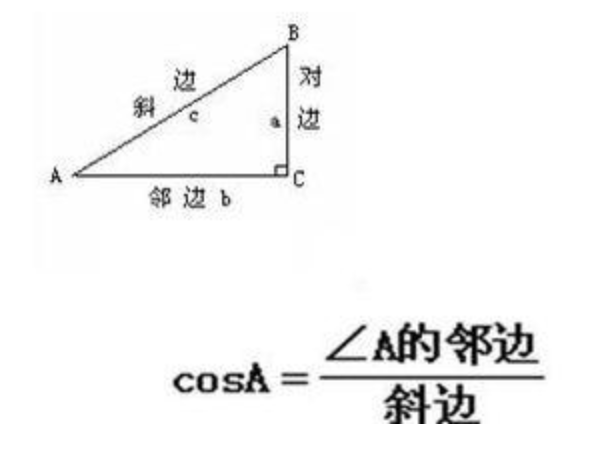
此时可以很轻松的算出蓝色邻边的大小为：

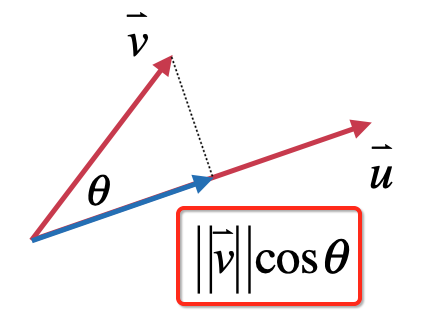
此时咱们就可以将向量点乘几何公式进行一下变化，如下：

 

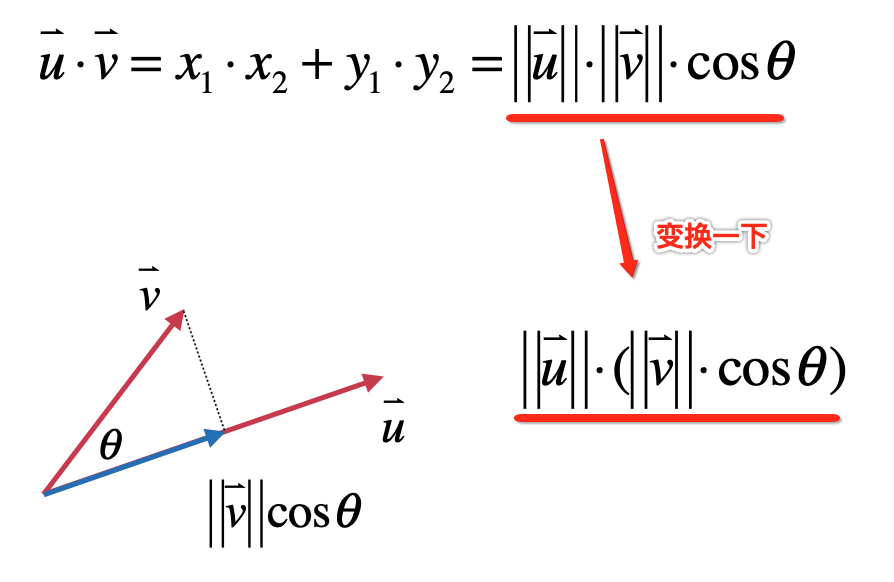
发现原来向量的点乘是使用投影的方式让两个向量都指向同一个方向两个向量大小的乘积，背后可以理解向量的点乘也就是想办法在处理向量是具有方向性这样一个事情，它认为不同方向的向量是不能直接做乘法的，将一个向量投影到另一个向量上不就具有相同的方向了么？此时再相乘不就有意义了，同理反过来，也可以将向量u投影到向量v上来，如下：

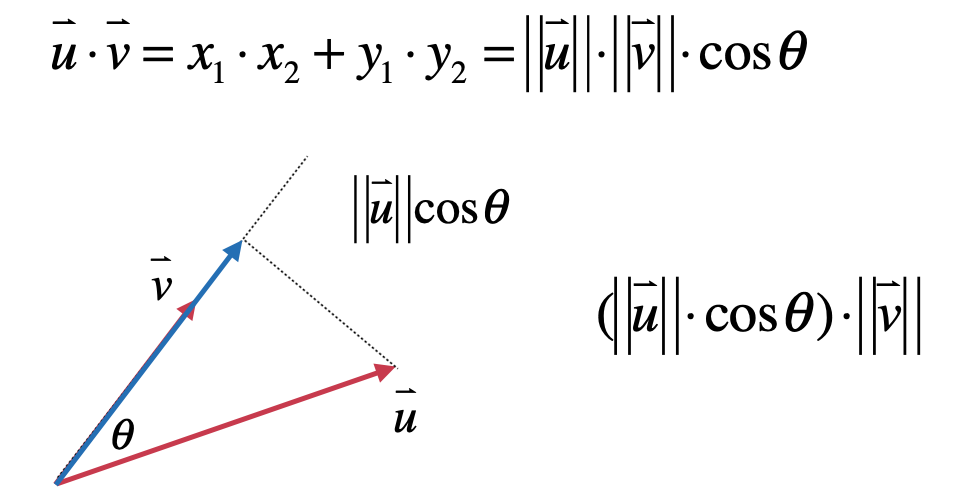
另外，其实也可以将向量投影以坐标系的x轴和y轴上来理解向量的点乘，比如：

 

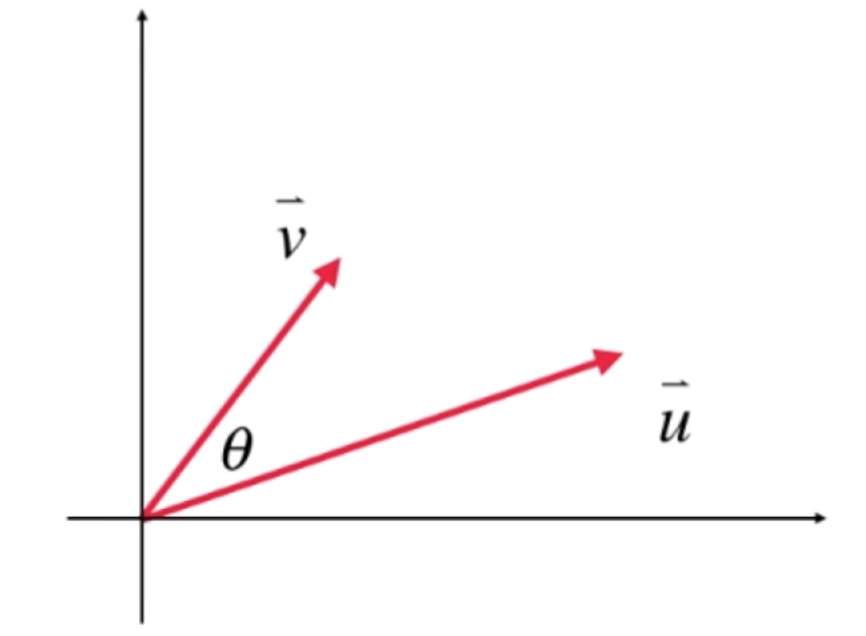
此时将向量u投影到x轴上为：

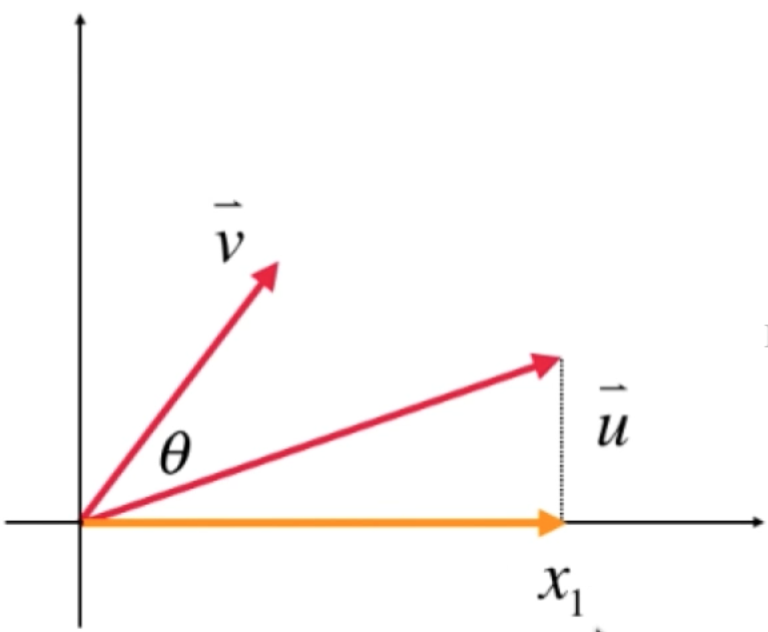
而将其投影到y轴上为：

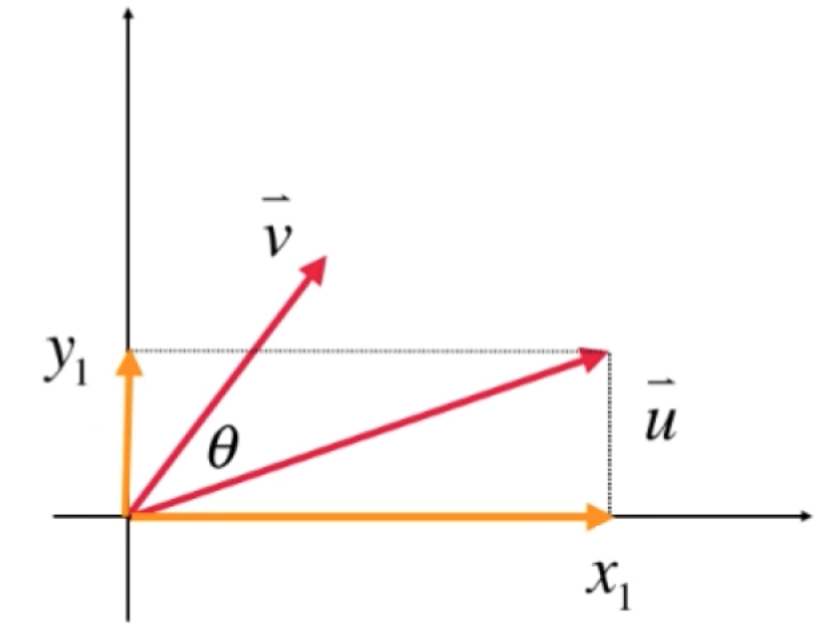
同理将向量v进行xy轴的投影如下：

 

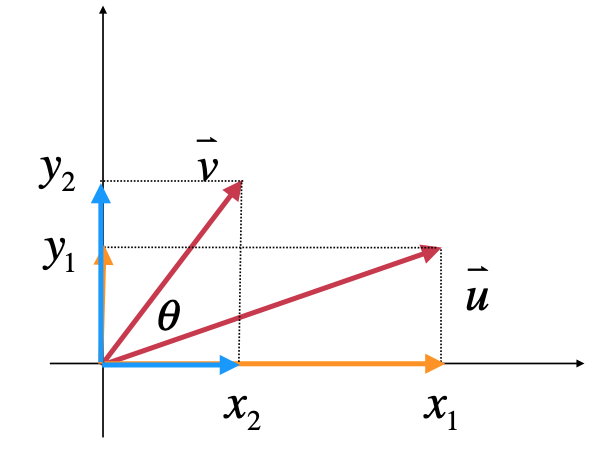
此时同方向的向量就可以做乘法了：

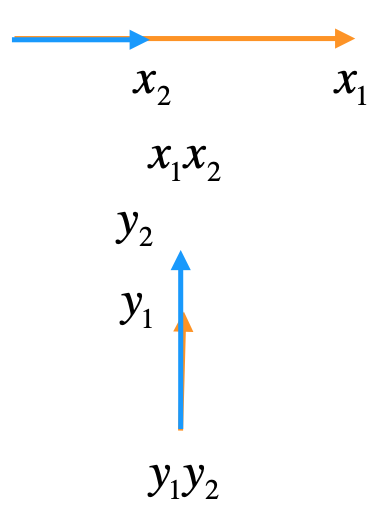
而对于另外两组搭配：

由于它们是完全不相同的方向，相互都没影响谁，所以相乘之后其实就是为0，所以这也是为啥向量的点乘中只有x1*x2+y1*y2的原因之所在了：

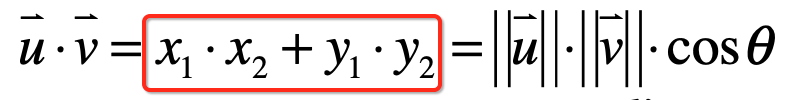
当然这种理解方式只是为了加深咱们对于向量点乘的理解，这个推导过程在实际使用时可以忽略~~

实现向量的点乘操作：

接下来则回到python中实现一下点乘：

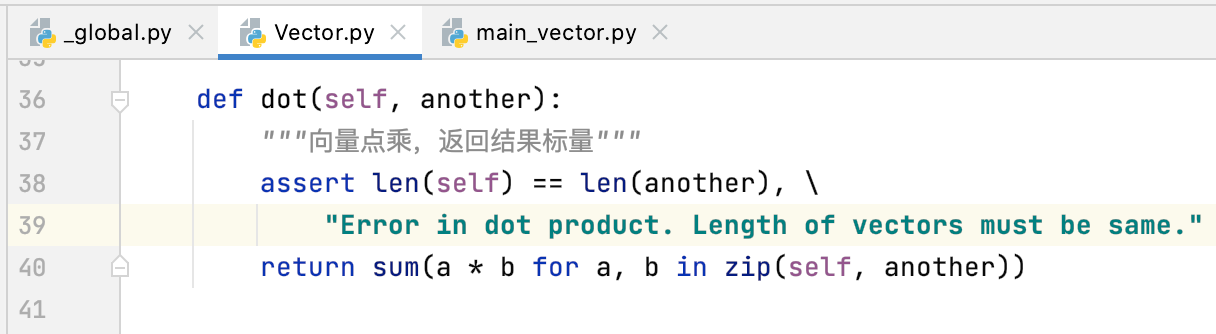
接下来调用运行一下：

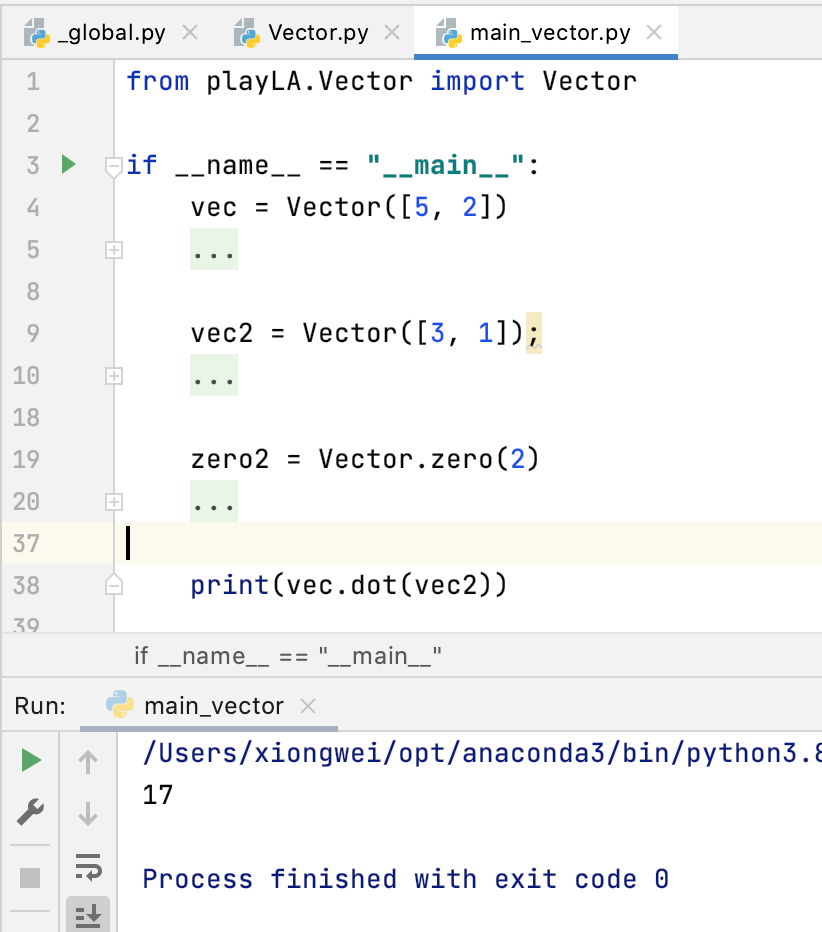
这里有一个注意点：有些数学库会将u * v定义为逐元素相乘的向量量，即：

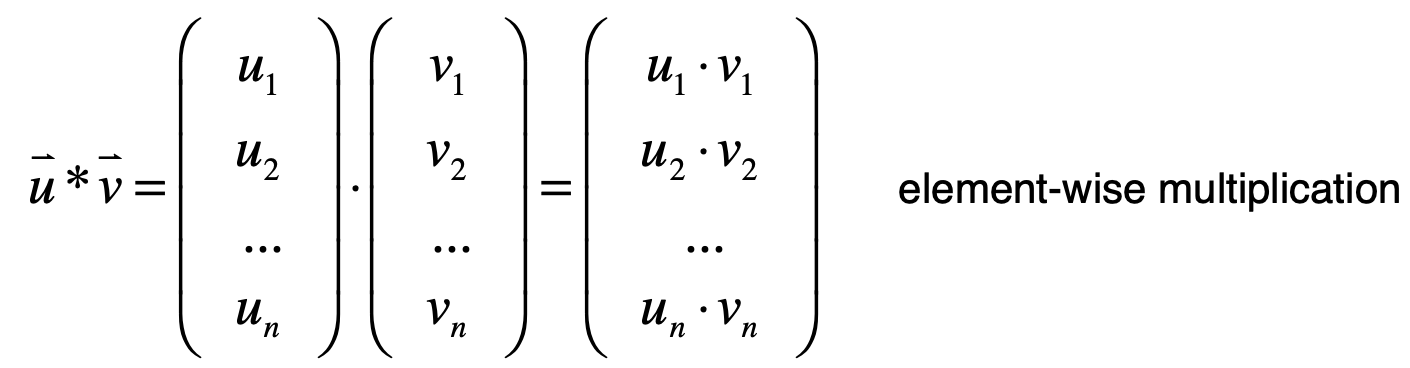
由于这种计算是不具备数学含义的，所以咱们的实现中就不实现了。 但是在实际使用数学库中可能会误认为提供的方法就是向量的点乘其实它是如上所说的这种，所以在实际使用数学库时需要小心。

向量点乘的应用：

学习了向量点乘有啥意义呢？下面则来探讨这样的一个话题。

向量的夹角：

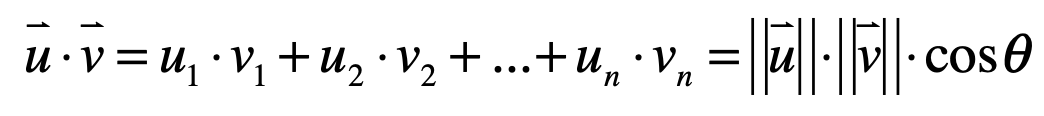
根据上面的公式发现可以很轻松的求出两向量的夹角，如下：

而根据余弦值，就可以判断夹角的类型了，如下：

此时就有如下结论了：

根据上面的这个特点，这里回忆一下之前所学的标准单位向量，其也可以判断所有标准单位向量都是垂直的：

 

判断两个向量的相似程度（推荐系统）：

正因为有上面这种可以判断向量夹角的关系，所以可以用它来判断两个物品的相似程度，如下：

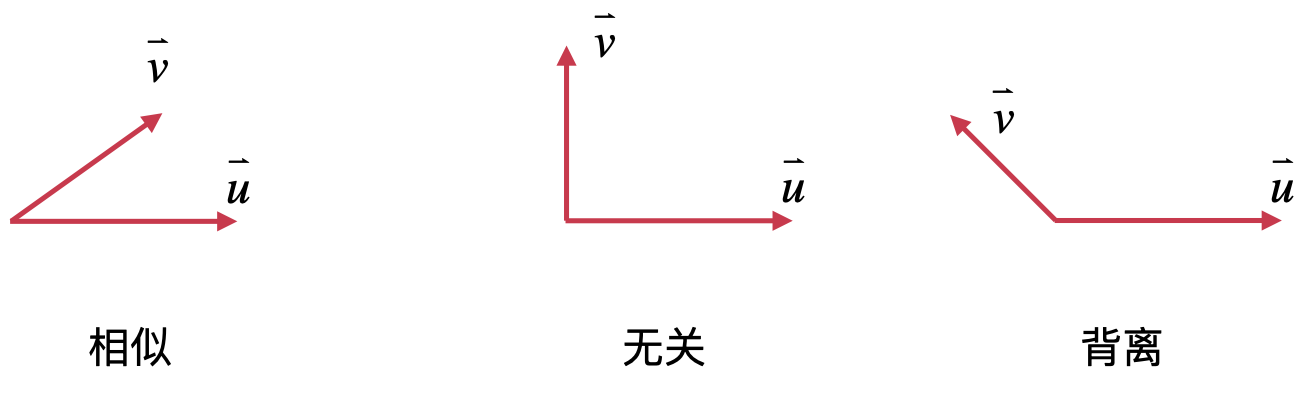
举个例子你在网上看了一部电影，然后呢之后系统就可以根据你的喜好进行电影推荐了，此时就可以把电影想象成一个向量，然后对多部电影进行向量的点乘运算就可以求出相似性，这里简单理解，当然真正的推荐系统不可以有这么简单的。

几何意义：

此时可以根据如下公式很轻松地算出来：

其中投影点的方向就是求向量u的单位向量，还记得之前说单位向量的意义主要是用来判断方向的么？

Numpy中向量的基本使用：

前言：

对于向量的各种运算目前都是我们自己来封装的，其实对于python中有一个非常著名的跟线性代数相关的库---Numpy，所以这里将来学习一下使用专业的数学库是如何完成向量的基本操作的。 这里新建一个新的文件：

说明环境木问题，那正式用numpy编写咱们的向量之前，先思考一下：在python中不是已经有列表的概念了：

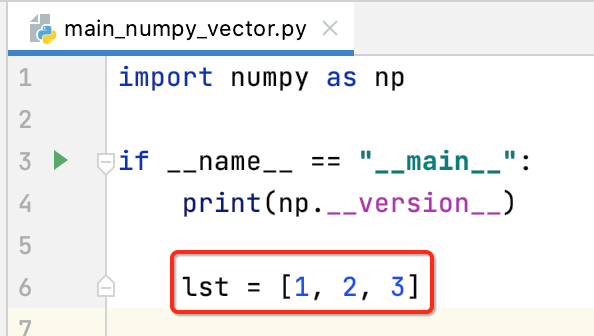
用它足以表达向量了，为啥还要搞个numpy出来呢？其实有一个非常重要的原因是在python中的这个列表里面可以存放任意类型，不同类型也可以存其中，比如说：

这是因为python的列表其实就是一个动态的数组，而数组这个数据结构本身就是用来存储数据用的，而并非为了数学计算所准备的，然后numpy中就不一样的，它纯是为了数学计算而生，它里面只能存储一种数据类型的，而正因为如此，使用numpy进行数学运算速度也是非常快的。

np.array的创建：

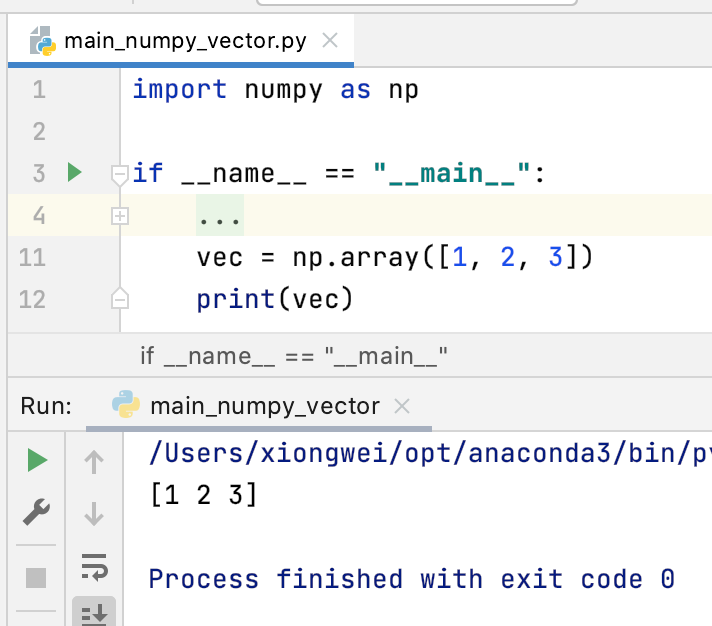
为了验证它里面只能存储同一种数据类型，下面来试一下：

另外numpy中生成的vector是可以变的，而我们之前设计的Vector类是不可变的，下面看一下：

创建零向量：

其中传的是向量的一个维度，从打印来看输出的是浮点数。

另外还有一个创建指定维度的向量，如下：

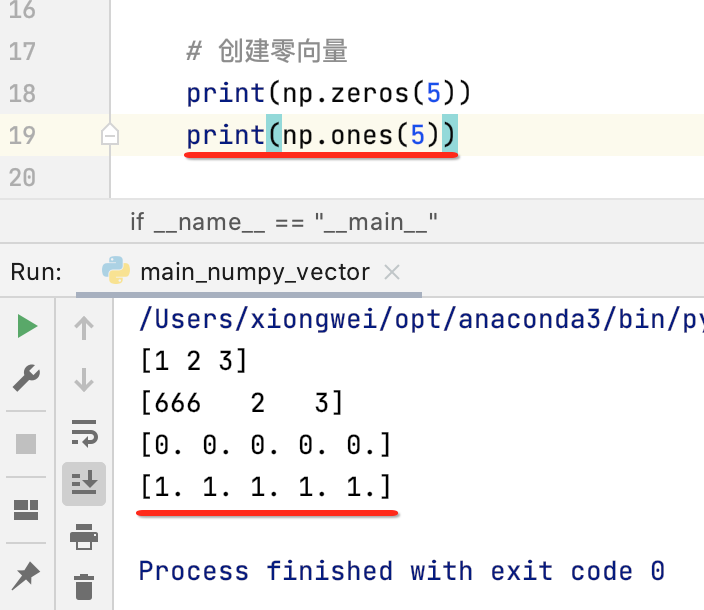
还有一种是我们可以在指定维度的基础上还能指定向量里面的值是多少，如下：

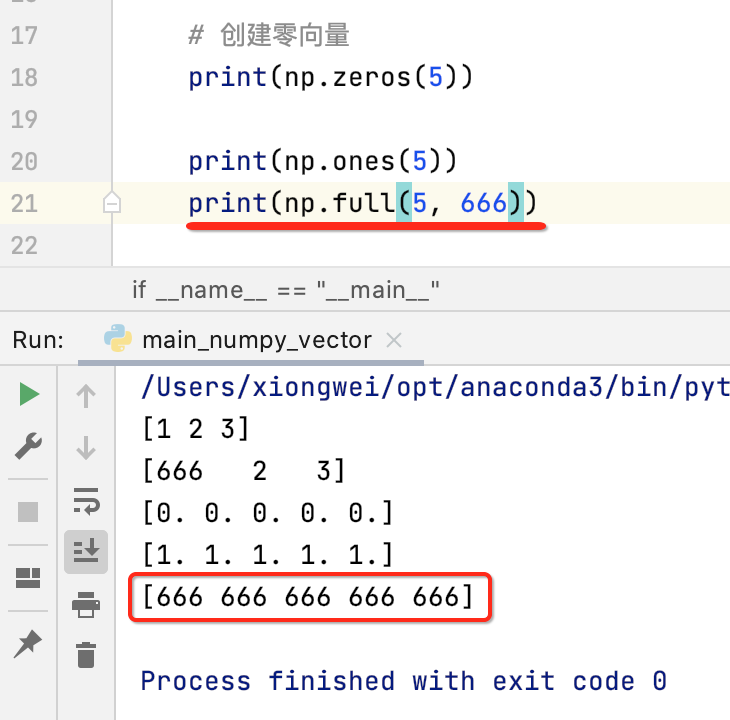
np.array的

基本属性：

首先能知道向量有多少个元素：

 

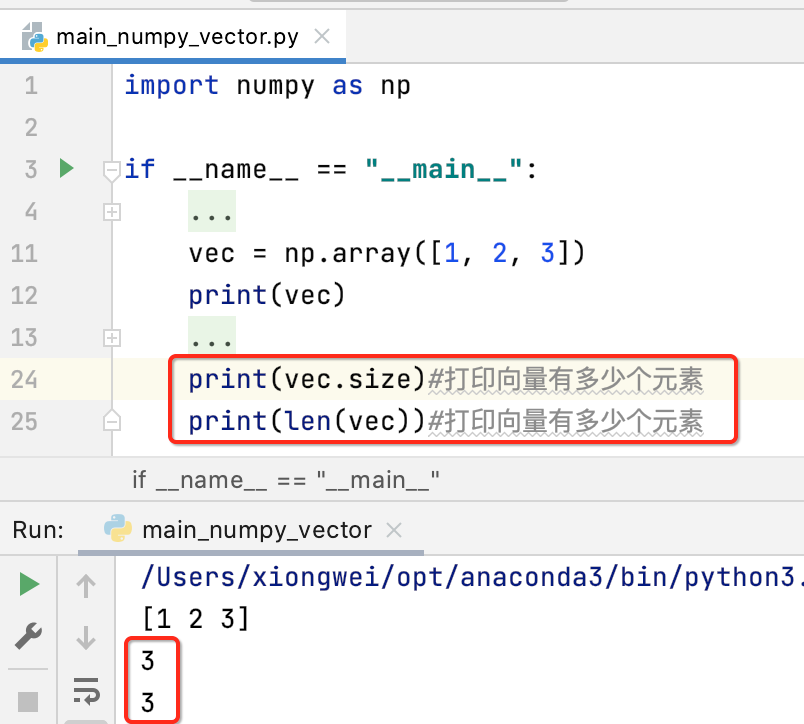
另外还可以取出向量中某个位置的元素：

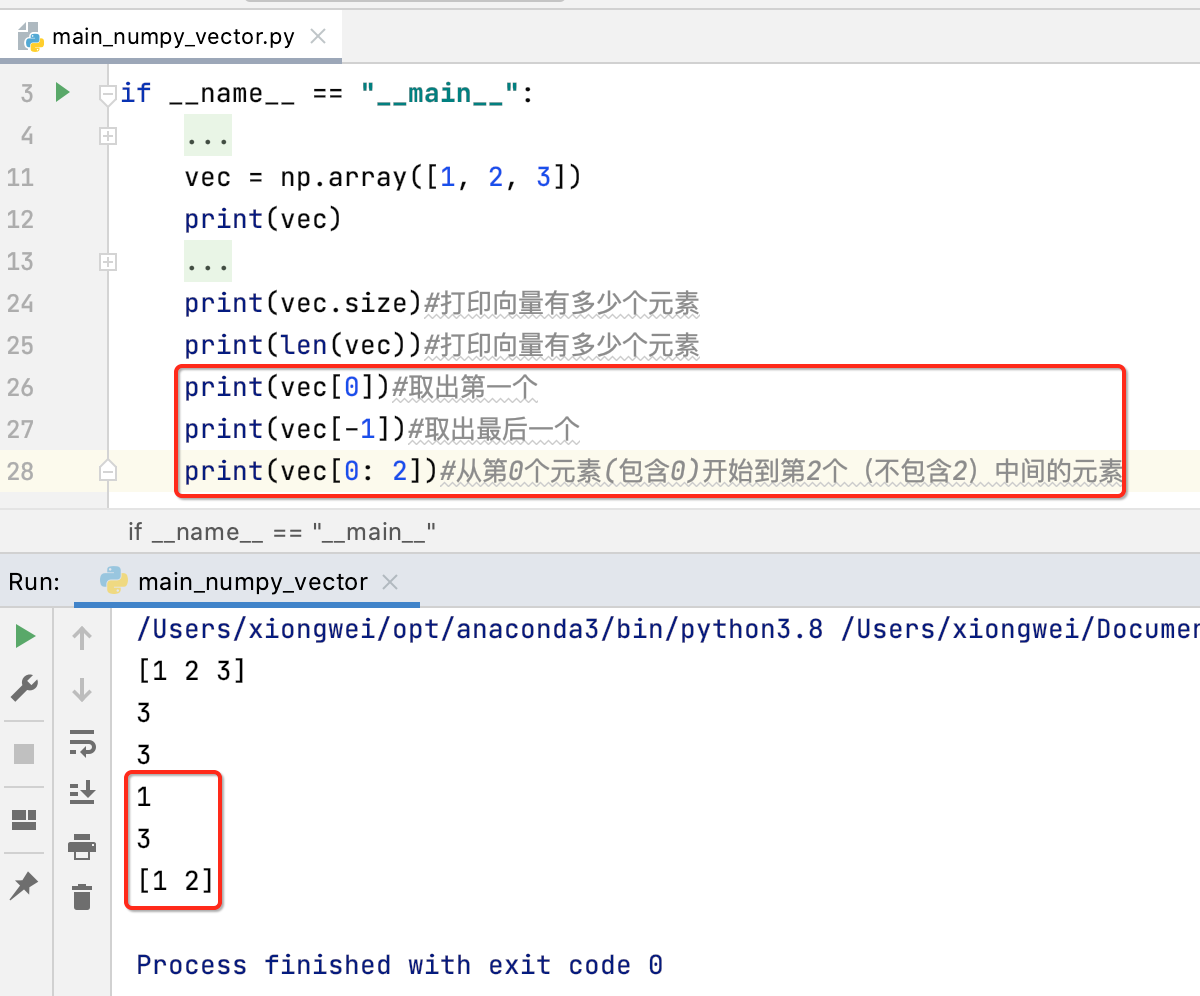
下面来看一下咱们取出的vec是不是numpy类型，打印一下：

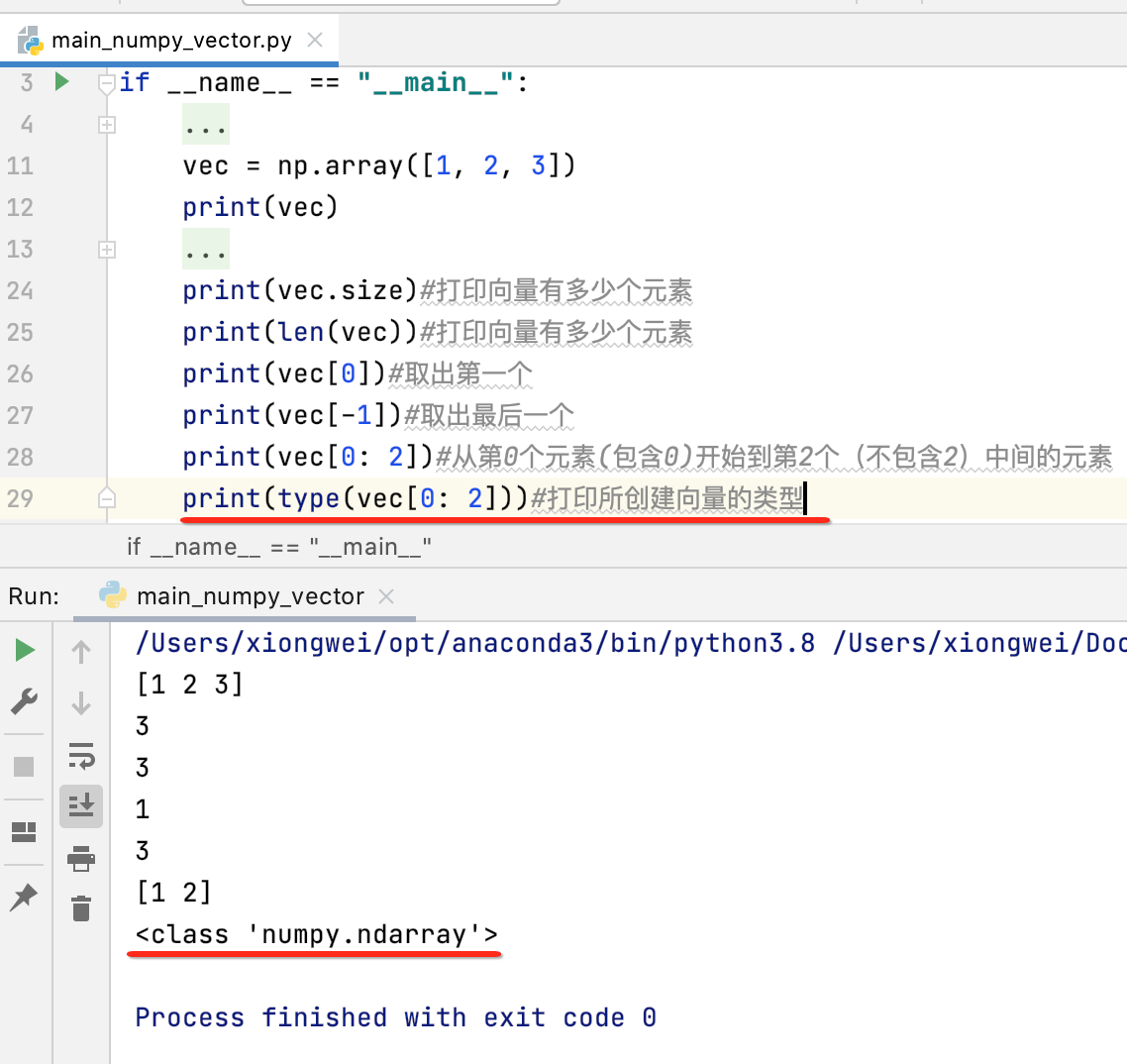
np.array的基本运算：

加法：

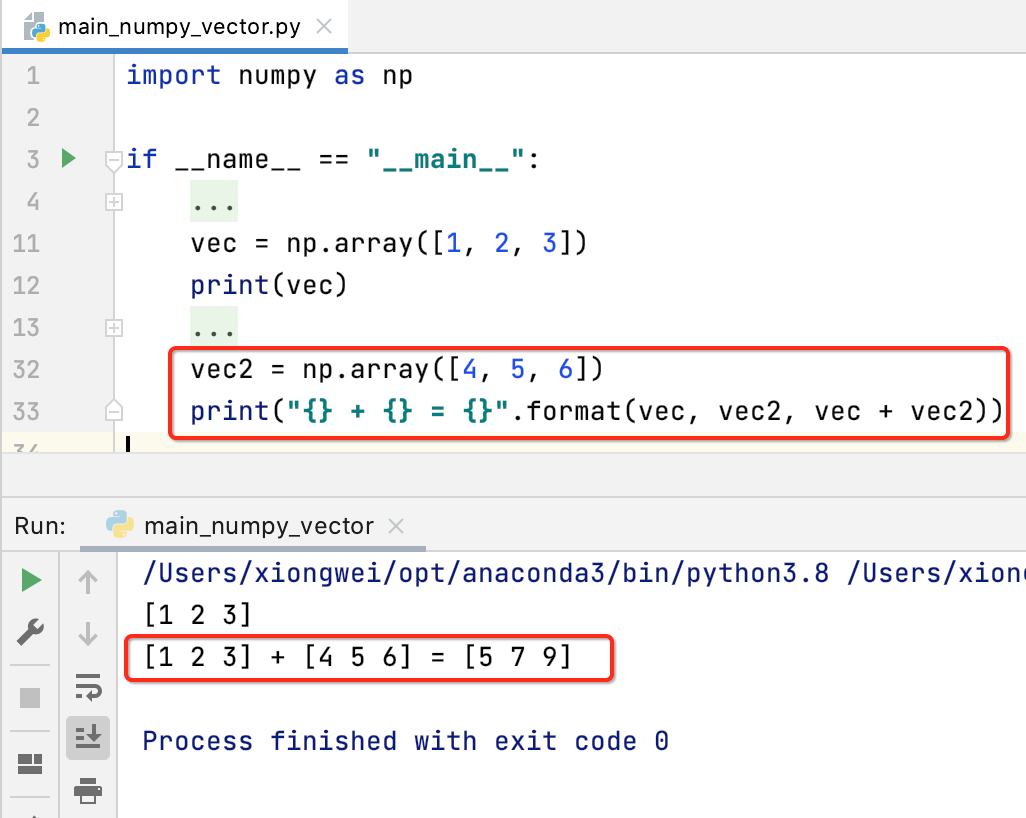
减法：

数量乘法：

 

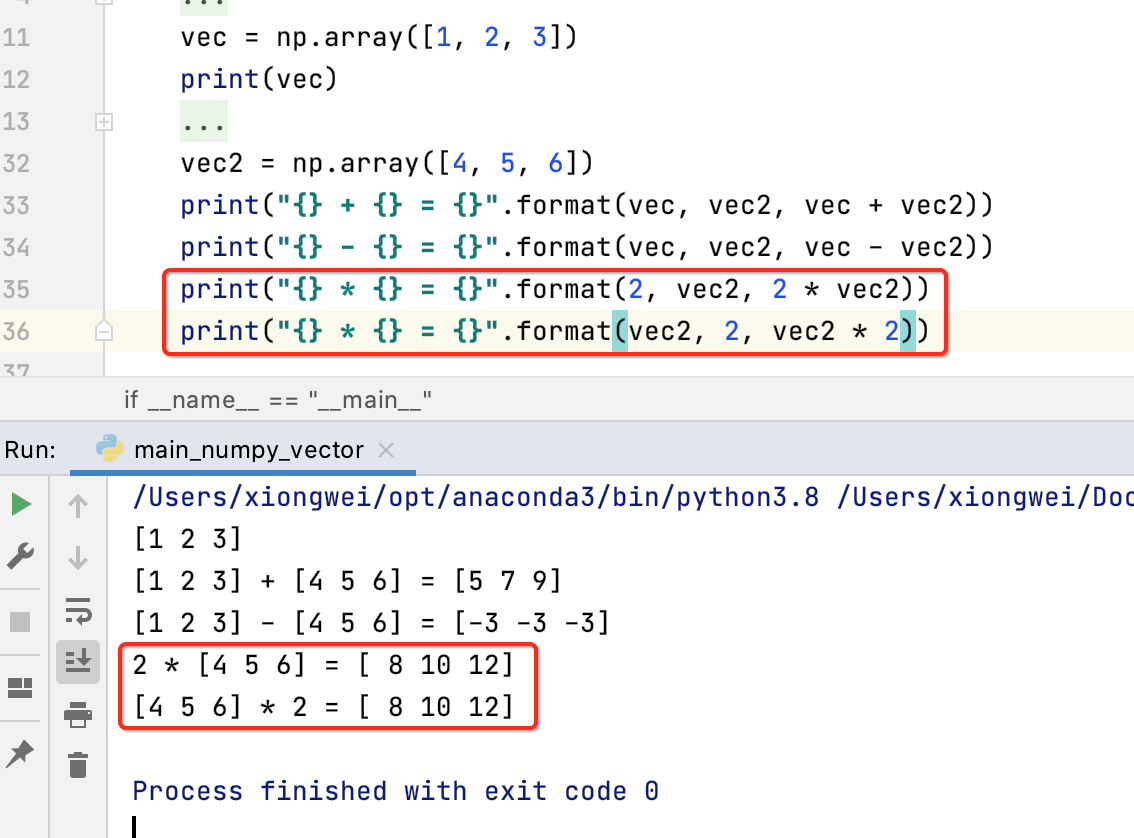
向量的点乘：

注意它的结果是一个数（标量），下面来看一下：

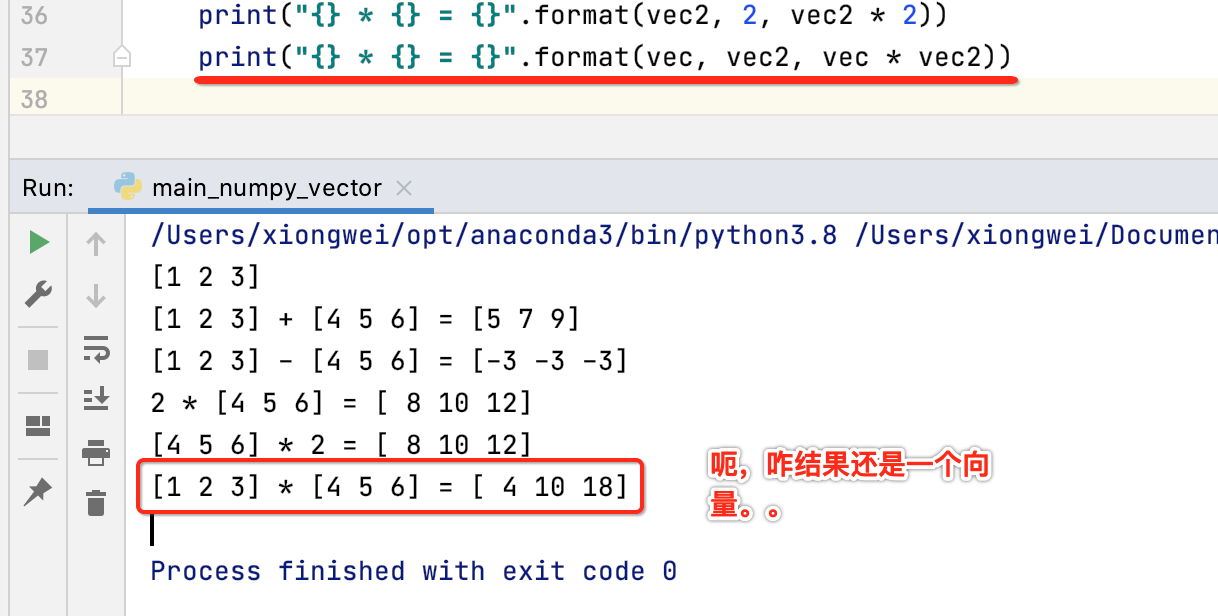
其实这就是在之前所说的：

所以说它不是真正意义上的点乘，那具体如何实现点乘呢？如下：

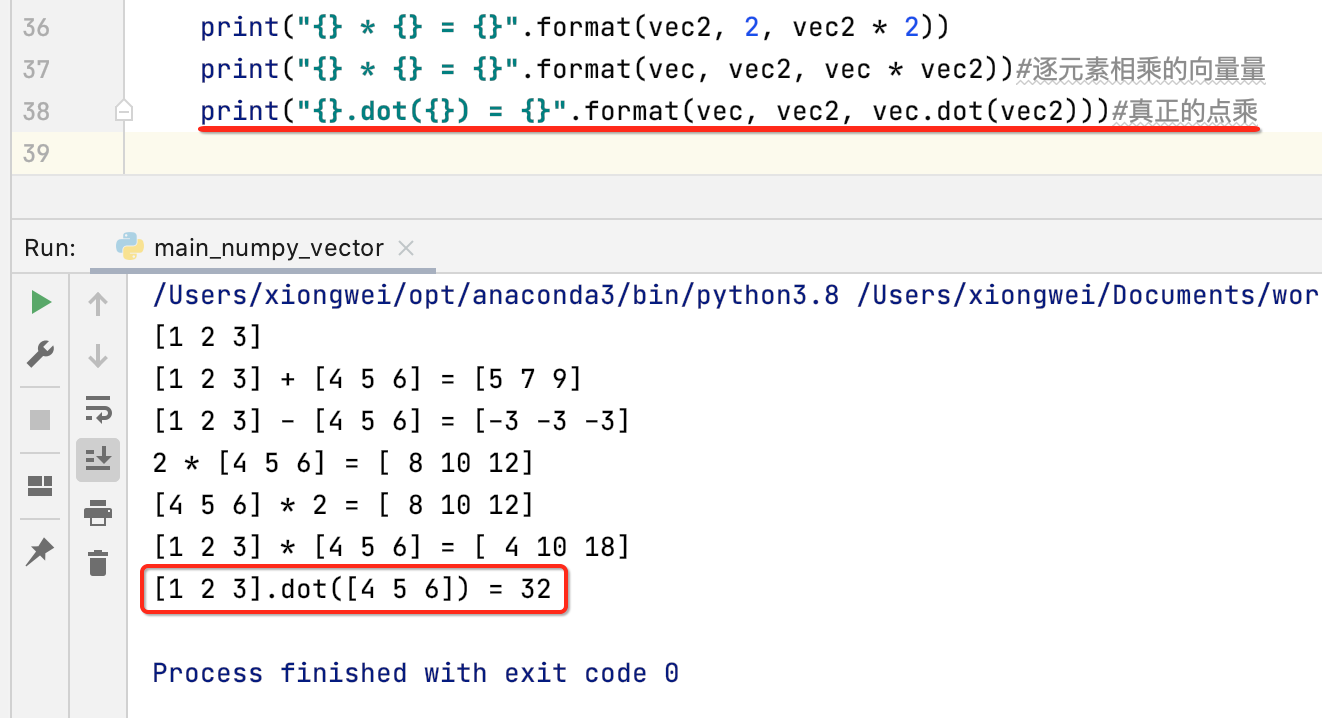
取模：

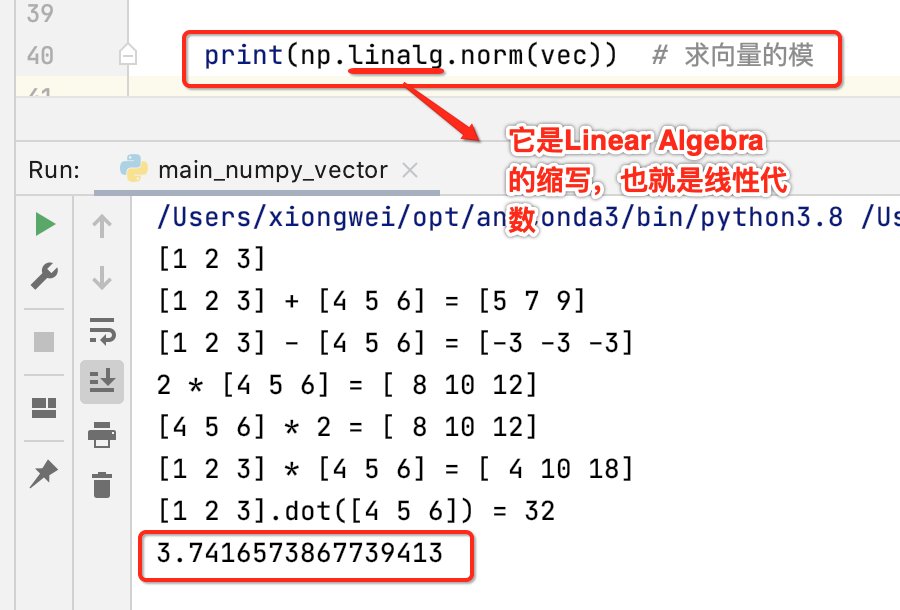
求单位向量：归一化、规范化

既然求出了向量的模，就可以求出它的单位向量了，注意单位向量的模永远是1，它的重点是关注方向，这里再三强调：

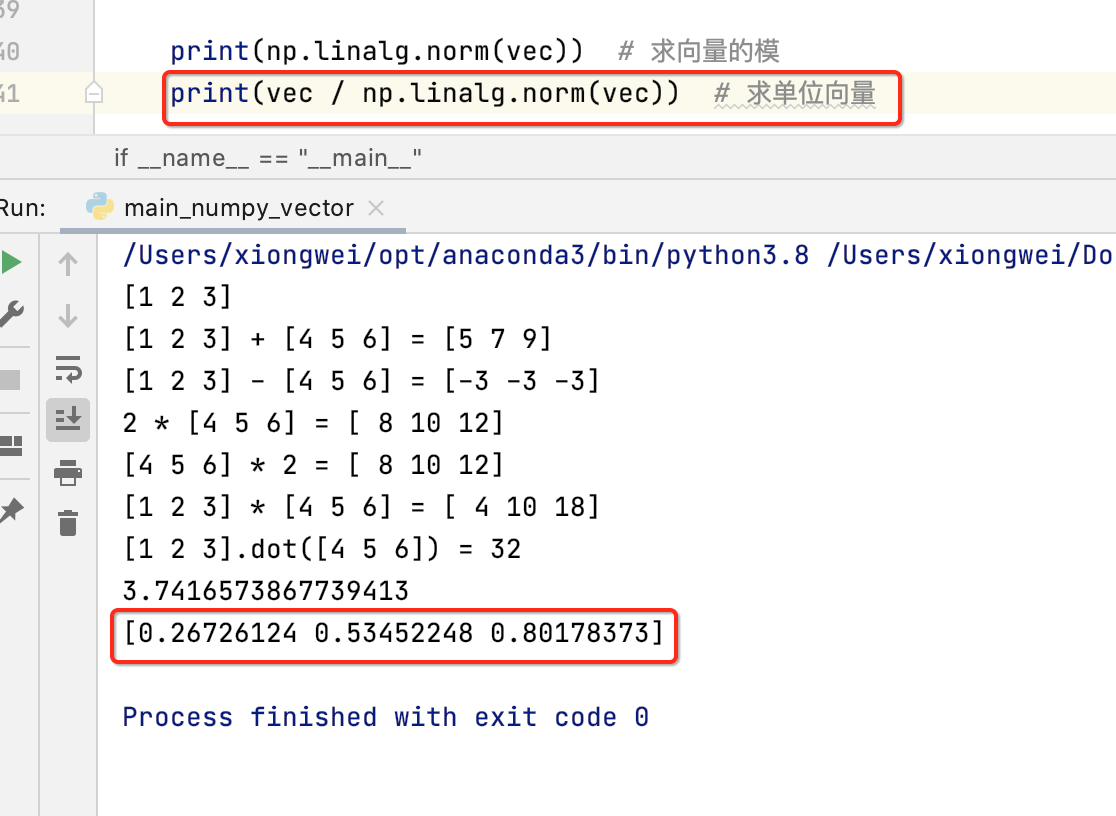
此时算一下单位向量的模，看一下它的大小是否是1：

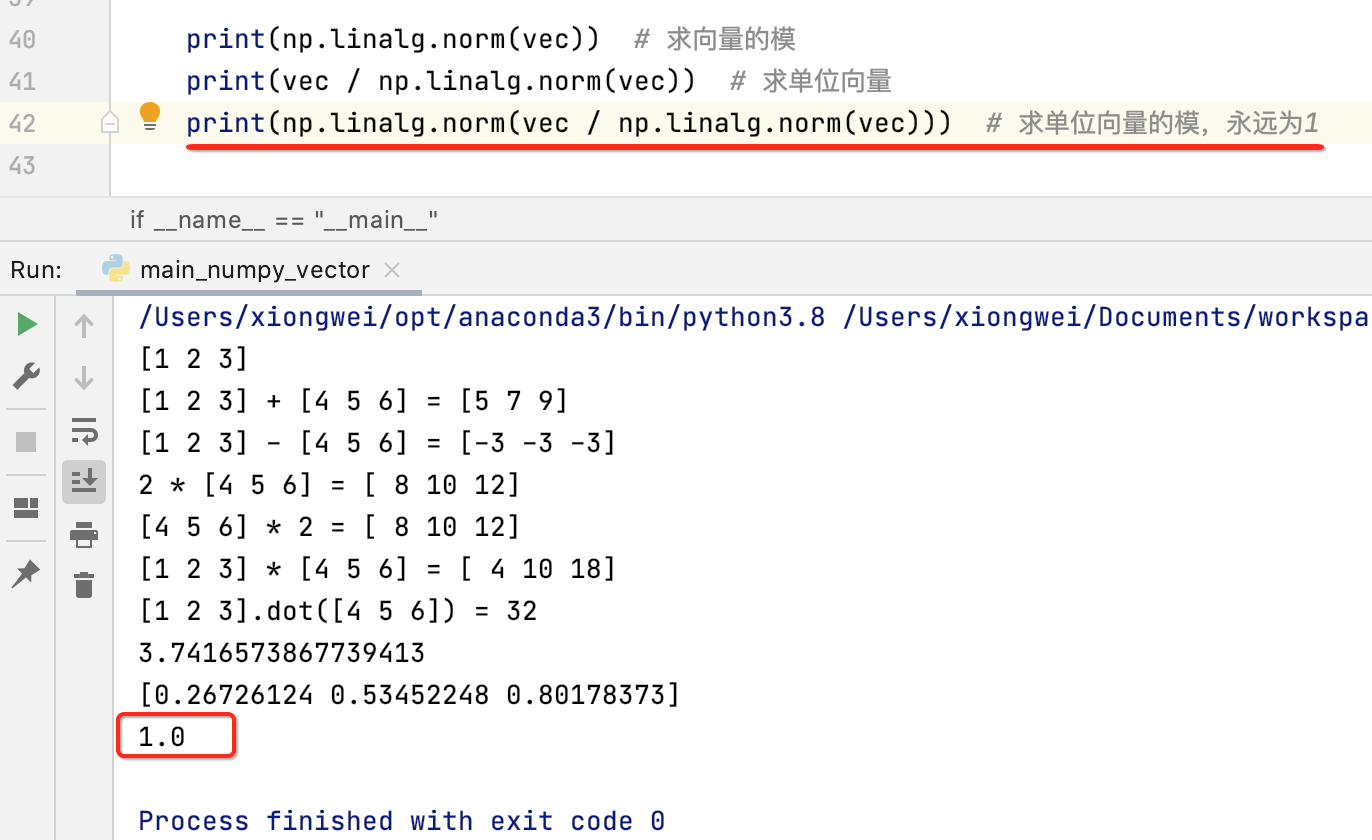
另外如果是零向量，numpy中是木有考虑这种异常情况的，所以此时算它的单位向量时就会报错：

 

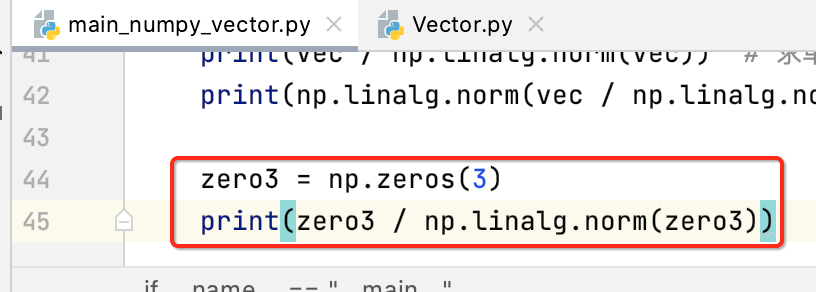
/Users/xiongwei/Documents/workspace/python/Play-with-Linear-Algebra/02-Vectors/03-Implement-Our-Own-Vector/main_numpy_vector.py:45: RuntimeWarning: invalid value encountered in true_divide
  print(zero3 / np.linalg.norm(zero3))

Process finished with exit code 0

所以如果在使用numpy求向量的单位向量时需要注意零向量的情况，异常需要咱们自己来处理。