算法与数据结构基础<三>----数据结构基础之动态数组

为什么要学习数据结构：

从今天开始则开始来接触数据结构，关于数据结构的概念应该人人皆知，下面先来宏观上再来概述一下。

定义：

数据结构研究的是数据如何在计算机中进行组织和存储，使得我们可以高效的获取数据或者修改数据。其中重点是要"高效"。

分类：

所以为了达到“高效”的目的就出现了N多种数据结构了，总体分为三大类：

线性结构：

• 数组【本次所学】
• 栈
• 队列
• 链表
• 哈希表
• ...

树结构：

• 二叉树
• 二分搜索树
• AVL
• 红黑树
• Treap
• Splay
• 堆
• Trie
• 线段树
• K-D树
• 并查集
• 哈夫曼树
• ... 

图结构：

• 邻接矩阵
• 邻接表 

对于这么多的数据结构，我们需要根据应用的不同，灵活地选择最合适的数据结构。

具体场景举例：

对于上面列的这些数据结构名词看起来是比较生硬的，学了它们有啥用呢？下面则以计算机实际场景为例具体看一下数组结构的用武之地。

数据库：

对于“SELECT * FROM Test where title = "数据结构"”这样一条数据库SQL语句，它底层其实就会用到树结构，比如：AVL、红黑树、B类树、哈希表。

操作系统：

其中操作系统中会涉及到以下几个方面：

• 优先队列
• 内存管理：内存堆栈
• 文件管理

这些都需要使用数据结构来解决。

文件压缩：

都需要使用一些压缩算法来实现，啊，你说的是“算法”，它又不是“数据结构”，其实要实现压缩算法也是需要借助数据结构来实现的，典型的数据结构：哈夫曼树。

游戏的最短路径：

其中这里就涉及到图论算法，而算法本身又得借助于数据结构来完成，典型的DFS(使用栈)、BFS(使用队列)

总结：

总的来说数据结构研究的是数据如何在计算机中进行组织和存储，使得我们可以高效的获取数据或者修改数据。而对于数据结构而言关注的核心操作是在内存世界的增删改查，其中“内存世界”是指未来研究的大多数的数据结构的数据都是存储内存当中，像数据库就是存储在“外存”当中的，当然它也不是咱们体系学习的重点。

使用 Java 中的数组【不要小瞧数组】：

接下来则来学习第一种数据结构----数组，可能第一印象就觉得数组有啥好学的，天天在用都用烂了， 如这标题所注，确实数组也有我们所不知道的，而且通过这个小小的数组结构会道出另一种分析复杂度的方式---均摊复杂度，另外什么是复杂度震荡呢？所以不要小瞧它了。

概述：

这里还是先从理论对数组进行一个审视，既然是系统地来学习，理论+实践都少不了，另外简单的知识再过一过无坏处。

数组其实就是把数据码成一排进行存放，如下：

这是一个可以存放8个数据的数组， 然后可以这个数组取一个名字：

比如这个数组是用来存放学生的成绩用的，而每个数组都有对应的一个下标索引：

而如果要访问某一个元素直接通过下标索引既可，比如：

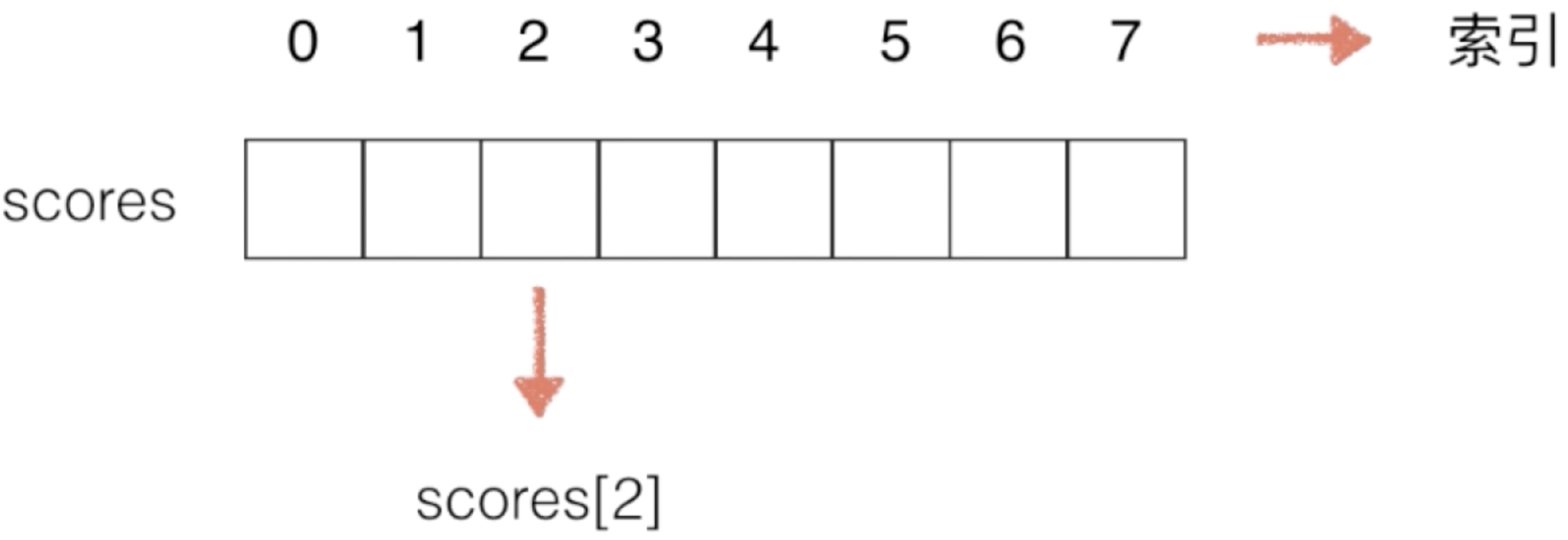
嗯，这些都是人人皆知的，就当个空气过一下既可。

使用：

接下来则来使用一下Java中的数组，也是纯java的语法，这里过一下是有目的的，因为要从标准的使用中来发现它的不足之处，然后再进行升级改造，然后封装一个类似于ArrayList这样效果的数组类，所以这里简单一带而过，先声明一个数组：

public class Main {
    public static void main(String[] args) {
        int[] arr = new int[10];
        for (int i = 0; i < arr.length; i++) {
            arr[i] = i;
        }
    }
}

然后数组还有另一种创建方式：

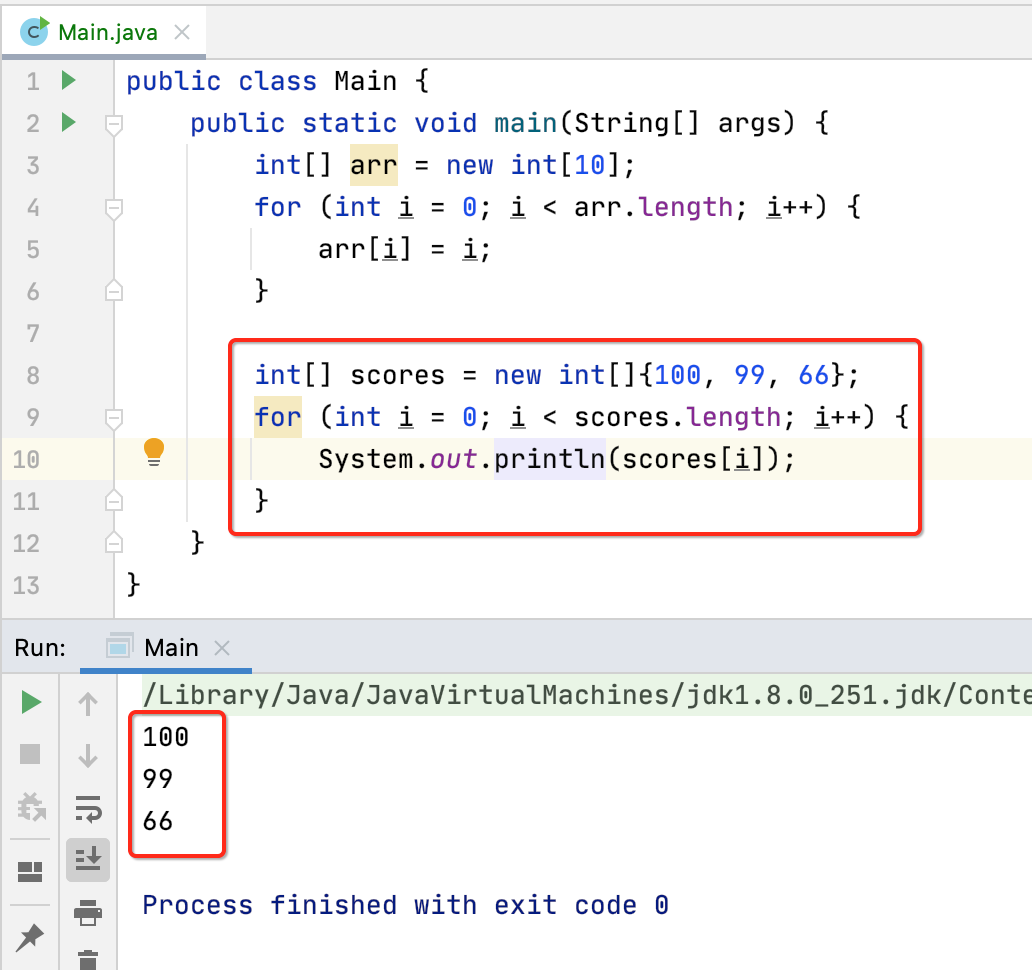
而数组元素的修改直接用下标进行：

非常非常基础的java语法啦，把自己当白痴~~

二次封装属于我们自己的数组：

概述：

上面咱们简单使用了一个Java中的数组，那这里要对这种数组的使用方式进行一下吐槽了。这里得先要从这个数组的索引开始说起，对于一个数组来说，它的索引可以有语意，也可以没有语意【这是关注的重点】，啥意思？还是拿这个数组举例：

其中的scores[2]的下标2没有任何语意的，它只是表示在数组中的2这个位置存了一个学生的成绩，而这个成绩存在数组中的任意位置都是可以的，这是“没有语意”的情况；而对于个数组来说它最大的优点是可以快速查询【直接拿下标快速定位】，所以数组最好要应用于“索引有语意”的情况，还是拿scores[2]来说，在有语意的角度下其中的下标2可以代表学号为2。对于没有语意的情况，其实是可以选择其它的数据结构，至于啥数据结构未来学到再提。

但是！！！并非所有有语意的索引都适用于数组的，举个极端的粟子：身份证号，比如说设计一个数组，该数组是存放不同人的工资情况，对于人来说身份证是唯一的嘛，那用身份证号码来当数组的索引那不妥妥的嘛，可你觉得合适么？一个身份证的数字这么大那数组得要开辟多大的空间才行呀，另外假说只需要存储几个人的工资，开辟的大量空间都会被浪费。

而我们这次主要是要来吐槽一下“索引没有语意”的情况数组的使用，因为在这种没有语意的情况下会有很多的问题存在，拿这样一个数组举例：

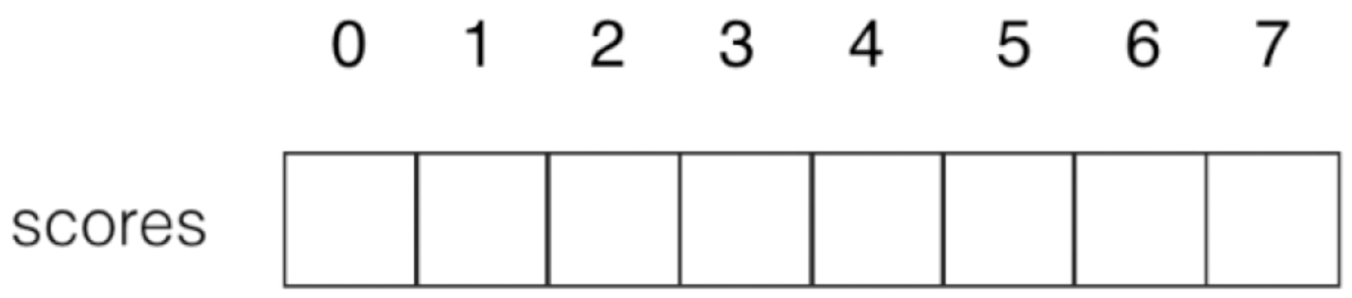
开辟了8个元素的空间对吧，但是呢里面只存放了部分元素，比如3个：

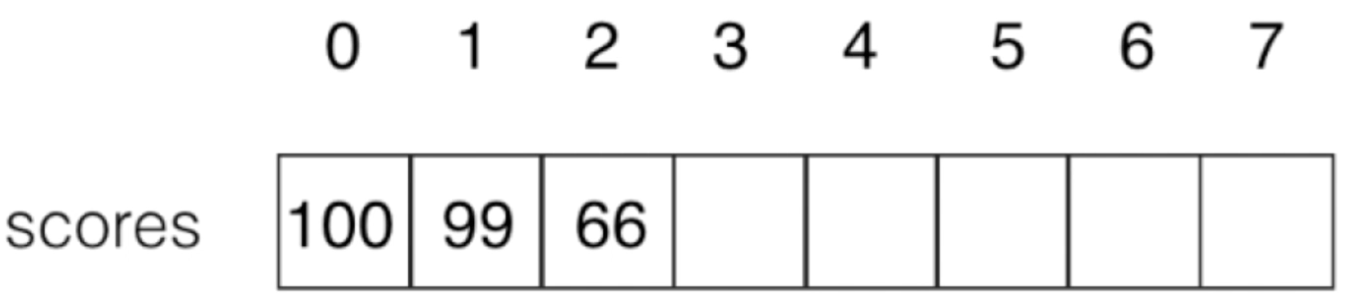
那么对于3~7索引没有存放元素在索引没有语意的情况下如何来表示没有元素呢？还有当数组满了之后再添加元素能否做到扩容呢【很显然java的数组是做不到的】？另外删除元素怎么能让其后面的元素进行位置调整等等一系列的问题，所以说有必要封装一个属于咱们自己的数组类。

封装思路：

其实封装思路也比较简单，其封装之后也就是要提供对于数组这个数据结构的增删改查操作，在未来学习其它数据结构时也是从增删改查这个层面进行考查。数组本身就静态的，也就是数组在创建时就必须指定大小，这个大小可以用容量来表示：

而它跟数组实际存放了多少元素是没有关系的，这里用它来表示实际数组存放元素的个数：

而增删改查则会来维护这个size了，目前先初步定义到这，接下来具体实现一下。

初步封装：

1、先定义两个成员变量：

看到它是不是很亲切，因为每天在使用的ArrayList其实底层也是使用了数组这个数据结构。

2、定义构造函数：

/**
 * 由于java数组本身的缺陷来封装一下属于自己的数组，效果类似于ArrayList
 */
public class Array {
    private int[] data;
    /* 数组实际存放的个数 */
    private int size;

    //构建函数，传入数组的容量capacity构造Array
    public Array(int capacity) {
        data = new int[capacity];
        size = 0;
    }
}

另外再声明一个默认的构造方法，简化使用方的使用：

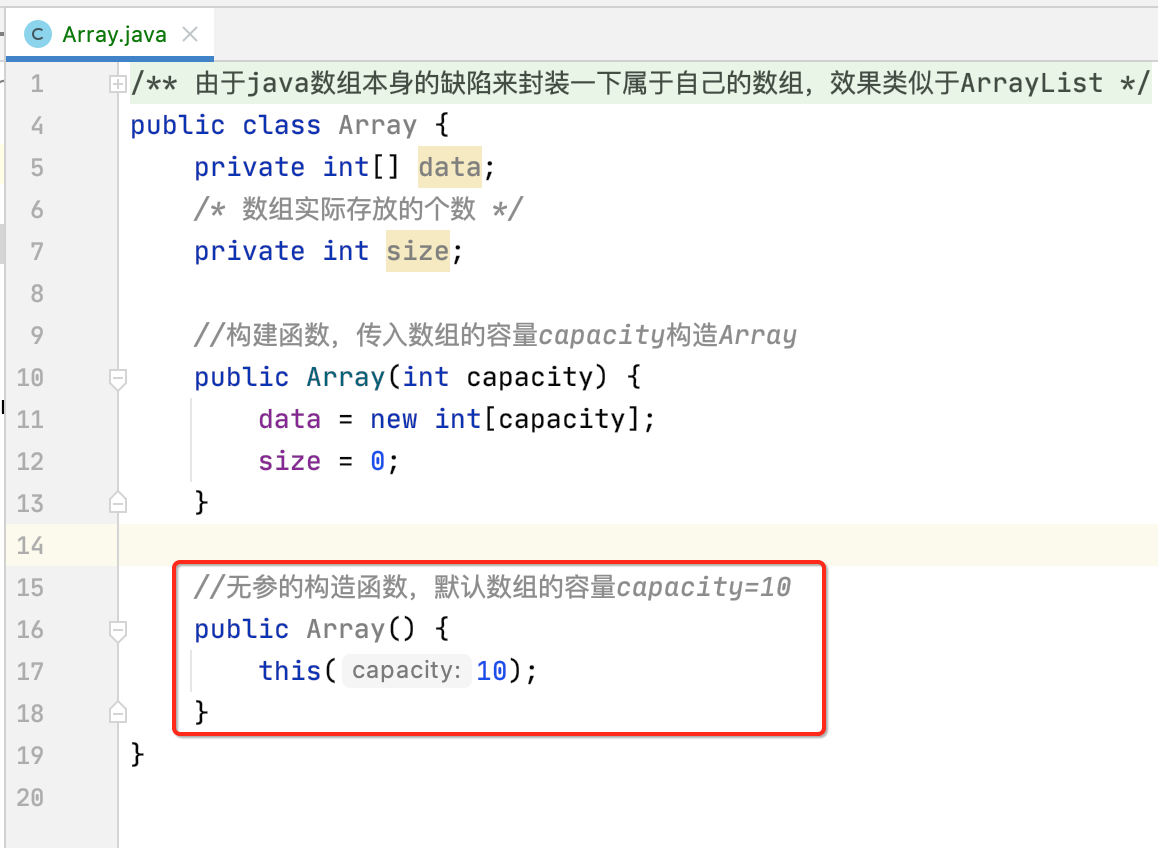
另外为了让代码更加有层次感，可以将构造函数归到一个类别，用它：

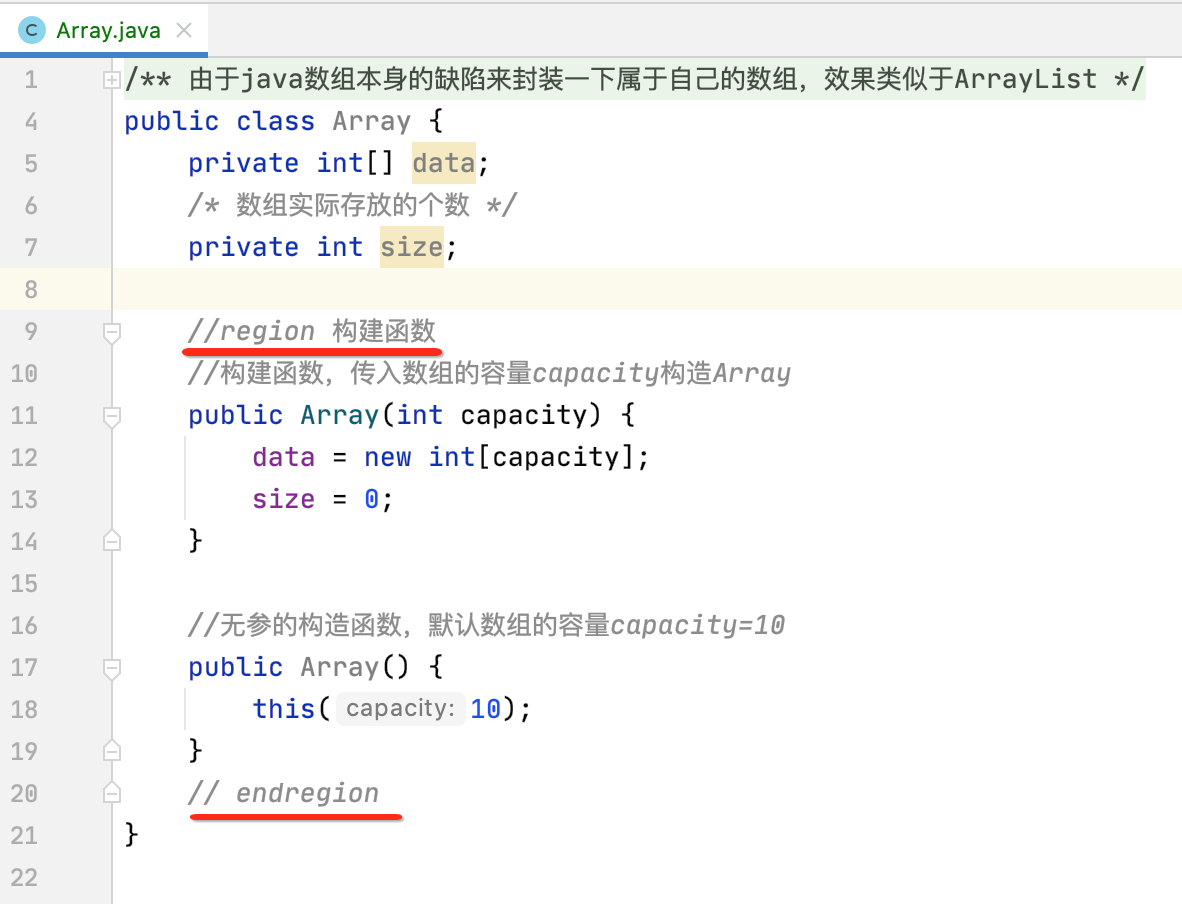
它的效果是可以折叠的，折叠之后如下：

这样当一个类代码较多时，用这种将代码进行功能划分的话，对于代码的可读性也会大大增强，在实际代码编写中可以善用这样的小技巧。

getSize()：

getCapacity()：

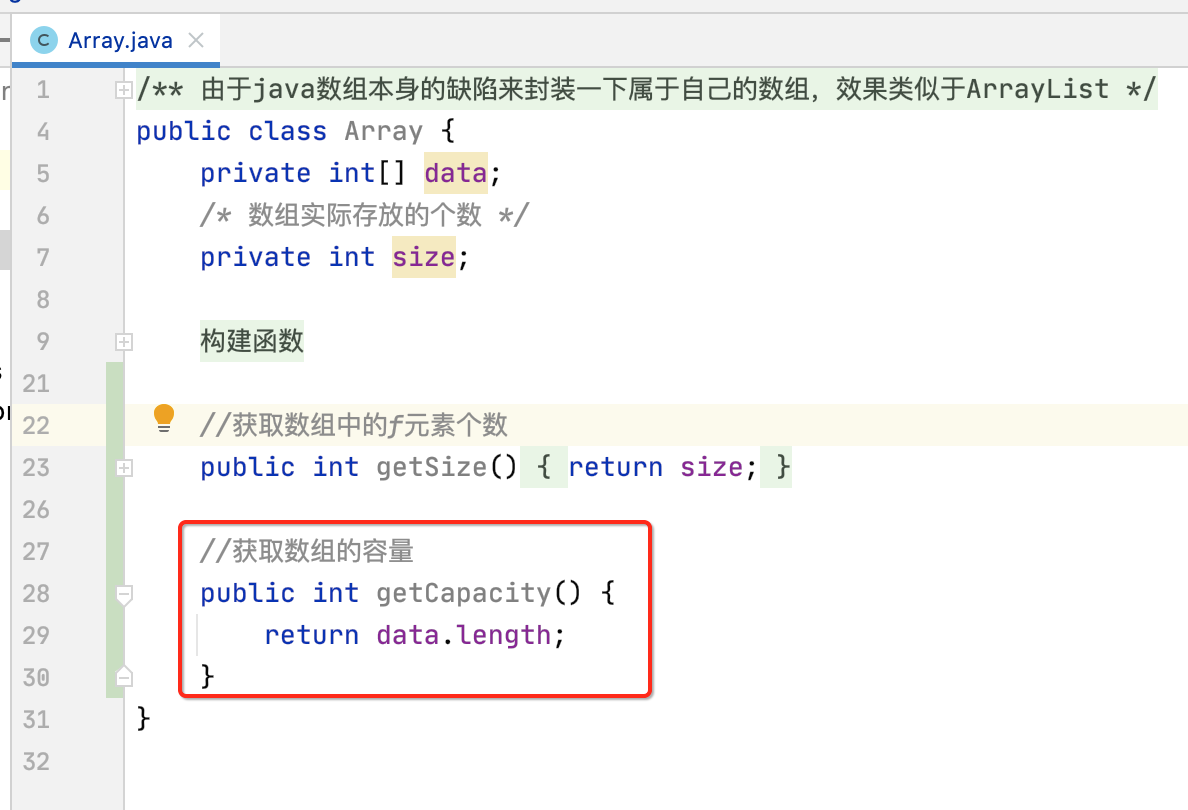
isEmpty()：

 

向数组中添加元素：

向数组末尾添加元素：

说明：

对于这样一个数组：

 

如果想要在数组末尾添加元素其实就是向size这个位置添加元素，比如要添加一个66，此时就往size=0的索引进行添加既可，如下：

此时需要维护一下size，让它size++，表示数组的元素已经有一个了：

接下来再想向数组末尾添加一个88，同样的直接放到size的位置既可：

同样需要维护一下size，size++：

【个人感想】：对于这么简单的一个操作还有必要把思路贴出来么？直接写不就ok了，还是那句话学习当中简单不可怕，可怕的是细节遗漏，既使是自己已经非常非常熟悉的知识点为了学习的效果再巩固一遍我也非常愿意，因为这是让知识化作你脑海当中的一个非常好的方法，当然每个人有每个人的学习方法，对于脑笨的我来说温故知新是学好某个技术的一大法宝，另外还有一个重点就是对于像算法与数据结构这门的学习图可能比代码还重要，图代表着一个思路，只有思路清晰在写算法时才不容易犯错，另外图是未来复习时最最好的一个东西，可以快速还原大脑，所以关于这块稍加说明一下~~

实现：

但是！！！此时该方法不够完善，因为没有考虑到数组满的情况，毕境目前数组是个静态的，开辟空间之后则不会再变了，目前先简单处理一下，如下：

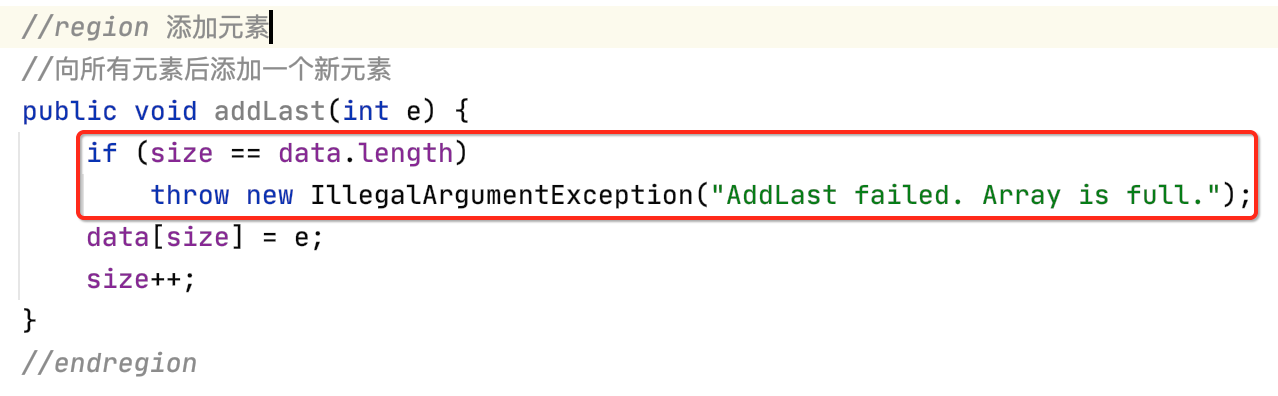
未来会有扩容处理，之后写到时再说。

向指定位置添加元素：

说明：

通常是像数组排序时就可能会用到这种添加方式，这块添加就稍微麻烦一些了，因为涉及到元素的挪动了，先来看一下整体的思路，比如这样的一个数组：

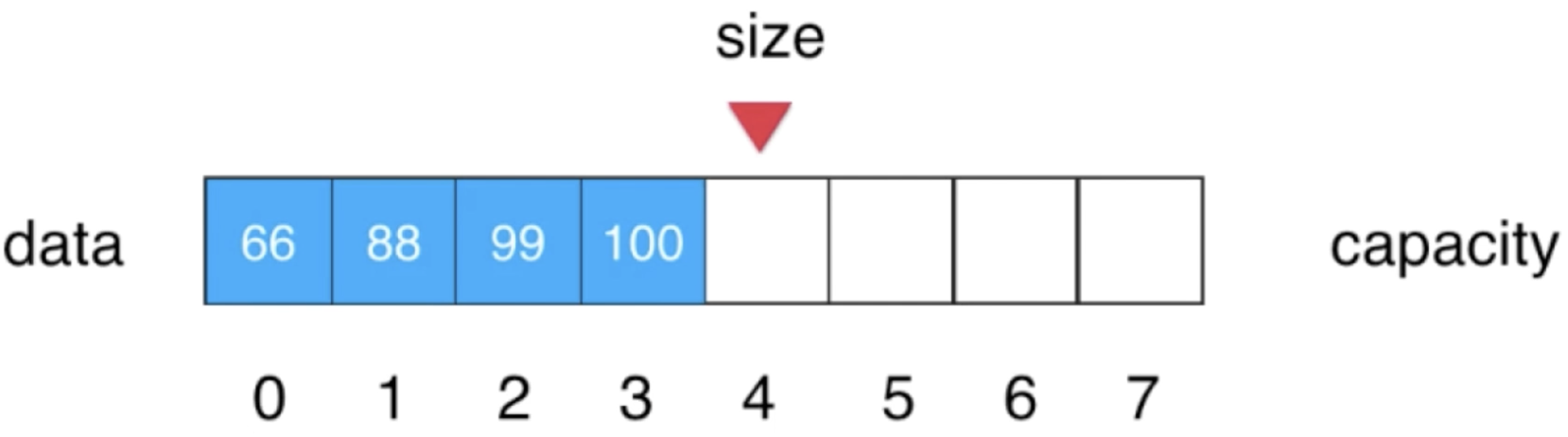
那我想将77这个数插入到索引为1的位置，那具体思路如下：

1、将索引为1的位置腾出来：

那要想将1的位置腾出来，则需要将88、99、100往后挪一个位置对吧？而要达到这种目的需要从后往前进行处理，因为如果从前往后则会出现问题：比如将88挪到99的位置上是不是99这个元素就会被88给“覆盖”掉了，那具体怎么个从后往前呢？如下：

先将最后一个索引3的元素100往后挪一个位置到4上面： 

然后再往前看一个元素，也就是99，再将它往后挪到3这个位置：

同样的道理，再往前看一个元素，也就是88，将它往后挪到2这个位置：

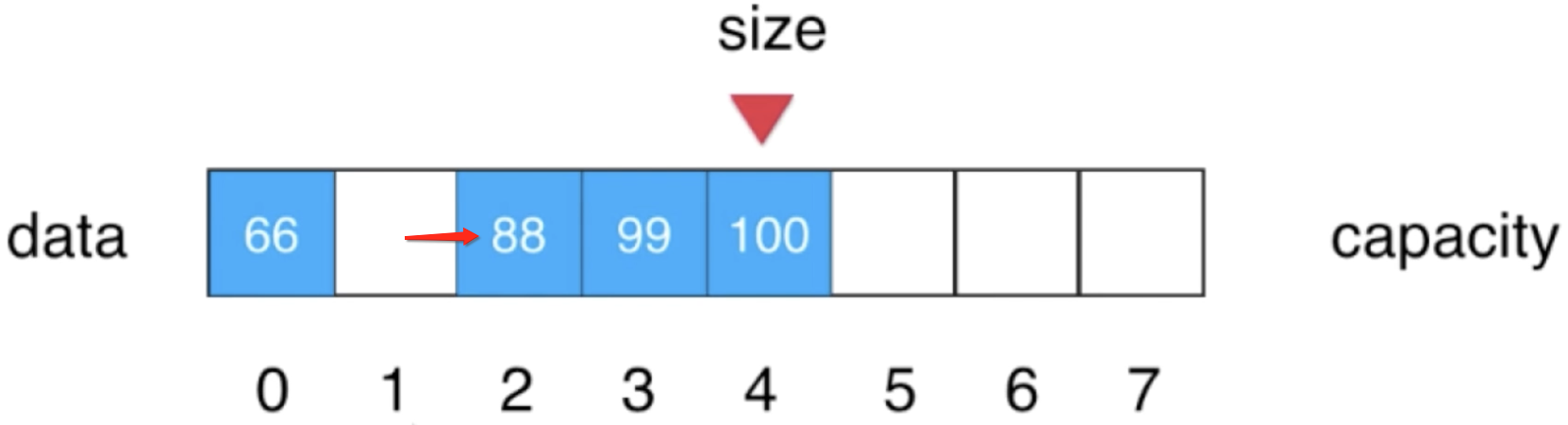
而当前已经是我们要添加的位置1了，所以此时1的位置就已经被腾出来啦。

2、再将待添加的元素放到索引1上：

直接将要添加的元素放到索引1上就ok了：

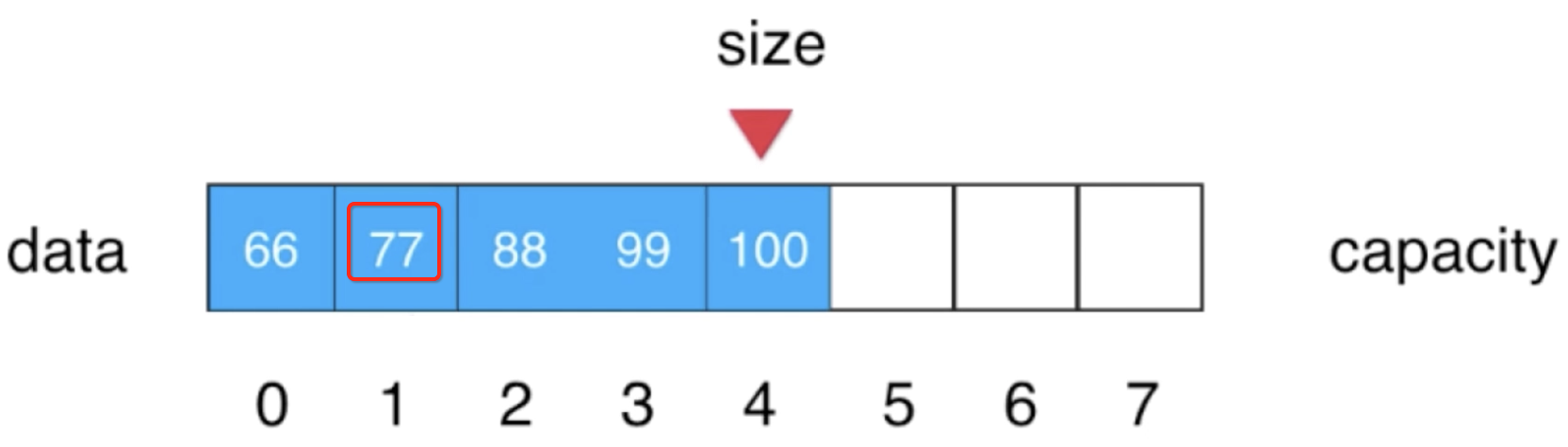
最后不要忘记要维护一下size，让它++:

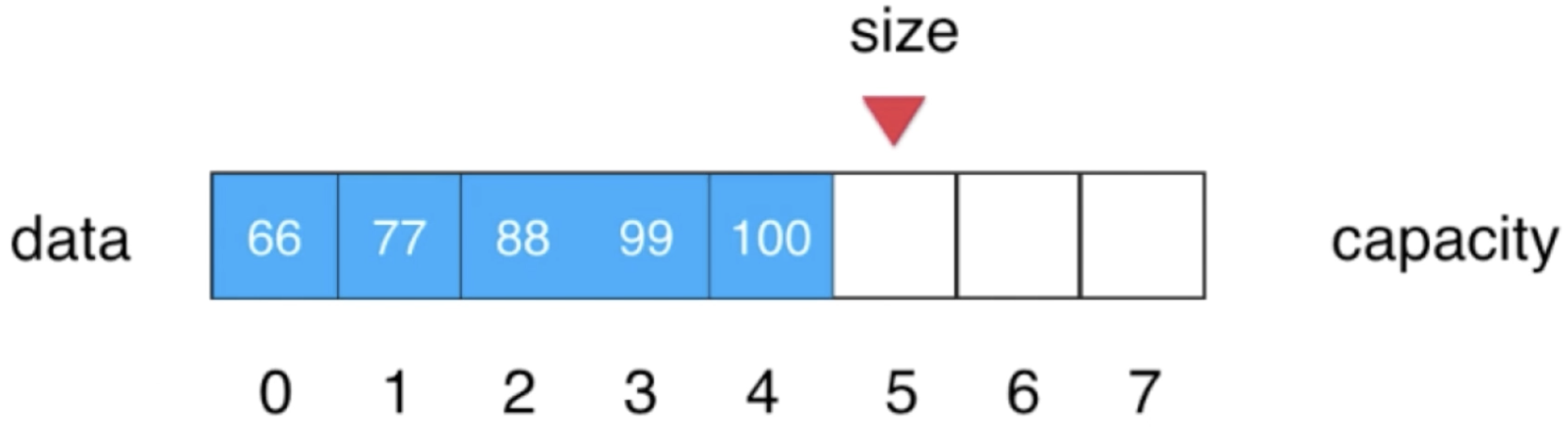
实现：

下面来实现一下，还是先做容错：

    //在第index个位置插入一个新元素e
    public void add(int index, int e) {
        if (size == data.length)
            throw new IllegalArgumentException("Add failed. Array is full.");
        if (index < 0 || index > size)
            throw new IllegalArgumentException("Add failed. Require index >= 0 and index <= size.");
    }

然后开始插入：

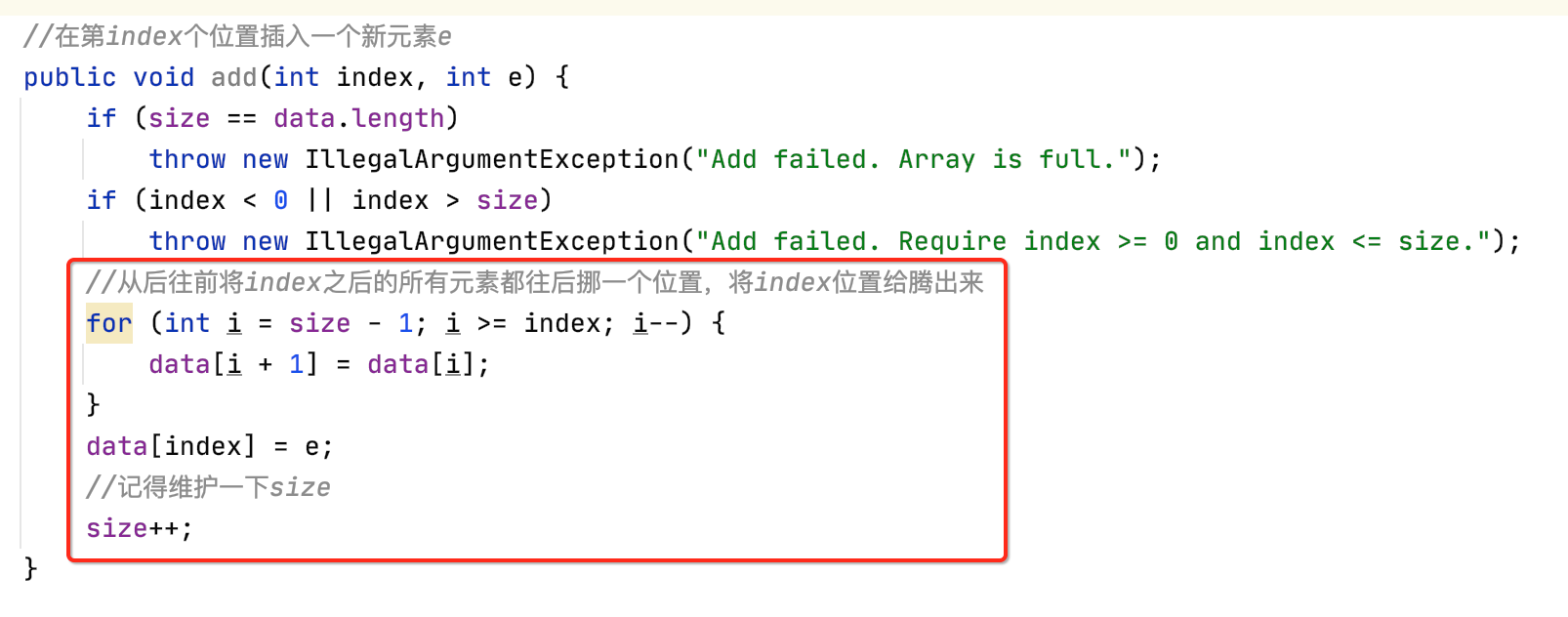
有了这个方法之后，对于向末尾添加的方法就可以调用此方法了，修改一下：

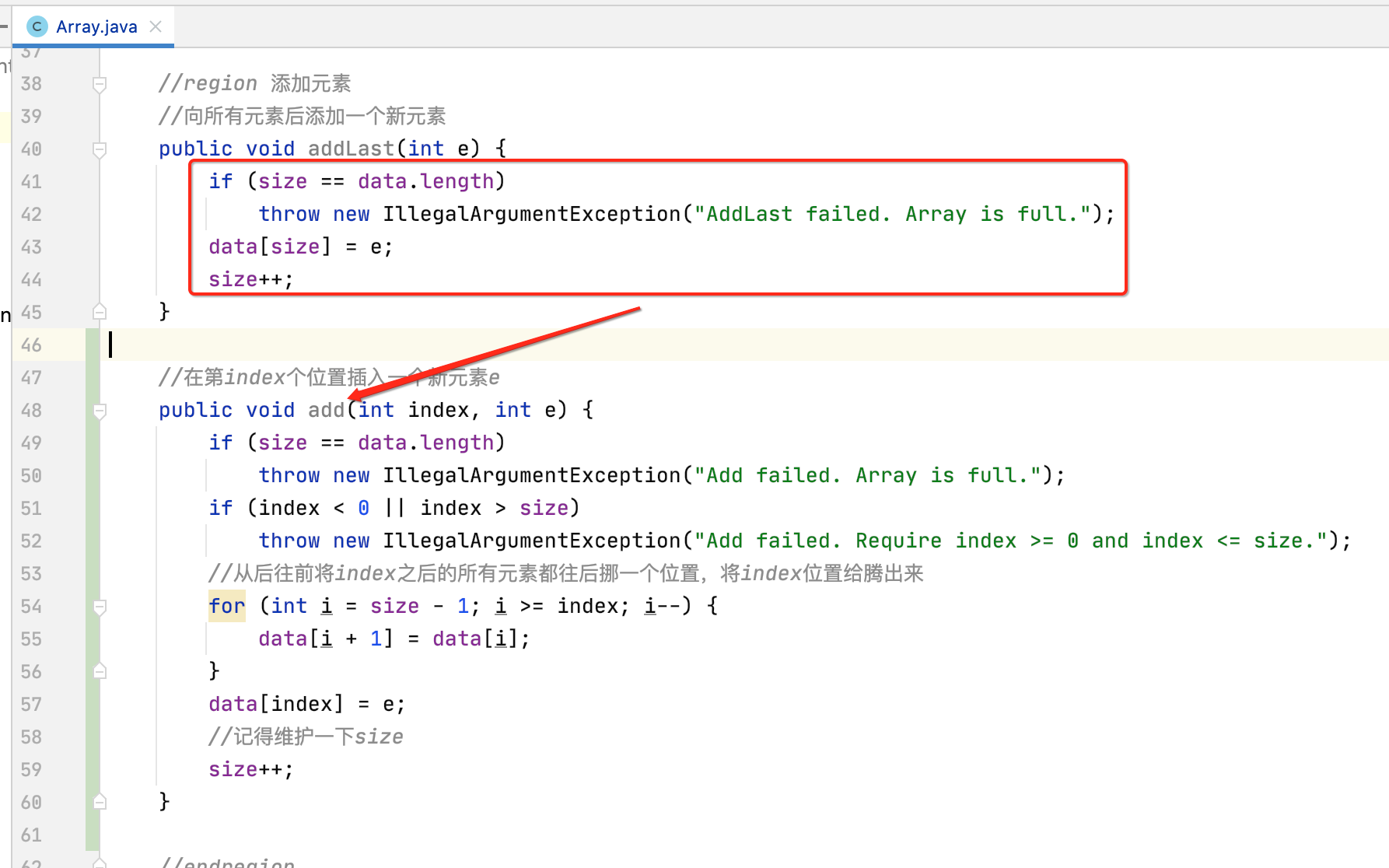
    //向所有元素后添加一个新元素
    public void addLast(int e) {
        add(size, e);
    }

同样还可以快速造另一个添加方法：

    //向所有元素前添加一个新元素
    public void addFirst(int e) {
        add(0, e);
    }

数组中查询元素和修改元素：

toString()：

为了在之后测试中能看到查询的结果，这里先来覆写一下toString()方法，这里不用工具生成 ，而是自己来实现一下，因为要打印自己的一些信息，直接贴出：

    @Override
    public String toString() {
        StringBuilder res = new StringBuilder();
        res.append(String.format("Array: size = %d , capacity = %d\n", size, data.length));
        res.append("[");
        for (int i = 0; i < size; i++) {
            res.append(data[i]);
            if (i != size - 1)
                res.append(", ");
        }
        res.append("]");
        return res.toString();
    }

接下来测试一下：

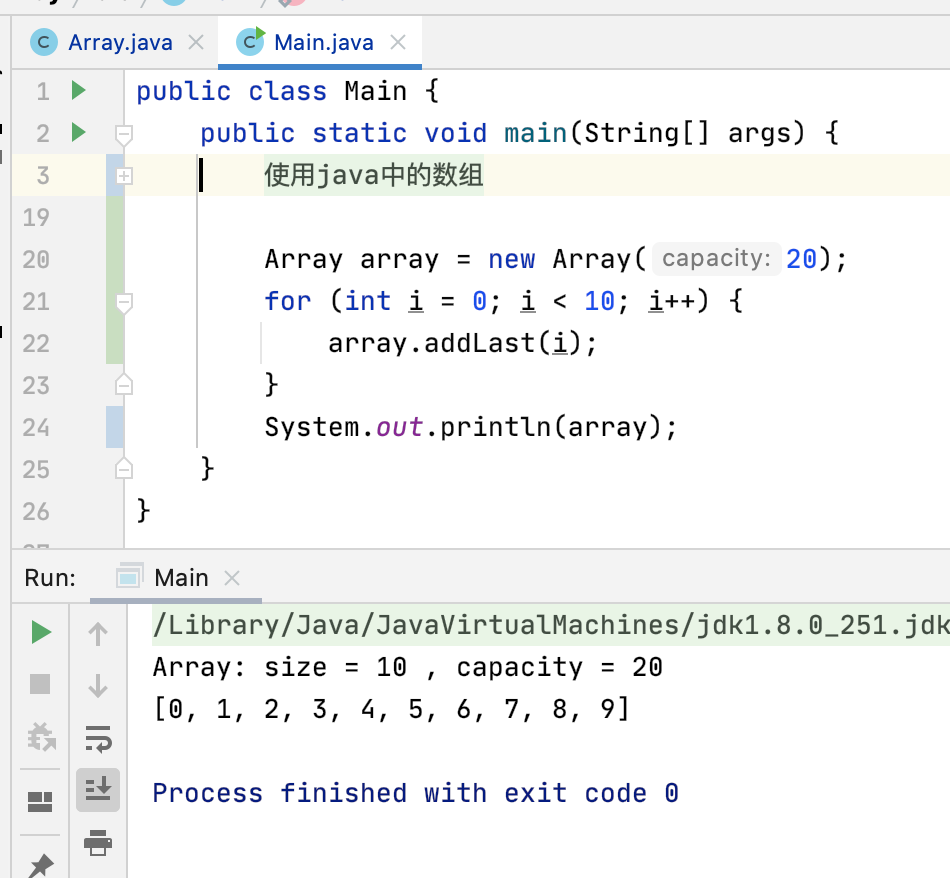
对于咱们已经编写好的一些方法也可以顺便做一下测试：

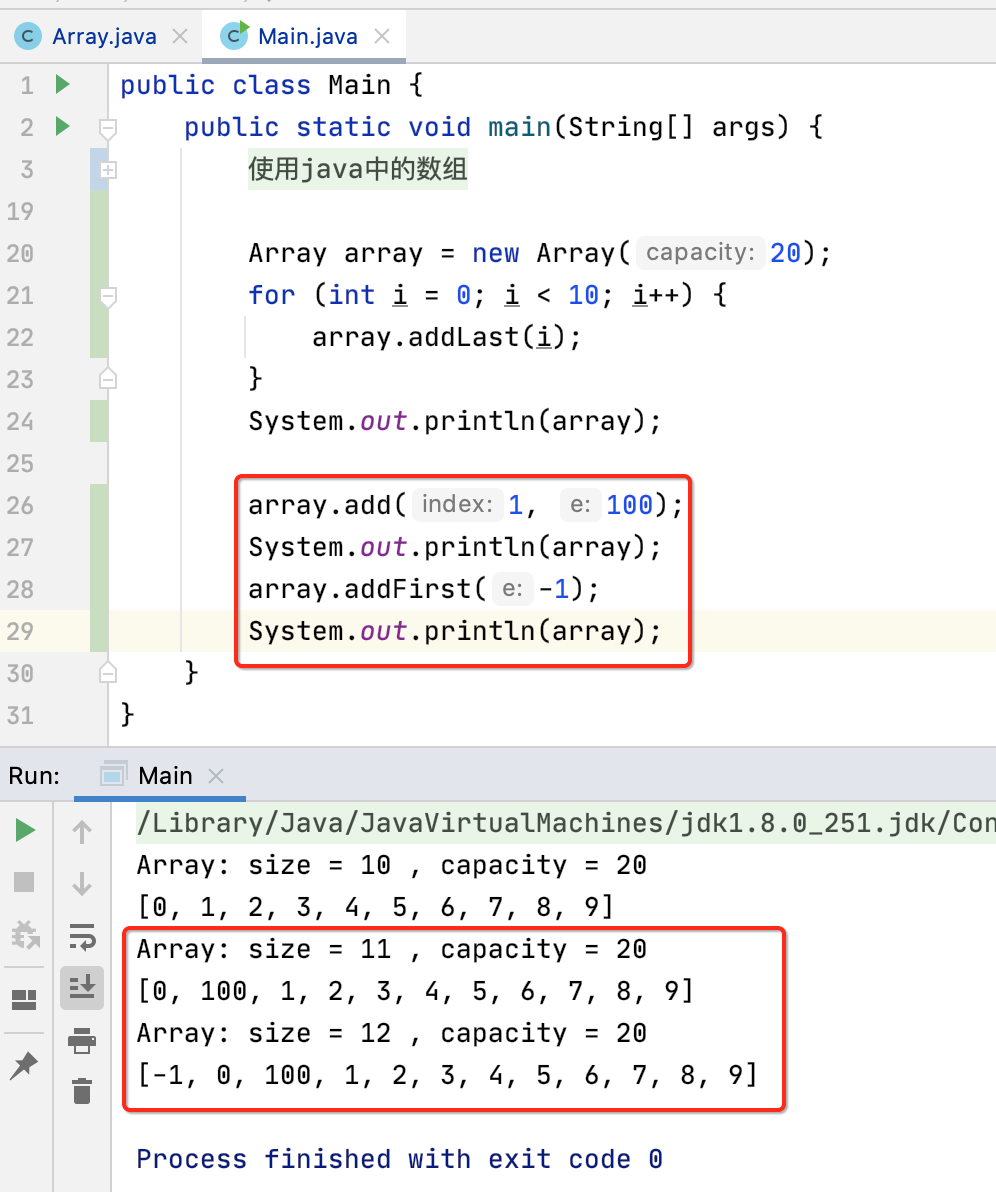
一切完美。

封装查询及修改数据的方法：

    //获取index索引位置的元素
    int get(int index) {
        if (index < 0 || index >= size)
            throw new IllegalArgumentException("Get failed. Index is illegal.");
        return data[index];
    }

    //修改index索引位置的元素为e
    void set(int index, int e) {
        if (index < 0 || index >= size)
            throw new IllegalArgumentException("Get failed. Index is illegal.");
        data[index] = e;
    }

下面测试一下：

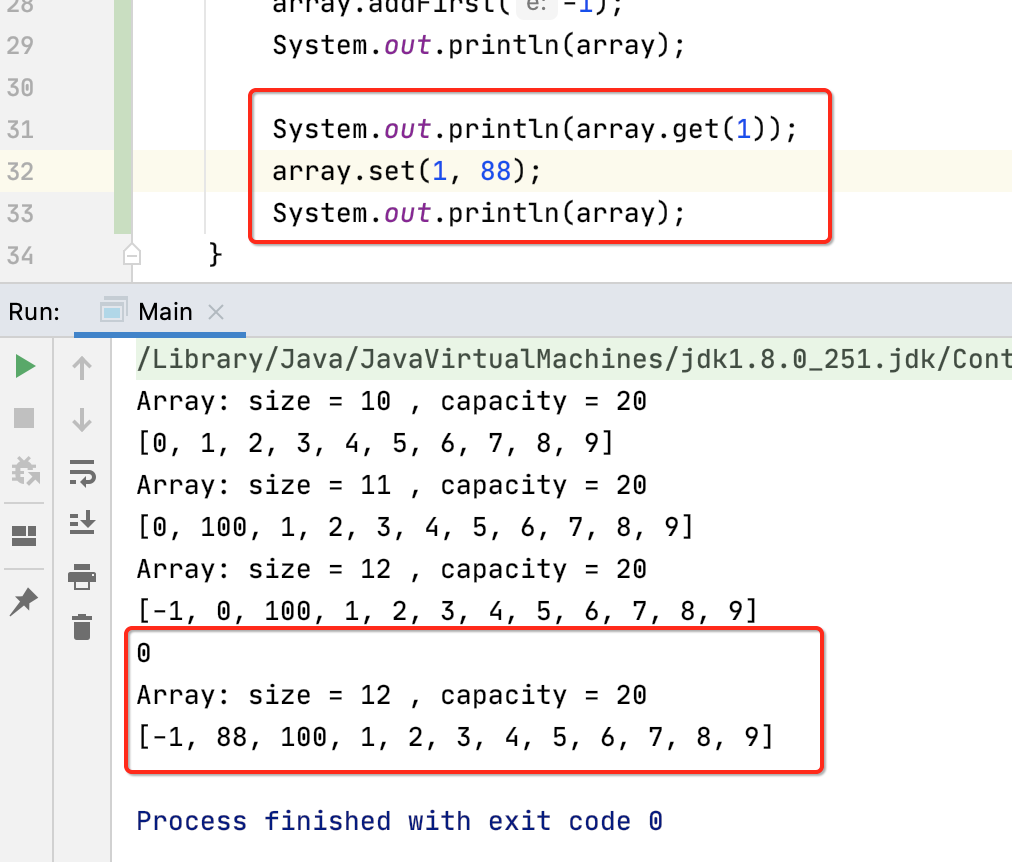
数组中的包含，搜索和删除：

contains()：是否包含某个元素

    //查找数组中是否包含有元素e
    public boolean contains(int e) {
        for (int i = 0; i < size; i++) {
            if (data[i] == e)
                return true;
        }
        return false;
    }

find()：查找元素的索引

    //查找数组中元素e所在的索引，如果不存在元素e，则返回-1
    public int find(int e) {
        for (int i = 0; i < size; i++) {
            if (data[i] == e)
                return i;
        }
        return -1;
    }

删除指定的元素：

分析：

这块先来分析一下删除的思路，对于这样一个数组：

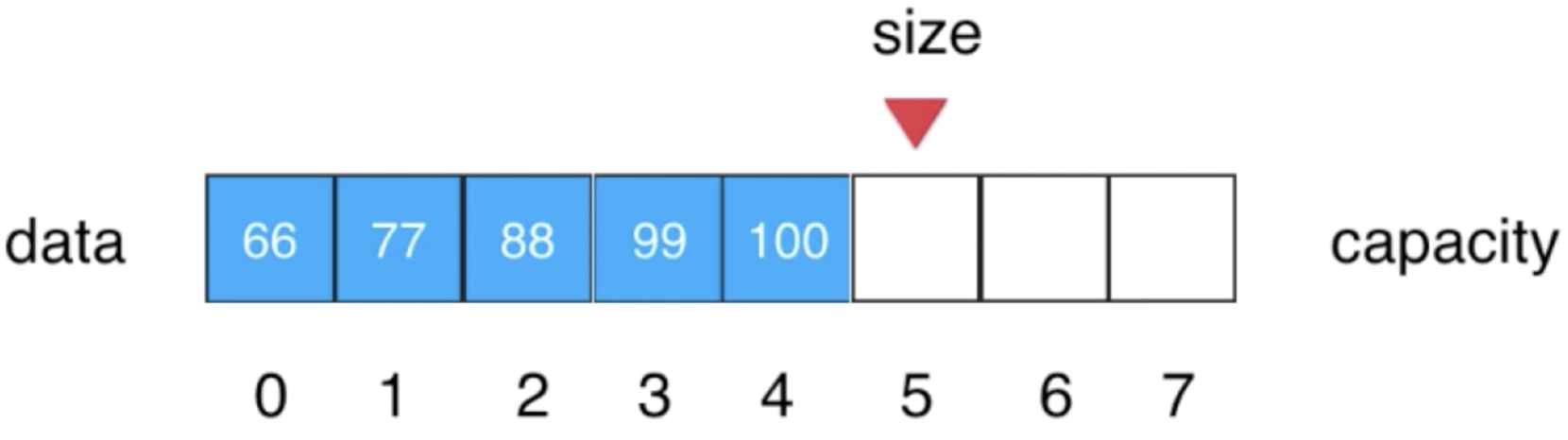
如果想删除索引为1的元素，只需要将索引为1之后的所有元素都往前挪一个位置既可，具体如下：

1、将索引为2的元素挪到索引为1的位置：

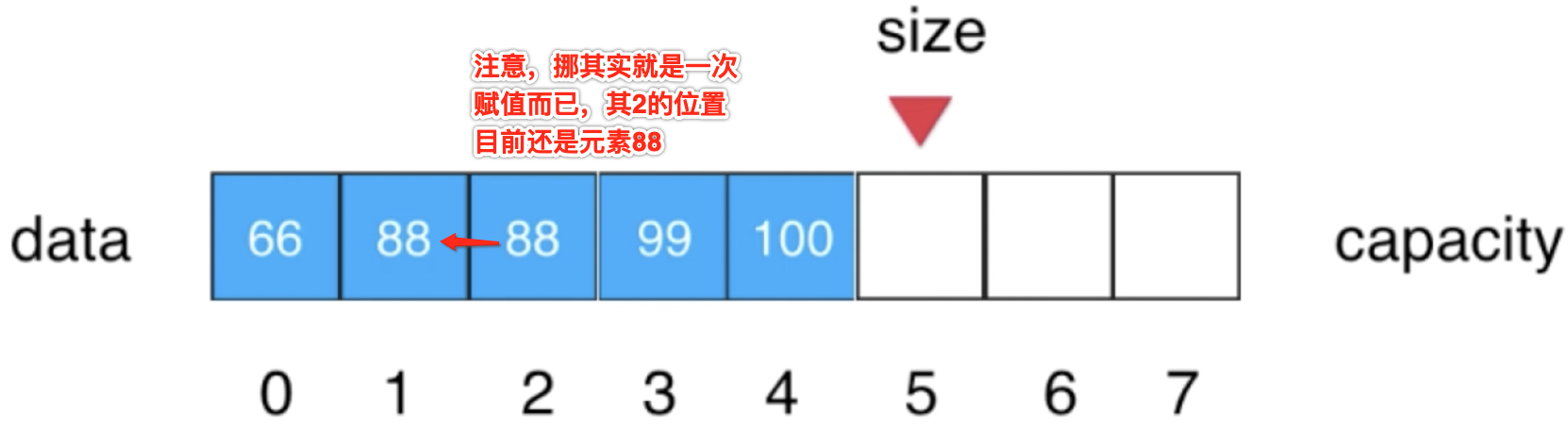
2、将索引2位置的元素被索引3位置的元素进行赋值：

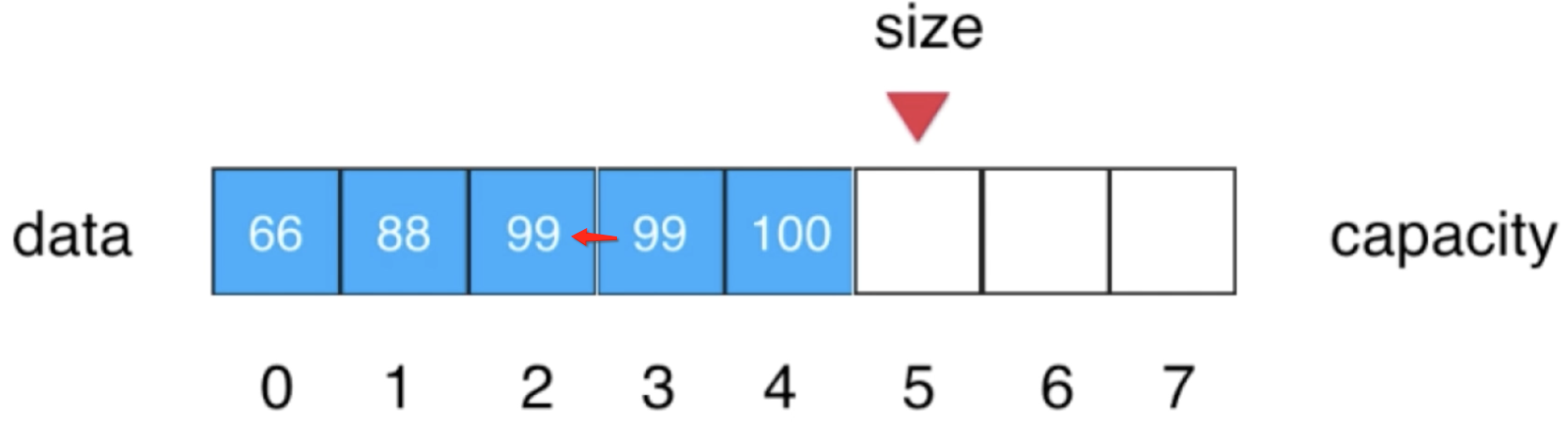
3、将索引3位置的元素被索引4位置的元素进行赋值：

4、将索引4位置的元素被索引5位置的元素进行赋值，而发现索引5已经没有元素了，所以整个删除任务结束，最后莫忘了维护一下size：

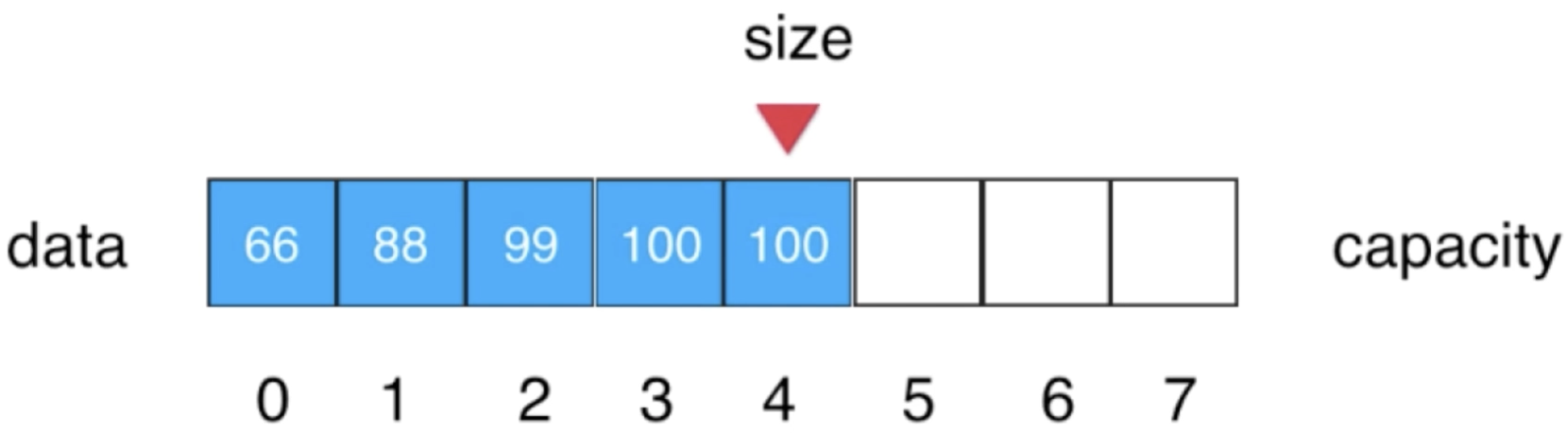
此时需要注意啦！！！对于size来说应该是指向一个第一个没有元素的位置，也就是如果咱们要想数组末尾再添加一个元素的话则应该是向size这个位置进行添加，但是！！！你有木有发现，当删除第1个元素之后，目前这个size指向的是一个有元素100的位置了：

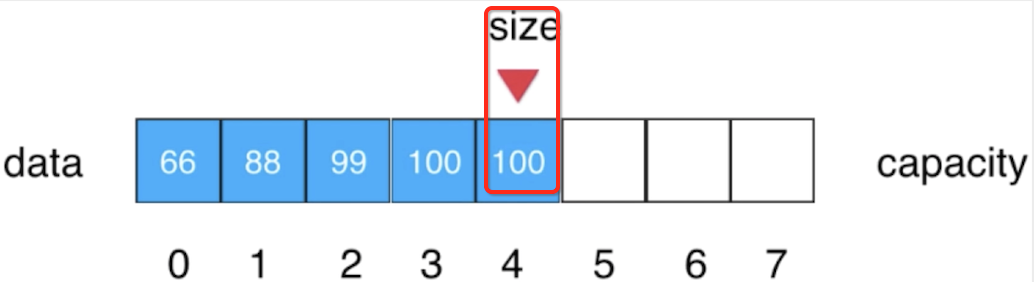
其实不用担心，因为我们暴露给用户取数据是做了索引合法性的检测的，如：

另一个层面，其实数组在开辟空间时默认每个索引位置都是有值的，其值为0，那跟目前值为100没有使用其实也没啥区别，这点要明白。

实现：

    //从数组中删除index位置的元素，返回删除的元素
    public int remove(int index) {
        if (index < 0 || index >= size)
            throw new IllegalArgumentException("Remove failed. Index is illegal.");
        int ret = data[index];
        for (int i = index + 1; i < size; i++) {
            data[i - 1] = data[i];
        }
        size--;
        return ret;
    }

同样的可以创建一个快捷方便的其它删除方法：

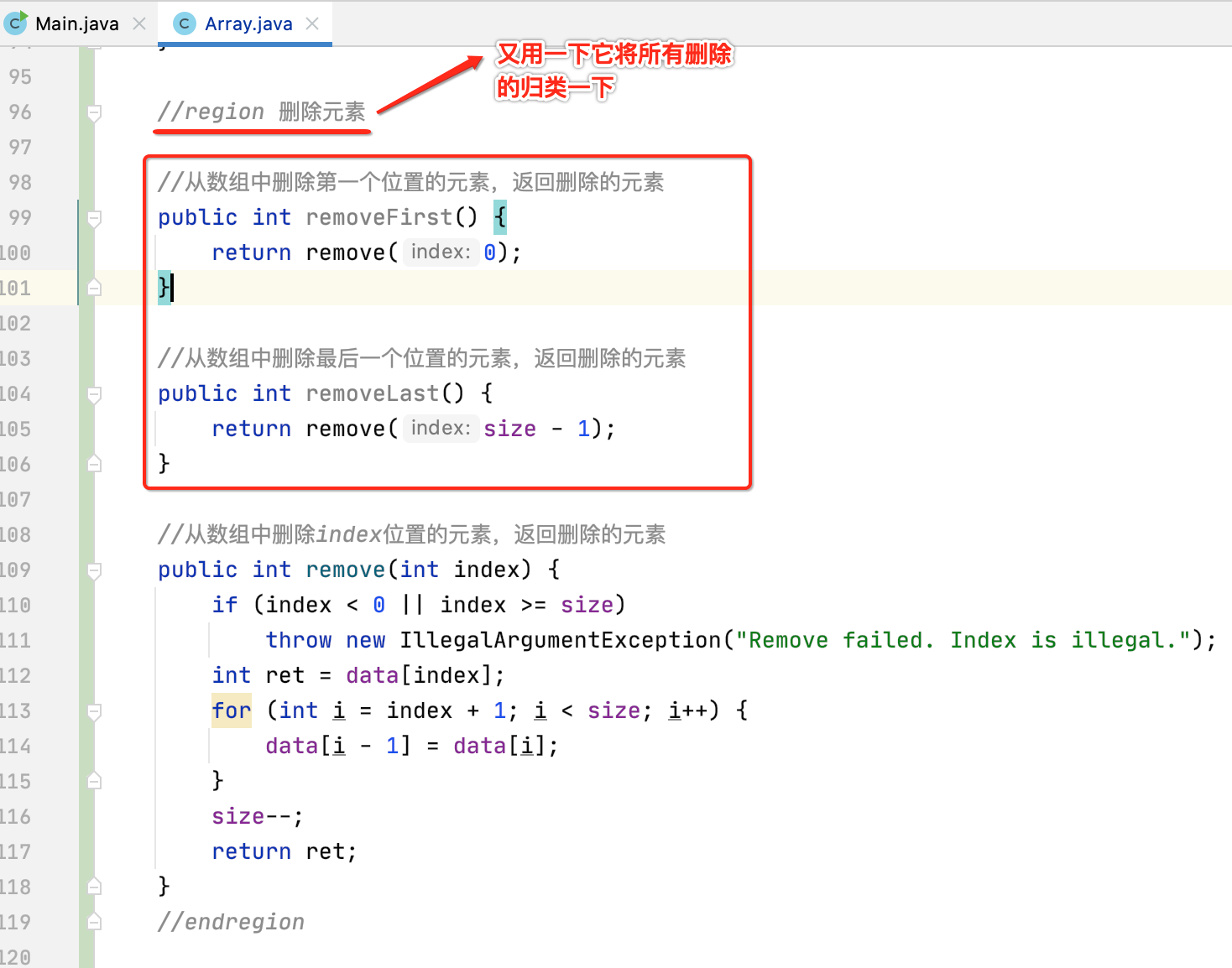
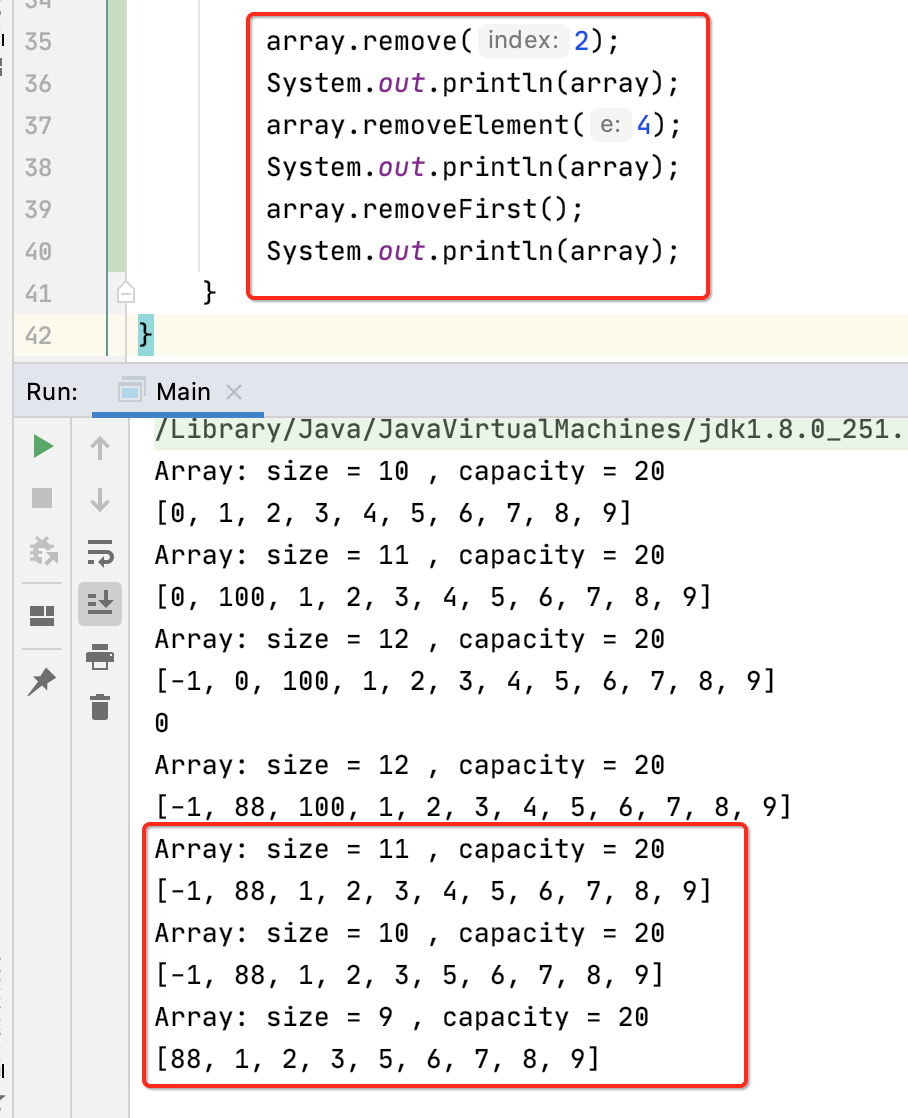
另外还可以创建一个删除某个元素的方法：

    //从数组中删除元素e
    public void removeElement(int e) {
        int index = find(e);
        if (index != -1)
            remove(index);
    }

测试：

泛型类：

目前咱们设计的数组类很明显的一个缺陷就是只能承载int类型的数据，像ArrayList它很明显可以存放任意类型的数据对吧？所以接下来将其泛型化：

1、类中声明泛型：

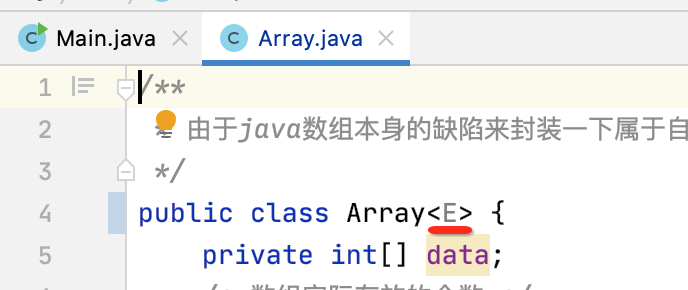
2、将数组声明成泛型：

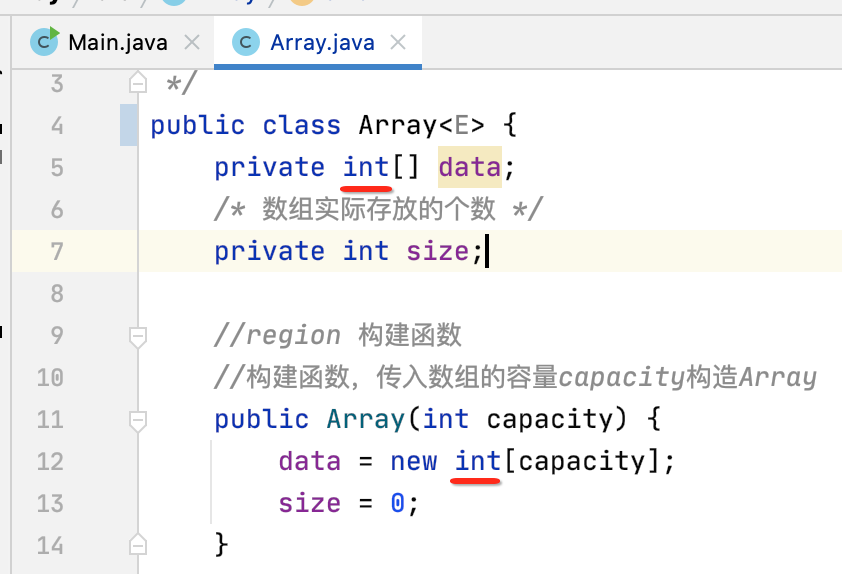
那怎么解决？其实需要绕一下弯才行，如下：

3、解决一系列报错：

将数组声明成泛型之后一系列报错就随之而来了，不过都很好解决，下面来改一下：

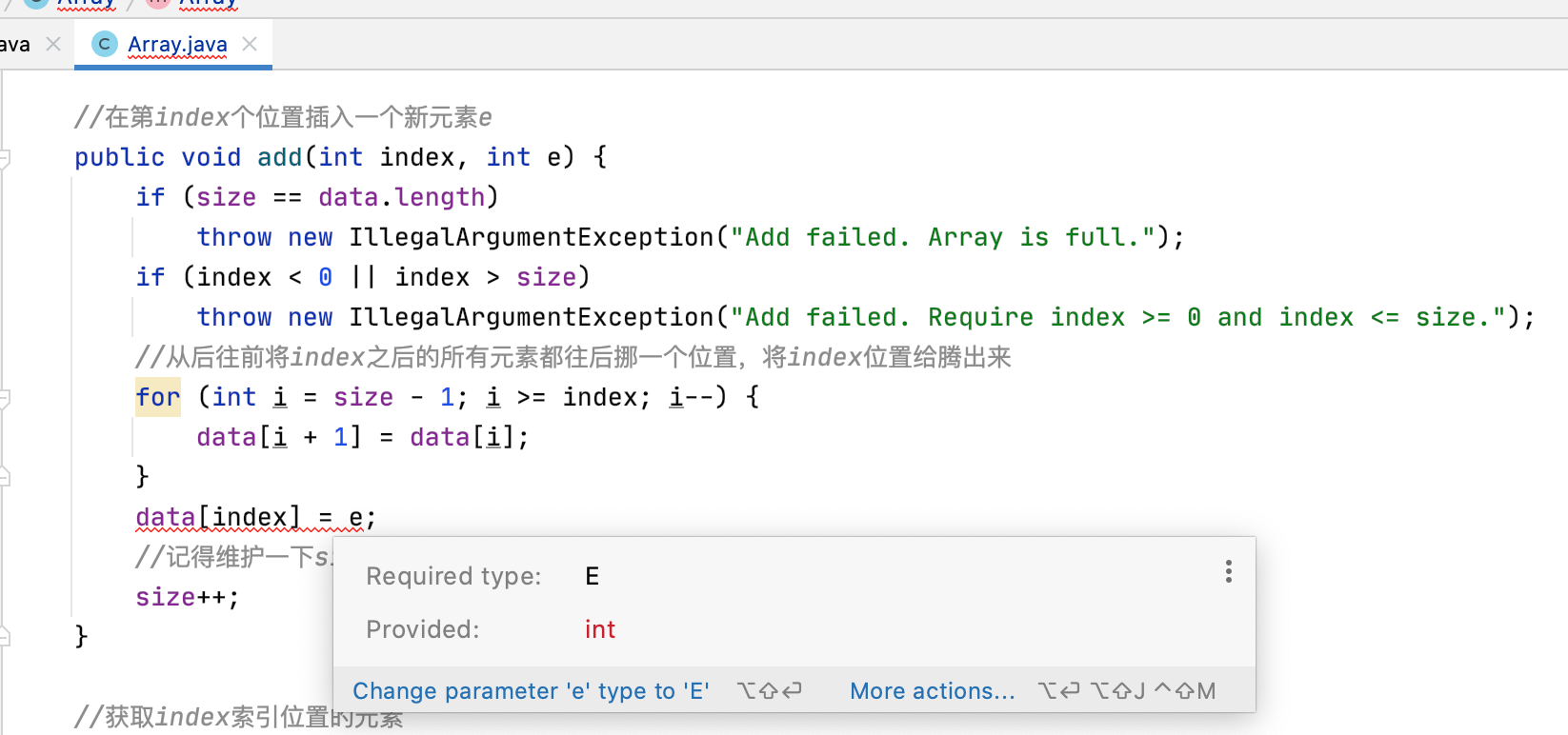
还有另外两个add方法：

 

 

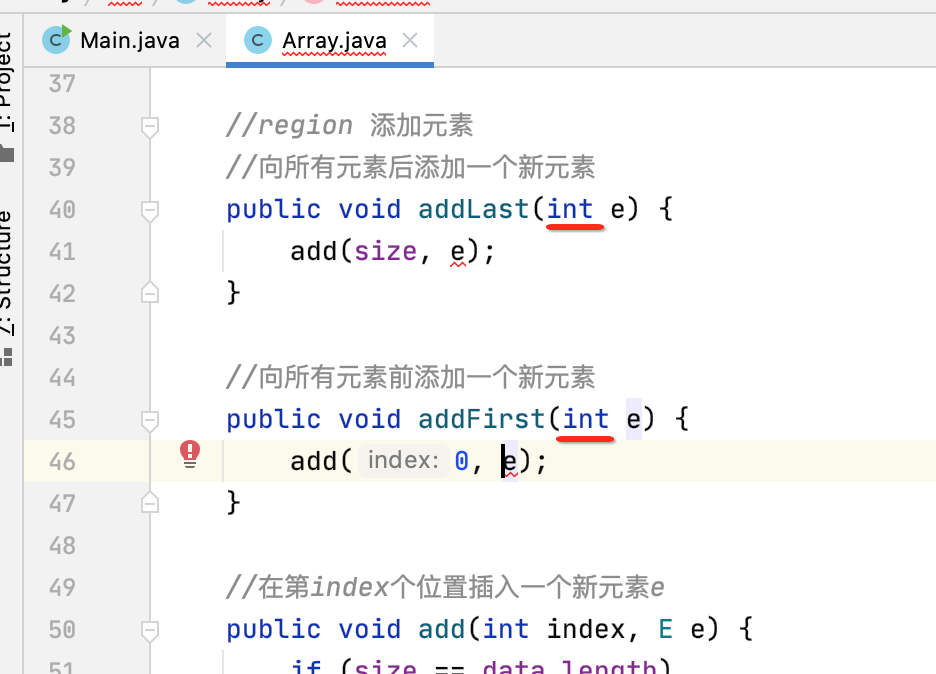
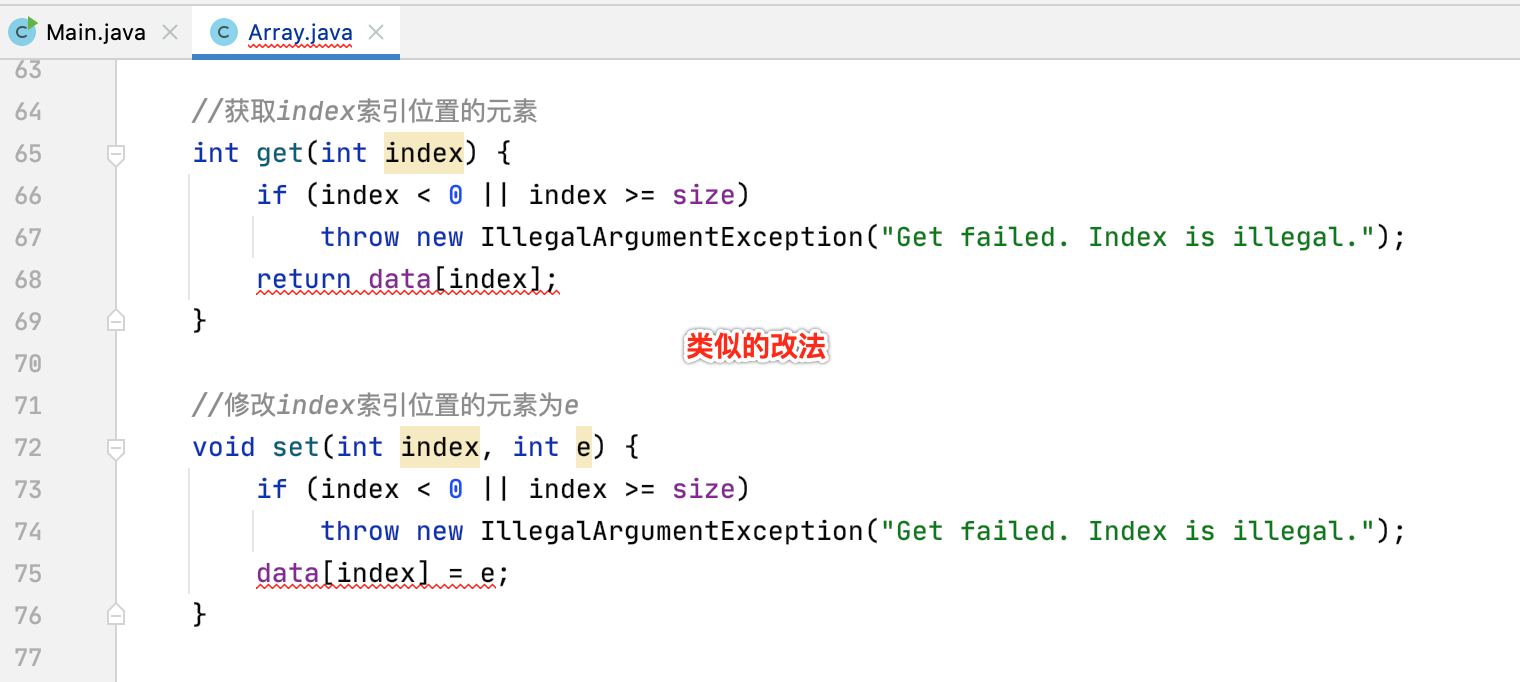
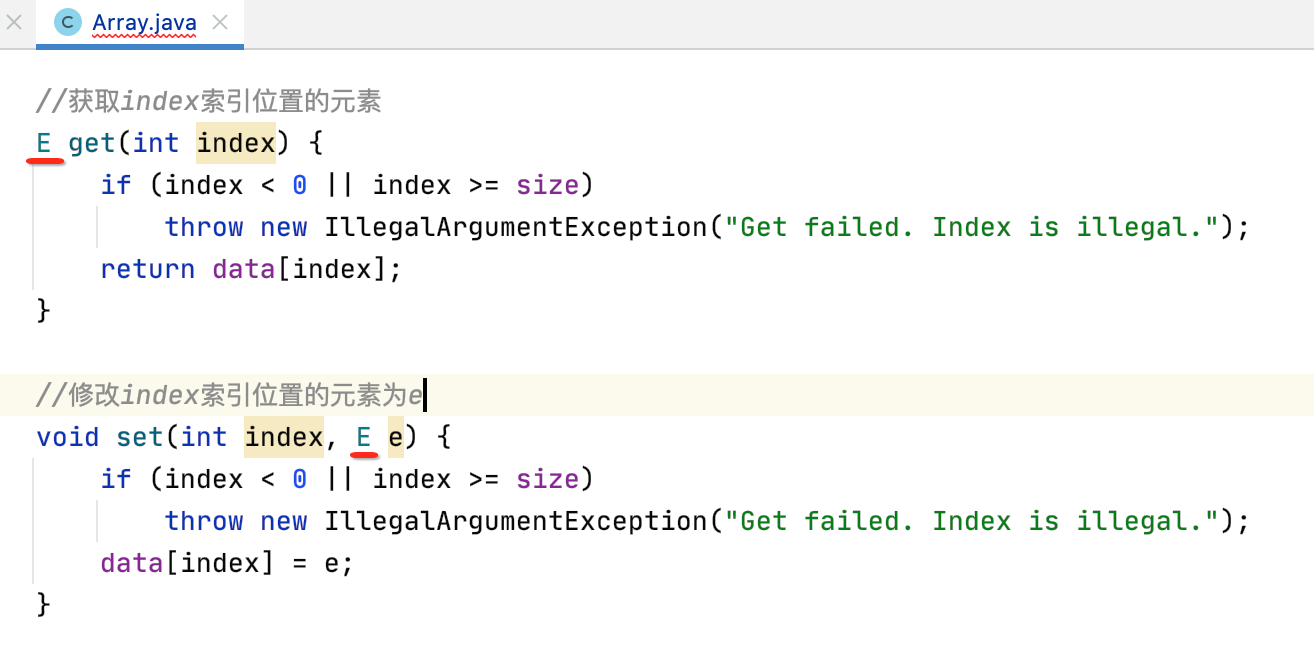
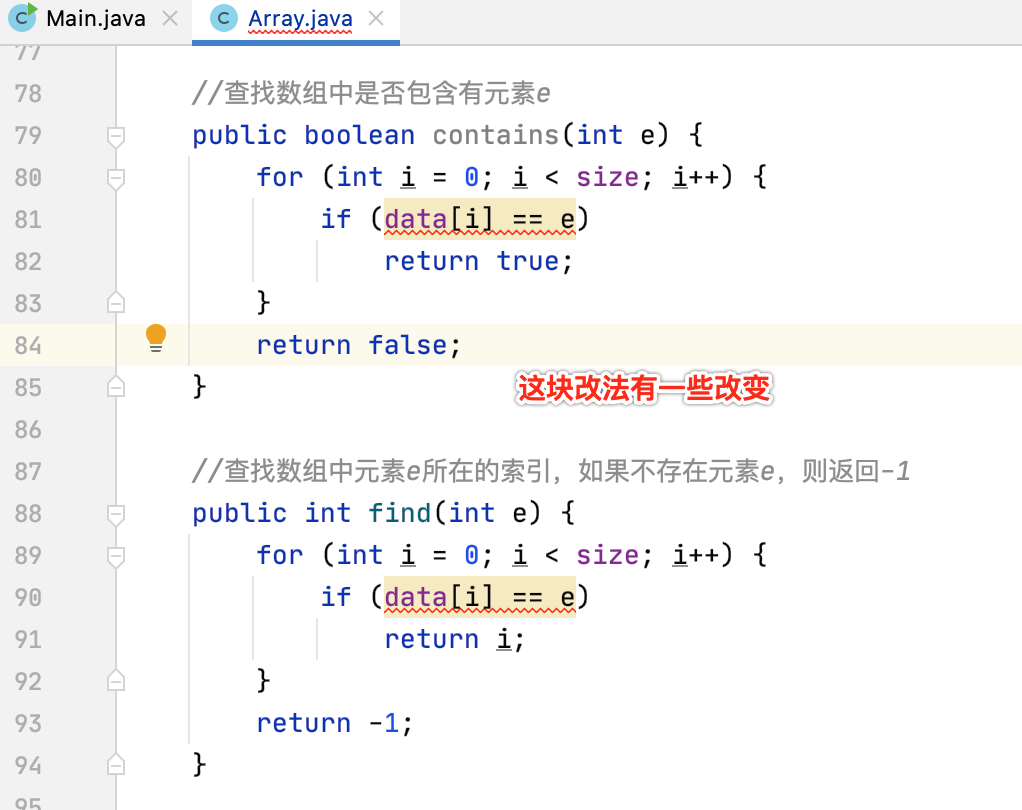
首先先改成泛型：

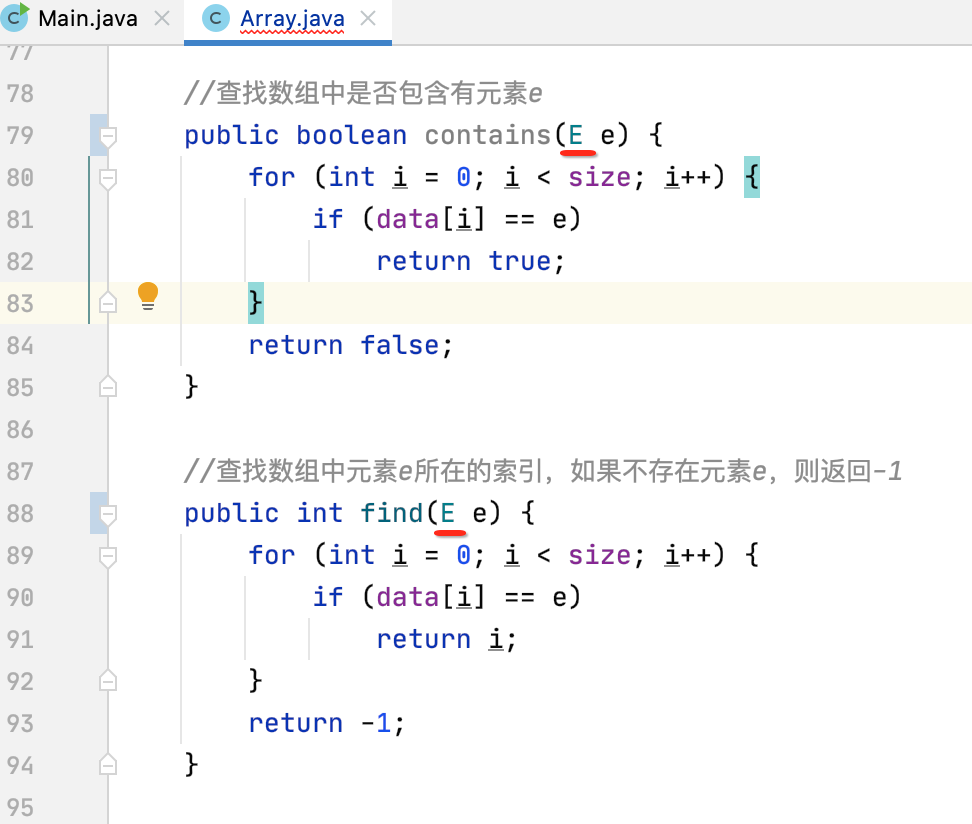
接着对于元素的比较就不能用==啦：

得改成它：

接下来则是删除相关的方法：

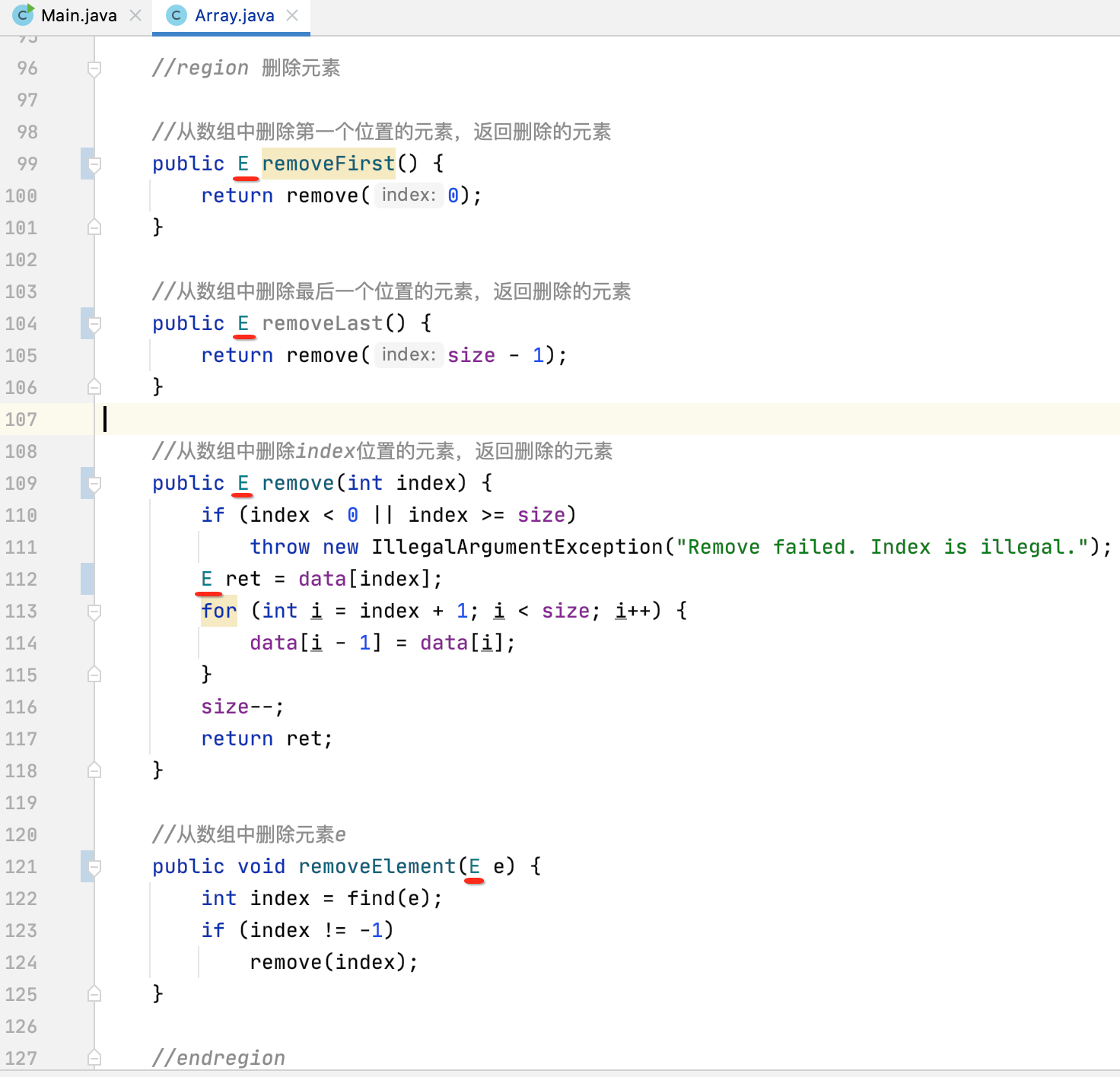
但是这里对于泛型修改之后删除方法有一个逻辑需要处理一下了，还记得对于整型数组当时在删除时size会指向一个有值的元素么？回忆一下：

当时说指向一个有值的元素无关系，但是！！！当变成了泛型类之后，由于里面存的是可以任意引用类型的对象了，那情况就不一样了，因为如果不处理会影响这个不用对象的GC操作的，所以咱们可以加一句话：

其实这样的对象有一个专业术语叫“loitering objects”：

它并不等于是内存泄漏，但是做为了一个良好的习惯最好是手动清除一下。

4、测试：

此时还是以咱们编写的整型数组改成带泛型的：

 

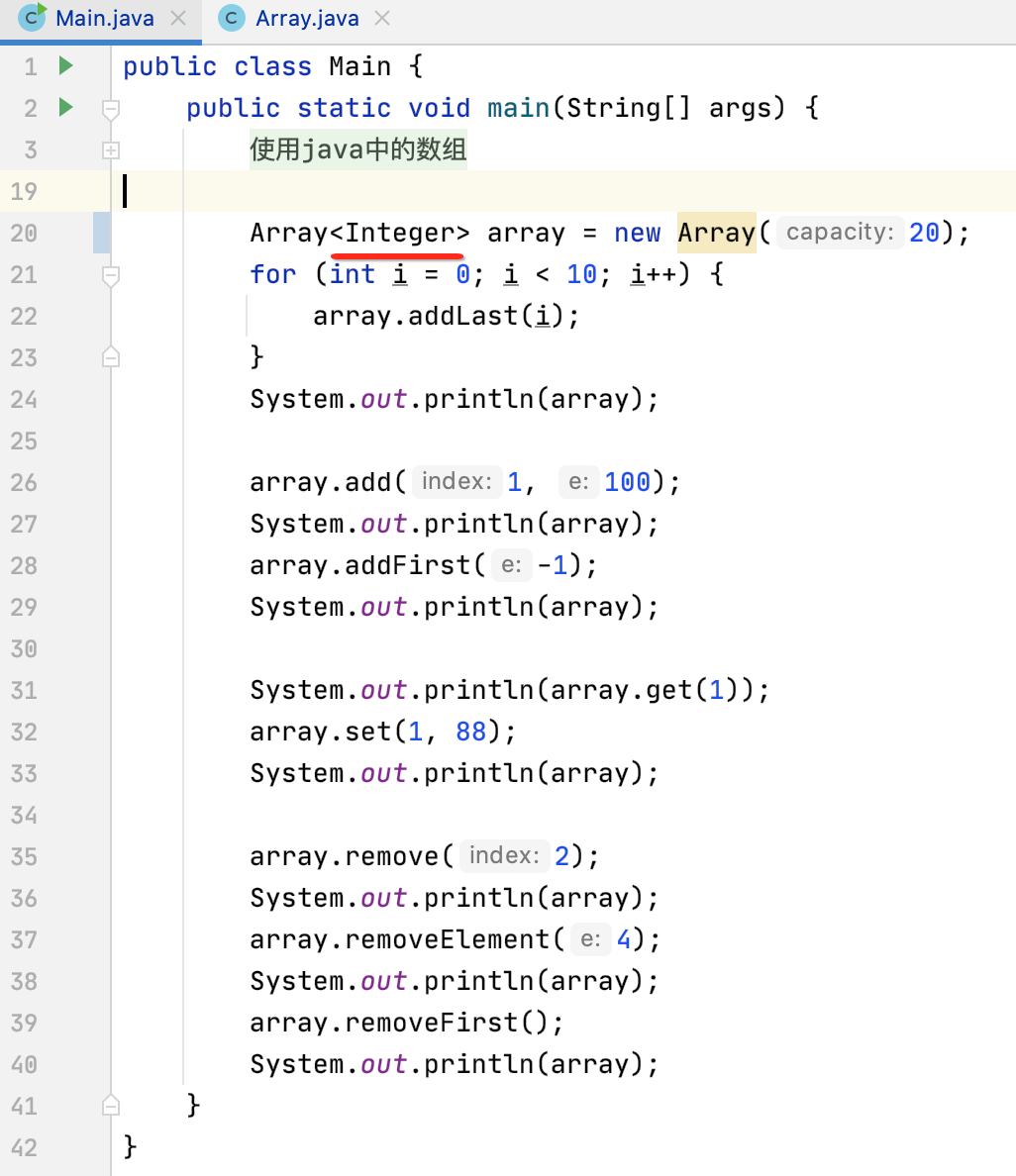
由于泛型不能使用基本数据类型，所以这里需要使用基本数据类型的包装类，整个运行结果跟之前一模一样，就不运行了。

接下来咱们使用一下自定义的类型来测试一下咱们编写的这个泛型数组，先将之前https://www.cnblogs.com/webor2006/p/14014542.html学习选择排序时的Student这个类拷过来：

其中它的代码为：

public class Student implements Comparable<Student> {
    private String name;
    private int score;

    public Student(String name, int score) {
        this.name = name;
        this.score = score;
    }

    @Override
    public boolean equals(Object o) {
        if (this == o) return true;
        if (o == null || getClass() != o.getClass()) return false;
        Student another = (Student) o;
        return this.name.equals(another.name);
    }

    @Override
    public int compareTo(Student another) {
//        if (this.score < another.score)
//            return -1;
//        else if (this.score == another.score)
//            return 0;
//        return 1;
//        return this.score - another.score;//从小到大排序
        return another.score - this.score;//从大到小排序
    }

    @Override
    public String toString() {
        return "Student{" +
                "name='" + name + '\'' +
                ", score=" + score +
                '}';
    }
}

接下来直接在Student类中的main方法中进行测试，如下：

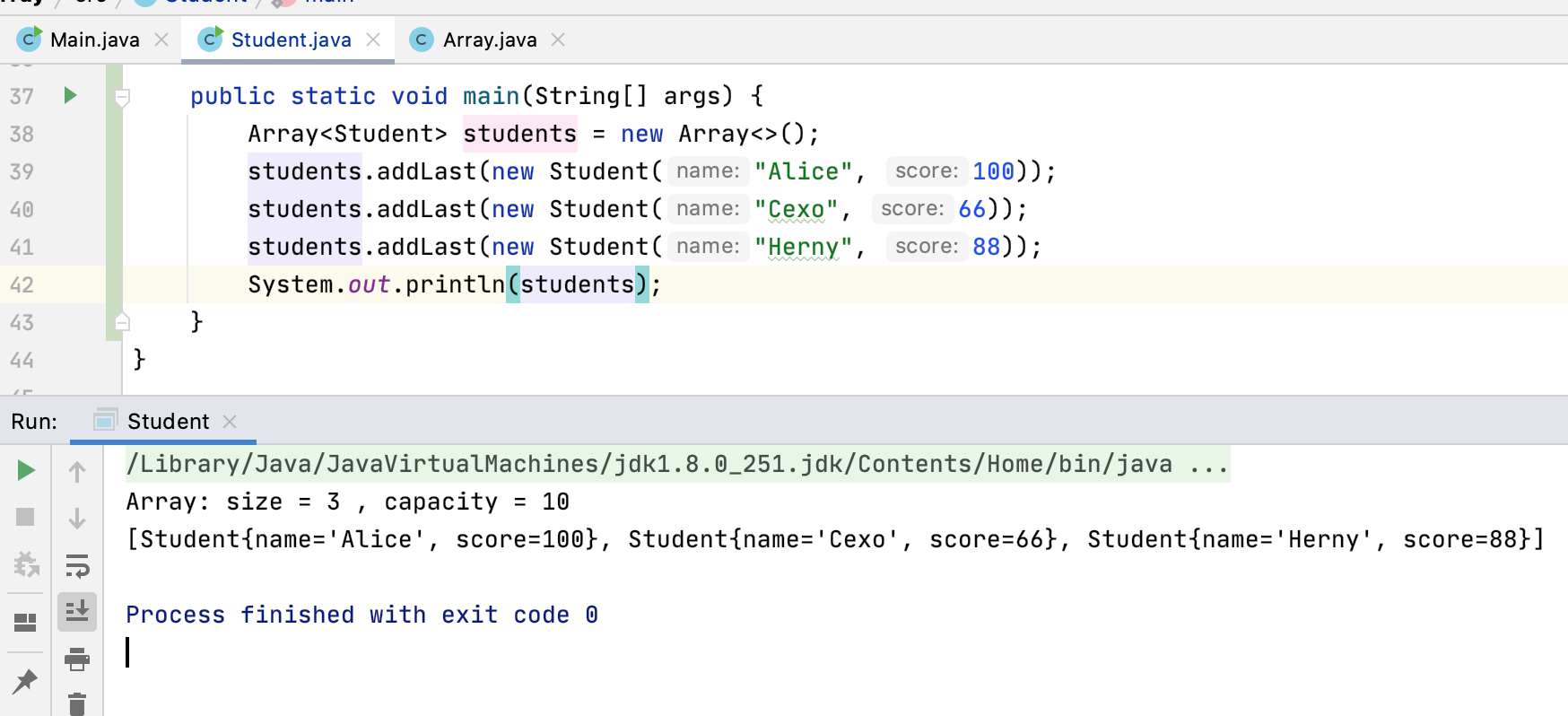
可见咱们设计的泛型类是很成功的，可以承载自定义的数据类型了。

动态数组：

概述：

目前咱们封装的这个数组类貌似是非常完美了，但是！！！它有一个非常致命的缺陷就是它底层还是使用的一个java静态数组来实现的，那就意味着咱们设计的这个数组只能存放有限的元素，而实际在进行数组存放时经常是无法预估空间的，如果说容量开得太大则有可能浪费很多用不到的空间，而如果容量开得过小则有可能导致空间不够用，所以需要有一种机制能做到数组的动态伸缩，也就是俗称的动态数组【类似于ArrayList】，所以接下来对种们的数组类进一步进行功能扩充。

思路：

那怎么能做到数组的动态伸缩呢？其实也不难，下面先来挼清思路，假设有这么个容量已经满了的数组：

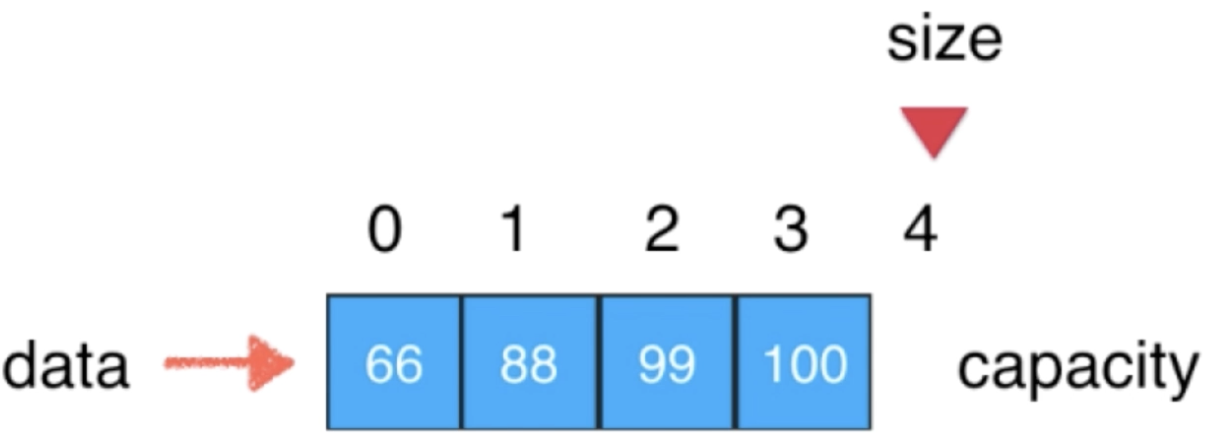
就目前的实现来说如果再添加元素很显然会抛出异常的，但是呢这里可以这样弄，当发现元素已经满了的时候此时可以再开辟一下容量比这个要大的“全新”的数组，如下：

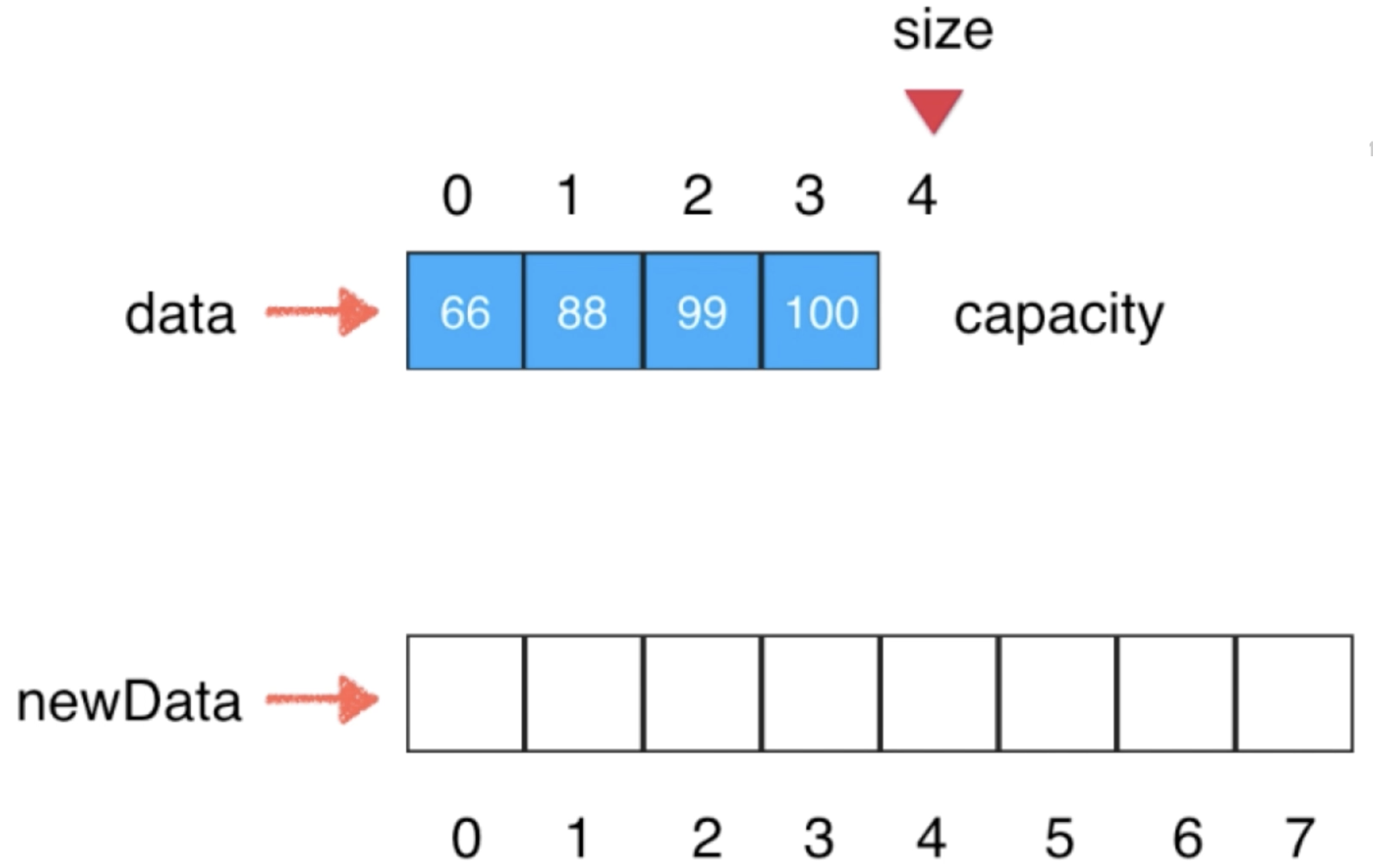
其中newData的空间比咱们正在使用的数组要大一些，然后将data中的所有元素都拷贝到newData当中，所以形态如下：

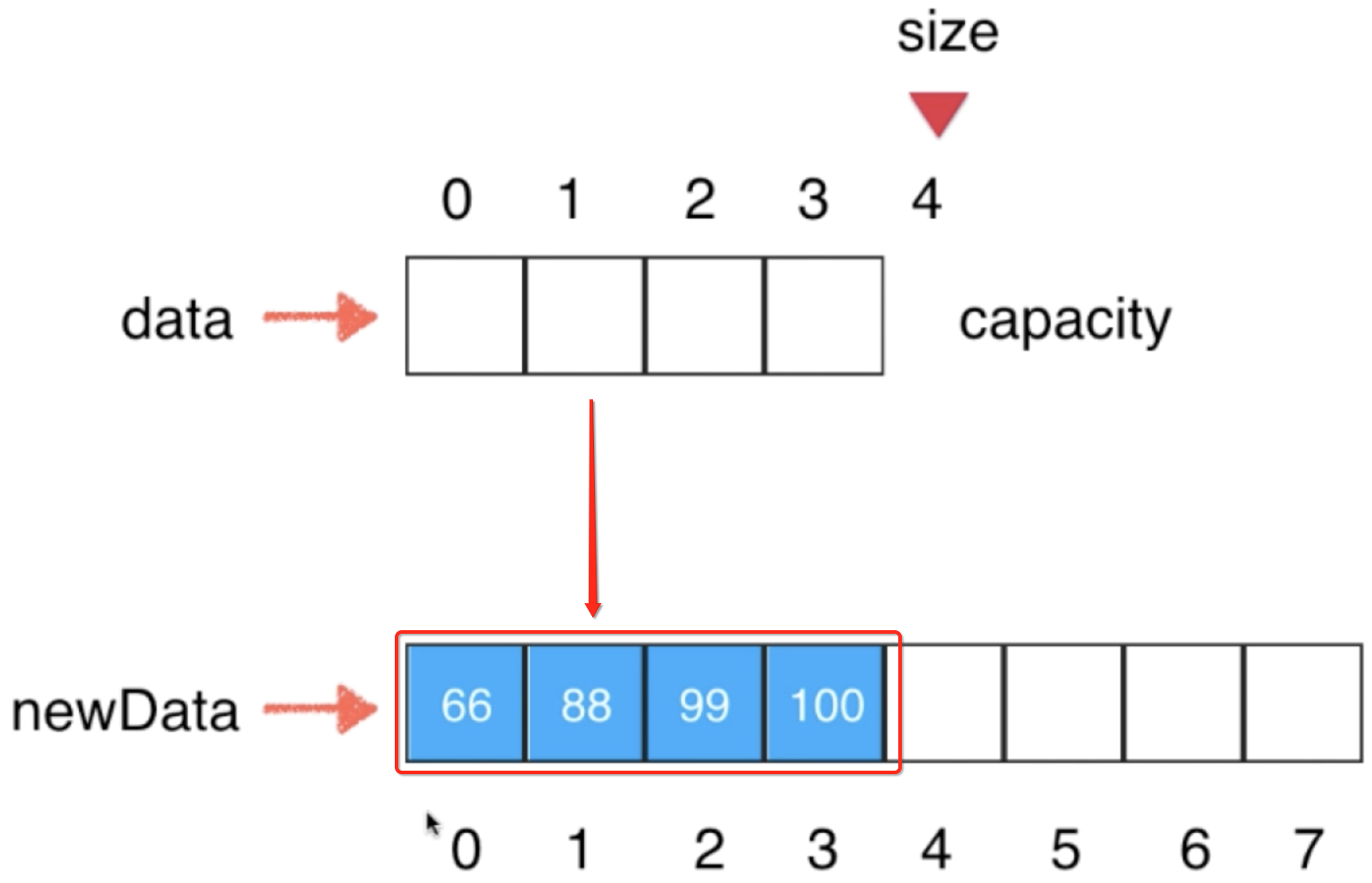
此时对于咱们的Array中的capacity和size也都指向了这个newData了，如下：

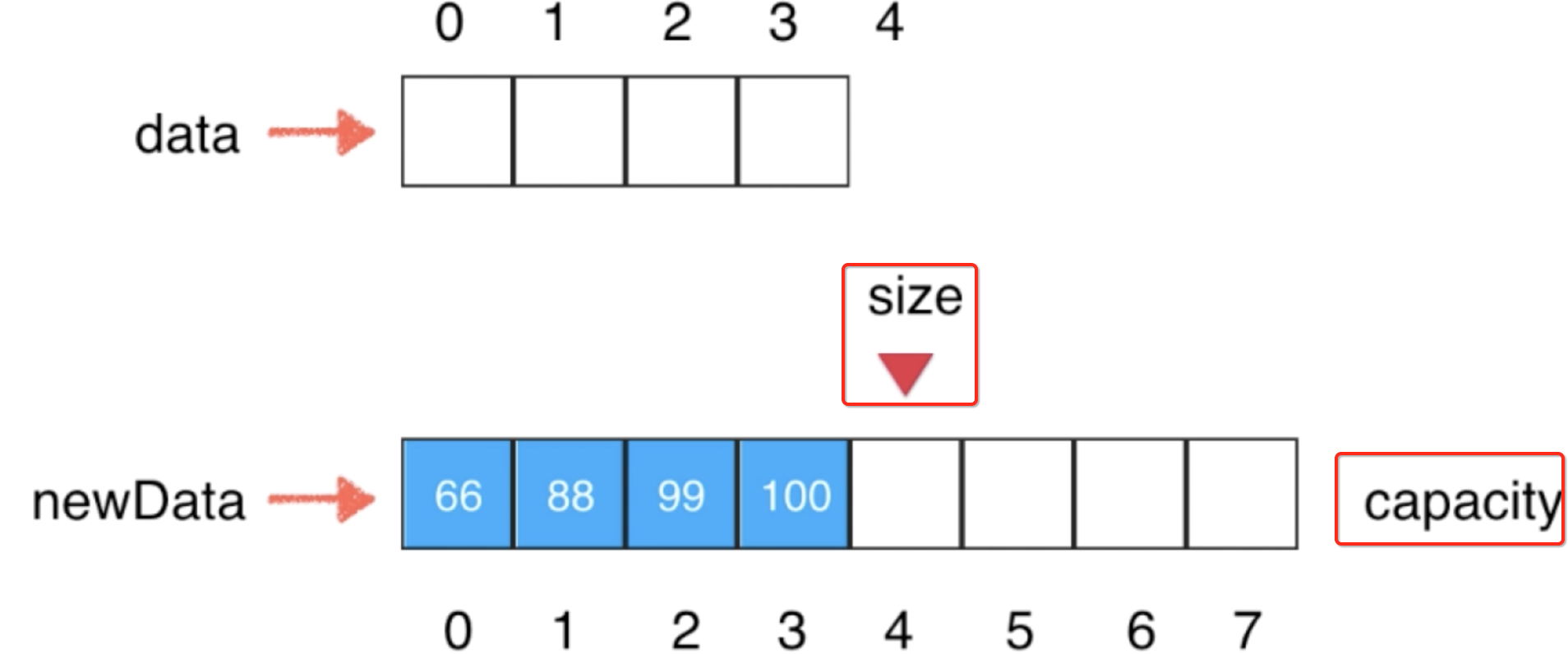
然后再做一个关键操作，就是让data的引用指向newData从而达到将原来容量不够的数组用全新空间足够的数组来代替，如下：

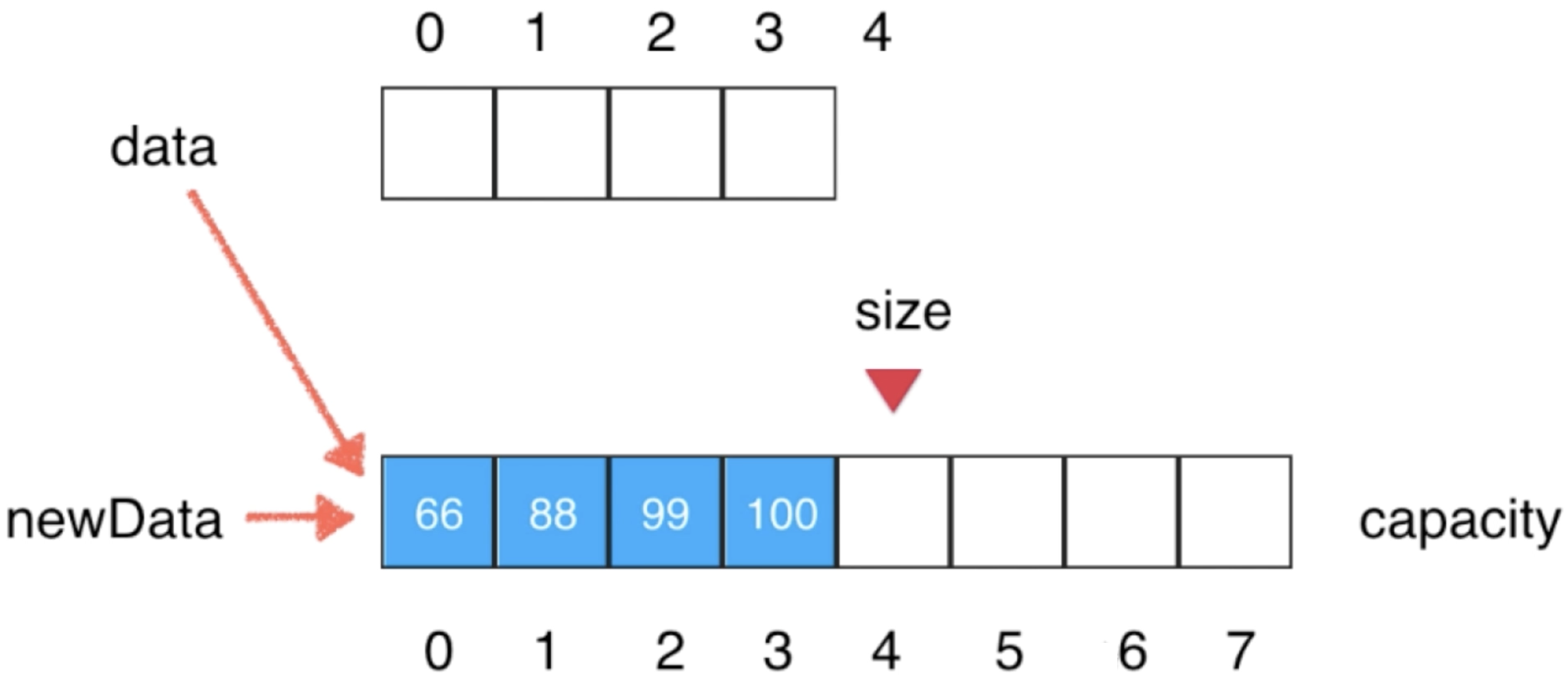
那原来空间不够的这个数组咋办呀？不用处理，因为已经没有引用指向它了，迟早会被GC所回收的，所以经过GC回收之后，最终的形态就变成了：

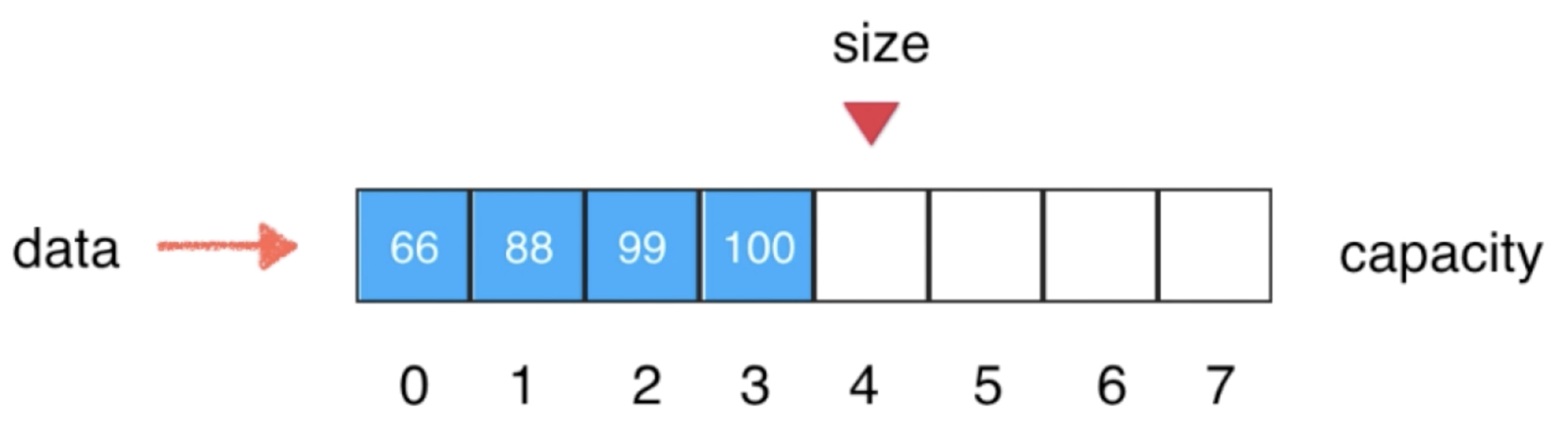
至此，整个数组扩容就已经可以实现了，其实有了这个思路之后，对于删除元素的数组“缩容”也可以类似的处理。

实现：

下面则来实现一下，首先来处理元素添加的情况：

 

 

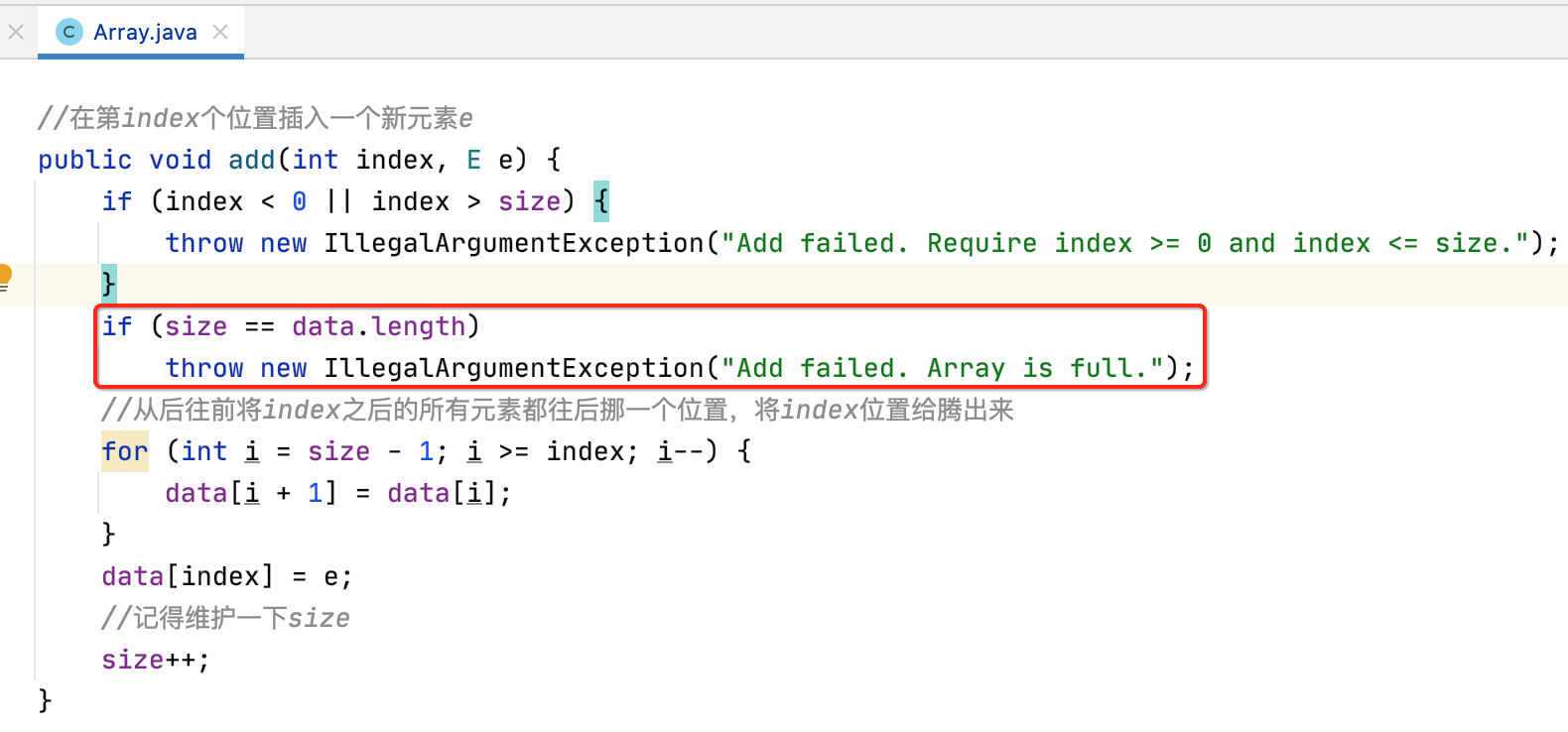
然后此时当空间不够时不能抛出异常了，而是需要进行扩容，如下：

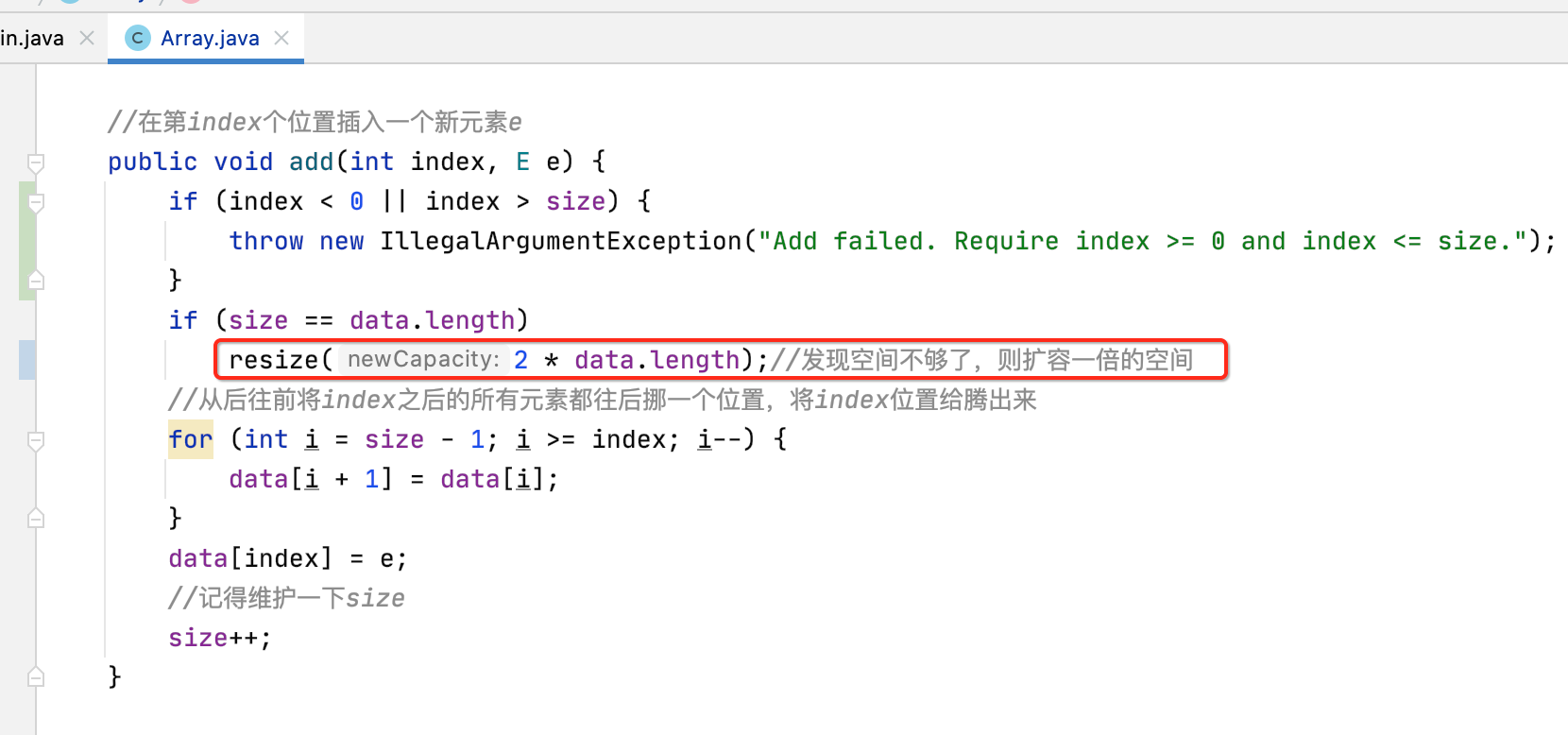
其中这里对于扩容为啥要定义成2 * data.length稍加说明一下，这是因为如果写一个固定的大小显然是不合适的，比如10000个这样体量的数组元素满了说明接下来可能还会来一大波元素，也就是增的能力会比较高，所以如果扩容只有一点点那这种扩容的意义就不是太好，相反如果对于10个这样体量的数组元素满了说明接下来新增的元素也就是一小波，如果扩容得过大则又会造成空间的浪费，所以这里直接让它扩容一倍，比较好的能照顾到两种极端情况，对于Java中的ArrayList它定义的是1.5倍。

接下来对于resize()实现比较简单，这里直接贴出：

    private void resize(int newCapacity) {
        E[] newData = (E[]) new Object[newCapacity];
        for (int i = 0; i < size; i++) {
            newData[i] = data[i];
        }
        data = newData;
    }

测试：

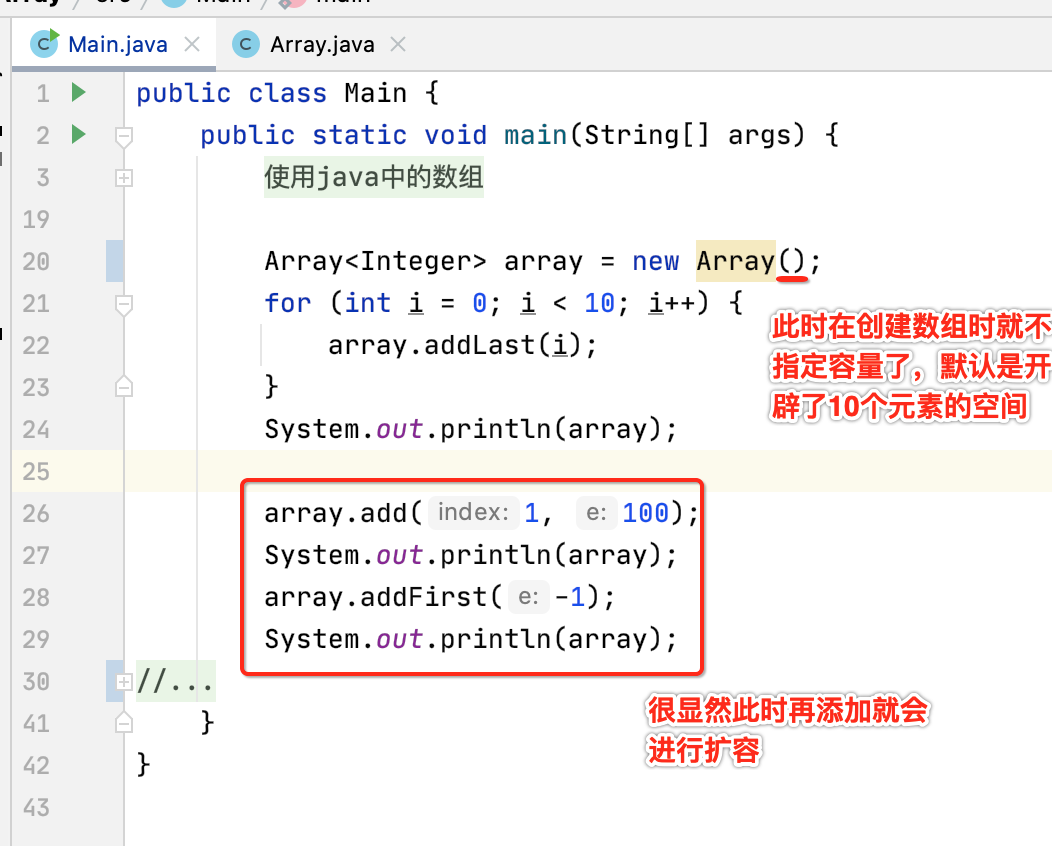
运行看一下：

 

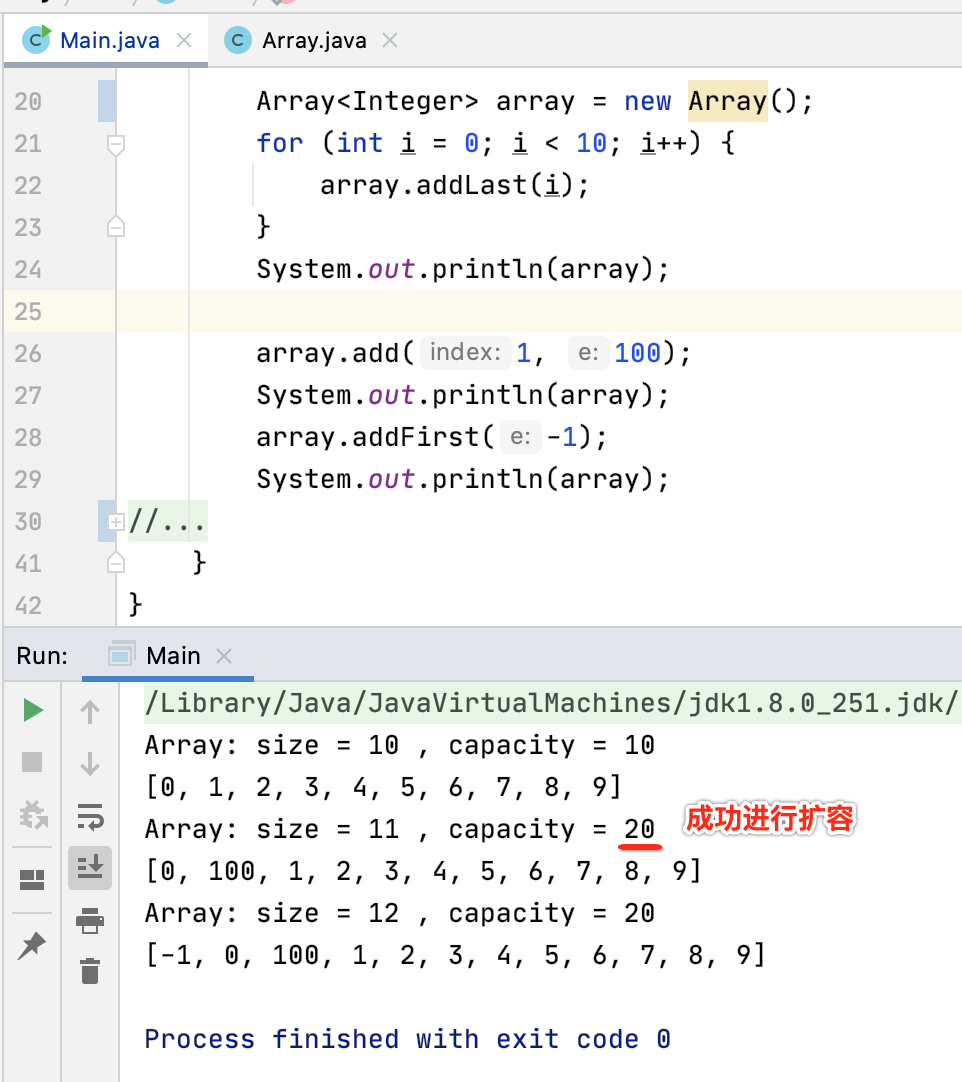
如之前所说，其实对于删除逻辑也可以加一个“缩容”机制，避免空间过于浪费，如下：

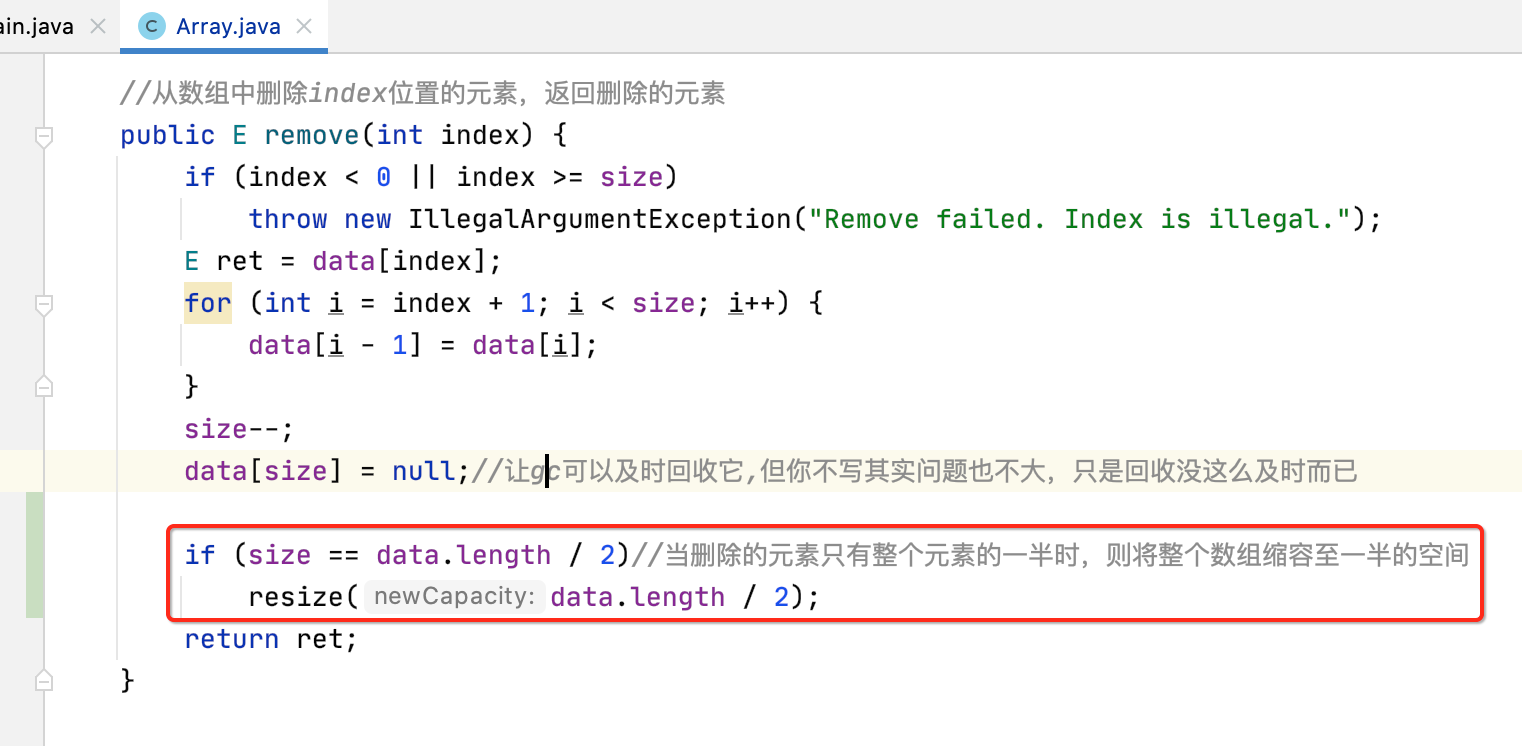
接下来再来测试一下缩容的情况：

 

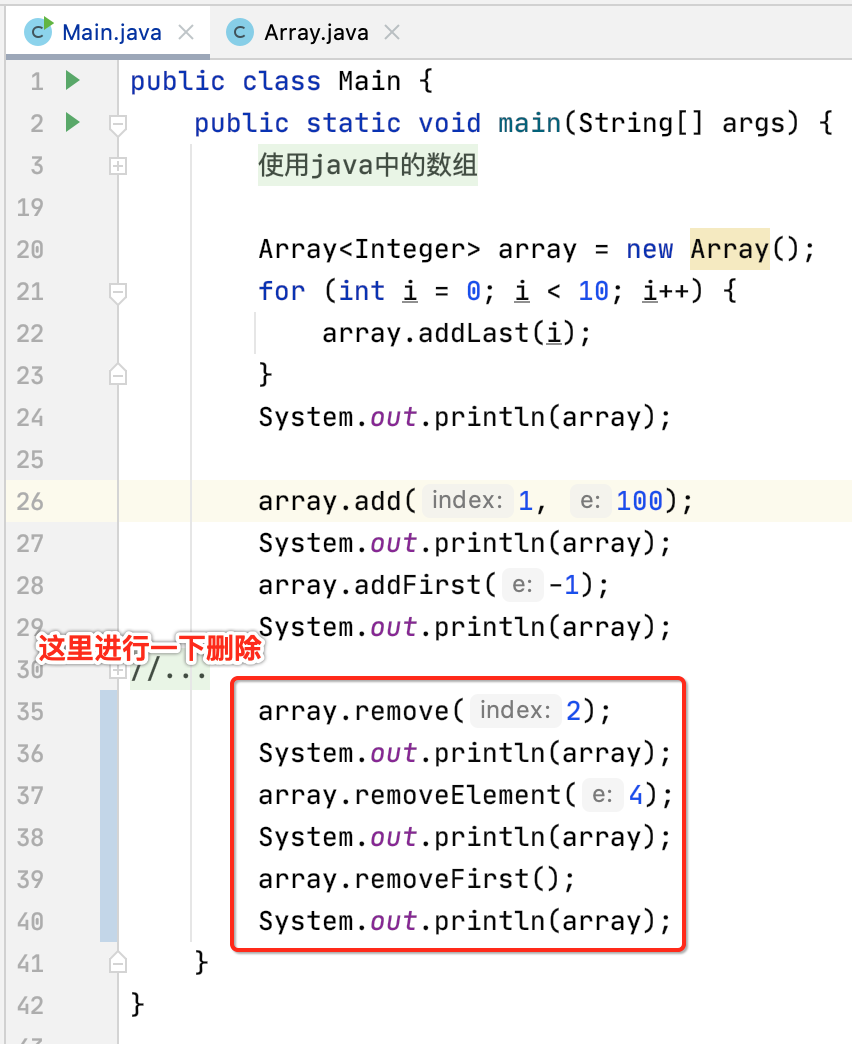
此时运行看一下结果：

简单的复杂度分析：

接下来则来对咱们封装的Array这个类中的方法进行一下复杂度分析，看看性能怎么样，这里就得从多个角度来进行分析了。

添加操作：O(n)

addLast(e)：

很明显它是O(1)级别的，因为此操作的时间复杂度跟数组的容量木有关系，常数级别，性能不用多说。

addFirst(e)：

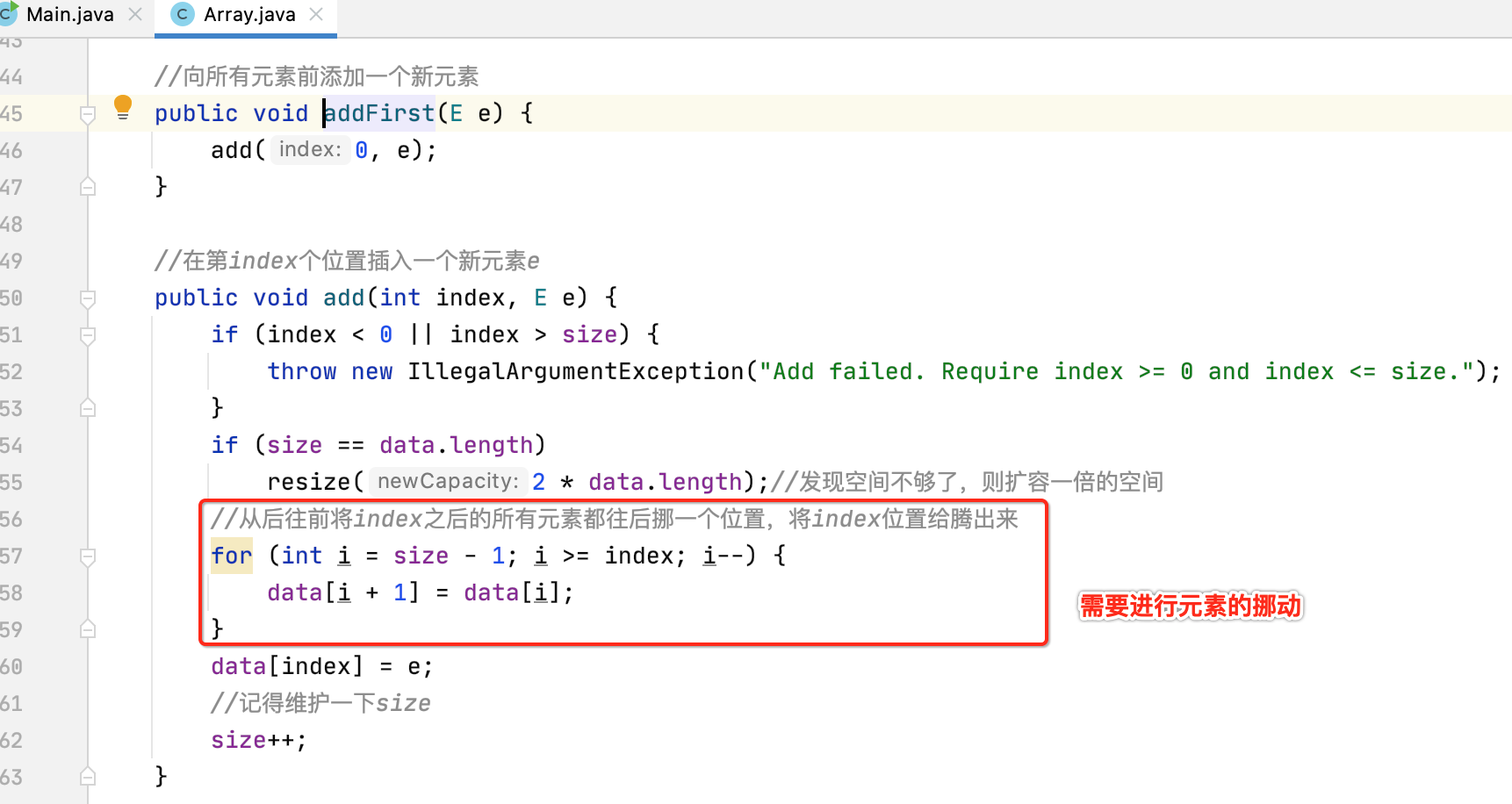
毫无疑问，将元素添加到第一个位置则将整个数组进行向后移动，所以它的时间复杂度是O(n)。 

add(index, e)：

由于这个index可以是任意数组的位置，很显然它的复杂度就没这么好分析了，比如如果index为size，那么就等于addLast(e)的复杂O(1)，而如果index为0，那么就等于addFirst(e)的复杂O(n)， 其实这里只能算一种概率，可以说这种操作的复杂度是O(n/2)，而对于时间复杂度中的常数是可以省掉的，最终整个的复杂度其实可以认为是O(n)。

而从整体来看，其实对于添加方法的时间复杂度为：

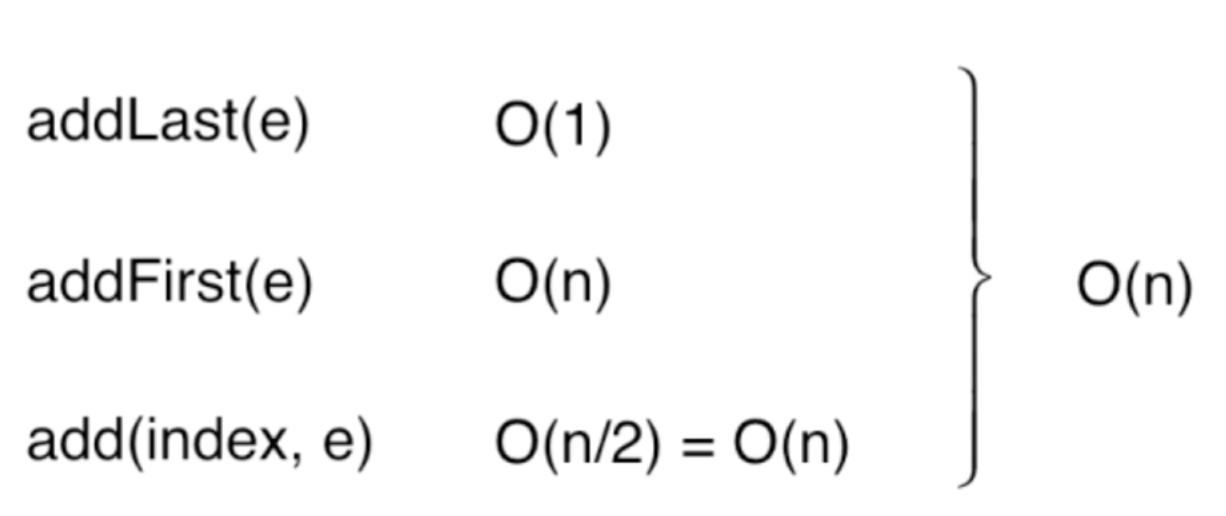
还是那句话，通常时间复杂度通常是“最坏”的情况【其中通常加粗了，因为还有一些特例情况不是按最坏来算时间复杂度的，其实也就是下面要道出的均摊复杂度】，另外还有一种情况还木有考虑，就是数组的扩容，很明显它是O(n)的，因为要将整个元素遍历拷贝到一个新的数组当中嘛，综合来看对于添加操作的时间复杂度就是O(n)。

删除操作：O(n)

其实跟添加操作类似，这里就把结果贴出来了：

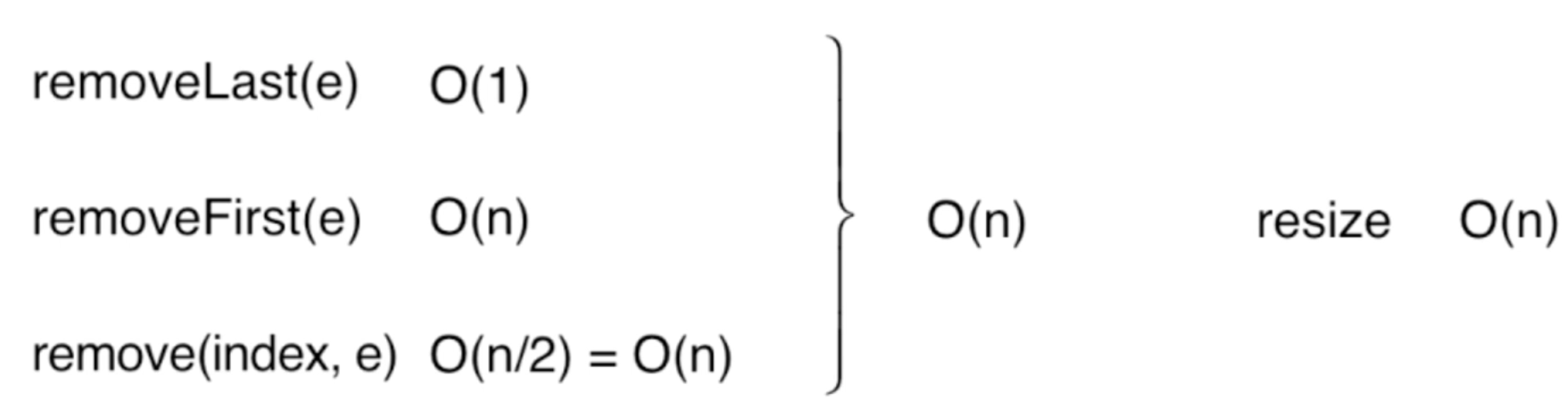
修改操作：O(1)

直接定位，直接修改，当然就是常用级别喽，O(1)妥妥的，这也是数组的一个非常大的优点。

查找操作：

get(index)：

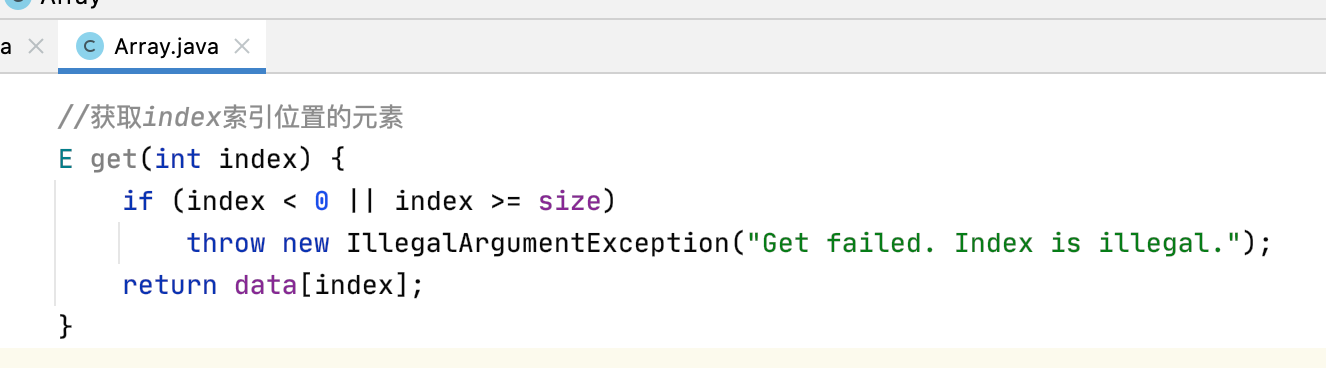
O(1)妥妥的。

contains(e)：

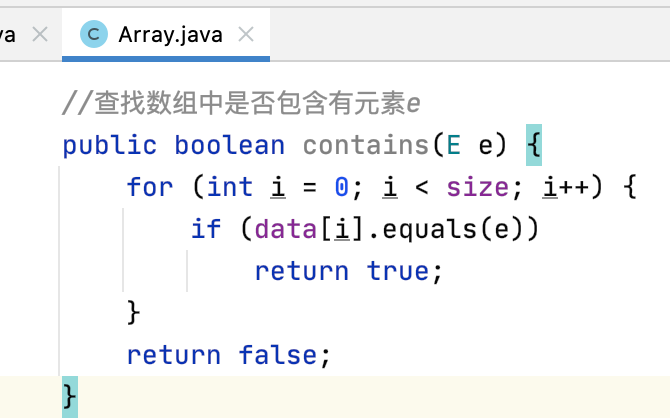
需要遍历，所以复杂度是O(n)。

find(e)：

 

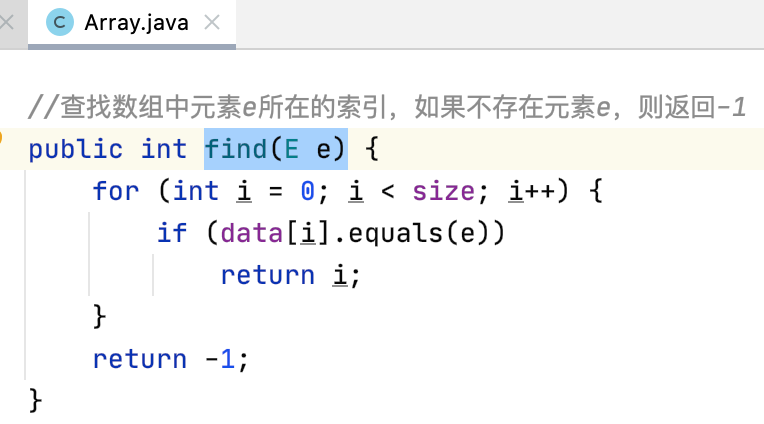
也是O(n)

结论：

其中可以看到在已知索引的情况下其性能是最好的，所以这应证了之前的描述：数组中的索引最好是要有语意的，这样使用数组检索就会有非常好的性能优势。

最后这里要强调一个细节，也是引出下面要进行探讨的话题的出处，就是对于增和删的时间复杂度：

如之前所分析当对最后一个元素进行增和删操作其实它们的复杂度其实是O(1)级别的，而为啥要说它们的复杂度是O(n)呢？因为会涉及到一个resize()的过程，此时就会涉及到数组的拷贝其复杂度瞬间就上升到了O(n)了，可见resize()是一个性能“不太好”的一个操作，这里的不太好打引号了，事实上对于resize()时间复杂度分析不能以最坏的O(n)来进行分析是不太合理的，需要引用均摊复杂度的分析方法，分析之后其实resize()操作性能并未想象中的那种次了。

均摊复杂度和防止复杂度的震荡【重点】：

均摊复杂度：

接下来终于来到了新知识的学习时间了，啥叫“均摊复杂度”呢？这里就得从上面分析resize()时间复杂度抛出的问题开始分析起，对于addLast()操作而言本身它是O(1)级别的，只是因为resize()是O(n)导致整个addLast()的时间复杂度上升到了O(n)了，这样分析是不太合理的，为啥？因为并不是每一次addLast()都会导致resize()操作呀，所以下面来优化一下这种复杂度的分析方法。下面注意其整个均摊复杂度分析的推理过程：

假设当前capacity = 8，并且每一次添加操作都使用addLast，这里的时间复杂度在容量没满时其实都是O(1)，这里用一个数字序列表示一下：

此时再addLast就得注意啦，得进行扩容对不对，然后此时它的复杂度就变成了：

 

而归纳总结一下：

 

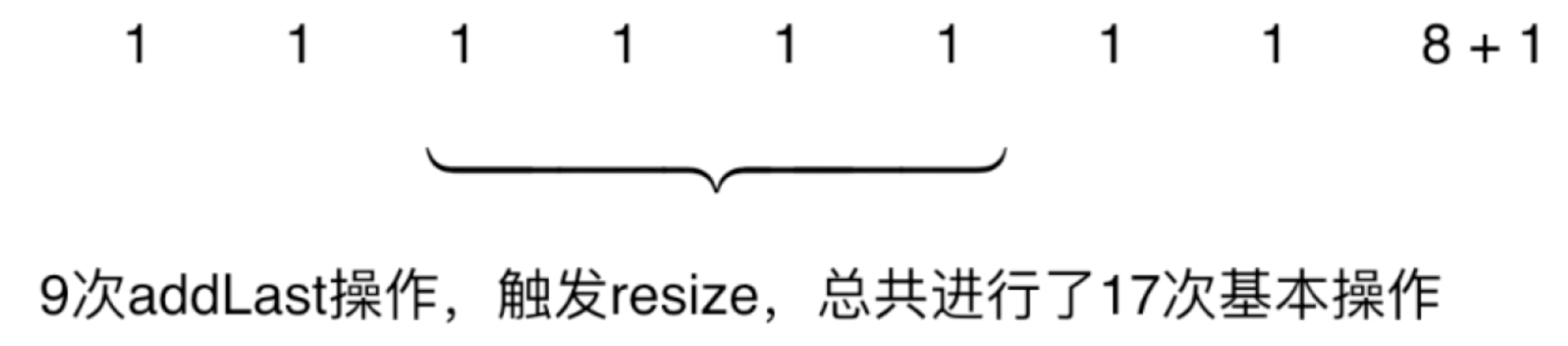
其中的基本操作就是给空间赋值，9次addLast触发的基本操作是17，17/9是不是差不多就是2倍？那平均分摊到每次addLast操作上是不是就是2次基本操作了？那我们是不是可以这样推断：

假设capacity = n，n+1次addLast，触发resize，总共进行2n+1次基本操作，那么平均来讲，每次addLast操作就进行了2次基本操作，也就是将一次时间较长的resize操作的时间均摊到了每一个元素上了，这就是所谓的“均摊复杂度【amortized time complexity】分析法”，经过这样一分摊，是不是此时的resize()的时间复杂度由O(n)变成了O(1)了？针对咱们这个场景来说，均摊计算比计算最坏情况是更有意义的，因为这个resize()是不会每次都触发的，对于这样的一个分析思想在实际复杂度的分析中记得要进行运用一下，而不要所有的复杂度一味地都用最杯的情况来进行计算。

复杂度的震荡：

概述：

那知道了resize()均摊之后的复杂度之后，同理，对于removeLast操作的均摊复杂度也为原来分析的O(n)降为O(1)了：

但是！！！凡事就怕但是~~如果我们同时看addLast()和removeLast()操作时，又会产生一个问题，啥问题呢？下面来阐述一下，比如有一个已经装满的数组：

此时再调用addLast()往数组尾部添加一个元素：

此时会触发扩容操作，此次的addLast操作的复杂度就是O(n)对吧？但是！！！此时又调用removeLast()操作，此时元素又变为整个容量的一半了：

此时咱们的Array又会触发一个resize()进行缩容，是不是此次的removeLast()的时间复杂度又是O(n)没毛病吧？好，此时再进行addLast()、removeLast()是不是这样的情况下全是会触发resize()操作了？那。。之前在均摊复杂度分析时还说n次操作时不是每次都会触发resize()操作，那目前咱们制造的这场景不是每次都触发的resize()操作了么？这种现像就叫“复杂度的震荡”，明明均摊的时候复杂度会是O(1)，但是在有一些场景下会因为复杂度的震荡而升为O(n)产生震荡了。

解决方案：

那如何解决这样的问题呢？这里就需要来分析一下问题之所在，其实就是由于removeLast时resize()过于着急（Eager）导致的，回到咱们写的逻辑来说：

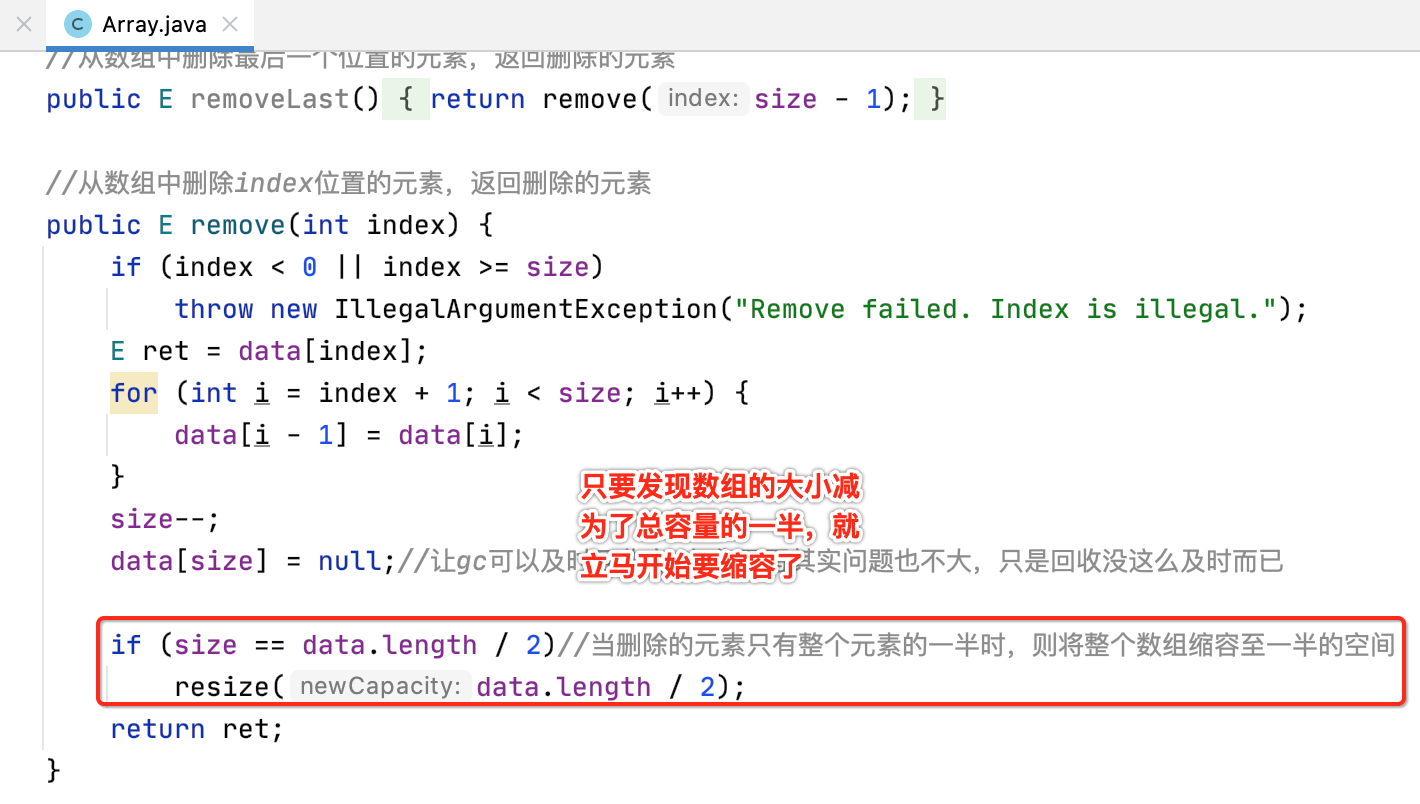
此时缩容之后刚好数组的大小跟数组的容量是一样的，那再添加时不就容易产生再一次的resize()了么？所以解决方案也比较简单，可以采取一种不那么着急缩容的机制来解决，怎么做？看下面：

首先初始数组时里面的元素是空的：

然后当我们把里面的数据都填满了：

此时再添加一个元素：

需要触发resize()进行扩容啦：

此时再删除末尾的元素：

好，此时优化的方案就要诞生了，不是立马就开始1/2的缩容了，而是先等等，等到后面删除到了整个数组的1/4的时候，这样：

此时才触发缩容操作，但是注意！！！缩容还是缩容整个容量的一半大小，也就是变成这样：

这样的好处就是如果再添加的话也不会立马触发resize()扩容了，所以总结一下其解决方案就是：当size == capacity / 4时，才将capacity减半， 也就是其resize()操作触发时机更加懒了，但是呢整个数组的性能却能大大的提升，这种思想在未来的学习中还会有遇到，等到时遇到时再说。

接下来则来优化一下咱们的代码，其实也比较简单，如下：

另外这块还有一个Bug需要修复一下，就是这块：

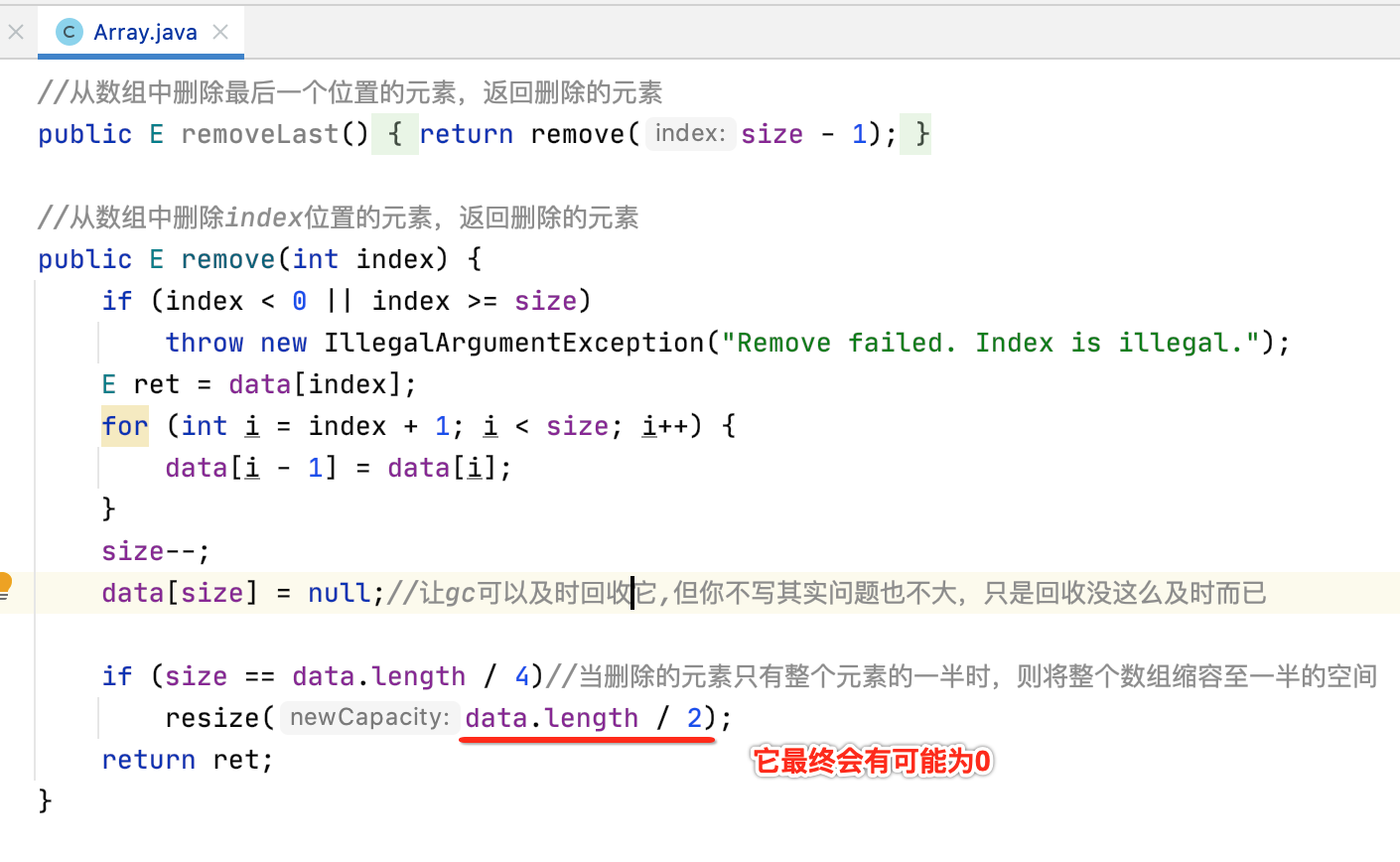
所以加一个判断既可：

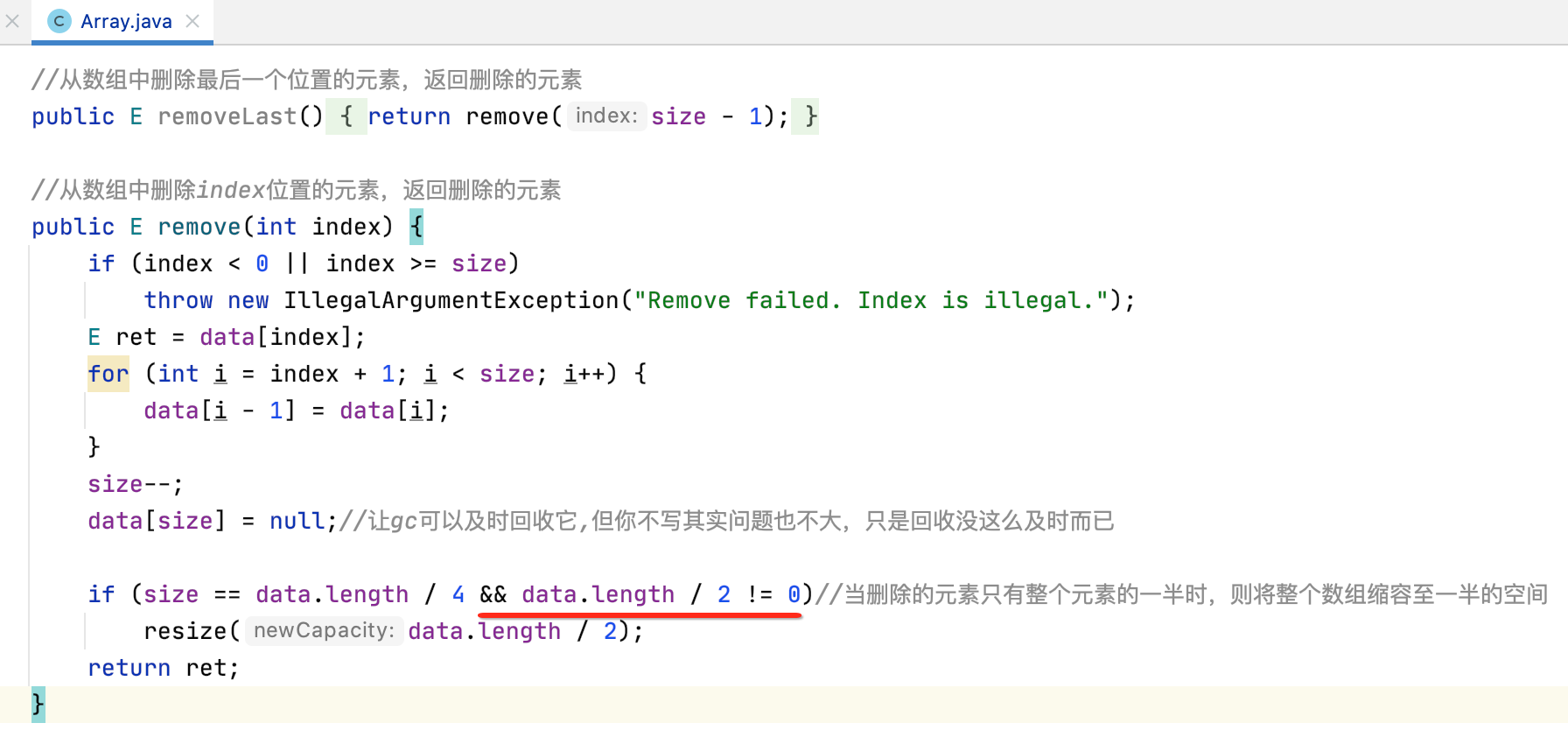
至此，关于Array这个类的封装就比较完美了，最后贴一下它的完整源码：

/**
 * 由于java数组本身的缺陷来封装一下属于自己的数组，效果类似于ArrayList
 */
public class Array<E> {
    private E[] data;
    /* 数组实际存放的个数 */
    private int size;

    //region 构建函数
    //构建函数，传入数组的容量capacity构造Array
    public Array(int capacity) {
        data = (E[]) new Object[capacity];
        size = 0;
    }

    //无参的构造函数，默认数组的容量capacity=10
    public Array() {
        this(10);
    }
    // endregion

    //region 对外暴露的公共方法
    //获取数组中的f元素个数
    public int getSize() {
        return size;
    }

    //获取数组的容量
    public int getCapacity() {
        return data.length;
    }

    //返回数组是否为空
    public boolean isEmpty() {
        return size == 0;
    }

    //region 添加元素
    //向所有元素后添加一个新元素
    public void addLast(E e) {
        add(size, e);
    }

    //向所有元素前添加一个新元素
    public void addFirst(E e) {
        add(0, e);
    }

    //在第index个位置插入一个新元素e
    public void add(int index, E e) {
        if (index < 0 || index > size) {
            throw new IllegalArgumentException("Add failed. Require index >= 0 and index <= size.");
        }
        if (size == data.length)
            resize(2 * data.length);//发现空间不够了，则扩容一倍的空间
        //从后往前将index之后的所有元素都往后挪一个位置，将index位置给腾出来
        for (int i = size - 1; i >= index; i--) {
            data[i + 1] = data[i];
        }
        data[index] = e;
        //记得维护一下size
        size++;
    }

    //获取index索引位置的元素
    E get(int index) {
        if (index < 0 || index >= size)
            throw new IllegalArgumentException("Get failed. Index is illegal.");
        return data[index];
    }

    //修改index索引位置的元素为e
    void set(int index, E e) {
        if (index < 0 || index >= size)
            throw new IllegalArgumentException("Get failed. Index is illegal.");
        data[index] = e;
    }

    //查找数组中是否包含有元素e
    public boolean contains(E e) {
        for (int i = 0; i < size; i++) {
            if (data[i].equals(e))
                return true;
        }
        return false;
    }

    //查找数组中元素e所在的索引，如果不存在元素e，则返回-1
    public int find(E e) {
        for (int i = 0; i < size; i++) {
            if (data[i].equals(e))
                return i;
        }
        return -1;
    }

    //region 删除元素

    //从数组中删除第一个位置的元素，返回删除的元素
    public E removeFirst() {
        return remove(0);
    }

    //从数组中删除最后一个位置的元素，返回删除的元素
    public E removeLast() {
        return remove(size - 1);
    }

    //从数组中删除index位置的元素，返回删除的元素
    public E remove(int index) {
        if (index < 0 || index >= size)
            throw new IllegalArgumentException("Remove failed. Index is illegal.");
        E ret = data[index];
        for (int i = index + 1; i < size; i++) {
            data[i - 1] = data[i];
        }
        size--;
        data[size] = null;//让gc可以及时回收它,但你不写其实问题也不大，只是回收没这么及时而已

        if (size == data.length / 4 && data.length / 2 != 0)//当删除的元素只有整个元素的一半时，则将整个数组缩容至一半的空间
            resize(data.length / 2);
        return ret;
    }

    //从数组中删除元素e
    public void removeElement(E e) {
        int index = find(e);
        if (index != -1)
            remove(index);
    }

    //endregion

    @Override
    public String toString() {
        StringBuilder res = new StringBuilder();
        res.append(String.format("Array: size = %d , capacity = %d\n", size, data.length));
        res.append("[");
        for (int i = 0; i < size; i++) {
            res.append(data[i]);
            if (i != size - 1)
                res.append(", ");
        }
        res.append("]");
        return res.toString();
    }

    //endregion

    //endregion

    private void resize(int newCapacity) {
        E[] newData = (E[]) new Object[newCapacity];
        for (int i = 0; i < size; i++) {
            newData[i] = data[i];
        }
        data = newData;
    }

}

经过这么一整，我去！！！一个不起眼的数组居然还能整出这么些个东东。。