数据结构与算法入门
在17年的时候曾经专门对数据结构跟算法进行了学习,不过,没有系统学完就半途而废了,当时我记得是学到了图相关的东东,转眼到19年过去两年了,对于这块的东东决定还是重拾起来从0开始系统完整的把它学完,不管是为了跳槽还是说为了工作,不能给自己技术树上留下遗憾。
数据结构与算法概念:
对于这些概念其实在大学都已经学过了,不过为了完整性还是得要大概对它们进行一个复习。
数据结构研究的内容:
定义:
数据结构是计算机存储、组织数据的方式。
数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。
通常情况下,精心选择的数据结构可以带来更高的运行或者存储效率。
数据结构往往同高效的检索算法和索引技术有关。
其中它有以下两个维度的结构:
逻辑结构:
- 集合结构
- 线性结构
- 树形结构
- 图形结构
存储结构:
- 表
- 堆栈
- 队列
- 数组
- 树
- 二叉树
- 图
算法研究的内容:
定义:
算法(Algorithm)是指解题方案的准确而完整的描述,是一系列解决问题的清晰指令,
算法代表着用系统的方法描述解决问题的策略机制。也就是说,能够对一定规范的输入,在有限时间内获得所要求的输出。
如果一个算法有缺陷,或不适合于某个问题,执行这个算法将不会解决这个问题。
不同的算法可能用不同的时间、空间或效率来完成同样的任务。
一个算法的优劣可以用空间复杂度与时间复杂度来衡量。
空间复杂度:
主要是指所写的算法在内存中占用的大小,不过由于目前的机器的内存越来越大,所以这个指标相比时间复杂度不是那么重要,如今看算法的好坏可能都是看时间复杂度。
时间复杂度:
定义:
算法的效率: 算法所处理的数据个数n 的函数,关键代码的执行次数。用大O表示法,如:
下面来看这两段伪代码的时间复杂度:
代码一:
function1() { for(int i = 0; i < n; i++) { for(int j = 0; j < n; j ++) { // dosomething;//这时间复杂度是n^2 } } for(int i = 0; i < n; i++) { //dosomething //这时间复杂度是n } // dosomething //这时间复杂度为1 }
该代码的O(n) = n^2 + n + 1。
代码二:
function2() { for(int i = 0; i < n; i++) { for(int j = 0; j < n; j ++) { // dosomething; //这时间复杂度为n^2 } }
FAQ:那以上两种算法,它们俩的时间复杂度哪个更好呢?
很明显代码二要比代码一要好嘛,其实在时间复杂度上它们俩是一样的,因为在n为无穷大时它们的时间复杂度都是n^2。所以这里需要注意。
如何把这两方面都控制到最合适?
我们在大学学习时都会听到这样一句话:“数据结构+算法=程序”,而衡量一个程序的好坏除了时间复杂度和空间复杂度之外,其实还有一个很重要的因素,那就是应用场景。为啥这样说,下面以“变量交换”简单的算法来举例来说明这个“应用场景”的重要性,如下:
第一种交换方法【最常用】:

第二种方法:不用中间临时变量,而是采用相加法:
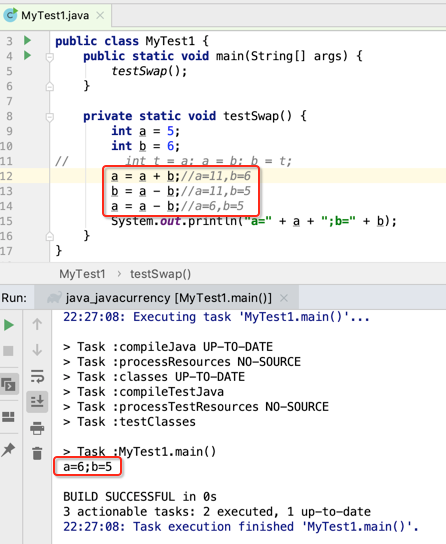
也同样达到了两数的交换,节省了一个临时变量,但是有个弊端,如果是对象貌似就没法这样弄了。。
第三种:上面第二种方法已经节省了空间,但时间上还有没有能进一步提升的呢?当然有,如下:
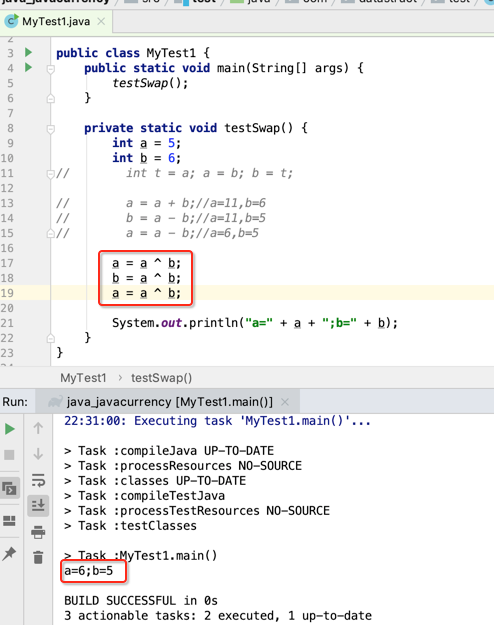
这种写法貌似平常接触得比较少,先来说一下它的原理,这里^是异或符,表示如果位数不同则返回1,相同则返回0,所以先将a=5和b=6换成二进制为:
a = 0101
b = 0110
而根据算法:
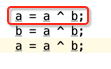
此时
a = 0011
b = 0110
再看第二句:
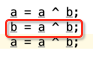
此时
a = 0011
b = 0101
再看第三句:

此时
a = 0110 = 6
b = 0101 = 5
所以通过位运算就将两数进行了替换了。
好,那思考一下以上三种实现方式哪种方式更好呢?可能大部分人都说肯定是第三种嘛,时间空间都最优,性能也最好,这里要说的是!!要结合“应用场景”来说,假如我们是在app里面来使用,第一种要比第三种强,因为第一种的可读性比较好,而第三种可读性比较差。并且运行的性能也相差不了太多;但是!!如果此段代码是运行在像无人机、跑步机这样配置不太高的设备上,那么第三种要优于第一种,因为这种场景更加看重性能。
线性表【数据结构的学习从它开始】:
顺序存储结构:
它长这样:
而用顺序存储的结构用个专用词则称之为“顺序表【这样是所有程序员沟通起来的一个通用名称】”,而对于顺序表,里面的元素还有以下这种关系,如下:

a1是a2的前驱,ai+1 是ai的后继,a1没有前驱,an没有后继
n为线性表的长度 ,若n==0时,线性表为空表。
知道了这些概念之后,那看下面这图是否是顺序表呢?
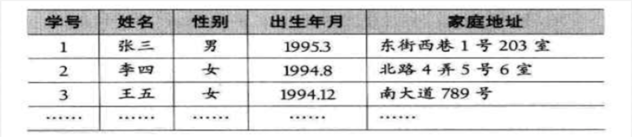
其实它就是顺序表,因为它可以表示为这样的结构:
class Students {
Student[40];
int size;
}
其实ArrayList就是典型的一个顺序表,它的源码的结构其实跟它类似,如下:
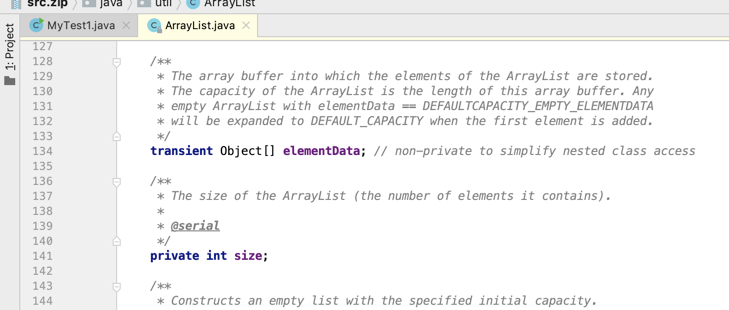
优缺点:
优点:
尾插效率高,支持随机访问。
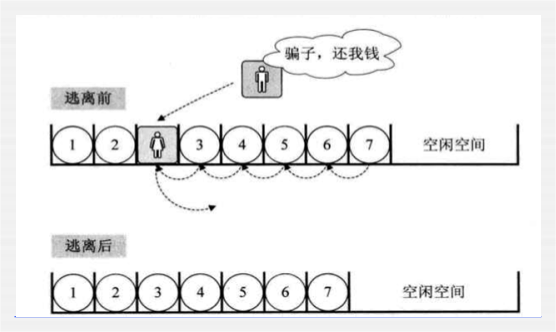
缺点:
中间插入或者删除效率低。
可以用图来感受一下:
下面用程序来模拟一下从数据中来查询数据,直接粗暴的轮循来查就成了:
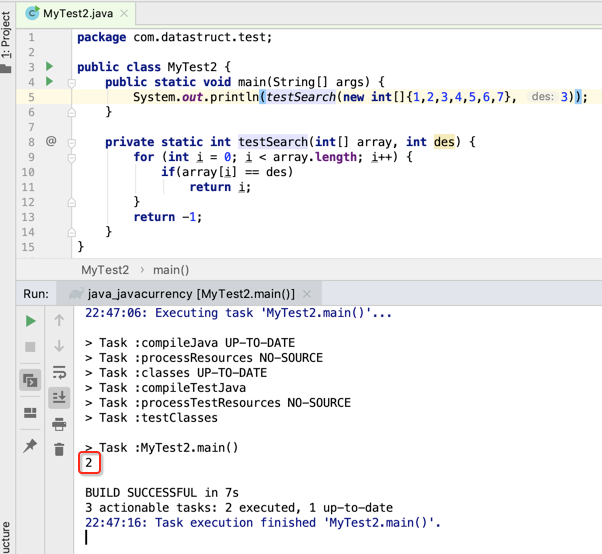
接着再来模拟一下数据插入:
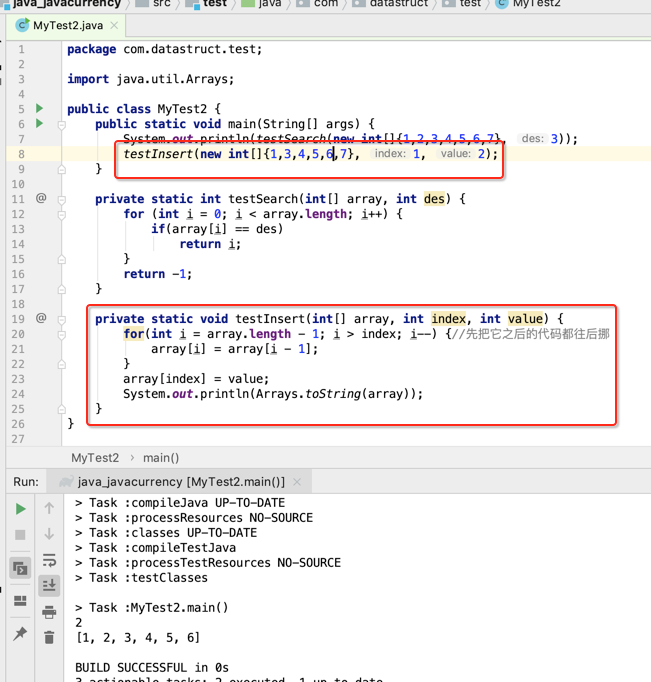
接下来则模拟一下删除操作:
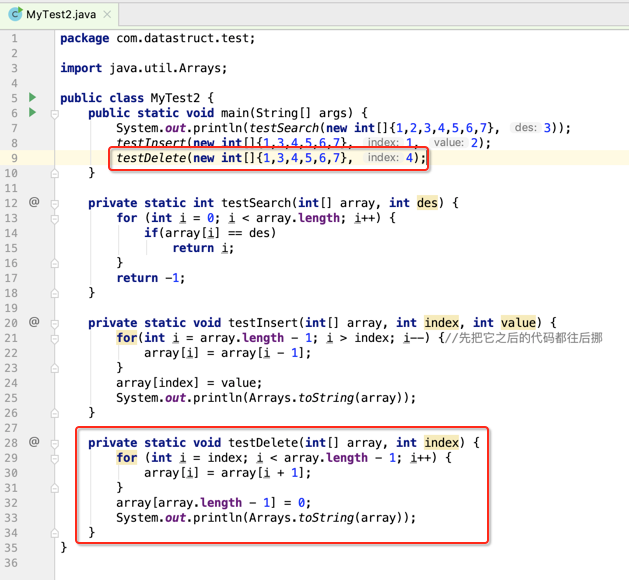
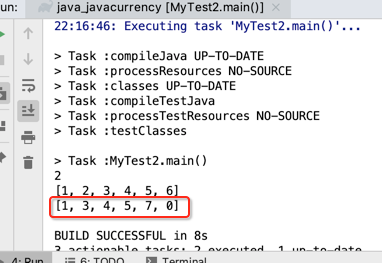
它的应用:
数组
ArrayList
排序开端:
像我们在玩斗牛时

手中会发5张牌,然后对其进行排序, 可见每次排序的元素比较小,其实这种场景使用冒泡排序是最快的,下面先来定义一个牌的类:
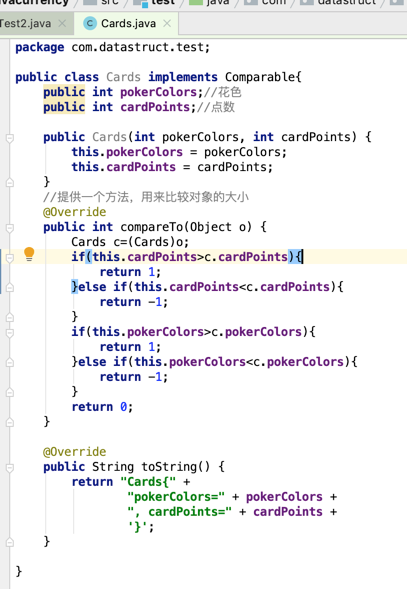
好,接下来比如我们收到的这几张牌,然后对其进行排序,超简单的:

嗯,貌似非常之完美,采用系统的API对其进行排序不天经定义的嘛, 但是!!其实系统的这个sort()方法是非常“重”的一个实现,可以大致的瞅一下它的实现:


也就是说采用系统的这个排序算法效率是比较低的,对于数据量这么小的排序来说性能不是太高,所以应该得用咱们自己的算法来实现,所以接下来就开始要接触线性表的排序算法了。
蛮力法:
啥叫蛮力法?先看一下它的定义:
蛮力法(brute force method,也称为穷举法或枚举法)
是一种简单直接地解决问题的方法,
常常直接基于问题的描述,
所以,蛮力法也是最容易应用的方法。
但是,用蛮力法设计的算法时间特性往往也是最低的,【指的是n接近于无穷大时】
典型的指数时间算法一般都是通过蛮力搜索而得到的 。(即输入资料的数量依线性成长,所花的时间将会以指数成长)
貌似该算法应该是比较low的,指数级别的,但是!!!对于数据量比较小,像我们这个每次才五个数据的场景,用这个蛮力法的排序效率是最高的,下面来看一下这种算法长啥样?冒泡排序和选择排序都算,下面具体来看一下:
冒泡排序:
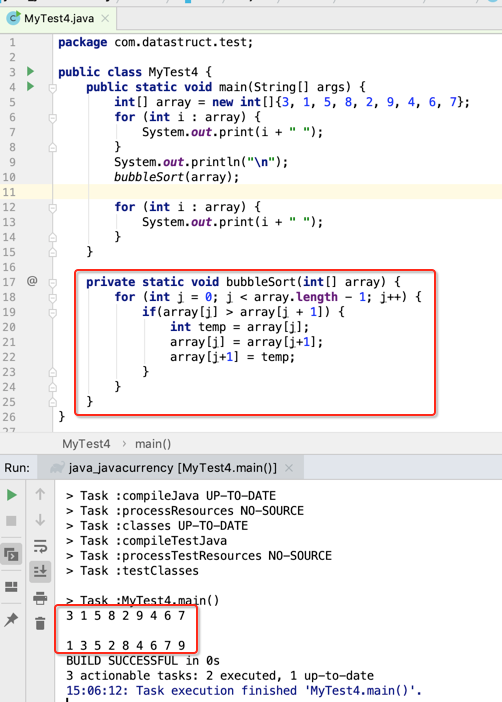
这里一点点来实现冒泡排序,先来说一下冒泡排序的第一步:
比如要对“3,1,5,8,2,9,4,6,7”这个数列进行从小到大的冒泡排序,首先是两两数进行比较,第二个数如果比第一个数小则就交换位置,具体为:
1、拿“3,1”进行比较,很显然3>1,所以此时对这俩数进行交换,就为:“1,3,5,8,2,9,4,6,7”;
2、拿“3,5”进行比较,由于3<5,则不交换,就为:“1,3,5,8,2,9,4,6,7”;
3、拿“5,8”进行比较,同样5<8,所以也不交换,就为:“1,3,5,8,2,9,4,6,7”;
4、拿"8,2"进行比较,由于8>3,所以将两数进行交换,就为:“1,3,5,2,8,9,4,6,7”;
5、拿"8,9"进行比较,由于8<9,所以不动,就为:“1,3,5,2,8,9,4,6,7”;
6、拿"9,4"进行比较,由于9>4,所以交换,就为:“1,3,5,2,8,4,9,6,7”;
7、拿"9,6"进行比较,由于9>6,所以交换,就为:“1,3,5,2,8,4,6,9,7”;
8、拿"9,7"进行比较,由于9>7,所以交换,最终为:“1,3,5,2,8,4,6,7,9”;
这样经过第一轮的俩俩比较就将最大的一个数浮到最后一位了,跟水冒泡一样从底部一点点往上浮,当然此时并未真正排好序,但是为了一步步实现,所以先不管这么多把这个步骤先实现了再之后进一步处理:
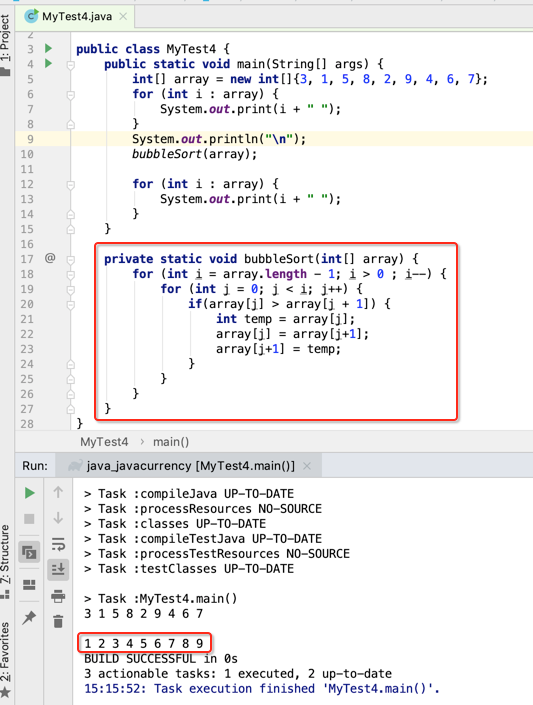
好,接下来第二轮比较则应该将这个“9”排除再进行俩俩比较,其实也只要改这块的条件既可:

所里这里再定义一个外层循环用它控制它,如下:
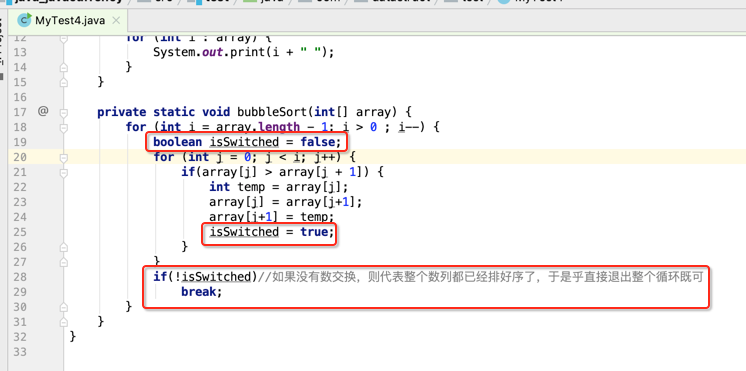
而它的时间复杂度可以算一下:
第一轮是要比较n-1次,第二轮是n-2次,第三轮是n-3次,依次类推,其实它的时间复杂度可以归结为:O(n)= n * (n - 1) / 2,其实可以将它优化成O(n) = n,加个判断如下:
接下来就可以将我们的纸排的排序改为咱们自己实现的冒泡排序了,如下:

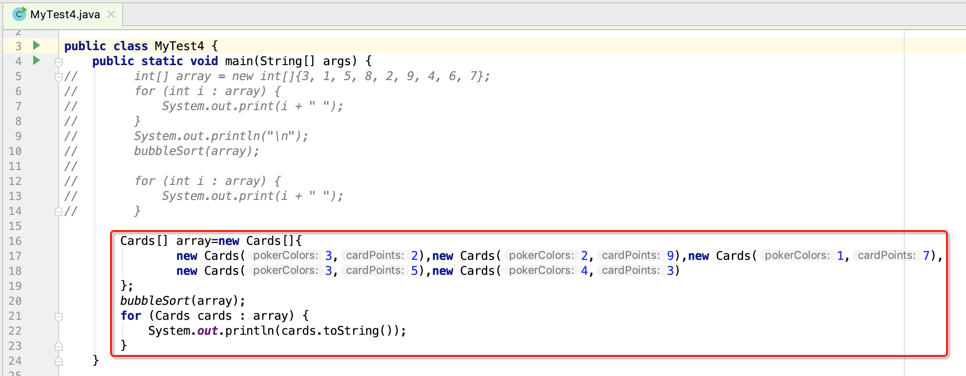

这种场景下利用冒泡就是一个非常之高效的算法了。
选择排序:
在n是个位数量的时候进行排序除了冒泡比较快之外,还有选择排序,而它是快速排序的基础功,所以需要好好学一下,所以下面来看一下用选择排序如何来实现。
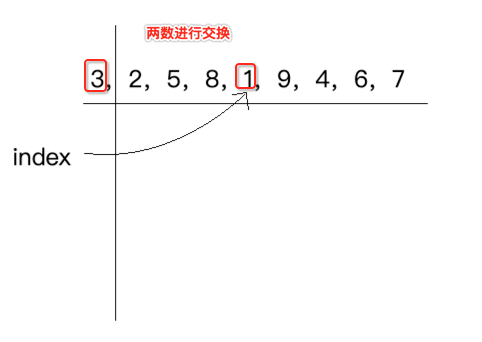
这里以“3,2,5,8,1,9,4,6,7”这个数列进行说明,跟冒泡算法一样先来看第一轮,一点点来,它的规则是先将数组的第一个元素定死,也就是:
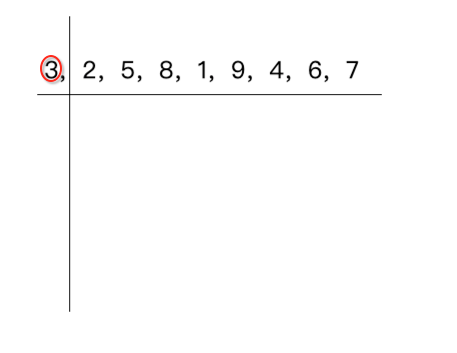
此时有个index指向它:
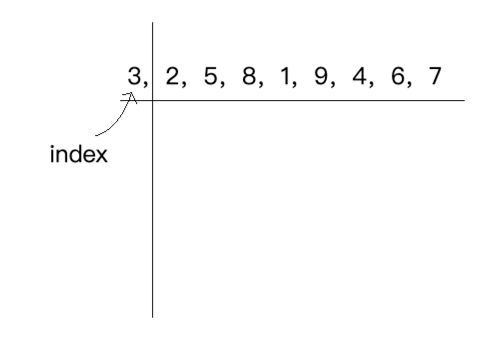
然后再从剩下的元素中找到一个最小元素的下标,并且index指向它,如下:

这里可以先把代码跟着写好:
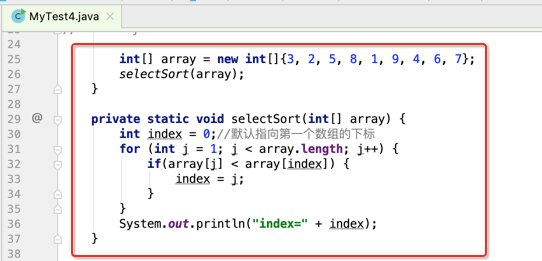
紧接着将这个index最小的元素和数组的第一个元素进行交换,如下:

好,代码跟上:
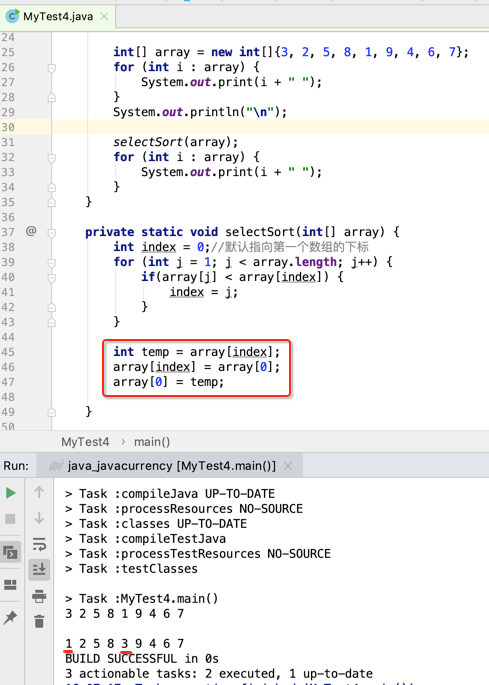

所以这里又得要个外层循环了:
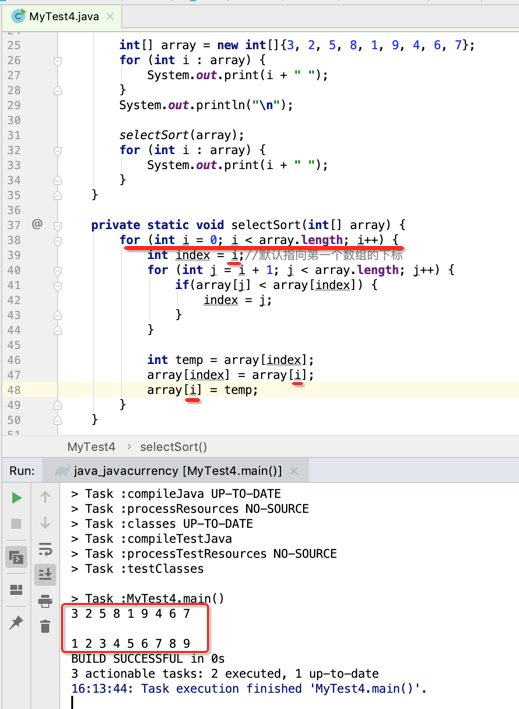
当然这里也可以进行优化一下:
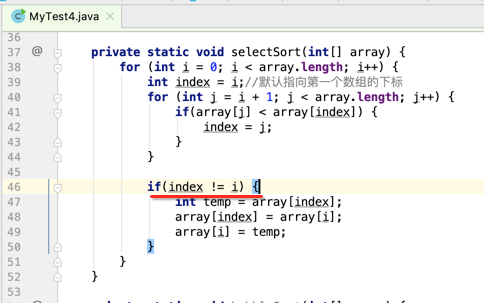
很明显用选择排序的交互次数要比冒泡排序的交换次数要少些,但是其实它们俩在数据量在个位数时其实是差不多的,下面则把这个选择排序应用到牌的排序中:

链式存储结构:
它长这样:

这次先不学它,因为东西有点多,下次再专门学习。



